下载文档原格式
预应力损失值计算预应力损失值计算是工程结构设计中的重要环节，它涉及到对于预应力混凝土结构的设计和分析。
准确计算预应力损失值可以帮助工程师评估结构的安全性和可靠性，从而保证建筑物的稳定性和使用寿命。
本文将介绍预应力损失值计算的主要方法和关键因素。
一、背景介绍预应力结构是通过在混凝土构件中施加预先拉紧的钢材，使得混凝土获得自身的预压力，以提高承载能力和抗震性能的建筑结构。
然而，在预应力系统的使用过程中，由于材料和施工工艺的原因，预应力损失是不可避免的。
预应力损失是指在施工和使用的过程中，预应力混凝土中的预应力损失所引起的预应力力值的减小。
二、预应力损失的分类根据预应力损失的原因和计算方法，预应力损失可以分为以下几类：1. 瞬时损失：指在预应力张拉完成时和切割钢束前的时间段内，由于混凝土收缩、蠕变等因素引起的预应力力值的减小。
2. 逐渐损失：指随着时间的推移，由于混凝土的收缩、蠕变、材料老化等因素引起的预应力力值的减小。
3. 长期损失：指从混凝土开始硬化后到结构使用寿命结束的整个时间段内，由于混凝土的收缩、蠕变、材料老化等因素引起的预应力力值的减小。
三、预应力损失的计算方法预应力损失的计算是一个复杂的过程，需要综合考虑多种因素。
一般来说，预应力损失的计算方法可以分为以下几种：1. 理论计算法：通过根据结构的材料性能和几何形状等参数，利用公式和模型进行理论计算。
2. 经验计算法：根据已有工程的实际经验总结出来的预应力损失值。
3. 验证计算法：通过对已有工程的预应力结构进行监测和测试，得到实际的预应力损失数据，进行验证和修正计算结果。
四、预应力损失影响因素预应力损失的计算结果受到多种因素的影响，主要包括以下几个方面：1. 材料因素：包括混凝土的材料性能、钢材的材料性能等。
2. 结构因素：包括结构的几何形状、构件的截面尺寸、构件的长度等。
3. 施工因素：包括预应力张拉的过程、预应力钢束的锚固长度、预应力钢束的切割等。
预应力混凝土预应力损失及计算方法预应力混凝土是一种常用于建筑结构中的高性能材料，其通过在混凝土构件中施加预应力，使其在受力过程中能够更好地承受荷载。
然而，由于各种原因，预应力混凝土中的预应力可能会发生一定的损失，影响结构的整体性能。
本文将就预应力混凝土预应力损失的原因以及计算方法进行探讨。
一、预应力混凝土预应力损失的原因预应力混凝土中的预应力损失主要包括材料损失、摩擦损失和开裂损失三个方面。
1. 材料损失材料损失是指预应力混凝土材料在施工、运输和使用过程中由于外界环境和条件的影响而导致的预应力损失。
常见的材料损失包括钢材弛豫损失、混凝土收缩和徐变等。
（1）钢材弛豫损失：在预应力混凝土构件的初张拉和释放过程中，钢材的初始应力会因为钢材的弛豫现象而逐渐减小，从而导致预应力的损失。
（2）混凝土收缩和徐变：混凝土存在收缩和徐变的现象，这也会导致预应力的损失。
混凝土在干燥过程中会发生收缩，而在受潮后则会发生徐变，这些变形会使得预应力逐渐减小。
2. 摩擦损失摩擦损失是指预应力混凝土构件中由于预应力钢束与混凝土之间的相对滑动而导致的预应力损失。
摩擦损失主要由于摩擦阻力和锚固器件的摩擦而引起。
（1）摩擦阻力：预应力钢束与混凝土之间存在一定的摩擦力，当受力端的锚固器件与混凝土之间的摩擦力大于预应力钢束处的摩擦力时，就会导致预应力损失。
（2）锚固器件的摩擦：锚固器件的摩擦也是导致预应力损失的原因之一。
锚固器件的设计和施工质量会直接影响摩擦损失的大小。
3. 开裂损失开裂损失是指预应力混凝土构件在施加预应力后由于荷载作用而引起的裂缝产生，从而导致预应力损失。
开裂会导致混凝土的强度明显下降，进而使得预应力损失。
二、预应力损失的计算方法为了准确计算预应力混凝土中的预应力损失，可以采用以下方法：1. 钢材弛豫损失的计算常用的计算钢材弛豫损失的方法包括弛豫系数法和易变程度法。
（1）弛豫系数法：根据预应力钢束的特性曲线，通过测量初始应力和一定时间后的应力变化，利用弛豫系数将时间换算积分得到弛豫损失。
预应力混凝土预应力损失及计算方法预应力混凝土是一种在混凝土构件承受使用荷载之前，预先对其施加压力的混凝土结构。
通过这种方式，可以有效地提高混凝土构件的抗裂性能、刚度和承载能力。
然而，在实际工程中，由于多种因素的影响，预应力会产生一定的损失。
准确计算和理解这些预应力损失对于保证预应力混凝土结构的安全性和可靠性至关重要。
预应力损失主要包括以下几个方面：锚具变形和钢筋内缩引起的预应力损失当预应力筋在锚固过程中，由于锚具的变形、钢筋与锚具之间的相对滑移以及混凝土的压缩等原因，会导致预应力的损失。
这种损失通常发生在预应力筋的锚固端，其大小与锚具的类型、锚具的尺寸、预应力筋的直径以及张拉控制应力等因素有关。
预应力筋与孔道壁之间的摩擦引起的预应力损失在预应力筋的张拉过程中，由于预应力筋与孔道壁之间存在摩擦力，使得预应力筋在沿孔道长度方向上的应力逐渐减小。
这种摩擦损失与孔道的形状、长度、预应力筋的类型以及施工工艺等因素有关。
混凝土加热养护时受张拉的钢筋与承受拉力的设备之间的温差引起的预应力损失在混凝土构件进行加热养护时，如果预应力筋已经张拉完成，由于钢筋与养护设备之间存在温差，会导致钢筋伸长，从而引起预应力的损失。
预应力筋的应力松弛引起的预应力损失预应力筋在长期保持高应力状态下，会产生应力松弛现象，即应力随时间逐渐降低。
这种损失与预应力筋的类型、初始应力水平、时间以及环境温度等因素有关。
混凝土的收缩和徐变引起的预应力损失混凝土在硬化过程中会发生收缩，在长期荷载作用下会产生徐变。
这些变形会导致预应力筋的回缩，从而引起预应力的损失。
收缩和徐变引起的预应力损失与混凝土的配合比、养护条件、构件的尺寸以及加载龄期等因素有关。
接下来，我们来探讨一下预应力损失的计算方法。
对于锚具变形和钢筋内缩引起的预应力损失，其计算公式通常为：＼（＼sigma_{l1} ＝ a\times\frac{l}｛E_{s}｝＼）其中，＼（＼sigma_{l1}＼）为锚具变形和钢筋内缩引起的预应力损失，＼（a\）为锚具变形和钢筋内缩值，＼（l\）为张拉端至锚固端之间的距离，＼（E_{s}＼）为预应力筋的弹性模量。
预应力损失计算我们主要采用分项计算法，就是根据预应力损失产生的不同原因分别计算各阶段的预应力损失，再把分项损失相加得出总损失。
这也是目前我国现行规范采用的损失计算法。
2.1锚具变形和钢筋内缩引起的应力损失（σl1）预应力钢筋张拉后锚固时，锚具将受到相当大的压力，一方面使锚具本身及锚具下垫板压密产生变形；另一方面混凝土结构的接缝缝隙在压力的作用下也将压密变形。
这些变形导致 预应力钢筋向内回缩，产生预应力损失。
按圆弧形曲线计算，反向摩擦影响长度：1x 2()(1-)l con f c fl l μσσκγ=+ γc --圆曲线预应力筋的曲率半径，以m 计；x--张拉端至计算截面的水平距离，以m 计；μ--预应力筋的与孔道壁的摩擦系数；κ--孔道每米长度局部偏差的摩擦系数；l f --反向摩擦影响长度，以m 计，可按下式计算l f2.2 预应力筋与孔道壁之间摩擦引起的应力损失（σl2）距离张拉端x 时的预应力筋的应力损失为：21(1)l con e κχμθσσ+=-式中：σcon --预应力钢筋的控制张拉应力；x--预应力筋张拉端至计算截面的水平投影距离，以m 计；μ--预应力筋的与孔道壁的摩擦系数； κ--孔道每米长度局部偏差的摩擦系数；θ--张拉端至计算截面曲线孔道部分切线的夹角，以弧度计；Ay--预应力钢筋的截面积。
2.4 预应力筋松弛引起的应力损失（σl4）钢筋在持续高应力作用下，会产生随时间变化而增加的变形（内部晶体结构蠕变）。
如果预应力筋束在一定的张拉应力作用下，长度保持不变，则预应力筋束中的应力将会随时间延长而降低，这就是钢筋的松驰引起的应力损失。
当0.7f ptk ≤σcon ≤0.8f ptk 时 40.2(0.575)conl con ptk f σσσ=-2.5混凝土收缩和徐变引起的应力损失（σl5）对于混凝土结构构件来说，在持续应力作用下，随着时间的延续，混凝土会产生收缩和徐变，导致预应力混凝土结构构件缩短，因而引起应力损失，其值为：,5,55300115pccu l σσσσ+=+式中：σl5—受拉区预应力筋中由于混凝土收缩徐变所产生的预应力损失；σpc —受拉区预应力筋在各自合力点所产生的混凝土法向压应力；σ’—受拉区预应力筋与非预应力筋的配筋率（其值为受拉区预应力筋和非预应力筋的截面面积与混凝土结构截面面积之比）；σ’cu -施加预应力时的混凝土立方体抗压强度。
第三章预应力与预应力损失计算预应力与预应力损失计算是结构工程领域中非常重要的一部分内容。
在第三章中，我们将深入探讨预应力的概念、计算方法和预应力损失的计算。
一、预应力概念预应力是指在结构正常使用过程中，在一定截面上施加的一种人为预先设置的压应力。
通过施加这种压应力，能够在结构中产生与它们相对应的弯矩和剪力，从而改善结构的控制性能、抗裂性能和承载性能。
二、预应力计算方法1. 预应力损失计算预应力损失是指预应力钢材所受的损失，主要分为两大类：瞬时损失和时间依赖性损失。
瞬时损失包括张拉初始损失、传递长度损失和锚固长度损失；时间依赖性损失包括徐变损失和材料损耗。
2. 预应力计算步骤（1）确定结构设计参数，包括材料参数、几何参数和受力状态等。
（2）计算预应力的大小和位置，根据结构受力分析确定所需的预应力大小和预应力钢材的位置。
（3）选择预应力的施加方式，包括预应力的初始张拉和锚固方式。
（4）进行预应力损失计算，按照相关规范和理论进行预应力损失的计算。
（5）校核预应力的效果，根据结构受力分析，检查预应力对结构性能的影响是否满足设计要求。
三、预应力损失计算1. 瞬时损失计算（1）张拉初始损失：包括初始张拉时应力的损失以及张拉应力在开锚后的递减。
（2）传递长度损失：由于预应力杆在传递过程中，受到局部应变的影响，导致预应力的损失。
（3）锚固长度损失：预应力锚固长度是指在预应力锚具有效长度之后的那部分长度，预应力损失主要发生在锚固长度的部分。
2. 时间依赖性损失计算（1）徐变损失：预应力杆所受到的长期荷载会导致预应力的逐渐减小，这部分损失称为徐变损失。
（2）材料损耗：主要指预应力钢材的弹性模量随时间的增加而减小，造成预应力的损失。
四、案例分析以某桥梁结构为例，根据设计参数进行预应力的计算和预应力损失的计算。
首先确定结构的受力状态、材料参数和几何参数，然后按照计算步骤进行预应力的计算，并考虑瞬时损失和时间依赖性损失的计算，最后校核预应力的效果是否满足设计要求。
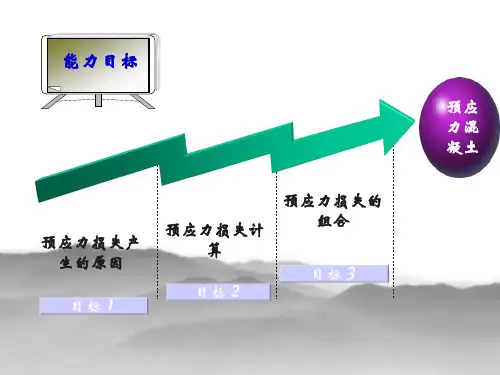
预应力损失的计算预应力损失的大小影响到已建立的预应力，当然也影响到结构的工作性能，因此，如何计算预应力损失值，是预应力混凝土结构设计的一个重要内容。
引起预应力损失的原因很多，而且许多因素相互制约、影响，精确计算十分困难。
我国新的《混凝土结构设计规范》GB50010-2002经历四年半修订,已顺利完成。
此次修订对原规范GBJ10-89进行补充和完善，增加和改动了不少内容。
现就其中预应力损失计算部分谈谈自己的理解，供大家参考指正。
1.预应力损失基本计算在预应力损失值的计算原则方面，各国规范基本一致，均采用分项计算然后叠加以求得总损失。
全部损失由两部分组成，即瞬时损失和长期损失。
其中，瞬时损失包括摩擦损失，锚固损失（包括锚具变形和预应力筋滑移）和混凝土弹性压缩损失。
长期损失包括混凝土的收缩，徐变和预应力钢材的松弛等三项，它们需要经过较长时间才能完成。
我国新规范采用分项计算然后按时序逐项叠加的方法。
下面将分项讨论引起预应力损失的原因，损失值的计算方法。
1.1孔道摩擦损失σl2孔道摩擦损失是指预应力钢筋与孔道壁之间的摩擦引起的预应力损失。
包括长度效应（kx）和曲率效应（μθ）引起的损失。
宜按下列公式计算：σl2=σcon(1-1/e kx+μθ)当(kx+μθ)≤0.2时(原规范GBJ10-89为0.3)，σl2可按下列近似公式计算：σl2=(kx+μθ)σcon1．张拉端 2.计算截面式中:X--张拉端至计算截面的孔道长度(m),可近似取该段孔道在纵轴上的投影长度；θ--张拉端至计算截面曲线孔道部分切线的夹角(rad);K--考虑孔道每米长度局部偏差的摩擦系数，按规范取值；μ--预应力钢筋与孔道壁之间的摩擦系数，按规范取值。
对摩擦损失计算用的K，μ值取为定值，是根据当前国内有关试验值确定的，与原规范GBJ10-89不同，与国外相比，μ值较高，是由于铁皮管质量不高或预压力筋与混凝土直接接触，从而增大摩擦力的缘故。
预应力损失计算1 引言由于受施工状况、材料性能和环境条件等因素的影响，预应力结构中预应力钢筋的预拉应力在施工和使用过程中将会逐渐减少。
这种减少的应力称为结构预应力损失[2]。
设计中所需的钢筋预应力值是扣除相应阶段的应力损失后钢筋中实际存在的有效应力值（pe σ）。
设钢筋初始张拉的预应力为con σ（称为张拉控制应力），相应的应力损失值为l σ，那么预应力钢筋的有效应力为：pe con lσσσ=-因此，要使结构获得所需的有效应力（peσ），除需要根据承受外荷载的情况和结构的使用性能确定张拉控制应力（con σ）外，关键是能准确估算出预应力损失值l σ。
引起结构预应力损失的因素是很多，要准确地估算预应力损失值是非常困难的。
根据目前的研究成果，预应力损失按损失完成时间分为瞬时损失和长期损失两大类。
瞬时损失是指施加预应力时短时内完成的损失，例如锚具变形和钢筋滑移、混凝土弹性压缩、分批张拉等引起的损失；长期损失指的是考虑了材料的时间效应所引起的预应力损失，主要包括混凝土的收缩、徐变、和钢筋预应力松弛引起的损失。
有关瞬时损失的计算在理论上已基本达成了一至的计算原则。
但是，对于长期损失的计算由于存在的不确定因素较多，有些因素（如混凝土的收缩、徐变及钢筋松弛）引起的预应力损失值是随着时间的增长和环境的变化而不断变化的；还有些因素之间互相影响导致预应力值降低，例如混凝土收缩、徐变使构件缩短，钢筋回缩引起预应力值降低；反过来，预应力值降低又将减小徐变损失；钢筋的松弛也将引起徐变损失的减小等。
各国学者、专家根据自己的试验结果及有关假设和推导提出了不同的的计算理论。
预应力损失估计准确与否，对预应力结构安全性能和使用性能（如结构的抗裂性、裂逢、挠度和反拱等）将有很大的影响。
预应力损失估计过大，结构中的混凝土将承受过高的持续压应力，产生过大的反拱度，对结构安全和使用产生不利的影响，同时造成材料的浪费；反之，则会造成局部预压应力不足，导致结构过早开裂，达不到预压的效果，甚至影响结构的安全性[15]。
由此可见，准确地估计和计算预应力损失在预应力结构设计中是非常重要的一环。
2 预应力损失计算方法根据预应力损失不同的阶段。
将各阶段预应力总损失的组成如图3-1所示。
目前有关预应力损失的计算方法大体上可分为三类：①预应力总损失估算法（综合估算法）；②分项预应力损失计算法；③精确估算法[15]。
瞬时损失长期损失图3-1 预应力损失的组成2.1 总损失估算法早在1958年，美国混凝土学会与土木学（ACI-ASCE）提出的“预应力混凝土结构设计建议”对混凝土弹性压缩、收缩、徐变和钢筋的松弛引起的总损失值作出规定：先张构件取241MPa，后张构件取172 MPa。
这一损失值是根据正常强度的混凝土、正常的钢绞线、正常的预加应力值以及正常的养护条件等情况确定的。
所计算的预应力损失值只包括：弹性压缩、钢筋松弛、混凝土收缩和徐变，不包括摩阻和锚具引起的损失。
这一规定在随后的十几年中在工程中得到广泛的应用，设计了大量的具有良好工作性能的房屋结构和桥梁结构。
随着工程实践的发展考虑到对松弛应力损失估计偏低，美国ACI规范和美国公路桥梁规范（AASHTO）在1975年对此做了修订，具体数值详见表3-1；1976年美国后张拉混凝土协会（PTI）也对预应力总损失值做出了修订[16]，具体数值详见表3-2所示。
表3-1 AASHTO规程总损失值注：后张拉钢丝或钢绞线的总应力损失不包括摩擦损失表3-2 PTI建议的总损失值上述表中的数值仅适用于中等条下的一般结构和构件。
如果混凝土在强度很低时就承受高预应力，或者混凝土外于非正常干燥或非常潮湿的暴露条件下，总损失值会有很大的差别。
由于混凝土和钢材和性能，养护与湿度条件，预加应力的时间和大小以及预应力工艺等到的诸多因素的影响，要定出一个统一的预应力总损失值勤是很困难的。
美籍华人林同炎提出总损失及各组成因素损失的平均值用张拉控制应力con σ的百分比表示，具体数值如表3-3所示。
表3-3 预加力百分比我国根据大量的工程实践经验对总预应力损失值也做了一些统计分析，提出在进行预应力混凝土结构设计时可以取如下值：单跨构件取0.8conσ；双跨和三跨克件的内支座截面，取0.7conσ；边支座及边跨跨中截面，取0.8conσ；三跨构件的内跨中截面，可取0.6conσ。
2.2 分项计算法分顶计算法就是根据预应力损失产生的不同原因分别计算各阶段的预应力损失，再把分项损失相加得出总损失。
这也是目前我国现行规范采用的损失计算法。
我国现行规范将预应力损失分为六项考虑。
2.2.1 锚具变形和钢筋内缩引起的应力损失（1l σ）预应力钢筋张拉后锚固时，锚具将受到相当大的压力，一方面使锚具本身及锚具下垫板压密产生变形；另一方面混凝土结构的接缝缝隙在压力的作用下也将压密变形。
这些变形导致预应力钢筋向内回缩，产生预应力损失，其值随钢筋为直线或曲线形面有所不同。
①、当为直线预应力钢筋时，1l σ可按下式计算[10]：1l s a E l σ=a --张拉端锚具变形和钢筋同缩值，以mm 计。
--张拉端至锚固端之间的距离，以mm 计。
可按下表3-4取值。
②、当为曲线预应力钢筋时由于受到曲线形孔道反向摩擦力的影响，使构件各截面所产生的损失值不同，离张拉端越远，其值越小。
至张拉端某一距离fl ，预应力损失降为零，此距离即为反向摩擦长度。
在该长度范围内的钢筋变形应等于锚具变形和钢筋内缩值。
《规范》对圆弧形预应力筋，且其对应圆心角θ不大于30°时的情况给出了距离端部为χ处表3-4 锚具变形和钢筋内缩值的1l σ计算公式为：12()(1)l con f cfxl l μσσκ=+-ϒ式中：cϒ--圆曲线预应力筋的曲率半径，以m 计；--张拉端至计算截面的水平距离，以m 计； --预应力筋的与孔道壁的摩擦系数，按表五取值；κ--孔道每米长度局部偏差的摩擦系数；fl --反向摩擦影响长度，以m 计，可按下式计算f l =2.2.2 预应力筋与孔道壁之间摩擦引起的应力损失（2l σ）在采用后张法工艺施工的无粘结预应力混凝土结构中，由于在张拉预应力筋时钢筋与孔壁的挤压产生摩擦阻力，从而导至预应力的损失。
后张法的预应力筋一般有直线和曲线两种形式。
张拉预应力钢筋时，预应力钢筋将沿混凝土管道壁滑移而产生摩擦力如图3-1a 所示；预应力筋中的预应力形成在张拉端高，向跨中方向逐渐减少如图3-1b 情况。
钢筋在任意两截面间的应力差值，就是此两截面间由摩擦所引起的预应力损失值。
摩擦损失主要由管道的弯曲和管道位置偏差两部分影响所产生。
对于直线管道，由于施工中位置偏差和孔壁不光滑等原因，在钢筋张拉时，局部孔壁仍将与钢筋接触而引起摩擦损失，一般称此为管道偏差影响（或称长度影响）摩擦损失，其数值较小；对于弯曲部分的管道，除存在上述管道偏差影响之外，还存在因管道弯转，预应力对弯道内壁的径向压力所起的摩擦损失，称此为弯道影响摩擦损失，其数值较大，并随钢筋弯曲角度之和的增加而增加。
曲线部分摩擦损失是由以上两部分影响所形成，故要比直线部分摩擦损失大得多。
①、弯道影响引起的摩擦力设钢筋与曲线管道内壁相贴，并取微段钢筋dl （如图3-2b ），dl 通常用其水平投影dx 代替）为研究对象，其对应的弯曲角为d θ，曲率半径为R ，则有dl ＝R d θ图3-2 预应力摩擦损失示意图由0Y =∑sin()sin 22R d d dN N N dN Nd θθθ=+-≈若设钢筋与管道壁间的摩擦系数为μ，微段dl 上的预应力损失为dN ， 摩擦力dF 则有：R dN dF dN Nd μμθ===式中： Ｎ— 预应力筋的张拉力；RdN — 单位长度内预应力筋对弯道内壁的径向压力；dF — 单位长度内预应力筋对弯道内壁的摩擦力；②、管道偏差影响引起的摩擦力设管道平均曲率半径为/R （如图3-2c ），钢筋与平均半径为/R 的管道壁相贴，且与微段直线钢筋dl 相应的弯曲角为'd θ，则钢筋在微段内径向压力////sin ()sin 22R d d dN N N dN Nd θθθ=+-≈/////R dldN dF dN Nd NR μμθμ====令/R μκ=（每米孔道单位力所产生的预应力损失），则有/dN Ndl κ=③、管道摩擦总损失综合②和③的推算结果，则可得到管道摩擦产生的预应力损失总值为：dN Nd Ndl μθκ=+由于θ一般都很小，所以可以用预应力筋在水一方向的投影值dx 近似地代替dl即有 dNd dxN μθκ=+对上式两边进行积分则有00conxN x N dNd dx N θμθκ=+⎰⎰⎰ln()xconN x CN κμθ=-++ 故有 ()x x N e C κμθ-+=+代入边界条件：当0x =时00,x s N N θ=== 可得0C =()x x con N N e κμθ-+=则可计算出距离张拉端x 时的预应力筋的应力损失为：()()2(1)x x con con l con yN N e e A κμθκμθσσ-+-+-==-式中：conσ--预应力钢筋的控制张拉应力；--预应力筋张拉端至计算截面的水平投影距离，以m 计； --预应力筋的与孔道壁的摩擦系数，按表五取值；κ--孔道每米长度局部偏差的摩擦系数；θ--张拉端至计算截面曲线孔道部分切线的夹角，以弧度计；yA --预应力钢筋的截面积。
④、折线形预应力筋摩擦损失的计算在上节中推导的摩擦损失计算公式（规范式）：当0.2x κμθ+≤时，公式按泰勒级数展开，并取第一项，则可简化为：2()l con x σκμθσ=+对于如图3-3所示的折线形预应力钢筋，AB 直线段(0)θ=，则按简化式可计算其预应力损失为：2()l AB con ABx σκσ=B 点处的转角水平投影很短（即0x =），设转角处的摩擦系数为μ，则在该点处的预应力损失为：22()()()(1)l B con con AB l B AB con x x σσκσμθσκσμθ=-⇒=-一般直线段的预应力损失比较少，即10x κ-≈，所以有：2()l B con σσμθ=。
同理直段CD 的损失为：22()()()()(1)()l CD con con AB con AB l CD AB con AB x x x x x x σσκσμθσκσκμθσ=---⇒=---图3-3 折线形预应力筋摩擦损失示意图 令(1)AB con x Kκμθσ--=（常数）则有：()2(1)x l con e κμθσσ-+=-2()()l CD AB K x x σ=-由上述分析可知，对于折线形预应力筋的预应力损失在直线段上是呈线性变化的，在折点处有突变。
