6预应力损失计算

预应力损失值计算预应力损失值计算是工程结构设计中的重要环节，它涉及到对于预应力混凝土结构的设计和分析。

准确计算预应力损失值可以帮助工程师评估结构的安全性和可靠性，从而保证建筑物的稳定性和使用寿命。

本文将介绍预应力损失值计算的主要方法和关键因素。

一、背景介绍预应力结构是通过在混凝土构件中施加预先拉紧的钢材，使得混凝土获得自身的预压力，以提高承载能力和抗震性能的建筑结构。

然而，在预应力系统的使用过程中，由于材料和施工工艺的原因，预应力损失是不可避免的。

预应力损失是指在施工和使用的过程中，预应力混凝土中的预应力损失所引起的预应力力值的减小。

二、预应力损失的分类根据预应力损失的原因和计算方法，预应力损失可以分为以下几类：1. 瞬时损失：指在预应力张拉完成时和切割钢束前的时间段内，由于混凝土收缩、蠕变等因素引起的预应力力值的减小。

2. 逐渐损失：指随着时间的推移，由于混凝土的收缩、蠕变、材料老化等因素引起的预应力力值的减小。

3. 长期损失：指从混凝土开始硬化后到结构使用寿命结束的整个时间段内，由于混凝土的收缩、蠕变、材料老化等因素引起的预应力力值的减小。

三、预应力损失的计算方法预应力损失的计算是一个复杂的过程，需要综合考虑多种因素。

一般来说，预应力损失的计算方法可以分为以下几种：1. 理论计算法：通过根据结构的材料性能和几何形状等参数，利用公式和模型进行理论计算。

2. 经验计算法：根据已有工程的实际经验总结出来的预应力损失值。

3. 验证计算法：通过对已有工程的预应力结构进行监测和测试，得到实际的预应力损失数据，进行验证和修正计算结果。

四、预应力损失影响因素预应力损失的计算结果受到多种因素的影响，主要包括以下几个方面：1. 材料因素：包括混凝土的材料性能、钢材的材料性能等。

2. 结构因素：包括结构的几何形状、构件的截面尺寸、构件的长度等。

3. 施工因素：包括预应力张拉的过程、预应力钢束的锚固长度、预应力钢束的切割等。

预应力混凝土预应力损失及计算方法预应力混凝土是一种常用于建筑结构中的高性能材料，其通过在混凝土构件中施加预应力，使其在受力过程中能够更好地承受荷载。

然而，由于各种原因，预应力混凝土中的预应力可能会发生一定的损失，影响结构的整体性能。

本文将就预应力混凝土预应力损失的原因以及计算方法进行探讨。

一、预应力混凝土预应力损失的原因预应力混凝土中的预应力损失主要包括材料损失、摩擦损失和开裂损失三个方面。

1. 材料损失材料损失是指预应力混凝土材料在施工、运输和使用过程中由于外界环境和条件的影响而导致的预应力损失。

常见的材料损失包括钢材弛豫损失、混凝土收缩和徐变等。

（1）钢材弛豫损失：在预应力混凝土构件的初张拉和释放过程中，钢材的初始应力会因为钢材的弛豫现象而逐渐减小，从而导致预应力的损失。

（2）混凝土收缩和徐变：混凝土存在收缩和徐变的现象，这也会导致预应力的损失。

混凝土在干燥过程中会发生收缩，而在受潮后则会发生徐变，这些变形会使得预应力逐渐减小。

2. 摩擦损失摩擦损失是指预应力混凝土构件中由于预应力钢束与混凝土之间的相对滑动而导致的预应力损失。

摩擦损失主要由于摩擦阻力和锚固器件的摩擦而引起。

（1）摩擦阻力：预应力钢束与混凝土之间存在一定的摩擦力，当受力端的锚固器件与混凝土之间的摩擦力大于预应力钢束处的摩擦力时，就会导致预应力损失。

（2）锚固器件的摩擦：锚固器件的摩擦也是导致预应力损失的原因之一。

锚固器件的设计和施工质量会直接影响摩擦损失的大小。

3. 开裂损失开裂损失是指预应力混凝土构件在施加预应力后由于荷载作用而引起的裂缝产生，从而导致预应力损失。

开裂会导致混凝土的强度明显下降，进而使得预应力损失。

二、预应力损失的计算方法为了准确计算预应力混凝土中的预应力损失，可以采用以下方法：1. 钢材弛豫损失的计算常用的计算钢材弛豫损失的方法包括弛豫系数法和易变程度法。

（1）弛豫系数法：根据预应力钢束的特性曲线，通过测量初始应力和一定时间后的应力变化，利用弛豫系数将时间换算积分得到弛豫损失。

预应力混凝土预应力损失及计算方法预应力混凝土是一种在混凝土构件承受使用荷载之前，预先对其施加压力的混凝土结构。

通过这种方式，可以有效地提高混凝土构件的抗裂性能、刚度和承载能力。

然而，在实际工程中，由于多种因素的影响，预应力会产生一定的损失。

准确计算和理解这些预应力损失对于保证预应力混凝土结构的安全性和可靠性至关重要。

预应力损失主要包括以下几个方面：锚具变形和钢筋内缩引起的预应力损失当预应力筋在锚固过程中，由于锚具的变形、钢筋与锚具之间的相对滑移以及混凝土的压缩等原因，会导致预应力的损失。

这种损失通常发生在预应力筋的锚固端，其大小与锚具的类型、锚具的尺寸、预应力筋的直径以及张拉控制应力等因素有关。

预应力筋与孔道壁之间的摩擦引起的预应力损失在预应力筋的张拉过程中，由于预应力筋与孔道壁之间存在摩擦力，使得预应力筋在沿孔道长度方向上的应力逐渐减小。

这种摩擦损失与孔道的形状、长度、预应力筋的类型以及施工工艺等因素有关。

混凝土加热养护时受张拉的钢筋与承受拉力的设备之间的温差引起的预应力损失在混凝土构件进行加热养护时，如果预应力筋已经张拉完成，由于钢筋与养护设备之间存在温差，会导致钢筋伸长，从而引起预应力的损失。

预应力筋的应力松弛引起的预应力损失预应力筋在长期保持高应力状态下，会产生应力松弛现象，即应力随时间逐渐降低。

这种损失与预应力筋的类型、初始应力水平、时间以及环境温度等因素有关。

混凝土的收缩和徐变引起的预应力损失混凝土在硬化过程中会发生收缩，在长期荷载作用下会产生徐变。

这些变形会导致预应力筋的回缩，从而引起预应力的损失。

收缩和徐变引起的预应力损失与混凝土的配合比、养护条件、构件的尺寸以及加载龄期等因素有关。

接下来，我们来探讨一下预应力损失的计算方法。

对于锚具变形和钢筋内缩引起的预应力损失，其计算公式通常为：＼（＼sigma_{l1} ＝ a\times\frac{l}｛E_{s}｝＼）其中，＼（＼sigma_{l1}＼）为锚具变形和钢筋内缩引起的预应力损失，＼（a\）为锚具变形和钢筋内缩值，＼（l\）为张拉端至锚固端之间的距离，＼（E_{s}＼）为预应力筋的弹性模量。

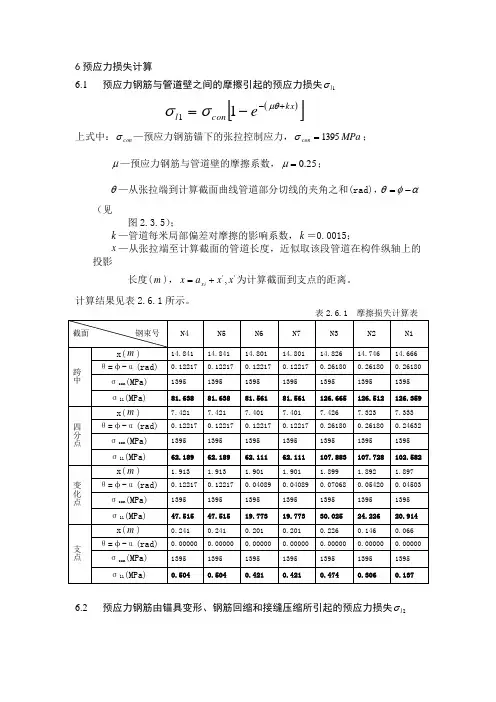
6预应力损失计算6.1 预应力钢筋与管道壁之间的摩擦引起的预应力损失1l σ()[]kx con l e+--=μθσσ11上式中：con σ—预应力钢筋锚下的张拉控制应力，MPa con 1395=σ；μ—预应力钢筋与管道壁的摩擦系数，25.0=μ；θ—从张拉端到计算截面曲线管道部分切线的夹角之和(rad)，αφθ-=（见图2.3.5）；k —管道每米局部偏差对摩擦的影响系数，k ＝0.0015；x —从张拉端至计算截面的管道长度，近似取该段管道在构件纵轴上的投影长度(m )，'',x x a x xi +=为计算截面到支点的距离。

计算结果见表2.6.1所示。

表2.6.1 摩擦损失计算表6.2 预应力钢筋由锚具变形、钢筋回缩和接缝压缩所引起的预应力损失2l σPl E ll ∆∑＝2σ上式中：l ∆∑—锚具变形值，OVM 夹片锚有顶压时取4mm ,这里采用两端张拉，mm l 8＝∆∑；l —张拉端到锚固端之间的距离,这里即预应力钢束的有效长度P E —预应力钢筋的弹性模量，MPa E P 5101.95⨯＝计算结果见表2.6.2所示。

6.3 由分批张拉所引起的预应力损失4l σpcEP l σασ∆∑=4上式中：EP α—预应力钢筋弹性模量与混凝土弹性模量的比值；pcσ∆—在计算截面先张拉的钢筋重心处，由后张拉各批钢筋产生的混凝土法向应力（MPa ）。

具体计算过程见附表，计算结果见表2.6.3所示。

表2.6.3 分批张拉损失计算表6.4 预应力钢筋由于钢筋松弛引起的预应力损失5l σpepkpel f σσζψσ⎪⎪⎭⎫⎝⎛-⋅=26.052.05上式中：ψ—张拉系数，此处取ψ＝1.0；ζ—钢筋松弛系数，这里采用低松弛钢铰线，取ζ＝0.3； peσ—传力锚固时的钢筋应力，421l l l con pe σσσσσ---＝。

计算结果见表2.6.4所示。

表2.6.4 钢筋松弛引起的应力损失计算表6.5 混凝土收缩、徐变所引起的预应力损失6l σ()()[]pspcEP cs P l t t t t E ρρφσαεσ151,,9.0006++=p Gkp npnppce IMe I M A N-+=σn n ps ps A I iie /,1222=+=ρ上式中：6l σ—受拉区全部纵向钢筋截面重心处由混凝土收缩、徐变引起的预应力损失；pcσ—受拉区全部纵向钢筋截面重心处由预应力产生的混凝土法向压应力；ρ—受拉区的全部纵向钢筋配筋率，这里即nP A A ＝ρ；pse —在这里即p e ，受拉区预应力钢筋截面重心都整个截面重心的距离；()0,t t cs ε—预应力钢筋传力锚固龄期为0t ,计算考虑龄期为t 时的混凝土收缩应变；()0,t t φ—加载龄期为0t ,计算考虑的龄期为t 时的混凝土徐变系数。

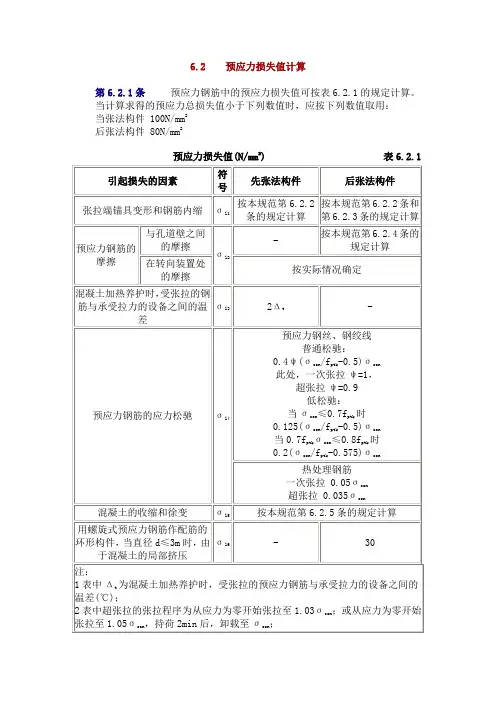
6.2 预应力损失值计算第6.2.1条预应力钢筋中的预应力损失值可按表6.2.1的规定计算。

当计算求得的预应力总损失值小于下列数值时，应按下列数值取用：当张法构件 100N/mm2后张法构件 80N/mm2预应力损失值(N/mm2) 表6.2.1第6.2.2条预应力直线钢筋由于锚具变形和预应力钢筋内缩引起的预应力损失值σl1可按下列公式计算：σl1=a/lEs(6.2.2)式中a--张拉端锚具变形和钢筋内缩值(mm),可按表6.2.2采用；l--张拉端至锚固端之间的距离(mm).锚具变形和钢筋内缩值a(mm) 表6.2.2块体拼成的结构，其预应力损失尚应计及块体间填缝的预压变形。

当采用混凝土或砂浆为填缝材料时，每条填缝的预压变形值可取为1mm.第6.2.3条后张法构件预应力曲线钢筋或折线由于锚具变形和预应力钢筋内缩引起的预应力损失值σl1,应根据预应力曲线钢筋或折线钢筋与孔道壁之间反向摩擦影响长度lf范围内的预应力钢筋变形值等于锚具变形和钢筋内缩值的条件确定，反向摩擦系数可按本规范表6.2.4中的数值采用。

常用束形的后张预应力钢筋在反向摩擦影响长度lf范围内的预应力损失值σl1可按本规范附录D计算。

第6.2.4条预应力钢筋与孔道壁之间的摩擦引起的预应力损失值σl2(图6.2.4)，宜按下列公式计算：σl2=σcon(1-1/e kx+μθ) (6.2.4-1)当(kx+μθ)≤0.2时，σl2可按下列近似公式计算：σl2=(kx+μθ)σcon(6.2.4-2)式中X--张拉端至计算截面的孔道长度(m),可近似取该段孔道在纵轴上的投影长度；θ--张拉端至计算截面曲线孔道部分切线的夹角(rad);K--考虑孔道每米长度局部偏差的摩擦系数，按表6.2.4采用；μ--预应力钢筋与孔道壁之间的摩擦系数，按表6.2.4采用。

摩擦系数表6.2.4第6.2.5条混凝土收缩、徐变引起受拉区和受压区纵向预应力钢筋的预应力损失值σl5、σ'l5可按下列方法确定：1对一般情况先张法构件σl5=45+280σpc/f'cu/1+15ρ(6.2.5-1)σ'l5=45+280σ'pc/f'cu/1+15ρ'(6.2.5-2)后张法构件σl5=35+280σpc/f'cu/1+15ρ(6.2.5-3)σ'l5=35+280σ'pc/f'cu/1+15ρ'(6.2.5-4)式中σpc 、σ'pc--在受拉区、受压区预应力钢筋合力点处的混凝土去向压应力；f'cu--施加预应力时的混凝土立方体抗压强度；ρ、ρ'--受拉区、受压区预应力钢筋和非预应力钢筋的配筋率：对先张法构件，ρ=(Ap +As)/A,ρ'=(A'p+A's)/A;对后张法构件，ρ=(Ap +As)/An,ρ'=(A'p+A's)/An;对于对称配置预应力钢筋和非预应力钢筋的构件，配筋率ρ、ρ'应按钢筋总截面面积的一半计算。

预应力混凝土预应力损失及计算方法范本一：预应力混凝土预应力损失及计算方法1. 引言预应力混凝土是一种能够提高混凝土受力性能的结构材料。

在预应力混凝土结构中，预应力钢束或钢索通过预先加载和应力传递使混凝土受到压应力，从而提高结构的承载能力。

然而，预应力混凝土在使用过程中会产生预应力损失，其影响了结构的性能。

2. 预应力损失及分类预应力损失是指预应力混凝土中预应力的大小随时间的变化而减小的现象。

根据损失的原因，预应力损失可以分为初始损失、长期损失和附加损失。

2.1 初始损失初始损失是指预应力损失在混凝土浇筑后短时间内发生的损失。

初始损失主要包括张拉损失、摩擦损失和锚固损失。

2.2 长期损失长期损失是指混凝土强度和固化引起的预应力损失。

长期损失主要包括徐变损失、收缩损失和蠕变损失。

2.3 附加损失附加损失是指在预应力混凝土结构使用过程中由于外界环境因素产生的预应力损失。

附加损失主要包括温度变化引起的损失、湿度变化引起的损失和荷载引起的损失。

3. 预应力损失的计算方法预应力损失的计算方法主要包括理论计算法和实测计算法。

3.1 理论计算法理论计算法是根据预应力损失的原理和公式对损失进行计算。

常用的理论计算方法有拉跨法、金属线法和修正损失法等。

3.2 实测计算法实测计算法是根据实测数据对预应力损失进行计算。

实测计算法主要基于监测数据和实测结果进行统计分析和计算。

4. 本文涉及附件本文中涉及到的附件包括预应力混凝土预应力损失计算表格和预应力损失实测数据表。

5. 法律名词及注释5.1 预应力混凝土结构：使用预应力技术构造的混凝土结构。

5.2 预应力钢束：用于施加预应力的钢索或钢缆。

5.3 预应力损失：预应力混凝土中预应力大小随时间变化而减小的现象。

6. 结束语预应力混凝土预应力损失是预应力混凝土结构设计和施工过程中需要考虑的重要问题。

本文介绍了预应力损失的分类和计算方法，并提供了相应的附件及法律名词及注释，以供参考。

预应力损失的计算预应力损失的大小影响到已建立的预应力，当然也影响到结构的工作性能，因此，如何计算预应力损失值，是预应力混凝土结构设计的一个重要内容。

引起预应力损失的原因很多，而且许多因素相互制约、影响，精确计算十分困难。

我国新的《混凝土结构设计规范》GB50010-2002经历四年半修订,已顺利完成。

此次修订对原规范GBJ10-89进行补充和完善，增加和改动了不少内容。

现就其中预应力损失计算部分谈谈自己的理解，供大家参考指正。

1.预应力损失基本计算在预应力损失值的计算原则方面，各国规范基本一致，均采用分项计算然后叠加以求得总损失。

全部损失由两部分组成，即瞬时损失和长期损失。

其中，瞬时损失包括摩擦损失，锚固损失（包括锚具变形和预应力筋滑移）和混凝土弹性压缩损失。

长期损失包括混凝土的收缩，徐变和预应力钢材的松弛等三项，它们需要经过较长时间才能完成。

我国新规范采用分项计算然后按时序逐项叠加的方法。

下面将分项讨论引起预应力损失的原因，损失值的计算方法。

1.1孔道摩擦损失σl2孔道摩擦损失是指预应力钢筋与孔道壁之间的摩擦引起的预应力损失。

包括长度效应（kx）和曲率效应（μθ）引起的损失。

宜按下列公式计算：σl2=σcon(1-1/e kx+μθ)当(kx+μθ)≤0.2时(原规范GBJ10-89为0.3)，σl2可按下列近似公式计算：σl2=(kx+μθ)σcon1．张拉端 2.计算截面式中:X--张拉端至计算截面的孔道长度(m),可近似取该段孔道在纵轴上的投影长度；θ--张拉端至计算截面曲线孔道部分切线的夹角(rad);K--考虑孔道每米长度局部偏差的摩擦系数，按规范取值；μ--预应力钢筋与孔道壁之间的摩擦系数，按规范取值。

对摩擦损失计算用的K，μ值取为定值，是根据当前国内有关试验值确定的，与原规范GBJ10-89不同，与国外相比，μ值较高，是由于铁皮管质量不高或预压力筋与混凝土直接接触，从而增大摩擦力的缘故。

预应力损失计算1 引言由于受施工状况、材料性能和环境条件等因素的影响，预应力结构中预应力钢筋的预拉应力在施工和使用过程中将会逐渐减少。

这种减少的应力称为结构预应力损失[2]。

设计中所需的钢筋预应力值是扣除相应阶段的应力损失后钢筋中实际存在的有效应力值（pe σ）。

设钢筋初始张拉的预应力为con σ（称为张拉控制应力），相应的应力损失值为l σ，那么预应力钢筋的有效应力为：pe con lσσσ=-因此，要使结构获得所需的有效应力（peσ），除需要根据承受外荷载的情况和结构的使用性能确定张拉控制应力（con σ）外，关键是能准确估算出预应力损失值l σ。

引起结构预应力损失的因素是很多，要准确地估算预应力损失值是非常困难的。

根据目前的研究成果，预应力损失按损失完成时间分为瞬时损失和长期损失两大类。

瞬时损失是指施加预应力时短时内完成的损失，例如锚具变形和钢筋滑移、混凝土弹性压缩、分批张拉等引起的损失；长期损失指的是考虑了材料的时间效应所引起的预应力损失，主要包括混凝土的收缩、徐变、和钢筋预应力松弛引起的损失。

有关瞬时损失的计算在理论上已基本达成了一至的计算原则。

但是，对于长期损失的计算由于存在的不确定因素较多，有些因素（如混凝土的收缩、徐变及钢筋松弛）引起的预应力损失值是随着时间的增长和环境的变化而不断变化的；还有些因素之间互相影响导致预应力值降低，例如混凝土收缩、徐变使构件缩短，钢筋回缩引起预应力值降低；反过来，预应力值降低又将减小徐变损失；钢筋的松弛也将引起徐变损失的减小等。

各国学者、专家根据自己的试验结果及有关假设和推导提出了不同的的计算理论。

预应力损失估计准确与否，对预应力结构安全性能和使用性能（如结构的抗裂性、裂逢、挠度和反拱等）将有很大的影响。

预应力损失估计过大，结构中的混凝土将承受过高的持续压应力，产生过大的反拱度，对结构安全和使用产生不利的影响，同时造成材料的浪费；反之，则会造成局部预压应力不足，导致结构过早开裂，达不到预压的效果，甚至影响结构的安全性[15]。

预应力损失计算预应力损失是指预应力混凝土中的张应力在时间和负荷作用下逐渐降低的现象。

它是影响预应力混凝土结构设计与安全的重要因素。

预应力损失的计算是预应力混凝土结构设计中的重要环节之一。

本文将介绍预应力损失的计算方法。

1. 预应力损失的分类预应力损失可分为两类： 1. 瞬时损失：由预应力杆弯曲形变、压缩和张拉过程中配合件弹性形变等因素引起的损失； 2. 长期损失：由混凝土的干缩、蠕变、徐变、温度变化和杆件氧化等因素引起的损失。

2. 预应力损失的计算方法预应力损失的计算方法主要有以下两种： 1. 经验公式法：根据预应力杆的长度、直径、工作时间、张拉应力等参数，查找相应的预应力损失系数表得出。

2. 数值模拟法：根据预应力混凝土结构的具体情况，应用数值方法进行模拟计算。

2.1 经验公式法经验公式法是一种常用的快速计算预应力损失的方法。

该方法的核心是利用预应力损失系数表进行计算。

预应力损失系数表中记录了不同工作时间、预应力杆直径、张拉应力等参数组合下的预应力损失系数，可以根据实际情况选择相应的系数进行计算。

预应力损失系数表的编制方法主要有以下两种： 1. 基于试验得出的经验关系进行编制； 2. 基于数值模拟结果进行编制。

经验公式法的主要计算公式为：$$ \\Delta P = k \\cdot fpu \\cdot A_{p}^{'} \\cdot \\frac{l}{E_{p}} $$其中， $\\Delta P$：预应力损失量；k：预应力损失系数；fpu：预应力杆应变量（或应力）；A p′：预应力杆工作期间考虑锚固代价的有效截面积（通常在初锚段的截面减少10%）；l：预应力杆工作长度；E p：预应力钢的弹性模量。

2.2 数值模拟法数值模拟法是通过建立预应力混凝土结构的有限元模型，针对不同因素的影响，进行数值模拟计算得出预应力损失量。

该方法计算精度较高，适用于大型、复杂的结构设计。

但由于计算复杂度较高，需要一定的计算能力和计算时间。

6.2 预应力损失值计算第6.2.1条预应力钢筋中的预应力损失值可按表6.2.1的规定计算。

当计算求得的预应力总损失值小于下列数值时，应按下列数值取用：当张法构件 100N/mm2后张法构件 80N/mm2预应力损失值(N/mm2) 表6.2.1第6.2.2条预应力直线钢筋由于锚具变形和预应力钢筋内缩引起的预应力损失值σl1可按下列公式计算：σl1=a/lEs(6.2.2)式中a--张拉端锚具变形和钢筋内缩值(mm),可按表6.2.2采用；l--张拉端至锚固端之间的距离(mm).锚具变形和钢筋内缩值a(mm) 表6.2.2块体拼成的结构，其预应力损失尚应计及块体间填缝的预压变形。

当采用混凝土或砂浆为填缝材料时，每条填缝的预压变形值可取为1mm.第6.2.3条后张法构件预应力曲线钢筋或折线由于锚具变形和预应力钢筋内缩引起的预应力损失值σl1,应根据预应力曲线钢筋或折线钢筋与孔道壁之间反向摩擦影响长度lf范围内的预应力钢筋变形值等于锚具变形和钢筋内缩值的条件确定，反向摩擦系数可按本规范表6.2.4中的数值采用。

常用束形的后张预应力钢筋在反向摩擦影响长度lf范围内的预应力损失值σl1可按本规范附录D计算。

第6.2.4条预应力钢筋与孔道壁之间的摩擦引起的预应力损失值σl2(图6.2.4)，宜按下列公式计算：σl2=σcon(1-1/e kx+μθ) (6.2.4-1)当(kx+μθ)≤0.2时，σl2可按下列近似公式计算：σl2=(kx+μθ)σcon(6.2.4-2)式中X--张拉端至计算截面的孔道长度(m),可近似取该段孔道在纵轴上的投影长度；θ--张拉端至计算截面曲线孔道部分切线的夹角(rad);K--考虑孔道每米长度局部偏差的摩擦系数，按表6.2.4采用；μ--预应力钢筋与孔道壁之间的摩擦系数，按表6.2.4采用。

摩擦系数表6.2.4第6.2.5条混凝土收缩、徐变引起受拉区和受压区纵向预应力钢筋的预应力损失值σl5、σ'l5可按下列方法确定：1对一般情况先张法构件σl5=45+280σpc/f'cu/1+15ρ(6.2.5-1)σ'l5=45+280σ'pc/f'cu/1+15ρ'(6.2.5-2)后张法构件σl5=35+280σpc/f'cu/1+15ρ(6.2.5-3)σ'l5=35+280σ'pc/f'cu/1+15ρ'(6.2.5-4)式中σpc 、σ'pc--在受拉区、受压区预应力钢筋合力点处的混凝土去向压应力；f'cu--施加预应力时的混凝土立方体抗压强度；ρ、ρ'--受拉区、受压区预应力钢筋和非预应力钢筋的配筋率：对先张法构件，ρ=(Ap +As)/A,ρ'=(A'p+A's)/A;对后张法构件，ρ=(Ap +As)/An,ρ'=(A'p+A's)/An;对于对称配置预应力钢筋和非预应力钢筋的构件，配筋率ρ、ρ'应按钢筋总截面面积的一半计算。

预应力损失计算预应力损失是指在预应力构件施工过程中由于各种原因导致的预应力损失的情况。

准确计算预应力损失对于工程的安全性和可靠性具有重要意义。

本文将介绍预应力损失的计算方法及其相关的内容。

1. 引言预应力技术在现代工程中得到广泛应用，其主要目的是通过施加预应力力量来提高结构的承载能力和变形性能。

然而，在预应力施工过程中，由于各种原因，如材料的初始应力损失、锚固滑移等，会导致预应力的损失，影响结构的设计效果和安全性。

2. 预应力损失的分类预应力损失可以分为初始应力损失、锚固应力损失和滑移应力损失三类。

2.1 初始应力损失初始应力损失是指在预应力构件施加初始应力后，在预应力锚固前由于材料的弹性和非弹性变形而产生的应力损失。

初始应力损失的计算可以采用材料本身的力学性能和试验数据来确定。

2.2 锚固应力损失锚固应力损失是指预应力钢束被锚固在构件内部时由于锚具的工作性能以及搭接长度的不同而导致的应力损失。

锚固应力损失的计算可借助于锚固试验和相关标准规范来确定。

2.3 滑移应力损失滑移应力损失是指在预应力钢束和混凝土之间产生滑移时，由于滑移长度和滑移阻力不同而导致的应力损失。

滑移应力损失的计算可以通过基于试验和经验公式来确定。

3. 预应力损失计算方法预应力损失的计算一般采用综合计算法，其基本原理是将初始应力损失、锚固应力损失和滑移应力损失综合考虑。

3.1 初始应力损失计算初始应力损失计算的一般步骤如下：- 根据预应力构件的几何特征、材料性能和施工工艺确定初始张拉时钢束的初始应力；- 根据预应力钢束的应力松弛特性和锚固后的应力变化规律，计算初始应力损失。

3.2 锚固应力损失计算锚固应力损失计算的一般步骤如下：- 根据预应力锚具的特性和设计要求确定锚固力的大小；- 根据预应力钢束与锚具之间的滑移长度和工作性能，计算锚固应力损失。

3.3 滑移应力损失计算滑移应力损失计算的一般步骤如下：- 根据预应力钢束与混凝土之间的滑移长度和试验数据，计算滑移应力损失；- 根据试验和经验公式，确定滑移应力损失的大小。

第6章 预应力损失及有效应力的计算本桥预采用后张法,应力损失包括： 摩阻损失、锚具变形及钢筋回缩、混凝土的弹性压缩、预应力筋的应力松弛、混凝土的收缩与徐变等5项。

根据《桥规》（JTG D62-2004）第6.2.1条规定，后张法预应力混凝土构件在正常使用极限状态计算中，应考虑由下列因素引起的预应力损失：预应力钢筋与管道壁之间的摩擦 σl1 锚具变形、钢筋回缩和接缝压缩 σl2 混凝土的弹性压缩 σl4 预应力钢筋的应力松弛 σl5 混凝土的收缩和徐变 σl6预应力损失的计算6.1.1 摩阻损失预应力钢筋与管道之间摩擦引起的应力损失可按下式计算：]1[)(1kx con l e +--=μθσσ (6-1)σcon ——张拉钢筋时锚下的控制应力（跟据《桥规》规定σcon ≤pk f ）； μ——预应力钢筋与管道壁的摩擦系数，对金属波纹管，取，具体取值见表6-1； θ——从张拉端至计算截面曲线管道部分切线的夹角之和，以rad 计； k ——管道每米局部偏差对摩擦的影响系数，取，具体取值见表6-1； x ——从张拉端至计算截面的管道长度,以米计。

表6-1 系数k 及μ的值管道类型K μ 橡胶管抽芯成型的管道 铁皮套管 金属波纹管～～6.1.2 锚具变形损失由锚具变形、钢筋回缩和接缝压缩引起的应力损失，可按下式计算：Pl Ell ∑∆=2σ (6-2)l ——锚具变形、钢筋回缩和接缝压缩值；统一取6mm ； L ——预应力钢筋的有效长度；E P ——预应力钢筋的弹性模量。

取195GPa 。

6.1.3 混凝土的弹性压缩后张预应力混凝土构件的预应力钢筋采用分批张拉时，先张拉的钢筋由于张拉后批钢筋所产生的砼弹性压缩引起的应力损失，可按下式计算pc EP l4ΔσΣασ= (6-3)式中， pc Δσ——在先张拉钢筋重心处，由后张拉各批钢筋而产生的混凝土法向应力；EP α——预应力钢筋与混凝土弹性模量比。

若逐一计算pc ΔσΣ的值则甚为繁琐，可采用下列近似计算公式412l EP PC N Nσασ-=⨯(6-4) 式中， N ——计算截面的分批张拉的钢束批数.钢束重心处混凝土法向应力：nn n n n p n P PCy I M y I e N A N 1-⎪⎪⎭⎫ ⎝⎛+=σ式中M 1为自重弯矩。

第6章 预应力损失及有效应力的计算本桥预采用后张法,应力损失包括： 摩阻损失、锚具变形及钢筋回缩、混凝土的弹性压缩、预应力筋的应力松弛、混凝土的收缩与徐变等5项。

根据《桥规》（JTG D62-2004）第6.2.1条规定，后张法预应力混凝土构件在正常使用极限状态计算中，应考虑由下列因素引起的预应力损失：预应力钢筋与管道壁之间的摩擦 σl1 锚具变形、钢筋回缩和接缝压缩 σl2 混凝土的弹性压缩 σl4 预应力钢筋的应力松弛 σl5 混凝土的收缩和徐变 σl66.1 预应力损失的计算6.1.1 摩阻损失预应力钢筋与管道之间摩擦引起的应力损失可按下式计算：]1[)(1kx con l e +--=μθσσ (6-1)σcon ——张拉钢筋时锚下的控制应力（跟据《桥规》规定σcon ≤0.75pk f ）； μ——预应力钢筋与管道壁的摩擦系数，对金属波纹管，取0.2，具体取值见表6-1； θ——从张拉端至计算截面曲线管道部分切线的夹角之和，以rad 计； k ——管道每米局部偏差对摩擦的影响系数，取0.0015，具体取值见表6-1； x ——从张拉端至计算截面的管道长度,以米计。

表6-1 系数k 及μ的值管道类型Kμ 橡胶管抽芯成型的管道 0.0015 0.55 铁皮套管 0.00300.35金属波纹管0.0020～0.00300.20～0.266.1.2 锚具变形损失由锚具变形、钢筋回缩和接缝压缩引起的应力损失，可按下式计算：Pl Ell ∑∆=2σ (6-2)∆l ——锚具变形、钢筋回缩和接缝压缩值；统一取6mm ； L ——预应力钢筋的有效长度；E P ——预应力钢筋的弹性模量。

取195GPa 。

6.1.3 混凝土的弹性压缩后张预应力混凝土构件的预应力钢筋采用分批张拉时，先张拉的钢筋由于张拉后批钢筋所产生的砼弹性压缩引起的应力损失，可按下式计算pc EP l4ΔσΣασ= (6-3)式中， pc Δσ——在先张拉钢筋重心处，由后张拉各批钢筋而产生的混凝土法向应力；EP α——预应力钢筋与混凝土弹性模量比。