角平分线定理及逆定理

角平分线的性质定理及其逆定理定理一、角平分线的性质定理及其逆定理1.角平分线的性质定理：角平分线上的点到这个角的两边的距离相等。

2.角平分线的逆定理：在角的内部，且到角的两边距离相等的点，在这个角的平分线上。

不难发现，定理1的条件是定理2的结论，同时它的结论又是定理2的条件，它们互为逆定理。

定理1说明了角平分线上点的纯粹性，即：只要是角平分线上的点，它到此角两边一定等距离，而无一例外；定理2反映了角平分线的完备性，即只要是到角两边距离相等的点，都一定在角平分线上，而绝不会漏掉一个。

在实际应用中，前者用来证明线段相等，后者用来证明角相等或证明点在一个角的平分线上。

用数学语言可表示如下：例题一：（1）∵OC平分∠AOB，点P在射线OC上，PD⊥OA于D，PE⊥OB于E∴PD=PE（定理1）（2）∵PD⊥OA，PE⊥OB，PD=PE∴OC平分∠AOB（定理2）例题二：如图，△ABC的ㄥB平分线BD与ㄥC的外角的平分线CE相较于点P。

求证：点P到三边AB、BC、CA所在直线的距离相等。

从P点向边AB做垂线,垂足为F,向BC边作垂线,垂足为G,向AC边作垂线,垂足为H因为BD是角ABC的角平分线所以PF=PG因为CE是角ACB的外角平分线所以PH=PG所以PF=PG=PH即,点P到三这AB,BC,CA所在直线的距离相等从P点向边AB做垂线,垂足为F,向BC边作垂线,垂足为G,向AC边作垂线,垂足为H因为BD是角ABC的角平分线所以PF=PG因为CE是角ACB的外角平分线所以PH=PG所以PF=PG=PH即,点P到三这AB,BC,CA所在直线的距离相等这题对吗？。

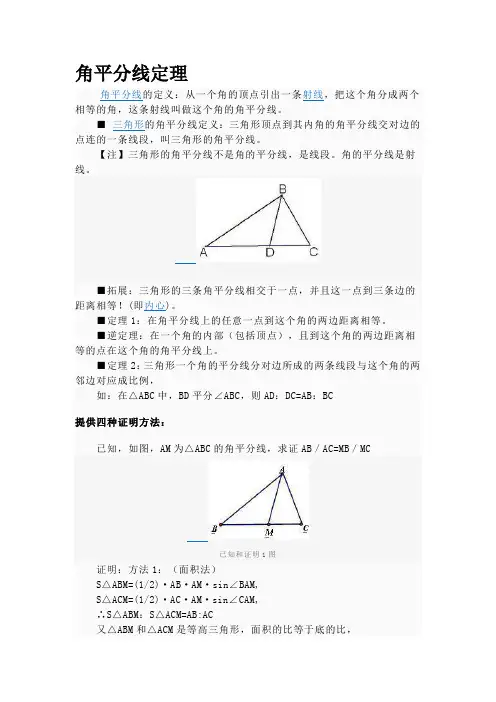
角平分线定理角平分线定义:从一个角顶点引出一条射线,把这个角分成两个相等角，这条射线叫做这个角角平分线。

■三角卷角平分线定义：三角形顶点到其内角角平分线交对边点连一条线段，叫三角形角平分线。

【注】三角形角平分线不是角平分线，是线段。

角平分线是射线。

B■拓展：三角形三条角平分线相交于一点，并且这一点到三条边距离相等！（即内心）。

■定理1:在角平分线上任意一点到这个角两边距离相等。

■逆定理：在一个角内部（包括顶点），且到这个角两边距离相等点在这个角角平分线上。

■定理2：三角形一个角平分线分对边所成两条线段及这个角两邻边对应成比例，如：在AABC 中，BD 平分ZABC,则AD： DC二AB： BC提供四种证明方法：已知，如图，AM为Z\ABC角平分线，求证AB / AC=MB / MC己知和证明1图证明：方法1:(面积法)SAABM=(l/2)・ AB ・ AM ・ sinZBAM,SAACM=(l/2)・ AC ・ AM ・ sinZCAM,AS A ABM： SAACM=AB:AC乂△ ABM和△ ACM是等高三角形，面积比等于底比,证明2图即三角形ABM面积S：三角形ACM面积S=BM:CM ・•・ AB / AC=MB / MC方法2（相似形）过C作CN II AB交AM延长线于N则厶ABM^ANCM・•・ AB/NC=BM/CM又可证明ZCAN=ZANC/. AC=CN・•・ AB / AC=MB / MC证明3图方法3 （相似形）过M作MN II AB交AC于N则厶ABC^ANMC,・•・ AB/AC二MN/NC, AN/NC二BM/MC 又可证明ZCAM=ZAMN・・・AN=MN・•・ AB/AC=AN/NC・•・ AB / AC=MB / MCA方法4 （正弦定理）作三角形外接圆，AM交圆于D,由正弦定理，得,AD证明4图AB/sinZ BMA=BM/ sinZBAM,A AC/sinZ CMA 二CM/ sinZCAM又ZBAM二ZCAM, ZBMA+ZAMC=180°sinZBAM^sinZCAM, sinZBMA^sinZAMC,/. AB / AC=MB / MC。

角平分线得性质定理及其逆定理一、基础概念学习目标:掌握角平分线得性质定理及其逆定理得证明与简单应用,掌握尺规作图做角平分线,规范证明步骤。

(1)角平分线得性质定理证明:角平分线得性质定理:角平分线上得点到这个角得两边得距离相等。

证明角平分线得性质定理时,将用到三角形全等得判定公理得推论:推论:两角及其中一角得对边对应相等得两个三角形全等。

(AAS)推导过程:已知:OC平分∠MON,P就是OC上任意一点,PA⊥OM,PB⊥ON,垂足分别为点A、点B.求证:PA＝PB.证明:∵PA⊥OM,PB⊥ON∴∠PAO＝∠PBO＝90°∵OC平分∠MON∴∠1＝∠2在△PAO与△PBO中,∴△PAO≌△PBO∴PA＝PB②几何表达:(角得平分线上得点到角得两边得距离相等)如图所示,∵OP平分∠MON(∠1＝∠2),PA⊥OM,PB⊥ON,∴PA＝PB.(2)角平分线性质定理得逆定理:到一个角得两边距离相等得点,在这个角得平分线上。

推导过程已知:点P就是∠MON内一点,PA⊥OM于A,PB⊥ON于B,且PA＝PB.求证:点P在∠MON得平分线上.证明:连结OP在Rt△PAO与Rt△PBO中,∴Rt△PAO≌Rt△PBO(HL)∴∠1＝∠2∴OP平分∠MON即点P在∠MON得平分线上.②几何表达:(到角得两边得距离相等得点在角得平分线上.)如图所示,∵PA⊥OM,PB⊥ON,PA＝PB∴∠1＝∠2(OP平分∠MON)(3) 角平分线性质及判定得应用①为推导线段相等、角相等提供依据与思路;②实际生活中得应用.例:一个工厂,在公路西侧,到公路得距离与到河岸得距离相等,并且到河上公路桥头得距离为300米.在下图中标出工厂得位置,并说明理由.(4)角平分线得尺规作图活动三:观察与思考: 尺规作角得平分线观察下面用尺规作角得平分线得步骤(如图),思考这种作法得依据。

步骤一:以点O为圆心,以适当长为半径画弧,弧与角得两边分别交于A,B两点。

角平分线定理角平分线的定义：从一个角的顶点引出一条射线，把这个角分成两个相等的角，这条射线叫做这个角的角平分线。

■ 三角形的角平分线定义：三角形顶点到其内角的角平分线交对边的点连的一条线段，叫三角形的角平分线。

【注】三角形的角平分线不是角的平分线，是线段。

角的平分线是射线。

■拓展：三角形的三条角平分线相交于一点，并且这一点到三条边的距离相等！(即内心)。

■定理1：在角平分线上的任意一点到这个角的两边距离相等。

■逆定理：在一个角的内部（包括顶点），且到这个角的两边距离相等的点在这个角的角平分线上。

■定理2：三角形一个角的平分线分对边所成的两条线段和这个角的两邻边对应成比例，如：在△ABC中，BD平分∠ABC，则AD：DC=AB：BC提供四种证明方法：已知，如图，AM为△ABC的角平分线，求证AB／AC=MB／MC已知和证明1图证明：方法1：（面积法）S△ABM=(1/2)·AB·AM·sin∠BAM,S△ACM=(1/2)·AC·AM·sin∠CAM,∴S△ABM：S△ACM=AB:AC又△ABM和△ACM是等高三角形，面积的比等于底的比，证明2图即三角形ABM面积S：三角形ACM面积S=BM:CM ∴AB／AC=MB／MC方法2（相似形）过C作CN‖AB交AM的延长线于N则△ABM∽△NCM∴AB/NC=BM/CM又可证明∠CAN=∠ANC∴AC=CN∴AB／AC=MB／MC证明3图方法3（相似形）过M作MN‖AB交AC于N则△ABC∽△NMC,∴AB/AC=MN/NC,AN/NC=BM/MC又可证明∠CAM=∠AMN∴AN=MN∴AB/AC=AN/NC∴AB／AC=MB／MC方法4（正弦定理）作三角形的外接圆，AM交圆于D，由正弦定理，得，证明4图AB/sin∠BMA=BM/sin∠BAM,∴AC/sin∠CMA=CM/sin∠CAM又∠BAM=∠CAM，∠BMA+∠AMC=180°sin∠BAM=sin∠CAM,sin∠BMA=sin∠AMC, ∴AB／AC=MB／MC。