角平分线定理的逆定理

初二数学角的平分线的性质及其逆定理通用版【本讲主要内容】角的平分线的性质及其逆定理【知识掌握】 【知识点精析】1. 角的平分线上的点到角的两边的距离相等；2. 到角的两边的距离相等的点在角的平分线上。

以上两个定理互为逆定理，要正确加以区分，性质1是指如果一个点在一个角的平分线上，可以得出它到角的两边的距离相等； 而性质2却与它恰好相反，如果一个点到角的两边距离相等，那么它的位置一定在这个角的平分线上。

通俗地说，性质1是先知点的位置，得到它的性质；性质2先由点满足某个性质，再确定它的位置。

【解题方法指导】例1. 已知：如图所示，E 是AD 上一点，∠=∠⊥⊥BAD CAD EB AB EC AC ，，。

求证：∠=∠DBE DCE分析：欲证∠=∠DBE DCE ，只要证DBE ∆≌DCE ∆即可。

由于DE 是它们的公共边，只要证出BE=CE ，∠=∠BED CED 即可，或证出BD=CD 。

已知AE 是∠BAC 的平分线，EB AB EC AC ⊥⊥，，可得出EB EC =，由∠=∠AEB AEC ，可得∠=∠BED CED 。

至此思路已通。

证明：∵AC EC AB EB CAD BAD ⊥⊥∠=∠，，∴=EB EC （角的平分线上的点到角的两边的距离相等）∵ABE BAE BED ∠+∠=∠，∠=∠+∠CED CAE ACE （三角形的外角等于不相邻的两个内角的和）DEDE CED BED =∠=∠∴又BDE ∆∴≌）（SAS CDE ∆ DCE DBE ∠=∠∴评析：如果由两次三角形全等来解决此题，实际上是把角平分线的性质又重新证了一遍，走了一个弯路，因此可直接由角平分线的性质，得出EB=EC 。

例2. 已知：如图所示，△ABC 中，D 是BC 的中点，F AC DF E AB DE 于，于⊥⊥，BE=CF 。

求证：AD 平分∠BAC 。

B D C分析：欲证AD 平分∠BAC ，由于DE ⊥AB ，DF ⊥AC ，因此只要证明DE=DF 即可，可通过△BDE ≌△CDF 加以解决。

角平分线得性质定理及其逆定理一、基础概念学习目标:掌握角平分线得性质定理及其逆定理得证明与简单应用,掌握尺规作图做角平分线,规范证明步骤。

(1)角平分线得性质定理证明:角平分线得性质定理:角平分线上得点到这个角得两边得距离相等。

证明角平分线得性质定理时,将用到三角形全等得判定公理得推论:推论:两角及其中一角得对边对应相等得两个三角形全等。

(AAS)推导过程:已知:OC平分∠MON,P就是OC上任意一点,PA⊥OM,PB⊥ON,垂足分别为点A、点B.求证:PA＝PB.证明:∵PA⊥OM,PB⊥ON∴∠PAO＝∠PBO＝90°∵OC平分∠MON∴∠1＝∠2在△PAO与△PBO中,∴△PAO≌△PBO∴PA＝PB②几何表达:(角得平分线上得点到角得两边得距离相等)如图所示,∵OP平分∠MON(∠1＝∠2),PA⊥OM,PB⊥ON,∴PA＝PB.(2)角平分线性质定理得逆定理:到一个角得两边距离相等得点,在这个角得平分线上。

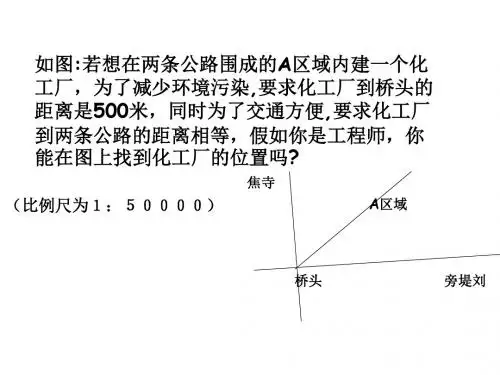
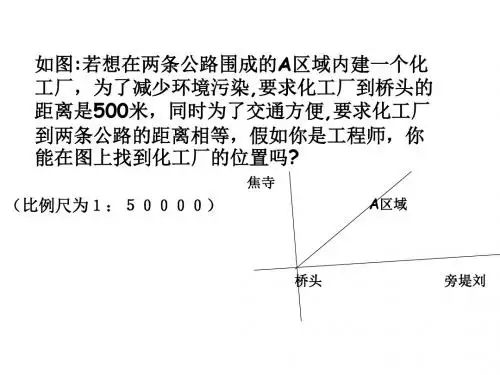
推导过程已知:点P就是∠MON内一点,PA⊥OM于A,PB⊥ON于B,且PA＝PB.求证:点P在∠MON得平分线上.证明:连结OP在Rt△PAO与Rt△PBO中,∴Rt△PAO≌Rt△PBO(HL)∴∠1＝∠2∴OP平分∠MON即点P在∠MON得平分线上.②几何表达:(到角得两边得距离相等得点在角得平分线上.)如图所示,∵PA⊥OM,PB⊥ON,PA＝PB∴∠1＝∠2(OP平分∠MON)(3) 角平分线性质及判定得应用①为推导线段相等、角相等提供依据与思路;②实际生活中得应用.例:一个工厂,在公路西侧,到公路得距离与到河岸得距离相等,并且到河上公路桥头得距离为300米.在下图中标出工厂得位置,并说明理由.(4)角平分线得尺规作图活动三:观察与思考: 尺规作角得平分线观察下面用尺规作角得平分线得步骤(如图),思考这种作法得依据。

步骤一:以点O为圆心,以适当长为半径画弧,弧与角得两边分别交于A,B两点。

19.5（1）角的平分线（角平分线的性质定理及逆定理） 要点归纳1.角平分线的性质定理给我们提供了证明两条线段相等的又一个重要方法，而且在已知中有角平分线时，往往在角平分线上选择适当的点向角的两边作垂线段。

2.角平分线性质定理的逆定理是证明两个角相等的一个重要方法。

3.利用以上两个定理可以得到：三角形三个角的平分线交于一点，且这点到三角形三边的距离相等。

疑难分析例1 已知：如图，BN 平分∠ABC ，P 为BN 上一点，PD ⊥BC 于点D ，AB+BC=2BD. 求证：∠BAP 与∠BCP 互补。

例2 已知：如图，在Rt △ABC 中，AD 是斜边BC 上的高，BF 平分∠ABC ，交AC 于点F 、AD 于点E ，EG ∥BC 交AC 于点G 。

求证：AF=CG 。

BB C A D基础训练1. ∠AOB 的平分线上的一点M ，点M 到OA 的距离为1.5厘米，则点M 到OB 的距离为＿＿＿＿；2. 如图，∠AOB=60°，CD ⊥OA 于点，CE ⊥OB 于点E ，且CD=CE ，则∠DOC 的度数为＿＿＿＿；（第2题） （第3题） （第4题）3. 如图，在△ABC 中，∠C=90°，AD 是∠BAC 的平分线，DE ⊥AB 于点E ，且DE=3厘米，BD=5厘米，则BC=＿＿＿＿厘米；4. 如图，CD 为△ABC 斜边上的高，∠BAC 的平分线分别交CD 、CB 于点E 、F ，FG ⊥AB ，垂足为G ，若CF=3厘米，则CE=＿＿＿＿；OBA B A B E D G5. 如图，已知AB 、CD 相交于点E ，过点E 作∠AEC 及∠AED 的平分线PQ 与MN ，则直线MN 与PQ 的位置关系是＿＿＿＿；（第5题） （第6题） （第7题）6. 如图，在△ABC 中，∠ACB=90°，BE 平分∠ABC ，DE ⊥AB 于点D ，如果AC=3厘米，那么AE+DE 等于（ ）A. 2厘米B. 3厘米C. 4厘米D. 5厘米7. 如图，已知AB=AC ，AE=AF ，BE 与CF 交于点D ，则①△ABE ≌△ACF ；②△BDF ≌△CDE ；③D 在∠BAC 的平分线上。

三角形角平分線逆定理
過一三角形頂點的線分(或外分)對邊所得的兩條線段與這頂點的兩邊對應成比例為這個角的內角(或外角
)平分線。

如圖，對于
給定的 ABC ，若BD DC =AB AC
，則AD 為∠BAC 的內角(或外角)平分線。

B
B
證明(1)
1.過C 作DA 的平行線，交BA 的延線于E ;
2.因與三角形一邊平行的直線截其它兩邊所得的對應線段成比
例，BA AE =BD DC ，
3.由于給定BA
AC
=BD DC ，得AC =AE,∠AEC =∠ACE
4.∠BAD =∠AEC =∠ACE =∠DAC ;
5.AD 平分∠BAC 。

B
證明(2)
1.過C 作DA 的平行線，交BA 于F ;
2.因與三角形一邊平行的直線截其它兩邊所得的對應線段
成比例，
BF F A =BC CD ,BF +F A AF =BC +CD DC ,BA AF =BD DC
=BA
AC 3.AC =AF,
∠EAD =∠AF C =∠ACF =∠DAC ;
4.AD 為∠BAC 的外角平分線。

B
參考資料
1.Durell.A New Geometry for Schools,1963.(P.475)
1。

角平分线定理逆定理
角平分线定理逆定理，又称作三角形角平分线定理反定理，是一种重要的几何定理。

它的关联定理为：若一个三角形的内角平分线的长度之和大于三角形的最长边的长度，则该三角形必然存在。

角平分线定理逆定理也可以解释为：若一个三角形不存在（即三角形角平分线长度和小于最长边长度），那么该三角形的最长边长度
是它内角平分线长度和的一半。

角平分线定理的反定理是角平分线定理的一种特殊情况，可以用来推导三角形的最长边长度，以及其他三角形规律。

角平分线定理逆定理描述的三角形一般有以下常见特征：
1）三角形的三条内角平分线相交于一点，即三角形的外心；
2）三角形的最长边长度等于内角平分线长度和的一半；
3）三角形的最长边长度等于它外心到最长边端点的距离；
4）其他两条边的总长度大于三角形的最长边的长度。

角平分线定理逆定理有着重要的应用。

例如，通过三角形的内角平分线长度可以推导最长边的长度，从而更轻松的解决三角形的主角平分线常见的问题，从而节省计算时间。

此外，角平分线定理逆定理同样能够用作求解凸三角形的外心和内心，直接求解最长边长度，也可以应用于计算最大椭圆面积等等。

角平分线定理逆定理在实际几何推理中有着重要的作用，可以用来简便地求解三角形的最长边长度，以及求解凸三角形的外心和内心。

同时，角平分线定理逆定理也给了我们一种简单的方法，可以快速推
断出一个三角形是否存在。

角平分线分线段成比例定理逆定理
角平分线分线段成比例定理是几何学中的重要定理，它告诉我们在三角形中，角平分线分出的线段成比例。

其中，角平分线是指从三角形角的中点出发，平分角的线段。

逆定理是指如果三角形中的线段满足角平分线分线段成比例关系，那么这个三角形就是角平分三角形。

这个定理和逆定理在证明上是互逆的，即如果知道一个定理, 就能推出另一个定理.
例如说, 如果已知三角形是角平分三角形, 那么就可以得出结论: 角平分线分出的线段成比例. 反之, 如果已知角平分线分出的线段成比例, 那么这个三角形就是角平分三角形.
这个定理和逆定理在几何学中有很多应用, 如利用这个定理来判断三角形是否是角平分三角形, 解决几何问题等.。

角平分线的性质与判定教学目标：1、 能够对角平分线的性质定理及逆定理进行严密的证明。

2、 能够灵活运用两个定理进行相关问题的计算或者证明。

教学重点：定理的证明及应用。

教学难点：定理的证明。

教学过程： 一.复习引入：在第二章，我们利用角的轴对称性质，通过实验的方法，探索出了角平分线的性质。

你还记得角平分线的性质吗？你能用推理的方法证明它们的真实性吗？角平分线的性质：___________________________________________________角平分线的性质的逆命题是： 二、新课学习：知识点一、证明：角平分线上的点到这个角的两边的距离相等.已知：OE 是∠AOB 的平分线，F 是OE 上一点，若CF ⊥OA 于点C ，DF ⊥OB 于点D 求证：CF ＝DF.证明：应用格式：例1.已知：如图，点B 、C 在∠A 的两边上，且AB=AC ，P 为∠A 内一点，PB=PC ， PE ⊥AB ，PF ⊥AC ，垂足分别是E 、F 。

求证：PE=PF知识点二、证明：到线段两个端点距离相等的点在这条线段的垂直平分线上。

图4已知：如图5，点P在∠AOB的内部，且PC⊥OA于C，PD⊥OB于D，PC＝PD求证：点P在∠AOB的平分线上.证明：应用格式：例2. 已知：PA、PC分别是△ABC外角∠MAC和∠NCA平分线，它们交于P，PD⊥BM于D，PF⊥BN于F，求证：BP为∠MBN的平分线。

知识点三. 关于三角形三条角平分线交点的定理：三角形三条角平分线相交于一点，并且这一点到三边的距离相等. 已知：如图6，AP、BQ、CR分别是△ABC的内角∠BAC、∠ABC、∠ACB的平分线求证：①AP、BQ、CR相交于一点I；②若ID、IE、IF分别垂直于BC、CA、AB 于点D、E、F，则DI＝EI＝FI.证明：三、课堂总结：总结本节课的收获四．课堂检测1、有一点P到三角形三条边的距离相等，则点P一定是的交点2．如图2，在△ABD中，AD=4，AB=3，AC平分∠BAD ，则=3．如图3，在△ABC中，∠C=，AD平分∠BAC，DE⊥AB于E，则下列结论：①AD 平分∠CDE；②∠BAC=∠BDE；③DE平分∠ADB；④BE+AC=AB。