实验一_霍尔位置传感器与弯曲法杨氏模量的测定
- 格式:doc
- 大小:1.77 MB
- 文档页数:11



用霍尔位置传感器测杨氏模量用霍尔位置传感器测量材料的杨氏模量利用霍尔位置传感器和弯曲法测量杨氏模量实验数据杨氏模量测量实验报告随着科技进步的蓬勃发展,微位移测量这一核心技术也日趋先进。
本次测试揭示了业界近年开发的先进霍尔位置传感器。
它通过电磁铁和集成霍尔元件之间不断变化的负载信号来测量微小的偏转。
这种控制技术主要用于杨氏弯曲法。
杨氏模量测试。
在此实验室报告中,模具的杨氏模量是使用霍尔位置传感器测量的。
合金铸铁的杨氏模量采用弯曲法测定。
除了测量铜的杨氏模量外,还要校准霍尔位置传感器以解决其精度问题。
利用霍尔位置传感器测量铁的杨氏模量等。
利用实验可以使学生增强对霍尔传感器基本原理的广泛应用、科学院新型传感器的标定、以及不同长度值的测量方法。
传感器法测量位移有什么优点霍尔位置传感器和弯曲法测量杨氏模量实验数据弯曲法测量杨氏模量实验中的主要测量值有哪些。
请计算每个环境因素的不确定性。
传感器测量位移的方法有什么特点?建议】使用千分尺时,2.使用高度计光学测量重物刀口架基线位置时,刀口架不能晃动。
4.使用霍尔位置霍尔传感器及弯曲法杨氏模量测量实验报告方法本实验在弯曲法良好基础上安装霍尔位置测量杨氏模量液态金属材料的模量。
传感器。
通过对霍尔位置传感器的输入阻抗与位移的微分关系的标定和微小位移的测量,使学生了解和掌握微小位移的非电测量新方法。
微位移测量技术也得到快速发展霍尔位置传感器标定及弯曲法测量杨氏模量误差分析SUES大学物理选修实验讲座笔记磁弯曲法测量杨氏模量及霍尔位置传感器校准随着科技进步的蓬勃发展,微挠度测量的电子技术也给经济带来了飞速的发展。
本科学实验介绍了近年来出现的新型先进霍尔位置传感器,利用负载的回波来测量电磁铁与霍尔传感器之间位置变化的微小偏移量。
该科学实验结合了电子技术测量金属梁的微小位移、霍尔位置传感器的校准和弯曲法测量铝的杨氏模量。
通过实验报告,小学生可以加深对霍尔传感器广泛应用的认识,学习新型传感器的标定、不同取值宽度的测量和不同宽度测量设备的采用。

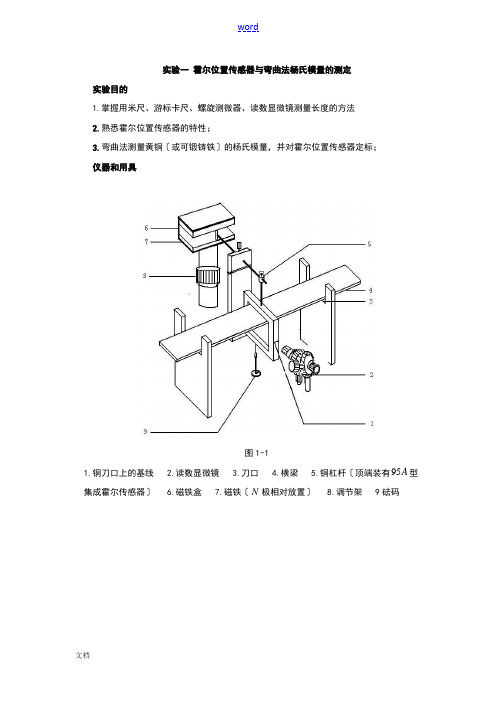
实验一霍尔位置传感器与弯曲法杨氏模量的测定实验目的1.掌握用米尺、游标卡尺、螺旋测微器、读数显微镜测量长度的方法2.熟悉霍尔位置传感器的特性;3.弯曲法测量黄铜〔或可锻铸铁〕的杨氏模量,并对霍尔位置传感器定标;仪器和用具图1-195型1.铜刀口上的基线 2.读数显微镜 3.刀口 4.横梁 5.铜杠杆〔顶端装有A 集成霍尔传感器〕 6.磁铁盒 7.磁铁〔N极相对放置〕 8.调节架 9砝码图1-2 实验装置的实物照片2、其他用用具米尺,游标卡尺,螺旋测微仪,砝码,待测材料〔一根黄铜、一根可铸锻铁〕 实验原理霍尔元件置于磁感应强度为B 的磁场中,在垂直于磁场方向通以电流I ,如此与这二者相垂直的方向上将产生霍尔电势差H U :B I K U H ⋅⋅= 〔1-1〕〔1-1〕式中K 为元件的霍尔灵敏度。
如果保持霍尔元件的电流I 不变,而使其在一个均匀梯度的磁场中移动时,如此输出的霍尔电势差变化量为:Z dZdBI K U H ∆⋅⋅⋅=∆ 〔1-2〕 〔1-2〕式中Z ∆为位移量,此式说明假如dZdB 为常数时,H U ∆与Z ∆成正比。
图1-3为实现均匀梯度的磁场,可以如图1-3所示,两块一样的磁铁〔磁铁截面积与外表磁感应强度一样〕相对放置,即N 极与N 极相对,两磁铁之间留一等间距间隙,霍尔元件平行于磁铁放在该间隙的中轴上。
间隙大小要根据测量X 围和测量灵敏度要求而定,间隙越小,磁场梯度就越大,灵敏度就越高。
磁铁截面要远大于霍尔元件,以尽可能的减小边缘效应影响,提高测量准确度。
假如磁铁间隙内中心截面处的磁感应强度为零,霍尔元件处于该处时,输出的霍尔电势差应该为零。
当霍尔元件偏离中心沿Z 轴发生位移时,由于磁感应强度不再为零,霍尔元件也就产生相应的电势差输出,其大小可以用数字电压表测量。
由此可以将霍尔电势差为零时元件所处的位置作为位移参考零点。
霍尔电势差与位移量之间存在一一对应关系,当位移量较小〔mm 2<〕,这一对应关系具有良好的线性。

实验名称霍尔传感器测杨氏模量【实验目的】1.了解霍尔位置传感器的结构原理、特性及使用方法。
2.学习掌握粱弯曲法测量金属板的杨氏弹性模量。
3.学会确定灵敏度的方法,并确定仪器的灵敏度。
4.掌握逐差法处理数据。
【实验仪器】霍尔位置传感器、霍尔位置传感器输出信号测量仪、游标卡尺、螺旋测微器。
【实验原理】霍尔传感器置于磁感应强度为B 的磁场中,在垂直于磁场的方向通入电流I ,则会产生霍尔效应,即在与这二者相互垂直的方向上将产生霍尔电势:IB K U H H = (5.2.1)其中H K 为霍尔传感器的灵敏度,单位为T mA mV ⋅。
如果保持通入霍尔元件的电流I 不变,而使其在一均匀梯度的磁场中移动,则输出的霍尔电势的变化量为:z dzdBIK U H H ∆=∆ (5.2.2) 其中:z ∆为位移量;dzdB为磁感应强度B 沿位移方向的梯度,为常数。
为了实现上述均匀梯度磁场,选用两块相同的磁铁。
磁铁平行相对而放,即N 极相对放置。
两磁铁之间的空隙内放入霍尔元件,并使此元件平行于磁铁,且与两磁铁的间距相等,即霍尔元件放置两磁铁空隙的中心,如图6.1所示。
若间隙中心截面的中心点A 的磁感应强度为零,霍尔元件处于该处时输出的霍尔电势应为零。
当霍尔元件偏离中心沿Z 轴发生位移,由于磁感应强度不再为零,霍尔元件也就有相应电势输出,其大小可由数字电压表读出。
一般地,将霍尔电势为零时元件所处的位置作为位移参考点。
霍尔电势与位移量之间存在一一对应的关系,当位移量较小时(小于2mm ),对应关系具有良好的线性,如图6.2所示。
mm在粱弯曲的情况下,杨氏模量E 用下列公式计算:zb a mg d E ∆=334 (6.1)式中:d 为两刀口间的距离,a 为粱的厚度,b 为粱的宽度,m 为砝码的质量,g 为重力加速度(2792.9s m g =),z ∆为粱中心由于外力的作用而下降的距离。
【实验装置】杨氏模量实验装置如图6.3所示。
用霍尔位置传感器测杨氏模量实验报告实验报告:用霍尔位置传感器测杨氏模量摘要:本实验通过使用霍尔位置传感器测量不同拉力下杆的长度变化,从而计算杨氏模量。
实验数据表明,杨氏模量的测量精度比传统方法更高。
引言:杨氏模量是描述材料弹性的重要参数,常用于评价材料的强度和刚度。
传统的测量方法通常是通过拉伸试验测量材料的长度变化,计算杨氏模量。
然而,这种方法需要使用高精度的测量设备,同时在实验过程中人为误差也比较大。
本实验采用霍尔位置传感器对杨氏模量进行测量,可以有效地提高测量精度和减少人为误差。
实验步骤:1. 准备工作:使用铁丝制作一根细长带有刻度的杆,其中的刻度距离为1cm;另外准备一块平整的板子和两个霍尔位置传感器。
2. 设置实验平台:将杆固定在平整的板子上,并且分别在两端用铁夹固定。
将两个霍尔位置传感器分别安装在杆子两端的铁夹上,并用电源适配器连接。
3. 实验测量:施加不同的拉力,分别记录杆子的长度变化和两个传感器的输出电压。
根据长度变化以及传感器输出电压计算出每个拉力下杨氏模量。
4. 实验记录:将实验数据记录在表格中,包括杆子的长度变化、两个传感器的输出电压以及计算出的杨氏模量。
实验数据:本实验进行了3次,每次都在不同的拉力下测量杨氏模量。
以下是实验数据:(表格)结果分析:通过数据分析可以看出,采用霍尔位置传感器测量杨氏模量的方法能够得到更加精确的结果。
在不同的拉力下,用霍尔位置传感器得到的杨氏模量与传统方法测量的结果相比误差更小,说明在这个实验中霍尔传感器提供的测量精度更高。
结论:通过实验结果可以得知,在测量杨氏模量时采用霍尔位置传感器比传统方法更具优势。
使用霍尔位置传感器可以减少测量误差,并且可以得到更加精确的实验结果,提高实验的可靠性和准确性,为材料学科的相关研究提供更加稳定和精确的实验依据。
实验(实训)报告辽宁科技大学 学院(系) 年 月 日 课程名称: 实验题目:班级:姓名:学号:机台号:同组人:任课教师:实验目的1、掌握基本长度和微小位移量测量的方法,学习游标卡尺、千分尺等常用长度测量仪器的使用;2、熟悉霍尔位置传感器的特性;3、弯曲法测量铁的杨氏模量;4、学会用逐差法、作图法处理数据。
<实验原理>杨氏模量的定义:反映材料应变(即单位长度变化量L L ∆)与物体内部应力(即单位面积所受到的力的大小F S )之间关系的物理量,反映材料的抗拉或抗压能力。
即:F LYS L∆= 测量杨氏模量的方法一般有拉伸法、梁弯曲法、振动法、内耗法等,还出现了利用光纤位移传感器、莫尔条纹、电涡流传感器和波动传递技术(微波或超声波)等实验技术和方法测量杨氏模量。
1、杨氏模量的测量杨氏模量测定仪主体装置如图3所示,在横梁弯曲的情况下,杨氏模量Y 可以用下式表示:Z b a Mgd Y ∆⋅⋅⋅=334; 其中:d 为两刀口之间的距离,M 为所加砝码的质量,a 为梁的厚度,b 为梁的宽度,Z ∆为梁中心由于外力作用而下降的距离,g 为重力加速度。
上面公式的具体推导见附录。
图1 实验装置图其中:1.铜刀口上的基线 2.读数显微镜 3.刀口 4.横梁 5.铜杠杆(顶端装有A 95型集成霍尔传感器) 6.磁铁盒 7.磁铁(N 极相对放置) 8.调节架 9砝码图2 实验原理图2、微小位移△z 的测量方法: (1)读数显微镜方法:(2)霍尔位置传感器方法:定义:一块半导体薄片处于垂直于它的磁场B 中,当通以电流I 时,则在垂直于B 、I 方向上产生霍耳电势差,这种现象称为霍耳效应。
图4 霍耳效应霍尔元件置于磁感应强度为B 的磁场中,在垂直于磁场方向通以电流I ,则与这二者相垂直的方向上将产生霍尔电势差H U :0H U K I B =⋅⋅ (1)(1)式中0K 为元件的霍尔灵敏度。
如果保持霍尔元件的电流I 不变,而使其在一个均匀梯度的磁场中移动时,则输出的霍尔电势差变化量为:0H dBU K I Z dZ∆=⋅⋅⋅∆ (2) (2)式中Z ∆为位移量,此式说明若dBI dZ⋅为常数时,H U ∆与Z ∆成正比,即: H U K Z ∆=⋅∆为实现均匀梯度的磁场,可以如图5所示,两块相同的磁铁(磁铁截面积及表面磁感应强度相同)相对放置,即N 极与N 极相对,两磁铁之间留一等间距间隙,霍尔元件平行于磁铁放在该间隙的中轴上。
霍耳位置传感器法测杨氏模量一、实验内容:1.了解霍耳效应及霍耳位置传感器的原理2.学会使用霍耳位置传感器法测杨氏模量二、实验仪器:杨氏模量测试仪、千分尺、游标卡尺三、实验原理:1.霍耳元件置于磁感应强度为B 的磁场中,在垂直于磁场方向通以电流I ,则与这二者平面垂直的方向上产生霍耳电势差:B I K U H ⋅⋅= (1)上式中K 为元件的霍耳灵敏度。
如果保持霍耳元件的电流I 不变,而使其在一均匀梯度的磁场中移动时,则输出的霍耳电势差变化量为:(2)杨氏模量测试仪上式中Z ∆为位移量,此式说明若dZdB 为常数时,U ∆与Z ∆成正比。
2.一段固体棒,在其两端沿轴发现施加大小相等、方向相反的外力F ,其长度L 发生改变L ∆,以S 表示横截面面积,称F/S 为胁强,相对长变L ∆/L 为胁变。
在弹性限度内,由胡克定律有:E 称为杨氏模量,其数值与材料性质有关。
在横梁受力弯曲的情况下,杨氏模量E 得测量表达式为:(3)其中:d 为两刀口之间的距离;M 为所加砝码的质量;a 为梁的厚度;b 为梁的宽度;Z ∆为梁中心由于外力作用而下降的距离;g 为重力加速度。
四、实验步骤:1.调节三维调节架的上下前后位置的调节螺丝,使传感器探测元件处于磁铁中间位置。
2.用水准器观察是否在平衡位置,若偏离可用底座螺丝调节到水平位置。
3.调节霍耳位置传感器的毫伏表。
磁铁盒可上下调节调节螺丝使磁铁上下移动,当毫伏表读数值很小时,停止调节并固定螺丝,最后调节零电位器使毫伏表读数为零。
4.调节读数显微镜,使眼睛观察十字线及分划板刻度线和数字清晰。
然后移动读数显微镜前后位置,使能清晰看到铜刀上的基线。
转动读数显微镜的鼓轮使刀口架上的基线与读数显微镜内十字刻度线重合,记下初始读数值。
5.逐次增加砝码,每次增加10.00g ,相应从读数显微镜读出梁中心的位置i Z (mm )及毫伏表的读数i U (mv )。
然后依次减少砝码,每次减少10.00g ,做同样的记录。
实验一霍尔位置传感器及弯曲法氏模量的测定实验目的1.掌握用米尺、游标卡尺、螺旋测微器、读数显微镜测量长度的方法2.熟悉霍尔位置传感器的特性;3.弯曲法测量黄铜(或可锻铸铁)的氏模量,并对霍尔位置传感器定标;仪器和用具1.氏模量测定仪主体装置如图1-1所示图1-195型1.铜刀口上的基线 2.读数显微镜 3.刀口 4.横梁 5.铜杠杆(顶端装有A 集成霍尔传感器) 6.磁铁盒 7.磁铁(N极相对放置) 8.调节架 9砝码图1-2 实验装置的实物照片2、其他用用具米尺,游标卡尺,螺旋测微仪,砝码,待测材料(一根黄铜、一根可铸锻铁) 实验原理 1.霍尔位置传感器霍尔元件置于磁感应强度为B 的磁场中,在垂直于磁场方向通以电流I ,则与这二者相垂直的方向上将产生霍尔电势差H U :B I K U H ⋅⋅= (1-1)(1-1)式中K 为元件的霍尔灵敏度。
如果保持霍尔元件的电流I 不变,而使其在一个均匀梯度的磁场中移动时,则输出的霍尔电势差变化量为:Z dZdBI K U H ∆⋅⋅⋅=∆ (1-2)(1-2)式中Z ∆为位移量,此式说明若dZdB 为常数时,H U ∆与Z ∆成正比。
图1-3为实现均匀梯度的磁场,可以如图1-3所示,两块相同的磁铁(磁铁截面积及表面磁感应强度相同)相对放置,即N 极与N 极相对,两磁铁之间留一等间距间隙,霍尔元件平行于磁铁放在该间隙的中轴上。
间隙大小要根据测量围和测量灵敏度要求而定,间隙越小,磁场梯度就越大,灵敏度就越高。
磁铁截面要远大于霍尔元件,以尽可能的减小边缘效应影响,提高测量精确度。
若磁铁间隙中心截面处的磁感应强度为零,霍尔元件处于该处时,输出的霍尔电势差应该为零。
当霍尔元件偏离中心沿Z 轴发生位移时,由于磁感应强度不再为零,霍尔元件也就产生相应的电势差输出,其大小可以用数字电压表测量。
由此可以将霍尔电势差为零时元件所处的位置作为位移参考零点。
霍尔电势差与位移量之间存在一一对应关系,当位移量较小(mm 2<),这一对应关系具有良好的线性。
2、氏模量固体、液体及气体在受外力作用时,形状或体积会发生或大或小的改变,称之为形变。
当外力不太大时,引起的形变也不会太大,若撤掉外力,形变随之会消失,这种形变称为弹性形变。
如一段固体棒,在其两端沿轴方向施加大小相等,方向相反的外力F ,其长度l 发生改变△11,以S 表示横截面面积,称F/S 为应力,相对长变(△!l/l )为应变,在弹性限度,根据胡克定律有llY S F ∆= Y 称为氏模量,其数值与材料性质有关。
如图2所示,在待测样品发生微小弯曲时,梁中存在一个中性面,面以上的部分发生压缩,面以下的部分发生拉伸。
总体来说,待测样品将发生应变,可用氏模量来描述材料的性质,氏模量为公式其中:d为两刀口之间的距离,M为所加砝码的质量,a为梁的宽度,戴尔特Z为梁中心由于外力作用而下降的距离,g为重力加速度。
实验容1.基本容:测量黄铜样品的氏模量和霍尔位置传感器的定标。
(1)调节三维调节架的调节螺丝,使集成霍尔位置传感器探测元件处于磁铁中间的位置。
(2)用水准器观察是否在水平位置,若偏离时可以用底座螺丝调节。
(3)调节霍尔位置传感器的毫伏表。
磁铁盒下的调节螺丝可以使磁铁上下移动,当毫伏表数值很小时,停止调节固定螺丝,最后调节调零电位器使毫伏表读数为零。
(4)调节读数显微镜,使眼镜观察十字线及分划板刻度线和数字清晰。
然后移动读数显微镜前后距离,使能够清晰看到铜架上的基线。
转动读数显微镜的鼓轮使刀口架的基线与读数显微镜十字刻度线吻合,记下初始读数值。
(5)逐次增加砝码(每次增加10g砝码),相应从读数显微镜上读出梁的弯曲位移及数字电压表相应的读数值(单位mV)。
以便于计算氏模量和霍尔位置传感器进行定标。
在进行测量之前,要求符合上述安装要求,并且检查杠杆的水平、刀口的垂直、挂砝码的刀口处于梁中间,要防止外加风的影响,杠杆安放在磁铁的中间,注意不要与金属外壳接触,一切正常后加砝码,使梁弯曲产生位移;精确测量传感器信号输出端的数值与固定砝码架的位置Z的关系,也就是用读数显微镜对传感器输出量进行定标,检验的关系。
(6)测量横梁两刀口间的长度d及测量不同位置横梁宽度b和梁厚度a。
(7)用逐差法按照公式(3)进行计算,求得黄铜材料的氏模量,并求出霍尔位置传感器的灵敏度,并把测量值与公认值进行比较。
2.选作容:用霍尔位置传感器测量可锻铸铁的氏模量。
查:数据记录与处理1.霍尔位置传感器的定标利用读数显微镜的读数和位置传感器输出电压U,用图解法求出霍尔位置传感器的灵敏度公式表1 霍尔位置传感器静态特性测量2.测量氏模量2.1 用逐差法求出加砝码质量M时,对应的梁中心由于外力作用而下降的距离戴尔特Z。
序号i 1 2 3 4 平均值公式2.2 计算平均值及不确定度:公式2.3 其他量:d=序号 1 2 3 4 5 6 7 8 9 10 梁宽b(mm)b=d=序号 1 2 3 4 5 6 7 8 9 10 梁厚a(mm)2.4利用式(4)计算,求得黄铜材料的氏模量及总不确定度公式2.5把测量结果与公认值(数值)进行比较【注意事项】(1)梁的厚度必须测准确。
在用千分尺测量黄铜厚度a时,将千分尺旋转时,当将要与金属接触时,必须用微调轮。
当听到答答答三声时,停止旋转。
有个别学生实验误差较大,其原因是千分尺使用不当,将黄铜梁厚度测得偏小;(2)读数显微镜的准丝对准铜挂件(有刀口)的标志刻度线时,注意要区别是黄铜梁的边沿,还是标志线;(3)霍尔位置传感器定标前,应先将霍尔传感器调整到零输出位置,这时可调节电磁铁盒下的升降杆上的旋钮,达到零输出的目的,另外,应使霍尔位置传感器的探头处于两块磁铁的正中间稍偏下的位置,这样测量数据更可靠一些;(4)加砝码时,应该轻拿轻放,尽量减小砝码架的晃动,这样可以使电压值在较短的时间达到稳定值,节省了实验时间;(5)实验开始前,必须检查横梁是否有弯曲,如有,应矫正。
【思考题】1.弯曲法测氏模量实验,测量误差主要有哪些?估算各因素的不确定度2.利用霍尔传感器法测位移有什么优点?弯曲法测氏模量实验,主要测量误差有哪些?请估算各测量的不确定度3.在本实验中最需要保证的实验条件是什么?为什么要有限制的增加砝码?4.实验中如何确定支撑横梁的两刀口是否平行?【参考资料】[1] 漆安慎 杜婵英 《力学》 高等教育[2] 方佩敏 《新编传感器原理、应用、电路详解》 电子工业[3] 游海洋 在忠 陆申龙 《霍尔位置传感器测量固体材料的氏模量》 《物理实验》,第20卷第8期[4] 龚镇雄 《普通物理实验》 人民教育【附录】弯曲法测量氏模量公式的推导固体、液体及气体在受外力作用时,形状与体积会发生或大或小的改变,这统称为形变。
当外力不太大,因而引起的形变也不太大时,撤掉外力,形变就会消失,这种形变称之为弹性形变。
弹性形变分为长变、切变和体变三种。
一段固体棒,在其两端沿轴方向施加大小相等、方向相反的外力F ,其长度l 发生改变l ∆,以S 表示横截面面积,称S F 为应力,相对长变ll∆为应变。
在弹性限度,根据胡克定律有:llY S F ∆⋅= (1-3) Y 称为氏模量,其数值与材料性质有关。
在横梁发生微小弯曲时,梁中存在一个中性面,面上部分发生压缩,面下部分发生拉伸,所以整体说来,可以理解横梁发生长变,即可以用氏模量来描写材料的性质。
如图1-4所示,虚线表示弯曲梁的中性面,易知其既不拉伸也不压缩,取弯曲梁长为dx 的一小段:图1-4设其曲率半径为)(x R ,所对应的角为θd ,再取中性面上部距为y 厚为dy 的一层面为研究对象,那么,梁弯曲后其长变为θd y x R ⋅-))((,所以,变化量为: dx d y x R -⋅-θ))((又)(x R dxd =θ;所以dx x R y dx x R dxy x R dx d y x R )()())(())((-=--=-⋅-θ;所以应变为:)(x R y-=ε;根据虎克定律有: )(x R yYdSdF -=; 又 dy b dS ⋅=;所以dy x R yb Y x dF )()(⋅⋅-=;对中性面的转矩为:dy y x R b Y y dF x d ⋅⋅=⋅=2)()(μ;积分得: ⎰-⋅⋅⋅=⋅⋅=2232)(12)()(a a x R a b Y dy y x R b Y x μ; (1-3)对梁上各点,有: []232)(1)()(1x y x y x R '+''=;因梁的弯曲微小: 0)(='x y ;所以有: )(1)(x y x R ''=;(4) 梁平衡时,梁在x 处的转矩应与梁右端支撑力2Mg对x 处的力矩平衡,所以有: )2(2)(x dMgx -=μ;(5) 根据(3)、(4)、(5)式可以得到: )2(6)(3x d a b Y Mgx y -⋅⋅='';据所讨论问题的性质有边界条件; 0)0(=y ;0)0(='y ;解上面的微分方程得到: );312(3)(323x x d a b Y Mgx y -⋅⋅= 将2d x =代入上式,得右端点的y值:334a b Y d Mg y ⋅⋅⋅=;又 Z y ∆=;所以,氏模量为: Z b a Mgd Y ∆⋅⋅⋅=334(6)。