用拉伸法测定钢丝的杨氏模量
- 格式:docx
- 大小:58.58 KB
- 文档页数:11

用拉伸法测钢丝杨氏模量――实验报告本实验使用拉伸法测定钢丝的杨氏模量。
实验过程包括测量原始尺寸和断裂强度,计算应力和应变,绘制应力-应变曲线,利用斜率计算杨氏模量。
一、实验原理1.杨氏模量:杨氏模量也称弹性模量,是研究力学学科中的一项重要物理量,它描述了物体在受力时,单位应力下的应变程度。
可以表示为弹性模量E,其计算公式为E=σ/ε,其中σ为应力,ε为单位应变。
2.拉伸法:拉伸法是测定材料弹性性质的常用方法之一。
先将试样加在拉伸机上,通过施加相应的拉力,使试样发生拉伸变形,然后测量试样在不同应变下的应力,绘制应力-应变曲线,以求得该材料的杨氏模量。
二、实验步骤1.准备实验设备,将钢丝放在拉伸机上。
2.用卡尺测量钢丝的初始长度、直径和断裂长度,记录数据。
3.用拉伸机分别在不同的拉力下进行拉伸,记录拉力和试样的应变。
4.计算每个密度下的应力,应力=拉力/试样横截面积。
5.计算每个密度下的应变,应变=延长长度/原始长度。
6.根据应力-应变曲线,计算杨氏模量。
三、实验数据试样长度:5m原始直径:2.5mm断裂长度:8m钢丝密度:7.85g/cm³拉伸试验数据如下:|拉力F(N)|延长长度L(mm)|试样直径D(mm)||:-:|:-:|:-:||0|0|2.5||50|2|2.5||100|4|2.6||150|6|2.7||200|8|2.8||250|10|2.9||300|12|3.0||350|14|3.1||400|16|3.2||450|18|3.3||500|20|3.4||550|22|3.5||600|24|3.6||650|26|3.7||700|28|3.8||750|30|3.9||800|32|4.0|四、实验计算1.计算实验数据中的横截面积试样横截面积=π*(D/2)²=π*(2.5/2)²=4.91mm² 2.计算每个密度下的应力应力=F/S=700/4.91=142.6N/mm²应变=L/L0=28/5000=0.00564.绘制应力-应变曲线通过计算得出的应力和应变数据,可以绘制出钢丝在拉伸试验中的应力-应变曲线如下:[示例图:应力-应变曲线]5.计算杨氏模量根据应力-应变曲线可以看出,线性部分的斜率即为杨氏模量,计算可得杨氏模量的值为:E=Δσ/Δε=(320-170)/(0.004-0.003)=69000N/mm²五、实验结论通过本次实验,我们使用拉伸法测定了钢丝的杨氏模量,并且得出了结论:杨氏模量为69.0×10⁹N/mm²。

用拉伸法测量钢丝的杨氏模量张翰晓 PB10011035实验目的(1)学会利用光杠杆法测定微小形变; (2)学会使用逐差法和作图法进行数据处理。
实验原理宏观物体在外力作用下都会发生形变,在弹性限度内,材料的应强与应变之比为一常数,称弹性模量。
杨氏模量(用E 表示)是条形物体沿纵向的弹性模量,定义为弹性限度内应力与应变之比(注:应力是力与作用的面积之比,应变是长度的变化与原长之比),即L S /FL )L /L /()S /F (E ∆∆== (1)在胡克定律成立的范围内,E 为常数,它仅决定于材料的属性,用于度量材料的刚性。
测量杨氏模量可用拉伸法、梁德弯曲法、振动法、内耗法等。
本实验采用拉伸法测量钢丝的样式模量,即,在截面积为S 的样品上的作用应力F ,测量引起的相对伸长量ΔL/L ,即可计算出材料的杨氏模量E 。
因伸长量ΔL 一般很小,常用光杠杆法先放大ΔL 再测量。
光杠杆装置是带有一个可旋转的平面镜的支架,平面镜的镜面与三个足尖决定的平面垂直,杠杆支脚与待测物接触。
当杠杆支脚随钢丝下降微小距离ΔL 时,镜面法线转过θ角,反射光线转动2θ角,当θ趋于0时(臂长为l )l /L tan ∆θθ=≈ (2)Dbtan =≈θθ22 (3) (D 为镜面到标尺的距离,b 是从望远镜中观察到的标尺移动的距离)由以上三式得到SlbDLFE 2=(4) 只要测量出L 、D 、l 和d (42/d S π=)及F 与b ,就可确定钢丝的杨氏模量E 。
实验仪器杨氏模量的测量装置包括光杠杆、砝码、望远镜和标尺。
实验装置如图所示,钢丝长约1m ,上端夹紧悬挂于支架顶部,下端夹在一个管制器底部,支架中部有一平台,平台中有一圆孔,管制器能在孔中上下移动,砝码加在管制器下的砝码托上,使金属丝伸长。
实验步骤1.调节仪器(1) 调节平台与望远镜的相对位置,使光杠杆镜面法线与望远镜轴线重合。
(2) 调节支架底脚螺丝,使平台水平;调节平台的竖直位置,使其上表面与管制器顶部共面。

一、实验目的1. 学习使用拉伸法测定钢丝的杨氏模量;2. 掌握光杠杆法测量微小伸长量的原理;3. 学会用逐差法处理实验数据;4. 学会计算不确定度,并正确表达实验结果。
二、实验原理杨氏模量(E)是材料在弹性限度内应力(σ)与应变(ε)的比值,即 E =σ/ε。
它是衡量材料刚度和抵抗形变能力的物理量。
本实验采用拉伸法测定钢丝的杨氏模量,利用光杠杆放大原理测量微小伸长量,通过计算得出杨氏模量。
三、实验仪器1. YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、砝码)2. 钢卷尺(0-200cm,0.1cm)3. 千分尺(0-150mm,0.02mm)4. 游标卡尺(0-25mm,0.01mm)5. 米尺四、实验步骤1. 调整杨氏模量测量仪,确保平台水平。
2. 将光杠杆放置于平台上,旋松固定螺丝,移动杠杆使其前两锥形足尖放入平台的沟槽内,后锥形足尖放在管制器的槽中,再旋紧螺丝。
3. 调节平面镜的仰角,使镜面垂直,即光杠杆镜面法线与望远镜轴线大致重合。
4. 利用望远镜上的准星瞄准光杠杆平面镜中的标尺刻度,调节望远镜的焦距,使标尺清晰可见。
5. 在钢丝下端悬挂砝码,使钢丝产生微小伸长。
6. 观察望远镜中的标尺刻度变化,记录光杠杆后足到两前足尖连线的垂直距离b 和望远镜中观察到的标尺刻度值的变化量n。
7. 重复步骤5和6,进行多次测量,记录数据。
8. 使用逐差法处理实验数据,计算杨氏模量的平均值。
五、数据处理1. 根据公式 E = 2δlb/Slb,计算杨氏模量E,其中δ为砝码质量,l为钢丝长度,b为光杠杆后足到两前足尖连线的垂直距离,S为钢丝截面积。
2. 计算不确定度,根据公式ΔE = Δδ/2δ + Δl/l + Δb/b + ΔS/S,其中Δδ、Δl、Δb、ΔS分别为δ、l、b、S的不确定度。
3. 根据计算结果,分析实验误差来源,讨论实验结果与理论值的差异。
六、实验结果与分析1. 通过实验,我们测定了钢丝的杨氏模量,计算结果为 E =2.02×10^5 MPa。


拉伸法测钢丝杨氏模量实验目的1. 掌握用光杠杆法测量微小量的原理和方法,并用以测定钢丝的杨氏模量;2. 掌握有效数字的读取、运算以及不确定度计算的一般方法.3. 掌握用逐差法处理数据的方法;4. 了解选取合理的实验条件,减小系统误差的重要意义.实验仪器YMC-l 型杨氏模量测定仪,如图所示(包括光杠杆、镜尺装置);量程为3m 或5m 钢卷尺;0-25mm 一级千分尺;分度值0.02mm 游标卡尺;水平仪;lkg 的砝码若干.1.标尺2.锁紧手轮3.俯仰手轮4.调焦手轮5.目镜6.内调焦望远镜7.准星8.钢丝上夹头9.钢丝 10.光杠杆 11.工作平台 12.下夹头 13.砝码 14.砝码盘 15.三角座 16.调整螺丝.实验原理设一粗细均匀的钢丝,长度为L 、横截面积为S ,沿长度方向作用外力F 后,钢丝伸长了ΔL .比值F /S 是钢丝单位横截面积上受到的作用力,称为应力;比值ΔL /L 是钢丝的相对伸长量,称为应变.根据胡克定律,在弹性限度内,钢丝的应力与应变成正比,即F L ES L ∆= 或 //F SE L L=∆ 式中E 称为杨氏模量,单位为N·m -2,在数值上等于产生单位应变的应力.由上式可知,对E 的测量实际上就是对F 、L 、S 、ΔL 的测量.其中F 、L 和S 都容易测量,而钢丝的伸长量ΔL 很小,很难用一般的长度测量仪器直接测量,因此ΔL 的准确测量是本实验的核心问题.本实验采用光杠杆放大法实现对钢丝伸长量ΔL 的间接测量.光杠杆是用光学转换放大的方法来实现微小长度变化的一种装置.它包括杠杆架和反射镜.杠杆架下面有三个支脚,测量时两个前脚放在杨氏模量测定仪的工作平台上,一个后脚放在与钢丝下夹头相连的活动平台上,随着钢丝的伸长(或缩短),活动平台向下(或向上)移动,带动杠杆架以两个前脚的连线为轴转动.设开始时,光杠杆的平面镜竖直,即镜面法线在水平位置,在望远镜中恰能看到标尺刻度s 0.当待测细钢丝受力作用而伸长ΔL 时,光杠杆的后脚下降ΔL ,光杠杆平面镜转过一较小角度θ,法线也转过同一角度θ,反射线转过2θ,此时在望远镜中恰能看到标尺刻度s 1(s 1为标尺某一刻度).由图可知2tan Ld θ∆=,1011tan 2s s s d d θ-∆== 式中,d 2为光杠杆常数(光杠杆后脚尖至前脚尖连线的垂直距离);d 1为光杠杆镜面至标尺的距离. 由于ΔL << d 2,Δs << d 1 ,偏转角度θ很小,所以近似地有θtan ≈θ2d L∆=,θ2tan θ2≈1101d s d s s ∆=-=由此可得 212d L s d ∆=∆ 实验中,外力F 由一定质量的砝码的重力产生,即F =mg ,钢丝横截面积为S =πD 2/4 (D 是钢丝直径),代入可得杨氏模量的计算公式:1228mgLd E D d s=π∆其中2d 1/ d 2为放大倍数,为保证大的放大倍数,实验时应有较大的d 1(一般为2m )和较小的d 2(一般为0.08m 左右). 将待测钢丝直径D 和原长L 、光杠杆镜面至标尺的距离d 1、光杠杆常数d 2、砝码产生的拉力mg 、以及对应的Δs 测出,便可计算出钢丝的杨氏模量E .实验内容1. 用千分尺测量钢丝的直径D ,在不同方位测六次,计算其不确定度;2. 用钢卷尺对钢丝的原长L (从支架上端钢丝上夹头开始到平台夹钢丝的下夹头之间的距离)及平面镜与标尺的距离d 1各测一次;3. 用游标卡尺测量光杠杆常数d 2一次;4. 采用逐个增加砝码和减去砝码的方法测量钢丝的伸长量,用逐差法求Δs 及其不确定度;5. 计算钢丝的杨氏模量E 及其不确定度,表达实验结果.实验步骤1. 杨氏模量测定仪的调整(1) 将待测钢丝固定好,调节杨氏模量仪的底脚螺丝,使两根支柱竖直,工作平台水平,并预加1-2块砝码使钢丝拉直;(2) 将光杠杆的两前脚放在工作平台的沟槽中,后脚放在下夹头的平面上,调整平面镜使镜面铅直.(3) 调节望远镜,使镜筒轴线水平,将其移近至工作平台,调节镜筒高度使其和平面镜等高,调好后将望远镜固定在支架上. 调整到平面镜法线和望远镜轴线等高共轴.(4) 移动望远镜支架距平面镜约2 m 处,调整标尺,使其竖直并与望远镜轴线垂直,且标尺0刻线与轴线等高. (5) 初步寻找标尺的像,从望远镜筒外观察平面镜中是否有标尺或镜筒的像,若没有,则左右移动望远镜、细心调节平面镜倾角,直到在平面镜中看到镜筒或标尺的像.(6) 调节望远镜找标尺的像.先调节目镜,看到清晰的十字叉丝,再调节调焦手轮,左右移动支架或转动方向,直到在望远镜中看到清晰的标尺刻线和十字叉丝.杠杆架反射镜固定平台砝码光杠杆结构图θθ光杠杆望远镜标尺s 0s 1d 1d 2ΔLθθΔs2. 用千分尺在不同方向、位置测量钢丝的直径D ,共测6次,测量前应先记录千分尺的零点读数;3. 用钢卷尺测量镜面到标尺的距离d 1;4. 在砝码钩上放上测量时要加的全部(共加7次)砝码(不包括预加的本底砝码)的一半(3-4块),细心调节平面镜倾角,使望远镜中看到的标尺像在零刻线附近,以保证在轴线附近的范围内测量.4. 去掉刚才所加的砝码,开始测量,记录初始值0s ',逐个增加砝码,记录每一步的读数i s ',再逐个减去砝码,记录每一步同一砝码数对应的读数i s '';5. 测量光杠杆常数d 2.可将光杠杆的三个脚放在数据记录纸上按下三个印,作连接前两脚的连线和后脚到该连线的垂线,用游标卡尺测量这一距离.6. 整理实验数据,交指导老师签字,整理仪器,完成实验.注意事项1. 实验系统调好后,一旦开始正式测量,在实验过程中不能再对系统任一部分进行任何调整,否则,所有数据将重新再测;2. 加减砝码时要轻拿轻放,槽口要相互错开,避免砝码钩晃动,在系统稳定后读数;3. 同一荷重(相同砝码数)下的两个读数要记在一起.增重与减重对应同一荷重下读数的平均值才是对应荷重下的最佳值,它消除了摩擦(圆柱体与圆孔之间的摩擦)与滞后(加减砝码时钢丝伸长与缩短滞后)等引起的系统误差.4. 实验完成后,应将砝码取下,防止钢丝疲劳.数据记录表一 L 、d 1、d 2测量数据表 单位: mm表二 钢丝直径D 的测量数据表千分尺零点读数 =仪ε mm 单位: mm表三 Δs 的测量数据表 单位:mm数据处理1.计算每增加一块砝码(1kg)的钢丝伸长量Δs 的最佳值及不确定度 (1) Δs 的最佳值(用逐差法))(41041s s s -=∆;)(41152s s s -=∆;)(41263s s s -=∆;)(41374s s s -=∆;)(414321s s s s s ∆+∆+∆+∆=∆(2) 计算 的实验标准差: ()Ss ∆= (3) 计算 平均值的实验标准差: ()S s ∆=(4) 标尺的示值极限误差: Δm=0.5mm(5) 合成不确定度:()u s ∆==2.D 的最佳值及不确定度的计算(1) D 的最佳值: ∑==6161i i D D(2) 计算D 的实验标准差: ()S D =(3) 计算 D 平均值的实验标准差: ()S D = (4) 千分尺的的示值极限误差:Δm =0.004mm(5) 计算D 的合成不确定度: ()u D ==3. E 的最佳值的计算和不确定度的计算 (1) E 的最佳值的计算: sd D mgLd E ∆=2218π(2) E 的合成不确定度的计算取u (d 2)=0.02mm ,u (d 1)=5mm , u (L )=5mm ,及2和3中的不确定度得到E S S u D D u L L u d d u d d u E u ⋅⎪⎭⎫⎝⎛∆∆+⎪⎭⎫ ⎝⎛+⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫ ⎝⎛=222222211)()(2)()()()((3) E 的相对不确定度的计算,将实验值与 E 的公认值 E 0=2.05×1011 N ·m -2比较,计算其相对不确定度:()100%EE E E =⨯。


大学物理实验-拉伸法测钢丝的杨氏模量(已批阅)-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN实验题目:用拉伸法测钢丝的杨氏模量 13+39+33=85实验目的:采用拉伸法测定杨氏模量,掌握利用光杠杆测定微小形变地方法。
在数据处理中,掌握逐差法和作图法两种数据处理的方法实验仪器: 杨氏模量测量仪(包括光杠杆,砝码,望远镜,标尺),米尺,螺旋测微计。
实验原理:在胡克定律成立的范围内,应力F/S 和应变ΔL/L 之比满足 E=(F/S )/(ΔL/L )=FL/(S ΔL )其中E 为一常量,称为杨氏模量,其大小标志了材料的刚性。
根据上式,只要测量出F 、ΔL/L 、S 就可以得到物体的杨氏模量,又因为ΔL 很小,直接测量困难,故采用光杠杆将其放大,从而得到ΔL 。
实验原理图如右图:当θ很小时,l L /tan ∆=≈θθ,其中l 是光杠杆的臂长。
由光的反射定律可以知道,镜面转过θ,反射光线转过2θ,而且有:Db =≈θθ22tan故:)2(D b lL =∆,即是)2(D bl L =∆那么SlbDLFE 2=,最终也就可以用这个表达式来确定杨氏模量E 。
实验内容: 1.调节仪器(1) 调节放置光杠杆的平台F 与望远镜的相对位置,使光杠杆镜面法线与望远镜轴线大体重合。
(2) 调节支架底脚螺丝,确保平台水平,调平台的上下位置,使管制器顶部与平台的上表面共面。
(3) 光杠杆的调节,光杠杆和镜尺组是测量金属丝伸长量ΔL 的关键部件。
光杠杆的镜面(1)和刀口(3)应平行。
使用时刀口放在平台的槽内,支脚放在管制器的槽内,刀口和支脚尖应共面。
(4) 镜尺组的调节,调节望远镜、直尺和光杠杆三者之间的相对位置,使望远镜和反射镜处于同等高度,调节望远镜目镜视度圈(4),使目镜内分划板刻线(叉丝)清晰,用手轮(5)调焦,使标尺像清晰。
2.测量(1) 砝码托的质量为m 0,记录望远镜中标尺的读数r 0作为钢丝的起始长度。

拉伸法测金属丝的杨氏模量实验报告引言:杨氏模量是描述某物质材料在受到拉伸或压缩时,弹性变形程度大小的一个物理量。
在实际应用中,杨氏模量常用于描述金属、合金、非晶态材料等材料的弹性特性。
在本次实验报告中,我们将通过拉伸法测量金属丝的杨氏模量。
实验目的:1. 了解拉伸法测定金属丝杨氏模量的基本原理。
2. 掌握拉伸法测定金属丝杨氏模量的实验方法。
3. 掌握实验数据的处理方法,确定金属丝的杨氏模量。
实验原理:当杆(或丝)在轴向受到拉伸力 F 后,其长度增加ΔL,应变为 E。
定义贯穿力 F、应变 E 和初始长度 L 的比值为一项物理量,称为杨氏模量 Y。
根据杨氏定律可得:$$ Y = \frac {F/A} {\Delta L/L} $$其中 A 为截面面积。
实验步骤:1. 用细钢丝制备试件,长度大于两倍的所需要的长度。
2. 将一个试件端固定,另一端悬挂一重物,使得钢丝呈直线状,测试钢丝的长度L0。
3. 用万能测量仪测试钢丝悬挂重物后的长度 L1。
4. 根据悬挂的重量计算钢丝的拉力 F。
5. 重复以上步骤,重复至少三次,记录不同重量下的拉力及钢丝的长度变化。
6. 计算每个拉力及钢丝长度变化的平均值,并绘制拉力-长度变化曲线。
7. 根据拉力-长度变化曲线计算钢丝杨氏模量 Y。
实验数据及处理:重量(kg)|拉力F(N)|长度变化ΔL(mm)|-|-|-|0.001|0.0098|0.15|0.002|0.0196|0.30|0.003|0.0294|0.45|0.004|0.0392|0.60|0.005|0.0490|0.74|计算钢丝的杨氏模量:平均截面积A = πd^2/4 = π(0.18mm)^2/4 = 2.54×10^(-5)m^2计算平均应变 E 平均长度变化ΔL/L =(0.15mm+0.30mm+0.45mm+0.60mm+0.74mm)/(200mm) = 0.0025E = ΔL/L = 0.0025/5 = 0.0005计算杨氏模量 Y Y = F/A/E =(0.0098N+0.0196N+0.0294N+0.0392N+0.0490N)/(5×2.54×10^(-5)m^2×0.0005) =1.96×10^11 Pa实验结果:经过实验测试,我们得到了金属丝的杨氏模量为 1.96×10^11 Pa。

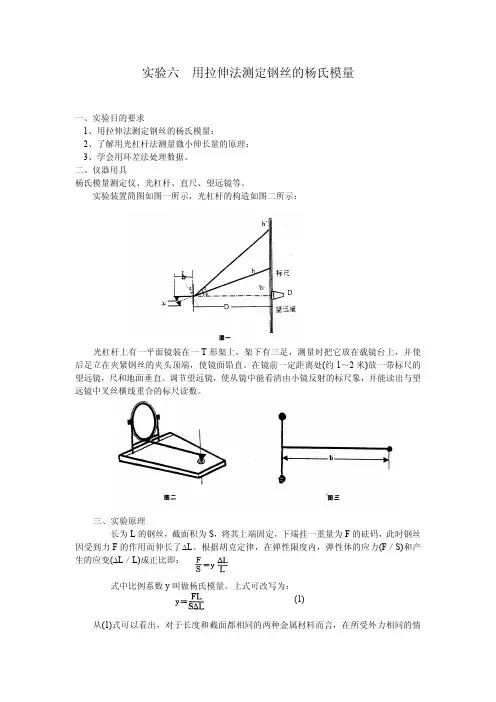
实验六用拉伸法测定钢丝的杨氏模量一、实验目的要求1、用拉伸法测定钢丝的杨氏模量:2、了解用光杠杆法测量微小伸长量的原理:3、学会用环差法处理数据。
二、仪器用具杨氏模量测定仪、光杠杆、直尺、望远镜等。
实验装置简图如图一所示,光杠杆的构造如图二所示:光杠杆上有一平面镜装在一T形架上,架下有三足,测量时把它放在载镜台上,并使后足立在夹紧钢丝的夹头顶端,使镜面铅直。
在镜前一定距离处(约1~2米)放一带标尺的望远镜,尺和地面垂直。
调节望远镜,使从镜中能看清由小镜反射的标尺象,并能读出与望远镜中叉丝横线重合的标尺读数。
三、实验原理长为L的钢丝,截面积为S,将其上端固定,下端挂一重量为F的砝码,此时钢丝因受到力F的作用而伸长了∆L。
根据胡克定律,在弹性限度内,弹性体的应力(F/S)和产生的应变(∆L/L)成正比即:式中比例系数y叫做杨氏模量。
上式可改写为:(1)从(1)式可以看出,对于长度和截面都相同的两种金属材料而言,在所受外力相同的情况下,杨氏模量大的一种材料变形∆L就小,杨氏模量小的变形就大,因此杨氏模量表示了材料抵抗形变的能力。
本实验是通过对L、S、及∆L的测量(F给定),按(1)式计算,从而测定钢丝的杨氏模量。
但由于∆L是一微小的长度变化量,不易直接测准,为此我们借助于光学放大的方法——光杠杆来测量。
在钢丝已被拉直的情况下,假定初始读数为h0,当在砝码盘上再加若干砝码时,钢丝由悬点到夹头一般将伸长∆L,同时光杠杆的后足也要随之向下移动∆L,因而使镜面向后抑了一微小角度φ,此时望远镜中标尺的读数也相应地变为h'(见图一)。
由光的反射定律知,设光杠杆两前足连线到后足的距离为b(见图),镜面到标尺的垂直距离为D,h'与h0间的距离为h,当长度变化量∆L很小时,由此可得:(2)可见通过光杠杆,∆L被放大了倍,将(2)式代人(1)式得:(3)若钢丝的直径为d,则(3)式可写成(4)在上述实验装置中,(4)式中L、D、d和b各量都是定值,唯有h随悬挂砝码重量F的增减作相应的改变。
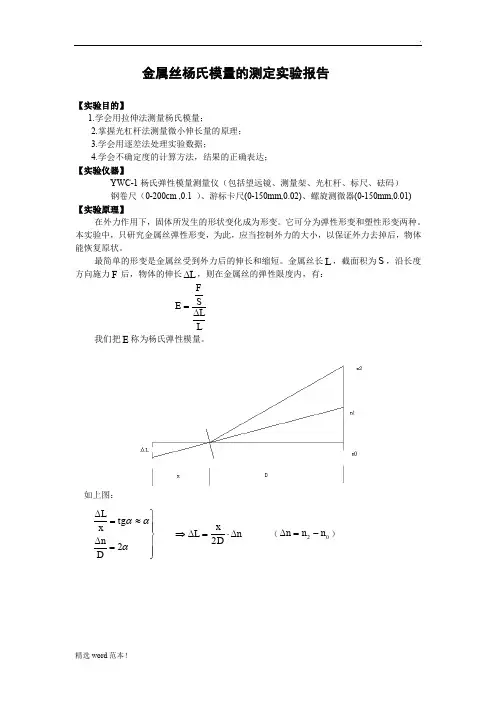
金属丝杨氏模量的测定实验报告【实验目的】1.学会用拉伸法测量杨氏模量;2.掌握光杠杆法测量微小伸长量的原理;3.学会用逐差法处理实验数据;4.学会不确定度的计算方法,结果的正确表达;【实验仪器】YWC-1杨氏弹性模量测量仪(包括望远镜、测量架、光杠杆、标尺、砝码) 钢卷尺(0-200cm ,0.1 )、游标卡尺(0-150mm,0.02)、螺旋测微器(0-150mm,0.01)【实验原理】在外力作用下,固体所发生的形状变化成为形变。
它可分为弹性形变和塑性形变两种。
本实验中,只研究金属丝弹性形变,为此,应当控制外力的大小,以保证外力去掉后,物体能恢复原状。
最简单的形变是金属丝受到外力后的伸长和缩短。
金属丝长L ,截面积为S ,沿长度方向施力F 后,物体的伸长L ∆,则在金属丝的弹性限度内,有:FS E LL=∆ 我们把E 称为杨氏弹性模量。
如上图:⎪⎪⎭⎪⎪⎬⎫=∆≈=∆ααα2D n tg x L n D x L ∆⋅=∆⇒2 (02n n n -=∆)n x d FLD Ln Dx d FL L S F E ∆⋅=∆=∆=228241ππ 真实测量时放大倍数为4倍,即E=2E【实验内容】<一> 仪器调整1、杨氏弹性模量测定仪底座调节水平;2、平面镜镜面放置与测定仪平面垂直;3、将望远镜放置在平面镜正前方1.5-2.0m 左右位置上;4、粗调望远镜:将镜面中心、标尺零点、望远镜调节等高,望远镜的缺口、准星对准平面镜中心,并能在望远镜外看到尺子的像;5、调节物镜焦距能看到尺子清晰的像,调节目镜焦距能清晰的看到叉丝;6、调节叉丝在标尺cm 2±以内,并使得视差不超过半格。
<二>测量1、 记下无挂物时刻度尺的读数0n ;2、依次挂上100g 的砝码,8次,计下7654321,,,,,,n n n n n n n ;3、依次取下100g 的砝码,8次,计下n 0‘,'7'65'4'3'2'1,,,,,,'n n n n n n n ; 4、用米尺测量出金属丝的长度L (两卡口之间的金属丝)、镜面到尺子的距离D ;5、用游标卡尺测量出光杠杆x 、用螺旋测微器测量出金属丝直径d 。
用拉伸法测钢丝杨氏模量——实验报告实验报告:用拉伸法测钢丝杨氏模量引言:拉伸试验是一种重要的材料力学测试方法,用于测量物体的杨氏模量。
钢丝作为一种常用的结构材料,其强度和刚度是工业应用的关键指标。
本实验旨在采用拉伸法来测量钢丝的杨氏模量,并通过实验结果来验证钢丝的力学性能。
实验原理:拉伸试验是通过对材料施加拉力,观察其应变与应力之间的关系来测量杨氏模量。
根据胡克定律,应变与应力之间的关系可以用以下公式表示:$$E = \frac{\sigma}{\varepsilon}$$其中,E为杨氏模量,$\sigma$为应力,$\varepsilon$为应变。
实验步骤:1. 准备工作:清洁并标识钢丝样品,准备拉力计、卡尺、示波器等实验设备。
2. 固定材料:将钢丝夹紧在拉力计上,确保钢丝受力均匀且垂直于拉力计。
3. 测量初始长度:使用卡尺测量钢丝的初始长度$L_0$,并记录。
4. 施加拉力:逐渐增加拉力施加在钢丝上,保持拉力保持稳定后记录下拉力计示数。
5. 测量应变:通过示波器等设备,测量钢丝的伸长量$\Delta L$。
6. 计算应变率:根据公式$\varepsilon = \frac{\Delta L}{L_0}$,计算出钢丝的应变率。
7. 计算应力:根据公式$\sigma = \frac{F}{A}$,计算出钢丝的应力,其中$F$为施加在钢丝上的拉力,$A$为钢丝的横截面积。
8. 绘制应力-应变曲线:将应变作为横坐标,应力作为纵坐标,绘制出钢丝的应力-应变曲线。
9. 计算杨氏模量:根据公式$E = \frac{\sigma}{\varepsilon}$,通过应力-应变曲线确定杨氏模量。
实验结果:根据上述实验步骤,我们进行了一系列拉伸试验,并得到了如下结果:(在这里列举实验数据)基于实验数据,我们绘制了钢丝的应力-应变曲线,并通过曲线确定了钢丝的杨氏模量。
讨论与结论:通过本实验,我们成功应用拉伸法测量了钢丝的杨氏模量。
用拉伸法测定钢丝的杨氏模量將理專验中心一•实验目的实验原理注意事项实验内容数据处理实验目的丄了解杨氏模量的物理概念,掌握其测量原理和方法。
丄学会用光杠杆测量微小伸长量的方法O实验原理一.胡克定律在外力作用下,固体所发生的形状变化称为形变。
形变可分为:弹性形变:外力撤除后,物体能完全恢复原状的形变。
范氏形变:外力较大,撤除后物体不能完全恢复原状,而留下剩余形变。
=1本实验只研究弹性形变。
最简单的弹性形变是棒状物体受外力后的拉长和缩短。
设物体的原长为厶横截面积为S,当在长度方向施加外力耐,其伸长 (或缩短)AL o按照胡克定律,在弹性限度内,物体的协强(F/S)与协变(AL/L)成正比。
二•杨氏模量条形物体(如钢丝)沿纵向的弹性模量叫杨氏模量。
测量杨氏模量的方法有:拉伸法、梁的弯曲法、振动 法、内耗法等等,本实验采用拉伸法测定杨氏模量。
比例系数E == ~~称为杨氏模量。
謎熬楚料性质的一个物理量,仅与材料的结构、化 学成分及其加工制造方法有关。
I=. J <l=. J三•光杠杆装置及放大原理小平面镜泌同直尺、望远镜共同构成光杠杆装置,它可把微小长度变化放大。
说雌线方向水平时,望远镜中看到的直尺上的相应刻度。
①为当钢丝因悬挂重物而下降21乙导致M的法线方向改变么角时,从望远镜中看到的直尺上的相应刻度。
b—平面镜M后一个支点到前两个支点的距离R—镜面到尺面的距离rm 亠小An n. —贝!l 有: -------------------- tg2oc = = -R R因为么角很小,故有:tga =a ;tgla = 2a・& = △</・一山/ b最后得:△乙= ----- A AZ =----------- (/?[—--- )AZ7 ~ b 42yreg)M*2R 2R V 1 07本实验的放大倍数:几十倍,R为1至2米;b为5至8 厘米.由前实验装置分析:厂F・L・FL 2LRF"5*AL"s^(H1-n o)"Z?S^-n o) 又:S = t";F =Mg 令:N = /\n = n i—n Q则:2LRMgb-7rD2N4*MgLR 7i E)2bN1 •调整杨氏弹性模量仪的支架底角螺旋H,使支架铅直(由支架的铅锤或水平气泡来确定),然后加重2千克(不记入作用力F内)将钢丝拉直,测量钢丝长度L。
拉伸法测量杨氏模量实验报告实验报告:拉伸法测量杨氏模量一、实验目的1.掌握拉伸法测量杨氏模量的原理和方法。
2.学会使用相关设备和测量仪器。
3.通过对实验数据的分析,提高实验数据处理和误差分析的能力。
二、实验原理杨氏模量是描述材料在弹性范围内受力时,应力与应变之间关系的物理量。
拉伸法测量杨氏模量是通过测量材料在拉伸力作用下的伸长量,结合应力-应变关系计算杨氏模量。
三、实验步骤1.准备实验器材:钢丝、张力计、尺子、砝码、支架、测量仪器等。
2.将钢丝固定在支架上,确保钢丝水平。
3.将张力计连接到钢丝上,并调整张力计至零点。
4.逐个增加砝码,并记录相应的伸长量。
5.重复实验,获取多组数据。
6.将实验数据输入测量仪器,计算杨氏模量。
7.分析实验数据,得出结论。
四、实验结果与数据分析实验数据如下表所示:根据实验数据,我们可以绘制出应力-应变曲线图。
横坐标为砝码质量(g),表示应力;纵坐标为钢丝伸长量(cm),表示应变。
通过该曲线图,我们可以直观地观察到应力和应变之间的关系。
通过测量仪器,我们可以计算出杨氏模量。
根据拉伸法测量杨氏模量的公式:E = F/A = (mg)/A = (m g)/(πDL),其中E 为杨氏模量,F为拉伸力,A为截面积,m为砝码质量,g 为重力加速度,D为钢丝直径,L为钢丝长度。
将实验数据代入公式进行计算,得到杨氏模量的值。
最后,将多组实验数据进行平均处理,得到最终的杨氏模量值。
五、结论与讨论通过本次实验,我们掌握了拉伸法测量杨氏模量的原理和方法,学会了使用相关设备和测量仪器。
通过对实验数据的分析,我们得出以下结论:钢丝的杨氏模量为XX×10³N/m²。
实验结果与理论值相符,表明我们的实验操作和数据处理是正确的。
同时,我们也发现实验中存在一些误差,如砝码质量测量误差、钢丝直径和长度测量误差等。
这些误差可能会对实验结果产生一定的影响。
为了减小误差,我们可以在实验中采用更高精度的测量仪器和更准确的测量方法。
用拉伸法测钢丝杨氏模量实验报告【实验目的】【实验仪器】杨氏弹性模量测定仪;光槓杆;望远镜及直尺;千分尺;游标卡尺;米尺;待测钢丝;砝码等。
【实验原理】1.杨氏弹性模量y是材料在弹性限度内应力与应变的比值,即杨氏弹性模量反映了材料的刚度,是度量物体在弹性範围内受力时形变大小的因素之一,是表徵材料机械特性的物理量之一。
2.光槓杆原理伸长量δl比较小,不易测準,本实验利用了光槓杆的放大原理对δl进行测量。
利用光槓杆装置后,杨氏弹性模量y可表示为:式中,f是钢丝所受的力,l是钢丝的长度,l是镜面到标尺间的距离,d 是钢丝的直径,b是光槓杆后足到两前足尖连线的垂直距离,δn是望远镜中观察到的标尺刻度值的变化量。
3. 隔项逐差法隔项逐差法为了保持多次测量优越性而採用的资料处理方法。
使每个测量资料在平均值内都起到作用。
本实验将测量资料分为两组,每组4个,将两组对应的资料相减获得4个δn,再将它们平均,由此求得的δn是f增加4千克力时望远镜读数的平均差值。
【实验步骤】1.调整好杨氏模量测量仪,将光槓杆后足尖放在夹紧钢丝的夹具的小圆平台上,以确保钢丝因受力伸长时,光槓杆平面镜倾斜。
2.调整望远镜。
调节目镜,使叉丝位于目镜的焦平面上,此时能看到清晰的叉丝像;调整望远镜上下、左右、前后及物镜焦距,直到在望远镜中能看到清晰的直尺像。
3.在钢丝下加两个砝码,以使钢丝拉直。
记下此时望远镜中观察到的直尺刻度值,此即为n0 值。
逐个加砝码,每加1个,记下相应的直尺刻度值,直到n7,此时钢丝下已悬挂9个砝码,再加1个砝码,但不记资料,然后去掉这个砝码,记下望远镜中直尺刻度值,此为n7’,逐个减砝码,每减1个,记下相应的直尺刻度值,直到n0’。
4. 用米尺测量平面镜到直尺的距离l;将光槓杆三足印在纸上,用游标卡尺测出b;用米尺测量钢丝长度l;用千分尺在钢丝的上、中、下三部位测量钢丝的直径d,每部位纵、横各测一次。
5. 测量完毕,整理各量具和器具。
一•实验目的
实验原理注意事项实验
内容数据处理
实验目的
丄了解杨氏模量的物理概念,掌握其测量原理和方法。
丄学会用光杠杆测量微小伸长量的方法O
实验原理
一.胡克定律
在外力作用下,固体所发生的形状变化称为形变。
形变可分为:弹性形变:外力撤除后,物体能完全恢复原状的形变。
范氏形变:外力较大,撤除后物体不能完全恢复原状,而留下剩余形变。
=1
本实验只研究弹性形变。
最简单的弹性形变是棒状物体受外力后的拉长和缩短。
设物体的原长为厶横截面积为S,当在长度方向施加外力耐,其伸长 (或缩短)AL o
按照胡克定律,在弹性限度内,物体的协强(F/S)与协变(AL/L)成正比。
二•杨氏模量
条形物体(如钢丝)沿纵向的弹性模量叫杨氏模量。
测量杨氏
模量的方法有:拉伸法、梁的弯曲法、振动 法、内耗法等等,本
实验采用拉伸法测定杨氏模量。
比例系数E =
= ~~称为杨氏模量。
謎熬楚料性质的一个物理量,仅与材料的结构、化 学成分及其
加工制造方法有关。
I=. J <
l=. J
2yr
本实验的放大倍数:几十倍,R为1至2米;b为5至8 厘米.
eg) M‘
\
\ M
\a
由前实验装置分析:
厂F
・L・FL 2LRF
"5*AL"s^(H1-n o)"Z?S^-n o) 又:S = t"; F = Mg 令:N = /\n = n{—n Q
则:
2LRMg
b-7rD2N
4
*MgLR 7i E)2bN
1 •调整杨氏弹性模量仪的支架底角螺旋H,使支架铅直(由支架的铅锤或
水平气泡来确定),然后加重2千克(不记入作用力F内)将钢丝拉直,测量钢丝长度L。
2.调节光杠杆装置。
(1)粗调
(2)细调
3. ---------------------------------------------------------------- 记下开始时望远镜中标尺的读数比o ,然后每增加500g祛码记录一次标尺读数,则标尺读数依次为® 小2,------------------------------------- ,n iO,直到增加了5000g 为止。
4•依次减少祛码,每次减500g ,分别记录各次所对应的标尺读数'卅
9,直到。
5.在不同位置对钢丝直径D测6次,并测量标尺到镜面的距离R及光杠杆
后支点到前两个支点的垂直距离b o
注意事项
丄充分重视光杠杆的粗调。
丄增减祛码时要轻放轻取,以防冲击和摆
动,应等标尺稳定后才可读数。
标尺读数若在零点两侧,应区分正负。
丄因祛码的重心不在其几何中心,所以要正确摆放祛码,以保证钢丝上悬挂的祛码串的稳定。
申逐差法
一般用于自变量等间隔测量且其测量误差可以略去情况下的数据处理。
优点是:充分利用各个测量数据,减小测量误差和扩大测量范围。
应用的一般条件是:处理等间隔线性变化的测量数据。
例如:声速的测定实验中,用行波法测量声波波长的以下一列数据:N1234567910
Xi X2X3X4X5“X7X8X9X10如果简单的将每一个波峰的距离直接计算出来,有:
—1 1
心二。
[(兀2 _兀1) + (兀3 _尤2)+ (兀4 _兀3)+…+ (兀10 _吗)]二0(兀10_兀1)由上式可以看出只有始末两次测量值起了作用,等效于只测E和X"。
为了充分利用测量数据,减小测量误差,应釆用逐差法:
(1)将测量列按次序分为高低两组
兀1,兀2,•…,毛兀6,兀7,…,兀10
(2)取对应项的差值后再求平均:
—1
A% =—[(兀6 _兀1 ) + (兀7 一兀)+ (兀8 _兀3)+・…+ (兀10 _兀5)]
€哄+勺+耳+兀9+心)-(坷+兀2+也+兀+乞)]..
其中Ax为5个峰值间的距离,即:2二Ax/5。