统计学第二章均值向量和协方差阵的检验.
- 格式:ppt
- 大小:1.20 MB
- 文档页数:81



第一章 多元正态分布的参数估计一、填空题1。
设X 、Y 为两个随机向量,对一切的u 、v,有 ,则称X 与Y 相互独立。
2。
多元分析处理的数据一般都属于 数据。
3.多元正态向量()'=p X X X ,,1 的协方差阵∑是 ,则X 的各分量是相互独立的随机变量。
4.一个p 元函数()p x x x f ,,,21 能作为pR 中某个随机向量的密度函数的主要条件是和 。
5.若p 个随机变量1X ,2X , ,p X 的联合分布等于 ,则称1X ,2X , ,p X 是相互独立的。
6。
多元正态分布的任何边缘分布为 。
7。
若()∑,~μp N X ,A 为p s ⨯阶常数阵,d 为s 维常数向量,则~d AX + 。
8.多元正态向量X 的任何一个分量子集的分布称为X 的 . 9.多元样本中,不同样品的观测值之间一定是 。
10。
多元正态总体均值向量和协差阵的极大似然估计量分别是 。
11.多元正态总体均值向量μ和协差阵∑的估计量X 、S n 11-具有 、 和 。
12.设X 和S 分别是多元正态总体()∑,μp N 的样本均值向量和离差阵,则~X ,X 和S 。
13。
若()()∑,~μαp N X ,n ,,2,1 =α且相互独立,则样本离差阵()()()()∑='--=nX X X X S 1~ααα .14.若()∑,~i p i n W S ,k i ,,1 =,且相互独立,则~21k S S S S +++= 。
二、判断题1。
多元分布函数()x F 是单调不减函数,而且是右连续的。
2.设X 是p 维随机向量,则X 服从多元正态分布的充要条件是:它的任何组合()p R X ∈'αα都是一元正态分布.3。
μ是一个P 维的均值向量,当A 、B 为常数矩阵时,具有如下性质: (1)E (AX )=AE (X ) (2)E (AXB)=AE (X )B4.若P 个随机变量X 1,…X P 的联合分布等于各自边缘分布的乘积,则称X 1,… X P 是相互独立的。

多元统计分析——均值向量和协方差阵检验均值向量检验是评估两个或多个总体均值是否相等的方法。
在多元统计分析中,均值向量检验常用于比较不同组别或条件下的均值是否有差异。
假设有k个样本组别,每个组别有n个观测值,那么总共有nk个观测值。
假设每个观测值有p个测量变量,那么每个样本组别的均值向量可以表示为一个p维的向量。
我们的目标是比较这k个均值向量是否相等。
常用的均值向量检验方法有Hotelling's T-squared统计量和Wilks' Lambda统计量。
Hotelling's T-squared统计量是基于方差-协方差阵的一个推广,它考虑了样本组别的大小和协方差结构。
它的计算公式为:T^2=n(p-k)/(k(n-1))*(x1-x)^TS^(-1)(x1-x)其中,n是每个组别的观测数,p是变量的个数,k是组别的个数,x1是第一个组别的均值向量,x是总体均值向量,S是协方差阵。
T^2的分布是一个自由度为k,维度为p的非中心F分布。
Wilks' Lambda统计量是基于协方差阵的特征值的一个变换,它的计算公式为:Lambda = ,W,/,B其中,W是所有组别的散布矩阵(Within-groups scatter matrix),B是总体的散布矩阵(Between-groups scatter matrix)。
Wilks' Lambda的分布是一个自由度为k和n-k-1的F分布。
协方差阵检验是评估两个或多个总体协方差阵是否相等的方法。
在多元统计分析中,协方差阵检验常用于比较不同组别或条件下的变量之间的协方差结构是否有差异。
假设有k个样本组别,每个组别有n个观测值,那么总共有nk个观测值。
假设每个观测值有p个测量变量,那么每个样本组别的协方差阵可以表示为一个p维的矩阵。
我们的目标是比较这k个协方差阵是否相等。
常用的协方差阵检验方法有Hotelling-Lawley's Trace统计量和Pillai-Bartlett's Trace统计量。


均值向量和协方差阵的检验实验报告嘿,大家好!今天咱们聊聊一个听上去挺高大上的话题,均值向量和协方差阵的检验。
这听起来就像在说外星人的语言,其实也没那么复杂,咱们慢慢来,轻松愉快地搞定它。
想象一下你在和朋友聚会,大家都在聊各自的生活,分享自己的故事。
每个人的经历就像一组数据,有的高高兴兴,有的郁郁寡欢,这些故事就形成了一个均值向量。
均值向量呢,就是这些故事的“平均水平”,能告诉我们大家的普遍状况。
比如说,某个朋友总是出去旅游,那他在这个聚会里的均值肯定就比其他人高。
这其实很有趣,感觉每个人的生活就像一根根串珠,串在一起的就是大家的均值。
再说到协方差阵,这玩意儿就像一个大网,把每个人的故事串联起来。
它能告诉你不同数据之间的关系。
想象一下,你和你的小伙伴经常一起吃饭,这种关系就像是协方差阵的体现。
它不仅仅告诉你们的吃饭频率,还能分析出你们吃什么、什么时候吃,以及这段友情对你们生活的影响。
换句话说,协方差阵帮我们理解这些数据是怎么互动的。
在我们的实验中,咱们主要是想检验一下这些均值和协方差是不是合理。
这时候,就需要一些统计的方法。
大家可能会觉得统计是个无聊的领域,满是公式和计算,简直让人打哈欠。
其实不然,这个过程就像侦探在寻找证据,解决一个个谜团。
我们拿到数据,就像是拿到了一张藏宝图。
通过计算均值、协方差,咱们一点点挖掘出其中的秘密。
检验均值向量和协方差阵的过程可不简单,得用到一些统计检验的方法,比如t检验和卡方检验。
这些方法就像是咱们的工具箱,各种工具都有其独特的用途。
有的用来比较均值,有的用来检查数据的分布。
想象一下,一个厨师在厨房里忙碌,调料、锅具、食材各司其职,最后做出一顿美味的大餐。
咱们在统计的世界里也是如此,得心应手才能得出正确的结论。
在这个过程中,数据可得经过一番“洗礼”。
有时,咱们会发现数据里藏着一些“异常值”,这些就像是在聚会上讲冷笑话的人,让人哭笑不得。
为了让我们的结果更靠谱,就得把这些“冷笑话”给去掉,保持数据的干净整洁。

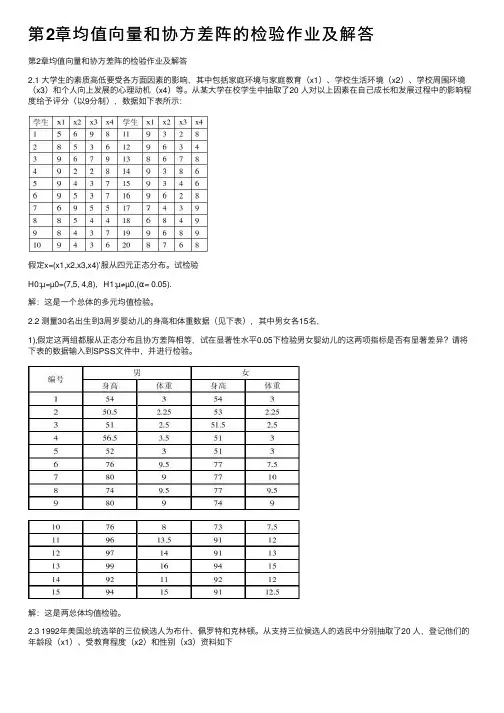
第2章均值向量和协⽅差阵的检验作业及解答
第2章均值向量和协⽅差阵的检验作业及解答
2.1 ⼤学⽣的素质⾼低要受各⽅⾯因素的影响,其中包括家庭环境与家庭教育(x1)、学校⽣活环境(x2)、学校周围环境(x3)和个⼈向上发展的⼼理动机(x4)等。
从某⼤学在校学⽣中抽取了20 ⼈对以上因素在⾃⼰成长和发展过程中的影响程度给予评分(以9分制),数据如下表所⽰:
假定x=(x1,x2,x3,x4)’服从四元正态分布。
试检验
H0:µ=µ0=(7,5, 4,8),H1:µ≠µ0,(α= 0.05).
解:这是⼀个总体的多元均值检验。
2.2 测量30名出⽣到3周岁婴幼⼉的⾝⾼和体重数据(见下表),其中男⼥各15名,
1),假定这两组都服从正态分布且协⽅差阵相等,试在显著性⽔平0.05下检验男⼥婴幼⼉的这两项指标是否有显著差异?请将下表的数据输⼊到SPSS⽂件中,并进⾏检验。
解:这是两总体均值检验。
2.3 1992年美国总统选举的三位候选⼈为布什、佩罗特和克林顿。
从⽀持三位候选⼈的选民中分别抽取了20 ⼈,登记他们的年龄段(x1)、受教育程度(x2)和性别(x3)资料如下
1),假定三组都服从多元正态分布,检验这三组的总体均值是否有显著性差异(α=0.05)。
2),检验三位候选⼈的协差阵是否相等(α=0.05)。
解:这是多总体均值检验。

统计学课后题第二章均值向量和协方差阵的检验1、试谈willks统计量在多元方差分析中的重要意义。
2、形象分析的基本思路是什么?形象又称轮廓图,是将总体样本的均值绘制到同一坐标轴里所得的折线图,每一个指标都表示为折线图上的一点。
形象分析是将两总体的形象绘制到同一个坐标下,根据形象的形状对总体的均值进行比较分析。
第三章聚类分析1、聚类分析的基本思想和功能是什么?聚类分析的核心思想是根据具体的指标对所研究的个体或者对象进行分类,使得同一类中的对象之间的相似性比其他类的对象的相似性更强。
聚类分析不仅可以用来对样品进行分类,也可以用来对变量进行分类。
对样品的分类常称为Q型聚类分析,对变量的分类常称为R型的聚类分析。
聚类分析的目的或功能就是把相似的研究对象归成类,即使类间对象的同质性最大化和类与类间对象的异质性最大化。
2、试述系统聚类法的原理和具体步骤系统聚类的基本思想是:距离相近的样品先聚成类,距离相远的后聚成类,过程一直进行下去,每个样品总能聚到合适的类中。
系统聚类的具体步骤:假设总共有N个样品第一步:将每个样品独自聚成一类,共有N类;第二步:根据所确定的样品“距离”公式,把距离较近的两个样品聚合为一类,其他的样品仍各自聚为一类,共聚成N-1类;第三步:将“距离”最近的两个类进一步聚成一类,共聚成N-2类;。
,以上步骤一直进行下去,最后将所有的样品全聚成一类。
3、试述K-均值聚类的方法原理这种聚类方法的思想是把每个样品聚集到其最近形心类中。
首先随机从数据集中选取 K个点作为初始聚类中心,然后计算各个样本到聚类中的距离,把样本归到离它最近的那个聚类中心所在的类。
计算新形成的每一个聚类的数据对象的平均值来得到新的聚类中心,如果相邻两次的聚类中心没有任何变化,说明样本调整结束,聚类准则函数已经收敛。
4、试述模糊聚类的思想方法模糊聚类分析是根据客观事物间的特征、亲疏程度、相似性,通过建立模糊相似关系对客观事物进行聚类的分析方法。
