均值向量和协方差阵的检验

霍特林统计量霍特林统计量（Hotelling's T-squared statistic）是多元统计分析中常用的一种统计量，用于评估两组或多组样本之间的差异性。

它是通过测量样本均值与总体均值之间的差异性来判断样本是否来自同一总体。

本文将介绍霍特林统计量的原理和应用，并探讨其在实际问题中的意义。

霍特林统计量的计算方法相对复杂，但我们可以通过一个简单的例子来说明其基本原理。

假设我们有两个不同的群体A和B，每个群体都有若干个观测值。

我们希望知道这两个群体之间是否存在显著差异。

首先，我们需要计算每个群体的均值向量和协方差矩阵。

然后，我们可以使用这些统计量来计算霍特林统计量。

霍特林统计量的计算公式如下：T^2 = n * (x̄_A - x̄_B)^T * S^(-1) * (x̄_A - x̄_B)其中，n是每个群体的样本量，x̄_A和x̄_B分别是群体A和B的均值向量，S是两个群体的协方差矩阵的加权平均。

霍特林统计量的值越大，表示两个群体之间的差异性越大。

当我们进行假设检验时，可以使用F分布来计算p值，进而判断两个群体之间是否存在显著差异。

如果p值小于设定的显著性水平，我们可以拒绝原假设，认为两个群体之间存在显著差异。

霍特林统计量在实际问题中有着广泛的应用。

例如，在医学研究中，我们可以使用霍特林统计量来比较不同药物治疗组和对照组的疗效差异。

在工业生产中，我们可以使用霍特林统计量来评估不同生产工艺对产品质量的影响。

在市场营销中，我们可以使用霍特林统计量来比较不同广告策略的效果。

除了以上应用外，霍特林统计量还可以用于多元回归分析中的模型选择。

在多元回归分析中，我们通常需要选择最优的模型，以便更好地解释和预测数据。

霍特林统计量可以作为一个评价指标，帮助我们选择最优的模型。

霍特林统计量是一种常用的多元统计分析工具，用于评估两组或多组样本之间的差异性。

它在假设检验、医学研究、工业生产和市场营销等领域都有着重要的应用。

n维随机变量的均值向量和协方差矩阵在统计学中，随机变量是指一个变量的取值是由概率决定的。

n维随机变量是指由n个随机变量组成的向量。

我们可以用一个n维向量来表示这个随机变量，其中每个元素表示对应随机变量的取值。

让我们来了解一下均值向量。

均值向量是由随机变量的期望值组成的向量，它反映了随机变量的中心趋势。

对于一个n维随机变量，其均值向量的第i个元素表示第i个随机变量的平均取值。

均值向量的计算方法是将每个随机变量的取值相加，然后除以n。

均值向量在统计分析中有很多重要的应用，比如用于描述数据的集中趋势和比较不同数据集之间的差异。

接下来，让我们来了解一下协方差矩阵。

协方差矩阵是一个对称矩阵，它描述了随机变量之间的线性关系。

对于一个n维随机变量，其协方差矩阵的第i行第j列元素表示第i个随机变量和第j个随机变量之间的协方差。

协方差矩阵的对角线元素表示各个随机变量的方差。

协方差矩阵可以帮助我们了解随机变量之间的相关性，以及它们对总体变异的贡献程度。

协方差矩阵在统计分析中有很多应用，比如主成分分析和线性回归分析。

均值向量和协方差矩阵在统计学中扮演着重要的角色，它们可以帮助我们理解和分析随机变量的特征。

通过计算均值向量和协方差矩阵，我们可以得到有关随机变量的很多信息，比如中心趋势、变异程度和相关性等。

这些信息对于我们进行统计推断和决策分析非常重要。

在实际应用中，我们经常需要根据样本数据来估计总体的均值向量和协方差矩阵。

通过对样本数据进行计算，我们可以得到样本的均值向量和协方差矩阵，并利用它们来推断总体的特征。

这在很多领域都有广泛的应用，比如金融投资、市场研究和医学统计等。

总结起来，均值向量和协方差矩阵是统计学中重要的概念和工具。

它们可以帮助我们理解和分析随机变量的特征，并在实际应用中提供有用的信息。

通过计算均值向量和协方差矩阵，我们可以得到关于随机变量的很多统计指标，从而进行统计推断和决策分析。

在未来的研究和实践中，我们可以进一步探索均值向量和协方差矩阵的性质和应用，以推动统计学的发展和应用。

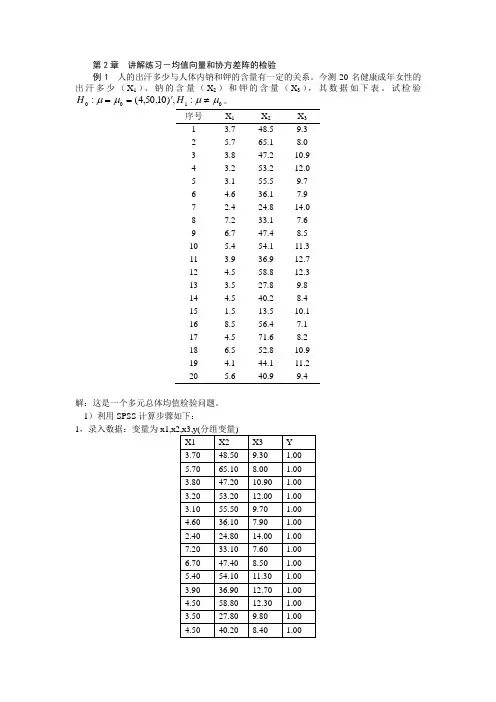
第2章 讲解练习－均值向量和协方差阵的检验例1 人的出汗多少与人体内钠和钾的含量有一定的关系。

今测20名健康成年女性的出汗多少（X 1）、钠的含量（X 2）和钾的含量（X 3），其数据如下表。

试检验0100:,)10,50,4(:μμμμ≠'==H H 。

序号 X 1 X 2 X 3 1 3.7 48.5 9.3 2 5.7 65.1 8.0 3 3.8 47.2 10.9 4 3.2 53.2 12.0 5 3.1 55.5 9.7 6 4.6 36.1 7.9 7 2.4 24.8 14.0 8 7.2 33.1 7.6 9 6.7 47.4 8.5 10 5.4 54.1 11.3 11 3.9 36.9 12.7 12 4.5 58.8 12.3 13 3.5 27.8 9.8 14 4.5 40.2 8.4 15 1.5 13.5 10.1 16 8.5 56.4 7.1 17 4.5 71.6 8.2 18 6.5 52.8 10.9 19 4.1 44.1 11.2 205.640.99.4解：这是一个多元总体均值检验问题。

1）利用SPSS 计算步骤如下：1，录入数据：变量为2将x1,x2,x3选入因变量，y选入固定因子，确定。

在输出窗口中得到在输出结果中“Multivariate Tests ”框中关于分组变量y 的“Hotelling ’s Trace ”（倒数第2行）得到 F=0.139，利用公式计算得到：2(1)T n F =+⋅＝(20+1)·0.139=2.929 （1） 与(,)F p n p α-=0.05(3,17) 3.196F =比较，若2T ＞1(,)F p n p α-，则拒绝原假设，否则接受原假设，本题中，20.05(3,17)T F <，故接受原假设。

说明：n 为样本数，p 为变量数。

公式（1）仅对单个总体均值的假设检验有效。

第三章多元正态分布均值向量和协方差的检验
1.基本思想和步骤
2.均值向量的检验
（1）分布：设且X与S相互独立，，则称统计量的分布为非中心分布
当时，称服从（中心）分布，记为
（2）转换为F分布：若且X与S相互独立，令，则
3.一个正态总体均值向量的检验
（1）协差阵已知，检验统计量为
（2）协差阵未知，检验统计量为
4.两个正态总体均值向量的检验
设为来自p维正态总体的容量为n的样本，
为来自p维正态总体的容量为m的样本，且两组样本相互独立
①针对共同已知协差阵，检验统计量为
②针对共同未知协差阵，检验统计量为
（2）协差阵不等
①针对n=m的情形，检验统计量为
②针对n≠m的情形，检验统计量为
5.多个正态总体均值向量的检验
（1）单因素方差分析：设k个正态总体分别为，从k个总体中取个独立样本，，假设H0成立，检验统计量为
其中，组间平方和为，组内平方和为，总平方和为，其中，
（2）若，则为X的广义方差，为样本广义方差
（3）Wilks分布：若且二者相互独立，
为Wilks统计量，分布为Wilks分布，简记为
（4）多元方差分析：检验统计量为
其中，，A为组间离差阵，E为组内离差阵，T为总离差阵，且T=A+E
6.协差阵的检验
（1）一个正态总体协差阵的检验：构造检验统计量
（2）多个协差阵相等的检验：构造检验统计量。

第1章 多元正态分布1、在数据处理时，为什么通常要进行标准化处理？数据的标准化是将数据按比例缩放，使之落入一个小的特定区间。

在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

其中最典型的就是0-1标准化和Z 标准化。

2、欧氏距离与马氏距离的优缺点是什么？欧氏距离也称欧几里得度量、欧几里得度量，是一个通常采用的距离定义，它是在m 维空间中两个点之间的真实距离。

在二维和三维空间中的欧氏距离的就是两点之间的距离。

缺点：就大部分统计问题而言，欧氏距离是不能令人满意的。

每个坐标对欧氏距离的贡献是同等的。

当坐标表示测量值时，它们往往带有大小不等的随机波动，在这种情况下，合理的方法是对坐标加权，使变化较大的坐标比变化较小的坐标有较小的权系数，这就产生了各种距离。

当各个分量为不同性质的量时，“距离”的大小与指标的单位有关。

它将样品的不同属性之间的差别等同看待，这一点有时不能满足实际要求。

没有考虑到总体变异对距离远近的影响。

马氏距离表示数据的协方差距离。

为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。

优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关。

由标准化数据和中心化数据计算出的二点之间的马氏距离相同。

马氏距离还可以排除变量之间的相关性的干扰。

缺点：夸大了变化微小的变量的作用。

受协方差矩阵不稳定的影响，马氏距离并不总是能顺利计算出。

3、当变量X1和X2方向上的变差相等，且与互相独立时，采用欧氏距离与统计距离是否一致？统计距离区别于欧式距离，此距离要依赖样本的方差和协方差，能够体现各变量在变差大小上的不同，以及优势存在的相关性，还要求距离与各变量所用的单位无关。

如果各变量之间相互独立,即观测变量的协方差矩阵是对角矩阵, 则马氏距离就退化为用各个观测指标的标准差的倒数作为权数的加权欧氏距离。

多元统计分析陈钰芬课后答案第1章多元正态分布1、在数据处理时，为什么通常要进行标准化处理？第1章多元正态分布1、在数据处理时，为什么通常要进行标准化处理？数据的标准化是将数据按比例缩放，使之落入一个小的特定区间。

在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

其中最典型的就是0-1标准化和Z标准化。

2、欧氏距离与马氏距离的优缺点是什么？欧氏距离也称欧几里得度量、欧几里得度量，是一个通常采用的距离定义，它是在m维空间中两个点之间的真实距离。

在二维和三维空间中的欧氏距离的就是两点之间的距离。

缺点：就大部分统计问题而言，欧氏距离是不能令人满意的。

每个坐标对欧氏距离的贡献是同等的。

当坐标表示测量值时，它们往往带有大小不等的随机波动，在这种情况下，合理的方法是对坐标加权，使变化较大的坐标比变化较小的坐标有较小的权系数，这就产生了各种距离。

当各个分量为不同性质的量时，“距离”的大小与指标的单位有关。

它将样品的不同属性之间的差别等同看待，这一点有时不能满足实际要求。

没有考虑到总体变异对距离远近的影响。

马氏距离表示数据的协方差距离。

为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。

优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关。

由标准化数据和中心化数据计算出的二点之间的马氏距离相同。

马氏距离还可以排除变量之间的相关性的干扰。

缺点：夸大了变化微小的变量的作用。

受协方差矩阵不稳定的影响，马氏距离并不总是能顺利计算出。

3、当变量X1和X2方向上的变差相等，且与互相独立时，采用欧氏距离与统计距离是否一致？统计距离区别于欧式距离，此距离要依赖样本的方差和协方差，能够体现各变量在变差大小上的不同，以及优势存在的相关性，还要求距离与各变量所用的单位无关。

第1章 多元正态分布1、在数据处理时，为什么通常要进行标准化处理？数据的标准化是将数据按比例缩放，使之落入一个小的特定区间。

在某些比较和评价的指标处理中经常会用到，去除数据的单位限制，将其转化为无量纲的纯数值，便于不同单位或量级的指标能够进行比较和加权。

其中最典型的就是0-1标准化和Z 标准化。

2、欧氏距离与马氏距离的优缺点是什么？欧氏距离也称欧几里得度量、欧几里得度量，是一个通常采用的距离定义，它是在m 维空间中两个点之间的真实距离。

在二维和三维空间中的欧氏距离的就是两点之间的距离。

缺点：就大部分统计问题而言，欧氏距离是不能令人满意的。

每个坐标对欧氏距离的贡献是同等的。

当坐标表示测量值时，它们往往带有大小不等的随机波动，在这种情况下，合理的方法是对坐标加权，使变化较大的坐标比变化较小的坐标有较小的权系数，这就产生了各种距离。

当各个分量为不同性质的量时，“距离”的大小与指标的单位有关。

它将样品的不同属性之间的差别等同看待，这一点有时不能满足实际要求。

没有考虑到总体变异对距离远近的影响。

马氏距离表示数据的协方差距离。

为两个服从同一分布并且其协方差矩阵为Σ的随机变量与的差异程度:如果协方差矩阵为单位矩阵,那么马氏距离就简化为欧氏距离,如果协方差矩阵为对角阵,则其也可称为正规化的欧氏距离。

优点：它不受量纲的影响，两点之间的马氏距离与原始数据的测量单位无关。

由标准化数据和中心化数据计算出的二点之间的马氏距离相同。

马氏距离还可以排除变量之间的相关性的干扰。

缺点：夸大了变化微小的变量的作用。

受协方差矩阵不稳定的影响，马氏距离并不总是能顺利计算出。

3、当变量X1和X2方向上的变差相等，且与互相独立时，采用欧氏距离与统计距离是否一致？统计距离区别于欧式距离，此距离要依赖样本的方差和协方差，能够体现各变量在变差大小上的不同，以及优势存在的相关性，还要求距离与各变量所用的单位无关。

如果各变量之间相互独立,即观测变量的协方差矩阵是对角矩阵, 则马氏距离就退化为用各个观测指标的标准差的倒数作为权数的加权欧氏距离。

n维随机变量的均值向量和协方差矩阵n维随机变量是指有n个分量的随机变量，每个分量都是一个随机变量。

这些分量可以代表不同的随机现象或者不同的特征。

而均值向量和协方差矩阵则是描述了这些随机变量的统计特征。

我们来介绍均值向量。

对于n维随机变量X=(X1, X2, ..., Xn)，其均值向量为μ=(μ1, μ2, ..., μn)，其中μi表示第i个分量的均值。

均值向量反映了每个分量的平均水平，可以用来描述随机变量的中心位置。

假设我们有一个5维随机变量X=(X1, X2, X3, X4, X5)，其中X1表示某公司的销售额，X2表示某公司的利润，X3表示某公司的市场份额，X4表示某公司的员工数量，X5表示某公司的产品种类数。

我们可以通过观察和记录，得到一系列的样本数据，然后计算每个分量的平均值。

得到的结果就是均值向量，它可以告诉我们这个公司的平均销售额、平均利润、平均市场份额、平均员工数量和平均产品种类数。

接下来，我们来介绍协方差矩阵。

对于n维随机变量X=(X1, X2, ..., Xn)，其协方差矩阵为Σ，其中Σij表示第i个分量和第j个分量的协方差。

协方差反映了两个分量之间的关联程度，可以用来描述随机变量之间的相关性。

继续以上面的例子为例，我们可以通过观察和记录，得到一系列的样本数据，然后计算每两个分量之间的协方差。

得到的结果就是协方差矩阵，它可以告诉我们销售额和利润之间的关联程度、销售额和市场份额之间的关联程度、销售额和员工数量之间的关联程度、销售额和产品种类数之间的关联程度，以及其他分量之间的关联程度。

均值向量和协方差矩阵是统计分析中常用的工具，它们可以帮助我们了解随机变量的分布特征和相关性。

通过对均值向量的分析，我们可以了解每个分量的平均水平，从而对随机变量的中心位置有一个直观的认识。

通过对协方差矩阵的分析，我们可以了解各个分量之间的关联程度，从而对随机变量之间的相关性有一个直观的认识。

在实际应用中，均值向量和协方差矩阵可以帮助我们进行数据分析和决策。

实验一SPSS软件的基本操作与均值向量和协方差阵的检验【实验目的】通过本次实验，了解SPSS的基本特征、结构、运行模式、主要窗口等，了解如何录入数据和建立数据文件，掌握基本的数据文件编辑与修改方法,对SPSS有一个浅层次的综合认识。

同时能够掌握对均值向量和协方差阵进行检验。

【实验性质】必修，基础层次【实验仪器及软件】计算机及SPSS软件【实验内容】1.操作SPSS的基本方法(打开、保存、编辑数据文件)2.问卷编码3.录入数据并练习数据相关操作4.对均值向量和协方差阵进行检验，并给出分析结论。

【实验学时】4学时【实验方法与步骤】1.开机2.找到SPSS的快捷按纽或在程序中找到SPSS，打开SPSS3.认识SPSS数据编辑窗、结果输出窗、帮助窗口、图表编辑窗、语句编辑窗4.对一份给出的问卷进行编码和变量定义5.按要求录入数据6.练习基本的数据修改编辑方法7.检验多元总体的均值向量和协方差阵8.保存数据文件9.关闭SPSS，关机。

【实验注意事项】1.实验中不轻易改动SPSS的参数设置，以免引起系统运行问题。

2.遇到各种难以处理的问题，请询问指导教师。

3.为保证计算机的安全，上机过程中非经指导教师和实验室管理人员同意，禁止使用移动存储器。

4.每次上机，个人应按规定要求使用同一计算机，如因故障需更换，应报指导教师或实验室管理人员同意。

5.上机时间，禁止使用计算机从事与课程无关的工作。

【上机作业】1.定义变量：试录入以下数据文件，并按要求进行变量定义。

表1学号姓名性别生日身高（cm）体重（kg）英语（总分100分）数学（总分100分）生活费（$代表人民币）200201 刘一迪男1982.01.12 156.42 47.54 75 79 345.00 200202 许兆辉男1982.06.05 155.73 37.83 78 76 435.00 200203 王鸿屿男1982.05.17 144.6 38.66 65 88 643.50 200204 江飞男1982.08.31 161.5 41.68 79 82 235.50 200205 袁翼鹏男1982.09.17 161.3 43.36 82 77 867.00 200206 段燕女1982.12.21 158 47.35 81 74200207 安剑萍女1982.10.18 161.5 47.44 77 69 1233.00 200208 赵冬莉女1982.07.06 162.76 47.87 67 73 767.80 200209 叶敏女1982.06.01 164.3 33.85 64 77 553.90 200210 毛云华女1982.09.12 144 33.84 70 80 343.00 200211 孙世伟男1981.10.13 157.9 49.23 84 85 453.80 200212 杨维清男1981.12.6 176.1 54.54 85 80 843.00 200213 欧阳已祥男1981.11.21 168.55 50.67 79 79 657.40 200214 贺以礼男1981.09.28 164.5 44.56 75 80 1863.90 200215 张放男1981.12.08 153 58.87 76 69 462.20 200216 陆晓蓝女1981.10.07 164.7 44.14 80 83 476.80 200217 吴挽君女1981.09.09 160.5 53.34 79 82200218 李利女1981.09.14 147 36.46 75 97 452.80 200219 韩琴女1981.10.15 153.2 30.17 90 75 244.70 200220 黄捷蕾女1981.12.02 157.9 40.45 71 80 253.00 要求：1）变量名同表格名，以“（）”内的内容作为变量标签。

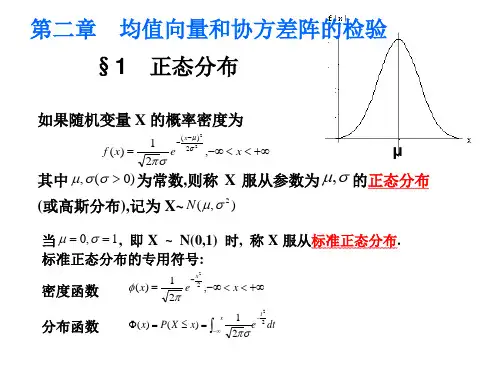
第三章3.1 试述多元统计分析中的各种均值向量和协差阵检验的基本思想和步骤。

其基本思想和步骤均可归纳为： 答： 第一，提出待检验的假设和H1；第二，给出检验的统计量及其服从的分布；第三，给定检验水平，查统计量的分布表，确定相应的临值，从而得到否定域；第四，根据样本观测值计算出统计量的值，看是否落入否定域中，以便对待判假设做出决策（拒绝或接受）。

均值向量的检验：统计量 拒绝域在单一变量中当2σ已知 0()X z n μσ-= /2||z z α>当2σ未知 0()X t n Sμ-=/2||(1)t t n α>-（2211()1ni i S X X n ==--∑作为2σ的估计量）一个正态总体00H =μμ：协差阵Σ已知 212000()()~()T n p χ-'=--X μΣX μ 220T αχ>协差阵Σ未知 2(1)1~(,)(1)n p T F p n p n p --+-- 2(1)n p T F n pα->-（200(()()]T n n n -'=---X μS X μ）两个正态总体012H =μμ：有共同已知协差阵 2120()()~()n m T p n mχ-⋅'=--+X Y ΣX Y 220T αχ> 有共同未知协差阵 2(2)1~(,1)(2)n m p F T F p n m p n m p+--+=+--+- F F α> （其中 21(2)())n m n m T n m n m n m -'⎡⎤⎡⎤⋅⋅=+---⎢⎥⎢⎥++⎣⎦⎣⎦X Y S X Y ）协差阵不等m n = -1()~(,)n p nF F p n p p-'=-Z S Z F F α>协差阵不等m n ≠ 1()~(,)n p nF F p n p p-'=--Z S Z F F α>多个正态总体k H μμμ===Λ210： 单因素方差 (1)~(1,)()SSA k F F k n k SSE n k -=--- F F α>多因素方差 ~(,,1)p n k k Λ==Λ--+E E T A E协差阵的检验 检验0=ΣΣ0p H =ΣI ： /2/21exp 2np n e tr n λ⎧⎫⎛⎫=-⎨⎬ ⎪⎩⎭⎝⎭S S00p H =≠ΣΣI ： /2/2**1exp 2np n e tr n λ⎧⎫⎛⎫=-⎨⎬ ⎪⎩⎭⎝⎭S S检验12k ===ΣΣΣL 012k H ===ΣΣΣL ：统计量/2/2/2/211i i kkn n pn np k iii i nnλ===∏∏SS3.2 试述多元统计中霍特林分布和威尔克斯分布分别与一元统计中t 分布和F 分布的关系。

第2章均值向量和协⽅差阵的检验作业及解答
第2章均值向量和协⽅差阵的检验作业及解答
2.1 ⼤学⽣的素质⾼低要受各⽅⾯因素的影响，其中包括家庭环境与家庭教育（x1）、学校⽣活环境（x2）、学校周围环境（x3）和个⼈向上发展的⼼理动机（x4）等。

从某⼤学在校学⽣中抽取了20 ⼈对以上因素在⾃⼰成长和发展过程中的影响程度给予评分（以9分制），数据如下表所⽰：
假定x=(x1,x2,x3,x4)’服从四元正态分布。

试检验
H0:µ=µ0=(7,5, 4,8)，H1:µ≠µ0,(α= 0.05).
解：这是⼀个总体的多元均值检验。

2.2 测量30名出⽣到3周岁婴幼⼉的⾝⾼和体重数据（见下表），其中男⼥各15名，
1),假定这两组都服从正态分布且协⽅差阵相等，试在显著性⽔平0.05下检验男⼥婴幼⼉的这两项指标是否有显著差异？请将下表的数据输⼊到SPSS⽂件中，并进⾏检验。

解：这是两总体均值检验。

2.3 1992年美国总统选举的三位候选⼈为布什、佩罗特和克林顿。

从⽀持三位候选⼈的选民中分别抽取了20 ⼈，登记他们的年龄段（x1）、受教育程度（x2）和性别（x3）资料如下
1），假定三组都服从多元正态分布，检验这三组的总体均值是否有显著性差异（α=0.05）。

2），检验三位候选⼈的协差阵是否相等（α=0.05）。

解：这是多总体均值检验。

统计学课后题第二章均值向量和协方差阵的检验1、试谈willks统计量在多元方差分析中的重要意义。

2、形象分析的基本思路是什么？形象又称轮廓图，是将总体样本的均值绘制到同一坐标轴里所得的折线图，每一个指标都表示为折线图上的一点。

形象分析是将两总体的形象绘制到同一个坐标下，根据形象的形状对总体的均值进行比较分析。

第三章聚类分析1、聚类分析的基本思想和功能是什么？聚类分析的核心思想是根据具体的指标对所研究的个体或者对象进行分类，使得同一类中的对象之间的相似性比其他类的对象的相似性更强。

聚类分析不仅可以用来对样品进行分类，也可以用来对变量进行分类。

对样品的分类常称为Q型聚类分析，对变量的分类常称为R型的聚类分析。

聚类分析的目的或功能就是把相似的研究对象归成类，即使类间对象的同质性最大化和类与类间对象的异质性最大化。

2、试述系统聚类法的原理和具体步骤系统聚类的基本思想是：距离相近的样品先聚成类，距离相远的后聚成类，过程一直进行下去，每个样品总能聚到合适的类中。

系统聚类的具体步骤：假设总共有N个样品第一步：将每个样品独自聚成一类，共有N类；第二步：根据所确定的样品“距离”公式，把距离较近的两个样品聚合为一类，其他的样品仍各自聚为一类，共聚成N-1类；第三步：将“距离”最近的两个类进一步聚成一类，共聚成N-2类；。

，以上步骤一直进行下去，最后将所有的样品全聚成一类。

3、试述K-均值聚类的方法原理这种聚类方法的思想是把每个样品聚集到其最近形心类中。

首先随机从数据集中选取 K个点作为初始聚类中心，然后计算各个样本到聚类中的距离，把样本归到离它最近的那个聚类中心所在的类。

计算新形成的每一个聚类的数据对象的平均值来得到新的聚类中心，如果相邻两次的聚类中心没有任何变化，说明样本调整结束，聚类准则函数已经收敛。

4、试述模糊聚类的思想方法模糊聚类分析是根据客观事物间的特征、亲疏程度、相似性，通过建立模糊相似关系对客观事物进行聚类的分析方法。

实验报告实验课程名称多元统计分析实验项目名称均值向量和协方差阵的检验年级 09级专业统计学生姓名周江学号 01理学院实验时间：2011年 10 月 4 日学生实验室守则一、按教学安排准时到实验室上实验课，不得迟到、早退和旷课。

二、进入实验室必须遵守实验室的各项规章制度，保持室内安静、整洁，不准在室内打闹、喧哗、吸烟、吃食物、随地吐痰、乱扔杂物，不准做与实验内容无关的事，非实验用品一律不准带进实验室。

三、实验前必须做好预习（或按要求写好预习报告），未做预习者不准参加实验。

四、实验必须服从教师的安排和指导，认真按规程操作，未经教师允许不得擅自动用仪器设备，特别是与本实验无关的仪器设备和设施，如擅自动用或违反操作规程造成损坏，应按规定赔偿，严重者给予纪律处分。

五、实验中要节约水、电、气及其它消耗材料。

六、细心观察、如实记录实验现象和结果，不得抄袭或随意更改原始记录和数据，不得擅离操作岗位和干扰他人实验。

七、使用易燃、易爆、腐蚀性、有毒有害物品或接触带电设备进行实验，应特别注意规范操作，注意防护；若发生意外，要保持冷静，并及时向指导教师和管理人员报告，不得自行处理。

仪器设备发生故障和损坏，应立即停止实验，并主动向指导教师报告，不得自行拆卸查看和拼装。

八、实验完毕，应清理好实验仪器设备并放回原位，清扫好实验现场，经指导教师检查认可并将实验记录交指导教师检查签字后方可离去。

九、无故不参加实验者，应写出检查，提出申请并缴纳相应的实验费及材料消耗费，经批准后，方可补做。

十、自选实验，应事先预约，拟订出实验方案，经实验室主任同意后，在指导教师或实验技术人员的指导下进行。

十一、实验室内一切物品未经允许严禁带出室外，确需带出，必须经过批准并办理手续。

学生所在学院：理学院专业：统计班级：09（1）班实验步骤：1．在SPSS软件的数据窗口依次定义变量，并输入要进行检验的数据。

2．首先要对数据是否遵从多元分布进行检验：Analyze-Descriptive Statistic-Explore....进入对话框，选中净资产收益率、总资产报酬率、资产负载率、总资产周转率、流动资产周转率、已获利息倍数、销售增长率及资本积累率八个变量到Dependend List框中，点击进入Plots对话框，选中Normality Plots with tests复选项以输出有关正态性检验的图表，Continue继续，OK运行，则得到结果。