人教版高中物理选修3-4 光的折射定律 折射率
- 格式:doc
- 大小:838.50 KB
- 文档页数:23







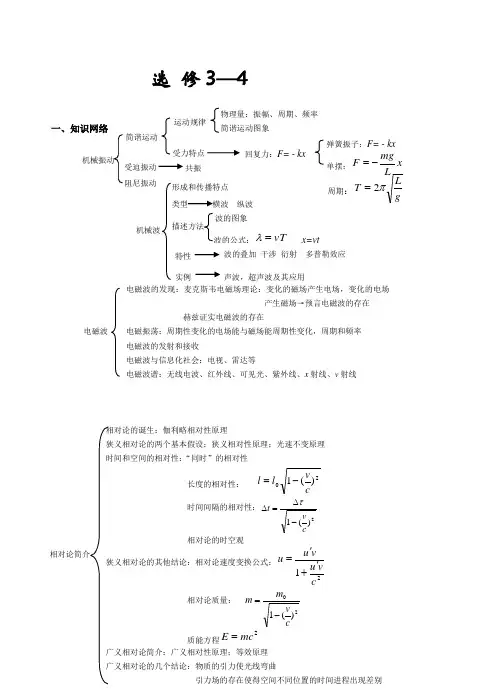
选 修3—4一、知识网络周期:gLT π2=机械振动简谐运动物理量:振幅、周期、频率 运动规律简谐运动图象阻尼振动受力特点回复力:F= - kx弹簧振子:F= - kx 单摆:x L mgF -= 受迫振动 共振 波的叠加 干涉 衍射 多普勒效应 特性 实例声波,超声波及其应用机械波形成和传播特点 类型横波 纵波 描述方法 波的图象 波的公式:vT =λx=vt电磁波电磁波的发现:麦克斯韦电磁场理论:变化的磁场产生电场,变化的电场产生磁场→预言电磁波的存在赫兹证实电磁波的存在电磁振荡:周期性变化的电场能与磁场能周期性变化,周期和频率 电磁波的发射和接收电磁波与信息化社会:电视、雷达等电磁波谱:无线电波、红外线、可见光、紫外线、x 射线、ν射线相对论简介相对论的诞生:伽利略相对性原理狭义相对论的两个基本假设:狭义相对性原理;光速不变原理 时间和空间的相对性:“同时”的相对性长度的相对性:20)(1cv l l -=时间间隔的相对性:2)(1cv t -∆=∆τ相对论的时空观狭义相对论的其他结论:相对论速度变换公式:21cv u v u u '+'=相对论质量: 20)(1cv m m -=质能方程2mc E=广义相对论简介:广义相对性原理;等效原理 广义相对论的几个结论:物质的引力使光线弯曲引力场的存在使得空间不同位置的时间进程出现差别二、考点解析 考点80 简谐运动 简谐运动的表达式和图象 要求:I1)如果质点所受的力与它偏离平衡位置位移的大小成正比,并且总是指向平衡位置,质点的运动就是简谐运动。
简谐运动的回复力:即F = – kx 注意:其中x 都是相对平衡位置的位移。
区分:某一位置的位移(相对平衡位置)和某一过程的位移(相对起点) ⑴回复力始终指向平衡位置,始终与位移方向相反⑵“k ”对一般的简谐运动,k 只是一个比例系数,而不能理解为劲度系数 ⑶F 回=-kx 是证明物体是否做简谐运动的依据 2)简谐运动的表达式: “x = A sin (ωt +φ)”3)简谐运动的图象:描述振子离开平衡位置的位移随时间遵从正弦(余弦)函数的规律变化的,要求能将图象与恰当的模型对应分析。



新课程新理念新设计人教版选修3-4《光的折射》教学设计(第一课时)永嘉中学肖飞燕yjxfy@一、设计思想“光的折射”主要内容是折射定律、折射率以及材料折射率的测定。
根据学习内容和学生实际情况本节课安排两课时,第一课时主要学习折射定律、折射率及初步应用;第二课时研究折射率的测量方法并测定玻璃的折射率。
“光的折射”是几何光学的主要内容,与以前教材相比,新人教版对几何光学内容删去较多,所以对“光的折射”的教学内容要更加重视。
设计时突出以下三方面:1、基于学生的已有知识,以实例和实验为基础,简单回顾光的反射定律和反射现象中光路可逆,初步形成光路概念。
在通过折射定律的应用培养分析光路图的能力,养成用光路研究几何光学的良好习惯。
2、用探究法得出折射定律,让学生经历规律发现的过程。
所以在折射定律的得出过程上多花些时间,首先用实验定性探究“折射角与入射角的定性关系”;接着重点定量分析折射角与入射角的定量关系,鼓励学生猜测并验证。
3、充分挖掘教材在情感态度价值观方面的教育功能。
通过“折射角与入射角的定量关系”的探究和历史足迹的介绍,使学生认识到科学的发现是经过曲折艰辛过程的,体验到认识发展的规律:实践——假设——再实践——修正假设,培养学生严谨的科学态度,同时使学生认识到各学科间是相互联系、互相促进,各学科全面发展的必要性,特别是数学与物理。
二、教材分析1、《课程标准》对本课教学内容“折射定律”的要求是“通过实验,理解光的折射定律;测定材料的折射率”。
《学科教学指导意见》对本课教学内容的教学要求如下:基本要求①知道光的反射与折射时光路可逆②掌握光的反射和折射定律③知道折射率的定义和表达式,知道折射率的决定因素发展要求①会用实验方法测出折射率②经历测定玻璃折射率的实验,体会其中蕴含的实验方法说明①不要求用惠更斯原理得出折射定律②不要求引入相对折射率的概念第一课时主要是达到基本要求,同时为第二课时铺垫。
2、本节课是光学的第一小节,教材在节前首先介绍了光学的发展史。
1 高中物理选修3-4知识点
光的折射定律 折射率
1)光的折射定律
①入射角、反射角、折射角都是各自光线与法线的夹角!
②表达式:2211sin sin θθn n =
③在光的折射现象中,光路也是可逆的
2)折射率
光从真空射入某种介质发生折射时,入射角的正弦与折射角的正弦之比,叫做这种介质的绝对折射率,用符号n 表示
sin sin n θθ=大
小
n 是反映介质光学性质的一个物理量,n 越大,表明光线偏折越厉害。
发生折射的原因是光在
不同介质中,速度不同 2.白光通过三棱镜时,会分解出各种色光,在屏上形成红→紫的彩色光带(注意:不同介质中,光的频率不变。
)
c n v
=。
高中物理选修3-4知识点总结:第十三章光(人教版)这一章内容比较多,重要的是光的几种特性,包括:折射、干涉、衍射、偏振和光的全反射。
本章的难点在于光的折射中有关折射率的问题,用双缝干涉测量光波的波长,以及光的全反射的有关计算问题。
理解性的内容主要有:光的色散,光的偏振等知识点。
考试的要求:Ⅰ、对所学知识要知道其含义,并能在有关的问题中识别并直接运用,相当于课程标准中的“了解”和“认识”。
Ⅱ、能够理解所学知识的确切含义以及和其他知识的联系,能够解释,在实际问题的分析、综合、推理、和判断等过程中加以运用,相当于课程标准的“理解”,“应用”。
要求Ⅰ:折射率、全反射、光导纤维、光的干涉、光的衍射、光的偏振以及色散等内容。
要求Ⅱ:光的折射定律、折射定律的运用、折射率的有关计算等有关的知识内容。
知识网络:内容详解:一、光的折射:反射定律:反射光线和入射光线以及法线在同一平面内,反射光线和入射光线分居法线两侧,反射角等于入射角。
折射定律:折射光线和入射光线以及法线在同一平面内,折射光线和入射光线分居法线两侧,入射角的正弦与折射角的正弦成正比。
在光的折射中光路是可逆的。
折射率:光从真空射入某介质时,入射角的正弦和折射角的正弦之比,称为折射率,用字母n表示。
测定玻璃的折射率:如图所示为两面平行的玻璃砖对光路的侧移,用插针法找出与入射光线AO对应的出射光线O′B,确定出O′点,画出O′O,量出入射角和折射角的度数。
根据公式:n=sinθ sinφ计算出玻璃的折射率。
对折射率的理解:介质折射率的大小取决于介质本身及入射光的频率,不同介质的折射率不同,与入射角、折射角的大小无关。
当光从真空射入介质中时,入射角、折射角以及它们的正弦值是可以改变的,但是正弦值之比是一个常数。
不同的介质,入射角的正弦跟折射角的正弦之比也是一个常数,但不同的介质具有不同的常数,说明常数反映着介质的光学特性。
介质的折射率跟光的传播速度有关,由于光在真空中的传播速度大于光在其他任何介质中的传播速度,所以任何介质的折射率都大于光从真空射入任何介质。
学案1光的折射定律[学习目标定位] 1.认识光的折射现象.2.理解光的折射定律,并能用其解释和计算有关问题.3.理解折射率的定义及其与光速的关系.1.波的反射:波遇到障碍物会返回来继续传播的现象.2.波的折射:当波由一种介质进入另一种介质后,传播方向发生偏折的现象.一、光的折射定律1.入射光线、折射光线和法线在同一平面内,入射光线与折射光线分居法线两侧:入射角的正弦值与折射角的正弦值之比为一常数,即sin isin r=n(式中n为比例常数)2.在光的折射现象中,光路可逆.二、介质的折射率n1.定义:光从真空射入某种介质发生折射时,入射角i的正弦值与折射角r的正弦值的比值.2.折射率与光速的关系:某种介质的折射率n等于光在真空中的传播速度c与光在这种介质中的传播速度v之比,即n=cv.任何介质的折射率n都大于1(填“大于”、“小于”或“等于”).一、反射定律和折射定律皎洁的月光下,在清澈的湖面上我们能通过水面看到月亮的倒影.同时,月光能够照亮水中的鱼和草,这说明光从空气射到水面时,一部分光射进水中,另一部分光返回到空气中,那么这两部分光的去向遵从什么规律呢?答案折射定律和反射定律.[要点提炼]1.光的反射(1)反射现象:光从一种介质射到它与第二种介质的分界面时,一部分光会返回到第一种介质的现象.(2)光的反射遵循反射定律:反射光线与入射光线、法线处在同一平面内,反射光线与入射光线分别位于法线的两侧;反射角等于入射角.(3)在光的反射现象中,光路可逆.2.光的折射(1)光的折射现象光从一种介质照射到两种介质的分界面时,一部分光进入另一种介质并改变传播方向的现象,称为光的折射现象.(2)折射定律(如图1所示)折射光线、入射光线和法线在同一平面内,入射光线与折射光线分居法线两侧;入射角的正弦值与折射角的正弦值之比为一常数,即sin isin r=n.图1(3)在光的折射现象中,光路可逆.3.注意:入射角、反射角和折射角不是光线与界面的夹角,而是光线与法线的夹角;光从一种介质进入另一种介质时,传播方向一般要发生变化,但并非一定要变化,当光垂直界面入射时光的传播方向就不变化.二、折射率[问题设计]光由真空以相同的入射角射向不同的介质时,折射角是不同的,为什么?答案因为不同介质对光的折射率不同.[要点提炼]1.折射率(1)定义式:n=sin isin r.(2)折射率与光速的关系:n=c v.2.对折射率n的理解(1)由于c>v,故任何介质的折射率都大于(填“大于”、“小于”或“等于”)1.(2)折射率n是反映介质光学性质的物理量,它的大小由介质本身及入射光的频率决定,与入射角、折射角的大小无关.(3)θ1为真空中的光线与法线的夹角,不一定为入射角;而θ2为介质中的光线与法线的夹角,也不一定为折射角,产生这种现象的原因是由于光路的可逆性. (4)介质的折射率与介质的密度没有必然联系.一、反射定律和折射定律的应用例1 一束光线从空气射入折射率为2的介质中,入射角为45°,在界面上入射光的一部分被反射,另一部分被折射,则反射光线和折射光线的夹角是( ) A .75° B .90° C .105° D .120° 解析 如图所示,根据折射定律sin i sin r =n ,则sin r =sin i n =sin45°2=12,r =30°,反射光线与折射光线的夹角θ=180°-45°-30°=105°,C 选项正确. 答案 C二、介质的折射率例2 一束光从空气射向折射率为3的某种介质,若反射光线与折射光线垂直,则入射角为________.真空中的光速为c ,则光在该介质中的传播速度为________.解析 设入射角为θ,折射角为90°-θ,根据n =sin θsin (90°-θ),可以得到θ=60°,再根据n =c v ,可得v =33c . 答案 60° 33c例3 如图2所示,一储油圆桶,底面直径与桶高均为d ,当桶内无油时,从某点A 恰能看到桶底边缘上的某点B ,当桶内油的深度等于桶高的一半时,在A 点沿AB 方向看去,看到桶底上的C 点,C 、B 相距14d .由此可得油的折射率n =________;光在油中传播的速度v =________m/s.(结果可用根式表示)图2解析 作出光路图如图所示.由题意知,sin α=22,sin β=d 4⎝⎛⎭⎫d 22+⎝⎛⎭⎫d 42=15=55,故油的折射率n =sin αsin β=102,光在油中传播的速度v =cn=610×107m/s.答案 102610×107光的反射和折射—⎪⎪⎪⎪⎪⎪⎪⎪—光的反射—⎪⎪⎪⎪ —反射定律—光路可逆—光的折射—⎪⎪⎪⎪—折射定律—光路可逆—折射率—⎪⎪⎪⎪—定义式n =sin isin r —与速度的关系n =cv1.(对折射率的理解)关于折射率,下列说法正确的是( )A .根据sin isin r =n 可知,介质的折射率与入射角的正弦值成正比B .根据sin isin r=n 可知,介质的折射率与入射角的正弦值成反比C .根据n =cv ,介质的折射率与介质中的光速成反比 D .介质的折射率与入射角、折射角的大小无关 答案 D解析 介质的折射率由介质材料本身和入射光的频率决定,与其他因素无关.故D 项正确. 2.(折射定律的应用)一个人站在湖边,观察离岸一段距离的水下的一条鱼,这个人看到的鱼的位置和鱼在水下真实的位置相比较,下列说法中正确的是( ) A .在鱼真实位置的正上方某处 B .在鱼真实位置上方偏向观察者的某处C .在鱼真实位置下方偏向观察者的某处D .所给条件不足,无法确定观察到的鱼的位置 答案 B解析 如图所示,人在岸上看离岸一段距离的水下的鱼,应是从鱼的位臵发出的光(实际上是鱼的反射光),经折射后射入人的眼睛,看到的是鱼的像.把鱼看做一个发光点S ,人看到的是折射光线的反向延长线交于发光点S 的右上方S ′点,这说明人看到的是鱼的虚像,且位臵是偏向右上方,所以选项B 正确.3.(折射定律的应用)光在某种玻璃中的传播速度是3×108m/s ,要使光由玻璃射入空气时折射光线与反射光线成90°夹角,则入射角应是( ) A .30°B .60°C .45°D .90° 答案 A解析 依题意作出光路图如图所示.折射角:θ2=90°-θ′=90°-θ1,玻璃的折射率:n =c v =3×1083×108= 3.由折射定律知:n sin θ1=sin θ2=sin(90°-θ1)=cos θ1,即tan θ1=1n =33,得θ1=30°.故答案为A.4.(折射定律的应用)现在高速公路上的标志牌都用“回归反光膜”制成.夜间行车时,它能把车灯射出的光逆向返回,标志牌上的字特别醒目.这种“回归反光膜”是用球体反射元件制成的,反光膜内均匀分布着一层直径为10μm 的细玻璃珠,所用玻璃的折射率为3,为使入射的车灯光线经玻璃珠折射——反射——折射后恰好和入射光线平行,如图3所示,那么第一次入射的入射角应是( )图3A .15°B .30°C .45°D .60° 答案 D解析 作光路图如图所示,设入射角为θ,折射角为α,则θ=2α,n =sin θsin α=2sin αcos αsin α,cos α=n 2=32,α=30°,所以θ=60°.故选项D 正确.题组一 光的折射定律和反射定律的应用1.如果光以同一入射角从真空射入不同介质,则折射率越大的介质( ) A .折射角越大,表示这种介质对光线的偏折程度越大 B .折射角越大,表示这种介质对光线的偏折程度越小 C .折射角越小,表示这种介质对光线的偏折程度越大 D .折射角越小,表示这种介质对光线的偏折程度越小 答案 C解析 由折射定律可知,在入射角相同的情况下,折射角越小,介质的折射率越大,介质对光线的偏折程度越大.2.关于光的折射现象,下列说法正确的是( ) A .光的传播方向发生改变的现象叫光的折射 B .光由一种介质进入另一种介质,传播方向一定改变 C .人观察盛水容器的底部,发现水变浅了D .若光从空气射入液体中,它的传播速度一定增大 答案 C3.关于光的反射与折射,以下说法正确的是( ) A .光发生反射时,光的传播方向一定改变 B .光发生反射时,光的传播方向可能偏转90° C .光发生折射时,一定伴随着反射现象 D .光发生折射时,光的传播方向可能偏转90° 答案 ABC解析 光发生反射时,光的传播方向一定改变,有人认为当入射角为0°时,也就是光线垂直界面入射时,反射角为零,光不改变传播方向,而实际上光的传播方向改变了180°,选项A 正确.当入射角为45°时,反射角也为45°,光的传播方向偏转90°,选项B 正确.光发生折射时,一定伴随着反射现象,C 正确;光发生折射时,传播的偏角方向一定小于90°,D 错误.4.如图1所示为地球及其大气层,高空有侦察卫星A接收到地球表面P处发出的光信号,则A感知到的发光物应在()图1A.图中P点B.图中P点靠近M的一侧C.图中P点靠近N的一侧D.以上位置都有可能答案 B解析由于大气层的存在,侦察卫星在A处接收到的P处发出的光信号的光路大致如图中实线所示,由图可知选项B正确,A、C、D错误.5.两束细平行光a和b相距为d,从空气中互相平行地斜射到长方体玻璃砖的上表面,如图2所示,若玻璃对a的折射率大于对b的折射率,当它们从玻璃砖的下表面射出后,有()图2A.两束光仍平行,间距等于dB.两束光仍平行,间距大于dC.两束光仍平行,间距小于dD.两束光不再平行答案 C解析光路如图所示.由光路图可知d′<d,故C项正确.6.如图3所示,井口大小和深度相同的两口井,一口是枯井,一口是水井(水面在井口之下),两井底部各有一只青蛙,则()图3A .水井中的青蛙觉得井口大些,晴天的夜晚,水井中的青蛙能看到更多的星星B .枯井中的青蛙觉得井口大些,晴天的夜晚,水井中的青蛙能看到更多的星星C .水井中的青蛙觉得井口小些,晴天的夜晚,枯井中的青蛙能看到更多的星星D .两只青蛙觉得井口一样大,晴天的夜晚,水井中的青蛙能看到更多的星星 答案 B解析 这是一道典型的视野问题,解决视野问题的关键是确定边界光线和确定是谁约束了视野等.如本题中由于井口边沿的约束,而不能看到更大的范围,据此作出边界光线如图所示.由图可看出α>γ,所以水井中的青蛙觉得井口小些;β>α,所以水井中的青蛙可看到更多的星星,故选项B 正确,A 、C 、D 错误. 题组二 介质的折射率7.如图4所示,玻璃三棱镜ABC 的顶角A 为30°,一束光线垂直于AB 射入棱镜,从AC 射出进入空气,测得出射光线与入射光线的夹角为30°,则棱镜的折射率为( )图4A.12B.22C.3D.33答案 C解析 顶角A 为30°,则光从AC 面射出时,在玻璃中的入射角i =30°.由于出射光线和入射光线的夹角为30°,所以折射角r =60°.由光路可逆和折射率的定义可知n =sin rsin i =3,C 项正确.8.如图5所示,等腰直角棱镜ABO 的两腰长都是16cm.为了测定它的折射率,棱镜放在直角坐标系中,使两腰与Ox 、Oy 轴重合.从OB 边的C 点注视A 棱,发现A 点的视位置在OA 边上的D 点,在C 、D 两点插上大头针,测出C 点的坐标位置(0,12),D 点的坐标位置(9,0),试由此计算出该棱镜的折射率.图5答案 43解析 从C 点注视A 点,发现A 点的视位臵在OA 边上的D 点,说明光线AC 经OB 边发生折射,反向延长线过D 点,由此可作出由A 点入射到C 点的光路如图所示,sin θ2=12122+92=45,sin θ1=12122+162=35,则n =sin θ2sin θ1=43. 题组三 综合应用9.如图6所示,一束激光从O 点由空气射入厚度均匀的介质,经下表面反射后,从上表面的A 点射出.已知入射角为i ,A 与O 相距l ,介质的折射率为n ,试求介质的厚度d .图6答案n 2-sin 2i2sin il解析 设射入介质时折射角为r ,由折射定律得sin isin r=n ,由几何关系得l =2d tan r ,解得:d=n 2-sin 2i 2sin i l10.如图7所示,半圆玻璃砖的半径R =10cm ,折射率为n =3,直径AB 与屏幕MN 垂直并接触于A 点.激光a 以入射角θ1=30°射向半圆玻璃砖的圆心O ,结果在水平屏幕MN 上出现两个光斑.求两个光斑之间的距离L .图7答案 23.1cm解析 画出如图所示的光路图,设折射角为θ2,根据折射定律,有 n =sin θ2sin θ1,解得θ2=60° 由几何知识得△OPQ 为直角三角形,所以两个光斑P 、Q 之间的距离L =P A +AQ =R tan30°+R tan60°,解得L =4033cm ≈23.1cm11.一半径为R 的1/4球体放置在水平桌面上,球体由折射率为3的透明材料制成.现有一束垂直于过球心O 的竖直平面内的光线,平行于桌面射到球体表面上,折射入球体后再从竖直表面射出,如图8所示.已知入射光线与桌面的距离为3R /2.求出射角θ.图8答案 60°解析 设入射光线与1/4球体的交点为C ,连接OC ,OC 即为入射点的法线.因此,图中的角α为入射角.过C 点作球体水平表面的垂线,垂足为B .依题意,∠COB =α.又由△OBC 知sin α=BC OC =32RR =32,α=60°.设光线在C 点的折射角为β,由折射定律得sin αsin β=3,联立以上两式得β=30°.由几何关系知,光线在球体的竖直表面上的入射角γ(如图)为30°.由折射定律得sin θsin γ=3,因此sin θ=32,θ=60°.12.一小孩站在宽6m 的河边,在他正对面的岸边有一距离河面高度为3m 的树,树的正下方河底有一块石头,小孩向河面看去,同时看到树顶和石头两者的像且重合.若小孩的眼睛离河面的高度为1.5m ,如图9所示,河水的折射率为43,试估算河水深度.图9答案 5.3m解析 光路图如图所示,得n =sin αsin β,由几何关系得1.5tan α+3tan α=6,解得tan α=43,sin α=45,P 点至树所在岸边的距离为3tan α=4m ,设河水深度为h , 则sin β=442+h 2, 由以上几式解得h =5.3m.。
第十三章第一节 光的折射定律 折射率课前自主学习(学案)一、请学生自主复习教材第十三章第一节P46至P50。
二、结合复习的内容思考如下问题:(3-5个问题)(编写说明:问题的设计请围绕要求学生掌握的概念、规律、重点、难点展开,让学生通过自主学习掌握基本内容)1、光的折射:光从 斜射入 时,传播方向会改变的现象叫光的折射。
2、光的折射遵循折射定律:也叫斯涅耳定律, 与入射光线、法线处于同一平面内,折射光线与入射光线分别位于 的两侧,入射角i 的 与折射角r 的 成 比。
折射现象中光路是可逆的。
3、光从真空射入介质发生 时,入射角的 与折射角的 之比,叫做这种介质的绝对折射率,简称 。
折射率是是表示介质折射光的本领大小的物理量。
折射率大小的决定因素有两个: 、 。
某介质折射率为vcn,式中n 为介质的折射率,n >1,故v <c 。
某一频率的光在不同介质中传播时,频率不变但折射率不同,所以光速不同,波长也不同(与机械波相同);不同频率的光在同一介质中传播时,折射率不同,所以光速不同,波长也不同(与机械波的区别).频率越高,折射率越大。
三、自主解答几道题目(3-5道)(编写说明:力图让学生提前掌握本课的一些基础达标题,当然也要有一定的思考性) 1、对于某单色光,玻璃的折射率比水大,则此单色光在玻璃中传播时A.其速度比在水中大,其波长比在水中长B.其速度比在水中大,其波长比在水中短C.其速度比在水中小,其波长比在水中短D.其速度比在水中小,其波长比在水中长解析:本题考查光在介质中传播时,速度、波长如何变化.据v =nc知,单色光在玻璃中的折射率比在水中大,因而速度比在水中小;由v =λν知,光的频率不变,速度v 变小,波长变短.C 正确. 答案:C2、细红光束和细蓝光束垂直于AB 面进入楔形棱镜,并能从AC 面射出,如图所示.这两束光从棱镜的AC 面射出后的情况是A.两束光一定相交B.两束光仍然平行C.两束光的反向延长线相交D.条件不足,无法确定解析:本题考查光的折射.由于光的折射,红蓝两束光从AC 面射出时均向BC 面偏折,但由于蓝光频率高于红光频率,其折射率大于红光的折射率,所以蓝光的偏转角大于红光的偏转角,所以从AC 面射出的两束光一定相交.故正确选项为A. 答案:A3、如图所示,光在真空和介质的界面MN 上发生偏折,那么下列说法正确是( ) A.光是从真空射向介质B.介质的折射率为1.73C.光在介质中的传播速度为1.73×108 m/sD.反射光线与折射光线成60°角答案:BC4、目前,一种用于摧毁人造卫星或空间站的激光武器已研制成功.如图所示,某空间站位于地平线上方,现准备用一束激光射向该空间站,则应把激光器()A.沿视线对着空间站瞄高一些B.沿视线对着空间站瞄低一些C.沿视线对准空间站直接瞄准D.条件不足,无法判别答案:C5、让光线通过一块长方形的玻璃砖,下列判断中错误的是A. 光线通过玻璃砖后发生的侧向位移与玻璃的厚度有关B. 光线通过玻璃砖后发生的侧向位移与玻璃的折射率有关C. 测玻璃砖折射率一定用上下面平行的玻璃砖D. 出射光线方向不变是因为没有发生折射答案:CD课堂主体参与(教案)(要求编写一个详案)【学习目标】1、认识光的折射现象,理解折射定律;2、理解介质折射率的定义、会有折射率公式进行有关计算。
【重点、难点】1、知道根据反射和折射定律正确画出光路图,进而根据几何关系求解是本节课的重点;2、(绝对)折射率的理解是本节课的难点。
【学习内容】 一、课前自主学习检查(编写说明:准备4-5个问题当堂考查,检查学生的课前自主学习情况,题目的难度比课前的题目要求高)1、例1、单色光从真空射入玻璃时,它的( ) A .波长变长、波速变小 B .波长变短、波速变大 C .波长变长、波速变大 D .波长变短、波速变小答案:D2、例2、(2003全国高考)如图所示,一玻璃柱体的横截面为半圆形,细的单色光束从空气射向柱体的O 点(半圆的圆心)产生反射光束1和2,已知玻璃折射率为3,入射角为450(相应的折射角为240),现保持入射光不变,将半圆柱绕通过O 点垂直于图面的轴线顺时针转过150,如图中虚线所示,则:A . 光束1转过150B . 光束1转过300150450入射光线1 2C.光束2转过的角度小于150D.光束2转过的角度大于150答案:B、C3、例3、假设地球表面不存在大气层,那么人们观察到日出时刻与实际存在大气层的情况相比()A.将提前B.将延后C.在某些地区将提前,在另一些地区将延后D.不变答案:B。
由几何光学知识可知,有大气层时,由于地表大气层不均匀,太阳光线经大气折射后向下弯曲,如图所示,地球上观察者看到日出的太阳要比实际位置高,也就是当太阳还在地平线以下时就可以看到太阳的像;而没有大气层时,太阳光线沿直线传播,当太阳在地平线以下时是看不到太阳的。
故有大气层时可提前看到日出。
4、如图7所示,一细光束中含有两种单色光(分别为红色和紫色),从空气斜射到透明的玻璃砖上,透过玻璃砖又射出到空气中,则A.出射光线中①是紫色,②是红色B.色光①在玻璃中的速度比色光②在玻璃中的速度慢C.这两种色光进入玻璃砖内速度都减小,它们的光子能量也都减少D.色光①在玻璃中的波长比色光②在玻璃中的波长大答案:AB5、关于可见光的传播速度,下列说法正确的是()(A)不同色光在真空中的速度相同,但在同一介质中速度不同(B)不同色光在真空中的速度不同,在同一介质中速度也不同(C)在玻璃中红光的速度最大(D)在玻璃中紫光的速度最大图7光束①②玻璃砖答案:AC(教师在学生完成后收上来进行批改,以了解学生学习情况) 二、构建知识框架、剖析典型概念(编写说明:教师采用启发式教学,帮助学生形成知识的逻辑体系,着重复习典型的概念和规律)考点1. 光的反射定律:光从一种介质射到另一种介质的分界面时发生反射。
光的反射定律:反射光线与入射光线、法线处在同一平面内,反射光线与入射光分别位于法线的两侧;反射角等于入射角。
考点2.光的折射现象,光的折射定律:1、光射到两种介质的分界面时可能同时发生反射和折射现象。
2、光的折射定律:折射光线与入射光线、法线处于同一平面内,折射光线与入射光线分别位于法线两侧,入射角i 的正弦与折射角r 的正弦成正比。
注意两角三线的含义折射率 (光线从介质Ⅰ——介质Ⅱ)12sin sin v v r i n ==折射现象的光路可逆性3、折射率:入射角的正弦与折射角的正弦的比。
①定义式:21sin sin θθ=n 研究表明:vcn = 反映光的本质Ⅰ Ⅱ②折射率的物理意义:表示介质折射光的本领大小的物理量③折射率大小由介质的种类、光源(频率即光的颜色)两个因素决定。
某一频率的光在不同介质中传播时,频率不变但折射率不同,所以光速不同,波长也不同(与机械波相同);不同频率的光在同一介质中传播时,折射率不同,所以光速不同,波长也不同(与机械波的区别)。
例在玻璃中,n红<n绿<n紫。
记忆方法:介质的折射率总大于1,故θ1>θ2,θ1一定是真空(或空气)中的角④对于光从一种介质进入另一种介质时,折射定律的表达式是n1sinθ1= n2sinθ2………⑤折射光路是可逆的考点3.折射时的色散:含有多种颜色的光被分解为单色光的现象叫光的色散。
(1)光通过棱镜时将向棱镜的横截面的底边方向偏折(2)通过棱镜折射后成像偏向顶点(3)实验表明,一束白光进入棱镜而被折射后,在屏上的光斑是彩色的,说明光在折射时发生了色散。
(4)光的色散规律:红光通过棱镜后偏折的程度比其他颜色的光的要小,而紫光的偏折程度比其他颜色的光要大。
说明透明物质对于波长不同的光的折射率是不同的。
波长越长,折射率越小。
三、自主研究例题(教师投影出典型例题,让学生先自主完成后再公布答案)例1、c 如图所示,一储油圆桶,底面直径与桶高均为d 。
当桶内无油时,从某点A 恰能看到桶底边缘上的某点B 。
当桶内油的深度等于桶高的一半时,在A 点沿AB 方向看去,看到桶底上的C 点,C 、B 相距4d,由此可得油的折射率n = ;光在油中传播的速度v = m/s 。
(结果可用根式表示) 答案:210;610×107 例2、如图,置于空气中的一不透明容器内盛满某种透明液体。
容器底部靠近器壁处有一竖直放置的6.0 cm 长的线光源。
靠近线光源一侧的液面上盖有一遮光板,另一侧有一水平放置的与液面等高的望远镜,用来观察线光源。
开始时通过望远镜不能看到线光源的任何一部分。
将线光源沿容器底向望远镜一侧平移至某处时,通过望远镜刚好可以看到线光源底端,再将线光源沿同一方向移动8.0 cm ,刚好可以看到其顶端。
求此液体的折射率n 。
思路分析:当折射角等于90时的入射角等于临界角,画出光路图,根据函数关系和几何关系即可求出折射率。
答案:若线光源底端在A 点时,望远镜内刚好可看到 线光源的底端,则有:/AOO α∠=其中α为此液体到空气的全反射临界角,由折 射定律得:1sin nα=同理,线光源顶端在B 1点时,望远镜内刚好可看到线光源的顶端,则:/1B OO α∠=遮光板望远镜线光源α AB 1 BO O/遮光板望远镜线光源由图中几何关系得:1sin ABAB α=解得:2211.3AB BB n AB+==[点评]该题属中档题,考查光的折射问题。
在分析折射现象时,要画出光路图。
利用几何关系和函数关系求解。
命题思路:本题主要考查的是光的折射和全反射,解决本题的关键在于依据题设条件,找出相应的几何关系,依据折射定律计算即可.例3、安全门上的观察孔,直径d=4 cm ,门的厚度L=3.464 cm ,为了扩大向外观察的范围,在孔中嵌入折射率为3的圆柱形玻璃,圆柱体轴线与门面垂直,如图所示。
从圆柱底面中心看出去,角。
可以看到的门外入射光线与轴线间的夹角称做视场角。
求:嵌入玻璃后的视场答案:由题中给出的视场角的定义,作出如图所示的光路,则图中θ角即为视场角。
由折射率公式得αθsin sin =n ,由几何关系得22)2(2sin dL d +=α联立解得234sin 22=+=d L nd θ,所以视场角为60°。
例4、某水池,实际深h ,垂直水面往下看,其视深多少?(设水折射率为n)答案:如图1作两条从水底S 发出的折射光线,一条垂直射出水面,一条入射角很小(眼睛对光点的张角很小),这两条折射光线延长的交点就是看到的S 的像,由图可见,在△AS'O 中,/tan h AO =α;在△ASO 中,hAOtg =γ ∴,hhtg tg =γα ∵α、r 小于5°,∴tg α≈sin α,tgr ≈sinr ,代入①得nhh h ==αγsin sin ,.四、小组讨论质疑(学生分组研讨刚才完成的典型例题,相互解决部分疑难问题,对个性问题,教师可直接帮助小组解决,对共性问题准备在全班研讨,对大家都争论较大的问题,教师要及时提醒学生停止争论,下一环节共同解决)(此内容在教案中不要编写,因为是课堂生成的)五、师生合作研讨(每个学习小组安排1个人,代表本组汇报本小组交流过程中仍然不能解决的、仍有困惑的、新生成的问题,教师先请能够解决的同学帮助解决,学生不能解决的,教师要引导学生掌握思考问题的方法。