2016年中考一模汇编：抛物线

2016年中考一模压轴题汇编28．在△ABC 中，AB =AC ，∠BAC =90︒，点D 在射线BC 上（与B 、C 两点不重合），以AD 为边作正方形ADEF ，使点E 与点B 在直线AD 的异侧，射线BA 与射线CF 相交于点G ． （1）若点D 在线段BC 上，如图1.①依题意补全图1；②判断BC 与CG 的数量关系与位置关系，并加以证明；（2）若点D 在线段BC 的延长线上，且G 为CF 中点，连接GE ，ABGE 的长为_______，并简述求GE 长的思路．图1 备用图29．在平面直角坐标系xOy 中，⊙C 的半径为r ，P 是与圆心C不重合的点，点P 关于⊙C 的限距点的定义如下：若P '为 直线PC 与⊙C 的一个交点，满足2r PP r '≤≤，则称P ' 为点P 关于⊙C 的限距点，右图为点P 及其关于⊙C 的限 距点P '的示意图．（1）当⊙O 的半径为1时．①分别判断点M (3,4)，N 5(,0)2，T 关 于⊙O 的限距点是否存在？若存在，求其坐标；②点D 的坐标为（2,0），DE ，DF 分别切⊙O 于点E ，点F ，点P 在△DEF 的 边上.若点P 关于⊙O 的限距点P '存在，求点P '的横坐标的取值范围；（2）保持（1）中D ，E ，F 三点不变，点P 在△DEF 的边上沿E →F →D →E 的方向运动，⊙C 的圆心C 的坐标为（1,0），半径为r .请从下面两个问题中任选一个作答. 温馨提示：答对问题1得2分，答对问题2得1分，两题均答不重复计分.28．在正方形ABCD 中，点P 是射线CB 上一个动点，连接PA ，PD ，点M ，N 分别为BC ，AP 的中点，连接MN 交PD 于点Q ．（1）如图1，当点P 与点B 重合时，QPM V 的形状是_____________________； （2）当点P 在线段CB 的延长线上时，如图2． ①依题意补全图2；②判断QPM V 的形状，并加以证明；（3）点P '与点P 关于直线AB 对称，且点P '在线段BC 上，连接AP '，若点Q 恰好在直线AP '上，正方形ABCD 的边长为2，请写出求此时BP 长的思路．（可以不写出计算结果）NAC DC图1 图2 图329．在平面直角坐标系xOy 中，对于点P 和图形W ,如果线段OP 与图形W 无公共点，则称点P 为关于图形W 的“阳光点”；如果线段OP 与图形W 有公共点，则称点P 为关于图形W 的“阴影点”． （1）如图1，已知点()13A ，，()11B ，，连接AB①在()11,4P ，()21,2P ，()32,3P ，()42,1P 这四个点中，关于线段AB 的“阳光点”是 ； ②线段11A B AB P ；11A B 上的所有点都是关于线段AB 的“阴影点”，且当线段11A B 向上或向下平移时，都会有11A B 上的点成为关于线段AB 的“阳光点”．若11A B 的长为4，且点1A 在1B 的上方，则点1A 的坐标为；（2）如图2，已知点(C，C e 与y 轴相切于点D ．若E e 的半径为32，圆心E 在直线l y =+：上，且E e 上的所有点都是关于C e 的“阴影点”，求圆心E 的横坐标的取值范围； （3）如图3，M e 的半径是3，点M 到原点的距离为5．点N 是Me 上到原点距离最近的点，点Q 和T 是坐标平面内的两个动点，且M e 上的所有点都是关于NQT ∆的“阴影点”，直接写出NQT ∆的周长的最小值．CBCB28. 如图，等边△ABC ，其边长为1， D 是BC 中点，点E ，F 分别位于AB ，AC 边上，且∠EDF =120°.（1）直接写出DE 与DF 的数量关系；（2）若BE ，DE ，CF 能围成一个三角形，求出这个三角形最大内角的度数；（要求：写出思路，画出图形，直接给出结果即可）（3）思考：AE +AF 的长是否为定值？如果是，请求出该值，如果不是，请说明理由.备用图29. 对于平面直角坐标系xOy 中的点P 和⊙C ，给出如下定义：若存在过点P 的直线l 交⊙C 于异于点P的A ，B 两点，在P ，A ，B 三点中，位于中间的点恰为以另外两点为端点的线段的中点时，则称点P 为⊙C 的相邻点，直线l 为⊙C 关于点P 的相邻线.（1）当⊙O 的半径为1时，○1分别判断在点D （21，14），E（0，），F （4，0）中，是⊙O 的相邻点 有__________；○2请从○1中的答案中，任选一个相邻点，在图1中做出⊙O 关于它的一条相邻线，并说明你的作图过程.○3点P 在直线3y x =-+上，若点P 为⊙O 的相邻点，求点P 横坐标的取值范围； （2）⊙C 的圆心在x 轴上，半径为1，直线y x =+与x 轴，y 轴分别交于点M ，N ，若线．段．MN 上存在⊙C 的相邻点P ，直接写出圆心C 的横坐标的取值范围．图1 备用图128．在等腰三角形ABC中，AC=BC，点P为BC边上一点（不与B、C重合），连接PA，以P为旋转中心，将线段PA顺时针旋转，旋转角与∠C相等，得到线段PD，连接DB．（1）当∠C=90º时，请你在图1中补全图形，并直接写出∠DBA的度数；（2）如图2，若∠C=α，求∠DBA的度数（用含α的代数式表示）；（3）连接AD，若∠C =30º，AC=2，∠APC=135º，请写出求AD长的思路．（可以不写出计算结果）29．在平面直角坐标系xOy中，A（t，0），B（t+，0），对于线段AB和x轴上方的点P给出如下定义：当∠APB=60°时，称点P为AB的“等角点”．（1）若t=-在点32C⎛⎫⎪⎝⎭，,2D⎛⎫⎪⎪⎝⎭，3,22E⎛⎫- ⎪⎪⎝⎭中，线段AB的“等角点”是；（2）直线MN分别交x轴、y轴于点M、N，点M的坐标是（6，0），∠OMN=30°．①线段AB的“等角点”P在直线MN上，且∠ABP=90°，求点P的坐标；②在①的条件下，过点B作BQ⊥PA，交MN于点Q，求∠AQB的度数；③若线段AB的所有“等角点”都在△MON内部，则t的取值范围是．图1PCB APCB A图2EA CD B 28．在正方形ABCD 中，E 为边CD 上一点，连接BE ．（1）请你在图1画出△BEM ，使得△BEM 与△BEC 关于直线BE 对称；（2）若边AD 上存在一点F ，使得AF+CE=EF ，请你在图2中探究∠ABF 与∠CBE 的数量关系并证明；（3）在（2）的条件下，若点E 为边CD 的三等分点，且CE<DE ，请写出求cos ∠FED 的思路．（可以不写出计算结果．．．．．．．．．）．图1 图2 备用图29．在平面直角坐标系xOy 中，图形W 在坐标轴上的投影长度定义如下：设点),(11y x P ，),(22y x Q 是图形W 上的任意两点．若21x x -的最大值为m ，则图形W 在x 轴上的投影长度m l x =；若21y y -的最大值为n ，则图形W 在y 轴上的投影长度n l y =．如右图，图形W 在x 轴上的投影长度213=-=x l ；在y 轴上的投影长度404=-=y l ．（1）已知点)3,3(A ，)1,4(B ．如图1所示，若图形W 为△OAB ，则=x l ，=y l ． （2）已知点)0,4(C ，点D 在直线26y x =-+上，若图形W 为△OCD ．当y x l l =时，求点D 的坐标．（3）若图形W 为函数2x y =）（b x a ≤≤的图象，其中0a b ≤<．当该图形满足1≤=y x l l 时，请直接写出a 的取值范围．AC DB28．已知：在△ABC 中，∠BAC =60°．（1）如图1，若AB =AC ，点P 在△ABC 内，且∠APC =150°，PA =3，PC =4，把△APC 绕着点A 顺时针旋转，使点C 旋转到点B 处，得到△ADB ，连接DP ①依题意补全图1； ②直接写出PB 的长；（2）如图2，若AB =AC ，点P 在△ABC 外，且PA =3，PB =5，PC =4，求∠APC 的度数；（3）如图3，若AB =2AC ，点P 在△ABC 内，且PA =3，PB =5，∠APC =120°，请直接写出PC 的长．ABB图1 图2 图329．在平面直角坐标系xOy 中，点P （a ，b ）的“变换点”Q 的坐标定义如下；当时b a ≥，Q 点坐标为（b ，-a ）；当a ＜b 时，Q 点的坐标为（a ，-b )． （1）求（-2，3），（6，-1）的变换点坐标；（2）已知直线l 与x 轴交于点A （4，0），与y 轴交于点B （0，2）．若直线l 上所有点的变换点组成一个新的图形，记作图形W ．请画出图形W ，并简要说明画图的思路； （3）若抛物线c x y +-=243与图形W有三个交点，请直接写出c 的取值范围．28.如图1，在四边形ABCD 中，BA =BC ，∠ABC =60°，∠ADC =30°，连接对角线BD .（1）将线段CD绕点C顺时针旋转60°得到线段CE，连接AE.①依题意补全图1；②试判断AE与BD的数量关系，并证明你的结论；（2）在（1）的条件下，直接写出线段DA、DB和DC之间的数量关系；（3）如图2，F是对角线BD上一点，且满足∠AFC=150°，连接FA和FC，探究线段FA、FB和FC之间的数量关系，并证明.（图1）（图2）29.在平面直角坐标系xoy中，对于任意三点A，B，C给出如下定义：如果正方形的任何一条边均与某条坐标轴平行，且A，B，C三点都在正方形的内部或边界上，那么称该正方形为点A，B，C的外延正方形，在点A，B，C所有的外延正方形中，面积最小的正方形称为点A，B，C的最佳外延正方形.例如，图1中的正方形A1B1C1D1，A2B2C2D2，A3B3CD3都是点A，B，C的外延正方形，正方形A3B3CD3是点A，B，C的最佳外延正方形.（图1）（图2）（图3 ）（图4）（1）如图1，点A（-1，0），B（2，4），C（0，t）（t为整数）.①如果t=3，则点A，B，C的最佳外延正方形的面积是；②如果点A，B，C的最佳外延正方形的面积是25，且使点C在最佳外延正方形的一边上，请写出一个符合题意的t值；（2）如图3，已知点M（3，0），N（0，4），P（x，y）是抛物线y=x2-2x-3上一点，求点M，N，P的最佳外延正方形的面积以及点P的横坐标x的取值范围；（3）如图4，已知点E（m，n）在函数x6y （x>0）的图象上，且点D的坐标为（1，1），设点O，D，E的最佳外延正方形的边长为a，请直接写出a的取值范围.28．在等边△ABC 外侧作直线AP ，点B 关于直线AP 的对称点为D ，连接AD ，BD ，CD ，其中CD 交直线AP 于点E ．设∠PAB ＝α，∠ACE ＝β，∠AEC ＝γ．(1) 依题意补全图1；(2) 若α＝15°，直接写出β和γ的度数； (3) 如图2，若60°<α<120°，①判断α，β的数量关系并加以证明；②请写出求γ大小的思路．（可以不写出计算结果．．．．．．．．．） 29．在平面直角坐标系xOy 中，给出如下定义：若点P 在图形M 上，点Q 在图形N 上，称线段PQ 长度的最小值为图形M ，N 的密距，记为d (M ，N )．特别地，若图形M ，N 有公共点，规定d (M ，N )＝0． (1) 如图1，⊙O 的半径为2，①点A (0，1)，B (4，3)，则d (A ，⊙O )＝ ，d (B ，⊙O )＝ ． ②已知直线l ：b x y +=43与⊙O 的密距d (l ，⊙O )＝56，求b 的值．(2) 如图2，C 为x 轴正半轴上一点，⊙C 的半径为1，直线33433+=x y －与x 轴交于点D ，与y 轴交于点E ，线段．．DE 与⊙C 的密距d (DE ，⊙C )<21．请直接写出圆心C 的横坐标m 的取值范围．图1图2图2A BPCAB CP图128. 在矩形ABCD 中，将对角线CA 绕点C 逆时针旋转得到CE ，连接AE ，取AE 的中点F ，连接BF ，DF . （1）若点E 在CB 的延长线上，如图1.①依题意补全图1；②判断BF 与DF 的位置关系并加以证明；（2）若点E 在线段BC 的下方，如果∠ACE =90°，∠ACB =28°，AC =6，请写出求BF 长的思路.（可以．．不写出计算结果．．．．．．．）29. 如图，点P ( x , y 1)与Q (x , y 2)分别是两个函数图象C 1与C 2上的任一点. 当a ≤ x ≤ b 时，有-1 ≤ y 1 - y 2≤ 1成立，则称这两个函数在a ≤ x ≤ b 上是“相邻函数”，否则称它们在a ≤ x ≤ b 上是“非相邻函数”. 例如，点P (x , y 1)与Q (x , y 2)分别是两个函数y = 3x +1与y = 2x - 1图象上的任一点，当-3 ≤ x ≤ -1时，y 1 - y 2 = (3x + 1) - (2x - 1) = x + 2，通过构造函数y = x + 2并研究它在-3 ≤ x ≤ -1上的性质，得到该函数值的范围是-1 ≤ y ≤ 1，所以-1 ≤ y 1 - y 2 ≤ 1成立，因此这两个函数在-3 ≤ x ≤ -1上是“相邻函数”.（1）判断函数y = 3x + 2与y = 2x + 1在－2 ≤ x ≤ 0上是否为“相邻函数”，并说明理由； （2）若函数y = x 2 - x 与y = x - a 在0 ≤ x ≤ 2上是“相邻函数”，求a 的取值范围；（3）若函数y =x a与y =－2x + 4在1 ≤ x ≤ 2上是“相邻函数”，直接写出a 的最大值与最小值.28. 在正方形ABCD 中，点H 在对角线BD 上（与点B 、D 不重合），连接AH ，将HA 绕点H顺时针图1备用图ABC D A BCD旋转 90º与边CD (或CD 延长线)交于点P ，作HQ ⊥BD 交射线DC 于点Q. (1)如图1:①依题意补全图1；②判断DP 与CQ 的数量关系并加以证明；(2)若正方形ABCD 的边长为3，当 DP=1时,试求∠PHQ 的度数.29．给出如下规定：两个图形G 1和G 2，点P 为G 1上任一点，点Q 为G 2上任一点，如果线段PQ 的长度存在最小值时，就称该最小值为两个图形G 1和G 2之间的“近距离”；如果线段PQ 的长度存在最大值时，就称该最大值为两个图形G 1和G 2之间的“远距离” ．请你在学习，理解上述定义的基础上，解决下面问题：在平面直角坐标系xOy 中，点A （-4， 3），B （-4，-3），C （4，-3），D （4， 3）．(1)请在平面直角坐标系中画出四边形ABCD ，直接写出线段AB 和线段CD 的“近距离”和“远距离”． (2)设直线b x y +=34（b>0）与x 轴，y 轴分别交于点E ，F ，若线段EF 与四边形ABCD 的“近距离”是1，求它们的“远距离” ；(3)在平面直角坐标系xOy 中，有一个矩形GHMN ，若此矩形至少有一个顶点在以O 为圆心，2为半径的圆上，其余各点可能在圆上或圆内.将四边形ABCD 绕着点O 旋转一周，在旋转的过程中，它与矩形GHMN 的“远距离”的最大值是 ；“近距离”的最小值是 ．28．在正方形ABCD 中，连接BD ．（1）如图1，AE ⊥BD 于E ．直接写出∠BAE 的度数．（2）如图1，在（1）的条件下，将△AEB 以A 旋转中心，沿逆时针方向旋转30°后得到△AB'E'，AB'与BD 交于M ，AE'的延长线与BD 交于N ． ① 依题意补全图1；② 用等式表示线段BM 、DN 和MN 之间的数量关系，并证明．（3）如图2，E 、F 是边BC 、CD 上的点，△CEF 周长是正方形ABCD 周长的一半，AE 、AF 分别与BD 交于M 、N ，写出判断线段BM 、DN 、MN 之间数量关系的思路．（不必写出完整推理过程）EDACBNMEDAC BF图1 图229．如图1，P 为∠MON 平分线OC 上一点，以P 为顶点的∠APB 两边分别与射线OM 和ON 交于A 、B两点，如果∠APB 在绕点P 旋转时始终满足OA ·OB =OP 2，我们就把∠APB 叫做∠MON 的关联角．A BO MNCPA N M O CPBAOM CNP B图1 图2 图3（1）如图2，P 为∠MON 平分线OC 上一点，过P 作PB ⊥ON 于B ，AP ⊥OC 于P ，那么∠APB∠MON 的关联角（填“是”或“不是”）． （2）① 如图3，如果∠MON =60°，OP =2，∠APB 是∠MON 的关联角，连接AB ，求△AOB 的面积和∠APB 的度数； ② 如果∠MON =α°（0°＜α°＜90°），OP =m ，∠APB 是∠MON 的关联角，直接用含有α和m的代数式表示△AOB 的面积．（3）如图4，点C 是函数2y x（x ＞0）图象上一个动点，过点C 的直线CD 分别交x 轴和y 轴于A ，B 两点，且满足BC =2CA ，直接写出∠AOB 的关联角∠APB 的顶点P 的坐标．OxyC图428．如图，在△ABC 中，∠ACB =90°，AC =BC=CD ，∠ACD =α，将线段CD 绕点C 顺时针旋转90°得到线段CE ，连接DE ，AE ，BD ．（1）依题意补全图1；（2）判断AE 与BD 的数量关系与位置关系并加以证明； （3）若0°＜α≤64°，AB =4，AE 与BD 相交于点G ，求点G 到直线AB 的距离的最大值．请写出求解的思路（可以不写出计算结果．．．．．．．．．）．29．对于两个已知图形G 1，G 2，在G 1上任取．．一点P ，在G 2上任取．．一点Q ，当线段PQ 的长度最小时，我们称这个最小长度为G 1，G 2的“密距”，用字母d 表示；当线段PQ 的长度最大时，我们称这个最大的长度为图形G 1，G 2的“疏距”，用字母f 表示．例如，当(1,2)M ，(2,2)N 时，点O 与线．段．MN ．．的“密距”O 与线．段．MN ．．的“疏距”为 （1）已知，在平面直角坐标系xOy 中，()2,0A -，()0,4B ，()2,0C ，()0,1D ， ①点O 与线段AB 的“密距”为，“疏距”为 ； ②线段AB 与△COD 的“密距”为，“疏距”为 ；（2）直线2y x b =+与x 轴，y 轴分别交于点E ，F ，以()0,1C -为圆心，1为半径作圆，当⊙C 与线段EF 的“密距”0<d <1时，求⊙C 与线段EF 的“疏距”f 的取值范围．28. 在平面直角坐标系xOy 中，对于点P （x ，y ）和Q （x ，y ′），给出如下定义：备用图图1 备用图图2图1A'B 如果()()0'0y x y y x ⎧⎪=⎨-⎪⎩≥＜，那么称点Q 为点P 的“妫川伴侣”．例如：点（5，6）的“妫川伴侣”为点（5，6），点（－5，6）的“妫川伴侣” 为点（－5，－6）．（1）① 点（2，1）的“妫川伴侣”为 ； ② 如果点A （3，－1），B （－1，3）的“妫川伴侣”中有一个在函数3y x=的图象上，那么这个点是 （填“点A ”或“点B ”）．（2）①点M *（－1，－2）的“妫川伴侣”点M 的坐标为 ；② 如果点N *（m +1，2）是一次函数y = x + 3图象上点N的“妫川伴侣”，求点N 的坐标．（3）如果点P 在函数24y x =-+（－2＜x ≤a ）的图象上，其“妫川伴侣”Q 的纵坐标y ′的取值范围是－4＜y ′≤4，那么实数a 的取值范围是 ．29. 阅读下面材料:小伟遇到这样一个问题：如图1，在△ABC （其中∠BAC 是一个可以变化的角）中，AB =2，AC =4，以BC 为边在BC 的下方作等边△PBC ，求AP 的最大值。

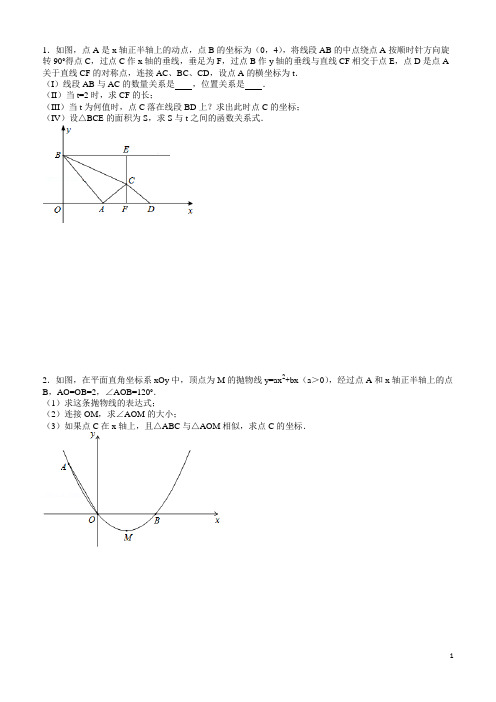
1．如图，点A是x轴正半轴上的动点，点B的坐标为（0，4），将线段AB的中点绕点A按顺时针方向旋转90°得点C，过点C作x轴的垂线，垂足为F，过点B作y轴的垂线与直线CF相交于点E，点D是点A 关于直线CF的对称点，连接AC、BC、CD，设点A的横坐标为t．（I）线段AB与AC的数量关系是，位置关系是．（II）当t=2时，求CF的长；（III）当t为何值时，点C落在线段BD上？求出此时点C的坐标；（IV）设△BCE的面积为S，求S与t之间的函数关系式．2．如图，在平面直角坐标系xOy中，顶点为M的抛物线y=ax2+bx（a＞0），经过点A和x轴正半轴上的点B，AO=OB=2，∠AOB=120°．（1）求这条抛物线的表达式；（2）连接OM，求∠AOM的大小；（3）如果点C在x轴上，且△ABC与△AOM相似，求点C的坐标．3．如图，已知△ABC的三个顶点坐标分别为A（﹣4，0）、B（1，0）、C（﹣2，6）．（1）求经过A、B、C三点的抛物线解析式；（2）设直线BC交y轴于点E，连接AE，求证：AE=CE；（3）设抛物线与y轴交于点D，连接AD交BC于点F，试问以A、B、F为顶点的三角形与△ABC相似吗？（4）若点P为直线AE上一动点，当CP+DP取最小值时，求P点的坐标．4．如图，抛物线y=ax2+b与x轴交于点A、B，且A点的坐标为（1，0），与y轴交于点C（0，1）．（1）求抛物线的解析式，并求出点B坐标；（2）过点B作BD∥CA交抛物线于点D，连接BC、CA、AD，求四边形ABCD的周长；（结果保留根号）（3）在x轴上方的抛物线上是否存在点P，过点P作PE垂直于x轴，垂足为点E，使以B、P、E为顶点的三角形与△CBD相似？若存在请求出P点的坐标；若不存在，请说明理由．5．如图，已知抛物线经过原点O，顶点为A（1，1），且与直线y=x﹣2交于B，C两点．（1）求抛物线的解析式及点C的坐标；（2）求证：△ABC是直角三角形；（3）若点N为x轴上的一个动点，过点N作MN⊥x轴与抛物线交于点M，则是否存在以O，M，N为顶点的三角形与△ABC相似？若存在，请求出点N的坐标；若不存在，请说明理由．6．如图，在平面直角坐标系中，抛物线y=ax2+x+c（a≠0）与x轴交于A、B两点（点A在点B的右侧），与y轴交于点C，点A的坐标为（4，0），抛物线的对称轴是直线x=．（1）求抛物线的解析式；（2）M为第一象限内的抛物线上的一个点，过点M作MG⊥x轴于点G，交AC于点H，当线段CM=CH 时，求点M的坐标；（3）在（2）的条件下，将线段MG绕点G顺时针旋转一个角α（0°＜α＜90°），在旋转过程中，设线段MG 与抛物线交于点N，在线段GA上是否存在点P，使得以P、N、G为顶点的三角形与△ABC相似？如果存在，请求出点P的坐标；如果不存在，请说明理由．7．如图，抛物线经过A（4，0），B（1，0），C（0，﹣2）三点．（1）求出抛物线的解析式；（2）P是抛物线上一动点，过P作PM⊥x轴，垂足为M，是否存在P点，使得以A，P，M为顶点的三角形与△OAC相似？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由；（3）在直线AC上方的抛物线上有一点D，使得△DCA的面积最大，求出点D的坐标．8．如图，在平面直角坐标系中，抛物线y=mx2﹣8mx+4m+2（m＞0）与y轴的交点为A，与x轴的交点分别为B（x1，0），C（x2，0），且x2﹣x1=4，直线AD∥x轴，在x轴上有一动点E（t，0）过点E作平行于y 轴的直线l与抛物线、直线AD的交点分别为P、Q．（1）求抛物线的解析式；（2）当0＜t≤8时，求△APC面积的最大值；（3）当t＞2时，是否存在点P，使以A、P、Q为顶点的三角形与△AOB相似？若存在，求出此时t的值；若不存在，请说明理由．9．如图，在平面直角坐标系xOy中，直线y=x+2与x轴交于点A，与y轴交于点C．抛物线y=ax2+bx+c 的对称轴是x=﹣且经过A、C两点，与x轴的另一交点为点B．（1）①直接写出点B的坐标；②求抛物线解析式．（2）若点P为直线AC上方的抛物线上的一点，连接PA，PC．求△PAC的面积的最大值，并求出此时点P 的坐标．（3）抛物线上是否存在点M，过点M作MN垂直x轴于点N，使得以点A、M、N为顶点的三角形与△ABC 相似？若存在，求出点M的坐标；若不存在，请说明理由．10．如图已知：直线y=﹣x+3交x轴于点A，交y轴于点B，抛物线y=ax2+bx+c经过A、B、C（1，0）三点．（1）求抛物线的解析式；（2）若点D的坐标为（﹣1，0），在直线y=﹣x+3上有一点P，使△ABO与△ADP相似，求出点P的坐标；（3）在（2）的条件下，在x轴下方的抛物线上，是否存在点E，使△ADE的面积等于四边形APCE的面积？如果存在，请求出点E的坐标；如果不存在，请说明理由．11．如图1，已知抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）两点．（1）求抛物线的解析式；（2）将直线OB向下平移m个单位长度后，得到的直线与抛物线只有一个公共点D，求m的值及点D的坐标；（3）如图2，若点N在抛物线上，且∠NBO=∠ABO，则在（2）的条件下，求出所有满足△POD∽△NOB 的点P坐标（点P、O、D分别与点N、O、B对应）．12．在平面直角坐标系中，抛物线y=ax2+bx+3与x轴的两个交点分别为A（﹣3，0）、B（1，0），过顶点C 作CH⊥x轴于点H．（1）直接填写：a=，b=，顶点C的坐标为；（2）在y轴上是否存在点D，使得△ACD是以AC为斜边的直角三角形？若存在，求出点D的坐标；若不存在，说明理由；（3）若点P为x轴上方的抛物线上一动点（点P与顶点C不重合），PQ⊥AC于点Q，当△PCQ与△ACH 相似时，求点P的坐标．13．如图所示，直线l：y=3x+3与x轴交于点A，与y轴交于点B．把△AOB沿y轴翻折，点A落到点C，抛物线过点B、C和D（3，0）．（1）求直线BD和抛物线的解析式．（2）若BD与抛物线的对称轴交于点M，点N在坐标轴上，以点N、B、D为顶点的三角形与△MCD相似，求所有满足条件的点N的坐标．（3）在抛物线上是否存在点P，使S△PBD=6？若存在，求出点P的坐标；若不存在，说明理由．14．如图，已知抛物线y=ax2+bx+c（a≠0）经过A（﹣1，0），B（4，0），C（0，2）三点．（1）求这条抛物线的解析式；（2）E为抛物线上一动点，是否存在点E，使以A、B、E为顶点的三角形与△COB相似？若存在，试求出点E的坐标；若不存在，请说明理由；（3）若将直线BC平移，使其经过点A，且与抛物线相交于点D，连接BD，试求出∠BDA的度数．15．已知抛物线y=x2+c与x轴交于A（﹣1，0），B两点，交y轴于点C．（1）求抛物线的解析式；（2）点E（m，n）是第二象限内一点，过点E作EF⊥x轴交抛物线于点F，过点F作FG⊥y轴于点G，连接CE、CF，若∠CEF=∠CFG．求n的值并直接写出m的取值范围（利用图1完成你的探究）．（3）如图2，点P是线段OB上一动点（不包括点O、B），PM⊥x轴交抛物线于点M，∠OBQ=∠OMP，BQ交直线PM于点Q，设点P的横坐标为t，求△PBQ的周长．16．如图，在平面直角坐标系中，顶点为A（1，﹣1）的抛物线经过点B（5，3），且与x轴交于C，D两点（点C在点D的左侧）．（1）求抛物线的解析式；（2）求点O到直线AB的距离；（3）点M在第二象限内的抛物线上，点N在x轴上，且∠MND=∠OAB，当△DMN与△OAB相似时，请你直接写出点M的坐标．17．如图，已知抛物线y=﹣（x+2）（x﹣m）（m＞0）与x轴相交于点A、B，与y轴相交于点C，且点A在点B的左侧．（1）若抛物线过点G（2，2），求实数m的值；（2）在（1）的条件下，解答下列问题：①求出△ABC的面积；②在抛物线的对称轴上找一点H，使AH+CH最小，并求出点H的坐标；（3）在第四象限内，抛物线上是否存在点M，使得以点A、B、M为顶点的三角形与△ACB相似？若存在，求m的值；若不存在，请说明理由．18．已知抛物线y=x2﹣2mx+m2+m﹣1（m是常数）的顶点为P，直线l：y=x﹣1（1）求证：点P在直线l上；（2）当m=﹣3时，抛物线与x轴交于A，B两点，与y轴交于点C，与直线l的另一个交点为Q，M是x轴下方抛物线上的一点，∠ACM=∠PAQ（如图），求点M的坐标；（3）若以抛物线和直线l的两个交点及坐标原点为顶点的三角形是等腰三角形，请直接写出所有符合条件的m的值．19．如图，已知抛物线y=（x+2）（x﹣4）与x轴交于点A、B（点A位于点B的左侧），与y轴交于点C，CD∥x轴交抛物线于点D，M为抛物线的顶点．（1）求点A、B、C的坐标；（2）设动点N（﹣2，n），求使MN+BN的值最小时n的值；（3）P是抛物线上一点，请你探究：是否存在点P，使以P、A、B为顶点的三角形与△ABD相似（△PAB 与△ABD不重合）？若存在，求出点P的坐标；若不存在，说明理由．20．设抛物线的解析式为y=ax2，过点B1（1，0）作x轴的垂线，交抛物线于点A1（1，2）；过点B2（，0）作x轴的垂线，交抛物线于点A2；…；过点B n（（）n﹣1，0）（n为正整数）作x轴的垂线，交抛物线于点A n，连接A n B n+1，得Rt△A n B n B n+1．（1）求a的值；（2）直接写出线段A n B n，B n B n+1的长（用含n的式子表示）；（3）在系列Rt△A n B n B n+1中，探究下列问题：①当n为何值时，Rt△A n B n B n+1是等腰直角三角形？②设1≤k＜m≤n（k，m均为正整数），问：是否存在Rt△A k B k B k+1与Rt△A m B m B m+1相似？若存在，求出其相似比；若不存在，说明理由．21．如图，直线y=kx+b（b＞0）与抛物线相交于点A（x1，y1），B（x2，y2）两点，与x轴正半轴相交于点D，与y轴相交于点C，设△OCD的面积为S，且kS+32=0．（1）求b的值；（2）求证：点（y1，y2）在反比例函数的图象上；（3）求证：x1•OB+y2•OA=0．22．如图，在平面直角坐标中，点O为坐标原点，直线y=﹣x+4与x轴交于点A，过点A的抛物线y=ax2+bx 与直线y=﹣x+4交于另一点B，且点B的横坐标为1．（1）求a，b的值；（2）点P是线段AB上一动点（点P不与点A、B重合），过点P作PM∥OB交第一象限内的抛物线于点M，过点M作MC⊥x轴于点C，交AB于点N，过点P作PF⊥MC于点F，设PF的长为t，MN的长为d，求d 与t之间的函数关系式（不要求写出自变量t的取值范围）；（3）在（2）的条件下，当S△ACN=S△PMN时，连接ON，点Q在线段BP上，过点Q作QR∥MN交ON于点R，连接MQ、BR，当∠MQR﹣∠BRN=45°时，求点R的坐标．23．如图1，在平面直角坐标系中，已知△AOB是等边三角形，点A的坐标是（0，4），点B在第一象限，点P是x轴上的一个动点，连接AP，并把△AOP绕着点A按逆时针方向旋转，使边AO与AB重合，得到△ABD．（1）求直线AB的解析式；（2）当点P运动到点（，0）时，求此时DP的长及点D的坐标；（3）是否存在点P，使△OPD的面积等于？若存在，请求出符合条件的点P的坐标；若不存在，请说明理由．24．在矩形ABCD中，点P是边AD上的动点，连接BP，线段BP的垂直平分线交边BC于点Q，垂足为点M，联结QP（如图）．已知AD=13，AB=5，设AP=x，BQ=y．（1）求y关于x的函数解析式，并写出x的取值范围；（2）当以AP长为半径的⊙P和以QC长为半径的⊙Q外切时，求x的值；（3）点E在边CD上，过点E作直线QP的垂线，垂足为F，如果EF=EC=4，求x的值．25．如图，在平面直角坐标系中，直线l：y=﹣2x+b（b≥0）的位置随b的不同取值而变化．（1）已知⊙M的圆心坐标为（4，2），半径为2．当b=时，直线l：y=﹣2x+b（b≥0）经过圆心M；当b=时，直线l：y=﹣2x+b（b≥0）与⊙M相切；（2）若把⊙M换成矩形ABCD，其三个顶点坐标分别为：A（2，0）、B（6，0）、C（6，2）．设直线l扫过矩形ABCD的面积为S，当b由小到大变化时，请求出S与b的函数关系式．26．如图，在Rt△ABC中，∠ACB=90°，AC=，BC=3，△DEF是边长为a（a为小于3的常数）的等边三角形，将△DEF沿AC方向平移，使点D在线段AC上，DE∥AB，设△DEF与△ABC重叠部分的周长为T．（1）求证：点E到AC的距离为一个常数；（2）若AD=，当a=2时，求T的值；（3）若点D运动到AC的中点处，请用含a的代数式表示T．27．如图，Rt△ABC中，∠C=90°，AB=15，BC=9，点P，Q分别在BC，AC上，CP=3x，CQ=4x（0＜x＜3）．把△PCQ绕点P旋转，得到△PDE，点D落在线段PQ上．（1）求证：PQ∥AB；（2）若点D在∠BAC的平分线上，求CP的长；（3）若△PDE与△ABC重叠部分图形的周长为T，且12≤T≤16，求x的取值范围．1.解：（I）∵如图，将线段AB的中点绕点A按顺时针方向旋转90°得点C，∵AB=2AC，∠BAC=90°，∴AB⊥AC．故答案是：AB=2AC，AB⊥AC；（II）由题意，易证Rt△ACF∽Rt△BAO，∴=．∵AB=2AM=2AC，∴CF=OA=t．当t=2时，CF=1；（III）由（1）知，Rt△ACF∽Rt△BAO，∴=，∴AF=OB=2，∴FD=AF=2，．∵点C落在线段BD上，∴△DCF∽△DBO，∴=，即=，整理得t2+4t﹣16=0解得t=2﹣2或t=﹣2﹣2（不合题意，舍去）∴当t=2﹣2时，点C落在线段BD上．此时，CF=t=﹣1，OF=t+2=2，∴点C的坐标为（2，﹣1+）；（IV）①当0＜t≤8时，如题图1所示：S=BE•CE=（t+2）•（4﹣t）=﹣t2+t+4；②当t＞8时，如答图1所示：CE=CF﹣EF=t﹣4S=BE•CE=（t+2）•（t﹣4）=t2﹣t﹣4；③如答图2，当点C与点E重合时，CF=OB=4，可得t=OA=8，此时S=0．2.解：（1）过点A作AE⊥y轴于点E，∵AO=OB=2，∠AOB=120°，∴∠AOE=30°，∴OE=，AE=1，∴A点坐标为：（﹣1，），B点坐标为：（2，0），将两点代入y=ax2+bx得：，解得：，∴抛物线的表达式为：y=x2﹣x；（2）过点M作MF⊥OB于点F，∵y=x2﹣x=（x2﹣2x）=（x2﹣2x+1﹣1）=（x﹣1）2﹣，∴M点坐标为：（1，﹣），∴tan∠FOM==，∴∠FOM=30°，∴∠AOM=30°+120°=150°；（3）当点C在x轴负半轴上时，则∠BAC=150°，而∠ABC=30°，此时∠C=0°，故此种情况不存在；当点C在x轴正半轴上时，∵AO=OB=2，∠AOB=120°，∴∠ABO=∠OAB=30°，∴AB=2EO=2，当△ABC1∽△AOM，∴=，∵MO==，∴=，解得：BC1=2，∴OC1=4，∴C1的坐标为：（4，0）；当△C2BA∽△AOM，∴=，∴=，解得：BC2=6，∴OC2=8，∴C2的坐标为：（8，0）．综上所述，△ABC与△AOM相似时，点C的坐标为：（4，0）或（8，0）．3.方法一：解：（1）设函数解析式为：y=ax2+bx+c，由函数经过点A（﹣4，0）、B（1，0）、C（﹣2，6），可得，解得：，故经过A、B、C三点的抛物线解析式为：y=﹣x2﹣3x+4；（2）设直线BC的函数解析式为y=kx+b，由题意得：，解得：，即直线BC的解析式为y=﹣2x+2．故可得点E的坐标为（0，2），从而可得：AE==2，CE==2，故可得出AE=CE；（3）相似．理由如下：设直线AD的解析式为y=kx+b，则，解得：，即直线AD的解析式为y=x+4．联立直线AD与直线BC的函数解析式可得：，解得：，即点F的坐标为（﹣，），则BF==，又∵AB=5，BC==3，∴=，=，∴=，又∵∠ABF=∠CBA，∴△ABF∽△CBA．故以A、B、F为顶点的三角形与△ABC相似．方法二：（1）略．（2）略．（3）若△ABF∽△ABC，则，即AB2=BF×BC，∵A（﹣4，0），D（0，4），∴l AD：y=x+4，l BC：y=﹣2x+2，∴l AD与l BC的交点F（﹣，），∴AB=5，BF=，BC=3，∴AB2=25，BF×BC=×3=25，∴AB2=BF×BC，又∵∠ABC=∠ABC，∴△ABF∽△ABC．（4）由（3）知：K AE=，K CE=﹣2，∴K AE×K CE=﹣1，∴AE⊥CE，过C点作直线AE的对称点C，点E为CC′的中点，∴，，∵C（﹣2，6），E（0，2），∴C′X=2，C′Y=﹣2，∵D（0，4），∴l C′D：y=﹣3x+4，∵l AE：y=x+2，∴l C′D与l AE的交点P（，）．4.方法一：解：（1）∵点A（1，0）和点C（0，1）在抛物线y=ax2+b上，∴，解得：a=﹣1，b=1，∴抛物线的解析式为：y=﹣x2+1，抛物线的对称轴为y轴，则点B与点A（1，0）关于y轴对称，∴B（﹣1，0）．（2）设过点A（1，0），C（0，1）的直线解析式为y=kx+b，可得：，解得k=﹣1，b=1，∴y=﹣x+1．∵BD∥CA，∴可设直线BD的解析式为y=﹣x+n，∵点B（﹣1，0）在直线BD上，∴0=1+n，得n=﹣1，∴直线BD的解析式为：y=﹣x﹣1．将y=﹣x﹣1代入抛物线的解析式，得：﹣x﹣1=﹣x2+1，解得：x1=2，x2=﹣1，∵B点横坐标为﹣1，则D点横坐标为2，D点纵坐标为y=﹣2﹣1=﹣3，∴D点坐标为（2，﹣3）．如答图①所示，过点D作DN⊥x轴于点N，则DN=3，AN=1，BN=3，在Rt△BDN中，BN=DN=3，由勾股定理得：BD=；在Rt△ADN中，DN=3，AN=1，由勾股定理得：AD=；又OA=OB=OC=1，OC⊥AB，由勾股定理得：AC=BC=；∴四边形ABCD的周长为：AC+BC+BD+AD=+++=+．（3）假设存在这样的点P，则△BPE与△CBD相似有两种情形：（I）若△EPB∽△BDC，如答图②所示，则有，即，∴PE=3BE．设OE=m（m＞0），则E（﹣m，0），BE=1﹣m，PE=3BE=3﹣3m，∴点P的坐标为（﹣m，3﹣3m）．∵点P在抛物线y=﹣x2+1上，∴3﹣3m=﹣（﹣m）2+1，解得m=1或m=2，当m=1时，点E与点B重合，故舍去；当m=2时，点E在OB左侧，点P在x轴下方，不符合题意，故舍去．因此，此种情况不存在；（II）若△EBP∽△BDC，如答图③所示，则有，即，∴BE=3PE．设OE=m（m＞0），则E（m，0），BE=1+m，PE=BE=（1+m）=+m，∴点P的坐标为（m，+m）．∵点P在抛物线y=﹣x2+1上，∴+m=﹣（m）2+1，解得m=﹣1或m=，∵m＞0，故m=﹣1舍去，∴m=，点P的纵坐标为：+m=+×=，∴点P的坐标为（，）．综上所述，存在点P，使以B、P、E为顶点的三角形与△CBD相似，点P的坐标为（，）．方法二：（1）略．（2）∵A（1，0），C（0，1），∴l AC：y=﹣x+1，∵BD∥CA，∴K BD=K AC=﹣1，∴l BD：y=﹣x﹣1，∴，∴x1=2，x2=﹣1（舍），∴D（2，﹣3），∴AC==，CB==，BD==3，DA==，∴四边形ABCD的周长为：5+．（3）∵C（0，1），B（﹣1，0），∴K BC==1，∵K BD=﹣1，∴K BC×K BD=﹣1，∴BD⊥BC，若△EPB∽△BDC，则或，①设点P（t，﹣t2+1），E（t，0），B（﹣1，0），PE=P Y=﹣t2+1，BE=E X﹣B X=t+1，∵BD=3，CB=，，∴，∴t=﹣2（此时点P位于x轴下方，故舍去）②∵，∴，∴t=，∴P（，）．5.解：（1）∵顶点坐标为（1，1），∴设抛物线解析式为y=a（x﹣1）2+1，又抛物线过原点，∴0=a（0﹣1）2+1，解得a=﹣1，∴抛物线解析式为y=﹣（x﹣1）2+1，即y=﹣x2+2x，联立抛物线和直线解析式可得，解得或，∴B（2，0），C（﹣1，﹣3）；（2）如图，分别过A、C两点作x轴的垂线，交x轴于点D、E两点，则AD=OD=BD=1，BE=OB+OE=2+1=3，EC=3，∴∠ABO=∠CBO=45°，即∠ABC=90°，∴△ABC是直角三角形；（3）假设存在满足条件的点N，设N（x，0），则M（x，﹣x2+2x），∴ON=|x|，MN=|﹣x2+2x|，由（2）在Rt△ABD和Rt△CEB中，可分别求得AB=，BC=3，∵MN⊥x轴于点N∴∠ABC=∠MNO=90°，∴当△ABC和△MNO相似时有=或=，①当=时，则有=，即|x||﹣x+2|=|x|，∵当x=0时M、O、N不能构成三角形，∴x≠0，∴|﹣x+2|=，即﹣x+2=±，解得x=或x=，此时N点坐标为（，0）或（，0）；②当=时，则有=，即|x||﹣x+2|=3|x|，∴|﹣x+2|=3，即﹣x+2=±3，解得x=5或x=﹣1，此时N点坐标为（﹣1，0）或（5，0），综上可知存在满足条件的N点，其坐标为（，0）或（，0）或（﹣1，0）或（5，0）．6.解：（1）∵x=﹣=，b=，∴a=﹣，把A（4，0），a=﹣代入y=ax2+x+c，可得（）×42+×4+c=0，解得c=2，则抛物线解析式为y=﹣x2+x+2．（2）如图1，连接CM，过C点作CE⊥MH于点E，，∵y=﹣x2+x+2，∴当x=0时，y=2，∴C点的坐标是（0，2），设直线AC解析式为y=kx+b（k≠0），把A（4，0）、C（0，2）代入y=kx+b，可得，解得：，∴直线AC解析式为y=﹣x+2，∵点M在抛物线上，点H在AC上，MG⊥x轴，∴设点M的坐标为（m，﹣m2+m+2），H（m，﹣m+2），∴MH=﹣m2+m+2﹣（﹣m+2）=﹣m2+2m，∵CM=CH，OC=GE=2，∴MH=2EH=2×[2﹣（﹣m+2）]=m，又∵MH=﹣m2+2m，∴﹣m2+2m=m，即m（m﹣2）=0，解得m=2或m=0（不符合题意，舍去），∴m=2，当m=2时，y=﹣×22+×2+2=3，∴点M的坐标为（2，3）．（3）存在点P，使以P，N，G为顶点的三角形与△ABC相似，理由为：∵抛物线与x轴交于A、B两点，A（4，0），A、B两点关于直线x=成轴对称，∴B（﹣1，0），∵AC==2，BC==，AB=5，∴AC2+BC2=+=25，AB2=52=25，∵AC2+BC2=AB2=25，∴△ABC为直角三角形，∴∠ACB=90°，线段MG绕G点旋转过程中，与抛物线交于点N，当NP⊥x轴时，∠NPG=90°，设P点坐标为（n，0），则N点坐标为（n，﹣n2+n+2），①如图2，当=时，∵∠N1P1G=∠ACB=90°，∴△N1P1G∽△ACB，∴=，解得：n1=3，n2=﹣4（不符合题意，舍去），∴P的坐标为（3，0）．②当=时，∵∠N2P2G=∠BCA=90°，∴△N2P2G∽△BCA，∴，解得：n1=1，n2=1﹣（不符合题意，舍去），∴P的坐标为（1+，0）．∴存在点P（3，0）或（1，0），使以P，N，G为顶点的三角形与△ABC相似．7.解：（1）∵该抛物线过点C（0，﹣2），设该抛物线的解析式为y=ax2+bx﹣2．将A（4，0），B（1，0）代入，得，解得，∴此抛物线的解析式为y=﹣x2+x﹣2．（2）存在．如图，设P点的横坐标为m，则点P的纵坐标为，当1＜m＜4时，AM=4﹣m，PM=，又∵∠COA=∠PMA=90°，∴①当==2时，△APM∽△ACO，∴=2，即|4﹣m|=2（），∴4﹣m=m2+5m﹣4，∴m2﹣6m+8=0，∴（m﹣2）（m﹣4）=0，解得：m1=2，m2=4（舍去）∴P（2，1）②当，△APM∽△CAO，那么有：2|4﹣m|=，∴2（4﹣m）=﹣m2+m﹣2，∴m2﹣9m+20=0，∴（m﹣4）（m﹣5）=0，解得：m1=4（舍去），m2=5（舍去），∴当1＜m＜4时，P（2，1），类似地可求出当m＞4时，P（5，﹣2），当m＜1时，P（﹣3，﹣14），当P，C重合时，△APM≌△ACO，P（0，﹣2）．综上所述，符合条件的点P为（2，1）或（5，﹣2）或（﹣3，﹣14）或（0，﹣2）；（3）如图，设D点的横坐标为t（0＜t＜4），则D点的纵坐标为﹣t2+t﹣2．过D作y轴的平行线交AC于E．由题意可求得直线AC的解析式为y=x﹣2．∴E点的坐标为（t，t﹣2）．∴DE=﹣t2+t﹣2﹣（t﹣2）=﹣t2+2t．∴S△DAC=×（﹣t2+2t）×4=﹣t2+4t=﹣（t﹣2）2+4．∴当t=2时，△DAC面积最大．∴D（2，1）．8.解：（1）由题意知x1、x2是方程mx2﹣8mx+4m+2=0的两根，∴x 1+x2=8，由解得：∴B（2，0）、C（6，0）则4m﹣16m+4m+2=0，解得：m=，∴该抛物线解析式为：y=；（2）可求得A（0，3）设直线AC的解析式为：y=kx+b，∵∴∴直线AC的解析式为：y=﹣x+3，要构成△APC，显然t≠6，分两种情况讨论：①当0＜t＜6时，设直线l与AC交点为F，则：F（t，﹣），∵P（t，），∴PF=，∴S=S△APF+S△CPF===，此时最大值为：，②当6＜t≤8时，设直线l与AC交点为M，则：M（t，﹣），∵P（t，），∴PM=，∴S △APC=S△APM﹣S△CPM===，当t=8时，取最大值，最大值为：12，综上可知，当0＜t≤8时，△APC面积的最大值为12；（3）方法一：如图，连接AB，则△AOB中，∠AOB=90°，AO=3，BO=2，Q（t，3），P（t，），①当2＜t＜8时，AQ=t，PQ=，若：△AOB∽△AQP，则：，即：，∴t=0（舍），或t=，若△AOB∽△PQA，则：，即：，∴t=0（舍）或t=2（舍），②当t＞8时，AQ′=t，PQ′=，若：△AOB∽△AQP，则：，即：，∴t=0（舍），或t=，若△AOB∽△PQA，则：，即：，∴t=0（舍）或t=14，方法二：若以A、P、Q为顶点的三角形与△AOB相似，则或，设P（t，）（t＞2）∴Q（t，3）①||=，∴||=，∴t1=2（舍），t2=14，②||=，∴||=，∴t1=，t2=，9.解：（1）①y=当x=0时，y=2，当y=0时，x=﹣4，∴C（0，2），A（﹣4，0），由抛物线的对称性可知：点A与点B关于x=﹣对称，∴点B的坐标为1，0）．②∵抛物线y=ax2+bx+c过A（﹣4，0），B（1，0），∴可设抛物线解析式为y=a（x+4）（x﹣1），又∵抛物线过点C（0，2），∴2=﹣4a∴a=∴y=x2x+2．（2）设P（m，m2m+2）．过点P作PQ⊥x轴交AC于点Q，∴Q（m，m+2），∴PQ=m2m+2﹣（m+2）=m2﹣2m，∵S△PAC=×PQ×4，=2PQ=﹣m2﹣4m=﹣（m+2）2+4，∴当m=﹣2时，△PAC的面积有最大值是4，此时P（﹣2，3）．（3）方法一：在Rt△AOC中，tan∠CAO=在Rt△BOC中，tan∠BCO=，∴∠CAO=∠BCO，∵∠BCO+∠OBC=90°，∴∠CAO+∠OBC=90°，∴∠ACB=90°，∴△ABC∽△ACO∽△CBO，如图：①当M点与C点重合，即M（0，2）时，△MAN∽△BAC；②根据抛物线的对称性，当M（﹣3，2）时，△MAN∽△ABC；③当点M在第四象限时，设M（n，n2n+2），则N（n，0）∴MN=n2+n﹣2，AN=n+4当时，MN=AN，即n2+n﹣2=（n+4）整理得：n2+2n﹣8=0解得：n1=﹣4（舍），n2=2∴M（2，﹣3）；当时，MN=2AN，即n2+n﹣2=2（n+4），整理得：n2﹣n﹣20=0解得：n1=﹣4（舍），n2=5，∴M（5，﹣18）．综上所述：存在M1（0，2），M2（﹣3，2），M3（2，﹣3），M4（5，﹣18），使得以点A、M、N为顶点的三角形与△ABC相似．方法二：∵A（﹣4，0），B（1，0），C（0，2），∴K AC×K BC=﹣1，∴AC⊥BC，MN⊥x轴，若以点A、M、N为顶点的三角形与△ABC相似，则，，设M（2t，﹣2t2﹣3t+2），∴N（2t，0），①||=，∴||=，∴2t1=0，2t2=2，②||=，∴||=2，∴2t1=5，2t2=﹣3，综上所述：存在M1（0，2），M2（﹣3，2），M3（2，﹣3），M4（5，﹣18），使得以点A、M、N为顶点的三角形与△ABC相似．10.解：（1）由题意得，A（3，0），B（0，3）∵抛物线经过A、B、C三点，∴把A（3，0），B（0，3），C（1，0）三点分别代入y=ax2+bx+c，得方程组解得：∴抛物线的解析式为y=x2﹣4x+3（2）由题意可得：△ABO为等腰三角形，如答图1所示，若△ABO∽△AP1D，则∴DP1=AD=4，∴P1（﹣1，4）若△ABO∽△ADP2 ，过点P2作P2 M⊥x轴于M，AD=4，∵△ABO为等腰三角形，∴△ADP2是等腰三角形，由三线合一可得：DM=AM=2=P2M，即点M与点C重合，∴P2（1，2）综上所述，点P的坐标为P1（﹣1，4），P2（1，2）；（3）不存在．理由：如答图2，设点E（x，y），则S△ADE=①当P1（﹣1，4）时，S四边形AP1CE=S△ACP1+S△ACE==4+|y|∴2|y|=4+|y|，∴|y|=4∵点E在x轴下方，∴y=﹣4，代入得：x2﹣4x+3=﹣4，即x2﹣4x+7=0，∵△=（﹣4）2﹣4×7=﹣12＜0∴此方程无解②当P2（1，2）时，S四边形AP2CE=S△ACP2+S△ACE==2+|y|，∴2|y|=2+|y|，∴|y|=2∵点E在x轴下方，∴y=﹣2，代入得：x2﹣4x+3=﹣2，即x2﹣4x+5=0，∵△=（﹣4）2﹣4×5=﹣4＜0∴此方程无解综上所述，在x轴下方的抛物线上不存在这样的点E．11.解：（1）∵抛物线y=ax2+bx（a≠0）经过A（3，0）、B（4，4）∴将A与B两点坐标代入得：，解得：，∴抛物线的解析式是y=x2﹣3x．（2）设直线OB的解析式为y=k1x，由点B（4，4），得：4=4k1，解得：k1=1∴直线OB的解析式为y=x，∴直线OB向下平移m个单位长度后的解析式为：y=x﹣m，∵点D在抛物线y=x2﹣3x上，∴可设D（x，x2﹣3x），又∵点D在直线y=x﹣m上，∴x2﹣3x=x﹣m，即x2﹣4x+m=0，∵抛物线与直线只有一个公共点，∴△=16﹣4m=0，解得：m=4，此时x1=x2=2，y=x2﹣3x=﹣2，∴D点的坐标为（2，﹣2）．（3）∵直线OB的解析式为y=x，且A（3，0），∴点A关于直线OB的对称点A′的坐标是（0，3），根据轴对称性质和三线合一性质得出∠A′BO=∠ABO，设直线A′B的解析式为y=k2x+3，过点（4，4），∴4k2+3=4，解得：k2=，∴直线A′B的解析式是y=，∵∠NBO=∠ABO，∠A′BO=∠ABO，∴BA′和BN重合，即点N在直线A′B上，∴设点N（n，），又点N在抛物线y=x2﹣3x上，∴=n2﹣3n，解得：n1=﹣，n2=4（不合题意，舍去）∴N点的坐标为（﹣，）．方法一：如图1，将△NOB沿x轴翻折，得到△N1OB1，则N 1（，），B1（4，﹣4），∴O、D、B1都在直线y=﹣x上．∵△P 1OD∽△NOB，△NOB≌△N1OB1，∴△P1OD∽△N1OB1，∴，∴点P1的坐标为（，）．将△OP1D沿直线y=﹣x翻折，可得另一个满足条件的点P2（，），方法二：如图2，将△NOB绕原点顺时针旋转90°，得到△N2OB2，则N2（，），B2（4，﹣4），∴O、D、B1都在直线y=﹣x上．∵△P 1OD∽△NOB，△NOB≌△N2OB2，∴△P1OD∽△N2OB2，∴，∴点P1的坐标为（，）．将△OP1D沿直线y=﹣x翻折，可得另一个满足条件的点P2（，），方法三：∵直线OB：y=x是一三象限平分线，∴A（3，0）关于直线OB的对称点为A′（0，3），∴得：x1=4（舍），x2=﹣，∴N（﹣，），∵D（2，﹣2），∴l OD：y=﹣x，∵l OD：y=x，∴OD⊥OB，∵△POD∽△NOB，∴N（﹣，）旋转90°后N1（，）或N关于x轴对称点N2（﹣，﹣），∵OB=4，OD=2，∴，∵P为ON 1或ON2中点，∴P1（，），P2（，）．12.解：（1）a=﹣1，b=﹣2，顶点C的坐标为（﹣1，4）；（2）假设在y轴上存在满足条件的点D，过点C作CE⊥y轴于点E．由∠CDA=90°得，∠1+∠2=90°．又∠2+∠3=90°，∴∠3=∠1．又∵∠CED=∠DOA=90°，∴△CED∽△DOA，∴．设D（0，c），则．变形得c2﹣4c+3=0，解之得c1=3，c2=1．综合上述：在y轴上存在点D（0，3）或（0，1），使△ACD是以AC为斜边的直角三角形．（3）①若点P在对称轴右侧（如图①），只能是△PCQ∽△CAH，得∠QCP=∠CAH．延长CP交x轴于M，∴AM=CM，∴AM2=CM2．设M（m，0），则（m+3）2=42+（m+1）2，∴m=2，即M（2，0）．设直线CM的解析式为y=k1x+b1，则，解之得，．∴直线CM的解析式．联立，解之得或（舍去）．∴．②若点P在对称轴左侧（如图②），只能是△PCQ∽△ACH，得∠PCQ=∠ACH．过A作CA的垂线交PC于点F，作FN⊥x轴于点N．由△CFA∽△CAH得，由△FNA∽△AHC得．∴AN=2，FN=1，CH=4，HO=1，则AH=2，∴点F坐标为（﹣5，1）．设直线CF的解析式为y=k2x+b2，则，解之得．∴直线CF的解析式．联立，解之得或（舍去）．∴．∴满足条件的点P坐标为或．13.解：（1）∵直线l：y=3x+3与x轴交于点A，与y轴交于点B，∴A（﹣1，0），B（0，3）；∵把△AOB沿y轴翻折，点A落到点C，∴C（1，0）．设直线BD的解析式为：y=kx+b，∵点B（0，3），D（3，0）在直线BD上，∴，解得k=﹣1，b=3，∴直线BD的解析式为：y=﹣x+3．设抛物线的解析式为：y=a（x﹣1）（x﹣3），∵点B（0，3）在抛物线上，∴3=a×（﹣1）×（﹣3），解得：a=1，∴抛物线的解析式为：y=（x﹣1）（x﹣3）=x2﹣4x+3．（2）抛物线的解析式为：y=x2﹣4x+3=（x﹣2）2﹣1，∴抛物线的对称轴为直线x=2，顶点坐标为（2，﹣1）．直线BD：y=﹣x+3与抛物线的对称轴交于点M，令x=2，得y=1，∴M（2，1）．设对称轴与x轴交点为点F，则CF=FD=MF=1，∴△MCD为等腰直角三角形．∵以点N、B、D为顶点的三角形与△MCD相似，∴△BND为等腰直角三角形．如答图1所示：（I）若BD为斜边，则易知此时直角顶点为原点O，∴N1（0，0）；（II）若BD为直角边，B为直角顶点，则点N在x轴负半轴上，∵OB=OD=ON2=3，∴N2（﹣3，0）；（III）若BD为直角边，D为直角顶点，则点N在y轴负半轴上，∵OB=OD=ON3=3，∴N3（0，﹣3）．∴满足条件的点N坐标为：（0，0），（﹣3，0）或（0，﹣3）．（3）方法一：假设存在点P，使S△PBD=6，设点P坐标为（m，n）．（I）当点P位于直线BD上方时，如答图2所示：过点P作PE⊥x轴于点E，则PE=n，DE=m﹣3．S△PBD=S梯形PEOB﹣S△BOD﹣S△PDE=（3+n）•m﹣×3×3﹣（m﹣3）•n=6，化简得：m+n=7 ①，∵P（m，n）在抛物线上，∴n=m2﹣4m+3，代入①式整理得：m2﹣3m﹣4=0，解得：m1=4，m2=﹣1，∴n1=3，n2=8，∴P1（4，3），P2（﹣1，8）；（II）当点P位于直线BD下方时，如答图3所示：过点P作PE⊥y轴于点E，则PE=m，OE=﹣n，BE=3﹣n．S△PBD=S梯形PEOD+S△BOD﹣S△PBE=（3+m）•（﹣n）+×3×3﹣（3﹣n）•m=6，化简得：m+n=﹣1 ②，∵P（m，n）在抛物线上，∴n=m2﹣4m+3，代入②式整理得：m2﹣3m+4=0，△=﹣7＜0，此方程无解．故此时点P不存在．综上所述，在抛物线上存在点P，使S△PBD=6，点P的坐标为（4，3）或（﹣1，8）．方法二：假设存在点P，使S△PBD=6，过点P作直线l平行BD，则l与BD的距离为d，∵BD==3，∴S△PBD=BD×d，∴d=2，∵BD与y轴夹角为45°，∴BB′=4，∴将BD上移或下移4个单位，①上移4个单位，l解析式为：y=﹣x+7，∵y=x2﹣4x+3，∴x2﹣3x﹣4=0，∴x1=4，x2=﹣1，②下移4个单位，l解析式为y=﹣x﹣1，∵y=x2﹣4x+3，∴x2﹣3x+4=0，△＜0，∴此方程无解，综上所述，点P的坐标为（4，3）或（﹣1，8）．14.方法一：解：（1）∵该抛物线过点C（0，2），∴可设该抛物线的解析式为y=ax2+bx+2．将A（﹣1，0），B（4，0）代入，得，解得，∴抛物线的解析式为：y=﹣x2+x+2．（2）存在．由图象可知，以A、B为直角顶点的△ABE不存在，所以△ABE只可能是以点E为直角顶点的三角形．在Rt△BOC中，OC=2，OB=4，∴BC==．在Rt△BOC中，设BC边上的高为h，则×h=×2×4，∴h=．∵△BEA∽△COB，设E点坐标为（x，y），∴=，∴y=±2将y=2代入抛物线y=﹣x2+x+2，得x1=0，x2=3．当y=﹣2时，不合题意舍去．∴E点坐标为（0，2），（3，2）．（3）如图2，连结AC，作DE⊥x轴于点E，作BF⊥AD于点F，∴∠BED=∠BFD=∠AFB=90°．设BC的解析式为y=kx+b，由图象，得，∴，y BC=﹣x+2．由BC∥AD，设AD的解析式为y=﹣x+n，由图象，得0=﹣×（﹣1）+n ∴n=﹣，y AD=﹣x﹣．∴﹣x2+x+2=﹣x﹣，解得：x1=﹣1，x2=5∴D（﹣1，0）与A重合，舍去；∴D（5，﹣3）．∵DE⊥x轴，∴DE=3，OE=5．由勾股定理，得BD=．∵A（﹣1，0），B（4，0），C（0，2），∴OA=1，OB=4，OC=2．∴AB=5在Rt△AOC中，Rt△BOC中，由勾股定理，得AC=，BC=2，∴AC2=5，BC2=20，AB2=25，∴AC2+BC2=AB2∴△ACB是直角三角形，∴∠ACB=90°．∵BC∥AD，∴∠CAF+∠ACB=180°，∴∠CAF=90°．∴∠CAF=∠ACB=∠AFB=90°，∴四边形ACBF是矩形，∴AC=BF=，在Rt△BFD中，由勾股定理，得DF=，∴DF=BF，∴∠ADB=45°．方法二：（1）略．（2）∵以A、B、E为顶点的三角形与△COB相似，∴AE⊥BE且或，∵E为抛物线上一动点，∴设E（t，﹣），A（﹣1，0），B（4，0），∴，∴t2﹣3t=0，解得：t1=0，t2=3，∴E1（0，2），E2（3，2），①当E1（0，2）时，AE=，BE=，∴，∵，∴，∴△ABE∽△COB，②当E2（3，2）时，同理△ABE∽△COB，∴E1（0，2），E2（3，2）．（3）过B点作AD的垂线，垂足为H，∵B（4，0），C（0，2），∴K BC==﹣，∵BC∥AD，∴K AD=﹣，l AD：y=﹣x﹣，∵BH⊥AD，∴K BH×K AD=﹣1，∴K BH=2，l BH：y=2x﹣8，∴l AD与l BH的交点H（3，﹣2），∴，解得x1=﹣1（舍），x2=5，∴D（5，﹣3），∵B（4，0），H（3，﹣2），∴BH=，BD=，∴sin∠BDH=，∴∠BDA=45°．15.解：（1）把A（﹣1，0）代入得c=﹣，∴抛物线解析式为（2）如图1，过点C作CH⊥EF于点H，∵∠CEF=∠CFG，FG⊥y轴于点G∴△EHC∽△FGC∵E（m，n）∴F（m，）又∵C（0，﹣）∴EH=n+，CH=﹣m，FG=﹣m，CG=m2又∵，则∴n+=2∴n=当F点位于E点上方时，则∠CEF＞90°；又∠CFG肯定为锐角，故这种情形不符合题意．由此当n=时，代入抛物线解析式，求得m=±2，又E点位于第二象限，所以﹣2＜m＜0．（3）由题意可知P（t，0），M（t，）∵PM⊥x轴交抛物线于点M，∠OBQ=∠OMP，∴△OPM∽△QPB．∴．其中OP=t，PM=，PB=1﹣t，∴PQ=．BQ=∴PQ+BQ+PB=．∴△PBQ的周长为2．16.解：（1）设抛物线的解析式为y=a（x﹣1）2﹣1，将B点坐标代入函数解析式，得（5﹣1）2a﹣1=3，解得a=．故抛物线的解析式为y=（x﹣1）2﹣1；（2）由勾股定理，得OA2=11+12=2，OB2=52+32=34，AB2=（5﹣1）2+（3+1）2=32，OA2+AB2=OB2，∴∠OAB=90°，O到直线AB的距离是OA=；（3）设M（a，b），N（a，0）当y=0时，（x﹣1）2﹣1=0，解得x1=3，x2=﹣1，D（3，0），DN=3﹣a．①当△MND∽△OAB时，=，即=，化简，得4b=a﹣3 ①M在抛物线上，得b=（a﹣1）2﹣1 ②联立①②，得，解得a1=3（不符合题意，舍），a2=﹣2，b=，M1（﹣2，），当△MND∽△BAO时，=，即=，化简，得b=12﹣4a ③，联立②③，得，解得a1=3（不符合题意，舍），a2=﹣17，b=12﹣4×（﹣17）=80，M2（﹣17，80）．综上所述：当△DMN与△OAB相似时，点M的坐标（﹣2，），（﹣17，80）．17.解：（1）∵抛物线过G（2，2），∴把G坐标代入抛物线解析式得：2=﹣（2+2）（2﹣m），解得：m=4；（2）①令y=0，得到﹣（x+2）（x﹣m）=0，解得：x1=﹣2，x2=m，∵m＞0，∴A（﹣2，0），B（m，0），把m=4代入得：B（4，0），∴AB=6，令x=9，得到y=2，即C（0，2），∴OC=2，则S△ABC=×6×2=6；②∵A（﹣2，0），B（4，0），∴抛物线解析式为y=﹣（x+2）（x﹣4）的对称轴为x=1，如图1，连接BC交对称轴于点H，由对称轴的性质和两点之间线段最短的性质可得：此时AH+CH=BH+CH=BC 最小，设直线BC的解析式为y=kx+b，把B与C坐标代入得：，解得：，∴直线BC解析式为y=﹣x+2，令x=1，得到y=，即H（1，）；（3）在第四象限内，抛物线上存在点M，使得以点A、B、M为顶点的三角形与△ACB相似，分两种情况考虑：（i）当△ACB∽△ABM时，则有=，即AB2=AC•AM，∵A（﹣2，0），C（0，2），即OA=OC=2，∴∠CAB=45°，∠BAM=45°，如图2，过M作MN⊥x轴，交x轴于点N，则AN=MN，∴OA+ON=2+ON=MN，设M（x，﹣x﹣2）（x＞0），把M坐标代入抛物线解析式得：﹣x﹣2=﹣（x+2）（x﹣m），∵x＞0，∴x+2＞0，∵m＞0，∴x=2m，即M（2m，﹣2m﹣2），∴AM==2（m+1），∵AB2=AC•AM，AC=2，AB=m+2，∴（m+2）2=2•2（m+1），解得：m=2±2，∵m＞0，∴m=2+2；（ii）当△ACB∽△MBA时，则=，即AB2=CB•MA，∵∠CBA=∠BAM，∠ANM=∠BOC=90°，∴△ANM∽△BOC，∴=，∵OB=m，设ON=x，∴=，即MN=（x+2），令M（x，﹣（x+2））（x＞0），把M坐标代入抛物线解析式得：﹣（x+2）=﹣（x+2）（x﹣m），∵x＞0，∴x+2＞0，∵m＞0，∴x=m+2，即M（m+2，﹣（m+4）），∵AB2=CB•MA，CB=，AN=m+4，MN=（m+4），∴（m+2）2=•，整理得：=0，显然不成立，18.（1）证明：∵y=x2﹣2mx+m2+m﹣1=（x﹣m）2+m﹣1，∴点P的坐标为（m，m﹣1），∵当x=m时，y=x﹣1=m﹣1，∴点P在直线l上；（2）解：当m=﹣3时，抛物线解析式为y=x2+6x+5，当y=0时，x2+6x+5=0，解得x1=﹣1，x2=﹣5，则A（﹣5，0），当x=0时，y=x2+6x+5=5，则C（0，5），可得解方程组，解得或，则P（﹣3，﹣4），Q（﹣2，﹣3），作ME⊥y轴于E，PF⊥x轴于F，QG⊥x轴于G，如图，∵OA=OC=5，∴△OAC为等腰直角三角形，∴∠ACO=45°，∴∠MCE=45°﹣∠ACM，∵QG=3，OG=2，∴AG=OA﹣OG=3=QG，∴△AQG为等腰直角三角形，∴∠QAG=45°，∵∠APF=90°﹣∠PAF=90°﹣（∠PAQ+45°）=45°﹣∠PAQ，∵∠ACM=∠PAQ，∴∠APF=∠MCE，∴Rt△CME∽Rt△PAF，∴=，设M（x，x2+6x+5），∴ME=﹣x，CE=5﹣（x2+6x+5）=﹣x2﹣6x，∴=，整理得x2+4x=0，解得x1=0（舍去），x2=﹣4，∴点M的坐标为（﹣4，﹣3）；（3）解：解方程组得或，则P（m，m﹣1），Q（m+1，m），∴PQ2=（m+1﹣m）2+（m﹣m+1）2=2，OQ2=（m+1）2+m2=2m2+2m+1，OP2=m2+（m﹣1）2=2m2﹣2m+1，当PQ=OQ时，2m2+2m+1=2，解得m1=，m2=；当PQ=OP时，2m2﹣2m+1=2，解得m1=，m2=；当OP=OQ时，2m2+2m+1=2m2﹣2m+1，解得m=0，综上所述，m的值为0，，，，．19.解：（1）令y=0得x1=﹣2，x2=4，∴点A（﹣2，0）、B（4，0）令x=0得y=﹣，∴点C（0，﹣）（2）将x=1代入抛物线的解析式得y=﹣∴点M的坐标为（1，﹣）∴点M关于直线x=﹣2的对称点M′的坐标为（﹣5，）设直线M′B的解析式为y=kx+b将点M′、B的坐标代入得：解得：所以直线M′B的解析式为y=．将x=﹣2代入得：y=﹣，所以n=﹣．（3）过点D作DE⊥BA，垂足为E．由勾股定理得：AD==3，BD=，如下图，①当P1AB∽△ADB时，即：∴P1B=6过点P1作P1M1⊥AB，垂足为M1．∴即：解得：P1M1=6，∵即：解得：BM1=12∴点P1的坐标为（﹣8，6）∵点P1不在抛物线上，所以此种情况不存在；②当△P2AB∽△BDA时，即：∴P2B=6过点P2作P2M2⊥AB，垂足为M2．∴，即：∴P2M2=2∵，即：∴M2B=8∴点P2的坐标为（﹣4，2）将x=﹣4代入抛物线的解析式得：y=2，∴点P2在抛物线上．由抛物线的对称性可知：点P2与点P4关于直线x=1对称，∴P4的坐标为（6，2），当点P3位于点C处时，两三角形全等，所以点P3的坐标为（0，﹣），综上所述点P的坐标为：（﹣4，2）或（6，2）或（0，﹣）时，以P、A、B为顶点的三角形与△ABD相似．20.解：（1）∵点A1（1，2）在抛物线的解析式为y=ax2上，∴a=2；（2）A n B n=2x2=2×[（）n﹣1]2=，B n B n+1=；（3）由Rt△A n B n B n+1是等腰直角三角形得A n B n=B n B n+1，则：=，2n﹣3=n，n=3，∴当n=3时，Rt△A n B n B n+1是等腰直角三角形，②依题意得，∠A k B k B k+1=∠A m B m B m+1=90°，有两种情况：i）当Rt△A k B k B k+1∽Rt△A m B m B m+1时，=，=，=，所以，k=m（舍去），ii）当Rt△A k B k B k+1∽Rt△B m+1B m A m时，=，=，=，∴k+m=6，∵1≤k＜m≤n（k，m均为正整数），∴取或；当时，Rt△A1B1B2∽Rt△B6B5A5，相似比为：==64，当时，Rt△A2B2B3∽Rt△B5B4A4，相似比为：==8，所以：存在Rt△A k B k B k+1与Rt△A m B m B m+1相似，其相似比为64：1或8：1．。

2016年上海市闵行区中考数学一模试卷一、选择题（本大题共6题，每题4分，共24分）1．在△ABC中，点D、E分别在边AB、AC上，下列条件中不能判定DE∥BC的是（）A．=B．=C．=D．=2．将二次函数y=x2﹣1的图象向右平移一个单位，向下平移2个单位得到（）A．y=（x﹣1）2+1 B．y=（x+1）2+1 C．y=（x﹣1）2﹣3 D．y=（x+1）2+33．已知α为锐角，且sinα=，那么α的余弦值为（）A．B．C．D．4．抛物线y=ax2+bx+c的图象经过原点和第一、二、三象限，那么下列结论成立的是（）A．a＞0，b＞0，c=0 B．a＞0，b＜0，c=0 C．a＜0，b＞0，c=0 D．a＜0，b＜0，c=05．在比例尺为1：10000的地图上，一块面积为2cm2的区域表示的实际面积是（）A．2000000cm2B．20000m2C．4000000m2D．40000m26．如图，矩形ABCD的长为6，宽为3，点O1为矩形的中心，⊙O2的半径为1，O1O2⊥AB于点P，O1O2=6．若⊙O2绕点P按顺时针方向旋转360°，在旋转过程中，⊙O2与矩形的边只有一个公共点的情况一共出现（）A．3次B．4次C．5次D．6次二、填空题（本大题共12小题，每题4分，满分48分）7．如果，那么=．8．如果两个相似三角形周长的比是2：3，那么它们的相似比是．9．已知线段AB的长为2厘米，点P是线段AB的黄金分割点（AP＜BP），那么BP的长是厘米．10．如图，在△ABC中，∠ACB=90°，点F在边AC的延长线上，且FD⊥AB，垂足为点D，如果AD=6，AB=10，ED=2，那么FD=．11．在Rt△ABC中，∠C=90°，cosA=，AC=2，那么BC=．12．已知一条斜坡，向上前进5米，水平高度升高了4米，那么坡比为．13．过△ABC的重心作DE∥BC，分别交AB于点D，AC于点E，如果=，=，那么=．14．方程ax2+bx+c=0（a≠0）的两根为﹣3和1，那么抛物线y=ax2+bx+c（a≠0）的对称轴是直线．15．在Rt△ABC中，∠C=90°，AC=12，BC=5，以点A为圆心作⊙A，要使B、C两点中的一点在圆外，另一点在圆内，那么⊙A的半径长r的取值范围为．16．已知⊙O1与⊙O2内切，⊙O1的半径长是3厘米，圆心距O1O2=2厘米，那么⊙O2的半径长等于厘米．17．闵行体育公园的圆形喷水池的水柱（如图1）如果曲线APB表示落点B离点O最远的一条水流（如图2），其上的水珠的高度）y（米）关于水平距离x（米）的函数解析式为y=﹣x2+4x+，那么圆形水池的半径至少为米时，才能使喷出的水流不落在水池外．18．将一副三角尺如图摆放，其中在Rt△ABC中，∠ACB=90°，∠B=60°，在Rt△EDF中，∠EDF=90°，∠E=45°．点D为边AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转角α（0°＜α＜60°）后得△E′DF′，DE′交AC于点M，DF′交BC于点N，那么的值为．三、解答题（本大题共7小题，满分78分）19．如图，已知Rt△ABC的斜边AB在x轴上，斜边上的高CO在y轴的正半轴上，且OA=1，OC=2，求经过A、B、C三点的二次函数解析式．20．已知：如图，在⊙O中，弦CD垂直于直径AB，垂足为点E，如果∠BAD=30°，且BE=2，求弦CD的长．21．如图，已知四边形ABCD，点P、Q、R分别是对角线AC、BD和边AB的中点，设=，=．（1）试用，的线性组合表示向量；（需写出必要的说理过程）（2）画出向量分别在，方向上的分向量．22．如图，一只猫头鹰蹲在树AC上的B处，通过墙顶F发现一只老鼠在E处，刚想起飞捕捉时，老鼠突然跑到矮墙DF的阴影下，猫头鹰立即从B处向上飞至树上C处时，恰巧可以通过墙顶F看到老鼠躲在M处（A、D、M、E四点在同一条直线上）．已知，猫头鹰从B点观测E点的俯角为37°，从C点观察M点的俯角为53°，且DF=3米，AB=6米．求猫头鹰从B处飞高了多少米时，又发现了这只老鼠？（结果精确到0.01米）（参考数据：sin37°=cos53°=0.602，cos37°=sin53°=0.799，tan37°=c ot53°=0.754，cot37°=tan53°=1.327）．23．如图，已知在△ABC中AB=AC，点D为BC边的中点，点F在边AB上，点E在线段DF的延长线上，且∠BAE=∠BDF，点M在线段DF上，且∠EBM=∠C．（1）求证：EB•BD=BM•AB；（2）求证：AE⊥BE．24．如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，B点的坐标为（3，0），与y轴交于点C（0，﹣3），点P是直线BC下方抛物线上的任意一点．（1）求这个二次函数y=x2+bx+c的解析式．（2）连接PO，PC，并将△POC沿y轴对折，得到四边形POP′C，如果四边形POP′C为菱形，求点P的坐标．（3）如果点P在运动过程中，能使得以P、C、B为顶点的三角形与△AOC相似，请求出此时点P 的坐标．25．如图，在直角梯形ABCD中，AB∥CD，∠ABC=90°，对角线AC、BD交于点G，已知AB=BC=3，tan∠BDC=，点E是射线BC上任意一点，过点B作BF⊥DE，垂足为点F，交射线AC于点M，射线DC于点H．（1）当点F是线段BH中点时，求线段CH的长；（2）当点E在线段BC上时（点E不与B、C重合），设BE=x，CM=y，求y关于x的函数解析式，并指出x的取值范围；（3）连接GF，如果线段GF与直角梯形ABCD中的一条边（AD除外）垂直时，求x的值．2016年上海市闵行区中考数学一模试卷参考答案与试题解析一、选择题（本大题共6题，每题4分，共24分）1．在△ABC中，点D、E分别在边AB、AC上，下列条件中不能判定DE∥BC的是（）A．=B．=C．=D．=【考点】平行线分线段成比例．【分析】根据平行线分线段成比例定理对各个选项进行判断即可．【解答】解：∵=，∴DE∥BC，选项A不符合题意；∵=，∴DE∥BC，选项B不符合题意；∵=，∴DE∥BC，选项C不符合题意；=，DE∥BC不一定成立，选项D符合题意．故选：D．【点评】本题考查平行线分线段成比例定理，如果一条直线截三角形的两边（或两边的延长线）所得的对应线段成比例，那么这条直线平行于三角形的第三边2．将二次函数y=x2﹣1的图象向右平移一个单位，向下平移2个单位得到（）A．y=（x﹣1）2+1 B．y=（x+1）2+1 C．y=（x﹣1）2﹣3 D．y=（x+1）2+3【考点】二次函数图象与几何变换．【专题】几何变换．【分析】先根据二次函数的性质得到抛物线y=x2﹣1的顶点坐标为（0，﹣1），再利用点平移的规律，点（0，﹣1）平移后的对应点的坐标为（1，﹣3），然后根据顶点式写出平移后的抛物线解析式．【解答】解：抛物线y=x2﹣1的顶点坐标为（0，﹣1），把点（0，﹣1）向右平移一个单位，向下平移2个单位得到对应点的坐标为（1，﹣3），所以平移后的抛物线解析式为y=（x﹣1）2﹣3．故选C．【点评】本题考查了二次函数图象与几何变换：由于抛物线平移后的形状不变，故a不变，所以求平移后的抛物线解析式通常可利用两种方法：一是求出原抛物线上任意两点平移后的坐标，利用待定系数法求出解析式；二是只考虑平移后的顶点坐标，即可求出解析式．3．已知α为锐角，且sinα=，那么α的余弦值为（）A．B．C．D．【考点】同角三角函数的关系．【专题】计算题．【分析】利用平方关系得到cosα=，然后把sinα=代入计算即可．【解答】解：∵sin2α+cos2α=1，∴cosα===．故选D．【点评】本题考查了同角三角函数的关系：sin2A+cos2A=1．4．抛物线y=ax2+bx+c的图象经过原点和第一、二、三象限，那么下列结论成立的是（）A．a＞0，b＞0，c=0 B．a＞0，b＜0，c=0 C．a＜0，b＞0，c=0 D．a＜0，b＜0，c=0【考点】二次函数图象与系数的关系．【专题】压轴题．【分析】先根据图象经过象限的情况判断出a的符号，由抛物线与y轴的交点判断c的符号，然后根据对称轴及抛物线与x轴交点情况进行推理．【解答】解：∵抛物线经过原点，∴c=0，∵抛物线经过第一，二，三象限，可推测出抛物线开口向上，对称轴在y轴左侧∴a＞0，∵对称轴在y轴左侧，∴对称轴为x=＜0，又因为a＞0，∴b＞0．故选A．【点评】解决此类题目，可现根据条件画出函数图象的草图再做解答．5．在比例尺为1：10000的地图上，一块面积为2cm2的区域表示的实际面积是（）A．2000000cm2B．20000m2C．4000000m2D．40000m2【考点】比例线段．【专题】常规题型．【分析】先根据面积的比等于比例尺的平方求出实际面积，然后再进行单位转化．【解答】解：设实际面积是x，则=（）2，解得x=200 000 000cm2，∵1m2=10000cm2，∴200 000 000cm2=20000m2．故选B．【点评】本题主要考查了比例线段中的比例尺，利用面积的比等于比例尺的平方是解题的关键，本题单位换算容易出错，需要特别注意．6．如图，矩形ABCD的长为6，宽为3，点O1为矩形的中心，⊙O2的半径为1，O1O2⊥AB于点P，O1O2=6．若⊙O2绕点P按顺时针方向旋转360°，在旋转过程中，⊙O2与矩形的边只有一个公共点的情况一共出现（）A．3次B．4次C．5次D．6次【考点】直线与圆的位置关系．【专题】分类讨论．【分析】根据题意作出图形，直接写出答案即可．【解答】解：如图，⊙O2与矩形的边只有一个公共点的情况一共出现4次，故选：B．【点评】本题考查了直线与圆的位置关系，解题的关键是了解当圆与直线相切时，点到圆心的距离等于圆的半径．二、填空题（本大题共12小题，每题4分，满分48分）7．如果，那么=．【考点】比例的性质．【分析】由，根据比例的性质，即可求得的值．【解答】解：∵，∴==．故答案为：．【点评】此题考查了比例的性质．此题比较简单，解题的关键是注意掌握比例的性质与比例变形．8．如果两个相似三角形周长的比是2：3，那么它们的相似比是2：3．【考点】相似三角形的性质．【分析】根据相似三角形周长的比等于相似比解答即可．【解答】解：∵两个相似三角形周长的比是2：3，∴两个相似三角形相似比是2：3，故答案为：2：3．【点评】本题考查的是相似三角形性质，掌握相似三角形周长的比等于相似比是解题的关键．9．已知线段AB的长为2厘米，点P是线段AB的黄金分割点（AP＜BP），那么BP的长是﹣1厘米．【考点】黄金分割．【分析】根据黄金比是进行计算即可．【解答】解：∵点P是线段AB的黄金分割点，AP＜BP，∴BP=AB=﹣1厘米．故答案为：﹣1．【点评】本题考查的是黄金分割的概念，把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值（）叫做黄金比．10．如图，在△ABC中，∠ACB=90°，点F在边AC的延长线上，且FD⊥AB，垂足为点D，如果AD=6，AB=10，ED=2，那么FD=12．【考点】相似三角形的判定与性质．【分析】根据垂直的定义得到∠BDE=∠ADF=90°，根据三角形的内角和得到∠F=∠B，推出△ADF∽△BDE，根据相似三角形的性质得到，代入数据即可得到结论．【解答】解：∵FD⊥AB，∴∠BDE=∠ADF=90°，∵∠ACB=90°，∠CEF=∠BED，∴∠F=∠B，∴△ADF∽△BDE，∴，即，解得：DF=12，故答案为：12．【点评】本题考查了直角三角形的性质，相似三角形的判定和性质，熟练掌握相似三角形的判定和性质是解题的关键．11．在Rt△ABC中，∠C=90°，cosA=，AC=2，那么BC=4．【考点】解直角三角形．【分析】根据∠C=90°，得出cosA=，再根据AC=2，求出AB，最后根据勾股定理即可求出BC．【解答】解：∵∠C=90°，∴cosA==，∵AC=2，∴AB=6，∴BC===4．故答案为：4．【点评】本题考查了解直角三角形，用到的知识点锐角三角函数、勾股定理，关键是根据题意求出AB．12．已知一条斜坡，向上前进5米，水平高度升高了4米，那么坡比为1：0.75．【考点】解直角三角形的应用-坡度坡角问题．【分析】先求出水平方向上前进的距离，然后根据坡比=竖直方向上升的距离：水平方向前进的距离，即可解题．【解答】解：如图所示：AC=5米，BC=4米，则AB==3米，则坡比===1：0.75．故答案为：1：0.75．【点评】本题考查了解直角三角形的应用﹣坡度坡角问题，坡度是坡面的铅直高度h和水平宽度l的比，又叫做坡比，它是一个比值，反映了斜坡的陡峭程度，一般用i表示，常写成i=1：m的形式．13．过△ABC的重心作DE∥BC，分别交AB于点D，AC于点E，如果=，=，那么=﹣．【考点】*平面向量；三角形的重心．【分析】由过△ABC的重心作DE∥BC，可得=，再利用三角形法则求解即可求得答案．【解答】解：∵过△ABC的重心作DE∥BC，∴=，∴==（﹣）=﹣．故答案为：﹣．【点评】此题考查了平面向量的知识以及三角形重心的性质．注意掌握三角形法则的应用．14．方程ax2+bx+c=0（a≠0）的两根为﹣3和1，那么抛物线y=ax2+bx+c（a≠0）的对称轴是直线x=﹣1．【考点】抛物线与x轴的交点．【分析】根据函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根及两根之和公式来解决此题．【解答】解：∵函数y=ax2+bx+c的图象与x轴的交点的横坐标就是方程ax2+bx+c=0的根，∵x1+x2=﹣3+1=﹣=﹣2．则对称轴x=﹣=×（﹣）=×（﹣2）=﹣1．【点评】要求熟悉二次函数与一元二次方程的关系和两根之和公式，并熟练运用．（利用二次函数的对称性解答更直接）15．在Rt△ABC中，∠C=90°，AC=12，BC=5，以点A为圆心作⊙A，要使B、C两点中的一点在圆外，另一点在圆内，那么⊙A的半径长r的取值范围为12＜r＜13．【考点】点与圆的位置关系．【分析】熟记“设点到圆心的距离为d，则当d=r时，点在圆上；当d＞r时，点在圆外；当d＜r时，点在圆内”即可求解，【解答】解：如果以点A为圆心作圆，使点C在圆A内，则r＞12，点B在圆A外，则r＜13，因而圆A半径r的取值范围为12＜r＜13．故答案为12＜r＜13．【点评】本题考查了对点与圆的位置关系的判断．设点到圆心的距离为d，则当d=r时，点在圆上；当d＞r时，点在圆外；当d＜r时，点在圆内．16．已知⊙O1与⊙O2内切，⊙O1的半径长是3厘米，圆心距O1O2=2厘米，那么⊙O2的半径长等于5或1厘米．【考点】圆与圆的位置关系．【专题】计算题．【分析】设⊙O2的半径为r，根据内切的判定方法得到r﹣3=2或3﹣r=2，然后解方程即可．【解答】解：设⊙O2的半径为r，∵⊙O1与⊙O2内切，∴r﹣3=2或3﹣r=2，∴r=5或r=1．故答案为5或1．【点评】本题考查了圆和圆的位置关系：设两圆的圆心距为d，两圆的半径分别为R、r：两圆外离⇔d＞R+r；两圆外切⇔d=R+r；两圆相交⇔R﹣r＜d＜R+r（R≥r）；两圆内切⇔d=R﹣r（R＞r）；两圆内含⇔d＜R﹣r（R＞r）．17．闵行体育公园的圆形喷水池的水柱（如图1）如果曲线APB表示落点B离点O最远的一条水流（如图2），其上的水珠的高度）y（米）关于水平距离x（米）的函数解析式为y=﹣x2+4x+，那么圆形水池的半径至少为米时，才能使喷出的水流不落在水池外．【考点】二次函数的应用．【分析】根据二次函数的解析式求得抛物线与x轴的交点坐标的横坐标，即为所求的结果．【解答】解：当y=0时，即﹣x2+4x+=0，解得x1=，x2=﹣（舍去）．答：水池的半径至少米时，才能使喷出的水流不落在水池外．故答案为：．【点评】本题考查了二次函数的应用，注意抛物线的解析式的三种形式在解决抛物线的问题中的作用．18．将一副三角尺如图摆放，其中在Rt△ABC中，∠ACB=90°，∠B=60°，在Rt△EDF中，∠EDF=90°，∠E=45°．点D为边AB的中点，DE交AC于点P，DF经过点C，将△EDF绕点D顺时针方向旋转角α（0°＜α＜60°）后得△E′DF′，DE′交AC于点M，DF′交BC于点N，那么的值为．【考点】旋转的性质．【分析】先根据直角三角形斜边上的中线性质得CD=AD=DB，则∠ACD=∠A=30°，∠BCD=∠B=60°，由于∠EDF=90°，可利用互余得∠CPD=60°，再根据旋转的性质得∠PDM=∠CDN=α，于是可判断△PDM∽△CDN，得到=，然后在Rt△PCD中利用正切的定义求解．【解答】解：∵点D为斜边AB的中点，∴CD=AD=DB，∴∠ACD=∠A=30°，∠BCD=∠B=60°，∵∠EDF=90°，∴∠CPD=60°，∴∠MPD=∠NC D，∵△EDF绕点D顺时针方向旋转α（0°＜α＜60°），∴∠PDM=∠CDN=α，∴△PDM∽△CDN，∴=，在Rt△PCD中，∵tan∠PCD=tan30°=，∴=tan30°=．故答案是：．【点评】本题考查了旋转的性质：对应点到旋转中心的距离相等；对应点与旋转中心所连线段的夹角等于旋转角；旋转前、后的图形全等．也考查了相似三角形的判定与性质．三、解答题（本大题共7小题，满分78分）19．如图，已知Rt△ABC的斜边AB在x轴上，斜边上的高CO在y轴的正半轴上，且OA=1，OC=2，求经过A、B、C三点的二次函数解析式．【考点】待定系数法求二次函数解析式．【分析】由同角的余角相等得到一对角相等，再由一对直角相等，得到三角形AOB与三角形AOC 相似，由相似得比例，求出OC的长，即可确定出C坐标；由B与C坐标设出抛物线的二根式，将A坐标代入求出a的值，确定出抛物线解析式即可．【解答】解：∵∠AOC=∠ACB=90°，∴∠CAO+∠ACO=90°，∠CAO+∠ABC=90°，∴∠ACO=∠ABC，又∵∠AOC=∠COB=90°，∴△ACO∽△CBO，∴=，即OC2=OB•OA，∵OA=1，OC=2，∴OB=4，则B（4，0），∵A（﹣1，0），C（0，2）设抛物线解析式为y=a（x+1）（x﹣4），将C（0，2）代入得：2=﹣4a，即a=﹣，则过A、B、C三点的抛物线的解析式为y=﹣（x+1）（x﹣4）=﹣x2+x+2，【点评】本题考查的是二次函数综合题，涉及到相似三角形的判定与性质以及用待定系数法求二次函数的解析式等知识，难度适中．20．已知：如图，在⊙O中，弦CD垂直于直径AB，垂足为点E，如果∠BAD=30°，且BE=2，求弦CD的长．【考点】垂径定理；解直角三角形．【分析】连接OD，设⊙O的半径为r，则OE=r﹣2，再根据圆周角定理得出∠DOE=60°，由直角三角形的性质可知OD=2OE，由此可得出r的长，在Rt△OED中根据勾股定理求出DE的长，进而可得出结论．【解答】解：连接OD，设⊙O的半径为r，则OE=r﹣2，∵∠BAD=30°，∴∠DOE=60°，∵CD⊥AB，∴CD=2DE，∠ODE=30°，∴OD=2OE，即r=2（r﹣2），解得r=4；∴OE=4﹣2=2，∴DE===2，∴CD=2DE=4．【点评】本题考查的是垂径定理，熟知平分弦的直径平分这条弦，并且平分弦所对的两条弧是解答此题的关键．21．如图，已知四边形ABCD，点P、Q、R分别是对角线AC、BD和边AB的中点，设=，=．（1）试用，的线性组合表示向量；（需写出必要的说理过程）（2）画出向量分别在，方向上的分向量．【考点】*平面向量．【分析】（1）由点P、Q、R分别是对角线AC、BD和边AB的中点，直接利用三角形中位线的性质，即可求得==﹣，==，再利用三角形法则求解即可求得答案；（2）利用平行线四边形法则求解即可求得答案．【解答】解：（1）∵点P、Q、R分别是对角线AC、BD和边AB的中点，∴==﹣，==，∴=+=﹣+；（2）如图：与即为所求．【点评】此题考查了平行向量的知识．注意掌握三角形法则与平行四边形法则的应用．22．如图，一只猫头鹰蹲在树AC上的B处，通过墙顶F发现一只老鼠在E处，刚想起飞捕捉时，老鼠突然跑到矮墙DF的阴影下，猫头鹰立即从B处向上飞至树上C处时，恰巧可以通过墙顶F看到老鼠躲在M处（A、D、M、E四点在同一条直线上）．已知，猫头鹰从B点观测E点的俯角为37°，从C点观察M点的俯角为53°，且DF=3米，AB=6米．求猫头鹰从B处飞高了多少米时，又发现了这只老鼠？（结果精确到0.01米）（参考数据：sin37°=cos53°=0.602，cos37°=sin53°=0.799，tan37°=cot53°=0.754，cot37°=tan53°=1.327）．【考点】解直角三角形的应用-仰角俯角问题．【分析】根据猫头鹰从B点观测E点的俯角为37°，可知∠E=37°，在△DEF中，已知DF的长度即可求得DE的长度，然后证得D是AE的中点，从而求得AE的长度，根据猫头鹰从C点观察M点的俯角为53°，可知∠AMC=53°，进而求得DM，即可求得AM，在△AMC中，根据余切函数求得AC，即可求得BC．【解答】解∵DF=3，∠E=37°，cot37°=，∴DE=3•cot37°，∵DF=3米，AB=6米，AC∥DF，∴D是AE的中点，∴AE=2DE=6•cot37°，∵cot53°=，∴DM=3•cot53°，∴AM=AD+DM=3（cot37°+cot53°），∵cot37°=，∴AC=AM•cot37°，∴BC=AC﹣6≈2.28（米）．【点评】本题考查了解直角三角形的应用，解答本题的关键是构造直角三角形并解直角三角形，利用三角函数求解相关线段，难度一般．23．如图，已知在△ABC中AB=AC，点D为BC边的中点，点F在边AB上，点E在线段DF的延长线上，且∠BAE=∠BDF，点M在线段DF上，且∠EBM=∠C．（1）求证：EB•BD=BM•AB；（2）求证：AE⊥BE．【考点】相似三角形的判定与性质．【专题】证明题．【分析】（1）根据等腰三角形的性质得到∠ABC=∠C，由已知条件得到∠EBM=∠C，等量代换得到∠EBM=∠ABC，求得∠ABE=∠DBM，推出△BEA∽△BDM，根据相似三角形的性质得到，于是得到结论；（2）连接AD，由等腰三角形的性质得到AD⊥BC，推出△ABD∽△EBM，根据相似三角形的性质得到∠ADB=∠EMB=90°，求得∠AEB=∠BMD=90°，于是得到结论．【解答】证明：（1）∵AB=AC，∴∠ABC=∠C，∵∠EBM=∠C，∴∠EBM=∠ABC，∴∠ABE=∠DBM，∵∠BAE=∠BDF，∴△BEA∽△BDM，∴，∴EB•BD=BM•AB；（2）连接AD，∵AB=AC，点D为BC边的中点，∴AD⊥BC，∵，∠ABD=∠EBM，∴△ABD∽△EBM，∴∠ADB=∠EMB=90°，∴∠AEB=∠BMD=90°，∴AE⊥BE．【点评】此题考查了相似三角形的判定与性质、勾股定理、等边三角形的判定与性质以及三角函数等知识．此题综合性较强，难度较大，解题的关键是准确作出辅助线，掌握转化思想与数形结合思想的应用．24．如图，在平面直角坐标系中，二次函数y=x2+bx+c的图象与x轴交于A、B两点，B点的坐标为（3，0），与y轴交于点C（0，﹣3），点P是直线BC下方抛物线上的任意一点．（1）求这个二次函数y=x2+bx+c的解析式．（2）连接PO，PC，并将△POC沿y轴对折，得到四边形POP′C，如果四边形POP′C为菱形，求点P的坐标．（3）如果点P在运动过程中，能使得以P、C、B为顶点的三角形与△AOC相似，请求出此时点P 的坐标．【考点】二次函数综合题．【分析】（1）根据待定系数法，可得函数解析式；（2）根据菱形的对角线互相垂直平分，可得P点的纵坐标，根据自变量与函数值的对应关系，可得答案；（3）分类讨论：①当∠PCB=90°，根据互相垂直的两条直线的一次项系数互为负倒数，可得BP的解析式，根据自变量与函数值的对应关系，可得P点坐标；根据勾股定理，可得BC，CP的长，根据两组对边对应成比例且夹角相等的两个三角形相似，可得答案；②当∠BPC=90°时，根据相似三角形的性质，可得P点的坐标，根据两组对边对应成比例且夹角相等的两个三角形相似，可得答案．【解答】解：（1）将B、C点代入函数解析式，得，解得，这个二次函数y=x2+bx+c的解析式为y=x2﹣2x﹣3；（2）四边形POP′C为菱形，得OC与PP′互相垂直平分，得y P=﹣，即x2﹣2x﹣3=﹣，解得x1=，x2=（舍），P（，﹣）；（3）∠PBC＜90°，①如图1，当∠PCB=90°时，过P作PH⊥y轴于点H，BC的解析式为y=x﹣3，CP的解析式为y=﹣x﹣3，设点P的坐标为（m，﹣3﹣m），将点P代入代入y═x2﹣2x﹣3中，解得m1=0（舍），m2=1，即P（1，﹣4）；AO=1，OC=3，CB==3，CP==，此时==3，△AOC∽△PCB；②如图2，当∠BPC=90°时，作PH⊥y轴于H，作BD⊥PH于D，BC的解析式为y=x﹣3，CP的解析式为y=﹣x﹣3，设点P的坐标为（m，﹣3﹣m），CH=﹣3﹣（m2﹣2m﹣3）=﹣m2+2m，PH=m，PD=3﹣m，BD=﹣（m2﹣2m﹣3）．△CHP∽△PDB，=，即=，解得m=，m=（不符合题意，舍），此时，==≠=3，以P、C、B为顶点的三角形与△AOC不相似；综上所述：P、C、B为顶点的三角形与△AOC相似，此时点P的坐标（1，﹣4）．【点评】本题考查了二次函数综合题，利用待定系数法求函数解析式；利用菱形的性质得出P点的坐标是解题关键；利用相似三角形的判定与性质得出关于m的方程是解题关键．25．如图，在直角梯形ABCD中，AB∥CD，∠ABC=90°，对角线AC、BD交于点G，已知AB=BC=3，tan∠BDC=，点E是射线BC上任意一点，过点B作BF⊥DE，垂足为点F，交射线AC于点M，射线DC于点H．（1）当点F是线段BH中点时，求线段CH的长；（2）当点E在线段BC上时（点E不与B、C重合），设BE=x，CM=y，求y关于x的函数解析式，并指出x的取值范围；（3）连接GF，如果线段GF与直角梯形ABCD中的一条边（AD除外）垂直时，求x的值．【考点】相似形综合题．【分析】（1））根据题意可先求出CD=6，根据BF⊥DE和F为线段BH中点的条件，由等腰三角形三线合一的性质得到△BHD为等腰三角形，从而求出BD=HD=3，再求CH=3﹣6；（2）设BE=x，CM=y，要求y关于x的函数解析式，先利用AB∥CH，得到成比例线段=，得到=，再根据△BCH∽△DCE，得到==，则可以用含x的式子表示CH=，代入=中，整理化简可得y=（根据点E在线段BC上，则可得到0＜x＜3）（3）①如下图2，当GF⊥BC时，此时GF∥AB∥CD，根据平行线等分线段定理得到==，根据题意易证△BCH∽△DCE，根据其相似比得BF=BH=DE，再根据△BFE∽△DCE的相似比=得到=，解方程即可得x=21﹣6（根据x=21+6＞3，舍去）②当E在射线BC上时（图3），GF∥BE，设GF与CD交点为K，先根据①中条件可求出GK=2，DK=4，设KF=a，则可得==，分别用含a的式子表示KH=，HC=，再利用tan∠KDF=tan∠CBH作为等量关系列方程=可解得a=（a=＜0故舍去）易求出CE=a=从而求出BE=CE+3=，再综合①②可知x的值为21﹣6或．【解答】解：（1）∵在直角梯形ABCD中，AB∥CD，∠ABC=90°∴∠DCB=90°∵AB=BC=3，tan∠BDC=∴CD=6∵BF⊥DE∴当F为线段BH中点时，△BHD为等腰三角形，∴BD=HD==3CH=DH﹣DC=3﹣6（2）∵AB∥CH，∴=又∵AC==3，∴=在△BCH与△DCE中，∠BCH=∠DCE=90°，∠HBC=∠EDC=90°﹣∠DHB，∴△BCH∽△DCE，∴==，则CH=，∴=，化简整理得：y=（0＜x＜3）；（3）①（图2）当GF⊥BC时，此时GF∥AB∥CD，==此时==∵△BCH∽△DCE∴===∴BF=BH=DE∴△BFE∽△DCE∴=∴=∴DE2=36x=（3﹣x）2+62，解得x=21﹣6（x=21+6＞3，故舍去）②当E在射线BC上时（图3），GF⊥DC即GF∥BE，设GF与CD交点为K，由①可知===，则GK=×3=2，DK=4设KF=a，则==，∴KH=，HC=，∵∠BCD=∠DKF=90°∴∠KDF=∠CBH∴tan∠KDF=tan∠CBH∴=解得a=（a=＜0故舍去）∵==∴CE=a=，BE=CE+3=综上可知：x的值为21﹣6或【点评】本题主要考查了平行线等分线段定理的应用和相似三角形的相似比作为等量关系列方程解方程的方法．（1）中根据条件判断出△BHD为等腰三角形是解题的关键；（2）中则主要是利用了相似三角形和平行线等分线段定理中的成比例线段作为等量关系，得到x与y之间的等量关系，整理即可得到y关于x的函数关系式；（3）中主要是根据线段GF与直角梯形ABCD中的一条边（AD 除外）垂直时的两种情况分类讨论，GF⊥BC和GF⊥DC时分别都有对应的相似三角形，根据相似三角形中的成比例线段作为等量关系列方程解方程即可．。

北京市2016年各区中考一模汇编抛物线1.【2016西城一模，第27题】在平面直角坐标系xOy 中，抛物线21C y x bx c ++：＝经过点()2,3A -，且与x 轴的一个交点为()30B ，． （1）求抛物线1C 的表达式；（2）D 是抛物线1C 与x 轴的另一个交点，点E 的坐标为()0m ，，其中0m >，ADE ∆的面积为214． ①求m 的值；②将抛物线1C 向上平移n 个单位，得到抛物线2C ，若当0x m ≤≤时，抛物线2C 与x 轴只有一个公共点，结合函数的图象，求n 的取值范围．2.【2016丰台一模，第27题】已知抛物线21(2)262y x m x m =+-+-的对称轴为直线x =1，与x 轴交于A ，B 两点（点A 在点B 的左侧），与y 轴交于点C . （1）求m 的值；（2）求A ，B ，C 三点的坐标；（3）过点C 作直线l ∥x 轴，将该抛物线在y 轴左侧的部分沿直线l 翻折，抛物线的其余部分保持不变，得到一个新的图象，记为G ．请你结合图象回答：当直线b x y +21=与图象G 只有一个公共点时，求b 的取值范围．3.【2016平谷一模，第26题】我们知道对于x 轴上的任意两点1(,0)A x ，2(,0)B x ，有AB =12x x -，而对于平面直角坐标系中的任意两点),(111y x P ，),(222y x P ，我们把2121y y x x -+-称为P l ，P 2两点间的直角距离，记作),(21P P d ，即),(21P P d =2121y y x x -+-.（1）已知O 为坐标原点，若点P 坐标为（1，3），则d (O ，P )＝____________；-3-2-1-1-2-3123321y xO（2）已知O 为坐标原点，动点()y x P ,满足(),2d O P =，请写出x 与y 之间满足的关系式，并在所给的直角坐标系中画出所有符合条件的点P 所组成的图形； （3）试求点M (2，3)到直线y =x +2的最小直角距离．4.【2016平谷一模，第27题】已知：直线l ：2y x =+与过点（0,﹣2），且与平行于x 轴的直线交于点A ，点A 关于直线1x =-的对称点为点B ．（1）求,A B 两点的坐标；（2）若抛物线2y x bx c =-++经过A ，B 两点，求抛物线解析式；（3）若抛物线2y x bx c =-++的顶点在直线l 上移动，当抛物线与线段AB 有一个公共点时，求抛物线顶点横坐标t 的取值范围．5.【2016朝阳一模，第27题】在平面直角坐标系xOy 中，抛物线c bx x y ++=2经过点（0，–3），（2，–3）． （1）求抛物线的表达式；（2）求抛物线的顶点坐标及与x 轴交点的坐标；（3）将c bx x y ++=2（y ≤0）的函数图象记为图象A ，图象A 关于x 轴对称的图象记为图象B ．已知一次函数y=mx +n ，设点H 是x 轴上一动点，其横坐标为a ，过点H 作x 轴的垂线，交图象A 于点P ，交图象B 于点Q ，交一次函数图象于点 N ．若只有当1<a<3时，点Q 在点N 上方，点N 在点P 上方，直接写出n 的值．6.【2016海淀一模，第27题】在平面直角坐标系xOy 中，抛物线224(0)y mx mx m m =-+-≠的顶点为A ，与x轴交于,B C 两点（点B 在点C 左侧），与y 轴交于点D 。

2016年初三一模知识点分类整理——二次函数一、选择题1. （宝山）抛物线542+-=x y 的开口方向………………（ ）A ．向上；B ．向下；C ．向左；D ．向右2. （宝山）已知二次函数y=ax 2+bx+c （a≠0）的图象如图1-2所示，则下列结论中正确的是（ ）A ．ac ＞0；B ．当x ＞-1时，y ＜0；C ． b=2a ；D ．9a+3b+c=0．3. （崇明）将抛物线2y x =先向右平移2个单位，再向下平移3个单位，所得抛物线的解析式是（ ） A. 2(2)3y x =++； B. 2(2)3y x =+-； C. 2(2)3y x =-+； D. 2(2)3y x =--；4. （奉贤）抛物线()212y x =-+的对称轴是（ ）A ．直线2x =；B ．直线2x =-；C ．直线1x =；D ．直线1x =-．5. （奉贤）抛物线223y x x =--与x 轴的交点个数是（ ）A. 0个 ； B ．1个； C ． 2个 ； D ． 3个． 6. （虹口）把二次函数241y x x =-+化成2()y a x m k =++的形式是（ ）A ．2(2)1y x =-+；B ．2(2)1y x =--；C ．2(2)3y x =-+； D.2(2)3y x =--． 7. （虹口）若将抛物线平移，得到新抛物线2(3)y x =+，则下列平移方法中，正确的是（ ）A ．向左平移3个单位；B ．向右平移3个单位；C ．向上平移3个单位；D ．向下平移3个单位． 8. （黄浦）下列函数中不是二次函数的有（ ）A. ()1y x x =- ；B.21y =- ； C. 2y x =- ； D. ()224y x x =+-． 9. （嘉定）已知二次函数23y x bx =++如图1-9，那么2(1)3y x b x =+-+的图像可能是（ ）A. B. C. D. 10. （闵行）将二次函数21y x =-的图像向右平移1个单位，向下平移2个单位得到（ ）A. 2(1)1y x =-+；B. 2(1)1y x =++；C. 2(1)3y x =--；D. 2(1)3y x =++；1-21-911. （闵行）抛物线2y ax bx c =++的图像经过原点和第一、二、三象限，则下列结论成立的是（ ）A. 0a >，0b >，0c =；B. 0a >，0b <，0c =；C. 0a <，0b >，0c =；D. 0a <，0b <，0c =； 12. （浦东）已知二次函数的图像如图1-12，那么a 、b 、c 的符号为( )A. a<0，b <0，c>0；B. a<0，b <0，c<0；C. a>0，b >0，c>0；D. a>0，b >0，c<0；13. （普陀）如果a 、b 同号，那么二次函数21y axbx =++的大致图像是（ ）A. B. C. D.14. （静安青浦）如果点(2,)A m 在抛物线2y x =上，将此抛物线向右平移3个单位后，点A 同时平移到点A '，那么A '坐标为（ ）A. (2,1)；B. (2,7)；C. (5,4)；D. (1,4)-15.（松江）如果二次函数2(0)y ax bx c a =++≠的图像如图1-15所示，那么（ A ．a ＜0，b ＞0，c ＞0； B ．a ＞0，b ＜0，c ＞0； C ．a ＞0，b ＞0，c ＜0； D ．a <0，b ＜0，c ＜0．16. （徐汇）将抛物线2)1(22-+=x y 向右平移2个单位，再向上平移2个单位后所得新抛物线的表达式是（ ）A. 2)3(2+=x y ；B. 2)3(+=x y ；C. 2)1(-=x y ；D. 2)1(2-=x y ． 17. （杨浦）将抛物线22y x =向上平移2个单位后所得抛物线的表达式是 （ ）A. 222+=x y ；B. 2)2(2+=x y ；C. 2)2(2-=x y ；D. 222-=x y ．18. （杨浦）下列图像中，有一个可能是函数20)y ax bx a b a =+++≠（的图像，它是 （ ）A.B. 19. （闸北）抛物线223y x =-+的顶点在（ ）111-1520. （闸北）已知，二次函数2y ax bx c =++（0a ≠）的图像如图1-20，则以下说法不正确的是（ ）A. 根据图像可得该函数y 有最小值；B. 当2x =-时，函数y 的值小于0C. 根据图像可得0a >，0b <；D. 当1x <-时，函数值y 随着x 的增大而减小；21. （长宁金山）二次函数1)2(2-+=x y 的图像可以由二次函数2x y =的图像平移得到，下列平移正确的是（ ）.A. 先向左平移2个单位，再向上平移1个单位B. 先向左平移2个单位，再向下平移1个单位C. 先向右平移2个单位，再向上平移1个单位D. 先向右平移2个单位，再向下平移1个单位 二、填空题1. （宝山）抛物线4)3(22+--=x y 的顶点坐标是 ．2. （宝山）若A(1，2)、B(3，2)、 C(0，5)、D(m ，5)是抛物线c bx ax y ++=2图像上的四点，则m = ．3. （宝山）已知A （4，y 1）、B （-4，y 2）是抛物线2)3(2-+=x y 的图像上两点，则y 1____y 2．4. （宝山）如图2-4抛物线322--=x x y 交x 轴于A(-1，0)、B （3，0），交y 轴于C （0，-3），M 是抛物线的顶点，现将抛物线沿平行于y 轴 的方向向上平移三个单位，则曲线CMB 在平移过程中扫过的面积 为 （面积单位）5. （崇明）抛物线2(2)3y a x x a =++-的开口向下，那么a 的取值范围是 ； 6. （奉贤）二次函数342+=x y 的顶点坐标为 ；7. （奉贤）如果抛物线k x k y -+=2)2(的开口向下，那么k 的取值范围是 ； 8. （奉贤）已知抛物线(4)y ax x =+，经过点A (5,9)和点B （m,9）,那么m = ； 9. （虹口）二次函数22y x x =-的图像的对称轴是直线 ． 10. （虹口）如果抛物线231y x x m =-+-+经过原点，那么m = ．11. （虹口） 已知点11(,)A x y 、22(,)B x y 为二次函数2(1)y x =-图像上的两点，若121x x <<，则y y （填“>”、“<”或“=”）；1-2012. （虹口）用“描点法”画二次函数2y ax bx c =++的图像时，列出了下面的表格：根据表格上的信息回答问题：当2x =时，y = ；13. （黄浦）已知抛物线 与 关于y 轴对称，我们称y 1与y 2互为“和谐抛物线”.请写出抛物线 的“和谐抛物线” ． 14. （嘉定） 如果抛物线 的最低点是原点，那么实数m 的取值范围是 ； 15. （嘉定） 抛物线 与y 轴的交点坐标是 ； 16. （嘉定）如果将抛物线 向上平移，使它经过原点，那么所得抛物线的表达式是 ；17. （闵行）方程20ax bx c ++=（0a ≠）的两根为-3和1，那么抛物线2y ax bx c =++（0a ≠）的对称轴是直线 ；18. （闵行）闵行体育公园的圆形喷水池的水柱（如图2-18-1），如果曲线APB 表示落点B 离点O 最远的一条水流（如图2-18-2），其上的水珠的高度y （米）关于水平距离x （米）的函数解析式为2944y x x =-++，那么圆形水池的半径至少为 米时，才能使喷出的水流不落在水池外；19. （浦东）二次函数2y ax bx c =++的图像如图2-20所示，对称轴为直线x=2，若此抛物线与x 轴的一个交点为(6,0)，则抛物线与x 轴的另一个交点坐标为__________________； 20. （浦东）将抛物线2(1)y x =+向下平移2个单位，得到的新抛物线解析式是______________； 21. （浦东）若抛物线2y ax c =+与x 轴交于点(,0),(,0),A m B n 与y 轴交于点(0,)C c ，则称ABC ∆为“抛物线三角形”。

2016年上海市闸北区中考数学一模试卷一、选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．】1．在下列四幅图形中，能表示两棵小树在同一时刻阳光下影子的图形的可能是( ) A．B．C．D．2．抛物线y=﹣2x2+3的顶点在( )A．x轴上B．y轴上C．第一象限 D．第四象限3．如图，已知点D、E分别在△ABC的边BA、CA的延长上，下列给出的条件中，不能判定DE∥BC的是( )A．BD：AB=CE：AC B．DE：BC=AB：AD C．AB：AC=AD：AE D．AD：DB=AE：EC4．已知点P是线段AB的黄金分割点（AP＞PB），AB=4，那么AP的长是( )A． B．C． D．5．如图，在Rt△ABC中，∠C=90°，AC=12，BC=5，CD⊥AB于点D，则cot∠BCD的值为( )A．B．C．D．6．已知，二次函数y=ax2+bx+c（a≠0）的图象如图所示，则以下说法不正确的是( )A．根据图象可得该函数y有最小值B．当x=﹣2时，函数y的值小于0C．根据图象可得a＞0，b＜0D．当x＜﹣1时，函数值y随着x的增大而减小二、填空题（本大题共12题，每题4分，满分48分）7．已知，则的值是__________．8．如图，在△ABC中，DE∥BC，当△ADE与△ABC的周长比为1：3时，那么DE：BC=__________．9．如图，已知在梯形ABCD中，AB∥CD，点E和点F分别在AD和BC上，EF是梯形ABCD的中位线，若，，则用表示=__________．10．求值：sin60°﹣tan30°=__________．11．汽车沿着坡度为1：7的斜坡向上行驶了50米，则汽车升高了__________米．12．已知抛物线y=（m﹣1）x2+4的顶点是此抛物线的最高点，那么m的取值范围是__________．13．周长为16的矩形的面积y与它的一条边长x之间的函数关系式为y=__________．（不需要写出定义域）14．在直角坐标系中，已知点P在第一象限内，点P与原点O的距离OP=2，点P与原点O 的连线与x轴的正半轴的夹角为60°，则点P的坐标是__________．15．如图，正方形CDEF内接于Rt△ABC，点D、E、F分别在边AC、AB和BC上，当AD=2，BF=3时，正方形CDEF的面积是__________．16．如图，在梯形ABCD中，AD∥BC，AC平分∠BCD，∠BAC=∠D，若AD=4，BC=10，则AC=__________．17．如图，△ABC的两条中线AD和BE相交于点G，过点E作EF∥BC交AD于点F，那么=__________．18．如图，将一张矩形纸片ABCD沿着过点A的折痕翻折，使点B落在AD边上的点F，折痕交BC于点E，将折叠后的纸片再次沿着另一条过点A的折痕翻折，点E恰好与点D 重合，此时折痕交DC于点G，则CG：GD的值为__________．三、解答题（本大题共7题，满分78分）19．解方程：．20．已知二次函数的图象的顶点在原点O，且经过点A（1，）．（1）求此函数的解析式；（2）将该抛物线沿着y轴向上平移后顶点落在点P处，直线x=2分别交原抛物和新抛物线于点M和N，且S△PMN=，求：MN的长以及平移后抛物线的解析式．21．如图，已知平行四边形ABCD的对角线相交于点O，点E是边BC的中点，联结DE交AC于点G．设=，=，（1）试用、表示向量；（2）试用、表示向量．22．如图，一棵大树在一次强台风中折断倒下，未折断树杆AB与地面仍保持垂直的关系，而折断部分AC与未折断树杆AB形成53°的夹角．树杆AB旁有一座与地面垂直的铁塔DE，测得BE=6米，塔高DE=9米．在某一时刻的太阳照射下，未折断树杆AB落在地面的影子FB长为4米，且点F、B、C、E在同一条直线上，点F、A、D也在同一条直线上．求这棵大树没有折断前的高度．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.33）23．如图，在△ABC中，AC=BC，∠BCA=90°，点E是斜边AB上的一个动点（不与A、B重合），作EF⊥AB交边BC于点F，联结AF、EC交于点G．（1）求证：△BEC∽△BFA；（2）若BE：EA=1：2，求∠ECF的余弦值．24．如图，在平面直角坐标系中，已知抛物线与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2），对称轴为直线x=1，对称轴交x轴于点E．（1）求该抛物线的表达式，并写出顶点D的坐标；（2）设点F在抛物线上，如果四边形AEFD是梯形，求点F的坐标；（3）联结BD，设点P在线段BD上，若△EBP与△ABD相似，求点P的坐标．25．（14分）如图，梯形ABCD中，AD∥BC，∠A=90°，AD=4，AB=8，BC=10，M在边CD上，且．（1）如图①，联结BM，求证：BM⊥DC；（2）如图②，作∠EMF=90°，ME交射线AB于点E，MF交射线BC于点F，若AE=x，BF=y．当点F在线段BC上时，求y关于x的函数解析式，并写出定义域；（3）若△MCF是等腰三角形，求AE的值．2016年上海市闸北区中考数学一模试卷一、选择题（本大题共6题，每题4分，满分24分）【下列各题的四个选项中，有且只有一个选项是正确的，选择正确项的代号并填涂在答题纸的相应位置上．】1．在下列四幅图形中，能表示两棵小树在同一时刻阳光下影子的图形的可能是( ) A．B．C．D．【考点】平行投影．【分析】根据平行投影得特点，利用两小树的影子的方向相反可对A、B进行判断；利用在同一时刻阳光下，树高与影子成正比可对C、D进行判断．【解答】解：A、两棵小树的影子的方向相反，不可能为同一时刻阳光下影子，所以A选项错误；B、两棵小树的影子的方向相反，不可能为同一时刻阳光下影子，所以B选项错误；C、在同一时刻阳光下，树高与影子成正比，所以C选项错误；D、在同一时刻阳光下，树高与影子成正比，所以D选项正确．故选D．【点评】本题考查了平行投影：由平行光线形成的投影是平行投影，如物体在太阳光的照射下形成的影子就是平行投影．2．抛物线y=﹣2x2+3的顶点在( )A．x轴上B．y轴上C．第一象限 D．第四象限【考点】二次函数的性质．【分析】因为y=﹣2x2+3可看作抛物线的顶点式，根据顶点式的坐标特点，得出顶点坐标为（0，3），即可知顶点在y轴上．【解答】解：抛物线y=﹣2x2+3是顶点式，根据顶点式的坐标特点可知，顶点坐标为（0，3），即顶点在y轴上．故选B．【点评】此题考查了二次函数的性质，二次函数y=a（x﹣h）2+k的顶点坐标为（h，k），对称轴为x=h．也考查了y轴上点的坐标特征．3．如图，已知点D、E分别在△ABC的边BA、CA的延长上，下列给出的条件中，不能判定DE∥BC的是( )A．BD：AB=CE：AC B．DE：BC=AB：AD C．AB：AC=AD：AE D．AD：DB=AE：EC 【考点】平行线分线段成比例．【分析】由平行线分线段成比例定理的逆定理得出A、C、D正确，B不正确，即可得出结论．【解答】解：∵BD：AB=CE：AC，∴DE∥BC，选项A正确；∵DE：BC=AB：AD不能判定DE∥BC，∴选项B不正确；∵AB：AC=AD：AE，∴DE∥BC，选项C正确；∵AD：DB=AE：EC，∴DE∥BC，选项D正确．故选：B．【点评】本题考查了平行线分线段成比例定理的逆定理；熟记平行线分线段成比例定理的逆定理是解决问题的关键．4．已知点P是线段AB的黄金分割点（AP＞PB），AB=4，那么AP的长是( )A． B．C． D．【考点】黄金分割．【分析】根据黄金分割点的定义，知AP是较长线段；则AP=AB，代入数据即可得出AP的长．【解答】解：由于P为线段AB=4的黄金分割点，且AP是较长线段；则AP=4×=2﹣2．故选A．【点评】本题考查了黄金分割的概念：把一条线段分成两部分，使其中较长的线段为全线段与较短线段的比例中项，这样的线段分割叫做黄金分割，他们的比值（）叫做黄金比．熟记黄金分割的公式：较短的线段=原线段的，较长的线段=原线段的是解题的关键．5．如图，在Rt△ABC中，∠C=90°，AC=12，BC=5，CD⊥AB于点D，则cot∠BCD的值为( )A．B．C．D．【考点】解直角三角形．【分析】根据在Rt△ABC中，∠C=90°，AC=12，BC=5，CD⊥AB于点D，可以得到∠A 和∠BCD的关系，由∠A的三角函数值可以得到∠BCD的三角函数值，从而可以解答本题．【解答】解：∵在Rt△ABC中，∠C=90°，∴∠B+∠A=90°，∵CD⊥AB于点D，∴∠CDB=90°，∴∠B+∠BCD=90°，∴∠A=∠BCD，∵在Rt△ABC中，∠C=90°，AC=12，BC=5，∴cot∠A=，∴cot∠BCD=．故选C．【点评】本题考查解直角三角形，解题的关键是找出各个角之间的关系，根据等角的三角函数值相等，运用数学转化的思想进行解答问题．6．已知，二次函数y=ax2+bx+c（a≠0）的图象如图所示，则以下说法不正确的是( )A．根据图象可得该函数y有最小值B．当x=﹣2时，函数y的值小于0C．根据图象可得a＞0，b＜0D．当x＜﹣1时，函数值y随着x的增大而减小【考点】二次函数的性质．【分析】由抛物线开口向上得a＞0，由当x=﹣2时，图象在x轴的下方，得出函数值小于0，对称轴x=﹣1在y轴的左侧得b＞0，根据二次函数的性质可得当x＜﹣1时，y随x的增大而减小；由此判定得出答案即可．【解答】解：由图象可知：A、抛物线开口向上，该函数y有最小值，此选项正确；B、当x=﹣2时，图象在x轴的下方，函数值小于0，此选项正确；C、对称轴x=﹣1，a＞0，则b＞0，此选项错误；D、当x＜﹣1时，y随x的增大而减小正确，此选项．故选：C．【点评】此题考查二次函数的性质，根据图象判定开口方向，得出对称轴，利用二次函数的增减性解决问题．二、填空题（本大题共12题，每题4分，满分48分）7．已知，则的值是．【考点】比例的性质．【分析】根据等比性质：⇒=，可得答案．【解答】解：由等比性质，得==，故答案为：．【点评】本题考查了比例的性质，利用等比性质是解题关键．8．如图，在△ABC中，DE∥BC，当△ADE与△ABC的周长比为1：3时，那么DE：BC=1：3．【考点】相似三角形的判定与性质．【分析】根据DE∥BC，得到△ADE∽△ABC，如何根据相似三角形的性质即可解题．【解答】解：∵DE∥BC，∴△ADE∽△ABC，∴=△ADE的周长：△ABC的周长比=1：3．故答案为：．【点评】本题考查了相似三角形的判定，考查了相似三角形对应边比例相等的性质，本题中求证△ADE∽△ABC是解题的关键．9．如图，已知在梯形ABCD中，AB∥CD，点E和点F分别在AD和BC上，EF是梯形ABCD的中位线，若，，则用表示=2﹣．【考点】*平面向量．【分析】由在梯形ABCD中，AB∥CD，EF是梯形ABCD的中位线，可得EF∥AB∥CD，EF=（AB+CD），则可得=2﹣，继而求得答案．【解答】解：∵在梯形ABCD中，AB∥CD，EF是梯形ABCD的中位线，∴EF∥AB∥CD，EF=（AB+CD），∴=2﹣=2﹣．故答案为：2﹣．【点评】此题考查了平面向量的知识以及梯形的中位线的性质．注意能灵活应用梯形中位线的性质是解此题的关键．10．求值：sin60°﹣tan30°=．【考点】特殊角的三角函数值．【专题】计算题．【分析】根据sin60°=，tan30°=得到原式=﹣，然后通分合并即可．【解答】解：原式=﹣=﹣=．故答案为．【点评】本题考查了特殊角的三角函数值：sin60°=，tan30°=．也考查了二次根式的运算．11．汽车沿着坡度为1：7的斜坡向上行驶了50米，则汽车升高了5米．【考点】解直角三角形的应用-坡度坡角问题．【分析】根据坡度即可求得坡角的正弦值，根据三角函数即可求解．【解答】解：∵坡度为1：7，∴设坡角是α，则sinα==∴上升的高度是：50×=5（米）．故答案是：5．【点评】本题主要考查了坡度的定义，正确求得坡角的正弦值是解题的关键．12．已知抛物线y=（m﹣1）x2+4的顶点是此抛物线的最高点，那么m的取值范围是m＜1．【考点】二次函数的最值．【分析】根据二次函数y=（m+1）x2+2的顶点是此抛物线的最高点，得出抛物线开口向下，即m+1＜0，即可得出答案．【解答】解：∵抛物线y=（m﹣1）x2+4的顶点是此抛物线的最高点，∴抛物线开口向下，∴m﹣1＜0，∴m＜1，故答案为m＜1．【点评】此题主要考查了利用二次函数顶点坐标位置确定图象开口方向，此题型是中考中考查重点，同学们应熟练掌握．13．周长为16的矩形的面积y与它的一条边长x之间的函数关系式为y=8x﹣x2．（不需要写出定义域）【考点】根据实际问题列二次函数关系式．【分析】首先根据矩形周长为16，一条边长x可表示出另一边长为8﹣x，再根据矩形面积=长×宽列出函数解析式即可．【解答】解：∵矩形周长为16，一条边长x，∴另一边长为8﹣x，∴面积：y=（8﹣x）x=8x﹣x2．故答案为：8x﹣x2．【点评】此题主要考查了根据实际问题列二次函数解析式，关键是掌握矩形的面积公式=长×宽．14．在直角坐标系中，已知点P在第一象限内，点P与原点O的距离OP=2，点P与原点O 的连线与x轴的正半轴的夹角为60°，则点P的坐标是（1，）．【考点】解直角三角形；坐标与图形性质．【分析】作PM⊥x轴于点M，构造直角三角形，根据三角函数的定义求解．【解答】解：作PM⊥x轴于点M，如图所示：∵OP=2，∴sin60°==，cos60°==，∴PM=，OM=1．故P点坐标为：（1，）．故答案为：（1，）．【点评】本题考查了解直角三角形和坐标与图形性质的知识，难度不大，注意掌握一个角的余弦和正弦的计算方法．15．如图，正方形CDEF内接于Rt△ABC，点D、E、F分别在边AC、AB和BC上，当AD=2，BF=3时，正方形CDEF的面积是6．【考点】相似三角形的判定与性质；正方形的性质．【分析】根据正方形的性质得到DE∥BC，由平行线的性质得到∠AED=∠B，∠ADE=∠EFB=90°，推出△ADE∽△BEF，根据相似三角形的性质得到，代入数据即可得到结论．【解答】解：∵四边形CDEF是正方形，∴DE∥BC，∴∠AED=∠B，∠ADE=∠EFB=90°，∴△ADE∽△BEF，∴，即，∴DE•EF=2×3=6，∴正方形CDEF的面积是6．故答案为：6．【点评】本题考查了相似三角形的判定和性质，正方形的性质，熟练掌握相似三角形的性质定理是解题的关键．16．如图，在梯形ABCD中，AD∥BC，AC平分∠BCD，∠BAC=∠D，若AD=4，BC=10，则AC=2．【考点】相似三角形的判定与性质．【分析】根据平行线的性质得出∠DAC=∠ACB，根据相似三角形的判定得出△ADC∽△CAB，得出比例式，代入求出即可．【解答】解：∵AD∥BC，∴∠DAC=∠ACB，∵∠BAC=∠D，∴△ADC∽△CAB，∴=，∴=，解得：AC=2．故答案为：2．【点评】本题考查了相似三角形的性质和判定，平行线的性质的应用，能求出△ADC∽△CAB是解此题的关键．17．如图，△ABC的两条中线AD和BE相交于点G，过点E作EF∥BC交AD于点F，那么=．【考点】平行线分线段成比例；三角形的重心．【分析】由三角形的重心定理得出=，=，由平行线分线段成比例定理得出=，即可得出结果．【解答】解：∵线段AD、BE是△ABC的中线，∴=，=，∵EF∥BC，=，∴=．故答案为：．【点评】本题考查了平行线分线段成比例定理、三角形的重心定理；熟练掌握三角形的重心定理，由平行线分线段成比例定理得出FG：DG=1：2是解决问题的关键18．如图，将一张矩形纸片ABCD沿着过点A的折痕翻折，使点B落在AD边上的点F，折痕交BC于点E，将折叠后的纸片再次沿着另一条过点A的折痕翻折，点E恰好与点D重合，此时折痕交DC于点G，则CG：GD的值为．【考点】翻折变换（折叠问题）．【分析】连接GE，由矩形的性质得出∠BAD=∠C=ADC=∠B=90°，AB=CD，AD=BC，由折叠的性质得出∠DAG=∠EAG=22.5°，AG⊥DE，由线段垂直平分线的性质得出GD=GE，得出∠GDE=∠GED=∠DAG=22.5°，由三角形的外角性质得出∠CGE=45°，证出△CEG是等腰直角三角形，得出GD=GE=CG，即可得出结果．【解答】解：如图所示：连接GE，∵四边形ABCD是矩形，∴∠BAD=∠C=ADC=∠B=90°，AB=CD，AD=BC，由折叠的性质得：∠DAE=∠BAE=45°，∠DAG=∠EAG=22.5°，AG⊥DE，∴GD=GE，∴∠GDE=∠GED=∠DAG=22.5°，∴∠CGE=∠GDE+∠GED=45°，∴△CEG是等腰直角三角形，∴GD=GE=CG，∴CG：GD=．故答案为：．【点评】本题考查了矩形的性质、翻折变换的性质、线段垂直平分线的性质、等腰三角形的性质、三角形的外角性质、等腰直角三角形的判定与性质；熟练掌握翻折变换和矩形的性质，证明△CEG是等腰直角三角形是解决问题的关键．三、解答题（本大题共7题，满分78分）19．解方程：．【考点】解分式方程．【专题】计算题；分式方程及应用．【分析】分式方程去分母转化为整式方程，求出整式方程的解得到x的值，经检验即可得到分式方程的解．【解答】解：去分母得：x﹣5+x2﹣1=3x﹣3，整理得：（x﹣3）（x+1）=0，解得：x1=3，x2=﹣1，经检验x=﹣1是增根，分式方程的解为x=3．【点评】此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．20．已知二次函数的图象的顶点在原点O，且经过点A（1，）．（1）求此函数的解析式；（2）将该抛物线沿着y轴向上平移后顶点落在点P处，直线x=2分别交原抛物和新抛物线于点M和N，且S△PMN=，求：MN的长以及平移后抛物线的解析式．【考点】二次函数图象与几何变换；待定系数法求二次函数解析式．【分析】（1）根据题意可直接设y=ax2把点（1，﹣3）代入得a=﹣3，所以y=﹣3x2；（2）设平移后y=x2+d（d＞0），则MN=d，根据题意得出S=×2×d=3，即可求得d的值，从而求得平移后的解析式．【解答】解：（1）∵抛物线顶点是原点，可设y=ax2，把点A（1，）代入，得a=，，所以这个二次函数的关系式为y=x2；（2）设平移后y=x2+d（d＞0），∴MN=d，S=×2×d=3，∴d=3，∴y=x2+3．【点评】主要考查了用待定系数法求函数解析式以及二次函数的图象与几何变换，熟练掌握待定系数法和平移的规律是解题的关键．21．如图，已知平行四边形ABCD的对角线相交于点O，点E是边BC的中点，联结DE 交AC于点G．设=，=，（1）试用、表示向量；（2）试用、表示向量．【考点】*平面向量．【分析】（1）由=，=，利用三角形法则，可求得，又由四边形ABCD是平行四边形，根据平行四边形的对角线互相平分，即可求得答案；（2）易得△ADG∽△CEG，然后由相似三角形的对应边成比例，证得AG：CG=AD：CE=2：1，继而求得，则可求得答案．【解答】解：（1）∵=，=，∴=+=+，∵四边形ABCD是平行四边形，∴==（+）=+；（2）∵四边形ABCD是平行四边形，∴AD∥BC，AD=BC，∴△ADG∽△CEG，∴AG：CG=AD：CE，∵点E是边BC的中点，∴AD：CE=2：1，∴AG：CG=2：1，∴AG：AC=2：3，∴==+，∴=﹣=+﹣=﹣．【点评】此题考查了平面向量的知识、相似三角形的判定与性质以及平行四边形的性质．注意掌握三角形法则的应用是关键．22．如图，一棵大树在一次强台风中折断倒下，未折断树杆AB与地面仍保持垂直的关系，而折断部分AC与未折断树杆AB形成53°的夹角．树杆AB旁有一座与地面垂直的铁塔DE，测得BE=6米，塔高DE=9米．在某一时刻的太阳照射下，未折断树杆AB落在地面的影子FB长为4米，且点F、B、C、E在同一条直线上，点F、A、D也在同一条直线上．求这棵大树没有折断前的高度．（参考数据：sin53°≈0.8，cos53°≈0.6，tan53°≈1.33）【考点】解直角三角形的应用．【分析】由题意得出AB∥DE，证出△ABF∽△DEF，由相似三角形的性质得出，求出AB，再由三角函数求出AC，即可得出结果．【解答】解：根据题意得：AB⊥EF，DE⊥EF，∴∠ABC=90°，AB∥DE，∴△ABF∽△DEF，∴，即，解得：AB=3.6米，∵cos∠BAC=，∴AC=≈=6（米），∴AB+AC=3.6+6=9.6米．答：这棵大树没有折断前的高度为9.6米．【点评】本题考查了解直角三角形的应用、相似三角形的应用；熟练掌握解直角三角形，由相似三角形的性质求出AB是解决问题的关键．23．如图，在△ABC中，AC=BC，∠BCA=90°，点E是斜边AB上的一个动点（不与A、B重合），作EF⊥AB交边BC于点F，联结AF、EC交于点G．（1）求证：△BEC∽△BFA；（2）若BE：EA=1：2，求∠ECF的余弦值．【考点】相似三角形的判定与性质；解直角三角形．【分析】（1）根据已知条件得到△BEF∽△ABC，根据相似三角形的性质得到，根据相似三角形判定定理即可得到结论；（2）由已知条件的，根据三角函数的定义得到tan∠EAF=，根据相似三角形的性质得到∠BAF=∠BCE，即可得到结论．【解答】解：（1）∵在△ABC中，AC=BC，∠BCA=90°，∵EF⊥AB，∴∠BEF=90°，∵∠B=∠B，∴△BEF∽△ABC，∴，∴△△BEC∽△BFA；（2）∵BE=EF，BE：EA=1：2，∴，∴tan∠EAF=，设EF=k，AE=2k，∴AF=，∵△BEC∽△BFA，∴∠BAF=∠BCE，∴cos∠ECF=cos∠EAF==．【点评】本题考查了相似三角形的判定和性质，锐角三角函数的定义，等腰直角三角形的性质，熟练掌握相似三角形的判定和性质是解题的关键．24．如图，在平面直角坐标系中，已知抛物线与x轴交于点A（﹣1，0）和点B，与y轴交于点C（0，2），对称轴为直线x=1，对称轴交x轴于点E．（1）求该抛物线的表达式，并写出顶点D的坐标；（2）设点F在抛物线上，如果四边形AEFD是梯形，求点F的坐标；（3）联结BD，设点P在线段BD上，若△EBP与△ABD相似，求点P的坐标．【考点】二次函数综合题．【分析】（1）根据函数值相等的亮点关于对称轴对称，可得B点坐标，根据待定系数法，可得函数解析式；（2）根据平行线的一次项的系数相等，可得EF的解析式，根据解方程组，可得答案；（3）根据两组对边对应成比例且夹角相等的两个三角形相似，可得PB的长，根据勾股定理，可得P点的横坐标，根据自变量与函数值的对应关系，可得P点坐标．【解答】解：（1）由A、B关于x=1对称，得B（3，0），设抛物线的解析式为y=ax2+bx+c （a≠0），将A、B、C点坐标代入，得，解得．抛物线的解析式为y=﹣x2+x+2，顶点坐标为D（1，）；（2）①当AE∥DF时，不存在，舍去；②当AD∥EF时，AD的解析式为y=x+，EF的解析式为y=x﹣，联立得，解得，F点坐标为（，），（3）∠PBE=∠DBA，如图：BD的解析式为y=﹣x+4，P在BD上，设P（m，﹣m+4）DB===，BA=3﹣（﹣1）=4，BE=3﹣1=2．①当△PBE∽△DBA时，=，即=，解得BP=，（3﹣m）2+（m﹣4）2=，解得m=2，m=4（不符合题意，舍），当m=2时，﹣m+4=，P1（2，）；②当△EBP∽△DBA时，=，即=，解得BP=，（3﹣m）2+（m﹣4）2=，解得m=，m=（不符合题意，舍），当m=时，﹣m+4=，P2（，），综上所述：P点坐标为P1（2，），P2（，）．【点评】本题考查了二次函数综合题，利用函数值相等的两点关于对称轴对称得出B点坐标是解题关键；利用平行线的一次项的系数相等得出EF的解析式是解题关键；利用两组对边对应成比例且夹角相等的两个三角形相似得出PB的长是解题关键，要分类讨论，以防遗漏．25．（14分）如图，梯形ABCD中，AD∥BC，∠A=90°，AD=4，AB=8，BC=10，M在边CD上，且．（1）如图①，联结BM，求证：BM⊥DC；（2）如图②，作∠EMF=90°，ME交射线AB于点E，MF交射线BC于点F，若AE=x，BF=y．当点F在线段BC上时，求y关于x的函数解析式，并写出定义域；（3）若△MCF是等腰三角形，求AE的值．【考点】相似形综合题．（1）连接BD，作DN⊥BC于N，则四边形ABND是矩形，得出DN=AB=8，BN=AD=4，【分析】求出CN=BC﹣BN=6，由勾股定理求出CD，得出CD=BC=10，由等腰三角形的性质和平行线的性质得出∠ADB=∠DBC=∠BDC，求出DM=4=AD，由SAS证明△ADB≌△MDB，得出对应角相等即可；（2）由角的互余关系得出∠C=∠MBA，∠CMF=∠BME，证出△CMF∽△BME，得出对应边成比例，即可得出结果；（3）分两种情况：①当点E在线段AB上时，△CMF∽△BME，△CMF为等腰三角形，得出△BME为等腰三角形，当BE=BM=8时，AE=0；当BM=ME时，由三角函数求出BE=＞AE，舍去；当BE=ME时，由三角函数求出BE=，得出AE=AB﹣BE=；②当点E在BC延长线上时，同（2）可证△CMF∽△BME，△BME为等腰三角形，由∠MBE ＞90°，得出BE=BM=8，因此AE=16；即可得出结果．【解答】（1）证明：连接BD，如图1所示：作DN⊥BC于N，则∠DNC=90°，四边形ABND是矩形，∴DN=AB=8，BN=AD=4，∴CN=BC﹣BN=10﹣4=6，CD==10，∴CD=BC=10，∴∠DBC=∠BDC，∵AD∥BC，∴∠ADB=∠DBC=∠BDC，∵，∴DM=4=AD，在△ADB和△MDB中，，∴△ADB≌△MDB（SAS），∴∠DMB=∠A=90°，BM=AB=8，∴BM⊥DC；（2）解：∵∠C=∠MBA=90°﹣∠MBC，∠CMF=∠BME=90°﹣∠FMB，∴△CMF∽△BME，∴，即，解得：y=x+4（0≤x≤8）；（3）解：分两种情况：①当点E在线段AB上时，△CMF∽△BME，△CMF为等腰三角形，∴△BME为等腰三角形，当BE=BM=8时，AE=0；当BM=ME时，BE=2×BM×cos∠MBA=2×8×=＞AE，舍去当BE=ME时，BE===，∴AE=AB﹣BE=8﹣=；②当点E在BC延长线上时，如图2所示：同（2）可证△CMF∽△BME，△BME为等腰三角形，又∵∠MBE＞90°，∴BE=BM=8，∴AE=16．综上所述：若△MCF是等腰三角形，AE的值为0或或16．【点评】本题是四边形综合题目，考查了梯形的性质、相似三角形的判定与性质、全等三角形的判定与性质、矩形的判定与性质、等腰三角形的判定与性质、三角函数等知识；本题综合性强，难度较大，特别是（3）中，需要进行分类讨论才能得出结果．。

2016年上海市杨浦区中考数学一模试卷2016年上海市杨浦区中考数学一模试卷一、选择题（本题共6个小题，每个小题4分，共24分）1．将抛物线y=2x2向上平移2个单位后所得抛物线的解析式是( )A．y=2x2+2B．y=2（x+2）2C．y=2（x﹣2）2D．y=2x2﹣2【解答】解：原抛物线的顶点为（0，0），向上平移2个单位，那么新抛物线的顶点为（0，2），可设新抛物线的解析式为：y=2（x﹣h）2+k，代入得：y=2x2+2．故选A．2．以下图形中一定属于互相放缩关系的是( )A．斜边长分别是10和5的两直角三角形B．腰长分别是10和5的两等腰三角形C．边长分别是10和5的两个菱形D．边长分别是10和5的两个正方形【解答】解：斜边长分别是10和5的两直角三角形，直角边不一定成比例，所以不一定属于互相放缩关系，A不正确；腰长分别是10和5的两等腰三角形不一定属于互相放缩关系，B不正确；边长分别是10和5的两个菱形不一定属于互相放缩关系，C不正确；边长分别是10和5的两个正方形属于互相放缩关系，D正确，故选：D．3．如图，已知在△ABC中，D是边BC的中点，，，那么等于( )A．B．C．D．【解答】解：△在△ABC中，D是边BC的中点，△==，△=﹣=﹣．故选B．4．坡度等于1：的斜坡的坡角等于( )A．30°B．40°C．50°D．60°【解答】解：坡角α，则tanα=1：，则α=30°．故选A．5．下列各组条件中，一定能推得△ABC与△DEF相似的是( )A．△A=△E且△D=△F B．△A=△B且△D=△FC．△A=△E且D．△A=△E且【解答】解：A、△D和△F不是两个三角形的对应角，故不能判定两三角形相似，故此选项错误；B、△A=△B，△D=△F不是两个三角形的对应角，故不能判定两三角形相似，故此选项错误；C、由可以根据两组对应边的比相等且夹角对应相等的两个三角形相似可以判断出△ABC与△DEF相似，故此选项正确；D、△A=△E且不能判定两三角形相似，因为相等的两个角不是夹角，故此选项错误；故选：C．6．下列图象中，有一个可能是函数y=ax2+bx+a+b（a≠0）的图象，它是( ) A．B．C．D．【解答】解：在函数y=ax2+bx+a+b（a≠0）中，当a＜0，b＜0时，则该函数开口向下，顶点在y轴左侧，一定经过点（0，a+b），点（0，a+b）一定在y轴的负半轴，故选项A、B错误；当a＞0，b＜0时，若函数过点（1，0），则a+b+a+b=0，得a与b互为相反数，则y=ax2﹣ax=ax（x﹣1），则该函数与x轴的两个交点是（0，0）或（1，0），故选项D错误；当a＞0，b＜0时，若函数过点（0，1），则a+b=1，只要a、b满足和为1即可，故选项C 正确；故选C．二、填空题（本大题共12个小题，每个小题4分，共48分）7．如果，那么=．【解答】解：△，△2y=3（x﹣y），整理，得3x=5y，△=．故答案为．8．如图，点G为△ABC的重心，DE过点G，且DE△BC，EF△AB，那么CF：BF=1：2．【解答】解：如图，连接AG并延长，交BC于H．△点G为△ABC的重心，△AG=2GH．△DE△BC，△CE：AE=GH：AG=1：2，△EF△AB，△CF：BF=CE：AE=1：2．故答案为1：2．9．已知在△ABC中，点D、E分别在AB和BC上，AD=2，DB=1，BC=6，要使DE和AC平行，那么BE=2．【解答】解：BE=2，理由是：如图：△AD=2，DB=1，△AB=2+1=3，△BC=6，BE=2，△=，△△B=△B，△△BED△△BCA，△△BED=△C，△DE△AC．故答案为：2．10．如果△ABC与△DEF相似，△ABC的三边之比为3：4：6，△DEF的最长边是10cm，那么△DEF的最短边是5cm．【解答】解：设△DEF的最短边为x，△ABC的三边分别为3a，4a，6a，△△ABC与△DEF相似，△3a：x=6a：10，△x=5，即△DEF的最短边是5cm．故答案为5．11．如果AB△CD，2AB=3CD，与的方向相反，那么=﹣．【解答】解：△AB△CD，2AB=3CD，与的方向相反，△2=﹣3，△=﹣．故答案为：﹣．12．计算：sin60°﹣cot30°=【解答】解：原式=﹣=﹣．13．在△ABC中，△C=90°，如果sinA=，AB=6，那么BC=2．【解答】解：sinA==，得BC=AB×=6×=2，故答案为：2．14．如果二次函数y=x2+bx+c配方后为y=（x﹣2）2+1，那么c的值为5．【解答】解：△y=（x﹣2）2+1=x2﹣4x+4+1=x2﹣4x+5，△c的值为5．故答案是：5．15．抛物线y=﹣2x2+4x﹣1的对称轴是直线x=1．【解答】解：抛物线y=﹣2x2+4x﹣1的对称轴是直线x=﹣=1．故答案为x=1．16．如果A（﹣1，y1），B（﹣2，y2）是二次函数y=x2+m图象上的两个点，那么y1＜y2（填“＜”或者“＞”）【解答】解：△二次函数y=x2+m中a=1＞0，△抛物线开口向上．△x=﹣=0，﹣1＜﹣2，△A（﹣1，y1），B（﹣2，y2）在对称轴的左侧，且y随x的增大而减小，△y1＜y2．故答案为：＜．17．请写出一个二次函数的解析式，满足：图象的开口向下，对称轴是直线x=﹣1，且与y轴的交点在x轴的下方，那么这个二次函数的解析式可以为y=﹣x2﹣2x﹣1．【解答】解：设所求二次函数的解析式为y=ax2+bx+c（a≠0）．△图象的开口向下，△a＜0，可取a=﹣1；△对称轴是直线x=﹣1，△﹣=﹣1，得b=2a=﹣2；△与y轴的交点在x轴的下方，△c＜0，可取c=﹣1；△函数解析式可以为：y=﹣x2﹣2x﹣1．故答案为：y=﹣x2﹣2x﹣1．18．如图，已知△ABC沿角平分线BE所在的直线翻折，点A恰好落在边BC的中点M 处，且AM=BE，那么△EBC的正切值是．【解答】解：设AM与BE交点为D，过M作MF△BE交AC于F，如图所示：△M为BC的中点，△F为CE的中点，△MF为△BCE的中位线，△MF=BE，由翻折变换的性质得：AM△BE，AD=MD，同理：DE是△AMF的中位线，△DE=MF，设DE=a，则MF=2a，AM=BE=4a，△BD=3a，MD=AM=2a，△△BDM=90°，△tan△EBC===．故答案为：．三、解答题（共78分）19．如图，已知两个不平行的向量．先化简，再求作：．（不要求写作法，但要指出所作图中表示结论的向量）【解答】解：=+3﹣﹣=﹣+2．如图：=2，=﹣，则=﹣+2，即即为所求．20．已知二次函数y=ax2+bx+c（a≠0）的图象上部分点的横坐标x与纵坐标y的对应值如下表所示：x…﹣1024…y…﹣511m…求：（1）这个二次函数的解析式；（2）这个二次函数图象的顶点坐标及上表中m的值．【解答】解：（1）依题意，得，解得；△二次函数的解析式为：y=﹣2x2+4x+1．（2）当x=4时，m=﹣2×16+16+1=﹣15，由y=﹣2x2+4x+1=﹣2（x﹣1）2+3，故其顶点坐标为（1，3）．21．如图，梯形ABCD中，AD△BC，BC=2AD，点E为边DC的中点，BE交AC于点F．求：（1）AF：FC的值；（2）EF：BF的值．【解答】解：（1）延长BE交直线AD于H，如图，△AD△BC，△△DEH△△CEB，△=，△点E为边DC的中点，△DE=CE，△DH=BC，而BC=2AD，△AH=3AD，△AH△BC，△△AHF△△CFB，△AF：FC=AH：BC=3：2；（2）△△DEH△△CEB，△EH：BE=DE：CE=1：1，△BE=EH=BH，△△AHF△△CFB，△FH：BF=AF：FC=3：2；设BF=2a，则FH=3a，BH=BF+FH=5a，△EH=a，△EF=FH﹣EH=3a﹣a=a，△EF：BF=a：2a=1：4．22．如图，某高楼顶部有一信号发射塔，在矩形建筑物ABCD的A，C两点测得该塔顶端F的仰角分别为和β，矩形建筑物宽度AD=20m，高度DC=33m．求：（1）试用α和β的三角比表示线段CG的长；（2）如果α=48°，β=65°，请求出信号发射塔顶端到地面的高度FG的值．（结果精确到1m）（参考数据：sin48°=0.7，cos48°=0.7，tan48°=1.1，sin65°=0.9，cos65°=0.4，tan65°=2.1）【解答】解：（1）设CG=xm，由图可知：EF=（x+20）•tanα，FG=x•tanβ，则（x+20）tanα+33=xtanβ，解得x=；（2）x===55，则FG=x•tanβ=55×2.1=115.5≈116．答：该信号发射塔顶端到地面的高度FG约是116m．23．已知：如图，在△ABC中，点D．E分别在AB，AC上，DE△BC，点F在边AB上，BC2=BF•BA，CF与DE相交于点G．（1）求证：DF•AB=BC•DG；（2）当点E为AC的中点时，求证：．【解答】证明：（1）△BC2=BF•BA，△BC：BF=BA：BC，而△ABC=△CBF，△△BAC△△BCF，△DE△BC，△△BCF△△DGF，△△DGF△△BAC，△DF：BC=DG：BA，△DF•AB=BC•DG；（2）作AH△BC交CF的延长线于H，如图，△DE△BC，△AH△DE，△点E为AC的中点，△AH=2EG，△AH△DG，△△AHF△△DGF，△=，△．24．已知在平面直角坐标系中，抛物线y=﹣+bx+c与x轴相交于点A，B，与y轴相交于点C，直线y=x+4经过A，C两点，（1）求抛物线的表达式；（2）如果点P，Q在抛物线上（P点在对称轴左边），且PQ△AO，PQ=2AO，求P，Q的坐标；（3）动点M在直线y=x+4上，且△ABC与△COM相似，求点M的坐标．【解答】解：（1）当x=0时，y=4，即C（0，4），当y=0时，x+4=0，解得x=﹣4，即A（﹣4，0），将A、C点坐标代入函数解析式，得，解得，抛物线的表达式为y=﹣x+4；（2）PQ=2AO=8，又PQ△AO，即P、Q关于对称轴x=﹣1对称，PQ=8，﹣1﹣4=﹣5，当x=﹣5时，y=×（﹣5）2﹣（﹣5）+4=﹣，即P（﹣5，﹣）；﹣1+4=3，即Q（3，﹣）；P点坐标（﹣5，﹣），Q点坐标（3，﹣）；（3）△MCO=△CAB=45°，①当△MCO△△CAB时，=，即=，CM=．如图1，过M作MH△y轴于H，MH=CH=CM=，当x=﹣时，y=﹣+4=，△M（﹣，）；当△OCM△△CAB时，=，即=，解得CM=3，如图2，过M作MH△y轴于H，MH=CH=CM=3，当x=3时，y=﹣3+4=1，△M（﹣3，1），综上所述：M点的坐标为（﹣，），（﹣3，1）．25．（14分）已知菱形ABCD的边长为5，对角线AC的长为6，点E为边AB上的动点，点F在射线AD上，且△ECF=△B，直线CF交直线AB于点M．（1）求△B的余弦值；（2）当点E与点A重合时，试画出符合题意的图形，并求出BM的长；（3）当点M在边AB的延长线上时，设BE=x，BM=y，求y关于x的函数解析式，并写出定义域．【解答】解：（1）连接BD、AC交于点O，作AH△BC于H，如图1所示：则AO=OC=3，BO=4，△S△ABC=BC×AH=AC×BO=×6×4=12，△×5×AH=12，解得：AH=，由勾股定理得：BH===，△cos△B===；（2）当点E与点A重合时，符合题意的图形，如图2所示：△四边形ABCD为菱形，△△FAC=△ACB，△△ECF=△B，△△ABC△△ECF，△=，即=，解得：EF=，△BC△AF，△△MBC△△MAF，△===，△=，解得：BM=；（3）作EH△BC于H，作EG△BC交CF于G，如图3所示：由（1）知cos△B=，BE=x，△BH=x，EH===x，△CE===，△EG△BC，△△GEC=△ECB，，△△BCE△△CEG，△，则EG==，△，整理得：y=，即y关于x的函数解析式为y=（＜x≤5）．。

上海市崇明县2016年中考数学一模试题(含解析)9．抛物线y=（a+2）x2+3x﹣a的开口向下，那么a 的取值范围是．10．一斜面的坡度i=1：0.75，一物体由斜面底部沿斜面向前推进了20米，那么这个物体升高了米．11．如果一个正多边形的一个外角是36°，那么该正多边形的边数为．12．已知AB是⊙O的直径，弦CD⊥AB于点E，如果AB=8，CD=6，那么OE= ．13．如图所示，某班上体育课，甲、乙两名同学分别站在C、D的位置时，乙的影子恰好在甲的影子里边，已知甲身高1.8米，乙身高1.5米，甲的影长是6米，则甲、乙同学相距米．14．如图，点A（3，t）在第一象限，OA与x轴所夹的锐角为α，tanα=，则t的值是．15．如图，▱ABCD中，E是CD的延长线上一点，BE 与AD交于点F，CD=2DE．若△DEF的面积为1，则▱ABCD的面积为．16．如图，在矩形ABCD中，AB=3，BC=5，以B为圆心BC为半径画弧交AD于点E，如果点F是弧EC的中点，联结FB，那么tan∠FBC的值为．17．新定义：我们把两条中线互相垂直的三角形称为“中垂三角形”．如图所示，△ABC中，AF、BE 是中线，且AF⊥BE，垂足为P，像△ABC这样的三角形称为“中垂三角形”，如果∠ABE=30°，AB=4，那么此时AC的长为．18．如图，等边△ABC中，D是边BC上的一点，且BD：DC=1：3，把△ABC折叠，使点A落在边BC上的点D处，那么的值为．三.解答题19．计算：﹣cot30°．20．已知，平行四边形ABCD中，点E在DC边上，且DE=3EC，AC与BE交于点F；（1）如果，，那么请用、来表示；（2）在原图中求作向量在、方向上的分向量．（不要求写作法，但要指出所作图中表示结论的向量）、21．如图，已知AD∥BE∥CF，它们依次交直线l1于点A、B、C和点D、E、F，，AC=14；l2（1）求AB、BC的长；（2）如果AD=7，CF=14，求BE的长．22．目前，崇明县正在积极创建全国县级文明城市，交通部门一再提醒司机：为了安全，请勿超速，并在进一步完善各类监测系统，如图，在陈海公路某直线路段MN内限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗？请说明理由．（参考数据：，）23．如图1，△ABC中，∠ACB=90°，CD⊥AB，垂足为D；（1）求证：△ACD∽△CBD；（2）如图2，延长DC至点G，联结BG，过点A作AF⊥BG，垂足为F，AF交CD于点E，求证：CD2=DE•DG．24．如图，在直角坐标系中，一条抛物线与x轴交于A、B两点，与y轴交于C点，其中B（3，0），C （0，4），点A在x轴的负半轴上，OC=4OA；（1）求这条抛物线的解析式，并求出它的顶点坐标；（2）联结AC、BC，点P是x轴正半轴上一个动点，过点P作PM∥BC交射线AC于点M，联结CP，若△CPM 的面积为2，则请求出点P的坐标．25．如图，已知矩形ABCD中，AB=6，BC=8，E是BC 边上一点（不与B、C重合），过点E作EF⊥AE交AC、CD于点M、F，过点B作BG⊥AC，垂足为G，BG 交AE于点H；（1）求证：△ABH∽△ECM；（2）设BE=x，，求y关于x的函数解析式，并写出定义域；（3）当△BHE为等腰三角形时，求BE的长．2016年上海市崇明县中考数学一模试卷参考答案与试题解析一.选择题1．已知=，那么的值为（）A．B．C．D．【考点】比例的性质．【分析】根据=，可设a=2k，则b=3k，代入所求的式子即可求解．【解答】解：∵ =，∴设a=2k，则b=3k，则原式==．故选B．【点评】本题考查了比例的性质，根据=，正确设出未知数是本题的关键．2．已知Rt△ABC中，∠C=90°，BC=3，AB=5，那么sinB的值是（）A．B．C．D．【考点】锐角三角函数的定义．【分析】首先利用勾股定理求得AC的长，然后利用正弦的定义求解．【解答】解：在直角△ABC中，AC===4，则sinB==．故选C．【点评】本题考查了正弦函数的定义，是所对的直角边与斜边的比，理解定义是关键．3．将抛物线y=x2先向右平移2个单位，再向下平移3个单位，那么得到的新的抛物线的解析式是（）A．y=（x+2）2+3 B．y=（x+2）2﹣3 C．y=（x﹣2）2+3 D．y=（x﹣2）2﹣3【考点】二次函数图象与几何变换．【分析】先确定出原抛物线的顶点坐标，然后根据向右平移横坐标加，向下平移纵坐标减求出新图象的顶点坐标，然后写出即可．【解答】解：抛物线y=x2的顶点坐标为（0，0），向右平移2个单位，再向下平移3个单位后的图象的顶点坐标为（2，﹣3），所以，所得图象的解析式为y=（x﹣2）2﹣3，故选：D．【点评】本题主要考查的是函数图象的平移，根据平移规律“左加右减，上加下减”利用顶点的变化确定图形的变化是解题的关键．4．如图，在△ABC中，点D、E分别在AB、AC上，∠AED=∠B，那么下列各式中一定正确的是（）A．AE•AC=AD•AB B．CE•CA=BD•AB C．AC•AD=AE•AB D．AE•EC=AD•DB【考点】相似三角形的判定与性质．【专题】证明题．【分析】在△ABC中，点D、E分别在AB、AC上，∠AED=∠B，而∠A公共，由此可以得到△ABC∽△AED，然后利用相似三角形的性质即可求解．【解答】解：∵在△ABC中，点D、E分别在AB、AC上，∠AED=∠B，而∠A公共，∴△ABC∽△AED，∴AB：AE=AC：AD，∴AB•AD=AC•AE．故选A．【点评】此题主要考查了相似三角形的下着雨判定，解题的关键是证明两个三角形相似即可解决问题．5．已知两圆的半径分别是3和5，圆心距是1，那么这两圆的位置关系是（）A．内切B．外切C．相交D．内含【考点】圆与圆的位置关系．【分析】先计算两圆的半径之差，然后根据圆和圆的位置关系的判定方法可确定这两圆的位置关系．【解答】解：∵5﹣3=2＞1，即圆心距小于两半径之差，∴这两圆内含．故选D．【点评】本题考查了圆和圆的位置关系：两圆的圆心距为d，两圆半径分别为R、r，：当两圆外离⇔d＞R+r；两圆外切⇔d=R+r；两圆相交⇔R﹣r＜d＜R+r（R≥r）；两圆内切⇔d=R﹣r（R＞r）；两圆内含⇔d＜R﹣r（R＞r）．6．如图所示，一张等腰三角形纸片，底边长18cm，底边上的高长18cm，现沿底边依次向下往上裁剪宽度均为3cm的矩形纸条，已知剪得的纸条中有一张是正方形，则这张正方形纸条是（）A．第4张B．第5张C．第6张D．第7张【考点】相似三角形的应用．【分析】根据相似三角形的相似比求得顶点到这个正方形的长，再根据矩形的宽求得是第几张．【解答】解：已知剪得的纸条中有一张是正方形，则正方形中平行于底边的边是3，所以根据相似三角形的性质可设从顶点到这个正方形的线段为x，则，解得x=3，所以另一段长为18﹣3=15，因为15÷3=5，所以是第5张．故选：B．【点评】本题主要考查了相似三角形的性质及等腰三角形的性质的综合运用；由相似三角形的性质得出比例式是解决问题的关键．二.填空题7．化简： = ﹣﹣7．【考点】*平面向量．【分析】直接利用平面向量的加减运算法则求解即可求得答案．【解答】解： =2﹣4﹣3﹣3=﹣﹣7．故答案为：．【点评】此题考查了平面向量的运算法则．注意掌握去括号时的符号变化是解此题的关键．8．如果在比例1：1000000的地图上，A、B两地的图上距离为2.4厘米，那么A、B两地的实际距离为24 千米．【考点】比例线段．【分析】实际距离=图上距离：比例尺，根据题意代入数据可直接得出实际距离．【解答】解：根据题意，2.4÷=2400000厘米=24千米．即实际距离是24千米．故答案为：24．【点评】本题考查了比例线段的知识，注意掌握比例线段的定义及比例尺，并能够灵活运用，同时要注意单位的转换．9．抛物线y=（a+2）x2+3x﹣a的开口向下，那么a 的取值范围是a＜﹣2 ．【考点】二次函数的性质；二次函数的定义．【专题】推理填空题．【分析】根据抛物线y=（a+2）x2+3x﹣a的开口向下，可得a+2＜0，从而可以得到a的取值范围．【解答】解：∵抛物线y=（a+2）x2+3x﹣a的开口向下，∴a+2＜0，得a＜﹣2，故答案为：a＜﹣2．【点评】本题考查二次函数的性质和定义，解题的关键是明确二次函数的开口向下，则二次项系数就小于0．10．一斜面的坡度i=1：0.75，一物体由斜面底部沿斜面向前推进了20米，那么这个物体升高了16 米．【考点】解直角三角形的应用-坡度坡角问题．【专题】推理填空题．【分析】根据一斜面的坡度i=1：0.75，可以设出一物体由斜面底部沿斜面向前推进了20米时对应的竖直高度和水平距离，然后根据勾股定理可以解答此题．【解答】解：设一物体由斜面底部沿斜面向前推进了20米时，对应的竖直高度为x，则此时的水平距离为0.75x，根据勾股定理，得x2+（0.75x）2=202解得x1=16，x2=﹣16（舍去），即一物体由斜面底部沿斜面向前推进了20米，此时这个物体升高了16米．故答案为：16．【点评】本题考查解直角三角形的应用﹣坡度坡角问题，解题的关键是明确什么是坡度，坡度是竖直高度与水平距离的比值．11．如果一个正多边形的一个外角是36°，那么该正多边形的边数为10 ．【考点】多边形内角与外角．【分析】利用外角和360°除以外角的度数36°可得正多边形的边数．【解答】解：360÷36=10，故答案为：10．【点评】此题主要考查了多边形的外角，关键是掌握多边形外角和为360°．12．已知AB是⊙O的直径，弦CD⊥AB于点E，如果AB=8，CD=6，那么OE= ．【考点】垂径定理；勾股定理．【分析】连接OC，根据垂径定理求出CE，在△OEC 中，根据勾股定理求出OE即可．【解答】解：连接OC．如图所示：∵AB是圆O的直径，AB⊥CD，∴CE=DE=CD=3，OC=OB=AB=4，在△OCE中，由勾股定理得：OE===；故答案为：．【点评】本题考查了勾股定理、垂径定理；关键是构造直角三角形，求出CE的长，用的数学思想是方程思想，把OE当作一个未知数，题目较好．13．如图所示，某班上体育课，甲、乙两名同学分别站在C、D的位置时，乙的影子恰好在甲的影子里边，已知甲身高1.8米，乙身高1.5米，甲的影长是6米，则甲、乙同学相距 1 米．【考点】相似三角形的应用．【专题】应用题．【分析】根据甲的身高与影长构成的三角形与乙的身高和影长构成的三角形相似，列出比例式解答．【解答】解：设两个同学相距x米，∵△ADE∽△ACB，∴，∴，解得：x=1．故答案为1．【点评】本题考查了相似三角形的应用，根据身高与影长的比例不变，得出三角形相似，运用相似比即可解答．14．如图，点A（3，t）在第一象限，OA与x轴所夹的锐角为α，tanα=，则t的值是．【考点】解直角三角形；坐标与图形性质．【分析】过点A作AB⊥x轴于B，根据正切等于对边比邻边列式求解即可．【解答】解：过点A作AB⊥x轴于B，∵点A（3，t）在第一象限，∴AB=t，OB=3，又∵tanα===，∴t=．故答案为：．【点评】本题考查了锐角三角函数的定义，过点A 作x轴的垂线，构造出直角三角形是利用正切列式的关键，需要熟记正切=对边：邻边．15．如图，▱ABCD中，E是CD的延长线上一点，BE 与AD交于点F，CD=2DE．若△DEF的面积为1，则▱ABCD的面积为12 ．【考点】相似三角形的判定与性质；平行四边形的性质．【分析】求出CE=3DE，AB=2DE，求出=， =，根据平行四边形的性质得出AB∥CD，AD∥BC，推出△DEF∽△CEB，△DEF∽△ABF，求出=（）2=，=（）2=，求出△CEB的面积是9，△ABF的面积是4，得出四边形BCDF的面积是8，即可得出平行四边形ABCD的面积．【解答】解：∵四边形ABCD是平行四边形，∴AD=BC，AB=CD，∵CD=2DE，∴CE=3DE，AB=2DE，∴=， =，∵四边形ABCD是平行四边形，∴AB∥CD，AD∥BC，∴△DEF∽△CEB，△DEF∽△ABF，∴=（）2=， =（）2=，∵△DEF的面积为1，∴△CEB的面积是9，△ABF的面积是4，∴四边形BCDF的面积是9﹣1=8，∴平行四边形ABCD的面积是8+4=12，故答案为：12．【点评】本题考查了平行四边形性质，相似三角形的性质和判定的应用，注意：相似三角形的面积比等于相似比的平方．16．如图，在矩形ABCD中，AB=3，BC=5，以B为圆心BC为半径画弧交AD于点E，如果点F是弧EC的中点，联结FB，那么ta n∠FBC的值为．【考点】全等三角形的判定与性质；角平分线的性质；矩形的性质；圆心角、弧、弦的关系；解直角三角形．【分析】连接CE交BF于H，连接BE，根据矩形的性质求出AB=CD=3，AD=BC=5=BE，∠A=∠D=90°，根据勾股定理求出AE=4，求出DE=1，根据勾股定理求出CE，求出CH，解直角三角形求出即可．【解答】解：连接CE交BF于H，连接BE，∵四边形ABCD是矩形，AB=3，BC=5，∴AB=CD=3，AD=BC=5=BE，∠A=∠D=90°，由勾股定理得：AE==4，DE=5﹣4=1，由勾股定理得：CE==，由垂径定理得：CH=EH=CE=，在Rt△BFC中，由勾股定理得：BH==，所以tan∠FBC===．故答案为：．【点评】本题考查了矩形的性质，勾股定理，解直角三角形，垂径定理的应用，能正确作出辅助线并构造出直角三角形是解此题的关键．17．新定义：我们把两条中线互相垂直的三角形称为“中垂三角形”．如图所示，△ABC中，AF、BE 是中线，且AF⊥BE，垂足为P，像△ABC这样的三角形称为“中垂三角形”，如果∠ABE=30°，AB=4，那么此时AC的长为2．【考点】三角形的重心；勾股定理．【专题】计算题；三角形．【分析】根据三角形中位线的性质，得到EF∥AB，EF=AB=2，再由勾股定理得到结果．【解答】解：如图，连接EF，∵AF、BE是中线，∴EF是△CAB的中位线，可得：EF=×4=2，∵EF∥AB，∴△PEF～△ABP，∴===，在Rt△ABP中，AB=4，∠ABP=30°，∴AP=2，PB=2，∴PF=1，PE=，在Rt△APE中，∴AE=，∴AC=2，故答案为：．【点评】本题考查了相似三角形的判定和性质、勾股定理等知识，熟练应用相似三角形的判定与性质是解题关键．18．如图，等边△ABC中，D是边BC上的一点，且BD：DC=1：3，把△ABC折叠，使点A落在边BC上的点D处，那么的值为．【考点】翻折变换（折叠问题）．【分析】由BD：DC=1：3，可设BD=a，则CD=3a，根据等边三角形的性质和折叠的性质可得：BM+MD+BD=5a，DN+NC+DC=7a，再通过证明△BMD∽△CDN即可证明AM：AN的值．【解答】解：∵BD：DC=1：3，∴设BD=a，则CD=3a，∵△ABC是等边三角形，∴AB=BC=AC=4a，∠ABC=∠ACB=∠BAC=60°，由折叠的性质可知：MN是线段AD的垂直平分线，∴AM=DM，AN=DN，∴BM+MD+BD=5a，DN+NC+DC=7a，∵∠MDN=∠BAC=∠ABC=60°，∴∠NDC+∠MDB=∠BMD+∠MBD=120°，∴∠NDC=∠BMD，∵∠ABC=∠ACB=60°，∴△BMD∽△CDN，∴（BM+MD+BD）：（DN+NC+CD）=AM：AN，即AM：AN=5：7，故答案为．【点评】本题考查了等边三角形的性质、全等三角形的判定和性质以及折叠的性质：折叠是一种对称变换，它属于轴对称，折叠前后图形的形状和大小不变，位置变化，对应边和对应角相等．三.解答题19．计算：﹣cot30°．【考点】特殊角的三角函数值．【分析】将特殊角的三角函数值代入求解．【解答】解：原式=﹣=﹣==2．【点评】本题考查了特殊角的三角函数值，解答本题的关键是掌握几个特殊角的三角函数值．20．已知，平行四边形ABCD中，点E在DC边上，且DE=3EC，AC与BE交于点F；（1）如果，，那么请用、来表示；（2）在原图中求作向量在、方向上的分向量．（不要求写作法，但要指出所作图中表示结论的向量）【考点】*平面向量；平行四边形的性质．【分析】（1）由四边形ABCD是平行四边形，根据平行四边形法则，易得，再由三角形法则，可求得，又由DE=3EC，CD∥AB，根据平行线分线段成比例定理，即可得，继而求得答案；（2）首先过点F作FM∥AD，FN∥AB，根据平行四边形法则即可求得答案．【解答】解：（1）∵四边形ABCD是平行四边形，∴AD∥BC且AD=BC，CD∥AB且CD=AB，∴，又∵，∴，∵DE=3EC，∴DC=4EC，又∵AB=CD，∴AB=4EC，∵CD∥AB，∴，∴，∴，∴；（2）如图，过点F作FM∥AD，FN∥AB，则，分别是向量在、方向上的分向量．【点评】此题考查了平面向量的知识以及平行四边形的性质．注意掌握平行四边形法则与三角形法则的应用是解此题的关键．、21．如图，已知AD∥BE∥CF，它们依次交直线l1l于点A、B、C和点D、E、F，，AC=14；2（1）求AB、BC的长；（2）如果AD=7，CF=14，求BE的长．【考点】平行线分线段成比例．【分析】（1）由平行线分线段成比例定理和比例的性质得出，即可求出AB的长，得出BC的长；（2）过点A作AG∥DF交BE于点H，交CF于点G，得出AD=HE=GF=7，由平行线分线段成比例定理得出比例式求出BH，即可得出结果．【解答】解：（1）∵AD∥BE∥CF，∴，∴，∵AC=14，∴AB=4，∴BC=14﹣4=10；（2）过点A作AG∥DF交BE于点H，交CF于点G，如图所示：又∵AD∥BE∥CF，AD=7，∴AD=HE=GF=7，∵CF=14，∴CG=14﹣7=7，∵BE∥CF，∴，∴BH=2，∴BE=2+7=9．【点评】本题考查了平行线分线段成比例：三条平行线截两条直线，所得的对应线段成比例；熟练掌握平行线分线段成比例，通过作辅助线运用平行线分线段成比例求出BH是解决问题的关键．22．目前，崇明县正在积极创建全国县级文明城市，交通部门一再提醒司机：为了安全，请勿超速，并在进一步完善各类监测系统，如图，在陈海公路某直线路段MN内限速60千米/小时，为了检测车辆是否超速，在公路MN旁设立了观测点C，从观测点C测得一小车从点A到达点B行驶了5秒钟，已知∠CAN=45°，∠CBN=60°，BC=200米，此车超速了吗？请说明理由．（参考数据：，）【考点】解直角三角形的应用．【分析】根据题意结合锐角三角函数关系得出BH，CH，AB的长进而求出汽车的速度，进而得出答案．【解答】解：此车没有超速．理由如下：过C作CH⊥MN，垂足为H，∵∠CBN=60°，BC=200米，∴CH=BC•sin60°=200×=100（米），BH=BC•cos60°=100（米），∵∠CAN=45°，∴AH=CH=100米，∴AB=100﹣100≈73（m），∴车速为m/s．∵60千米/小时=m/s，又∵14.6＜，∴此车没有超速．【点评】此题主要考查了勾股定理以及锐角三角函数关系的应用，得出AB的长是解题关键．23．如图1，△ABC中，∠ACB=90°，CD⊥AB，垂足为D；（1）求证：△ACD∽△CBD；（2）如图2，延长DC至点G，联结BG，过点A作AF⊥BG，垂足为F，AF交CD于点E，求证：CD2=DE•DG．【考点】相似三角形的判定与性质．【专题】证明题．【分析】（1）根据垂直的定义得到∠ADC=∠CDB=90°，根据余角的性质得到∠ACD=∠B，由于∠ADC=∠CDB，即可得到结论；（2）根据∠ACB=90°，CD⊥AB，得到∠CAD=∠BCD，推出Rt△ACD∽Rt△CBD，于是得到CD2=AD•BD，根据AF⊥B G，GD⊥AB，证得∠EDA=∠EFG=∠GDP=90°，推出△BGD∽△ADE，于是得到AD•BD=DG•DE即可得到结论．【解答】证明：（1）∵CD⊥AB，∴∠ADC=∠CDB=90°，∴∠BCD+∠B=90°，∵∠ACB=90°，∴∠ACD+∠BCD=90°，∴∠ACD=∠B，又∵∠ADC=∠CDB，∴△ACD∽△CBD；（2）∵AF⊥BG，∴∠AFB=90°，∴∠FAB+∠GBA=90°，∵∠GDB=90°，∴∠G+∠GBA=90°，∴∠G=∠FAB，又∵∠ADE=∠GDB=90°，∴△ADE∽△GDB，∴，∴AD•BD=DE•DG，∵△ACD∽△CBD，∴，∴CD2=AD•BD，∴CD2=DE•DG．【点评】此题主要考查的是相似三角形的判定和性质，垂直的定义，熟练掌握相似三角形的判定和性质是解题的关键．24．如图，在直角坐标系中，一条抛物线与x轴交于A、B两点，与y轴交于C点，其中B（3，0），C （0，4），点A在x轴的负半轴上，OC=4OA；（1）求这条抛物线的解析式，并求出它的顶点坐标；（2）联结AC、BC，点P是x轴正半轴上一个动点，过点P作PM∥BC交射线AC于点M，联结CP，若△CPM 的面积为2，则请求出点P的坐标．【考点】二次函数综合题．【分析】（1）根据OA与OC的关系，可得A点坐标，根据待定系数法，可得函数解析式；（2）根据锐角三角函数，可得PH的长，根据相似三角形的性质，可得MC的长，根据三角形的面积，可得关于x的方程，根据解方程，可得答案．【解答】解：（1）∵C（0，4），O（0，0），∴OC=4．∵OC=4OA，∴OA=1．∵点A在x轴的负半轴上，∴A（﹣1，0）．设这条抛物线的解析式为y=ax2+bx+c，∵抛物线过点 A（﹣1，0），B（3，0），C（0，4）∴，解得，∴这条抛物线的解析式为y=﹣x+x+4，它的顶点坐标为（1，）；（2）过点P作PH⊥AC，垂足为H．∵P点在x轴的正半轴上，∴设P（x，0）．∵A（﹣1，0），∴PA=x+1．∵在Rt△AOC中，OA2+OC2=AC2又∵OA=1，OC=4，∴AC===，∵∠AOC=90°，∴sin∠CAO===∵∠PHA=90°，∴sin∠CAO===∴PH=．∵PM∥BC，∴=∵B（3，0），P （x ，0）①点P 在点B 的左侧时，BP=3﹣x∴=，∴CM=．∵S △PCM =2，∴CM•PH=2，∴••=2．解得x=1．∴P（1，0）；②点P 在点B 的右侧时，BP=x ﹣3∴=，∴CM=，∵S △PCM =2，∴CM•PH=2，∴••=2．解得x 1=1+2，x 2=1﹣2（不合题意，舍去）∴P（，0）．综上所述，P 的坐标为（1，0）或（，0）．【点评】本题考查了二次函数综合题，利用待定系数法求函数解析式；利用锐角三角函数得出PH的长是解题关键，又利用相似三角形的性质得出CM的长，利用三角形的面积得出关于x的方程．25．如图，已知矩形ABCD中，AB=6，BC=8，E是BC 边上一点（不与B、C重合），过点E作EF⊥AE交AC、CD于点M、F，过点B作BG⊥AC，垂足为G，BG 交AE于点H；（1）求证：△ABH∽△ECM；（2）设BE=x，，求y关于x的函数解析式，并写出定义域；（3）当△BHE为等腰三角形时，求BE的长．【考点】相似形综合题．【专题】综合题；图形的相似．【分析】（1）由矩形的四个角为直角，得到∠ABC 为直角，再由BG垂直于AC，AE垂直于EF，得到一对直角相等，利用同角的余角相等得到一对角相等，再利用外角性质得到另一对角相等，利用两角相等的三角形相似即可得证；（2）延长BG，交AD于点K，利用两角相等的三角形相似得到三角形ABK与三角形ABC相似，由相似得比例求出AK的长，由AK与BE平行，得到三角形AHK 与三角形BHE相似，表示出EH，由第一问的结论，利用相似三角形对应边成比例表示出，即可确定出y与x的函数解析式，并求出定义域即可；（3）当△BHE为等腰三角形时，分三种情况考虑：①当BH=BE时，利用等腰三角形的性质，角平分线定义及锐角三角函数定义求出BE的长；②当HB=HE 时，利用等腰三角形的性质及锐角三角函数定义求出BE的长；③当EB=EH时，利用等腰三角形的性质及勾股定理求出BE的长即可．【解答】（1）证明：∵四边形ABCD是矩形，∴∠ABC=90°，即∠ABG+∠CBG=90°，∵EF⊥AE，BG⊥AC，∴∠AEF=∠BGA=90°，∴∠AEF=∠ABC，∠ACB+∠CBG=90°，∴∠ABG=∠ACB，∵∠AEC=∠ABC+∠BAE，即∠AEF+∠CEF=∠ABC+∠BAE，∴∠BAE=∠CEF，又∵∠ABG=∠ACB，∴△ABH∽△ECM；（2）解：延长BG交AD于点K，∵∠ABG=∠ACB，又∵在矩形ABCD中，∠BAK=∠ABC=90°，∴△ABK∽△BCA，∴=，即=，∴AK=，∵在矩形ABCD中，AD∥BC，且BE=x，∴==，∴EH=•AH，∵△ABH∽△ECM，∴==，∵=y，∴y==•=•=（0＜x＜8）；（3）解：当△BHE为等腰三角形时，存在以下三种情况：①当BH=BE时，则有∠BHE=∠BEH，∵∠BHE=∠AHG，∴∠BEH=∠AHG，∵∠ABC=∠BGA=90°，∴∠BEH+∠BAE=∠AHG+∠EAM=90°，∴∠BAE=∠EAM，即AE为∠BAC的平分线，过点E作EQ⊥AC，垂足为Q，如图2所示，则EQ=EB=x，CE=8﹣x，∵sin∠ACB===，∴x=3，即BE=3；②当HB=HE时，则有∠HBE=∠HEB，∵∠ABC=∠BGC=90°，∴∠BAE+∠HEB=∠BCG+∠HBE=90°，∴∠BAE=∠BCG，∴tan∠BAE=tan∠BCA==，∴x=，即BE=；③当EB=EH时，则有∠EHB=∠EBH，又∵∠EHB=∠AHG，∴∠AHG=∠EBH，∵∠BGA=∠BGC=90°，∴∠CAE+∠AHG=∠BCG+∠EBH=90°，∴∠CAE=∠BCG，∴EA=EC=8﹣x，∵在Rt△ABE中，AB2+BE2=AE2，即62+x2=（8﹣x）2，解得：x=，即BE=，综上所述，当△BHE是等腰三角形时，BE的长为3或或．【点评】此题属于相似形综合题，涉及的知识有：矩形的性质，相似三角形的判定与性质，平行线等分线段定理，勾股定理，锐角三角函数定义，以及等腰三角形的性质，熟练掌握相似三角形的判定与性质是解本题的关键．。

2016届中考数学一模考试试卷（练习）中考复习最忌心浮气躁，急于求成。

指导复习的教师，应给学生一种乐观、镇定、自信的精神面貌。

要扎扎实实地复习，一步一步地前进，下文为大家准备了中考数学一模考试试卷的内容。

一.仔细选一选(本题有10个小题，每小题3分，共30分)下面每小题给出的四个选项中，只有一个是正确的.注意可以用多种不同的方法来选取正确答案.1.的倒数是()(A)(B)(C)(D)2.解一元二次方程得到它的根是()(A)(B)或(C)(D)或3.事件A：若a是实数，则事件B：若实数x满足，则x正实数。

则下列关于事件A和事件B的说法正确的是()(A)事件A是必然事件，而事件B是随机事件(B)事件A是随机事件，而事件B是必然事件(C)事件A是必然事件，而事件B是必然事件(D)事件A是随机事件，而事件B是随机事件4.下列各数：①;②;③;④中是负数的是()(A)①②③(B)①②④(C)②③④(D)①②③④5.如图①，有6张写有实数的卡片，它们的背面都相同，现将它们背面朝上洗匀后如图②摆放，从中任意翻开两张都是无理数的概率是()(A)(B)(C)(D)6.如图是某几何体的三视图及相关数据，则判断正确的是(A)(B)(C)(D)7.如图，A、B、C是⊙O上的三点，且A是优弧BAC上与点B、点C不同的一点，若△BOC是直角三角形，则△BAC必是()(A)等腰三角形(B)锐角三角形(C)有一个角是的三角形(D)有一个角是的三角形8.如右图所示，三角形ABC的面积为1cm2。

AP垂直B的平分线BP于P。

则与三角形PBC的面积相等的长方形是()9.两个正数满足，，设，则P关于t的函数图像是A.射线(不含端点)B.线段(不含端点)C.直线D.抛物线的一部分10.如图，边长为2的正方形EFGH在边长为6的正方形ABCD 所在平面上移动，始终保持EF∥AB.线段CF的中点为M，DH的中点为N，则线段MN的长为()A、B、C、D、二.认真填一填(本题有6个小题，每小题4分，共24分)要注意认真看清题目的条件和要填写的内容,尽量完整地填写答案.11.如图，直线a//b，直角三角板的直角顶点P在直线b上，若，则的度数。

2016年黄浦区一模18、如图6，在梯形ABCD 中，AD//BC ，45=∠B ,点E 是AB 的中点，DE=DC ，90=∠EDC 若AB=2，则AD 的长是_____24、在平面直角坐标系中，抛物线c ax ax y +-=32与x 轴交于A （-1,0）、B 两点（A 在B 点左侧),与y 轴交于点C （0,2）（1）求抛物线的对称轴及B 点坐标 （2）求证：BCO CAO ∠=∠（3）点D 是射线BC 上一点（不与B 、C 重合），联结OD ，过点B 作OD BF ⊥，垂足为BOD ∆外一点E ，若BDE ∆与ABC ∆相似，求点D 的坐标25、已知直线1l 、2l ，1l //2l ,点A 是1l 上的点，B 、C 是2l 上的点BC AC ⊥,60=∠ABC ,AB=4，O 是AB 中点，D 是CB 延长线上的点，将DOC ∆沿直线CO 翻折，点D 与'D 重合（1）如图12，当点'D 落在直线1l 上时，求DB 的长（2）延长DO 交1l 于点E ，直线'OD 分别交1l 、2l 于点M 、N①如图13，当点E 在线段AM 上时，设AE=x,DN=y ，求y 关于x 的函数解析式及其定义域 ②若DON ∆的面积为323时，求AE 的长2016年杨浦区一模18、如图，已知将ABC ∆沿角平分线BE 所在的直线翻折，点A 恰好落在边BC 的中点M 处，且AM=BE ，那么EBC ∠的正切值为_____24、在平面直角坐标系中，抛物线c bx x y ++-=221与x 轴交于A 、B 两点，与y 轴交于点C ，直线4+=x y 经过A,C 两点（1）求抛物线的表达式（2）如果点P 、Q 在抛物线上（P 点在对称轴的左边），且PQ//AO,PQ=2AO,求点P 、Q 的坐标 （3）动点M 在直线4+=x y 上，且ABC ∆与COM ∆相似，求点M 的坐标25、已知菱形ABCD 的边长为5，对角线AC 的长为6,（如图1），点E 为边AB 上的动点，点F 在射线AD 上，且B ECF ∠=∠，直线CF 交直线AB 于点M,的余弦值(1)求B（2）当点E与点A重合时，试画出符合题意的图形，并求BM的长（3）当点M在边AB的延长线上时，设BE=x，BM=y,求y关于x的函数解析式并写出定义域2016年徐汇区一模18、如图8，在Rt△ABC中，∠BAC=90°，AB=3，cosB=，将△ABC绕着点A旋转得△ADE，点B的对应点D落在边BC上，联结CE，那么CE的长是________.24、如图12，在Rt△AOB中，∠AOB=90°，已知点A(-1，-1)，点B在第二象限，OB=，抛物线经过点A和点B.(1)求点B的坐标；(2)求抛物线的对称轴；(3)如果该抛物线的对称轴分别和边AO、BO的延长线交于点C、D，设点E在直线AB上，当△BOE和△BCD相似时，直接写出点E的坐标。