下载文档原格式
以下是一些常见函数的导数：
1. 常数函数：f(x)=c的导数为0。
2. 幂函数：f(x)=x^n的导数为f'(x)=nx^(n-1)。
3. 指数函数：f(x)=a^x的导数为f'(x)=a^x*lna。
4. 对数函数：f(x)=lnx的导数为f'(x)=1/x。
5. 三角函数：
* 正弦函数：f(x)=sinx的导数为f'(x)=cosx。
* 余弦函数：f(x)=cosx的导数为f'(x)=-sinx。
* 正切函数：f(x)=tanx的导数为f'(x)=sec^2x。
6. 反三角函数：
* 反正弦函数：f(x)=arcsinx的导数为f'(x)=1/√(1-x^2)。
* 反余弦函数：f(x)=arccosx的导数为f'(x)=-1/√(1-x^2)。
* 反正切函数：f(x)=arctanx的导数为f'(x)=1/(1+x^2)。
7. 双曲函数：
* 自然双曲正弦函数：f(x)=shx的导数为f'(x)=chx。
* 自然双曲余弦函数：f(x)=chx的导数为f'(x)=shx。
8. 幂函数：对于形如f(x)=ax^n的幂函数，其导数为
f'(x)=nax^(n-1)。
9. 分式函数：对于形如f(x)=u/v的函数，其中u和v都是可导的，其导数为f'(x)=(u'v-uv')/v^2。
这只是一部分常见函数的导数，实际上还有很多其他类型的函数，这些函数的导数都需要根据具体情况进行计算。
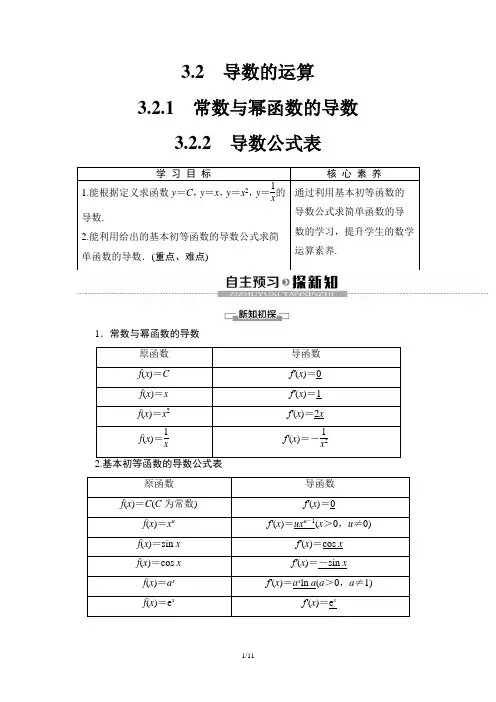
3.2导数的运算3.2.1常数与幂函数的导数3.2.2导数公式表学习目标核心素养1.能根据定义求函数y＝C，y＝x，y＝x2，y＝1 x的导数.2.能利用给出的基本初等函数的导数公式求简单函数的导数．(重点、难点) 通过利用基本初等函数的导数公式求简单函数的导数的学习，提升学生的数学运算素养.1．常数与幂函数的导数原函数导函数f(x)＝C f′(x)＝0f(x)＝x f′(x)＝1f(x)＝x2f′(x)＝2xf(x)＝1x f′(x)＝－1x2原函数导函数f(x)＝C(C为常数)f′(x)＝0 f(x)＝x u f′(x)＝ux u－1(x＞0，u≠0) f(x)＝sin x f′(x)＝cos xf(x)＝cos x f′(x)＝－sin xf(x)＝a x f′(x)＝a x ln a(a＞0，a≠1) f(x)＝e x f′(x)＝e xf (x )＝log a x f′(x )＝1x ln a (a ＞0，a ≠1，x ＞0)f (x )＝ln xf′(x )＝1x1．下列结论：①(sin x )′＝cos x ；②(x 53)′＝x 23； ③(log 3x )′＝13ln x ；④(ln x )′＝1x .其中正确的有( )A ．0个B ．1个C ．2个D ．3个C [∵②(x 53)′＝53x 23；③(log 3x )＝1x ln 3；∴②③错误，故选C.] 2．若函数f (x )＝x ，则f′(1)等于( ) A ．0 B ．－12 C ．12D ．1C [∵f′(x )＝(x )′＝(x12)′＝12x 12－1＝12x，∴f′(1)＝12，故选C.]3．曲线y ＝sin x 在⎝ ⎛⎭⎪⎫π4，22处的切线方程为________．42x －8y ＋2(4－π)＝0 [∵k ＝(sin x )′|x ＝π4＝cos π4＝22，∴切线方程为y －22＝22⎝ ⎛⎭⎪⎫x －π4，即42x －8y ＋2(4－π)＝0.]利用导数公式求函数的导数(1)y ＝x 12；(2)y ＝1x 4；(3)y ＝5x 3； (4)y ＝2sin x 2cos x2；(5)y ＝log 12x . [思路探究] 先将解析式化为基本初等函数的形式，再利用公式求导． [解] (1)y ′＝(x 12)′＝12x 12－1＝12x 11. (2)y ′＝(x －4)′＝－4x －4－1＝－4x －5＝－4x 5. (3)y ′＝(5x 3)′＝(x 35)′＝35x 35－1＝35x －25＝355x 2.(4)∵y ＝2sin x 2cos x2＝sin x ，∴y ′＝cos x . (5)y ′＝(log 12x )′＝1x ln 12＝－1x ln 2.用导数公式求导，可以简化运算过程、降低运算难度.解题时根据所给函数的特征，将题中函数的结构进行调整，再选择合适的求导公式.提醒：若题目中所给出的函数解析式不符合导数公式，需通过恒等变换对解析式进行化简或变形后求导，如根式化成指数幂的形式求导.导数公式的综合应用1．若y ＝c ，y ＝x 和y ＝x 2都表示路程关于时间的函数，则其导数的物理意义是什么？提示：若y ＝c 表示路程关于时间的函数，则y ′＝0可以解释为某物体的速度始终为0，即物体一直处于静止状态；若y ＝x 表示路程关于时间的函数，则y ′＝1可以解释为某物体做速度为1的匀速运动；若y ＝x 2表示路程关于时间的函数，则y ′＝2x 可以解释为某物体做变速运动，它在x 时刻的瞬时速度为2x .2．指数函数与对数函数的导数公式各具有什么特点？[提示] (1)指数函数的导数等于指数函数本身乘以底数的自然对数，y ＝e x 的导数是y ＝a x (a >0，a ≠1)导数的特例．(2)对数函数的导数等于x 与底数的自然对数乘积的倒数，y ＝ln x 的导数是y ＝log a x (a ＞0，a ≠1，x ＞0)导数的特例．【例2】 已知点P (－1,1)，点Q (2,4)是曲线y ＝x 2上两点，是否存在与直线PQ 垂直的切线，若有，求出切线方程；若没有，说明理由．[思路探究] 先求导数，再根据导数的几何意义求解． [解] 因为y ′＝(x 2)′＝2x ，假设存在与直线PQ 垂直的切线． 设切点坐标为(x 0，y 0)，由PQ 的斜率为k ＝4－12＋1＝1，又切线与PQ 垂直，所以2x 0＝－1，即x 0＝－12，所以切点坐标为⎝ ⎛⎭⎪⎫－12，14.所以所求切线方程为 y －14＝(－1)()x ＋12， 即4x ＋4y ＋1＝0.1．(变结论)若本例条件不变，求与直线PQ 平行的曲线y ＝x 2的切线方程． [解] 因为y ′＝(x 2)′＝2x ， 设切点为M (x 0，y 0)， 则y ′|x ＝x 0＝2x 0. 又因为PQ 的斜率为k ＝4－12＋1＝1， 而切线平行于PQ ，所以k ＝2x 0＝1， 即x 0＝12.所以切点为M ⎝ ⎛⎭⎪⎫12，14， 所以所求切线方程为y －14＝x －12， 即4x －4y －1＝0.2．(变条件)若函数改为y ＝ln x ，试求与直线PQ 平行的切线方程． [解] 设切点为(a ，b )，因为k PQ ＝1， 则由f′(a )＝1a ＝1，得a ＝1， 故b ＝ln 1＝0，则与直线PQ 平行的切线方程为y ＝x －1，即x －y －1＝0.解决切线问题，关键是确定切点，要充分利用：(1)切点处的导数是切线的斜率.(2)切点在切线上.(3)切点又在曲线上这三个条件联立方程解决.1．思考辨析(1)若函数f (x )＝log 2π，则f′(x )＝1πln 2.( ) (2)若函数f (x )＝3x ，则f′(x )＝x ·3x －1.( ) (3)若函数f (x )＝4x ，则f′(x )＝4x 2.( ) [提示] (1)× π为常数． (2)× f′(x )＝3x ln 3. (3)× f′(x )＝－4x 2.2．函数f (x )＝x ，则f′(3)等于( ) A ．36 B ．0 C ．12xD ．32A [∵f′(x )＝12x ，∴f′(3)＝123＝36.]3．设函数f (x )＝log a x ，f′(1)＝－1，则a ＝________. 1e [∵f′(x )＝1x ln a ，∴f′(1)＝1ln a ＝－1，∴a ＝1e.] 4．过曲线y ＝sin x 上的点P ⎝ ⎛⎭⎪⎫π6，12的切线方程为________．63x －12y －3π＋6＝0 [曲线y ＝sin x 在点P ⎝ ⎛⎭⎪⎫π6，12处的切线斜率为k ＝y ′|x ＝π6＝cos π6＝32. 所以切线方程为y －12＝32⎝ ⎛⎭⎪⎫x －π6，即63x －12y －3π＋6＝0.]5．求下列函数的导数：(1)y ＝cos π6；(2)y ＝1x 5；(3)y ＝x 2x ；(4)y ＝lg x ；(5)y ＝5x ；(6)y ＝cos ⎝ ⎛⎭⎪⎫π2－x .[解] (1)y ′＝0. (2)∵y ＝1x 5＝x －5，∴y ′＝(x －5)′＝－5x －6＝－5x 6. (3)∵y ＝x 2x＝x 32.∵y ′＝(x 32)′＝32x 12＝32x . (4)y ′＝1x ln 10. (5)y ′＝5x ln 5.(6)∵y ＝cos ⎝ ⎛⎭⎪⎫π2－x ＝sin x ，∴y ′＝(sin x )′＝cos x ．课时分层作业(十七) 常数与幂函数的导数导数公式表(建议用时：40分钟)[基础达标练]1．已知f (x )＝1x ，则f ′(3)＝( ) A ．－13 B ．－19 C ．19D ．13B [∵f (x )＝1x ，∴f ′(x )＝－1x 2，∴f ′(3)＝－132＝－19，故选B.] 2．已知f (x )＝ln x ，则f ′(e)＝( ) A ．0 B ．1e C ．1D ．eB [∵f (x )＝ln x ，∴f ′(x )＝1x ，则f ′(e)＝1e ，故选B.] 3．已知f (x )＝x α(α∈Q )，若f ′(－1)＝4，则α等于( ) A ．3 B ．－3 C ．4D ．－4D [∵f (x )＝x α，∴f ′(x )＝αx α－1. ∴f ′(－1)＝α(－1)α－1＝4. ∴α＝－4.]4．已知直线y ＝kx 是曲线y ＝e x 的切线，则实数k 的值为( ) A ．1e B ．－1e C ．－eD ．eD [y ′＝e x ，设切点为(x 0，y 0)，则⎩⎨⎧y 0＝k x 0，y 0＝e x 0，k ＝e x 0，∴e x 0·x 0＝e x 0，∴x 0＝1，∴k ＝e.]5．若幂函数f (x )＝mx α的图象经过点A ⎝ ⎛⎭⎪⎫14，12，则它在点A 处的切线方程是( )A ．2x －y ＝0B ．2x ＋y ＝0C ．4x －4y ＋1＝0D ．4x ＋4y ＋1＝0C [因为函数f (x )＝mx α为幂函数，所以m ＝1.又幂函数f (x )＝x α的图象经过点A ⎝ ⎛⎭⎪⎫14，12，所以α＝12，所以f (x )＝x 12，f ′(x )＝12x ，f ′⎝ ⎛⎭⎪⎫14＝1，所以f (x )的图象在点A 处的切线方程为y －12＝x －14，即4x －4y ＋1＝0.]6．已知函数f (x )＝x m －n (m ，n ∈Q )的导数为f ′(x )＝nx 3，则m ＋n ＝________. 12 [∵f (x )＝x m －n ，∴f ′(x )＝(m －n )x m －n －1， ∴⎩⎨⎧m －n ＝n ，m －n －1＝3，解得m ＝8，n ＝4，∴m ＋n ＝12.] 7．设曲线y ＝e x 在点(0,1)处的切线与曲线y ＝1x (x ＞0)上点P 处的切线垂直，则点P 的坐标为________．(1,1) [因为y ′＝e x ，所以曲线y ＝e x 在点(0,1)处的切线的斜率为k 1＝e 0＝1. 设P (m ，n )，y ＝1x (x ＞0)的导数为y ′＝－1x 2(x ＞0)，曲线y ＝1x (x ＞0)在点P 处的切线斜率为k 2＝－1m 2(m ＞0)，因为两切线垂直，所以k 1·k 2＝－1，所以m ＝1，n ＝1，则点P 的坐标为(1,1)．]8．函数y ＝x 2(x ＞0)的图象在点(a k ，a 2k )处的切线与x 轴的交点的横坐标为a k＋1，其中k ∈N *，若a 1＝16，则a 1＋a 3＋a 5的值是________．21 [∵y ′＝2x ，∴y ＝x 2(x ＞0)的图象在点(a k ，a 2k )处的切线方程为y －a 2k ＝2a k (x －a k )．又该切线与x 轴的交点为(a k ＋1,0)，∴a k ＋1＝12a k ，即数列{a k }是首项a 1＝16，公比q ＝12的等比数列，∴a 3＝4，a 5＝1，∴a 1＋a 3＋a 5＝21.]9．已知曲线C ：y ＝x 3.(1)求曲线C 上点(1,1)处的切线方程；(2)在(1)中的切线与曲线C 是否还有其他公共点？ [解] (1)因为y ′＝3x 2， 所以切线斜率k ＝3，所以切线方程为y －1＝3(x －1)， 即3x －y －2＝0. (2)由⎩⎨⎧3x －y －2＝0，y ＝x 3， 所以(x －1)(x 2＋x －2)＝0， 所以x 1＝1，x 2＝－2，所以公共点为(1,1)及(－2，－8)，即其他公共点为(－2，－8)． 10．若曲线y ＝x－12在点(a ，a－12)处的切线与两个坐标轴围成的三角形的面积为9，求实数a 的值．[解] ∵y ＝x －12，∴y ′＝－12x －32， ∴曲线在点(a ，a－12)处的切线的斜率为k ＝－12a －32， ∴切线方程为y －a－12＝－12a －32 (x －a )．令x ＝0，得y ＝32a －12；令y ＝0， 得x ＝3a .由题意知，a >0，该切线与两个坐标轴围成的三角形的面积为S ＝12×3a ×32a －12＝94a 12＝9，∴a ＝16.[能力提升练]1．设曲线y ＝x 在点(2，2)处的切线与直线ax ＋y ＋1＝0垂直，则a ＝( ) A ．22B ．24C ．－2 2D ．2 2D [∵y ＝x ＝x 12，∴y ′＝12x －12＝12x ，∴切线的斜率k ＝y ′|x ＝2＝122，由已知，得－a ＝－22，即a ＝22，故选D.]2．设f 0(x )＝sin x ，f 1(x )＝f 0′(x )，f 2(x )＝f 1′(x )，…，f n ＋1(x )＝f n ′(x )，n ∈N ，则f 2 020(x )等于( )A ．sin xB ．－sin xC ．cos xD ．－cos xA [f 1(x )＝f 0′(x )＝(sin x )′＝cos x ， f 2(x )＝f 1′(x )＝(cos x )′＝－sin x ， f 3(x )＝f 2′(x )＝(－sin x )′＝－cos x ， f 4(x )＝(－cos x )′＝sin x ， f 5(x )＝(sin x )′＝f 1(x )， f 6(x )＝f 2(x )，…， f n ＋4(x )＝f n (x )，可知周期为4，所以f 2 020(x )＝f 505×4(x )＝sin x ．]3．曲线y ＝log 2x 在点(1,0)处的切线与两坐标轴所围成的三角形的面积为________．12log 2e [y ′＝1x ln 2＝1x ·log 2e ，所以切线的斜率k ＝y ′|x ＝1＝log 2e ，切线方程为y ＝(x －1)log 2e ，令x ＝0，得y ＝－log 2e ，令y ＝0，得x ＝1，因此所求三角形的面积S ＝12×1×log 2e ＝12log 2e.]4．已知函数f (x )＝⎩⎨⎧x 3，x ≤0，ln x ，0＜x ＜1，，f ′(a )＝12，则实数a 的值为________．112或－2 [由题意得 f ′(x )＝⎩⎪⎨⎪⎧3x 2，x ≤0，1x ，0＜x ＜1，若 f ′(a )＝12，则⎩⎪⎨⎪⎧0＜a ＜1，1a＝12或⎩⎨⎧a ≤0，3a 2＝12，解得a ＝112或a ＝－2.]5．点P是曲线y＝e x上任意一点，求点P到直线y＝x的最小距离．[解]如图，当曲线y＝e x在点P(x0，y0)处的切线与直线y＝x平行时，点P 到直线y＝x的距离最近．则曲线y＝e x在点P(x0，y0)处的切线斜率为1，又y′＝(e x)′＝e x，所以e x0＝1，得x0＝0，代入y＝e x，得y0＝1，即P(0,1)．由点到直线的距离公式，得最小距离为d＝|－1|2＝22.11/11。
3.2.1-3.2.2常数与幂函数的导数、导数公式表教学过程：创设情景我们知道,导数的几何意义是曲线在某一点处的切线斜率,物理意义是运动物体在某一时刻的瞬时速度.那么,对于函数()y f x =,如何求它的导数呢？由导数定义本身,给出了求导数的最基本的方法,但由于导数是用极限来定义的,所以求导数总是归结到求极限这在运算上很麻烦,有时甚至很困难,为了能够较快地求出某些函数的导数,这一单元我们将研究比较简捷的求导数的方法,下面我们求几个常用的函数的导数. 新课讲授一、函数()y f x c ==的导数根据导数定义,因为()()0y f x x f x c c x x x∆+∆--===∆∆∆ 所以00lim lim 00x x y y ∆→∆→∆'===0y '=表示函数y c =图像(图3.2-1)上每一点处的切线的斜率都为0.若y c =表示路程关于时间的函数,则0y '=可以解释为某物体的瞬时速度始终为0,即物体一直处于静止状态.二、函数()y f x x ==的导数因为()()1y f x x f x x x x x x x∆+∆-+∆-===∆∆∆ 所以00lim lim 11x x y y ∆→∆→∆'===∆1y '=表示函数y x =图像(图3.2-2)上每一点处的切线的斜率都为1,若y x =表示路程关于时间的函数,则1y '=可以解释为某物体做瞬时速度为1的匀速运动.三、函数2()y f x x ==的导数 因为22()()()y f x x f x x x x x x x ∆+∆-+∆-==∆∆∆2222()2x x x x x x x x+∆+∆-==+∆∆ 所以00lim lim (2)2x x y y x x x ∆→∆→∆'==+∆=∆2y x '=表示函数y x =图像(图3.2-3)上点(,)x y 处的切线的斜率都为2x ,说明随着x 的变化,切线的斜率也在变化.另一方面,从导数作为函数在一点的瞬时变化率来看,表明:当0x <时,随着x 的增加,函数2y x =减少得越来越慢;当0x >时,随着x 的增加,函数2y x =增加得越来越快.若2y x =表示路程关于时间的函数,则2y x '=可以解释为某物体做变速运动,它在时刻x 的瞬时速度为2x . 四、函数1()y f x x==的导数 因为11()()y f x x f x x x x x x x-∆+∆-+∆==∆∆∆ 2()1()x x x x x x x x x x-+∆==-+∆∆+⋅∆ 所以220011lim lim ()x x y y∆→∆→∆'==-=-∆ 课本练习A 、B 五、基本初等函数的导数公式表：课本练习A 、B 1.2.()3.4.5.ln 6.7.8.n R a ∈'n 'n-1''x 'x x 'x 'a '若f(x)=c，则f(x)=0若f(x)=x ，则f(x)=nx 若f(x)=sinx，则f(x)=cosx 若f(x)=cosx，则f(x)=-sinx 若f(x)=a ，则f(x)=a 若f(x)=e ，则f(x)=e 1若f(x)=log x，则f(x)=xlna1若f(x)=lnx，则f(x)=x。
