下载文档原格式
一维势箱中粒子的波函数
一维势箱是量子力学中一种比较基础的模型，通常被用来研究粒子在有限空间内的运动情况。
本文将介绍一维势箱中粒子的波函数。
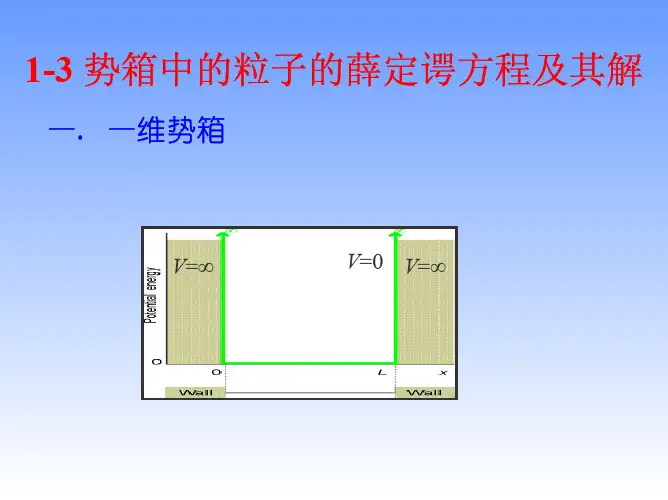
一维势箱是一个长度为L的无限深势阱，也就是说当粒子在势箱内部时，势能为零，当粒子处于势箱外部时，势能为无穷大。
这样的势场约束了粒子只能在势箱内部运动，此外无处可去。
为了求解一维势箱中粒子的波函数，我们可以利用薛定谔方程。
根据波粒二象性，一个粒子可以看作是一个波包，如果用y(x,t)表示粒子的波函数，则粒子的能量E与角频率w的关系为E=hw，其中h为普朗克常数。
而薛定谔方程可以表示为：
i(h/2π)·∂y(x,t)/∂t=（-h^2/2m）·∂^2y(x,t)/∂x^2
式子中，i是虚数单位，m为粒子的质量。
这个方程可以看做是描述粒子在一维势箱中的运动情况的基本方程。
对这个方程进行数学求解，我们可以得到一维势箱中粒子的波函数：
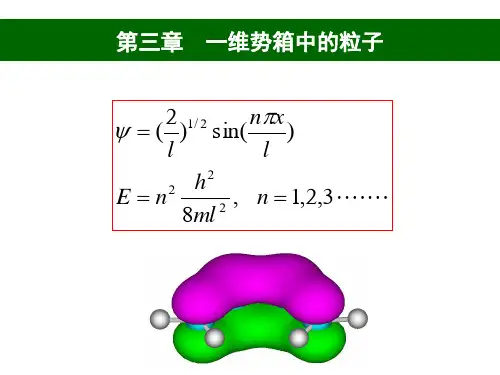
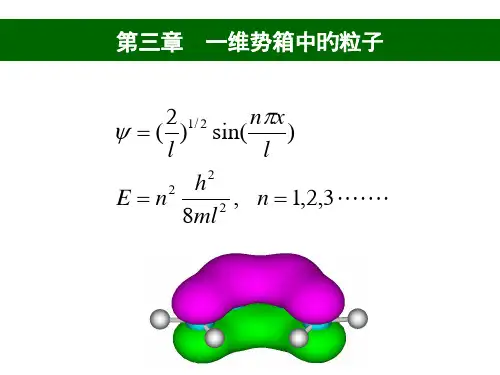
y(x,t)=Asin(nπx/L)·exp(-i(Et/h))
式中，A为归一化因子，n为正整数，代表是势箱内的第n个能级。
此外，由于一维势箱中的边界条件，波函数必须满足在x=0和x=L 处的边界条件。
总的来说，一维势箱中粒子的波函数与粒子的能量以及势场的形状密切相关。
对于能级有限的势场，可以通过求解薛定谔方程，得到粒子的波函数。
通过对波函数的分析，我们可以了解粒子在一维势箱中的运动和行为。
一维势箱中粒子的最大德布罗意波长量子力学是一门探究原子和分子行为的学科，其中粒子的波动性质是其研究的核心。
而德布罗意波长则是表征粒子波动特性的物理量，它在一维势箱中的最大值更是具有重要的物理意义。
一维势箱是一种理想模型，它能够清晰而简洁地展现物质的量子力学性质。
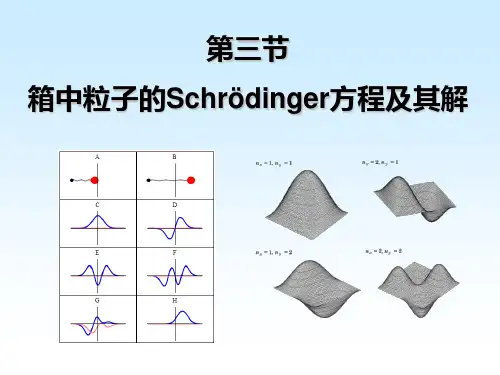
当一个粒子被限制在能够容纳其的一维势箱内时，其波函数必须满足一些特殊的条件。
首先，波函数必须为零，当粒子离开势箱的两端时；其次，波函数必须是正弦曲线的形式，在势箱内部的位置与时间的关系上。
由于波函数的存在，粒子被视为是一种波动现象，而德布罗意波长就是描述这种波动特性的物理量。
它是一个粒子的普朗克常数除以其动量得到的值，即λ = h/p，其中h是普朗克常数，p是粒子的动量。
在一维势箱中，粒子的动量p是由其波长λ决定的：p = h/λ。
因此，当粒子在势箱内的波长变短时，其动量就必须变大。
但由于势箱的尺寸是固定的，因此存在一定的限制。
当粒子的波长λ等于势箱长度L时，它的动量也就达到了最大值。
因此，一维势箱中粒子的最大德布罗意波长为L。
这个结论对于量子力学的研究具有重要的物理意义。
它代表着粒子所具有的最大分辨率，即这个粒子最小的特征大小。
在现代科技中，可以应用于许多地方，例如扫描电子显微镜等高分辨率科学设备的研制。
除此之外，这一论断也为量子力学提供了更深入的理解。
由于波函数的存在，粒子的特殊行为被更好地解释了。
波函数是波动性的载体，它描述了粒子的位置、动量、角动量等各种物理属性。
在势箱中的波函数示范了波动性质的极限，这对于探究粒子的本质具有重要的意义。
总之，一维势箱中粒子的最大德布罗意波长，是量子力学中的一个重要概念，它展示了波动性质在量子世界中的重要性。
也因此，科学家们对这一原理的理解深化，不断应用于科学探索中，以期更好地理解自然界。
