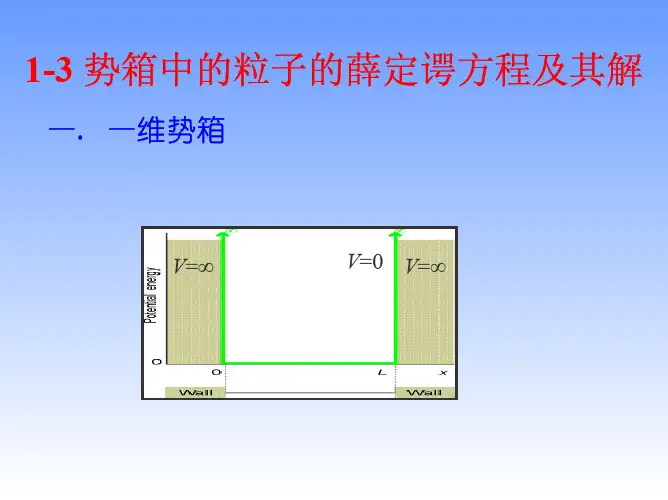
势箱中的粒子的薛定谔方程及其解
- 格式:pdf
- 大小:330.21 KB
- 文档页数:18

关于薛定谔方程一. 定义及重要性薛定谔方程(Schrdinger equation )是由奥地利物理学家薛定谔提出的量子力学中的一个基本方程,也是量子力学的一个基本假定,其正确性只能靠实验来检验.是将物质波的概念和波动方程相结合建立的二阶偏微分方程,可描述微观粒子的运动,每个微观系统都有一个相应的薛定谔方程式,通过解方程可得到波函数的具体形式以及对应的能量,从而了解微观系统的性质。
薛定谔方程是量子力学最基本的方程,亦是量子力学的一个基本假定,它的正确性只能靠实验来检验.二. 表达式三. 定态方程()()222V r E r m ηψψ+⎡⎤-∇=⎢⎥⎣⎦所谓势场,就是粒子在其中会有势能的场,比如电场就是一个带电粒子的势场;所谓定态,就是假设波函数不随时间变化。
其中,E 是粒子本身的能量;v(x ,y ,z )是描述势场的函数,假设不随时间变化。
2222222z y x ∂∂∂∂∂∂++=∇可化为d 0)(222=-+ψψv E h m dx薛定谔方程的解法一. 初值解法;欧拉法,龙格库塔法二. 边值解法;差分法,打靶法,有限元法龙格库塔法(对欧拉法的完善)给定初值问题).()()((3)),(),()( ,,(2))(),( 3112122111021h O t y t y hk y h t f k y t f k k c k c h y y y c c a y b t a y t f dt dyi i i i i i i i =-⎪⎪⎩⎪⎪⎨⎧++==++==⎪⎩⎪⎨⎧=≤≤=++的局部截断误差使以下数值解法的值及确定常数ββαβα.))(,(,,(3) )()(2)()( ,))(,())(,())(,()( ))(,()( )()(2)()()( )( 3213211处的函数值分别表示相应函数在点其中得代入上式将处展成幂级数在首先将i i y t y t i i y t i i i i i i t y t f f f h O ff f h hf t y t y t y t f t y t f t y t f t y t y t f t y h O t y h t y h t y t y t t y '++++=+'=''='+''+'+=+++.)(21 1 ,,021,01 ),()()())(21()1()( ,)( 3221212213113222111的计算公式局部截断误差为可得到但只有两个方程,因此方程组有三个未知数,满足条件即常数当且仅当要使局部截断误差得下假设在局部截断误差的前提h O c c c c c c c c h O y t y h O ff f c h f c c h y t y t y y i i y t i i i i ==+=-=-+=-++-+-+-=-=++++ββββ有限元方法有限元的概念早在几个世纪前就已产生并得到了应用,例如用多边形(有限个直线单元)逼近圆来求得圆的周长,但作为一种方法而被提出,则是最近的事。

薛定谔方程的含义和求解方法薛定谔方程是量子力学中的基本方程之一,描述了微观粒子(如电子)的行为。
本文将介绍薛定谔方程的含义及其求解方法。
一、薛定谔方程的含义薛定谔方程是由奥地利物理学家薛定谔于1926年提出的,用来描述微观粒子的运动和性质。
该方程是一个偏微分方程,包含粒子的波函数(Ψ)和哈密顿量(H)。
薛定谔方程的一般形式为:iℏ∂Ψ/∂t = HΨ其中,i是虚数单位,ℏ是约化普朗克常数,t是时间。
Ψ是粒子的波函数,H是系统的哈密顿量。
薛定谔方程描述了一个量子系统的演化过程。
通过对波函数的求解,我们可以得到粒子在不同位置和时间的概率分布,从而理解其行为和性质。
二、薛定谔方程的求解方法薛定谔方程是一个高度复杂的偏微分方程,一般情况下无法通过解析方法求解。
但可以通过一些近似方法和数值方法来求解。
1. 解析方法对于简单的系统,可以通过解析方法求解薛定谔方程。
例如,对于自由粒子,可以得到平面波的解。
对于一维谐振子,可以得到谐振子波函数的解。
然而,对于复杂的系统,如多电子体系或相互作用体系,解析方法往往不适用。
因此,需要使用近似方法和数值方法来求解。
2. 近似方法常用的近似方法包括变分法、微扰法和量子力学近似等。
变分法通过选取适当的波函数的形式和参数,使得波函数的能量最小化。
微扰法将系统的哈密顿量分解为一个已知的部分和一个微扰项,通过级数展开的方式求解波函数。
3. 数值方法数值方法是求解薛定谔方程的重要手段之一。
常用的数值方法包括有限差分法、有限元法和动态变分法等。
这些方法通过将波函数和哈密顿量离散化,将偏微分方程转化为一组代数方程,然后通过迭代求解来得到波函数的数值解。
数值方法的优点是适用于各种复杂系统,并且可以提供较高的精度。
但需要注意选择合适的离散化方法和参数,以及控制误差和收敛性。
总之,薛定谔方程是研究微观粒子的基本工具之一,可以描述粒子的运动和性质。
通过适当的求解方法,我们可以获得粒子的波函数,从而深入理解量子力学中的各种现象和行为。

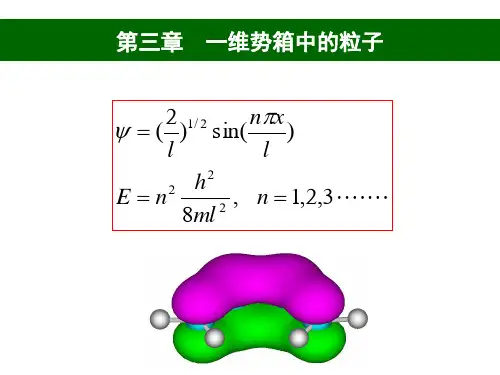

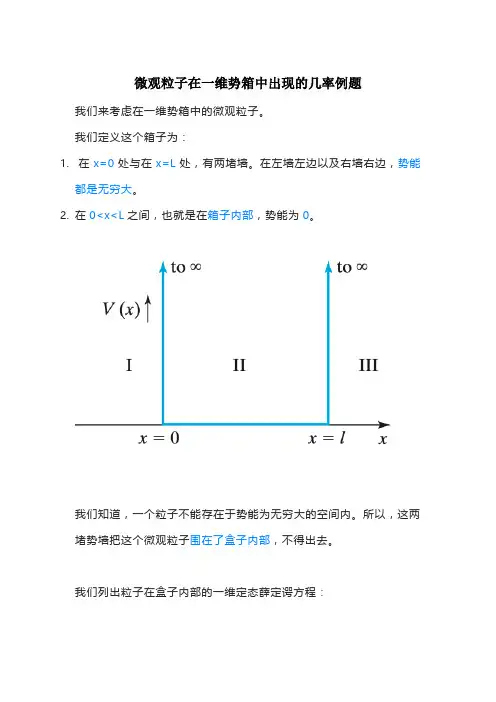
微观粒子在一维势箱中出现的几率例题我们来考虑在一维势箱中的微观粒子。
我们定义这个箱子为:1.在x=0处与在x=L处,有两堵墙。
在左墙左边以及右墙右边,势能都是无穷大。
2.在0<x<L之间,也就是在箱子内部,势能为0。
我们知道,一个粒子不能存在于势能为无穷大的空间内。
所以,这两堵势墙把这个微观粒子围在了盒子内部,不得出去。
我们列出粒子在盒子内部的一维定态薛定谔方程:因为我们定义箱内势能为0,那么我们可以删除势能项,只剩下动能项:如果我们设波函数的表达式为:(其中C与D为参数)代入方程,再重排得到动能的表达式:现在,我们得到了动能的表达式,我们转过头来看看这个一维势箱中粒子的波函数有什么限制。
可以看出,在x=0与x=L这两个点的位置,势能就已经取了无穷大值。
说明波函数在这两点处必定为0。
代表着,粒子出现在这两个绝对的位置的概率为0。
用数学语言表达,便是下式:因为这一条件限制的是波函数在盒子边界处的行为(behaviour),所以这一条件也属于边界条件(Boundary Condition)。
波函数满足边缘条件的必要性说明只有特定的波函数是可接受的,所以这把可观测量的值限制到了离散的值。
因为波函数在盒子的边缘处值必须为0,而我们如果用一个正弦函数来描述波函数,这个问题就变得很简单了。
这意味着,正弦函数的频率只能是一些特定的值,而只有这些值能使正弦函数在盒子的边缘通过0点。
量化这个结论,就是:盒子的长度,L,必须是一个正整数,n,乘以波函数的半波长:而对于一个正弦函数sin(kx)来说,(在本系列文章第二篇中也提到过),其波长等于两倍圆周率除以正弦函数内,x前面的系数,也就是k。
所以我们有:(如果我们忽略Dcos(kx))于是,对于不同的n值,波函数的波长会越来越短,但是如果n还是满足正整数条件,那么这个正弦函数一定会满足边界条件,且总是会在盒子的两个边缘值为0,就像如下:到了这一步,既然C是任意常数,我们就令其等于归一化常数吧。




薛定谔方程求解步骤薛定谔方程(Schrodinger Equation)是描述量子力学中粒子运动的基本方程。
它的求解可以得到粒子的能量和波函数,从而揭示出粒子在各种势场中的性质。
下面将介绍薛定谔方程的求解步骤。
1. 建立薛定谔方程薛定谔方程的一般形式为:$$ \\hat{H} \\psi = E \\psi $$其中,$\\hat{H}$ 表示哈密顿算符,$\\psi$ 是粒子的波函数,E是粒子的能量。
2. 利用哈密顿算符哈密顿算符可以根据具体情况而定,对不同的系统具有不同的形式。
例如,对自由粒子,将动能算符代入哈密顿算符中,可以得到:$$ \\hat{H} = -\\frac{{\\hbar}^2}{2m} \ abla^2 $$其中,$\\hbar$ 是约化普朗克常数,m是粒子的质量,abla2是拉普拉斯算符。
3. 将波函数代入薛定谔方程将波函数 $\\psi$ 带入薛定谔方程中,得到:$$ -\\frac{{\\hbar}^2}{2m} \ abla^2 \\psi = E \\psi $$4. 分离变量为了求解上述薛定谔方程,通常采用分离变量的方法。
假设波函数可以表示为:$$ \\psi(x, y, z) = X(x) \\cdot Y(y) \\cdot Z(z) $$将分离变量的结果代入薛定谔方程中,得到:$$ -\\frac{{\\hbar}^2}{2m} \\left (\\frac{1}{X}\\frac{{d}^2X}{{d}x^2} +\\frac{1}{Y}\\frac{{d}^2Y}{{d}y^2} + \\frac{1}{Z}\\frac{{d}^2Z}{{d}z^2} \\right ) = E $$5. 将方程化简为一系列互相独立的微分方程由于上式左侧的每一项只涉及一个独立变量,而右侧的E是常数,因此左侧和右侧的各项必须都等于同一个常数,称为分离常数。
假设该常数为k,则上述薛定谔方程可以分解为三个独立的微分方程:$$ \\frac{1}{X}\\frac{{d}^2X}{{d}x^2} = -\\frac{{2mk}}{{\\hbar}^2} \\\\\\frac{1}{Y}\\frac{{d}^2Y}{{d}y^2} = -\\frac{{2mk}}{{\\hbar}^2} \\\\\\frac{1}{Z}\\frac{{d}^2Z}{{d}z^2} = -\\frac{{2mk}}{{\\hbar}^2} $$ 解这些微分方程可以得到每个方向上的波函数和能量。
由一维势箱粒子的薛定谔方程所得到能量量
子化的概念
一维势箱是一种理想化模型,它假设存在一个无限高的势垒,粒子只能在有限的空间范围内运动。
根据薛定谔方程,粒子在一维势箱内的波函数满足以下方程:
[-(h^2/8π^2m)]*(d^2ψ/dx^2) + V(x)ψ = Eψ
其中,h是普朗克常数,m是粒子的质量,V(x)是势能函数,E是能量。
根据边界条件,波函数在势垒两侧必须为零。
这意味着势箱内的波函数必须满足以下条件:
ψ(0) = ψ(L) = 0
其中L是势箱的长度。
通过求解薛定谔方程,我们可以得到势箱内的波函数和对应的能量值。
波函数的形式取决于势能函数V(x)。
对于势能函数为零的情况,即自由粒子,波函数的解是平面波,能量是连续的。
然而,对于势能函数为无限高的势垒,波函数只能在有限范围内存在。
由于边界条件,只有特定的波长才能在势箱内满足波函数为零的条件。
这导致能量的量子化,即只有特定的能量值能够被粒子所具有。
根据波函数的形式,可以得到以下能量量子化公式:
E = (n^2 * h^2) / (8π^2mL^2)
其中n为正整数,代表能级的编号。
这意味着在一维势箱中,粒子的能量只能取离散的数值,而不是连续的。
这种离散化的能量就是能级,每个能级对应一个特定的波函数。
不同的能级对应着不同的粒子状态和运动特性。