7状态空间设计法极点配置观测器解析
- 格式:doc
- 大小:953.50 KB
- 文档页数:17





实用文档之"基于MATLAB 的状态观测器设计"预备知识: 极点配置基于状态反馈的极点配置法就是通过状态反馈将系统的闭环极点配置到期望的极点位置上,从而使系统特性满足要求。
1. 极点配置原理假设原系统的状态空间模型为:⎩⎨⎧=+=Cxy Bu Ax x 若系统是完全可控的,则可引入状态反馈调节器,且:Kx u input -=这时,闭环系统的状态空间模型为:⎩⎨⎧=+-=Cx y Bu x )BK A (x 2. 极点配置的MATLAB 函数 在MATLAB 控制工具箱中,直接用于系统极点配置的函数有acker()和place()。
调用格式为:K=acker(A,C,P) 用于单输入单输出系统其中:A ,B 为系统矩阵,P 为期望极点向量,K 为反馈增益向量。
K=place(A,B,P)(K,prec,message)=place(A,B,P)place()用于单输入或多输入系统。
Prec 为实际极点偏离期望极点位置的误差;message 是当系统某一非零极点偏离期望位置大于10%时给出的警告信息。
3. 极点配置步骤:(1)获得系统闭环的状态空间方程;(2)根据系统性能要求,确定系统期望极点分布P ;(3)利用MATLAB 极点配置设计函数求取系统反馈增益K ; (4)检验系统性能。
已知系统模型如何从系统的输入输出数据得到系统状态?初始状态:由能观性,从输入输出数据确定。
不足:初始状态不精确,模型不确定。
思路:构造一个系统,输出逼近系统状态称为是的重构状态或状态估计值。
实现系统状态重构的系统称为状态观测器。
观测器设计状态估计的开环处理:但是存在模型不确定性和扰动!初始状态未知!应用反馈校正思想来实现状态重构。
通过误差来校正系统:状态误差,输出误差。
基于观测器的控制器设计系统模型若系统状态不能直接测量,可以用观测器来估计系统的状态。
L是观测器增益矩阵,对偏差的加权。
真实状态和估计状态的误差向量误差的动态行为:的极点决定了误差是否衰减、如何衰减?通过确定矩阵L来保证。


现代控制实验状态反馈器和状态观测器的设计现代控制实验中,状态反馈器和状态观测器是设计系统的重要组成部分。
状态反馈器通过测量系统的状态变量,并利用反馈回路将状态变量与控制输入进行耦合,以优化系统的性能指标。
状态观测器则根据系统的输出信息,估计系统的状态变量,以便实时监测系统状态。
本文将分别介绍状态反馈器和状态观测器的设计原理和方法。
一、状态反馈器的设计:状态反馈器的设计目标是通过调整反馈增益矩阵,使得系统的状态变量在给定的性能要求下,达到所需的一组期望值。
其设计步骤如下:1.系统建模:通过对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
通常表示为:ẋ=Ax+Buy=Cx+Du其中,x为系统状态向量,u为控制输入向量,y为系统输出向量,A、B、C、D为系统的状态矩阵。
2.控制器设计:根据系统的动态性能要求,选择一个适当的闭环极点位置,并计算出一个合适的增益矩阵。
常用的设计方法有极点配置法、最优控制法等。
3.状态反馈器设计:根据控制器设计得到的增益矩阵,利用反馈回路将状态变量与控制输入进行耦合。
状态反馈器的输出为:u=-Kx其中,K为状态反馈增益矩阵。
4.性能评估与调整:通过仿真或实验,评估系统的性能表现,并根据需要对状态反馈器的增益矩阵进行调整。
二、状态观测器的设计:状态观测器的设计目标是根据系统的输出信息,通过一个状态估计器,实时估计系统的状态变量。
其设计步骤如下:1.系统建模:同样地,对被控对象进行数学建模,得到描述系统动态行为的状态空间表达式。
2.观测器设计:根据系统的动态性能要求,选择一个合适的观测器极点位置,以及一个合适的观测器增益矩阵。
常用的设计方法有极点配置法、最优观测器法等。
3.状态估计:根据观测器设计得到的增益矩阵,通过观测器估计系统的状态变量。
状态观测器的输出为:x^=L(y-Cx^)其中,L为观测器增益矩阵,x^为状态估计向量。
4.性能评估与调整:通过仿真或实验,评估系统的状态估计精度,并根据需要对观测器的增益矩阵进行调整。

基于M A T L A B的状态观测器设计预备知识:极点配置基于状态反馈的极点配置法就是通过状态反馈将系统的闭环极点配置到期望的极点位置上,从而使系统特性满足要求。
1. 极点配置原理假设原系统的状态空间模型为:若系统是完全可控的,则可引入状态反馈调节器,且:这时,闭环系统的状态空间模型为:2. 极点配置的MATLAB函数在MATLAB控制工具箱中,直接用于系统极点配置的函数有acker()和place()。
调用格式为:K=acker(A,C,P) 用于单输入单输出系统其中:A,B为系统矩阵,P为期望极点向量,K为反馈增益向量。
K=place(A,B,P)(K,prec,message)=place(A,B,P)place()用于单输入或多输入系统。
Prec为实际极点偏离期望极点位置的误差;message 是当系统某一非零极点偏离期望位置大于10%时给出的警告信息。
3. 极点配置步骤:(1)获得系统闭环的状态空间方程;(2)根据系统性能要求,确定系统期望极点分布P;(3)利用MATLAB极点配置设计函数求取系统反馈增益K;(4)检验系统性能。
已知系统模型如何从系统的输入输出数据得到系统状态?初始状态:由能观性,从输入输出数据确定。
不足:初始状态不精确,模型不确定。
思路:构造一个系统,输出逼近系统状态称为是的重构状态或状态估计值。
实现系统状态重构的系统称为状态观测器。
观测器设计状态估计的开环处理:但是存在模型不确定性和扰动!初始状态未知!应用反馈校正思想来实现状态重构。
通过误差来校正系统:状态误差,输出误差。
基于观测器的控制器设计系统模型若系统状态不能直接测量,可以用观测器来估计系统的状态。
L是观测器增益矩阵,对偏差的加权。
真实状态和估计状态的误差向量误差的动态行为:的极点决定了误差是否衰减、如何衰减?通过确定矩阵L来保证。
也即极点配置问题。
要使得误差衰减到零,需要选取一个适当的矩阵L,使得A-LC是稳定的。

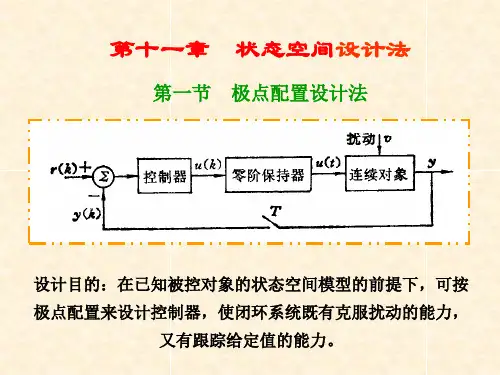

第7章线性定常离散时间状态空间设计法7.1引言7.2状态反馈配置极点7.3状态估值和状态观测器7.4利用状态估值构成状态反馈以配置极点7.5扰动调节7.6无差调节7.1引言一个被控对象:(1)()()()()():1,():1,:,:,:x k Fx k Gu k y k Cx k x k n u k m F n n G n m C r n+=+⎧⎨=⎩⨯⨯⨯⨯⨯ 7.1当设计控制器对其控制时,需要考虑如下各因素: ● 扰动,比如负载扰动 ● 测量噪声● 给定输入的指令信号 ● 输出 如图7.1所示。
给d L (k )扰动图7.1 控制系统示意图根据工程背景的不同,控制问题可分为调节问题和跟踪问题,跟踪问题也称为伺服问题。
调节问题的设计目标是使输出迅速而平稳地运行于某一平衡状态。
包括指令变化时的动态过程,和负载扰动下的动态过程。
但是这二者往往是矛盾的,需要折衷考虑。
伺服问题的设计目标是对指令信号的快速动态跟踪。
本章研究基于离散时间状态空间模型的设计方法。
7.2研究通过状态变量的反馈对闭环系统的全部特征值任意配置——稳定性与快速线。
7.3考虑当被控对象模型的状态无法直接测量时,如何使用状态观测器对状态进行重构。
7.4讨论使用重构状态进行状态反馈时闭环系统的特征值。
7.5简单地讨论扰动调节问题。
7.6状态空间设计时的无差调节问题。
7.2 状态反馈配置极点工程被控对象如式7.1,考虑状态反馈()()()u k v k Lx k =+7.2如图7.2所示。
式7.2带入式7.1,得(1)()()()()()()()x k Fx k Gu k y k Cx k u k v k Lx k +=+⎧⎪=⎨⎪=+⎩7.3整理得()(1)()()()()x k F GL x k Gv k y k Cx k +=++⎧⎨=⎩7.4(k )v(k )图7.2 状态反馈任意配置闭环系统的极点闭环系统的特征方程为[]det ()0zI F GL -+=7.5问题是在什么情况下式7.5的特征根是可以任意配置的?即任给工程上期望的n 个特征根λ1, λ2, ..., λn ,有[]1det ()()0ni i zI F GL z λ=-+=-=∏7.6定理:状态反馈配置极点若被控对象式7.1是状态完全能达的,即(F , G )是一个能达对(能达性矩阵-1[...]N c W F G FG G =满秩),则一定存在一个r 行n 列的状态反馈矩阵L ,使得在状态反馈()()()u k v k Kx k =+下,闭环系统式7.4具有任意给定的n 个期望的特征根λ1, λ2, ..., λn 。
状态空间分析及设计姓名:周海波学号:200740297(15)班级:自控实验0701班日期:2010-5-2目录一.系统能控性和能观性判定二.主导极点法进行状态反馈极点配置三.对称根轨迹法(SRL)进行状态反馈极点配置四.主导极点法和SRL状态反馈极点配置对比五.全维观测器设计和分析1.观测器设计2.分离定理验证六.带全维观测器的状态反馈与直接状态反馈对比七.降阶观测器和带降阶观测器的状态反馈系统的设计和分析八.全维观测器的状态反馈与降阶观测器的状态反馈对比1.抗过程干扰能力2.抗测量噪声能力九.采用内模原则设计状态反馈系统1.跟踪性能分析2.抗干扰性能分析状态空间分析及设计有以下系统122201101011x x µ−−−⎡⎤⎡⎤⎢⎥⎢⎥=−+⎢⎥⎢⎥⎢⎥⎢⎥−⎣⎦⎣⎦i[]100y x=要求:对系统设计状态反馈使得系统闭环阶跃响应的超调量小于5%,且在稳态误差值为1%范围内的调节时间小于4.6s.一.系统能控性和能观性判定由系统能控性判别矩阵:224001013115rank BAB A B rank −⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥−⎣⎦由系统能观性判别矩阵:21001223142C rank CA rank CA ⎡⎤⎡⎤⎢⎥⎢⎥=−−−=⎢⎥⎢⎥⎢⎥⎢⎥−⎣⎦⎣⎦所以系统既是能控的又是能观的。
二.主导极点法进行状态反馈极点配置1.当 4.61% 4.6s nt s ζω∆==<%5%e πζσ−=<解得:0.691n ζζω>⎧⎨>⎩取0.752n ζω==则:2222340n n s s s s ζωω++=++=所以1,2 1.5 1.323s j =−±,取非主导极点38s =−,则期望特征多项式为:232(34)(8)112832s s s s s s +++=+++设[]123K k k k =又1231233213123123122222det()01111(32)(524)(5233)s k k k sI A BK s k k s k s k k s k k k s k k k ++++−+=+−−++=++++++++−++所以:13123123321152428523332k k k k k k k k ++=⎧⎪+++=⎨⎪−++=⎩解得:123392k k k =⎧⎪=⎨⎪=⎩[]392K ∴=因此在无参考输入下的状态反馈响应曲线为:y/uss versus time State versus time由于期望闭环极点的选择是在误差向量的快速性和干扰以及测量噪声的灵敏度之间的一种折中,因此在决定反馈增益K 时,我们选取几组不同的期望闭环极点,所以去取另外两组期望闭环极点为:(1)1,2 1.40.8s j =−±取非主导极点38s =−,通过Matlab 函数acker求得:[2.6000 4.4000 2.6000]K =,无参考输入下的状态反馈响应曲线:y/uss versus time State versus time(2)1,23 2.5s j =−±取非主导极点38s =−,通过Matlab 函数acker 求得[] 4.1250 39.0000 2.7500K =,无参考输入下的状态反馈响应曲线:y/uss versus time State versus time将三组不同期望极点对应的状态响应曲线进行比较,可以得出以下结论:期望极点在S 平面上向左移动,响应速度加快,但控制信号明显加大,且超调量也有所增加,反之如果期望极点靠近原点,则控制信号较小,但响应时间加长。
基于MATLAB的状态观测器设计之蔡仲巾千创作预备知识:极点配置基于状态反馈的极点配置法就是通过状态反馈将系统的闭环极点配置到期望的极点位置上,从而使系统特性满足要求。
1. 极点配置原理假设原系统的状态空间模型为:若系统是完全可控的,则可引入状态反馈调节器,且:这时,闭环系统的状态空间模型为:2. 极点配置的MATLAB函数在MATLAB控制工具箱中,直接用于系统极点配置的函数有acker()和place()。
调用格式为:K=acker(A,C,P) 用于单输入单输出系统其中:A,B为系统矩阵,P为期望极点向量,K为反馈增益向量。
K=place(A,B,P)(K,prec,message)=place(A,B,P)place()用于单输入或多输入系统。
Prec为实际极点偏离期望极点位置的误差;message是当系统某一非零极点偏离期望位置大于10%时给出的警告信息。
3. 极点配置步调:(1)获得系统闭环的状态空间方程;(2)根据系统性能要求,确定系统期望极点分布P;(3)利用MATLAB极点配置设计函数求取系统反馈增益K;(4)检验系统性能。
已知系统模型如何从系统的输入输出数据得到系统状态?初始状态:由能观性,从输入输出数据确定。
缺乏:初始状态不精确,模型不确定。
思路:构造一个系统,输出迫近系统状态称为是的重构状态或状态估计值。
实现系统状态重构的系统称为状态观测器。
观测器设计状态估计的开环处理:但是存在模型不确定性和扰动!初始状态未知!应用反馈校正思想来实现状态重构。
通过误差来校正系统:状态误差,输出误差。
基于观测器的控制器设计系统模型若系统状态不克不及直接丈量,可以用观测器来估计系统的状态。
L是观测器增益矩阵,对偏差的加权。
真实状态和估计状态的误差向量误差的动态行为:的极点决定了误差是否衰减、如何衰减?通过确定矩阵L来包管。
也即极点配置问题。
要使得误差衰减到零,需要选取一个适当的矩阵L,使得A-LC是稳定的。
第7章线性定常离散时间状态空间设计法7.1引言7.2状态反馈配置极点7.3状态估值和状态观测器7.4利用状态估值构成状态反馈以配置极点7.5扰动调节7.6无差调节7.1引言一个被控对象:(1)()()()()():1,():1,:,:,:x k Fx k Gu k y k Cx k x k n u k m F n n G n m C r n+=+⎧⎨=⎩⨯⨯⨯⨯⨯ 7.1当设计控制器对其控制时,需要考虑如下各因素: ● 扰动,比如负载扰动 ● 测量噪声● 给定输入的指令信号 ● 输出 如图7.1所示。
给d L (k )扰动图7.1 控制系统示意图根据工程背景的不同,控制问题可分为调节问题和跟踪问题,跟踪问题也称为伺服问题。
调节问题的设计目标是使输出迅速而平稳地运行于某一平衡状态。
包括指令变化时的动态过程,和负载扰动下的动态过程。
但是这二者往往是矛盾的,需要折衷考虑。
伺服问题的设计目标是对指令信号的快速动态跟踪。
本章研究基于离散时间状态空间模型的设计方法。
7.2研究通过状态变量的反馈对闭环系统的全部特征值任意配置——稳定性与快速线。
7.3考虑当被控对象模型的状态无法直接测量时,如何使用状态观测器对状态进行重构。
7.4讨论使用重构状态进行状态反馈时闭环系统的特征值。
7.5简单地讨论扰动调节问题。
7.6状态空间设计时的无差调节问题。
7.2 状态反馈配置极点工程被控对象如式7.1,考虑状态反馈()()()u k v k Lx k =+7.2如图7.2所示。
式7.2带入式7.1,得(1)()()()()()()()x k Fx k Gu k y k Cx k u k v k Lx k +=+⎧⎪=⎨⎪=+⎩7.3整理得()(1)()()()()x k F GL x k Gv k y k Cx k +=++⎧⎨=⎩7.4(k )v(k )图7.2 状态反馈任意配置闭环系统的极点闭环系统的特征方程为[]det ()0zI F GL -+=7.5问题是在什么情况下式7.5的特征根是可以任意配置的?即任给工程上期望的n 个特征根λ1, λ2, ..., λn ,有[]1det ()()0ni i zI F GL z λ=-+=-=∏7.6定理:状态反馈配置极点若被控对象式7.1是状态完全能达的,即(F , G )是一个能达对(能达性矩阵-1[...]N c W F G FG G =满秩),则一定存在一个r 行n 列的状态反馈矩阵L ,使得在状态反馈()()()u k v k Kx k =+下,闭环系统式7.4具有任意给定的n 个期望的特征根λ1, λ2, ..., λn 。
证明:略在实际工程应用中,动态系统式7.1的阶数n 不会太高。
在式7.6中L 是一个r 行n 列的矩阵,有nr 个待定参数,分别令式中等号左右的n 阶首一多项式的n 个系数对应相等,可得n 个线性方程。
当单输入单输出情况时,l 是一个n 元行向量,此时l 是唯一确定的。
当多输入多输出情况时,L 是一个r 行n 列的矩阵,此时L 不是唯一的。
有限拍闭环控制器当选择闭环系统的n 个特征根均为零,即λi =0,i =1,2,…,n ,则式7.6成为[]det ()0n zI F GL z -+==7.7根据矩阵代数中的Cayley-Hamilton 定理,此时有0n F =7.8上式表明,由任何扰动引起的状态偏差,系统都会在最多n 拍以内使之衰减为零。
关于有限拍控制器,有两点需要注意: ①n 拍意味着过度过程不大于nT ,T 为采样周期。
这一点似乎意味减小采样周期就可以提高系统的动态速度。
但是,减小采样周期同时意味着控制信号的幅值急剧增大。
如果控制信号的幅值超出了系统允许的范围,实际上达不到预期的控制效果。
因此,谨慎地选取采样周期非常重要。
②就动态性能而言,离散时间系统中的零特征值(同时采样T 周期趋于零)等价于连续时间系统中的特征值为 “-∞”,二者都是无法实现的。
7.3 状态估值和状态观测器用一组代数运算器(无动态运算)通过状态反馈实现被控对象的动态特性任意配置,似乎是一种很完美的控制方法。
但是尚有几个非理想的因素需要解决。
比如,● 状态是否可以直接测得? ● 是否可以实现无差调节? ● 对扰动的调节能力如何?工程控制中,状态反馈的实现需要被控对象的n 个状态可以实时测得。
这一点对于一般的系统大多是不现实的。
而在经典控制理论的输出反馈中,系统的输出总是可以检测的。
因此,能否实现通过状态反馈实现任意配置极点,首先需要设法实时获得n 个状态的值 7.3.1全维观测器假设被控对象式7.1的状态x 无法直接测得,一个合理的办法是人为地对x 进行重构,如图7.3所示。
重构系统具有和式7.1完全相同的结构、参数、和输入量,其状态记为ˆx,输出记为ˆy。
理论上讲,由于重构的系统和原系统结构和参数均完全相同,如果x 和ˆx 的初始状态也相同,则有ˆ()()xk x k =;由ˆx 取代x 进行状态反馈即可。
实际上却存在三个问题: ● 一是对象中的扰动会改变其状态;● 二是原系统可能存在稳定性问题,因而重构系统也会不稳定; ● 三是原系统参数可能并不太准确。
为了保证ˆ()xk 动态跟踪()x k ,引入输出误差ˆ()()y k y k -的反馈 ()ˆˆˆ(1)()()()()ˆˆ()()xk Fx k Gu k K y k y k y k Cx k +=++-⎧⎪⎨=⎪⎩7.9图7.3 全维观测器结构化简后后得到()ˆˆ(1)()()()ˆˆ()()xk F KC x k Gu k Ky k y k Cx k +=-++⎧⎪⎨=⎪⎩7.10现在考虑(定义)估值误差ˆˆˆ()()()xk x k x k =- 7.11将式7.1和式7.10带入上式,得()ˆˆˆˆ(1)()xk F KC x k +=- 7.12显然,如果可以选择矩阵K 使得矩阵(F-KC )具有稳定且足够小的特征值,ˆˆ()xk 就会足够快地趋于零;就是说,ˆ()xk 会足够快地趋于()x k 。
这就是渐进状态观测器,简称观测器。
定理:观测器的动态特性若被控对象式7.1是状态完全能观的,即(F , C )是一个能观对(能观性矩阵1O ...()TTT T T N TW CF C F C -=⎡⎤⎣⎦满秩),则一定存在一个n 行m 列的输出反馈矩阵K ,使得状态观测器式7.10或式7.12具有任意给定的n 个期望的特征根γ, γ2, ..., γn 。
即有[]1det ()()0ni i zI F KC z γ=--=-=∏7.13就是说,总可以通过选取适当的矩阵K 使得观测器具有期望的稳定性 无论原来的系统式7.1是否稳定!在上式中K 是一个n 行m 列的矩阵,有nm 个待定参数,分别令式中等号左右的n 阶首一多项式的n 个系数对应相等,可得n 个线性方程。
当单输入单输出情况时,K 是一个n 元行向量,此时K 是唯一确定的。
当多输入多输出情况时,K 是一个n 行m 列的矩阵,此时K 不是唯一的。
式7.9的观测器与原系统式7.1具有相同的维数,因而称为全维观测器。
7.3.2降维观测器(Luenberger 观测器)观测器实际上是控制器的一部分。
降低观测器的维数可以简化控制器的设计和实现。
降维观测器的思路是,式7.1中的输出y (k )中已经“直接”包含了部分状态x (k )的信息,这些对应的状态就可直接测得,只需对剩余无法测得的状态进行观测,观测器的维数就可降低,称为降维观测器。
假设输出矩阵C 是满秩的,则一定存在一个相似变换12()()()()x k x k Px k x k ⎡⎤==⎢⎥⎣⎦7.14其中,1()x k 和2()x k 分别为n-m 维和m 维。
于是,式7.1成为11111212221122122(1)()()(1)()()()[0]()()x k x k F F G u k x k x k F F G x k y k I x k x k ⎧+⎡⎤⎡⎤⎡⎤⎡⎤=+⎪⎢⎥⎢⎥⎢⎥⎢⎥+⎪⎣⎦⎣⎦⎣⎦⎣⎦⎨⎡⎤⎪==⎢⎥⎪⎣⎦⎩7.15展开得11111221221112222(1)()()()(1)()()()()()x k F x k F x k G u k x k F x k F x k G u k y k x k ⎧+=++⎪+=++⎨⎪=⎩ 7.16对应有111122112112[0]F F F P FP F F C CP I B G P G B --⎧⎡⎤==⎪⎢⎥⎣⎦⎪⎪==⎨⎪⎡⎤⎪==⎢⎥⎪⎣⎦⎩7.17注意到2()()y k x k =,已经直接得到了2()x k 的估值,即2ˆ()()xk y k = 7.18为了对1()x k 设计观测器,令1()x k 子系统的输出为()()121122222222()()(1)()()(1)()()y k F x k x k F x k G u k y k F y k G u k ==+-+=+-+ 7.19则待观测的1()x k 子系统成为()111112211211222(1)()()()()()(1)()()x k F x k F x k G u k y k F x k y k F y k G u k ⎧+=++⎪⎨==+-+⎪⎩ 7.20仿照式7.10对上式中的1()x k 设计n-m 维降维观测器,得()1111122111112112ˆˆˆˆ(1)()()()()()ˆˆ()()ˆ()()x k F x k F x k G u k K y k y k y k F x k x k y k ⎧+=+++-⎪⎪=⎨⎪=⎪⎩7.21将式7.20带入上式,得()()()11112111121212212ˆˆ(1)()()()(1)ˆ()()x k F K F x k G K G u k F K F y k K y k x k y k ⎧+=-+-⎪⎪+-++⎨⎪=⎪⎩ 7.22将上式用结构图表示如下图7.4。
图中有一个增序算子z ,将该支路移到减序支路之后(必须在反馈分支之前,为什么?)二者相互抵消;相应的状态改记为1ˆ()wk ;再考虑线性变换式7.14,最后得到x (k )的状态估值ˆ()xk ;如图7.5所示。
)图7.4 降维观测器式7.23的结构u图7.5 降维观测器式7.23的等效简化再对上图进行简化,将K 1输入支路移到反馈分支之后,最后得降维状态观测器动态方程如下式,亦如下图7.6所示。
()()()1111211112121221112111111ˆˆ(1)()()()ˆˆ()()()ˆ()ˆ()()w k F K F w k G K G u k F K F F K F K y k x k w k K y k x k x k P y k ⎧+=-+-⎪⎪⎡⎤+-+-⎣⎦⎪⎨=+⎪⎡⎤⎪=⎢⎥⎪⎣⎦⎩7.23得到x (k )的状态估值ˆ()x k 后,即可实现7.2节中由式7.2定义的状态反馈以实现极点配置,示于图7.8。