第七章平面图形的认识(初一)

平面图形的认识7.4认识三角形课标知识与能力目标1.认识三角形，会用字母表示三角形2.知道三角形的个组成部分，并会用字母表示3.了解三角形的分类4.知道三角形的性质5.知道三角形高、中线、角平分线的定义6.会做任意三角形高、中线、角平分线知识点1：三角形的性质1.三角形定义由三条不在同一直线上的三条线段首尾依次相接组成的图形叫做三角形.2.三角形的性质①三角形的任意两边之和大于第三边（由此得三角形的两边的差一定小于第三边）②三角形三个内角的和等于180度（在三角形中至少有一个角大于等于60度，也至少有一个角小于等于60度）（一个三角形的3个内角中最少有2个锐角）③直角三角形的两个锐角互余④三角形的一个外角等于与它不相邻的两个内角之和（三角形的一个外角大于任何一个与它不相邻的内角）⑤等腰三角形的顶角平分线，底边的中线，底边的高重合，即三线合一⑥三角形的三条角平分线交于一点，三条高线的所在直线交于一点，三条中线交于一点⑦三角形的外角和是360°⑧等底等高的三角形面积相等⑨三角形的任意一条中线将这个三角形分为两个面积相等的三角形.三角形具有稳定性.3.三角形的分类（1）按边分①不等边三角形②等腰三角形（含等腰直角三角形、等边三角形）按角分①锐角三角形②直角三角形③钝角三角形（锐角三角形和钝角三角形可统称为斜三角形）知识点2：三角形的有关定义1.三角形的高：在三角形中，从一个顶点向它的对边所在的直线作垂线，顶点和垂足间的线段叫做三角形的高线，简称为高.三角形的三条高交于一点，这一点叫三角形的垂心.垂心到三角形三个顶点的距离相等2.三角形的角平分线：三角形的一个内角的平分线与它的对边相交，这个角的顶点和交点之间的线段叫三角形的角平分线.（也叫三角形的内角平分线.）三角形的三条角平分线都在三角形的内部，并交于一点，这一点叫三角形的内心.三角形的内心到三边的距离相等.3.三角形的中线：三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线.三角形的三条中线在三角形的内部，并交于一点，这一点叫三角形的重心.每条三角形中线分得的两个三角形面积相等.典型例题考点1：三角形边的大小例1为估计图中池塘A、B 之间的距离，阳阳在池塘一侧选取了一点P，测得PA=1:2cm，PB=16cm，那么PB 可以取什么样的范围？考点2：三角形形状判断例1已知在△ABC 中有两个角的大小分别为40°和70°，则这个三角形是()A．直角三角形B．等边三角形C 钝角三角形D．等腰三角形例2如果AD .AE .AF 分别是△ABC 的中线、高和角平分线，且有一条在△ABC 的外部，则这个三角形是（）A．锐角三角形B．直角三角形C．钝角三角形D．任意三角形例3在△ABC 中，若∠A＝2∠B＝3∠C，则△ABC 是()A．锐角三角形B．直角三角形C．钝角三角形D．不能确定考点3：三角形的角平分线与高例1如图，在△ABC 中，∠1=∠2，G 为AD 的中点，延长BG 交AC 于E 点，F 为AB 上的一点，CF⊥AD 于H，下列判断正确的有①AD 为△ABE 的角平分线；②BE 为△ABD 边AD 上的中线；③CH 为△ACD 边AD 上的高；④AH 是△ACF 的角平分线和高线.AP BE 12ABCDE F考点4：三角形三边关系（两边之和大于第三边，两边只差小于第三边）例1下列长度的3条线段，能构成三角形的是（）A．1cm,2cm,3cm B．2cm,9cm,9cm C．4cm,3cm,8cmD．5cm,5cm,10cm例2一个三角形的两边长分别是5cm 和2cm ，则它的第三边不可能是（）A.5cmB.4cmC.6cmD.2cm例3在满足下列条件的线段a 、b 、c 中，能作为一个三角形的三边的是（）A．a c b c b a >+>+,B．3:2:1::=c b a C．c b a 21==D．2cb a 43==例4从1cm 、3cm 、5cm 、7cm 、9cm 的五根小棒中任取三根,能围成______个三角形.拓展提优题型1：三角形周长例1等腰三角形的一边等于3，一边等于6，则它的周长为()A．12B．12或15C．15或18D．15例1一个等腰三角形的周长为8，则腰长x 的取值范围是_______．例1已知三角形的两边长分别为7和2，第三边的数值是奇数，则该三角形的周长为．题型2：三角板相关求角度例1小明把一个含有450角的直角三角板放在如图所示的两条平行线m n ，上，测得0120α∠=，则β∠的度数是()A．450B．550C．650D．750例2把一块直尺与一块三角板如图放置，若∠1=50°，则∠2的度数为（）A．115°B．120°C ．130°D ．140°ba3412题型3：三角形求角度问题例1若一个三角形的三个内角不相等，则它的最小角不能大于()A．45°B．60°C．90°D．120°例2如图7，在△ABC 中，∠C =50°，按图中虚线将∠C 剪去后，∠1+∠2等于()A.230°B.210°C.130°D.310°例3如图所示,∠1=72°,∠2=72°,∠3=70°,求∠4的度数为（）A．72°B．70°C．108°D．110°例4如图，已知在三角形ABC 中，∠C＝∠ABC＝2∠A，BD 是AC 边上的高，求∠DBC 的度数．2CA 1图7例5如图1，已知线段AB、CD相交于点O，连接AD、CB，我们把形如图1的图形称之为“8字形”，试解答下列问题：(1)在图1中，写出∠A、∠B、∠C、∠D之间关系为＋＝＋；(2)如图2，在(1)的结论下，∠DAB和∠BCD的平分线AP和CP相交于点P，并且与CD、AB 分别相交于点M、N．①若∠D＝40°，∠B＝36°，则∠P＝_______；②探究∠P与∠D、∠B之间有何数量关系，并说明理由．例6（1）如图1，△ABC中∠ABC与∠ACB的平分线相交于点P试探索∠BPC与∠A的数量关系.（2）如图2，点P是△ABC中两外角∠DBC与∠ECB平分线的交点.试探索∠BPC与∠A的数量关系.（3）如图3，点P是△ABC中内角∠ABC平分线与外角∠ACD平分线的交点.试探索∠BPC与∠A的数量关系.题型4：求三角形一边取值范围例1已知a，b，c 是△ABC 的三边长；且满足a 2＋b 2－10a－8b＋41＝0，求c 的取值范围．例2已知：c b a ,,分别为ΔABC 的三条边的长度，请你猜想2222b a c ac --+的值是正数、负数还是零？你能用所学的知识说明为什么吗？例3已知a ，b ，c 是△ABC 的三边长，满足a 2＋b 2＝10a ＋8b －41，且c 是△ABC 中最长的边，求c 的取值范围．。

七年级第七章：平面图形的认识（二）课标要求：1．相交线与平行线（1）识别同位角、内错角、同旁内角。

（2）理解平行线概念；掌握基本事实：两条直线被第三条直线所截，如果同位角相等，那么两直线平行。

（3）掌握基本事实：过直线外一点有且只有一条直线与这条直线平行。

（4）掌握平行线的性质定理：两条平行直线被第三条直线所截，同位角相等。

*了解平行线性质定理的证明。

（5）能用三角尺和直尺过已知直线外一点画这条直线的平行线。

（6）探索并证明平行线的判定定理：两条直线被第三条直线所截，如果内错角相等（或同旁内角互补），那么两直线平行；平行线的性质定理：两条平行直线被第三条直线所截，内错角相等（或同旁内角互补）。

（7）了解平行于同一条直线的两条直线平行。

2．图形的平移（1）通过具体实例认识平移，探索它的基本性质：一个图形和它经过平移所得的图形中，两组对应点的连线平行（或在同一条直线上）且相等。

（2）认识并欣赏平移在自然界和现实生活中的应用。

（3）运用图形的轴对称、旋转、平移进行图案设计。

3．三角形（1）理解三角形及其内角、外角、中线、高线、角平分线等概念，了解三角形的稳定性。

（2）探索并证明三角形的内角和定理。

掌握它的推论：三角形的外角等于与它不相邻的两个内角的和。

证明三角形的任意两边之和大于第三边。

4．多边形（1）了解多边形的定义，多边形的顶点、边、内角、外角、对角线等概念；探索并掌握多边形内角和与外角和公式。

重点难点：重点：掌握直线平行的条件与性质；掌握平移的基本性质；掌握三角形相关概念（内角、外角、中线、高线、角平分线），会画出任意三角形的角平分线、中线、高线；掌握多边形的内角和与外角和定理，并能利用此进行相关角度的计算。

难点：平行线条件与性质的探索过程，平行线间的距离，能进行相关线段和差及角度和差的计算。

知识梳理一．三线八角：两条直线AB、CD与直线EF相交，交点分别为E、F，如图，则称直线AB、CD被直线EF所截，直线为截线，直线___ 、___称为被截线，两条直线AB、CD被直线EF所截可得8个角，这样的图形就是我们通常所说的“三线八角”.（一）、这八个角中有：1、对顶角：∠1与∠3，∠2与∠4，∠5与∠7，∠6与∠8.2、邻补角有：∠1与∠2，∠2与∠3，∠3与∠4，∠4与∠1，∠5与∠6，∠6与∠7，∠7与∠8，∠8与∠5.（二）、同位角，内错角，同旁内角：1、同位角：两条直线被第三条直线所截，在二条直线的同侧，且在第三条直线的同旁的二个角叫。

平面图形的认识（二）知识点总复习及强化练习【知识梳理】1.平行线的认识（1）认识三线八角：如图，两条直线被第三条直线所截，分成了八个角。

（2）平行的判定：同位角相等，两直线平行；内错角相等，两直线平行；同旁内角互补，两直线平行。

（3）平行的性质：两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补。

2.三角形的认识（1）三角形的三边关系：两边之和大于第三边，两边之差小于第三边。

（2）三角形的内角和：三角形的内角和是180°（3）三角形内外角关系：一个外角大于和它不相邻的任意一个内角，等于和它不相邻的两个内角和。

（4）三角形的分类：直角三角形；锐角三角形；钝角三角形。

（5）三角形的三线：角平分线；中线；高线。

3.多边形的外角和与内角和公式。

【例题精讲】题型一：平行的判定与性质例1.如图所示，AB∥CD，AF平分∠CAB，CF平分∠ACD．计算(1)∠B+∠E+∠D=________；(2)∠AFC=________.例2.如图，AB∥CD，∠A=120°，∠1=72°，则∠D的度数为__________．题型二：折叠问题例1.如图，将一张长方形纸片沿EF折叠后，点D、C分别落在D′、C′的位置，ED′的延长线与BC交于点G．若∠EFG=55°，则∠1=__________．与AD交于点G，例2.如图，把矩形ABCD沿EF折叠，点A、B分别落在A′、B′处．A′B′若∠1 =50°，则∠AEF=（）A．110°B．115°C．120°D．130°题型三：多边形的内角和与外角和例1.一多边形内角和为2340°，若每一个内角都相等，求每个外角的度数．．．．．．．。

例2.一个零件的形状如图，按规定∠A=90°，∠ABD和∠ACD，应分别是32°和21°，检验工人量得∠BDC=148°，就断定这个零件不合格，运用三角形的有关知识说明零件不合格的理由．例3.如图，已知∠DAB+∠D=180°，AC平分∠A，且∠CAD=25°，∠B=95°（1）求∠DCA的度数；（2）求∠ACE的度数．题型四：拓展延伸例1.如图①是长方形纸带，将纸带沿EF折叠成图②，再沿BF折叠成图③.（1）若∠DEF=200，则图③中∠CFE度数是多少？（2）若∠DEF=α，把图③中∠CFE用α表示.例2.如图，△ABC中，BE，CD为角平分线且交点为点O，当∠A=600时，（1）求∠BOC的度数；（2）当∠A=1000时，求∠BOC的度数；（3）若∠A=α时，求∠BOC的度数。

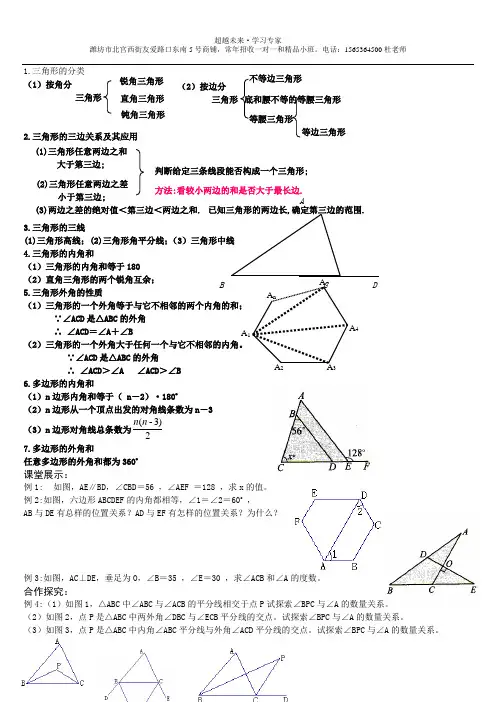
1.三角形的分类（1）按角分三角形2.三角形的三边关系及其应用3.三角形的三线(1)三角形高线；(2)三角形角平分线；（3）三角形中线4.三角形的内角和（1）三角形的内角和等于180（2）直角三角形的两个锐角互余；5.三角形外角的性质（1）三角形的一个外角等于与它不相邻的两个内角的和；∵∠ACD是△ABC的外角∴∠ACD＝∠A＋∠B（2）三角形的一个外角大于任何一个与它不相邻的内角。

∵∠ACD是△ABC的外角∴∠ACD＞∠A ∠ACD＞∠B6.多边形的内角和（1）n边形内角和等于（ n－2）·180o（2）n边形从一个顶点出发的对角线条数为n－3（3）n边形对角线总条数为2)3-(nn7.多边形的外角和任意多边形的外角和都为360o课堂展示：例1:如图，AE∥BD，∠CBD＝56 ，∠AEF ＝128 ，求x的值。

例2:如图，六边形ABCDEF的内角都相等，∠1＝∠2＝60o，AB与DE有总样的位置关系？AD与EF有怎样的位置关系？为什么？例3:如图，AC⊥DE，垂足为O，∠B＝35 ，∠E＝30 ，求∠ACB和∠A的度数。

合作探究：例4:（1）如图1，△ABC中∠ABC与∠ACB的平分线相交于点P试探索∠BPC与∠A的数量关系。

（2）如图2，点P是△ABC中两外角∠DBC与∠ECB平分线的交点。

试探索∠BPC与∠A的数量关系。

（3）如图3，点P是△ABC中内角∠ABC平分线与外角∠ACD平分线的交点。

试探索∠BPC与∠A的数量关系。

锐角三角形直角三角形钝角三角形（2）按边分底和腰不等的等腰三角形三角形不等边三角形等腰三角形等边三角形(1)三角形任意两边之和大于第三边;(2)三角形任意两边之差小于第三边;(3)两边之差的绝对值＜第三边＜两边之和.判断给定三条线段能否构成一个三角形;已知三角形的两边长,确定第三边的范围.方法:看较小两边的和是否大于最长边.AB C DA1A2A3A4A5A n巩固拓展：1、在△ABC 中， ∠A ＝40°，∠B ＝∠C ，则∠C ＝ 。

七年级数学下册第七章平面图形的认识一、选择题:(每题3分，共30分)1、下列图形中，不能通过其中一个四边形平移得到的是： ( )2、在下列各图的△ABC中，正确画出AC边上的高的图形是：( )3、如图，在宽为20m，长为30m的矩形地面上修建两条同样宽的道路，余下部分作为耕地.根据图中数据，计算耕地的面积为： ( )A、600m2B、551m2C、550m 2D、500m24、将一张长方形纸片如图所示折叠后，再展开.如果1=56，那么2等于： ( )A、56B、68C、62D、665、a、b、c、d四根竹签的长分别为2cm、3cm、4cm、6cm.从中任意选取三根首尾依次相接围成不同的三角形,则围成的三角形共有： ( )A、1个B、2个C、3个D、4个6、若一个多边形每一个外角都与它的相邻的内角相等，则这个多边形的边数是： ( )A、6B、5C、4D、37、下列叙述中，正确的有： ( )①三角形的一个外角等于两个内角的和;②一个五边形最多有3个内角是直角;③任意一个三角形的三条高所在的直线相交于一点，且这点一定在三角形的内部;④ABC中，若A=2B=3C，则这个三角形ABC为直角三角形.A、0个B、1个C、2个D、3个8、如图，OP∥QR∥ST，则下列各式中正确的是： ( )A、2+3=180B、2-3=90C、2+3=90D、3-1=1809、如图是一块电脑主板的示意图，每一转角处都是直角，数据如图所示，则该主板的周长是：( )A、88mmB、96mmC、80mmD、84mm10、一幅三角板如图所示叠放在一起，则图中的度数为： ( )A、75B、60C、65D、55二、填空题(每题2分，共20分)1、如图，面积为6cm2的直角三角形ABC沿BC方向平移至三角形DEF的位置，平移距离是BC的2倍，则图中四边形ACED的面积为_______ cm2.2、如图，l1∥l2，ABl2，垂足为O，BC交l2于点E，若ABC=140，则1=_____.3、光线a照射到平面镜CD上，然后在平面镜AB和CD之间来回反射，这时光线的入射角等于反射角。