遗传算法的0-1背包问题(c语言)
- 格式:doc
- 大小:177.50 KB
- 文档页数:26

问题描述0/1 背包问题 :现有 n 种物品,对 1<=i<=n ,已知第 i 种物品的重量为正整数 W i ,价值为正整数 V i , 背包能承受的最大载重量为正整数 W ,现要求找出这 n 种物品的一个子集,使得子集中物 品的总重量不超过 W 且总价值尽量大。
(注意:这里对每种物品或者全取或者一点都不取, 不允许只取一部分)算法分析根据问题描述,可以将其转化为如下的约束条件和目标函数:nw i x i W i 1 i i(1)x i { 0,1}( 1 i n)nmax v i x i (2) i1于是,问题就归结为寻找一个满足约束条件( 1 ),并使目标函数式( 2 )达到最大的 解向量 X (x 1, x 2 ,x 3, ........... , x n ) 。
首先说明一下 0-1 背包问题拥有最优解。
假设 (x 1,x 2,x 3, ........ ,x n ) 是所给的问题的一个最优解, 则(x 2,x 3, ............... ,x n )是下面问题的n n n个问 题 的 一 个 最 优解 , 则v i y iv i x i , 且 w 1x 1w i y i W 。
因此 ,i 2 i 2 i 2一个最优解:w i x i Wi2w 1x 1nmax v i x i 。
如果不是的话,设(y 2,y 3, , y n ) 是这x i {0,1}( 2 i n)i2n n nv1x1 v i y i v1x1 v i x i v i x i ,这说明(x1,y2,y3, ............. ,y n) 是所给的0-1 背包问i 2 i 2 i 1题比( x1 , x 2 , x3 , ... , x n ) 更优的解,从而与假设矛盾。
穷举法:用穷举法解决0-1 背包问题,需要考虑给定n 个物品集合的所有子集,找出所有可能的子集(总重量不超过背包重量的子集) ,计算每个子集的总重量,然后在他们中找到价值最大的子集。

遗传算法解决01背包问题2015 ~2016 学年第二学期学生姓名专业学号2016年 6 月目录一:问题描述 (3)二:遗传算法原理及特点 (3)三:背包问题的遗传算法求解 (3)1.文字描述 (3)2.遗传算法中的抽象概念在背包问题的具体化 (3)3.算法求解的基本步骤 (4)四:算法实现 (4)1.数据结构 (4)2.部分代码 (5)五:结论 (8)六:参考文献 (8)一、问题描述0-1背包问题属于组合优化问题的一个例子,求解0-1背包问题的过程可以被视作在很多可行解当中求解一个最优解。
01背包问题的一般描述如下:给定n个物品和一个背包,物品i的重量为Wi,其价值为Vi,背包的容量为C。
问应如何选择合适的物品装入背包,使得背包中装入的物品的总价值最大。
注意的一点是,背包内的物品的重量之和不能大于背包的容量C。
在选择装入背包的物品时,对每种物品i只有两种选择:即装入背包或者不装入背包,不能讲物品i装入背包多次,也不能只装入部分的物品,称此类问题为0/1背包问题。
二、遗传算法原理及特点遗传算法(Genetic Algorithm)是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型,是一种通过模拟自然进化过程搜索最优解的方法。
遗传算法有着鲜明的优点:(1)遗传算法的操作对象是一组可行解,而非单个可行解;搜索轨道有多条,而非单条,因而具有良好的并行性.(2)遗传算法只需利用目标的取值信息,而无需递度等高价值信息,因而适用于任何规模,高度非线形的不连续多峰函数的优化以及无解析表达式的目标函数的优化,具有很强的通用性.(3)遗传算法择优机制是一种“软”选择,加上良好的并行性,使它具有良好的全局优化性和稳健性.(4)遗传算法操作的可行解集是经过编码化的(通常采用二进制编码),目标函数解释为编码化个体(可行解)的适应值,因而具有良好的可操作性与简单性.三、背包问题的遗传算法求解1、文字描述0-1背包问题传统的解决方法有动态规划法、分支界限法、回溯法等等。

遗传算法求解背包问题程序实现一、背包问题描述背包问题是著名的NP 完备类困难问题,对这个问题的求解前人已经研究出了不少的经典的方法,对该问题确实能得到很好的结果。
近年来蓬勃发展起来的遗传算法已被广泛地应用于优化领域,其全局最优性、可并行性、高效性在函数优化中得到了广泛地应用遗传算法克服了传统优化方法的缺点,借助了大自然的演化过程,是多线索而非单线索的全局优化方法,采用的是种群和随机搜索机制. 本程序将遗传算法应用于背包问题。
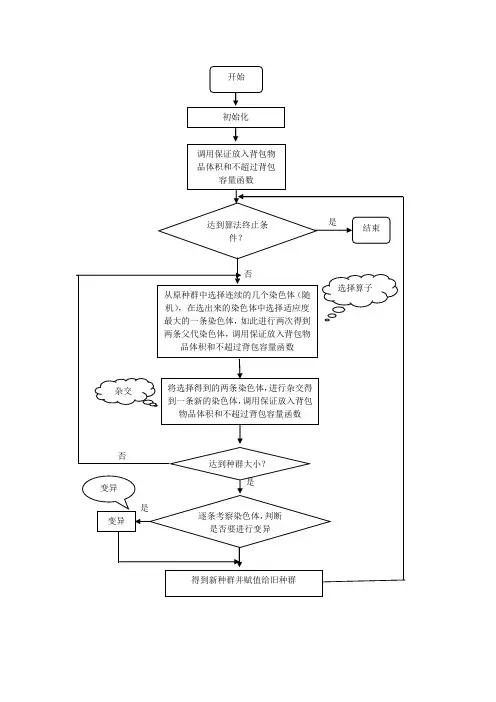
二、实验程序1、编程语言:C++2、开发环境:Microsoft Visual Studio 20053、程序整体流程:步1初始化过程1. 1确定种群规模scale、杂交概率pc、变异概率pm、染色体长度chN及最大进化代数maxgen。
1. 2取x1′(0) = u (0 ,1) , x2′(0) = u (0 ,1) , …, xchN′(0) = u (0 ,1) ,其中函数u (0 ,1) 表示随机地产生数0 或1 ,则x (0) = ( x1 (0) , x2 (0) ,⋯, xN (0) ) .若不满足约束条件,则拒绝接受. 由(1. 2) 重新产生一个新的染色体; 如果产生的染色体可行,则接受它作为种群的一名成员,经过有限次抽样后, 得到scale个可行的染色体xj (0) , j =1 ,2 , ⋯, M ,设xj (0) 的染色体编码为vj (0) ,并记为v (0) = ( v1 (0) , ⋯, vchN (0) ) .1. 3计算各个染色体的适值1. 4 置k = 0步2选择操作2. 1采用转轮法选择下一代。
.步3杂交变异操作3. 1 事先定义杂交操作的概率pc ,为确定杂交操作的父代,从j = 1 到M 重复以下过程:从[0 ,1 ] 中产生随机数r ,若r < pc ,则选择cj′( k)作为一个父代.3. 2 产生两个[1 , N ] 上的随机整数i 、j ,变异的结果为染色体vj′( k)的第i 位基因的值变为其第j 位基因的值,同样将染色体的vj′( k)第j 位基因的值变为其第i 位基因的值.3. 3 检验该染色体的可行性,若可行则作为变异的结果;如不可行,重复3. 2 直至该染色体可行.3. 4 事先定义变异概率pm ,对经过杂交操作的中间个体进行变异操作: ,如果r < pm ,则选择vi″( k) 作为变异的父代.3. 5 产生一个[1 , N ] 上的随机整数i ,及随机地产生数0 或1 , 记为b , 变异的结果为染色体vi″( k) 的第i 位基因的值变为b.3. 6 检验该染色体的可行性,若可行则作为变异的结果:如不可行,重复3. 5 直至该染色体可行.3. 7 计算新个体的适应值,并把它们同时放回,和步2 选择操作中剩余的个体一起构成新一代种群v ( k + 1) = { v1 ( k + 1) , v2 ( k + 1) , ⋯, vM ( k + 1) } .步4 终止检验如果达到最大进化代数maxgen 则终止演化,否则置k : = k + 1 ,转步2.4、程序流程图程序流程图5、程序代码1)主程序代码:KnapsacksProblem.cpp文件#include "GAonKP.h"#include <iostream>using namespace std;void main(){FILE* fp;CGAonKP gakp;int scale; //种群规模double MaxWeight; //背包允许最大财宝质量double pc; //杂交概率double pm; //变异概率int maxgen; //最大进化代数char filename[256];cout<<"遗传算法解决背包问题程序使用说明:"<<endl;cout<<"1、该背包问题采用遗传算法"<<endl;cout<<"2、-1编码的方法,其中代表选中所对应的物品,代表不选中该物品"<<endl;cout<<"3、背包允许最带重量,种群规模(解空间大小),";cout<<"杂交概率,变异概率,最大进化代数需自己给";cout<<"定,程序会提示输入"<<endl;cout<<"4、程序提供一个输入示例"<<endl;cout<<"5、输入文件可加单行或多行注释"<<endl;cout<<"例如:#添加单行注释内容#"<<endl;cout<<"例如:#添加多行注释内容"<<endl;cout<<" 添加多行注释内容#"<<endl;cout<<"6、输入文件头位置需指定物品个数为int型数据。
遗传算法的过程:初始化:将计划装入背包的每个物品看成一个二进制串的一位,为1表示放入该物品,为0表示不放入该物品。
初始种群的产生:初始化前对放入背包物品数的一个预测(背包容积/物品最大体积),接下来只要在种群每条染色体中保证有(背包容积/物品最大体积)个为1的位初始化就完成了。
选择:选择进行杂交的父代染色体,被选中的父代染色体总是若干个染色体中最优(适应度最高)的,来保证向优化的方向发展。
详细的选择方法:随机产生2个数:Chrom_Cross_From, Chrom_Cross_To,当然得采用一定的手段来保证前者比后者小。
从Chrom_Cross_From到Chrom_Cross_To这Chrom_Cross_To-Chrom_Cross_From+1条染色体中选择最优(适应度最大)的染色体作为父代之一。
需要进行两次选择得到杂交的两条父代染色体。
这样做可以保证算法不会过早收敛。
函数实现:Individual Select(int ChromSize,Individual Pop[]){int Num_Selected,i,j,Chrom_Selected_From,Chrom_Selected_To,temp;Individual *Chrom_Selected;do{Chrom_Selected_From=rand()%PopSize;Chrom_Selected_To=rand()%PopSize;if(Chrom_Selected_From>Chrom_Selected_To){temp=Chrom_Selected_From;Chrom_Selected_From=Chrom_Selected_To;Chrom_Selected_To=temp;}Num_Selected=Chrom_Selected_To-Chrom_Selected_From+1;}while(Num_Selected<=0);Chrom_Selected=new Individual[Num_Selected];for(i=0;i<Num_Selected;i++)Chrom_Selected[i].chrom=new int[ChromSize];for(i=0,j=Chrom_Selected_From;i<Num_Selected,j<Chrom_Selected_To+1;i++,j++){Chrom_Selected[i]=Pop[j];}Order_Best_First(ChromSize,Num_Selected,Chrom_Selected);Chrom_Selected[0].fitness=Fitness(Chrom_Selected[0].chrom,ChromSize);return Chrom_Selected[0];}杂交:将两次选择得到的父代染色体进行杂交得到一条新的染色体,作为较新种群(并非新的种群)的一条染色体,杂交直到较新种群的染色体数等于原种群的染色体数。

算法设计与分析实验报告—0/1背包问题-【问题描述】给定n 种物品和一个背包。
物品i 的重量是iw ,其价值为i v,背包容量为C 。
问应该如何选择装入背包的物品,使得装入背包中物品的总价值最大?【问题分析】0/1背包问题的可形式化描述为:给定C>0, i w >0, i v >0,1i n ≤≤,要求找出n 元0/1向量{}12(,,...,),0,1,1n i x x x x i n ∈≤≤,使得n1i i i w x c =≤∑,而且n1i ii v x=∑达到最大。
因此0/1背包问题是一个特殊的整数规划问题。
0n k w ≤≤1max ni i i v x =∑n1i ii w xc =≤∑{}0,1,1i x i n ∈≤≤【算法设计】设0/1背包问题的最优值为m( i, j ),即背包容量是j ,可选择物品为i,i+1,…,n 时0/1背包问题的最优值。
由0/1背包问题的最优子结构性质,可以建立计算m( i, j )的递归式如下:max{m( i+1, j ), m( i+1, j-i w )+i v } i j w ≥m( i, j )=m(i+1,j)n v n j w >m(n,j)=0 0n k w ≤≤【算法实现】#include <iostream.h> #include<string.h> #include<iomanip.h>int min(int w, int c) {int temp; if (w < c) temp = w;elsetemp = c;return temp;}Int max(int w, int c) {int temp; if (w > c) temp = w;elsetemp = c;return temp;}void knapsack(int v[], int w[], int** m, int c, int n) //求最优值 {int jmax = min(w[n]-1, c);for (int j = 0; j <= jmax; j++)m[n][j] = 0;for (int jj = w[n]; jj <= c; jj++)m[n][jj] = v[n];for(int i = n-1; i > 1; i--)//递归部分{jmax = min(w[i]-1, c);for(int j = 0; j <= jmax; j++)m[i][j] = m[i+1][j];for(int jj = w[i]; jj <= c; jj++)m[i][jj] = max(m[i+1][jj], m[i+1][jj-w[i]]+v[i]);}m[1][c] = m[2][c];if(c >= w[1])m[1][c] = max(m[1][c], m[2][c-w[1]]+v[1]);cout << endl << "最优值:" << m[1][c] << endl;cout<<endl;cout<< "&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&&" << endl;}int traceback(int x[], int w[], int** m, int c, int n) //回代,求最优解{out << endl << "得到的一组最优解如下: " << endl;for(int i = 1; i < n; i++){if(m[i][c] == m[i+1][c]) x[i] = 0;else{x[i] = 1;c -= w[i];}}x[n] = (m[n][c]) ? 1:0;for(int y = 1; y <= n; y++)cout << x[y] << "\t";cout << endl;return x[n];}void main(){int n, c;int **m;cout << "&&&&&&&&&&&&&&&&&&&&&欢迎使用0-1背包问题程序&&&&&&&&&&&&&&&&&&&" << endl;cout << "请输入物品个数: ";cin >> n ;cout << endl << "请输入背包的承重:";cin >> c;int *v = new int[n+1];cout << endl << "请输入每个物品的价值 (v[i]): " << endl;for(int i = 1; i <= n; i++)cin >> v[i];int *w = new int[n+1];cout << endl << "请输入每个物品的重量 (w[i]): " << endl;for(int j = 1; j <= n; j++)cin >> w[j];int *x = new int[n+1];m = new int* [n+1]; //动态的分配二维数组for(int p = 0; p < n+1; p++)m[p] = new int[c+1];knapsack (v, w, m, c, n);traceback(x, w, m, c, n);}【运行结果】。

以下是使用C语言实现01背包问题的回溯法代码:```c#include <stdio.h>#include <stdlib.h>// 初始化背包struct knapsack {int maxWeight; // 背包最大承重int *items; // 物品数组int n; // 物品数量};// 定义物品重量、价值和数量int weights[] = {2, 2, 6, 5, 4};int values[] = {6, 3, 5, 4, 6};int quantities[] = {3, 2, 2, 1, 1};// 初始化背包最大承重和当前承重int maxWeight = 10;int currentWeight = 0;// 初始化最大价值为0int maxValue = 0;// 遍历物品数组void traverseItems(struct knapsack *knapsack, int index) { // 对于每个物品,遍历其数量for (int i = 0; i < knapsack->quantities[index]; i++) {// 如果当前物品可以放入背包装且当前承重不超过背包最大承重,计算放入该物品后的总价值,并更新最大价值if (currentWeight + weights[index] <= knapsack->maxWeight) {int currentValue = values[index] * knapsack->quantities[index];if (currentValue > maxValue) {maxValue = currentValue;}}// 回溯,将当前物品从背包装中移除,递归地尝试下一个物品knapsack->quantities[index]--;if (index < knapsack->n - 1) {traverseItems(knapsack, index + 1);}knapsack->quantities[index]++; // 恢复物品数量,以便下次遍历尝试放入其他物品}}// 主函数int main() {// 初始化背包装和物品数组struct knapsack knapsack = {maxWeight, weights, 5};knapsack.items = (int *)malloc(sizeof(int) * knapsack.n);for (int i = 0; i < knapsack.n; i++) {knapsack.items[i] = values[i] * quantities[i]; // 根据价值和数量计算物品价值,并存储在物品数组中}knapsack.n = quantities[4]; // 由于最后一个物品的数量为1,因此只需遍历前n-1个物品即可得到所有可能的结果// 使用回溯法求解01背包问题,返回最大价值traverseItems(&knapsack, 0);printf("The maximum value is %d.\n", maxValue);free(knapsack.items); // 释放内存空间return 0;}```希望以上信息能帮助到你。

c语言算法--贪婪算法---0/1背包问题在0 / 1背包问题中,需对容量为c 的背包进行装载。
从n 个物品中选取装入背包的物品,每件物品i 的重量为wi ,价值为pi 。
对于可行的背包装载,背包中物品的总重量不能超过背包的容量,最佳装载是指所装入的物品价值最高,即n ?i=1pi xi 取得最大值。
约束条件为n ?i =1wi xi≤c 和xi?[ 0 , 1 ] ( 1≤i≤n)。
在这个表达式中,需求出xt 的值。
xi = 1表示物品i 装入背包中,xi =0 表示物品i 不装入背包。
0 / 1背包问题是一个一般化的货箱装载问题,即每个货箱所获得的价值不同。
货箱装载问题转化为背包问题的形式为:船作为背包,货箱作为可装入背包的物品。
例1-8 在杂货店比赛中你获得了第一名,奖品是一车免费杂货。
店中有n 种不同的货物。
规则规定从每种货物中最多只能拿一件,车子的容量为c,物品i 需占用wi 的空间,价值为pi 。
你的目标是使车中装载的物品价值最大。
当然,所装货物不能超过车的容量,且同一种物品不得拿走多件。
这个问题可仿照0 / 1背包问题进行建模,其中车对应于背包,货物对应于物品。
0 / 1背包问题有好几种贪婪策略,每个贪婪策略都采用多步过程来完成背包的装入。
在每一步过程中利用贪婪准则选择一个物品装入背包。
一种贪婪准则为:从剩余的物品中,选出可以装入背包的价值最大的物品,利用这种规则,价值最大的物品首先被装入(假设有足够容量),然后是下一个价值最大的物品,如此继续下去。
这种策略不能保证得到最优解。
例如,考虑n=2, w=[100,10,10], p =[20,15,15], c = 1 0 5。
当利用价值贪婪准则时,获得的解为x= [ 1 , 0 , 0 ],这种方案的总价值为2 0。
而最优解为[ 0 , 1 , 1 ],其总价值为3 0。
另一种方案是重量贪婪准则是:从剩下的物品中选择可装入背包的重量最小的物品。

0/1 背包问题动态规划详解及C代码动态规划是用空间换时间的一种方法的抽象。
其关键是发现子问题和记录其结果。
然后利用这些结果减轻运算量。
比如01背包问题。
/* 一个旅行者有一个最多能用M公斤的背包,现在有N件物品,它们的重量分别是W1,W2,...,Wn,它们的价值分别为P1,P2,...,Pn.若每种物品只有一件求旅行者能获得最大总价值。
输入格式:M,NW1,P1W2,P2......输出格式:X*/因为背包最大容量M未知。
所以,我们的程序要从1到M一个一个的试。
比如,开始任选N 件物品的一个。
看对应M的背包,能不能放进去,如果能放进去,并且还有多的空间,则,多出来的空间里能放N-1物品中的最大价值。
怎么能保证总选择是最大价值呢?看下表。
测试数据:10,33,44,55,6c[i][j]数组保存了1,2,3号物品依次选择后的最大价值.这个最大价值是怎么得来的呢?从背包容量为0开始,1号物品先试,0,1,2,的容量都不能放.所以置0,背包容量为3则里面放4.这样,这一排背包容量为4,5,6,....10的时候,最佳方案都是放4.假如1号物品放入背包.则再看2号物品.当背包容量为3的时候,最佳方案还是上一排的最价方案c为4.而背包容量为5的时候,则最佳方案为自己的重量5.背包容量为7的时候,很显然是5加上一个值了。
加谁??很显然是7-4=3的时候.上一排 c3的最佳方案是4.所以。
总的最佳方案是5+4为9.这样.一排一排推下去。
最右下放的数据就是最大的价值了。
(注意第3排的背包容量为7的时候,最佳方案不是本身的6.而是上一排的9.说明这时候3号物品没有被选.选的是1,2号物品.所以得9.)从以上最大价值的构造过程中可以看出。
f(n,m)=max{f(n-1,m), f(n-1,m-w[n])+P(n,m)}这就是书本上写的动态规划方程.这回清楚了吗?下面是实际程序(在VC 6.0环境下通过):#include<stdio.h>int c[10][100];/*对应每种情况的最大价值*/int knapsack(int m,int n){int i,j,w[10],p[10];printf("请输入每个物品的重量,价值:\n");for(i=1;i<=n;i++)scanf("%d,%d",&w[i],&p[i]);for(i=0;i<10;i++)for(j=0;j<100;j++)c[i][j]=0;/*初始化数组*/for(i=1;i<=n;i++)for(j=1;j<=m;j++){if(w[i]<=j) /*如果当前物品的容量小于背包容量*/{if(p[i]+c[i-1][j-w[i]]>c[i-1][j])/*如果本物品的价值加上背包剩下的空间能放的物品的价值*//*大于上一次选择的最佳方案则更新c[i][j]*/c[i][j]=p[i]+c[i-1][j-w[i]];elsec[i][j]=c[i-1][j];}else c[i][j]=c[i-1][j];}return(c[n][m]);}int main(){int m,n;int i,j;printf("请输入背包的承重量,物品的总个数:\n");scanf("%d,%d",&m,&n);printf("旅行者背包能装的最大总价值为%d",knapsack(m,n)); printf("\n");return 0;}。

遗传算法求解0-1背包问题。
(步骤)#include "iostream.h"#include "iomanip.h"#include "stdlib.h"#include "math.h"#include "time.h"//定义问题的最大规模#define max 100//问题规模,即共有多少个包int packageNum;//每个包的重量int packageWeight[max];//每个包的价值int packageValue[max];//约束,背包的最大容量int limitWeight;//群体的规模int colonySize;//colonyState[i][k] 表示一个染色体//colonyState[1...colonySize][ 0|1 ] 表示一代群体int colonyState[max][2][max];// currAge 表示当前代的编号// (currAge+1)%2 表示下一代的编号int currAge = 0;//个体评价信息表typedef struct tagIndividualMsg{int index;int value;} IndividualMsg;IndividualMsg individualMsg[max];//////////////////////////////////////////////////////////// // 函数声明void printColonyState( int nextAge );//////////////////////////////////////////////////////////// //初始化群体void colonyInit(){int i , j;int w;for( i = 0 ; i < colonySize ; i++ ){//保证找到一个符合约束的染色体w = limitWeight + 1;while( w > limitWeight ){w = 0;for( j = 0 ; j < packageNum && w <= limitWeight ; j++ ){colonyState[i][currAge][j] = rand() % 2;w += packageWeight[j] * colonyState[i][currAge][j];}}}}//对个体进行评价int cmp( const void *a , const void *b ){IndividualMsg *x = (IndividualMsg *)a;IndividualMsg *y = (IndividualMsg *)b;return y->value - x->value;}void individualEstimate(){int i , j;for( i = 0 ; i < colonySize ; i++ ){individualMsg[i].index = i;individualMsg[i].value = 0;for( j = 0 ; j < packageNum ; j++ )individualMsg[i].value += packageValue[j] * colonyState[i][currAge][j]; }qsort( individualMsg , colonySize , sizeof(IndividualMsg) , cmp );}//终止循环的条件bool stopFlag(){//进行n 代进行后停止static int n = 50;if( n-- <= 0 )return true;elsereturn false;}//赌轮选择int gambleChoose(){int wheel[max] = { 0 };int i = colonySize - 1;int choose;wheel[i] = individualMsg[i].value;for( i-- ; i >= 0 ; i-- )wheel[i] = ( individualMsg[i].value + wheel[i+1] ) + colonySize * ( colonySize - i ); int seed = abs( wheel[0] - ( rand() % ( 2 * wheel[0] ) + 1 ) );choose = colonySize - 1;while( seed > wheel[choose] )choose--;// cout<<"----------------------------------------"<<endl;// cout<<"wheel :"<<endl;// for( i = 0 ; i < colonySize ; i++ )// cout<<setw(5)<<wheel[i];// cout<<endl;// cout<<"seed = "<<seed<<endl;// cout<<"choose "<<choose<<endl;return choose;}//交叉void across( int male , int female , int index ){int nextAge = (currAge+1)%2;int i , j , t;int acrossBit = rand() % (packageNum-1) + 1;for( j = 0 ; j < packageNum ; j++ ){colonyState[index][nextAge][j] =colonyState[individualMsg[male].index][currAge][j];colonyState[index+1][nextAge][j] =colonyState[individualMsg[female].index][currAge][j];}for( i = 0 ; i < acrossBit ; i++ ){t = colonyState[index][nextAge][i];colonyState[index][nextAge][i] = colonyState[index+1][nextAge][i];colonyState[index+1][nextAge][j] = t;}}//变异void aberrance( int index ){int seed , nextAge;nextAge = (currAge+1)%2;//只有1/3 的概率发生异变seed = rand() % ( packageNum * 3 );if( seed < packageNum )colonyState[index][nextAge][seed] = ( colonyState[index][nextAge][seed] + 1 ) % 2;}//处理死亡个体void dealDeath(){int i , j;int weight , w;int nextAge = (currAge+1)%2;for( i = 0 ; i < colonySize ; i++ ){weight = 0;for( j = 0 ; j < packageNum ; j++ )weight += packageWeight[j] * colonyState[i][nextAge][j];if( weight > limitWeight ){//随机生成新的个体w = limitWeight + 1;while( w > limitWeight ){w = 0;for( j = 0 ; j < packageNum && w <= limitWeight ; j++ ){colonyState[i][nextAge][j] = rand() % 2;w += packageWeight[j] * colonyState[i][nextAge][j];}}}}printColonyState( nextAge );}//最优个体保护void saveBest(){int i , j;int min , minp , value;int nextAge = ( currAge+1)%2;min = individualMsg[0].value;minp = -1;for( i = 0 ; i < colonySize ; i++ ){value = 0;for( j = 0 ; j < packageNum ; j++ )value += packageValue[j] * colonyState[i][nextAge][j]; if( value <= min ){min = value;minp = i;}}if( minp >= 0 ){for( j = 0 ; j < packageNum ; j++ ){colonyState[minp][nextAge][j] =colonyState[individualMsg[0].index][currAge][j];}}}//////////////////////////////////////////////////////////// void setProblem(){int i;packageNum = 5;int w[] = { 5 , 4 , 3 , 2 , 1 };int v[] = { 8 , 9 , 3 , 1 , 2 };for( i = 0 ; i < packageNum ; i++ ){packageWeight[i] = w[i];packageValue[i] = v[i];}limitWeight = 13;colonySize = 5;}void printProblem(){int i;cout<<"----------------------------------------"<<endl;cout<<"problem state:"<<endl;cout<<"packageNum = "<<packageNum<<endl;cout<<"limitWeight = "<<limitWeight<<endl;cout<<"Weight: ";for( i = 0 ; i < packageNum ; i++ )cout<<setw(3)<<packageWeight[i];cout<<endl;cout<<"Value: ";for( i = 0 ; i < packageNum ; i++ )cout<<setw(3)<<packageValue[i];cout<<endl;}void printColonyState( int k ){cout<<"----------------------------------------"<<endl;cout<<"colonyState-->";if( k == currAge )cout<<"currAge:"<<endl;elsecout<<"next age:"<<endl;int i , j;for( i = 0 ; i < colonySize ; i++ ){for( j = 0 ; j < packageNum ; j++ )cout<<setw(2)<<colonyState[i][k][j];cout<<endl;}}void printIndividualMsg(){int i;cout<<"----------------------------------------"<<endl;cout<<"Individual Msg:"<<endl;for( i = 0 ; i < colonySize ; i++ ){cout<<individualMsg[i].index<<"\t"<<individualMsg[i].value<<endl; }}////////////////////////////////////////////////////////////void main(){srand( (unsigned int)time(NULL) );setProblem();printProblem();//初始群体colonyInit();printColonyState( currAge );while( !stopFlag() ){//评价当前群体individualEstimate();//生成下一代for( int i = 0 ; i < colonySize ; i += 2 ){int male = gambleChoose();int female = gambleChoose();across( male , female , i );aberrance( i );aberrance( i + 1 );}//处理死亡个体dealDeath();//最优个体保护saveBest();//现在的下一代变成下一轮的当前代currAge = ( currAge + 1 ) % 2;//printColonyState( currAge );}//输出问题解individualEstimate();cout<<"近似解:"<<endl;int j , w = 0;cout<<setw(10)<<"Value:";for( j = 0 ; j < packageNum ; j++ )cout<<setw(5)<<packageValue[j];cout<<endl;cout<<setw(10)<<"Weight:";for( j = 0 ; j < packageNum ; j++ ){w += packageWeight[j] * colonyState[individualMsg[0].index][currAge][j]; cout<<setw(5)<<packageWeight[j];}cout<<endl;cout<<setw(10)<<"Choose:";for( j = 0 ; j < packageNum ; j++ )cout<<setw(5)<<colonyState[individualMsg[0].index][currAge][j];cout<<endl;cout<<"limitWeight: "<<limitWeight<<endl;cout<<"总重量: "<<w<<endl;cout<<"总价值: "<<individualMsg[0].value<<endl; }////////////////////////////////////////////////////////////。

0-1背包问题(回溯法)实验报告姓名:学号:指导老师:一.算法设计名称:0-1背包问题(回溯法)二.实验内容问题描述:给定n 种物品和一背包。
物品i 的重量是w i ,其价值为v i ,背包的容量为C 。
问应如何选择装入背包的物品,使得装入背包中物品的总价值最大?在选择装入背包的物品时,对每种物品i 只有两种选择,即装入背包或不装入背包。
不能将物品装入背包多次,也不能只装入部分的物品。
三.实验目的1.运用回溯思想,设计解决上述问题的算法,找出最大背包价值的装法。
2.掌握回溯法的应用四.算法设计:问题求解思路1.由0-1背包问题的最优子结构性质,建立计算m[i][j]的递归式如下:i i i w j w j j i m i v w j i m j i m j i m <≤≥⎩⎨⎧-+---=0],1[]}[],1[],,1[max{),(2.查找装入背包物品的回溯函数:从0-1二叉树的根开始搜索:若是叶子节点,则判断此时的价值是否比当前最优的价值大,否则将之替换,并获得最优解向量且返回;若不是叶子节点,则向左右子树搜索,先改变当前的数据状态,递归的调用自己,然后恢复数据状态表示回溯。
3.边界函数bound主要是当还未搜索到叶子节点时,提前判断其子树是否存可能存在更优的解空间,否则进行回溯,即裁剪掉子树的解空间。
关键数据结构及函数模块:(Backtrack.h )#ifndef __BACKTRACK_H__#define __BACKTRACK_H__class BP_01_P{public:∑=ni i i x v 1max ⎪⎩⎪⎨⎧≤≤∈≤∑=n i x C x w i n i i i 1},1,0{1BP_01_P(int w,int n):m_Sum_weitht(0),m_Number(0) {m_Sum_weitht=w;m_Number=n;bestHav=0;bestVal=0;curVal=0;curHav=0;m_hav=new int[n];m_val=new int[n];temop=new int[n];option=new int[n];}~BP_01_P(){delete []m_hav;delete []m_val;delete []temop;delete []option;}void traceBack(int n);int bound(int n);void printBestSoulation();int *m_hav;//每个物品的重量int *m_val;//每个物品的价值int *temop;//01临时解int *option;//01最终解int bestHav;//最优价值时的最大重量int bestVal;//最优的价值int curVal;//当前的价值int curHav;//当前的重量private:int m_Sum_weitht;//背包的总容量int m_Number;//物品的种类};#endif __BACKTRACK_H__五:主要的算法代码实现:(Backtrack.cpp)边界函数:bound( )int BP_01_P::bound(int n){int hav_left=m_Sum_weitht-curHav;int bo=curVal;while(n<m_Number && m_hav[n]<=hav_left){hav_left-=m_hav[n];bo+=m_val[n];n++;}if(n<m_Number){bo+=m_val[n]*hav_left/m_hav[n];//bo+=hav_left;}return bo;}回溯递归函数:traceBack( )void BP_01_P::traceBack(int n){if(n>=m_Number){if(curVal>=bestVal){bestVal=curVal;for(int i=0;i<n;i++){option[i]=temop[i];}return ;}}if(curHav+m_hav[n]<=m_Sum_weitht)//向左子树搜索 {curHav=curHav+m_hav[n];curVal=curVal+m_val[n];temop[n]=1;//标记要选择这个物品traceBack(n+1);curHav=curHav-m_hav[n];curVal=curVal-m_val[n];}if(bound(n+1)>bestVal)//向右子树搜索{temop[n]=0;//标记要丢弃这个物品traceBack(n+1);}}主控函数:(main.cpp)#include <iostream>#include "Backtrack.h"using namespace std;int main(){int number,weigth;cout<<"包的总容量:";cin>>weigth;cout<<"物品的种类:";cin>>number;BP_01_P *ptr=new BP_01_P(weigth,number);cout<<"各种物品的重量:"<<endl;for(int i=0;i<number;i++)cin>>ptr->m_hav[i];cout<<"各种物品的价值:"<<endl;for(i=0;i<number;i++)cin>>ptr->m_val[i];ptr->traceBack(0);ptr->printBestSoulation();cout<<"总重量:"<<ptr->bestHav<<"\t总价值:"<<ptr->bestVal<<endl;return 0;}六:算法分析采用回溯法解决0-1背包问题,明显比动态规划法更优良。
P01: 01背包问题题目有N件物品和一个容量为V的背包。
第i件物品的费用是c[i],价值是w[i]。
求解将哪些物品装入背包可使价值总和最大。
基本思路这是最基础的背包问题,特点是:每种物品仅有一件,可以选择放或不放。
用子问题定义状态:即f[i][v]表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。
则其状态转移方程便是:f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}这个方程非常重要,基本上所有跟背包相关的问题的方程都是由它衍生出来的。
所以有必要将它详细解释一下:“将前i件物品放入容量为v的背包中”这个子问题,若只考虑第i件物品的策略(放或不放),那么就可以转化为一个只牵扯前i-1件物品的问题。
如果不放第i件物品,那么问题就转化为“前i-1件物品放入容量为v的背包中”,价值为f[i-1][v];如果放第i件物品,那么问题就转化为“前i-1件物品放入剩下的容量为v-c[i]的背包中”,此时能获得的最大价值就是f[i-1][v-c[i]]再加上通过放入第i件物品获得的价值w[i]。
优化空间复杂度以上方法的时间和空间复杂度均为O(VN),其中时间复杂度应该已经不能再优化了,但空间复杂度却可以优化到O。
先考虑上面讲的基本思路如何实现,肯定是有一个主循环i=1..N,每次算出来二维数组f[i][0..V]的所有值。
那么,如果只用一个数组f[0..V],能不能保证第i次循环结束后f[v]中表示的就是我们定义的状态f[i][v]呢?f[i][v]是由f[i-1][v]和f[i-1][v-c[i]]两个子问题递推而来,能否保证在推f[i][v]时(也即在第i次主循环中推f[v]时)能够得到f[i-1][v]和f[i-1][v-c[i]]的值呢?事实上,这要求在每次主循环中我们以v=V..0的顺序推f[v],这样才能保证推f[v]时f[v-c[i]]保存的是状态f[i-1][v-c[i]]的值。
遗传算法求解01背包问题一、问题描述01背包问题属于组合优化问题的一个例子,求解01背包问题的过程可以被视作在很多可行解当中求解一个最优解。
01背包问题的一般描述如下:给定n个物品和一个背包,物品i的重量为W i,其价值为V i,背包的容量为C。
选择合适的物品装入背包,使得背包中装入的物品的总价值最大。
注意的一点是,背包内的物品的重量之和不能大于背包的容量C。
在选择装入背包的物品时,对每种物品i只有两种选择:装入背包或者不装入背包,即只能将物品i装入背包一次。
称此类问题为0/1背包问题。
01背包问题是NP问题,传统的解决方法有动态规划法、分支界限法、回溯法等等。
传统的方法不能有效地解决01背包问题。
遗传算法(Genetic Algorithms)则是一种适合于在大量的可行解中搜索最优(或次优)解的有效算法。
二、遗传算法1、遗传算法的基本思想遗传算法的搜索从一个被称作种群的候选解集开始,新的种群由旧的种群中产生以期得到更好的种群。
从旧种群中按照解的适应度来选择解以产生新的解;适应度越大,解被选择生成后代的机率也越大。
这个从已有种群中选择双亲并产生后代的迭代过程持续到遗传算法的停止条件满足为止。
2、遗传算法的基本元素。
遗传算法由以下几个原素组成:由染色体组成的种群,根据适应度进行选择以及交叉产生后代。
三、用遗传算法求解01背包问题1、01背包问题中染色体的表示。
用向量X来表示染色体,X = {x1,x2,……,x n}。
,x i∈{0,1},x i=1表示物品i装入了背包,x i =0表示物品i未装入背包。
每个染色体对应其当前装入背包的物品的总价值和总重量。
背包中物品的中价值代表了该物品的适应度。
程序中定义了这样的一个结构来表示染色体:typedef struct{int Weight; //染色体代表的物品的总重量int Fitness; //染色体代表的物品的价值(适应度)int Gene[NUMG]; //用元素取值于定义域{0,1}的数组表示染色体。
01背包问题回溯法c语言背包问题是一个很经典的动态规划问题,其中最常见的一种形式就是 01 背包问题。
在该问题中,给定一组物品的重量和价值,以及一个背包的容量限制,要求选择一些物品,使得在不超过背包容量的前提下,背包中物品的总价值最大。
这里我们将讨论如何使用回溯法解决01 背包问题,使用C 语言进行编程实现。
首先,我们需要定义问题的数据结构。
我们可以使用一个数组来表示不同物品的重量和价值,背包的容量可以通过一个常量来表示。
```c#define N 5 // 物品的个数#define MAX_WEIGHT 10 // 背包的容量int weights[N] = {2, 3, 4, 5, 9}; // 物品的重量int values[N] = {3, 4, 5, 8, 10}; // 物品的价值int bestValue = 0; // 最优解的价值int bestSelection[N]; // 最优解中物品的选择情况```接下来,我们可以定义一个递归函数来实现回溯法。
该函数将遍历所有可能的物品选择情况,并更新当前的最优解。
```cvoid backtrack(int depth, int weight, int value, int selection[]) {if (depth == N) {if (weight <= MAX_WEIGHT && value > bestValue) {bestValue = value;for (int i = 0; i < N; i++) {bestSelection[i] = selection[i];}}return;}// 不选择当前物品selection[depth] = 0;backtrack(depth + 1, weight, value, selection);// 选择当前物品selection[depth] = 1;backtrack(depth + 1, weight + weights[depth], value + values[depth], selection); }```最后,我们可以在主函数中调用回溯函数,得到最优解。
分支限界法——01背包问题12软工028 胡梦颖一、问题描述0-1背包问题:给定n种物品和一个背包。
物品i的重量是Wi,其价值为Vi,背包的容量为C。
应如何选择装入背包的物品,使得装入背包中物品的总价值最大?在选择装入背包的物品时,对每种物品i只有2种选择,即装入背包或不装入背包。
不能将物品i装入背包多次,也不能只装入部分的物品i。
二、问题分析分支限界法类似于回溯法,也是在问题的解空间上搜索问题解的算法。
一般情况下,分支限界法与回溯法的求解目标不同。
回溯法的求解目标是找出解空间中满足约束条件的所有解,而分支限界法的求解目标则是找出满足约束条件的一个解,或是在满足约束条件的解中找出使某一目标函数值达到极大或极小的解,即在某种意义下的最优解。
由于求解目标不同,导致分支限界法与回溯法对解空间的搜索方式也不相同。
回溯法以深度优先的方式搜索解空间,而分支限界法则以广度优先或以最小耗费优先的方式搜索解空间。
分支限界法的搜索策略是,在扩展结点处,先生成其所有的儿子结点(分支),然后再从当前的活结点表中选择下一扩展结点。
为了有效地选择下一扩展结点,加速搜索的进程,在每一个活结点处,计算一个函数值(限界),并根据函数值,从当前活结点表中选择一个最有利的结点作为扩展结点,使搜索朝着解空间上有最优解的分支推进,以便尽快地找出一个最优解。
这种方式称为分支限界法。
人们已经用分支限界法解决了大量离散最优化的问题。
三.源代码#include <stdio.h>#include<malloc.h>#define MaxSize 100 //结点数的最大值typedef struct QNode{float weight;float value;int ceng;struct QNode *parent;bool leftChild;}QNode,*qnode;typedef struct{qnode Q[MaxSize];int front,rear;}SqQueue; //存放结点的队列SqQueue sq;float bestv=0; //最优解int n=0; //实际物品数float w[MaxSize]; //物品的重量float v[MaxSize]; //物品的价值int bestx[MaxSize]; // 存放最优解qnode bestE;void InitQueue(SqQueue &sq ) //队列初始化{sq.front=1;sq.rear=1;}bool QueueEmpty(SqQueue sq) //队列是否为空{if(sq.front==sq.rear)return true;elsereturn false;}void EnQueue(SqQueue &sq,qnode b) //入队{if(sq.front==(sq.rear+1)%MaxSize){printf("队列已满!");return;}sq.Q[sq.rear]=b;sq.rear=(sq.rear+1)%MaxSize;} qnode DeQueue(SqQueue &sq) //出队{qnode e;if(sq.front==sq.rear){printf("队列已空!");return 0;}e=sq.Q[sq.front];sq.front=(sq.front+1)%MaxSize;return e;}void EnQueue1(float wt,float vt, int i ,QNode *parent, bool leftchild) {qnode b;if (i==n) //可行叶子结点{ if (vt==bestv){ bestE=parent;bestx[n]=(leftchild)?1:0;}return;}b=(qnode)malloc(sizeof(QNode)); //非叶子结点b->weight=wt;b->value=vt;b->ceng=i;b->parent=parent;b->leftChild=leftchild;EnQueue(sq,b);}void maxLoading(float w[],float v[],int c){float wt=0;float vt=0;int i=1; //当前的扩展结点所在的层float ew=0; //扩展节点所相应的当前载重量float ev=0; //扩展结点所相应的价值qnode e=NULL;qnode t=NULL;InitQueue(sq);EnQueue(sq,t); //空标志进队列while (!QueueEmpty(sq)){wt=ew+w[i];vt=ev+v[i];if (wt <= c){if(vt>bestv)bestv=vt;EnQueue1(wt,vt,i,e,true); // 左儿子结点进队列} EnQueue1(ew,ev,i,e,false); //右儿子总是可行;e=DeQueue(sq); // 取下一扩展结点if (e == NULL){if (QueueEmpty(sq))break;EnQueue(sq,NULL); // 同层结点尾部标志e=DeQueue(sq); // 取下一扩展结点i++;}ew=e->weight; //更新当前扩展结点的值ev=e->value;}printf("最优取法为:\n");for( int j=n-1;j>0;j--) //构造最优解{bestx[j]=(bestE->leftChild?1:0);bestE=bestE->parent;}for(int k=1;k<=n;k++){if(bestx[k]==1)printf("物品%d:重量:%.1f,价值:%.1f\n",k,w[k],v[k]);}printf("最大价值为:%.1f\n",bestv);}void main(){int c;float ewv[MaxSize];printf("请输入背包的最大容量v:");scanf("%d",&c);printf("请输入物品总数n:");scanf("%d",&n);printf("请输入物品的重量和单位重量价值:\n");for(int i=1;i<=n;i++){printf("第%d件物品:",i);scanf("%f%f",&w[i],&ewv[i]);v[i]=w[i]*ewv[i];}maxLoading(w,v,c);}五.实验结果。
“遗传算法”解决“背包问题”遗传算法基本思想:1) ⼀个种群有多个个体,每个个体有染⾊体和对应的基因为了繁殖进⾏:2) 选择:在残酷的世界中,适者⽣存,优胜略汰。
3) 重组:染⾊体交叉,基因重组4) 突变:染⾊体上的基因⼩概率的突变(⼀般给⼩数点后两位)背包问题:背包只能容得下⼀定重量b的物品,物品有m种,每种物品有⾃⼰的重量w(i)和价值v(i)(0<i<=m),从这些物品中选择装⼊背包,是背包不超过重量b,但价值⼜要最⼤。
运⽤动态规划,分⽀限界都可以达到效果,但不佳。
我⽤遗传算法解决:⼀般⼈有多条染⾊体,但对于背包问题,⼀个解我们将看成⼀个个体,所以,⼀个个体只有⼀个染⾊体,⼀个染⾊体对应多个基因。
如:100101010100111 表⽰装⼊背包的可能解。
(具体情况具体分析)遗传所做准备:1) ⽤0表⽰“不选择装⼊”,1表⽰“装⼊”,形成⼀条基因链;100101010100111则表⽰“15种物品”装⼊或不装⼊背包的可能解。
------- 此处⽤chrom[]存放基因,代表染⾊体2) ⼀个基因对应⼀个个体。
------- 此处⽤Population类或结构体声明其含有chrom[]等信息3) 可能的解有很多,构成⼀个种群。
------- ⽤Population类定义⼀个数组代表个体构成的种群newPop[]:存放新⽣代,oldPop[]:存放上⼀代4) 适应度:适应度和⽬标函数是正相关的,所以需要物品价值和重量。
------- fitness,weight包含在Population类中最⼤适应度:maxFitness,最⼩适应度:minFitness,总适应度:sumFitness,(帮助求突变和交叉的染⾊体)平均适应度:avgFitness遗传算法的函数:基本:1) InitPop() 初始化个体,使每个个体都有基因组2) Statistics(*pop) 计算适应度(最⼤,最⼩,总的,平均的)3) Selection(*pop) 通过选择种群中符合要求的⽗母去繁殖新代,返回这对⽗母的位置4) crossover(*parent1,*parent2,pos) 传⼊要改的个体位置,随机产⽣交叉位置,⽤优良⽗母繁殖优良后代并替代传⼊个体位置5) mutation(i) i为基因组基因的位置,逐个基因看是否要变异6) generation() 对个体进⾏判断,若不符合要求,进⾏选择,重组,突变。
基于遗传算法的0-1背包问题的求解摘要:一、前言组合优化问题的求解方法研究已经成为了当前众多科学关注的焦点,这不仅在于其内在的复杂性有着重要的理论价值,同时也在于它们能在现实生活中广泛的应用。
比如资源分配、投资决策、装载设计、公交车调度等一系列的问题都可以归结到组合优化问题中来。
但是,往往由于问题的计算量远远超出了计算机在有效时间内的计算能力,使问题的求解变为异常的困难。
尤其对于NP 完全问题,如何求解其最优解或是近似最优解便成为科学的焦点之一。
遗传算法已经成为组合优化问题的近似最优解的一把钥匙。
它是一种模拟生物进化过程的计算模型,作为一种新的全局优化搜索算法,它以其简单、鲁棒性强、适应并行处理以及应用范围广等特点,奠定了作为21世纪关键智能计算的地位。
背包问题是一个典型的组合优化问题,在计算理论中属于NP-完全问题, 其计算复杂度为)2(O n ,传统上采用动态规划来求解。
设w[i]是经营活动 i 所需要的资源消耗,M 是所能提供的资源总量,p[i]是人们经营活动i 得到的利润或收益,则背包问题就是在资源有限的条件下, 追求总的最大收益的资源有效分配问题。
二、问题描述背包问题( Knapsack Problem)的一般提法是:已知n 个物品的重量(weight )及其价值(或收益profit )分别为0>i w 和0>i p ,背包的容量(contain )假设设为0>i c ,如何选择哪些物品装入背包可以使得在背包的容量约束限制之内所装物品的价值最大?该问题的模型可以表示为下述0/1整数规划模型:目标函数:∑==ni i i n x c x x x f 121),,(max Λ⎪⎩⎪⎨⎧=∈≤∑=),2,1(}1,0{t .s 1n i x p x w i n i i i i Λ (*)式中i x 为0-1决策变量,1=i x 时表示将物品i 装入背包中,0=i x 时则表示不将其装入背包中。
三、求解背包问题的一般方法解决背包问题一般是采取动态规划、递归回溯法和贪心方法。
动态规划可以把困难得多阶段决策变换为一系列相互联系比较容易的单阶段问题。
对于背包问题可以对子过程用枚举法求解,而且约束条件越多,决策的搜索范围越小,求解也越容易。
它的主要缺点是用数值方法求解时会随着状态变量的个数呈指数级的增长,往往对于求解背包问题的实际问题是不现实的。
使用递归回溯法解决背包问题的优点在于它算法思想简单, 而且它能完全遍历搜索空间,肯定能找到问题的最优解;但是由于此问题解的总组合数有n 2个,因此,随着物件数 n 的增大,其解的空间将以n2级增长,当 n 大到一定程度上,用此算法解决背包问题将是不现实的。
使用贪心方法求解时计算的复杂度降低了很多,但是往往难以得到最优解,有时所得解与最优解相差甚远。
因此, 我们可以探索使用遗传算法解决物件数较大的背包问题。
四、遗传算法简介遗传算法( Genetic Algorithms ,GA) 是在1975 年首次由美国密西根大学的D 。
J 。
Holland 教授和他的同事们借鉴生物界达尔文的自然选择法则和孟德尔的遗传进化机制基础之上提出的。
经过近30年的研究、应用,遗传算法已被广泛地应用于函数优化、机器人系统、神经网络学习过程、模式识别、图象处理、工业优化控制等领域。
遗传算法是将问题的每一个可能性解看作是群体中的一个个体(染色体),并将每一个染色体编码成串的形式,再根据预定的目标函数对每个个体进行评价,给出一个适应值。
算法将根据适应度值进行它的寻优过程,遗传算法的寻优过程是通过选择、杂交和变异三个遗传算子来具体实现的。
它的搜索能力由选择算子和杂交算子决定,变异算子则保证了算法能够搜索到问题空间的尽可能多的点,从而使其具有搜索全局最优的能力。
遗传算法的高效性和强壮性可由Holland 提出的模式定理( Schema Therem) 和隐式并行性得以解释。
在遗传算法中,定义长度较短、低阶且适应值超过平均适应值的模式在群体中数目的期望值按指数递增,这个结论称为遗传算法的基本定理。
遗传算法是通过定义长度短、确定位数少、适应度值高的模式的反复抽样、组合来寻找最佳点,称这些使遗传算法有效工作的模式为积木块,是遗传算法构造答案的基本材料。
但归根到底,要使遗传算法有效工作必须按照遗传算法的模式定理(或积木块假设) 根据具体问题设计合理的编码方案。
在运行遗传算法程序时,需要对一些参数作事先选择,它们包括种群的大小、染色体长、交叉率、变异率、最大进化代数等,这些参数对GA 的性能都有很重要的影响。
在试验中参数一般选取如下:种群大小N= 20~100 ,交叉概率c p = 0.4 ~0.9 ,变异概率m p = 0.001~0.1 ,最大进化代数maxgen = 100~500。
遗传算法是具有“生成+检测”的迭代过程的搜索算法。
它的基本处理流程如图1所示。
图1、遗传算法的基本流程遗传算法的基本流程描述如下:初始化种群评估种群中个体适应度选 择编 码交 叉变 异演化(1)编码:将解空间的解数据进行二进制编码,表达为遗传空间的基因型串(即染色体)结构数据,如将数据9编码为“1001”;(2)初始化种群:定义整数pop_size 作为染色体的个数,并且随机产生pop_size个染色体作为初始种群;(3)评估种群中个体适应度:评价函数对种群中的每个染色体(chromosome )求得其个体适应度)(fitness f i ;(4)选择:选择把当前群体中适应度较高的个体按某种规则或者模型遗传到下一代种群中,这里所用的规则是:染色体在种群中被选择的可能性与其个体的适应度的大小成正比;(5)交叉:定义参数c p 作为交叉操作的概率,由(4)选择得到的两个个体以概率c p 交换各自的部分染色体,得到新的两个个体;(6)变异:定义参数m p 作为变异操作的概率,由(5)得到每个个体中的每个基因值都以概率m p 进行变异;(7)演化:经过选择、交叉和变异操作,得到一个新的种群,对上述步骤经过给定的循环次数(maxgen )的种群演化,遗传算法终止。
五、背包问题的遗传算法求解描述基于背包问题的模型(*),我们设计了针对于背包问题的染色体编码方法:将待求解的各量X 表示成长为n 的二进制字符串]j [x ,j=1,2, …,n 。
0]j [x =表示物体j 不放入背包内,1]j [x =表示物体j 放入背包内。
例如:111001100…000111代表一个解,它表示将第1、2、3、6、7…n-2,n-1,n 号物体放入背包中,其它的物体则不放入。
根据遗传算法的基本流程,我们确定了求解背包问题的遗传算法:步骤1、初始化过程1.1 确定种群规模popsize 、杂交概率c p 、变异概率m p 、染色体长度lchrom 及最大进化代数maxgen ;1.2 读入背包问题的相关信息,如每个物体的重量weight[j]、每个物体的收益profit[j]和背包的容量contain ,其中1)lchrom (,1,0j -=Λ; 1.3 取1)lchrom (,1,0j )1,0(u ]j [x -==Λ,其中)1,0(u 表示0-1整数的均匀分布函数,即随机地生成数0或1,生成的]j [x 串即可看为一个染色体个体。
若不满足模型(*)的约束条件,则拒绝接受,由1.2重新生成一个新的染色体个体chrom ;如果产生的染色体可行,则接受它作为种群的一名成员,经过有限次的1.2抽样后,得到popsize 个可行的染色体chrom ,形成新的种群。
1.4 置种群的代数gen=0;步骤2、计算种群中个体适应度以及统计种群适应度情况2.1 按照下列公式计算种群中个体适应度:)1(1lchrom 0j ]j [chrom *]j [weight weight ∑-==;)2(containifweight )contain weight (*alpha ]j [chrom *]j [profit contain ifweight ]j [chrom *]j [profit fitness 1lchrom 0j 1lchrom 0j ⎪⎪⎩⎪⎪⎨⎧>--≤=∑∑-=-= 公式(2)的下半部分即为适应度的惩罚函数,其中参数 1.0alpha >。
2.2 按公式(3)计算种群的总体适应度,)3(]i [fitness sumfitness 1popsize 0i ∑-==并且按照排序的方法统计出种群中的最大、最小适应度的染色体个体,分别标记为maxpop 、minpop ;步骤3、选择操作3.1 生成一个随机数rand_Number ,要求1_0<<Nuber rand ;3.2 按照赌轮法选择个体,赌轮法的算法描述如下:int selection( ){i=0; //个体的编号sum=0; //部分个体适应度的累加和//根据随机数和群体的总适应度确定赌轮的位置wheel-pos=rand_Number*sufitness;while sum<wheel-pos && i<=popsize{ i=i+1;sum=sum+fitness[i]; //fitness 为第i 个个体的适应度}return i-1; //选择了个体i-1}3.3 重复两次操作3.1、3.2,生成两个个体作为交叉操作的父代;步骤四、交叉操作4.1 根据事先定义好的交叉概率c p ,为了确定是否进行交叉操作,则生成[0,1]的随机数pp ,若c p pp <,则进行4.2交叉操作,否则将两个父代保留为下一代的两个个体;4.2 随机生成]1lchrom ,[0-的整数作为交叉点,对两个父代个体交叉生成新的两个个体;4.3 重复pop_size/2次4.1、4.2便可生成pop_size 个个体组成新的种群; 步骤五、 变异操作5.1 根据事先定义好的变异概率m p ,为了确定新种群上的每个个体上的每个基因是否进行变异操作,则生成[0,1]的随机数pp ,若m p pp <,则进行5.2变异操作,否则基因不变异;5.2 基因变异操作为原基因若为1,则新基因则变异为0,若原基因为0,则新基因变异为0;步骤6、 演化6.1 按步骤2的方法计算新种群的个体适应度和总体适应度情况,尤其是找出新种群中最大适应度的个体和最小适应度的个体;6.2 若旧种群的最大个体适应度〉新种群的最大个体适应度,把旧种群的最大适应度的个体代替新种群中的最小适应度的个体,否则进行6.3;6.3 种群的代数gen=genm+1,若gen 〉Maxgen ,则结束种群的演化,否则转到步骤2。