遗传算法解决01背包问题

数学建模遗传算法例题数学建模中，遗传算法是一种基于进化思想的优化算法，可以应用于复杂的优化问题中。

本文将介绍一些遗传算法的例题，帮助读者更好地理解遗传算法的应用。

例题一：背包问题有一个体积为V的背包和n个物品，第i个物品的体积为vi，价值为wi。

求这个背包最多能装多少价值的物品。

遗传算法的解决步骤：1. 初始化种群：随机生成一定数量的个体作为初始种群。

2. 适应度函数：将每个个体代入适应度函数，计算其适应度值。

3. 选择：根据每个个体的适应度值，选择一定数量的个体进入下一代。

4. 交叉：对被选中的个体进行交叉操作，生成新的个体。

5. 变异：对新的个体进行变异操作，引入新的基因。

6. 重复以上步骤，直到符合终止条件。

在背包问题中，适应度函数可以定义为：背包中物品的总价值。

交叉操作可以选择单点交叉或多点交叉，变异操作可以选择随机变异或非随机变异。

例题二：旅行商问题有n个城市，旅行商需要依次经过这些城市，每个城市之间的距离已知。

求旅行商经过所有城市的最短路径。

遗传算法的解决步骤：1. 初始化种群：随机生成一定数量的个体作为初始种群，每个个体代表一种旅行路线。

2. 适应度函数：将每个个体代入适应度函数，计算其适应度值。

3. 选择：根据每个个体的适应度值，选择一定数量的个体进入下一代。

4. 交叉：对被选中的个体进行交叉操作，生成新的个体。

5. 变异：对新的个体进行变异操作，引入新的基因。

6. 重复以上步骤，直到符合终止条件。

在旅行商问题中，适应度函数可以定义为：旅行商经过所有城市的总距离。

交叉操作可以选择顺序交叉或部分映射交叉，变异操作可以选择交换或反转基因序列。

总结：遗传算法是一种强大的优化算法，可以应用于多种复杂的优化问题中。

在数学建模中，遗传算法的应用也越来越广泛。

本文介绍了背包问题和旅行商问题的遗传算法解决步骤，希望对读者有所帮助。

遗传算法解决01背包问题2015 ～2016 学年第二学期学生姓名专业学号2016年 6 月目录一：问题描述 (3)二：遗传算法原理及特点 (3)三：背包问题的遗传算法求解 (3)1.文字描述 (3)2.遗传算法中的抽象概念在背包问题的具体化 (3)3.算法求解的基本步骤 (4)四：算法实现 (4)1.数据结构 (4)2.部分代码 (5)五：结论 (8)六：参考文献 (8)一、问题描述0-1背包问题属于组合优化问题的一个例子，求解0-1背包问题的过程可以被视作在很多可行解当中求解一个最优解。

01背包问题的一般描述如下：给定n个物品和一个背包，物品i的重量为Wi，其价值为Vi，背包的容量为C。

问应如何选择合适的物品装入背包，使得背包中装入的物品的总价值最大。

注意的一点是，背包内的物品的重量之和不能大于背包的容量C。

在选择装入背包的物品时，对每种物品i只有两种选择：即装入背包或者不装入背包，不能讲物品i装入背包多次，也不能只装入部分的物品，称此类问题为0/1背包问题。

二、遗传算法原理及特点遗传算法（Genetic Algorithm）是模拟达尔文生物进化论的自然选择和遗传学机理的生物进化过程的计算模型，是一种通过模拟自然进化过程搜索最优解的方法。

遗传算法有着鲜明的优点：(1)遗传算法的操作对象是一组可行解,而非单个可行解;搜索轨道有多条,而非单条,因而具有良好的并行性.(2)遗传算法只需利用目标的取值信息,而无需递度等高价值信息,因而适用于任何规模,高度非线形的不连续多峰函数的优化以及无解析表达式的目标函数的优化,具有很强的通用性.(3)遗传算法择优机制是一种“软”选择,加上良好的并行性,使它具有良好的全局优化性和稳健性.(4)遗传算法操作的可行解集是经过编码化的(通常采用二进制编码),目标函数解释为编码化个体(可行解)的适应值,因而具有良好的可操作性与简单性.三、背包问题的遗传算法求解1、文字描述0-1背包问题传统的解决方法有动态规划法、分支界限法、回溯法等等。

背包问题报告小组成员：张灿、吴雪涛、高坤、占强、习慧平小组分工情况小组成员查找资料制作ppt 编写程序讲解ppt 制作报告张灿ⅴⅴⅴⅴⅴ吴雪涛ⅴ高坤ⅴⅴ占强ⅴ习慧平ⅴ背包问题一、背包问题的历史由来它是在1978年由Merkel和Hellman提出的。

它的主要思路是假定某人拥有大量物品，重量各不同。

此人通过秘密地选择一部分物品并将它们放到背包中来加密消息。

背包中的物品中重量是公开的，所有可能的物品也是公开的，但背包中的物品是保密的。

附加一定的限制条件，给出重量，而要列出可能的物品，在计算上是不可实现的。

背包问题是熟知的不可计算问题，背包体制以其加密，解密速度快而其人注目。

在解决大量的复杂组合优化问题时，它常常作为一个子问题出现，从实际的观点看，许多问题可以用背包问题来描述，如装箱问题，货仓装载，预算控制，存储分配，项目选择决策等，都是典型的应用例子。

随着网络技术的不断发展，背包公钥密码在电子商务中的公钥设计中也起着重要的作用。

然而当问题的规模较大时，得到最优解是极其困难的。

但是，大多数一次背包体制均被破译了，因此现在很少有人使用它。

二、背包问题的描述背包问题(Knapsack problem)是一种组合优化的NP完全问题。

问题可以描述为：给定一组物品，每种物品都有自己的重量和价格，在限定的总重量内，我们如何选择，才能使得物品的总价格最高。

问题的名称来源于如何选择最合适的物品放置于给定背包中。

相似问题经常出现在商业、组合数学，计算复杂性理论、密码学和应用数学等领域中。

也可以将背包问题描述为决定性问题，即在总重量不超过W的前提下，总价值是否能达到V？三、背包问题的定义我们有n种物品，物品j的重量为w j，价格为p j。

我们假定所有物品的重量和价格都是非负的。

背包所能承受的最大重量为W。

如果限定每种物品只能选择0个或1个，则问题称为0-1背包问题。

可以用公式表示为：maximizesubject to如果限定物品j最多只能选择b j个，则问题称为有界背包问题。

遗传算法求解背包问题程序实现一、背包问题描述背包问题是著名的NP 完备类困难问题,对这个问题的求解前人已经研究出了不少的经典的方法,对该问题确实能得到很好的结果。

近年来蓬勃发展起来的遗传算法已被广泛地应用于优化领域,其全局最优性、可并行性、高效性在函数优化中得到了广泛地应用遗传算法克服了传统优化方法的缺点,借助了大自然的演化过程,是多线索而非单线索的全局优化方法,采用的是种群和随机搜索机制. 本程序将遗传算法应用于背包问题。

二、实验程序1、编程语言：C++2、开发环境：Microsoft Visual Studio 20053、程序整体流程：步1初始化过程1. 1确定种群规模scale、杂交概率pc、变异概率pm、染色体长度chN及最大进化代数maxgen。

1. 2取x1′(0) = u (0 ,1) , x2′(0) = u (0 ,1) , …, xchN′(0) = u (0 ,1) ,其中函数u (0 ,1) 表示随机地产生数0 或1 ,则x (0) = ( x1 (0) , x2 (0) ,⋯, xN (0) ) .若不满足约束条件,则拒绝接受. 由(1. 2) 重新产生一个新的染色体; 如果产生的染色体可行,则接受它作为种群的一名成员,经过有限次抽样后, 得到scale个可行的染色体xj (0) , j =1 ,2 , ⋯, M ,设xj (0) 的染色体编码为vj (0) ,并记为v (0) = ( v1 (0) , ⋯, vchN (0) ) .1. 3计算各个染色体的适值1. 4 置k = 0步2选择操作2. 1采用转轮法选择下一代。

.步3杂交变异操作3. 1 事先定义杂交操作的概率pc ,为确定杂交操作的父代,从j = 1 到M 重复以下过程:从[0 ,1 ] 中产生随机数r ,若r < pc ,则选择cj′( k)作为一个父代.3. 2 产生两个[1 , N ] 上的随机整数i 、j ,变异的结果为染色体vj′( k)的第i 位基因的值变为其第j 位基因的值,同样将染色体的vj′( k)第j 位基因的值变为其第i 位基因的值.3. 3 检验该染色体的可行性,若可行则作为变异的结果;如不可行,重复3. 2 直至该染色体可行.3. 4 事先定义变异概率pm ,对经过杂交操作的中间个体进行变异操作: ,如果r < pm ,则选择vi″( k) 作为变异的父代.3. 5 产生一个[1 , N ] 上的随机整数i ,及随机地产生数0 或1 , 记为b , 变异的结果为染色体vi″( k) 的第i 位基因的值变为b.3. 6 检验该染色体的可行性,若可行则作为变异的结果:如不可行,重复3. 5 直至该染色体可行.3. 7 计算新个体的适应值,并把它们同时放回,和步2 选择操作中剩余的个体一起构成新一代种群v ( k + 1) = { v1 ( k + 1) , v2 ( k + 1) , ⋯, vM ( k + 1) } .步4 终止检验如果达到最大进化代数maxgen 则终止演化,否则置k : = k + 1 ,转步2.4、程序流程图程序流程图5、程序代码1）主程序代码：KnapsacksProblem.cpp文件#include "GAonKP.h"#include <iostream>using namespace std;void main(){FILE* fp;CGAonKP gakp;int scale; //种群规模double MaxWeight; //背包允许最大财宝质量double pc; //杂交概率double pm; //变异概率int maxgen; //最大进化代数char filename[256];cout<<"遗传算法解决背包问题程序使用说明："<<endl;cout<<"1、该背包问题采用遗传算法"<<endl;cout<<"2、-1编码的方法，其中代表选中所对应的物品，代表不选中该物品"<<endl;cout<<"3、背包允许最带重量，种群规模（解空间大小），";cout<<"杂交概率，变异概率，最大进化代数需自己给";cout<<"定，程序会提示输入"<<endl;cout<<"4、程序提供一个输入示例"<<endl;cout<<"5、输入文件可加单行或多行注释"<<endl;cout<<"例如：#添加单行注释内容#"<<endl;cout<<"例如：#添加多行注释内容"<<endl;cout<<" 添加多行注释内容#"<<endl;cout<<"6、输入文件头位置需指定物品个数为int型数据。

遗传算法求解0-1背包问题一、问题描述给定n种物品和容量为C的背包。

物品i的重量是wi，其价值为vi。

问应如何选择装入背包的物品，使得装入背包中物品的总价值最大?二、知识表示1、状态表示（1）个体或染色体：问题的一个解，表示为n个比特的字符串，比特值为0表示不选该物品，比特值为1表示选择该物品。

（2）基因：染色体的每一个比特。

（3）种群：解的集合。

（4）适应度：衡量个体优劣的函数值。

2、控制参数（1）种群规模：解的个数。

（2）最大遗传的代数（3）交叉率：参加交叉运算的染色体个数占全体染色体的比例，取值范围一般为0.4～0.99。

（4）变异率：发生变异的基因位数所占全体染色体的基因总位数的比例，取值范围一般为0.0001～0.1。

3、算法描述（1）在搜索空间U上定义一个适应度函数f(x)，给定种群规模N，交叉率Pc和变异率Pm，代数T；（2）随机产生U中的N个个体s1, s2, …, sN，组成初始种群S={s1, s2, …, sN}，置代数计数器t=1；（3）计算S中每个个体的适应度f() ；（4）若终止条件满足，则取S中适应度最大的个体作为所求结果，算法结束。

（5）按选择概率P(xi)所决定的选中机会，每次从S中随机选定1个个体并将其染色体复制，共做N次，然后将复制所得的N个染色体组成群体S1；（6）按交叉率Pc所决定的参加交叉的染色体数c，从S1中随机确定c个染色体，配对进行交叉操作，并用产生的新染色体代替原染色体，得群体S2；（7）按变异率P m所决定的变异次数m，从S2中随机确定m个染色体，分别进行变异操作，并用产生的新染色体代替原染色体，得群体S3；（8）将群体S3作为新一代种群，即用S3代替S，t = t+1，转步3。

三、算法实现1、主要的数据结构染色体：用一维数组表示，数组中下标为i的元素表示第（i+1）个物品的选中状态，元素值为1，表示物品被选中，元素值为0表示物品不被选中。

种群：用二维数组表示，每一行表示一个染色体。

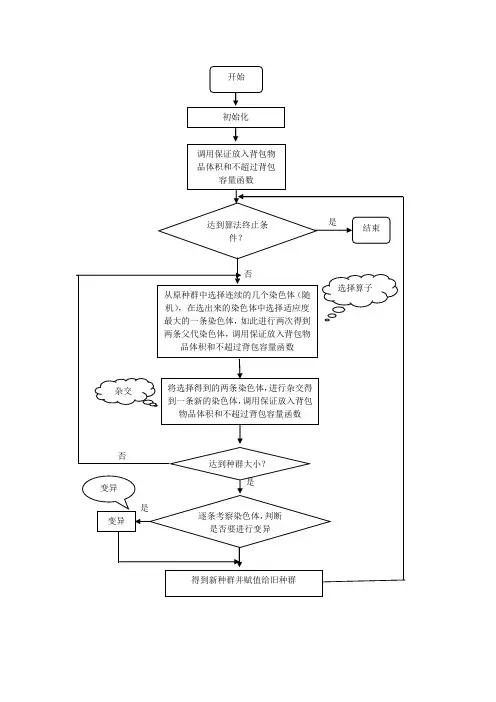
遗传算法的过程：初始化：将计划装入背包的每个物品看成一个二进制串的一位，为1表示放入该物品，为0表示不放入该物品。

初始种群的产生：初始化前对放入背包物品数的一个预测（背包容积/物品最大体积），接下来只要在种群每条染色体中保证有（背包容积/物品最大体积）个为1的位初始化就完成了。

选择：选择进行杂交的父代染色体，被选中的父代染色体总是若干个染色体中最优（适应度最高）的，来保证向优化的方向发展。

详细的选择方法：随机产生2个数：Chrom_Cross_From, Chrom_Cross_To,当然得采用一定的手段来保证前者比后者小。

从Chrom_Cross_From到Chrom_Cross_To这Chrom_Cross_To-Chrom_Cross_From+1条染色体中选择最优（适应度最大）的染色体作为父代之一。

需要进行两次选择得到杂交的两条父代染色体。

这样做可以保证算法不会过早收敛。

函数实现：Individual Select(int ChromSize,Individual Pop[]){int Num_Selected,i,j,Chrom_Selected_From,Chrom_Selected_To,temp;Individual *Chrom_Selected;do{Chrom_Selected_From=rand()%PopSize;Chrom_Selected_To=rand()%PopSize;if(Chrom_Selected_From>Chrom_Selected_To){temp=Chrom_Selected_From;Chrom_Selected_From=Chrom_Selected_To;Chrom_Selected_To=temp;}Num_Selected=Chrom_Selected_To-Chrom_Selected_From+1;}while(Num_Selected<=0);Chrom_Selected=new Individual[Num_Selected];for(i=0;i<Num_Selected;i++)Chrom_Selected[i].chrom=new int[ChromSize];for(i=0,j=Chrom_Selected_From;i<Num_Selected,j<Chrom_Selected_To+1;i++,j++){Chrom_Selected[i]=Pop[j];}Order_Best_First(ChromSize,Num_Selected,Chrom_Selected);Chrom_Selected[0].fitness=Fitness(Chrom_Selected[0].chrom,ChromSize);return Chrom_Selected[0];}杂交：将两次选择得到的父代染色体进行杂交得到一条新的染色体，作为较新种群（并非新的种群）的一条染色体，杂交直到较新种群的染色体数等于原种群的染色体数。

遗传算法经典实例遗传算法是一种从若干可能的解决方案中自动搜索最优解的算法，它可以用来解决各种复杂的优化问题，是进化计算的一种。

它的基本过程是：对初始种群的每个个体都估计一个适应度值，并从中选择出最优的个体来作为新一代的父本，从而实现进化的自然演化，经过几代的迭代最终得到最优的解。

在许多复杂的优化问题中，遗传算法能产生比其它方法更优的解。

下面，我们将列出几个典型的遗传算法经典实例，以供参考。

1.包问题背包问题可以分解为：在一定的物品中选择出最优的物品组合需求，在有限的背包中装入最大价值的物品组合。

针对这个问题，我们可以使用遗传算法来求解。

具体而言，首先，需要构建一个描述染色体的数据结构，以及每个染色体的适应度评估函数。

染色体的基本单元是每个物品，使用0-1二进制编码表示该物品是否被选取。

然后，需要构建一个初始种群，可以使用随机生成的方式，也可以使用经典进化方法中的锦标赛选择、轮盘赌选择或者较优概率选择等方法生成。

最后，使用遗传算法的基本方法进行迭代，直至得出最优解。

2.着色问题图着色问题是一个比较复杂的问题，它涉及到一个无向图的节点和边的颜色的分配。

其目的是为了使相邻的节点具有不同的颜色，从而尽可能减少图上边的总数。

此问题中每种可能的颜色可以看作一个个体。

染色体中每个基因对应一条边，基因编码可以表示边上节点的着色颜色。

求解这个问题，我们可以生成一个初始群体，通过计算它们的适应度量，然后使用遗传算法的基本方法进行迭代，直至收敛于最优解。

3.舍尔旅行商问题费舍尔旅行商问题是一个求解最短旅行路径的问题，它可以分解为：从起点到终点访问给定的一组城市中的每一个城市，并且回到起点的一个最短旅行路径的搜索问题。

用遗传算法求解费舍尔旅行商问题，通常每个个体的染色体结构是一个由城市位置索引构成的序列，每个索引对应一个城市，表示在旅行路径中的一个节点，那么该路径的适应度就是城市之间的距离和，通过构建一个初始种群，然后结合遗传算法中的进化方法，如变异、交叉等进行迭代，最终得出最优解。

毕业设计（论文）基于遗传算法求解背包问题院别专业名称班级学号学生姓名指导教师2012年6月15日基于遗传算法求解背包问题摘要背包问题(Knapsack problem)是一种组合优化的NP完全问题,本文首先介绍了基本遗传算法的基本原理、特点及其基本实现技术，接着针对背包问题，论述了遗传算法在编码表示和遗传算子（包括选择算子、交叉算子变异算子这三种算子）等方面的应用情况。

并且结合背包问题实例，给出了具体的编码方法，运行参数，群体大小，最大迭代次数，以及合适的遗传算子。

最后，简单说明了遗传算法在求解背包问题中的应用并对遗传算法解决背包问题的前景提出了展望。

关键词：背包问题，遗传算法，遗传算子Genetic Algorithm for KPAuthor：Yang DongTutor：Kong ZhiAbstractKP (Knapsack Problem) is a combinatorial optimization of NP - complete problem. The primary knowledge, characteristics and the basic techniques of GA are introduced firstly. The encoding model and genetic operators (including selection operation, crossover operation and mutation operation) solving KP are discussed secondly. Combined with examples of knapsack problem, we have given the specific encoding method, operating parameters, popsize, maxgeneration, and suitable genetic operator. At last, the application of genetic algorithm is simple presented, and the prospect for the future of genetic algorithm in solving KP has been given.Key Words: KP, genetic algorithm, genetic operators目录1绪论 (III)1.1 引言 (1)1.2 背包问题概述 (1)1.2.1 背包问题的描述 (2)1.2.2 研究背包问题的意义 (9)1.3 遗传算法 (10)1.3.1 遗传算法概述 (10)1.3.2 遗传算法的特点 (10)1.3.3 遗传算法的应用领域 (11)2遗传算法的基本原理 (13)2.1 基本流程 (14)2.2 编码 (14)2.3 适应度函数 (15)2.4 遗传算子 (15)2.4.1 选择算子 (15)2.4.2 交叉算子 (17)2.4.3 变异算子 (17)2.5 参数控制 (18)2.5.1 群体规模 (18)2.5.2 交叉概率 (18)2.5.3 变异概率 (18)2.6 算法结束条件控制 (19)3求解实现背包问题的遗传算法 (20)3.1 0_1背包问题中染色体的表示 (20)3.2 算法求解01背包问题时用到的参数 (20)3.3 选择操作 (20)3.4 交叉操作 (21)3.5 精英策略 (22)3.6 变异操作 (22)3.7 代际更新 (23)3.8 算法的终止 (23)3.9 仿真结果与测试 (24)3.9.1 不同交叉概率下所的测试结果 (25)3.9.2 极端数据对结果的影响 (27)3.9.3 仿真结果总结 (29)结论 (31)致谢 (32)参考文献 (33)附录 (34)1绪论1.1引言现代科学理论研究与实践中存在着大量与优化、自适应相关的问题，但除了一些简单的情况之外，人们对于大型复杂系统的优化和自适应问题仍然无能为力。

遗传算法求解0-1背包问题。

（步骤）#include "iostream.h"#include "iomanip.h"#include "stdlib.h"#include "math.h"#include "time.h"//定义问题的最大规模#define max 100//问题规模，即共有多少个包int packageNum;//每个包的重量int packageWeight[max];//每个包的价值int packageValue[max];//约束，背包的最大容量int limitWeight;//群体的规模int colonySize;//colonyState[i][k] 表示一个染色体//colonyState[1...colonySize][ 0|1 ] 表示一代群体int colonyState[max][2][max];// currAge 表示当前代的编号// (currAge+1)%2 表示下一代的编号int currAge = 0;//个体评价信息表typedef struct tagIndividualMsg{int index;int value;} IndividualMsg;IndividualMsg individualMsg[max];//////////////////////////////////////////////////////////// // 函数声明void printColonyState( int nextAge );//////////////////////////////////////////////////////////// //初始化群体void colonyInit(){int i , j;int w;for( i = 0 ; i < colonySize ; i++ ){//保证找到一个符合约束的染色体w = limitWeight + 1;while( w > limitWeight ){w = 0;for( j = 0 ; j < packageNum && w <= limitWeight ; j++ ){colonyState[i][currAge][j] = rand() % 2;w += packageWeight[j] * colonyState[i][currAge][j];}}}}//对个体进行评价int cmp( const void *a , const void *b ){IndividualMsg *x = (IndividualMsg *)a;IndividualMsg *y = (IndividualMsg *)b;return y->value - x->value;}void individualEstimate(){int i , j;for( i = 0 ; i < colonySize ; i++ ){individualMsg[i].index = i;individualMsg[i].value = 0;for( j = 0 ; j < packageNum ; j++ )individualMsg[i].value += packageValue[j] * colonyState[i][currAge][j]; }qsort( individualMsg , colonySize , sizeof(IndividualMsg) , cmp );}//终止循环的条件bool stopFlag(){//进行n 代进行后停止static int n = 50;if( n-- <= 0 )return true;elsereturn false;}//赌轮选择int gambleChoose(){int wheel[max] = { 0 };int i = colonySize - 1;int choose;wheel[i] = individualMsg[i].value;for( i-- ; i >= 0 ; i-- )wheel[i] = ( individualMsg[i].value + wheel[i+1] ) + colonySize * ( colonySize - i ); int seed = abs( wheel[0] - ( rand() % ( 2 * wheel[0] ) + 1 ) );choose = colonySize - 1;while( seed > wheel[choose] )choose--;// cout<<"----------------------------------------"<<endl;// cout<<"wheel :"<<endl;// for( i = 0 ; i < colonySize ; i++ )// cout<<setw(5)<<wheel[i];// cout<<endl;// cout<<"seed = "<<seed<<endl;// cout<<"choose "<<choose<<endl;return choose;}//交叉void across( int male , int female , int index ){int nextAge = (currAge+1)%2;int i , j , t;int acrossBit = rand() % (packageNum-1) + 1;for( j = 0 ; j < packageNum ; j++ ){colonyState[index][nextAge][j] =colonyState[individualMsg[male].index][currAge][j];colonyState[index+1][nextAge][j] =colonyState[individualMsg[female].index][currAge][j];}for( i = 0 ; i < acrossBit ; i++ ){t = colonyState[index][nextAge][i];colonyState[index][nextAge][i] = colonyState[index+1][nextAge][i];colonyState[index+1][nextAge][j] = t;}}//变异void aberrance( int index ){int seed , nextAge;nextAge = (currAge+1)%2;//只有1/3 的概率发生异变seed = rand() % ( packageNum * 3 );if( seed < packageNum )colonyState[index][nextAge][seed] = ( colonyState[index][nextAge][seed] + 1 ) % 2;}//处理死亡个体void dealDeath(){int i , j;int weight , w;int nextAge = (currAge+1)%2;for( i = 0 ; i < colonySize ; i++ ){weight = 0;for( j = 0 ; j < packageNum ; j++ )weight += packageWeight[j] * colonyState[i][nextAge][j];if( weight > limitWeight ){//随机生成新的个体w = limitWeight + 1;while( w > limitWeight ){w = 0;for( j = 0 ; j < packageNum && w <= limitWeight ; j++ ){colonyState[i][nextAge][j] = rand() % 2;w += packageWeight[j] * colonyState[i][nextAge][j];}}}}printColonyState( nextAge );}//最优个体保护void saveBest(){int i , j;int min , minp , value;int nextAge = ( currAge+1)%2;min = individualMsg[0].value;minp = -1;for( i = 0 ; i < colonySize ; i++ ){value = 0;for( j = 0 ; j < packageNum ; j++ )value += packageValue[j] * colonyState[i][nextAge][j]; if( value <= min ){min = value;minp = i;}}if( minp >= 0 ){for( j = 0 ; j < packageNum ; j++ ){colonyState[minp][nextAge][j] =colonyState[individualMsg[0].index][currAge][j];}}}//////////////////////////////////////////////////////////// void setProblem(){int i;packageNum = 5;int w[] = { 5 , 4 , 3 , 2 , 1 };int v[] = { 8 , 9 , 3 , 1 , 2 };for( i = 0 ; i < packageNum ; i++ ){packageWeight[i] = w[i];packageValue[i] = v[i];}limitWeight = 13;colonySize = 5;}void printProblem(){int i;cout<<"----------------------------------------"<<endl;cout<<"problem state:"<<endl;cout<<"packageNum = "<<packageNum<<endl;cout<<"limitWeight = "<<limitWeight<<endl;cout<<"Weight: ";for( i = 0 ; i < packageNum ; i++ )cout<<setw(3)<<packageWeight[i];cout<<endl;cout<<"Value: ";for( i = 0 ; i < packageNum ; i++ )cout<<setw(3)<<packageValue[i];cout<<endl;}void printColonyState( int k ){cout<<"----------------------------------------"<<endl;cout<<"colonyState-->";if( k == currAge )cout<<"currAge:"<<endl;elsecout<<"next age:"<<endl;int i , j;for( i = 0 ; i < colonySize ; i++ ){for( j = 0 ; j < packageNum ; j++ )cout<<setw(2)<<colonyState[i][k][j];cout<<endl;}}void printIndividualMsg(){int i;cout<<"----------------------------------------"<<endl;cout<<"Individual Msg:"<<endl;for( i = 0 ; i < colonySize ; i++ ){cout<<individualMsg[i].index<<"\t"<<individualMsg[i].value<<endl; }}////////////////////////////////////////////////////////////void main(){srand( (unsigned int)time(NULL) );setProblem();printProblem();//初始群体colonyInit();printColonyState( currAge );while( !stopFlag() ){//评价当前群体individualEstimate();//生成下一代for( int i = 0 ; i < colonySize ; i += 2 ){int male = gambleChoose();int female = gambleChoose();across( male , female , i );aberrance( i );aberrance( i + 1 );}//处理死亡个体dealDeath();//最优个体保护saveBest();//现在的下一代变成下一轮的当前代currAge = ( currAge + 1 ) % 2;//printColonyState( currAge );}//输出问题解individualEstimate();cout<<"近似解:"<<endl;int j , w = 0;cout<<setw(10)<<"Value:";for( j = 0 ; j < packageNum ; j++ )cout<<setw(5)<<packageValue[j];cout<<endl;cout<<setw(10)<<"Weight:";for( j = 0 ; j < packageNum ; j++ ){w += packageWeight[j] * colonyState[individualMsg[0].index][currAge][j]; cout<<setw(5)<<packageWeight[j];}cout<<endl;cout<<setw(10)<<"Choose:";for( j = 0 ; j < packageNum ; j++ )cout<<setw(5)<<colonyState[individualMsg[0].index][currAge][j];cout<<endl;cout<<"limitWeight: "<<limitWeight<<endl;cout<<"总重量: "<<w<<endl;cout<<"总价值: "<<individualMsg[0].value<<endl; }////////////////////////////////////////////////////////////。