上海市中学生业余数学学校招生试题含答案

2017年上海市中学生业余数学学校预备年级招生考试试题（10月21日上午8:30~9:30）得分评分复核本卷满分100分（10’×10=100’）1、计算：（1）2017 × 20162016 - 2016 × 20172017=________（2）13312155132642586538++++++=________2、有一个四位正整数，在它的某位数字前加上一个小数点，再与这个四位数相加，得到数2037、17，则这个四位数是________3、已知一列数：2017，2016，1，2015，2014，1，2013，2012，1，…，3，2，1，则这一列数中，从左向右数，第2017个数是________4、五年级某班有26名男生、在一次考试中，该班有30人得分超过85分，则这次考试中，该班女生中得分超过85分的人数比男生中得分没有超过85分的人数多________人5、某人工作一月（按30天计算）的酬金是1800元加一台自动洗衣机、实际上，他做了12天，得到60元和一台自动洗衣机，则这台自动洗衣机的价值为________元6、如图，在四边形ABCD中，已知AB=BC=a cm，AD=DC=b cm（a，b 为整数），∠DAB=∠BCD=90°，且四边形ABCD的面积为385cm2，则四边形ABCD周长的最小值是________cm7、有三堆棋子，每堆棋子一样多，且都由黑白两色棋子组成、已知第一堆的黑棋和第二堆的白棋数目相等，第三堆的黑棋占三堆全部黑棋的25、若把三堆棋子并成一堆，则在这一堆棋子中，白棋占全部棋子的________（填一个分数）8、如图，由12条线段搭成一个空间框架、框架中两条没有公共端点的线段是不相交的，例如AC与BD是一对不相交的线段（这里AC，BD没有次序之分），则这个框架的12条线段中，不相交的线段有________对9、在如图的10个小方格里分别填上1，2，3，4，5，11，12，13，14，15十个数，使三个2×2的正方形中的四个数的和都相等，则这个和的最大值是________10、有64个1×1×1的小正方体，其中34个是白色的，30个是黑色的、现将它们拼成一个4×4×4的大正方体，则大正方体表面黑色部分面积的最小是________2017年上海市中学生业余数学学校招生试题答案 预备年级1、（1）0;（2）242、20173、6734、45、11006、927、948、36 9、33 10、22。

2000年上海市中学生业余数学学校预备年级招生试题解答1、如图，它是由火柴棒组成的三角形图案，如果在这个三角形图案中，用了2001根火柴，那么它共有三角形 1000 个。

解：设共有三角形x 个则1+2x=2001x=10002、三个正方形连成如图所示，求x °= 41 °解：如图∠1=90°+30°=120°，∠2=540°－90°－90°－120°－124°＝116°则∠3=64°，∴∠4=360°－90°－75°－64°＝131°∴x ＝131°－90°＝41°3、图中的阴影部分由三条圆弧围成，大圆弧的半径是4，两个小圆弧的半径都是2，那么阴影部分的面积是 4.56 (取π=3.14)解：利用割补法可得，阴影部分的面积是一个弓形面积21144448 4.5642ππ⨯⨯⨯－＝－＝4、如果有n 个1构成n 位数11111n个是7的倍数，那么n 最小可能值是 6 解：可以通过试的方法。

因为求n 的最小可能值，所以分别用1 1、111、1111、……去除以7，第一个整除的就是。

可得n 最小可能值是6。

5、两个自然数的和是7299，这两个自然数的积和首、末两个数码之和的最大值是6、从甲地开往乙地，一辆载重5吨的大货车要用汽油10升，一辆载重3吨的小货车要用汽油7升。

甲地有27吨货物要运往乙地，用大货车和小货车运，至少要用汽油 57 升。

解：设用大货车x 辆，小货车y 辆则5x+3y ≥27x=0，1，2，3，4，5，6y=9，8，6，4，3，1，0对应的汽油用量分别是：63,66,62,58,61,57,60，所以至少要用汽油57升7、如图，在长方形内画一些线段，使得边上有三个图形的面积分别是13、35、49，那么图中阴影部分的面积是97 。

2003年上海市中学生业余数学学校预备年级招生试题（10月11日上午8∶30—9∶30）本卷满分100分（7/×4+8/×4+10/×4 =100/）1、A、B两城市相距625千米，小王从A市于上午5:30出发，以每小时100千米的速度驶向B市．小王出发15分钟后，小张从B市以每小时80千米的速度驶向A市．则两人于点分在途中相遇．解：小王出发15分钟，走了100×0.25小时=25千米；余下项羽距离625-25=600千米；600÷（100+80）=10/3小时=200分钟∴215分钟后（3小时35分钟后）相遇，即9点05分2、某城市的外环公路总长61千米，为了联络需要在环路边设置应急电话亭，要求每两个电话亭之间的距离不超过2千米，那么外环路边最少需要设置个电话亭．解：[61÷2]+1=313、运相同的78箱货物，如果用能装5箱货物的大卡车运一次，运费为130元，如果用能装2箱货物的小卡车运一次，运费为60元，合理选择大、小卡车的辆数，可使得总运费最省，最省的总运费为．解：大卡车折合每箱26元、小卡车每箱30元，所以尽量要用大卡车。

4、在如图所示的街道示意图中，从A到B的最短路线共有条．解：最短路线就是不走回头路，只往右、只网上。

标数法，9条AB5、如图所示，两个等腰直角三角形ABC和DEF叠放在一起，如果BC = 10，EF = 8，CE = FC + BE，那么图中阴影部分的面积是．解：CE = FC + BE => 3 CE = BC + EF = 10+8 => CE=6、FC=2、BE=4、FB=12S阴影=S△NBF- S△FMC- S△PBE=（12×12÷2-4×4-2×2）÷2=526、某个质数与6，8，12，14之和都仍然是质数，一共有个满足上述条件的质数．解：把x依据处以5所得余数分为以下五种情况：当X=5k+1，则X+14=5×（k+3）为合数当X=5k+2，则X+8=5×(k+2) 为合数当X=5k+3，则X+12=5×（k+3）为合数当X=5k+4，则X+6=5×（k+2）为合数因此只能取X=5k，且k取1即X=5 ∴1个A BECFMNDP7、据说美国有一位铁路职员花了50多年业余时间，研究得到了一个六角形幻方，如图所示的每一个圆中分别填写了1，2，…，19中的一个数字（不同的圆中填写的数字各不相同），使得图中每一个横或斜方向的线段上几个圆内的数之和都相等，现在已知该图中七个圆内的数字，则图中的x= ．解：①确定红色的两个数比较容易(11+18=14+15;16+12=13+15)。

2006年上海市中学生业余数学学校预备年级招生考试2006年上海市中学生业余数学学校预备年级招生考试（10月6日 上午8:309:30-）本卷满分100分（7'48'410'4100'⨯+⨯+⨯=）【第1题】有一列数8，88，888，…，888888 个，它们的和的百位数字是_______。

【分析与解】888888888888++++ 个的和的百位数字与88286888888888888-=++++ 个的和的百位数字相同；868888888888888888888676464++++=++⨯= 个；即86888888888888++++ 个的和的百位数字是4；故888888888888++++ 个的和的百位数字是4。

【第2题】若数20062006200620061006n个能被11整除，则n 的最小值是_______。

【分析与解】因为200611|2006200620061006n个； 所以()()062011|0606060620202010662145n n n n n ++⎛⎫⎛⎫++++++++-++++++++=+-+=+ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭个个； n 的最小值是7。

2006年上海市中学生业余数学学校预备年级招生考试【第3题】如图，ABCD ，AMOQ ，MBNO ，ONCP ，QOPD 都是矩形，若矩形QOPD 的面积为251cm ，矩形ONCP 的面积为217cm ，矩形MBNO 的面积为229cm ，则四边形MNPQ 的面积2_______cm 。

OQPNM DCBA【分析与解】因为()()()()OQ OP ON OM ON OP OQ OM ⨯⨯⨯=⨯⨯⨯； 所以QOPD MBNO ONCP AMOQ S S S S ⨯=⨯矩形矩形矩形矩形；所以251291787AMOQ QOPD MBNO ONCP S S S S cm =⨯÷=⨯÷=矩形矩形矩形矩形；所以251172987184ABCD QOPD ONCP MBNO AMOQ S S S S S cm =+++=+++=矩形矩形矩形矩形矩形； 因为PQO PQD S S ∆∆=，PNO PNC S S ∆∆=，MNO MNB S S ∆∆=，QMO QMA S S ∆∆=； 所以22184292MNPQ ABCD S S cm =÷=÷=四边形矩形。

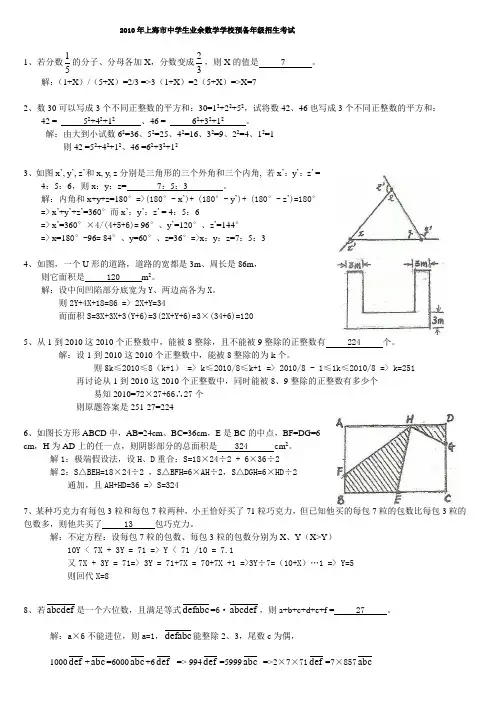
2010年上海市中学生业余数学学校预备年级招生考试1、若分数51的分子、分母各加X ，分数变成32，则X 的值是 7 。

解：（1+X ）/（5+X ）=2/3 =>3（1+X ）=2（5+X ）=>X=72、数30可以写成3个不同正整数的平方和：30=12+22+52，试将数42、46也写成3个不同正整数的平方和：42 = 52+42+12 、46 = 62+32+12 。

解：由大到小试数62=36、52=25、42=16、32=9、22=4、12=1则42 =52+42+12、46 =62+32+123、如图x ’, y ’, z ’和x, y, z 分别是三角形的三个外角和三个内角, 若x ’：y ’：z ’ =4：5：6，则x ：y ：z= 7：5：3 。

解：内角和x+y+z=180°=>(180°- x ’)+ (180°- y ’)+ (180°- z ’)=180°=> x ’+y ’+z ’=360°而x ’：y ’：z ’ = 4：5：6=> x ’=360°×4/(4+5+6)= 96°、y ’=120°、z ’=144°=> x=180°-96= 84°、y=60°、z=36°=>x ：y ：z=7：5：34、如图，一个U 形的道路，道路的宽都是3m 、周长是86m ，则它面积是 120 m 2。

解：设中间凹陷部分底宽为Y 、两边高各为X 。

则2Y+4X+18=86 => 2X+Y=34而面积S=3X+3X+3(Y+6)=3(2X+Y+6)=3×(34+6)=1205、从1到2010这2010个正整数中，能被8整除，且不能被9整除的正整数有 224 个。

解：设1到2010这2010个正整数中，能被8整除的为k 个。

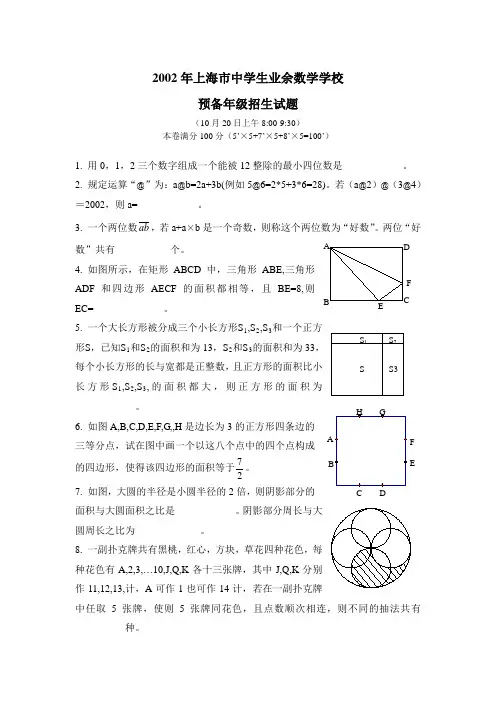
上海市中学生业余数学学校历年初中招生试题汇编（含参考答案）目录01．1987年初一年级招生试题 ------------------------------------ 03 02．1988年初一年级招生试题------------------------------------- 05 03．1989年初一年级招生试题------------------------------------- 07 04．1990年初一年级招生试题--------------------------------------09 05．1991年初一年级招生试题------------------------------------- 1106．1992年初一年级招生试题------------------------------------- 13 07．1993年初一年级招生试题------------------------------------- 15 08．1994年初一年级招生试题------------------------------------- 17 09．1995年初一年级招生试题------------------------------------- 19 10．1996年初一年级招生试题------------------------------------- 21 11．1997年初中预备年级招生试题--------------------------------- 23 12．1997年初一年级招生试题------------------------------------- 25 13．1998年初中预备年级招生试题--------------------------------- 2714．1998年初一年级招生试题------------------------------------- 29 15．1999年初中预备年级招生试题--------------------------------- 3116．2000年初中预备年级招生试题--------------------------------- 3317．2001年初中预备年级招生试题--------------------------------- 3518．2002年初中预备年级招生试题--------------------------------- 3719．2003年初中预备年级招生试题--------------------------------- 3920．2004年初中预备年级招生试题--------------------------------- 4121．2005年初中预备年级招生试题--------------------------------- 4322．2006年初中预备年级招生试题--------------------------------- 4523．2007年初中预备年级招生试题--------------------------------- 4724．2008年初中预备年级招生试题--------------------------------- 4925．参考答案---------------------------------------------------- 512005年上海市中学生业余数学学校预备年级招生试题本卷满分100分（7/×4+8/×4+10/×4 =100/）1、 在平面上画一个长方形能把平面分成两个部分，如果画三个长方形，那么最多能把平面分成部分。

2010年上海市中学生业余数学学校预备年级招生考试2010年上海市中学生业余数学学校预备年级招生考试【第1题】若分数15的分子、分母各加X ，分数变成23，则X 的值是_______。

【分析与解】（方法一）()()125331257X X X X X +=++=+=即X 的值是7。

（方法二）约分之前，分母比分子大514-=；分数15的分子、分母各加X ，分数的分子为()43228÷-⨯=，分母为()432312÷-⨯=；即18512X X +=+； 故X 的值是7。

【第2题】数30可以写成三个不同正整数的平方和：22230125=++试将数42，46也写成三个不同正整数的平方和： 42_____________=；46_____________=。

【分析与解】211=，224=，239=，2416=，2525=，2636=； 先考虑最大的整数的平方；经尝试，22242145=++，22246136=++。

2010年上海市中学生业余数学学校预备年级招生考试【第3题】如图，'x ，'y ，'z 和x ，y ，z 分别是三角形的三个外角和三个内角，若':':'4:5:6x y z =，则::_______x y z =。

z' y'x'yx z【分析与解】因为':':'4:5:6x y z =；所以设'4x k = ，'5y k = ，'6z k = （0k ≠）；则()180'1804x x k =-=-，()180'1805y y k =-=-，()180'1806z z k =-=-； 三角形内角和等于180 ；()()()180418051806180k k k -+-+-=； 三角形外角和等于360 ；456360k k k ++=； 24k =；84x = ，60y = ，36z = ； ::84:60:367:5:3x y z == 。

2008 年上海市中学生业余数学学校 预备年级招生考试
城隍喵
【第 6 题】 如图， 四个一样大小的正方形和七个一样的小长方形拼成一个大长方形， 如果大长方形的面积是 30 平方分 米，那么这个大长方形的周长是 _______ 分米。
【分析与解】
3 个小长方形组成的小长方形与 4 个小正方形组成的小长方形的长、宽分别相等，故面积也相等； 那么大长方形的面积相当于 10 个小长方形的面积； 小长方形的面积为 30 10 3 平方分米； 4 个小正方形的面积为 3 3 9 平方分米； 即 3 个小长方形的面积为 9 平方分米；
2008 年上海市中学生业余数学学校 预备年级招生考试
城隍喵
【第 4 题】 1 ， 2 ， 3 ，…， 2007 ， 2008 这 2008 个数中，数码 0 共有 _______ 。 【分析与解】 先考虑 0 ~ 1999 中的数； 将所有 0 ~ 1999 所有的数都看成四位数，不足四位的在前面补 0 ，即看成 0000 ~ 1999 ； 个位数字是 0 的，千位、百位、十位可以是 000 ~ 199 ，有 200 个数； 十位数字是 0 的，千位、百位、个位可以是 000 ~ 199 ，有 200 个数； 百位数字是 0 的，千位、十位、个位可以是 000 ~ 199 ，有 200 个数； 千位数字是 0 的，百位、十位、个位可以是 000 ~ 999 ，有 1000 个数； 则 0000 ~ 1999 中，一共有 200 200 200 1000 1600 个数字 0 ； 0 ~ 9 ，每个数多算了 3 个数字 0 ，一共有多算了 3 10 30 个数字 0 ； 10 ~ 99 ，每个数多算了 2 个数字 0 ，一共有多算了 2 90 180 个数字 0 ； 100 ~ 999 ，每个数多算了 1 个数字 0 ，一共有多算了 1 900 900 个数字 0 ； 0 ~ 1999 中，一共有 1600 30 180 900 490 个数字 0 ； 因为 0 有 1 个数字 0 ， 2000 ~ 2008 一共有 3 2 2 2 19 个数字 0 ；

中任取 5 张牌，使则 5 张牌同花色，且点数顺次相连，则不同的抽法共有 __________种。
9. 小胡和小涂计算甲，乙两个两位数的乘积。小胡看错了甲数的个位数字，计 算结果为 1274 ，小涂看错了甲数的十位数字，计算结果为 819 ，则甲数是 _____________。 10. 把一个长方形菜地分成三块，如图所示，已 知第二块比第一块宽 10 米，第二块面积为 1000 平方米；第三块比第一块窄 4 米，第三块面积是 650 平方米，那么第一块的面积是_____________平方米。 11. 一 条 单 轨 铁 路 线 上 有
本卷满分 100 分（7 ×4+8 ×4+10/×4 =100/）
1、A、B 两城市相距 625 千米，小王从 A 市于上午 5:30 出发，以每小时 100 千米的速 度驶向 B 市．小王出发 15 分钟后，小张从 B 市以每小时 80 千米的速度驶向 A 市．则两人 点 分在途中相遇． 于 2、某城市的外环公路总长 61 千米，为了联络需要在环路边设置应急电话亭，要求每两 个电话亭． 个电话亭之间的距离不超过 2 千米，那么外环路边最少需要设置 3、运相同的 78 箱货物，如果用能装 5 箱货物的大卡车运一次，运费为 130 元，如果用 能装 2 箱货物的小卡车运一次，运费为 60 元，合理选择大、小卡车的辆数，可使得总运费 ． 最省，最省的总运费为 4、在如图所示的街道示意图中，从 A 到 B 的最短路线共有 条．
5 ，则 m＝ 13
。
B
5
I
3
ቤተ መጻሕፍቲ ባይዱ
C
5、在正方形 ABCD 中，切去四个三角形得到一个 五边形 EFGHI （如右图， 其中所标的数表示各线段 的长度） ， 线段 IJ 将五边形 EFGHI 分成两个面积相 等的部分，那么 FJ 的长度是 。

1999年上海市中学生业余数学学校预备年级试题（10月24日 上午9:00~10:30）1. 已知b a=⨯++⨯+⨯+⨯62611541431321，其中a ，b 是互质的正整数，那么a+b ＝ 。

2. 如图所示，ABCD 是一个正方形，它是由四个相同的小正方形所组成的，如果△EFC 的面积是54，那么AB ＝ 。

3. 如果正整数n 使得717-+n n 也是正整数，那么这样的正整数n 有 个。

HF G E DCB A FE D CBA4. 在5、6、7、8、9、10这六个数字之间分别填上加减乘除四则运算符号，并允许添括号， 但是不能改变数的顺序， 使最后结果为2000， 这样的算式可以是5 6 7 8 9 10 ＝2000。

5. 边长分别是6、7、9、10、11、14的等角六边形ABCDEF ，内接于一个边长为30的等边三角形中，如图所示。

同样这个等角六边形也能内接于另一个边长为n 的等边三角形，n ≠30，那么n ＝ 。

6. 8个互不相等的分数，其中每7个的和都是分母为24的正的既约真分数（分子和分母的最大公约数是1的真分数），那么8个分数的和是 。

7. 一个长方体，表面全部涂上红色以后，被分割成若干个体积都等于1立方厘米的小正方体。

如果在这些小正方体中，不带红色的小正方体的个数等于7，那么两面带红色的小正方体的个数是 。

8. 在100到999这900个自然数中，使得每一个数中的一个数码是另外两个数码的平均数，那么这样的三位数共有 个。

9. 如图的四边形ABCD 被对角线AC 、BD 分为甲、乙、丙、丁四个三角形。

如果AE ＝80，BE ＝60，CE ＝40，DE ＝30。

那么丙丁两个三角形的面积的和是甲乙两个三角形面积的和的 倍。

10. 数1919…19（100个19）除以6所得的余数是 。

丙丁乙甲E A BD C 16432111. 从0，1，2，…，1000000。

那么这些数的所有数码的和是 。

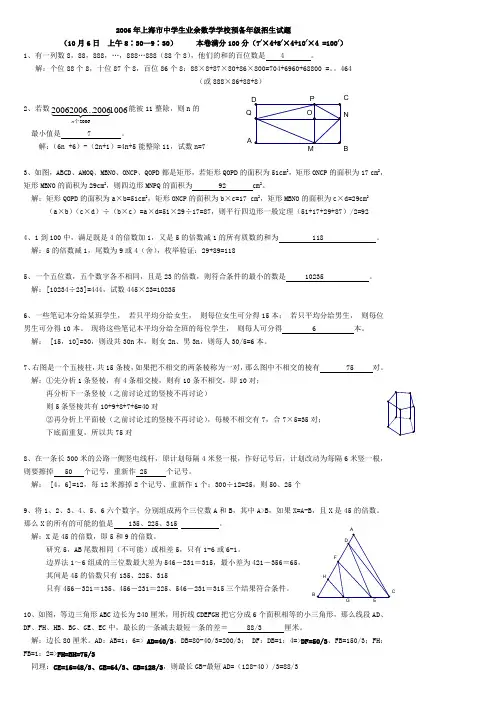
2006年上海市中学生业余数学学校预备年级招生试题（10月6日 上午8∶30—9∶30） 本卷满分100分（7/×4+8/×4+10/×4 =100/）1、有一列数8，88，888，…，888…888（88个8），他们的和的百位数是 4 。

解：个位88个8，十位87个8，百位86个8：88×8+87×80+86×800=704+6960+68800 =。

464（或888×86+88+8）2、若数10062006 (200620062006)个n 能被11整除，则n 的最小值是 7 。

解：（6n +6）-（2n+1）=4n+5能整除11，试数n=73、如图，ABCD 、AMOQ 、MBNO 、ONCP 、QOPD 都是矩形，若矩形QOPD 的面积为51cm 2，矩形ONCP 的面积为17 cm 2，矩形MBNO 的面积为29cm 2，则四边形MNPQ 的面积为 92 cm 2。

解：矩形QOPD 的面积为a ×b=51cm 2，矩形ONCP 的面积为b ×c=17 cm 2，矩形MBNO 的面积为c ×d=29cm 2（a ×b ）（c ×d ）÷（b ×c ）=a ×d=51×29÷17=87，则平行四边形一般定理（51+17+29+87）/2=924、1到100中，满足既是4的倍数加1，又是5的倍数减1的所有质数的和为 118 。

解：5的倍数减1，尾数为9或4（舍），枚举验证：29+89=1185、一个五位数，五个数字各不相同，且是23的倍数，则符合条件的最小的数是 10235 。

解：[10234÷23]=444，试数445×23=102356、一些笔记本分给某班学生， 若只平均分给女生， 则每位女生可分得15本； 若只平均分给男生， 则每位男生可分得10本。

上海市中学生业余数学学校预备年级招生试题1. 某学校共有1000名学生，其中男学生人数与女学生人数的比是2:3，女学生人数与教师人数的比是8:1。

那么教师有___________名。

2. 有一筐苹果和一筐梨，如果每天吃掉1个苹果2个梨，那么梨吃完时还剩下3个苹果;如果每天吃掉2个苹果3个梨，那么苹果吃完时还剩下5个梨，这筐苹果有_________个，这筐梨有__________个。

3. 若为一个四位数，且a=d，b=c，则称这个数为四位对称数。

四位对称数共有__________个。

4. 在一个圆周上有7个点，正好将圆周七等分，以这些点为顶点作三角形，可以作___________个等腰三角形。

5. 已知Sn=1-2+3-4+5-6+…+(-1)n+1n，其中n是正整数。

那么S2001+S2002=________。

6. 一个两位数N具有性质：N与颠倒N的数字后的数之和为完全平方数，则这样的N有___________个。

7. 数119具有以下性质：当它被2除余1;被3除余2;被4除余3;被5除余4;被6除余5;那么，具有这样性质的三位数(包括数119在内)共有_____个。

8. 有两部自动换币机，第一部能将一枚硬币换成二枚其它硬币;第二部能将一枚硬币换成五枚其它硬币，某人进行了14次换币，将一枚硬币换成了42枚硬币。

则他在第一，第二部换币机上分别换了________，________次。

9. 某人一块手表比家里的钟每小时快15秒，已知家里的钟比标准时间每小时慢15秒，则这快手表比标准时间一昼夜____________秒(填快或慢多少秒)10. A，B，C，D，E五个人中，其中任取4个人的平均年龄再加上余下一个人的年龄所得的和分别为37，40，49，58，64，则这五个人中年龄最大的比年龄最小的大___________岁。

11. 一次乒乓球比赛有A，B，C，D，E五名选手参加，他们来自湖北，广东，福建，北京和上海，经调查知道：(1)A仅与另外两名运动员比赛过;(2)上海运动员与另外三名运动员比赛过;(3)B没有和广东运动员比赛过;(4)福建运动员和C比赛过;(5)广东，福建。

2017年上海市中学生业余数学学校预备年级招生考试试题（10月21日上午8:30~9:30）本卷满分100分（10’×10=100’）1.计算：（1）2017×20162016-2016×20172017=________.（2）1331215++++++=________.51326425865382.有一个四位正整数，在它的某位数字前加上一个小数点，再与这个四位数相加，得到数2037.17，则这个四位数是________.3.已知一列数：2017,2016,1,2015,20XX,1,20XX,20XX,1，…，3,2,1，则这一列数中，从左向右数，第2017个数是________.4.五年级某班有26名男生.在一次考试中，该班有30人得分超过85分，则这次考试中，该班女生中得分超过85分的人数比男生中得分没有超过85分的人数多________人.5.某人工作一月（按30天计算）的酬金是1800元加一台自动洗衣机.实际上，他做了12天，得到60元和一台自动洗衣机，则这台自动洗衣机的价值为________元.6.如图，在四边形ABCD中，已知AB=BC=a cm，AD=DC=b cm（a，b为整数），∠DAB=∠BCD=90°，且四边形ABCD的面积为385cm2，则四边形ABCD周长的最小值是________cm.7.有三堆棋子，每堆棋子一样多，且都由黑白两色棋子组成.已知第一堆的黑棋和第二堆的白棋数目相等，第三堆的黑.若把三堆棋占三堆全部黑棋的25棋子并成一堆，则在这一堆棋子中，白棋占全部棋子的________（填一个分数）.8.如图，由12条线段搭成一个空间框架.框架中两条没有公共端点的线段是不相交的，例如AC与BD是一对不相交的线段（这里AC，BD没有次序之分），则这个框架的12条线段中，不相交的线段有________对.9.在如图的10个小方格里分别填上1,2,3,4,5,11,12,13,14,15十个数，使三个2×2的正方形中的四个数的和都相等，则这个和的最大值是________. 10.有64个1×1×1的小正方体，其中34个是白色的，30个是黑色的.现将它们拼成一个4×4×4的大正方体，则大正方体表面黑色部分面积的最小是________.2017年上海市中学生业余数学学校高一年级招生考试试题（10月21日上午10:00~11:30）________区__________________学校，姓名___________准考证号________________得分评分 复核本卷满分100分（10’×10=100’） 1.如图，直线122y x =--与G 轴、y 轴分别交于 A 点、B 点，把△AOB （O 为坐标原点）沿直线AB翻折，点O 落在点C 处，则点C 的坐标是________.2.如图，直线AB 、AC 切圆O 于B 、C 两点，点P 在圆O 上，且到AB 、AC 的距离PM 、PN 分别为1、2，则点P 到直线BC 的距离PQ 的长为________.3.已知23()2|1|1,02f x x x x =---≤≤，则()f x 的值域是________. 4.已知a 、b 、G 、y 都是实数，且aG +by =4，aG 2+by 2=2，aG 3+by 3=1，则aG 4+by 4的值是________.5.如图，正方形DEFG 内接于△ABC ，正方形HIJ K内接于△AGF ，若BC=a ，KJ=m ，则正方形DEFG的面积为________.6.如图，在△ABC 中，∠ACB=90°，CA=CB=2，O 为AC 的中点，以AC 为直径作⊙O ，OB 交⊙O 于点D ，AD 的延长线交CB 于点E ，则CE 的长为________.7.一个五位数乘以某一整数k （28k ≤≤），得到该五位数的反序数（把一个n 位正整数的各位数码顺序颠倒过来得到的新的n 位整数称为原数的反序数. 例如12345的反序数为54321），则原来的五位数是________________.8.已知a 、b 为实数，且224a ab b ++=，则22a ab b -+的取值范围为 ________________.9.从集合{|,11000}x x N x ∈≤≤中取出k 个数，使得取出的k 个数中，任意三 个数之和总能被18整除，则k 的最大值为________.10.已知凸五边形ABCDE 的面积为1，且△ABC,△BCD,△CDE,△DEA,△EAB 的 面积都相等，则△ABC 的面积为________.2017年上海市中学生业余数学学校招生试题答案预备年级1.（1）0;（2）242.20173.6734.45.11006.927.948.36 9.3310.22高一年级 1.)516,58(-- 2.2 3.[-2,1]4.21 5.am6.15- 7.219788.[34,12] 9.5610.1055-。

2004年上海市中学生业余数学学校高一年级招生试题（考试时间：2014年10月12日）1、如图，在直角坐标平面中，30AOX ∠=︒，AB AO ⊥，2AO =，BO =，则点B 的坐标为 ▲ ． 2、记N i k *∈，且12n k k k >>>L ，若122014222n k k k =+++L ，试求12n k k k +++L 的值为 ▲ ． 3、如图，在矩形ABCD 中，5AB =，12BC =，将矩形沿对角线AC 翻折，记D 的对应点为点E ，联结AE 交BC 于点F ，则△ECF 的面积为 ▲ ．4、若方程220x ax ++=，20x ax a +-=，2(1)0x a x a +--=中至少有一个方程有实数根，则a 的取值范围是 ▲ ．5、若111111(20)a b c d e a b c d e =++++<<<<<，满足 ,,,,N a b c d e *∈，试写出满足条件的其中一个算式 ▲ ．6、如图，四边形ABCD 是正方形，E 是边BC 上的一点，且40DME S =△，20AB =，则BE 的长为 ▲ ．7、若方程20x mx n --=的正根小于5，且,N m n *∈，则满足条件的方程共有 ▲ 个8、令函数110()10100x f x x +=-，记()()((()))n n ff x f f f f x =L 14243个，则 (2)(3)(1000)11112222f f f f ⎛⎫⎛⎫⎛⎫⎛⎫++++ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭L 的值为 ▲ ． 9、若正整数n 满足如下条件：①不等式220130x x n -+>对于N x *∈恒成立；②存在N x *∈，使得220140x x n -+≤成立。

则满足条件的n 的个数是 ▲ ．10、已知x 是无理数，且满足2x x +、322x x +都是整数，则x 的值为 ▲ ．AB CD E F A B CDE M。

1998年上海市中学生业余数学学校预备年级试题（10月18日 上午10:30~11:30）1. 一本书共有1998页，在这本书的页码上，数字7一共出现了 次2. 在矩形ABCD 中，E 、F 分别是AD 、AB 的中点，四边形AFCE 的面积是18cm 2，则矩形ABCD 的面积是________cm 2.3. 一个十位数字为0的三位数等于它各位数字之和的P 倍（P 为已知的自然数），交换它的个位和百位后所得的新三位数等于它的各位数字之和的 倍。

4. 八个自然数排成一排，从第三个数开始，每个数都是它前面的两个数的和。

已知第五个数是7，则第八个数是 。

5. 有一列分数：; (44);43;42;41;33;32;31;22;21;11其中第1998个数是 。

6. 下图中三角形ABC 的面积是75cm 2，把三角形ABC 的边AB 和AC 都五等分，阴影部分的面积是 cm 2。

F CB A DE GH7. 上图中正方形ABCD 的边长是5cm ，AEGD 是长方形，三角形ECH 的面积为10cm 2，则FG ＝ cm 。

8. 甲、乙两人沿长方形道路ABCD 匀速相对而行，开始时甲在A 处，乙在C 处，同时出发。

第一次相遇时甲走了50米，第二次相遇时，乙再走20米就回到C 处，这条道路的周长是 米。

9. 125个1×1×1的正方体，其中60个为白色的，65个为红色的，将它们拼搭成一个大正方体，大正方形的表面上，白色部分的面积最少为。

10. 甲、乙两车同时从A、B两地相对开出，4小时以后相遇，甲车再开3小时到达B地。

已知甲车每小时比乙车快20千米，A、B两地相距千米。

11. 某地按以下规定收取煤气费：（1）每月所用煤气按整立方米计算；（2）若该月用煤气不超过24立方米，按每立方米0.9元收费，若超过24立方米，超过部分按每立方米2.0元收费。

已知本月甲家比乙家多交煤气费9.6元，则甲家交了煤气费元。