直角三角形全等判定HL

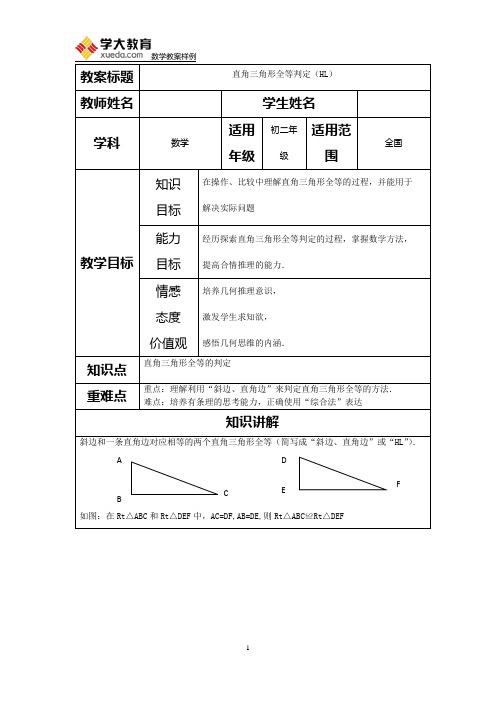
教案标题 直角三角形全等判定（HL ）教师姓名 学生姓名学科数学适用年级初二年级适用范围全国教学目标知识 目标 在操作、比较中理解直角三角形全等的过程，并能用于 解决实际问题能力目标 经历探索直角三角形全等判定的过程，掌握数学方法， 提高合情推理的能力． 情感 态度 价值观培养几何推理意识， 激发学生求知欲， 感悟几何思维的内涵．知识点 直角三角形全等的判定重难点重点：理解利用“斜边、直角边”来判定直角三角形全等的方法． 难点：培养有条理的思考能力，正确使用“综合法”表达知识讲解斜边和一条直角边对应相等的两个直角三角形全等（简写成“斜边、直角边”或“HL ”）．如图：在Rt △ABC 和Rt △DEF 中，AC=DF,AB=DE,则Rt △ABC ≌Rt △DEFA BCDEF例题讲解例1. AC ⊥BC ，BD ⊥AD ，AC=BD ，求证BC=AD ．[答案]BC=AD ． [详细答案】【思路点拨】欲证BC=•AD ，•首先应寻找和这两条线段有关的三角形，•这里有△ABD 和△BAC ，△ADO 和△BCO ，O 为DB 、AC 的交点，经过条件的分析，△ABD 和△BAC•具备全等的条件． 证明：∵AC ⊥BC ，BD ⊥BD ， ∴∠C 与∠D 都是直角．在Rt △ABC 和Rt △BAD 中，,,AB BA AC BD =⎧⎨=⎩ ∴Rt △ABC ≌Rt △BAD （HL ）． ∴BC=AD ．例2.下列说法正确的是（ ）A.面积相等的两个直角三角形全等B.周长相等的两个直角三角形全等C.斜边相等的两个直角三角形全等D.有一个锐角和斜边上的高对应相等的两个直角三角形全等 [答案] D[详细答案]周长和面积相等的两个三角形全等是错误的，斜边相等的两个三角形全等不具备全等的条件，只有D 答案具备全等的条件。

例3.有两个长度相同的滑梯，左边滑梯的高度AC•与右边滑梯水平方面的长度DF 相等，两个滑梯的倾斜角∠ABC 和∠DFE 的大小有什么关系？[答案] ∠ABC 与∠DEF 是互余的．[详细答案] 解： 在Rt △ABC 和Rt △DEF 中, ⎩⎨⎧==DFAC EFBC∴△ABC ≌△DEF ∴∠ABC=∠DEF ∵∠DEF+∠DFE=90°∴∠ABC+∠DFE=90°． ∴∠ABC 与∠DEF 是互余的．例4.AE ⊥BC ，DF ⊥BC ，E ，F 是垂足，且AE=DF ，AB=DC ，求证：∠ABC=∠DCB.[答案]∠ABC=∠DCB ．[详细答案]证明：∵AE ⊥BC ，DF ⊥BC ，∴∠AEB=∠CFD=90° 在Rt △ABE 和Rt △DCF 中， ∵AE=DF,AB=DC∴Rt △ABE ≌Rt △DCF ∴∠ABC=∠DCB ．例5. AB=CD ，AE ⊥BC ，DF ⊥BC ，垂足分别为E ，F ，CE=BF.求证：AB ∥CD ．[答案]AB ∥CD ．[详细答案]证明：CE=BF ，所以CE+EF=BF+EF ， 即BE=CF ，在Rt △AEB 和Rt △DCF 中， ,,AB CD BE CF =⎧⎨=⎩ ∴△ABE ≌△DCF ，所以∠B=∠C ， ∴AB ∥CD ．例6.在△ABC 中，∠B=∠C ，D 是BC 中点，DE ⊥AB ，DF ⊥AC ，E ，F 为垂足，求证：AD 平分∠BAC ． [答案]AD 平分∠BAC. [详细答案]证明：DF ⊥AC ，DE ⊥AB ，所以∠BED=∠CFD=90°。

《直角三角形全等的判定》教学设计中心发言人：DH教学目标:（1）明确两个直角三角形的全等，可以利用“边边边，边角边，角边角，角角边”来证明；但是由于直角相等，所以两个直角三角形全等的判定，只需要增加两个条件即可。

（2）探索和掌握直角三角形全等的特殊判定方法：斜边和一条直角边对应相等的两个直角三角形全等，并会用“SSS，SAS，ASA，AAS及HL”证明两个直角三角形全等。

教学重点：探索和掌握直角三角形全等的特殊判定方法：斜边和一条直角边对应相等的两个直角三角形全等，并会用“SSS，SAS，ASA，AAS及HL”证明两个直角三角形全等。

教学难点：（1）满足“边边角”分别对应相等的两个三角形不一定全等，但满足“斜边和一条直角边对应相等的两个直角三角形”符合“边边角”的条件，两个直角三角形却是全等的。

（2）要注意用HL直角三角形全等的证明格式集体备教教学过程：1、复习与回顾：（1）判定两个三角形全等的方法是，，，（2）回顾直角三角形的边、角的名称及相关性质。

2、尝试归纳两个直角三角形全等的判定方法：如图，A B⊥BE于B，D E⊥BE于E，（1）若∠A=∠D，AB=DE，则△ABC与△DEF （填“全等”或“不全等”），根据（用简写法）。

（2）若∠A=∠D，BC=EF，则△ABC与△DEF （填“全等”或“不全等”），个性补教AB CE FD根据（用简写法）。

（3）若AB=DE，BC=EF，则△ABC与△DEF （填“全等”或“不全等”），根据（用简写法）。

（4）若∠A=∠D，AC=DF则△ABC与△DEF （填“全等”或“不全等”），根据（用简写法）。

归纳：两个直角三角形全等的类型：ASA ,AAS ,SAS ,AAS (一锐角一直角边，一锐角一斜边，两直角边，共四种情形) 3、探究：一斜边一直角边对应相等，两直角三角形是否全等？（1）情景引入如图，两根长度为12米的绳子，一端系在旗杆上，另一端分别固定在地面两个木桩上，两个木桩离旗杆底部的距离相等吗？请说明你的理由。

hl定理是证明两个直角三角形全等的定理, 是的，HL定理是证明两个直角三角形全等的定理。

HL定理的内容是：如果两个直角三角形的斜边和一条直角边分别对应相等，那么这两个直角三角形全等。

HL定理的简写是“Hypotenuse-Leg”，其中H是斜边（Hypotenuse），L是直角边（Leg）。

这个定理是证明两个直角三角形全等的一种特殊判定方法，可以通过证明两个三角形的斜边和一条直角边对应相等来证明两个三角形全等。

它可以通过SSS （Side-Side-Side）或者SAS（Side-Angle-Side）等其他全等判定定理进行转换。

在证明两个直角三角形全等时，HL定理可以提供一种简单而有效的方法。

前提是一定要确保所比较的两个三角形都是直角三角形，否则这个定理不适用。

学会用“HL”说明直角三角形全等一般三角形全等判定方法（SSS，SAS，ASA，AAS）对于直角三角形同样适用，除此之外，还有一种特殊的方法“HL”，即有斜边和一条直角边对应相等的两个直角三角形全等．下面举例说明“HL”的应用．一、说明直线平行例1如图1 ，已知AE⊥BD，CF⊥BD，且AD=BC，BE=DF，试判断AD 和BC的位置关系.说明你的结论．图1分析：只要说明△AED≌△CBF，就可以得到∠D=∠B，进一步得到AD//BC．解：AD//BC．因为BE=DF，所以BE+EF=DF+E，即BF=DE.在Rt△ADE和Rt△CAF中，AD=CB，DE=BF，所以Rt△ADE≌Rt△CAF（HL），所以∠D=∠B，所以AD//BC．评注：本题是探索两直线的位置关系，解决问题时，可先通过观察获得猜想，然后再尝试证明．二、说明角相等例2如图2，∠ACB=∠BDA=90°，AD=BC，AB//CD．试说明：∠1=∠2．分析：要证明∠1=∠2，根据AB//CD，可得∠1=∠DBA，∠2=∠CAB，所以只要证明∠CAB=∠DBA即可，为此要证明Rt△ABC≌Rt△BDA，根据已知AD=BC并结合公共边AB=BA可以利用“HL”证明两个三角形全等．图2解：在Rt△ABC和Rt△BAD中，因为∠ACB=∠BDA=90°，BC=AD，AB=BA，所以Rt△ABC≌Rt△BAD（HL），所以∠BAC=∠ABD，又AB//CD，所以∠1=∠DBA，∠2=∠CAB，所以∠1=∠2．评注：本题在证明两个三角形全等时，利用了公共边AB=BA这一隐含条件，注意不要写成AB=AB．三、证垂直例3如图3，AC⊥BD，AC=DC，CB=CE，试说明：DE⊥AB．分析：观察图形，发现已知AC=DC，CB=CE就在Rt△ACB和Rt△DCE中，恰好符合“HL”的条件，可得Rt△ACB≌Rt△DCE。

而要证DE⊥AB，只需证∠B+∠D=90°，由已知可得∠A+∠B=90°，只需证∠A=∠D，要证∠A=∠D，只需证Rt△ACB≌Rt△DCE图3解：因为AC⊥BD，所以∠ACB=∠DCE=90°，所以∠A+∠B=90°，又在Rt△ACB和Rt△DCE中，AC=DC，BC=EC，所以Rt△ACB≌Rt△DCE，所以∠A=∠D，所以∠B+∠D=90°，所以DE⊥AB．评注：当图形中有直角三角形存在时，且有斜边与一直角边对应相等时，可考虑利用“HL”证明其全等，又在证明直线垂直问题，可以通过证出三角形中有一个角是直角，或证三角形中两个锐角互余．。

直角三角形全等的判定方法hl证明嘿，咱今天就来好好唠唠直角三角形全等的判定方法 HL 证明。

你说这直角三角形啊，就像是一个特别的小团队，它们有着自己独特的规则和特点呢。

HL 证明呢，就好像是一把神奇的钥匙，能打开直角三角形全等的大门。

咱先想想，两个直角三角形，它们有一条直角边相等，斜边也相等，那这俩三角形不就全等了嘛！这就好比是两个人，都有一条一样长的腿，然后身子的长度也一样，那这俩人不就是一模一样的嘛。

你可能会问啦，为啥有了这两条边相等就能说它们全等呢？嘿嘿，这就得好好琢磨琢磨啦。

你看啊，直角三角形本身就有个直角在那摆着呢，这可是个重要的标志呀。

有了这个直角，再加上那相等的直角边和斜边，就像是给这个三角形定了型一样，其他的边和角也就都确定啦。

咱可以想象一下，有两个直角三角形，它们就像是两个形状特别的积木，当它们的那条直角边和斜边能完美重合的时候，那不就说明它们是一样的嘛。

这 HL 证明啊，就是让我们能准确地判断出这两个积木是不是同一个。

你说这数学世界多奇妙呀，就这么几条边几个角的事儿，就能有这么多有趣的发现和证明。

这 HL 证明就像是在直角三角形的世界里点亮了一盏明灯，让我们能更清楚地看清它们的模样。

而且啊，这HL 证明在实际生活中也有用呢。

比如说盖房子的时候，工人们要保证一些结构是完全一样的，这时候不就可以用 HL 证明来判断嘛。

或者是做一些模型的时候，也得保证各个部分全等呀，这 HL 证明就能派上大用场啦。

你再想想，如果没有这个 HL 证明，那我们怎么能确定两个直角三角形是不是全等呢？那可就麻烦啦，得去一点点量其他的边和角，多费劲呀。

但是有了 HL 证明，一下子就简单明了啦。

总之呢，直角三角形全等的判定方法 HL 证明可真是个好东西呀，它让我们能更轻松地理解和掌握直角三角形的奥秘。

怎么样，是不是觉得挺有意思的呀？下次再看到直角三角形，可别忘了 HL 证明哦！。