数字信号处理第三版(姚天任、江太辉) 答案 第三章
- 格式:pdf
- 大小:770.60 KB
- 文档页数:14



数字信号处理(姚天任江太辉)第三版课后习题答案第二章2.1判断下列序列是否是周期序列。
若是,请确定它的最小周期(1)x(n)二Acos( 5 n86)(2)x(n )= e j(- 8 )(3) x(n )=Asi n(3 n4 3)解(1)对照正弦型序列的-般公式x(n)二 Acos( n ),得出5。
因此82 16是有理数,所以是周期序列。
5 最小周期等于N=^k 16(k取5)。
5(2)对照复指数序列的般公式x(n)二exp[ j ]n,得出1。
因此2168是无理数,所以不是周期序列。
(3)对照正弦型序列的般公式x(n)二 Acos( 3n ),又x(n)二Asin( n ) =Acos(— .门—)=Acos( —n 丄),得出3。
因此2 8是有理数,所以2 434 6 4 3是周期序列。
最小周期等于N=-k38(k 取3)2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解利用线性卷积公式y(n )= x(k)h( n k)k按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值(a) y(0)=x(0)h(0)=1y(l)=x(0)h(1)+x(1)h(0)=3y(n)=x(O)h( n)+x(1)h( n-1)+x(2)h( n-2)=4,n (b) x(n )=2 (n)- (n-1)h(n)=- (n)+2 (n-1)+ (n-2)y(n)=-2(n )+5(n-1)= (n-3)(c) y(n )=u(k)kn ka u(n k):n k 1 a n 1/ \=a = . a u(n)k i a2.3计算线性线性卷积(1) y(n )=u( n)*u( n)(2) y(n)= n u(n)*u(n)解:(1) y(n)二u(k)u(n k)ku(k)u(n k)=(n+1),n >0 k 0 即y(n)=(n+1)u(n)(2) y(n )=kku(k)u( n k)2.4图P2.4所示的是单位取样响应分别为 九(n)和h 2(n)的两个线性非移变系统的级联,已知 x(n)=u(n), h ^n)二(n)-(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出 y(n).解(n)=x( n)*h Jn)u(k)[(n-k)- (n-k-4)]k=u( n)-u( n-4)y(n)= (n)*h 2 (n)a k u(k)[u( n-k)-u( n-k-4)]k算线性卷积的方法,求系统的单位阶跃响应即 y(n)二ku(k)u(n1n 1——,n >n 1—u(n)2.5已知一个线性非移变系统的单位取样响应为h(n)二a n u(-n),0<a<1 用直接计2.6 试证明线性卷积满足交换率、结合率和加法分配率。

第三章离散傅里叶变换及其快速算法习题答案参考3.1 图P3.1所示的序列(xn 是周期为4的周期性序列。
请确定其傅里叶级数的系数(X k。
解:(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.2 (1设(xn 为实周期序列,证明(x n 的傅里叶级数(X k 是共轭对称的,即*((X k X k =− 。
(2证明当(xn 为实偶函数时,(X k 也是实偶函数。
证明:(1 111**((([(]((N nk N n N N nk nkNNn n Xk x n W Xk x n W xn W X−−=−−−==−=−===∑∑∑ k(2因(xn 为实函数,故由(1知有 *((Xk X k =− 或*((X k X k −= 又因(xn 为偶函数,即((x n x n =− ,所以有(111*0((((((N N N nk nk nk N N N n n n X k x n W x n W x n W X k X k −−−−−=====−= =−=∑∑∑3.3 图P3.3所示的是一个实数周期信号(xn 。
利用DFS 的特性及3.2题的结果,不直接计算其傅里叶级数的系数(Xk ,确定以下式子是否正确。
(1,对于所有的k; ((10Xk X k =+ (2((Xk X k =− ,对于所有的k; (3; (00X=(425(jkX k eπ,对所有的k是实函数。
解:(1正确。
因为(x n 一个周期为N =10的周期序列,故(X k 也是一个周期为N=10的周期序列。
(2不正确。
因为(xn 一个实数周期序列,由例3.2中的(1知,(X k 是共轭对称的,即应有*((Xk X = k −,这里(X k 不一定是实数序列。
(3正确。
因为(xn (0n ==在一个周期内正取样值的个数与负取样值的个数相等,所以有 10(0N n Xx −=∑ (4不正确。

数字信号处理课后习题答案HEN system office room 【HEN16H-HENS2AHENS8Q8-HENH1688】数字信号处理(姚天任江太辉)第三版课后习题答案第二章判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n )(2)x(n)=)8(π-ne j(3)x(n)=Asin(343ππ+n )解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =在图中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n) 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λn u(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0即y(n)=λλ--+111n u(n)图所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a n u(n),|a|<1,求系统的输出y(n). 解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥3已知一个线性非移变系统的单位取样响应为h(n)=a n -u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。

第二章2.1 判断下列序列是否是周期序列。
若是,请确定它的最小周期。
(1)x(n)=Acos(685ππ+n ) (2)x(n)=)8(π-ne j(3)x(n)=Asin(343ππ+n ) 解 (1)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),得出=ω85π。
因此5162=ωπ是有理数,所以是周期序列。
最小周期等于N=)5(16516取k k =。
(2)对照复指数序列的一般公式x(n)=exp[ωσj +]n,得出81=ω。
因此πωπ162=是无理数,所以不是周期序列。
(3)对照正弦型序列的一般公式x(n)=Acos(ϕω+n ),又x(n)=Asin(343ππ+n )=Acos(-2π343ππ-n )=Acos(6143-n π),得出=ω43π。
因此382=ωπ是有理数,所以是周期序列。
最小周期等于N=)3(838取k k =2.2在图2.2中,x(n)和h(n)分别是线性非移变系统的输入和单位取样响应。
计算并列的x(n)和h(n)的线性卷积以得到系统的输出y(n),并画出y(n)的图形。
(a)1111(b)(c)111110 0-1-1-1-1-1-1-1-1222222 33333444………nnn nnnx(n)x(n)x(n)h(n)h(n)h(n)21u(n)u(n)u(n)a n ===22解 利用线性卷积公式y(n)=∑∞-∞=-k k n h k x )()(按照折叠、移位、相乘、相加、的作图方法,计算y(n)的每一个取样值。
(a) y(0)=x(O)h(0)=1y(l)=x(O)h(1)+x(1)h(O)=3y(n)=x(O)h(n)+x(1)h(n-1)+x(2)h(n-2)=4,n ≥2 (b) x(n)=2δ(n)-δ(n-1)h(n)=-δ(n)+2δ(n-1)+ δ(n-2)y(n)=-2δ(n)+5δ(n-1)= δ(n-3) (c) y(n)=∑∞-∞=--k kn k n u k u a)()(=∑∞-∞=-k kn a=aa n --+111u(n)2.3 计算线性线性卷积 (1) y(n)=u(n)*u(n) (2) y(n)=λnu(n)*u(n)解:(1) y(n)=∑∞-∞=-k k n u k u )()(=∑∞=-0)()(k k n u k u =(n+1),n ≥0即y(n)=(n+1)u(n) (2) y(n)=∑∞-∞=-k k k n u k u )()(λ=∑∞=-0)()(k kk n u k u λ=λλ--+111n ,n ≥0 即y(n)=λλ--+111n u(n)2.4 图P2.4所示的是单位取样响应分别为h 1(n)和h 2(n)的两个线性非移变系统的级联,已知x(n)=u(n), h 1(n)=δ(n)-δ(n-4), h 2(n)=a nu(n),|a|<1,求系统的输出y(n).解 ω(n)=x(n)*h 1(n) =∑∞-∞=k k u )([δ(n-k)-δ(n-k-4)]=u(n)-u(n-4)y(n)=ω(n)*h 2(n) =∑∞-∞=k kk u a )([u(n-k)-u(n-k-4)]=∑∞-=3n k ka,n ≥32.5 已知一个线性非移变系统的单位取样响应为h(n)=an-u(-n),0<a<1 用直接计算线性卷积的方法,求系统的单位阶跃响应。

第三章答案3.1解: (1):由题设:h (n) =)()(10n h n hy (n)=)1()(-n yn y 则u (n) =h (n) y (n)所以可得最陡下降法解:h (n=1) =h *+(I-2μR )2h (0)- h *其中R =)0()1()1()0(yy yy yy yy R R R = 3223(2):h *= R1-P =3 =1-(3):由于R =5225 则可得λ1=1,λ2=5;所以μ的取值范围为:0<μ<51当μ=61时迭代公式收敛。
(4):μ=61时h (n) = 14- + 100132× h (0) - 14-=14- +32--(0) - 14-3.2解:(1)空(2)e (n) = x (n)-y (n)[2μe (n-1)y (n-1)+h (n-1)] = x (n)-u (n)[2μe (n-1)y (n-1)+h (n-1)] 对e (n)进行z 变换: e (Z) = x (z) - 2μZ1-e (Z) - Z1-h (Z)由h (n)=2μe (n-1)u (n-1)+h (n-1) 得 h (Z)=2μZ1-e (Z) + Z1-h (Z)h (Z)=1-11)(Z 2--ZZ e μ 所以:e (Z) = x (Z)-2μZ1-e (Z)- Z1-1-11)(z 2--zz e μH (Z) = 11)1(211---+-ZZ μ 所以零点在单位园上,极点在Z = 1-2μ园上。
(3):要使H(Z)稳定,则极点在单位园内即: 0121><-μμ且3.3(1)性能曲面函数:[][][]⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡---+=-+=+-=-==+-=-=-=-====-==⎥⎦⎤⎢⎣⎡---==-+=1022202222010222)1([)]()1([)]1()([)([102)]([)()55(2125)]1()([0)]()([10)]([85585)]()1([)]1()([25)]1([25)]([)2cos(2)()2sin()()()()()1()()()()]()([)1([)]()1([)]1()([)([)]()([2)]([)(W W n x E n x n x E n x n x E n x E W W WP RW W n d E n n x n d E n x n d E n d E n x n x E n x n x E n x E n x E n N n d n N n x n W n W n W n x n d n x n d E n X n d E P n x E n x n x E n x n x E n x E n X n X E R WP RW W n d E n T T TTT T ξππξ[]⎥⎦⎤⎢⎣⎡--10)1()()()(2W W n x n d n x n d[]⎥⎦⎤⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+-+-+=10202585585]855852510W W W W⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+--10)55(212502W W1211020)55(21525)45545(2510w w w w w ++++-++=(2)误差性能曲面matlab 程序: (3)[][][][][])1(*)(*2)1(**2)(*)1(**2)(*)(*2)(*)1(**2)(**2 210112001---+-=∂∂-+-+=∂∂⎥⎦⎤⎢⎣⎡∂∂∂∂=∂∂=∇n x n d n x E w n x n X E w w n x n d n x n X E w n X E w w w w w Tξξξξξ (4)⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡-⎥⎥⎦⎤⎢⎢⎣⎡==---* 2.1029-0.6498 7553.40 0.4422 0.1367-0.1367- 0.4422 7553.402.5 0.77250.7725 2.5 )1()()()(1)-(n x 1)-x)n *x(n)1)-x(n *n) x( )( *11221n x n d n x n d n x pR w(5)[][]91-10 1029.2698.04.7553- 0-10 *)(2min ==⎥⎦⎤⎢⎣⎡-=-=*w p n d E T ξ 3.4[][]2725.3*2*27275.1*2*20.70717071.0 0.7071- 7071.02725.3 7275.1 2.5 .0.77250.7725 2.5 1)-(n x 1)-x(n *x(n)1)-x(n * x(n) )(1120102111021w2==∂∂==∂∂====⎥⎦⎤⎢⎣⎡=⎥⎥⎦⎤⎢⎢⎣⎡=λλξλλξV V V V n x E R TT[][][][]4216142)2( 8722242 8722112 )]([ 2)]([)(15..3101021201010101010101022+--++=+-⎥⎦⎤⎢⎣⎡+++=⎥⎦⎤⎢⎣⎡-⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=-+=ωωωωωωωωωωωωωωωωωωωωωωωεn d E P R n d E n T )解:([][][][]()()()[]6222)5(30014'300113122112'21124 )4(438423287)]([)]([ )3(323296872112872112 210'1''1'0min 2min 2110min 2*2min *1*03131*1*011*2'122'02====⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=Λ+=⎥⎦⎤⎢⎣⎡=Λ∴--=--=⎥⎦⎤⎢⎣⎡--=-Λ+=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+=+==-=⎥⎦⎤⎢⎣⎡-=-==⇒⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡⇒⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡==∂∂∂∂--λλεελλλλλλεεεεωεωωωωωεεv v T T TTv v v v v v R E v v v v v v Rv v n d E P n d E P R )、(3.6 解:(1)[][]()()[][][][][][][][][]NN N NN NN N N N N N T NN NN N N N N n N N N TT TT T T T n d E n n E n d E E n E n n E n n E n r n x n d n r n x n d E n X n d E P R n n n n x n E n r n x E n x n x E n r n x n r n x E n r n x E n nr E n r E n E n r n E n r n x E n r n x n r n x E n r n x n r n x E E n X n X E R n n n X n d E n n X n X E n n n y n d E n e E n ππππππππππππππππππππππππωωωωωϕωωωωϕϕωωεϕϕϕφωωωωωωεπ212021*********221221211022222242222212212212122124221222212cos -122222222210222sin 2cos ))(5.0(2sin 02cos cos )]([)(2]cos 4[)]([sin 0][sin ][sin )]1(sin )1([cos sin cos 2[)]1()1()(())()()(([)]()([cos cos cos ))]cos((cos E[ )]1(sin sin E[1)]-E[x(n)x(n 1)]-E[r(n)r(n )]1()[()]1()([)]1()([))]1()1())(()([(]))1()1([(E )(sin 2)(sin ))((sin ]r(n))E[(x(n)]))1()1([())]()())(1()1([())]1()1())(()([(]r(n))E[(x(n) ]1)-r(n 1)-x(n r(n)x(n)1)-r(n 1)-x(n r(n)x(n)[])()([1)-r(n 1)-x(n r(n)x(n)X(n) )()()]()([2)(])()([)()](E[d ]))()([()]([)(N 4+++++=⎥⎦⎤⎢⎣⎡--⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡+++=∴====--=-+-+==⎥⎦⎤⎢⎣⎡++=∴=--=-==+-+-+-=-+-+-+-=+=+⎥⎦⎤⎢⎣⎡=++=+=+⎥⎦⎤⎢⎣⎡-+-+-+--+-++=++++==++==-+=-==[]05.0][1044/1T 14.54/1(4)T )21/(1u 0 : ][021][)cos(2/11/2 0 ]cos cos [R -E ]cos cos [)3())cos()21/(()sin()21(2))cos()21/(()sin()cos(20)sin(2)cos(2)5.0(0)cos(2)5.0( )2(2mse21mse112122122122121212212212122221*222220*2201210101======+<<∴<<+=+=+==------=++=⎪⎩⎪⎨⎧-++-=-+=⇒⎪⎩⎪⎨⎧=+++==++===∇-+=∂∂∂∂∂∂∂∂∂∂R ut M u u u R t u R t R r r r N N NN N N N N N N N N N T λλϕϕλλϕλϕλϕλλϕϕϕϕωϕωωωϕωωϕππππππππππππωεπωεωεωεωε值范围为系统收敛的3.11答案:11)(4)(4.0)()]()([2))(()()]([)(min))(()()()()()()1(22222+-=-+===-=n h n h n h n y n x E n y E n h n x E n n e E n n y n h n x n e ξξ5)(04)(8.0)()(==-=n h n h n dh n d ξ (2)μμμξ4)()2.31())(8.04()())(()()1(48.0)(+-=-+=-∇+=+-=∂∂=∇n h n h u n h n n h n h h hn 数迭代计算公式为:最陡下降法推导加权系(3)求加权系数表达式]10)0([)8.01(10])0([)2()(**--+=--+=h h h R I h n h nn μμ要求1max 0-<<λμ5.204.010<<<<∴μμ即3.12答案:2102][][0)1(1011<<==<<∑=--μλμμ即满足为保证收敛应使k k R tr R tr器的收敛速度相同。



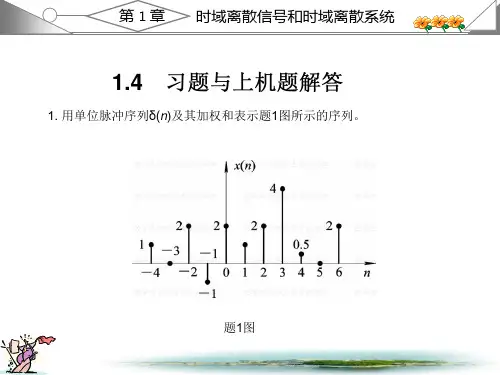
数字信号处理课后答案1.2 教材第一章习题解答1. 用单位脉冲序列()n δ及其加权和表示题1图所示的序列。
解:()(4)2(2)(1)2()(1)2(2)4(3) 0.5(4)2(6)x n n n n n n n n n n δδδδδδδδδ=+++-+++-+-+-+-+-2. 给定信号:25,41()6,040,n n x n n +-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n 序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n 序列; (3)令1()2(2)x n x n =-,试画出1()x n 波形; (4)令2()2(2)x n x n =+,试画出2()x n 波形; (5)令3()2(2)x n x n =-,试画出3()x n 波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)()3(4)(3)(2)3(1)6() 6(1)6(2)6(3)6(4)x n n n n n n n n n n δδδδδδδδδ=-+-+++++++-+-+-+-(3)1()x n 的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n 的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n 时,先画x(-n)的波形,然后再右移2位,3()x n 波形如题2解图(四)所示。
3. 判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14; (2)12,168w wππ==,这是无理数,因此是非周期序列。
5. 设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
数字信号处理课后答案教材第一章习题解答1.用单位脉冲序列()nδ及其加权和表示题1图所示的序列。
解:2.给定信号:25,41 ()6,040,n nx n n+-≤≤-⎧⎪=≤≤⎨⎪⎩其它(1)画出()x n序列的波形,标上各序列的值;(2)试用延迟单位脉冲序列及其加权和表示()x n序列;(3)令1()2(2)x n x n=-,试画出1()x n波形;(4)令2()2(2)x n x n=+,试画出2()x n波形;(5)令3()2(2)x n x n=-,试画出3()x n波形。
解:(1)x(n)的波形如题2解图(一)所示。
(2)(3)1()x n的波形是x(n)的波形右移2位,在乘以2,画出图形如题2解图(二)所示。
(4)2()x n的波形是x(n)的波形左移2位,在乘以2,画出图形如题2解图(三)所示。
(5)画3()x n时,先画x(-n)的波形,然后再右移2位,3()x n波形如题2解图(四)所示。
3.判断下面的序列是否是周期的,若是周期的,确定其周期。
(1)3()cos()78x n A n ππ=-,A 是常数;(2)1()8()j n x n e π-=。
解:(1)3214,73w w ππ==,这是有理数,因此是周期序列,周期是T=14;(2)12,168w wππ==,这是无理数,因此是非周期序列。
5.设系统分别用下面的差分方程描述,()x n 与()y n 分别表示系统输入和输出,判断系统是否是线性非时变的。
(1)()()2(1)3(2)y n x n x n x n =+-+-; (3)0()()y n x n n =-,0n 为整常数; (5)2()()y n x n =; (7)0()()nm y n x m ==∑。
解:(1)令:输入为0()x n n -,输出为'000'0000()()2(1)3(2)()()2(1)3(2)()y n x n n x n n x n n y n n x n n x n n x n n y n =-+--+---=-+--+--=故该系统是时不变系统。