地基沉降与时间关系

沉降与时间的关系曲线是工程地质和土木工程中的重要工具，它描述了地基或土体在荷载作用下的沉降量如何随时间变化。

这种关系对于预测土壤或地基的稳定性以及制定合理的设计和施工决策至关重要。

首先，我们需要理解沉降的概念。

沉降是指土壤或地基在受到外力作用后，其高度发生降低的现象。

这种现象通常是由于土壤中的水分被挤出，或者土壤颗粒之间的空隙被压缩所导致的。

沉降的程度通常用沉降量来表示，单位通常是毫米或厘米。

然后，我们来看看沉降与时间的关系。

在开始阶段，沉降速度通常会很快，随着时间的推移，沉降速度会逐渐减慢。

这是因为在开始阶段，土壤中的水分和空隙较多，容易发生变形；而在后期，土壤已经接近其固结状态，变形的空间较小。

因此，沉降与时间的关系通常呈现出先快后慢的趋势。

为了更直观地描述这种关系，我们可以绘制沉降与时间的关系曲线。

在这个曲线中，沉降量s为纵轴，时间t为横轴。

我们可以通过观测每次的沉降量，然后将这些数据点连接起来，形成一条曲线。

这条曲线就代表了沉降与时间的关系。

通过观察这条曲线，我们可以得出很多有用的信息。

例如，我们可以通过找到曲线的拐点来确定沉降的速度何时开始减慢；我们还可以通过比较不同时间的沉降量来评估土壤的稳定性；此外，我们还可以通过预测未来的沉降量来制定相应的设计和施工计划。

总的来说，沉降与时间的关系曲线是一种非常实用的工具，它可以帮助工程师更好地理解和控制土壤和地基的变形。

然而，要准确地绘制这条曲线，我们需要有精确的观测数据和深入的理论分析。

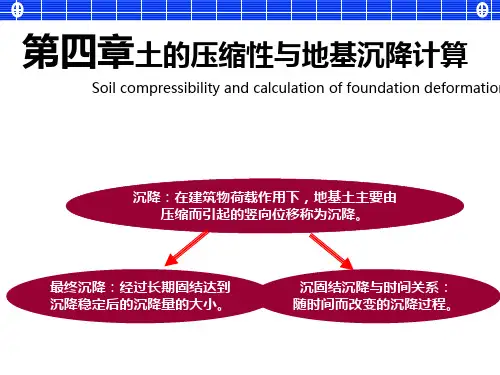
饱和粘性土地基沉降与时间的关系第四节 饱和粘性土地基沉降与时间的关系前面介绍的方法确定地基的沉降量，是指地基土在建筑荷载作用下达到压缩稳定后的沉降量，因而称为地基的最终沉降量。

然而，在工程实践中，常常需要预估建筑物完工及一般时间后的沉降量和达到某一沉降所需要的时间，这就要求解决沉降与时间的关系问题，下面简单介绍饱和土体依据渗流固结理论为基础解决地基沉降与时间的关系。

一、饱和土的有效应力原理用太沙基渗透固结模型很能说明问题。

当t ＝0时，u =σ，0='σ 当t ﹥0时，u +'=σσ，0≠'σ当t ＝∞时，σσ'=，u ＝0结论：u +'=σσ'，饱和土的渗透固结过程就是孔隙水压力向有效力应力转化的过程。

在渗透固结过程中，伴随着孔隙水压力逐渐消散，有效应力在逐渐增长，土的体积也就逐渐减小，强度随着提高。

二、饱和土的渗流固结整个模型（饱和土体）⎪⎩⎪⎨⎧→→→土的渗透性活塞小孔的大小孔隙水水固体颗粒骨架弹簧三、太沙基一维渗流固结理论（最简单的单向固结）——1925年太沙基提出一．基本假设：将固结理论模型用于反映饱和粘性土的实际固结问题，其基本假设如下： 1．土层是均质的，饱和水的2．在固结过程中，土粒和孔隙水是不可压缩的； 3．土层仅在竖向产生排水固结（相当于有侧限条件）；4．土层的渗透系数k 和压缩系数a 为常数； 5．土层的压缩速率取决于自由水的排出速率，水的渗出符合达西定律；6．外荷是一次瞬时施加的，且沿深度z 为均匀分布。

二．固结微分方程式的建立在饱和土体渗透固结过程中，土层内任一点的孔隙水应力),(t z u 所满足的微分方程式称为固结微分方程式。

在粘性土层中距顶面z 处取一微分单元，长度为dz ，土体初始孔隙比为e 1，设在固结过程中的某一时刻t ，从单元顶面流出的流量为q ＋dz zq ∂∂则从底面流入的流量将为q 。

于是，在dt 时间内，微分单元被挤出的孔隙水量为：dzdt zqdt q dz z q q dQ )(])[(∂∂=-∂∂+=设渗透固结过程中时间t 的孔隙比为e t ， 孔隙体积为：dz e e Vtv11+=在dt 时间内，微分单元的孔隙体积的变化量为：dzdt e e dt dz e et dt t V dV ttt v v ∂∂+=+∂∂=∂∂=1111)1(由于土体中土粒，水是不可压缩的，故此时间内流经微分单元的水量变化应该等于微分单元孔隙体积的变化量， 即：vdV dQ =或dzdt te e dzdt z q t∂∂+=∂∂111)(即：te ez q t∂∂+=∂∂111根据渗流满足达西定律的假设zu r k z h kki VA q w ∂∂=∂∂===式中：A 为微分单元在渗流方向上的载面积，A ＝1；i ：为水头梯度，zhi ∂∂=其中h 为侧压管水头高度μ：为孔隙水压力，h r u w =根据压缩曲线和有效应力原理，dp de a -=而up u z-=-=σσ'所以： tu a t e t ∂∂=∂∂ 并令ware k Cv )1(1+= 则得t uzu Cv ∂∂=∂∂22此式即为饱和土体单向渗透固结微分方程式 。

第3章地基沉降计算本章主要介绍土的压缩特性及其影响因素、土的压缩性指标及测定方法；地基最终沉降量计算，地基沉降与时间关系的计算等。

学习本章的目的：能根据建筑地基土层的分布、厚度、物理力学性质和上部结构的荷载，进行地基变形值的计算。

土层在荷载作用下将产生压缩变形，使建筑物产生沉降。

而沉降值的大小，取决于建筑物荷载的大小与分布；也取决于地基土层的类型、分布、各土层厚度及其压缩性。

为了计算地基变形，必须了解土的压缩性。

若地基基础的沉降超过建筑物所允许的范围，或者是建筑物各部分之间由于荷载不同或土层压缩性不均而引起的不均匀沉降，都会影响建筑物的安全和正常使用。

第一节土的压缩性一、土的压缩性及影响因素土的压缩性是指土在外部压力和周围环境作用下体积减小的特性。

土体体积减少包括三个方面：①土颗粒本身被压缩；②封闭在土中的水和气体被压缩；③土孔隙体积减小，土颗粒发生相对位移，孔隙中水和气体向外排出体积随之减少。

研究表明，工程实践中如遇到的压力<600kPa, 则土颗粒与土中水和气体本身的压缩极小，可以忽略不计。

故土的压缩被认为只是由于孔隙体积减小的结果。

对于透水性较大的无黏性土，土中水易于排出，压缩过程很快就可完成；对于饱和黏性土，由于透水性小，排水缓慢，达到压缩稳定需要较长时间。

土体在压力作用下，其压缩量随时间增长的过程，称为土的固结。

二、土的有效应力原理甲、乙两个完全相同的量筒的底部放置一层松砂土。

在甲量筒松砂顶面加若干钢球，使松砂承受σ的压力，松砂顶面下降，表明砂土已发生压缩，即砂土的孔隙比减小。

乙量筒松砂顶面小心缓慢地注水，在砂面以上高度h正好使砂层表面也增加σ的压力，结果发现砂层顶面不下降，表明砂土未发生压缩，即砂土的孔隙比e不变。

土体中存在两种不同性质应力：（1）由钢球施加的应力，通过砂土的骨架传递的部分称为有效应力（σ′），这种有效应力能使土层发生压缩变形。

（2）由水施加的应力通过孔隙中的水来传递，称为孔隙水压力（u），这种孔隙水压力不能使土层发生压缩变形。

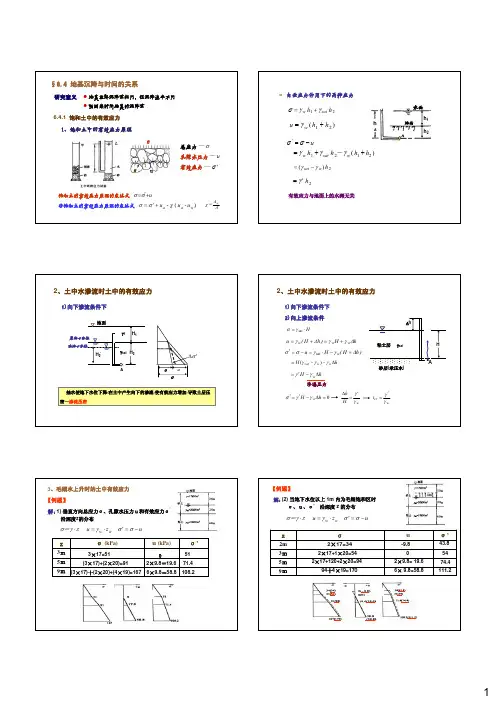
6.4.1 饱和土中的有效应力1、饱和土中的有效应力原理σσ’u非饱和土的有效应力原理的表达式饱和土的有效应力原理的表达式)- ( -w a a u u u χσσ+′=AA w＝χ总应力孔隙水压力有效应力σ —u—σ′—u+′=σσ研究意义§6.4 地基沉降与时间的关系z 地基最终沉降量相同，但沉降速率不同z 预测某时间地基的沉降量自重应力作用下的两种应力21h h sat w γγσ+=)(21h h u w +=γ)( 2121h h h h uw sat w ++=−=′γγγσσ－2)(h w sat γγ−=2h γ′=地面水面h 1h 2hA有效应力与地面上的水深无关H 2’σ’uσ1)向下渗流条件下σ′Δ2、土中水渗流时土中的有效应力H2H 1γ1γsat A地面抽水使地下水位下降,在土中产生向下的渗流,使有效应力增加,导致土层压密—渗流压密原地下水位现地下水位1)向下渗流条件下2、土中水渗流时土中的有效应力2)向上渗流条件H⋅=sat γσhH )h H (u w w w ΔγγΔγ+=+= )h H (H u w Δγγσσ+−⋅=−=′sat hH w w sat Δ−−=γγγ)(hH w Δ−′=γγ0=Δ−′=′h H w γγσwH h γγ′=Δwcr i γγ′=渗透压力砂层(承压水)粘土层γsatHΔhA9ｍ5ｍ3ｍσ’u (kPa)σ(kPa)ｚ1) 垂直方向总应力σ、孔隙水压力ｕ和有效应力σ’沿深度z 的分布【例题】解：uz u w w −=′⋅=⋅σσγγσ ｚ＝3×17=51(3×17)+(2×20)=91(3×17)十(2×20)+(4×19)=167０2×9.8＝19.66×9.8＝58.85171.4108.23、毛细水上升时的土中有效应力σ’uσｚ9ｍ5ｍ3ｍ2m 解：(2) 当地下水位以上1m 内为毛细饱和区时σ、ｕ、σ’沿深度z 的分布2×17=342×17+1×20=542×17+120+2×20=9494十4×19=170-9.82×9.8= 19.66×9.8=58.8111.2043.8 5474.4uz u w w −=′⋅=⋅σσγγσ ｚ＝【例题】6.4.2 一维固结理论1、饱和土渗流固结过程(3) 水的运动是层流，服从达西定律(6) 附加应力一次瞬时施加(5) 在渗流固结中，土的K和Es不变饱和土(2) 土的排水和压缩为竖直向的，即一维的(1) 土层均匀, 各向同性，完全饱和(4) 土颗粒和土中水都是不可压缩的(7) 土体的变形完全是孔隙水压力消散引起的基本假设2、太沙基一维固结理论在dt时间内流经微元体的水量变化：dzdtz q qdt dt dz z q q q ∂∂=−⎟⎠⎞⎜⎝⎛∂∂+=Δ根据达西定律，从而得dzdt zuγK q ∂∂−=Δdz zq q ∂∂+qzu γK w ∂∂−=KiA q =⎟⎠⎞⎜⎝⎛∂∂−=z h K 单向渗流固结微分方程推导wuh γ=在dt 时间内微元体的压缩量为dz e deV 11+=Δ()u σd a σd a de −=′=dt t u aadu ∂∂−=−=dzdtt ue a V ∂∂⋅+−=Δ11tue a z u γK w ∂∂+−=∂∂−1221△q =△Vtuz u a γe K w ∂∂=∂∂+221)(1tu z u C v∂∂=∂∂22——饱和土单向渗流固结微分方程v C ——土的固结系数，(cm 2/s, m 2/y r )根据初始条件和边界条件求微分方程的特解0 ,000000 00=≤≤∞==∂∂=∞<<==∞<<=≤≤=u H z t zuH z t u z t u H z t 时和时，和时，和时，和当σtu z u C v∂∂=∂∂22应用傅立叶级数，采用分离变量法求得特殊解如下(kPa)eH z m πsin mσπu T πm m z t ,z 41214−∞=⋅=∑m ——正奇整数（1，3，5，…）；e ——自然对数底；H ——最大排水距离，双面排水取(1/2)H ；T V ——时间因数。

第一章1. 土是由固体颗粒、水和气体组成的三相体。

2. 土颗粒粒径之间大小悬殊越大，颗粒级配曲线越平缓，不均匀系数越大，颗粒级配越好。

为了获得较大的密实度，应选择级配良好的土料作为填方或砂垫层的土料。

3. 塑性指数是指粘性土处于可塑状态时的含水量变化范围。

4. 根据液性指数可将粘性土划分为坚硬、硬塑、可塑、软塑、和流塑五种不同的软硬状态。

5. 反映无粘性土工程性质的主要指标是土的密实度，工程上常用指标孔隙比结合指标相对密实度来衡量。

6. 在土的三相指标中，可以通过试验直接测定的指标有比重、含水量和密度，分别可用比重瓶法、烘干法和环刀法测定。

7. 土的物理状态，对于无粘性土，一般指其密实度；而对于粘性土，则是指它的稠度。

8. 土的结构是指由土粒单元的大小、形状、相互排列及其连接关系等因素形成的综合特征，一般分为单粒结构、蜂窝结构和絮状结构三种基本类型。

9. 土的灵敏度越高，结构性越强，其受扰动后土的强度降低就越多。

10. 工程上常用不均匀系数表示土的颗粒级配，一般认为，不均匀系数小于5 的土属级配不良，不均匀系数大于10 的土属级配良好。

有时还需要参考曲率系数值。

11. 土的含水量为土中水的质量与土固体颗粒的质量之比。

12. 某砂层天然饱和重度为20KN/m3，土粒比重为2.68，并测得该砂土的最大干密度为1.71g/cm3，最小干密度为1.54g/cm3，则天然孔隙比为 0.68 ，最大孔隙比为 0.74 ，最小孔隙比为 0.57 。

13. 岩石按风化程度划分为微风化，中等风化，强风化；按其成因可分为岩浆岩，沉积岩，变质岩；按坚固程度可划分为硬质岩石，软质岩石。

14.砂土是指粒径大于 2 mm的颗粒累计含量不超过总质量的 50％，而粒径大于 0.075 mm的颗粒累计含量超过总质量的 50％的土。

15. 土由可塑状态转到流动状态的界限含水量叫做液限，可用锥式液限仪或碟式液限仪测定；土由半固态转到可塑状态的界限含水量叫做塑限，可用搓条法或液、塑限联合测定法测定。

《土力学与地基基础》习题解答学习项目1 土中应力计算任务1.1 土中自重应力的计算学习评价（1）土中自重应力计算的假定是什么？【答】计算土中自重应力时，假定土体为半无限体，即土体的表面尺寸和深度都是无限大，土体自重应力作用下的地基为均质的线性变形的半无限体，即任何一个竖直平面均可视为半无限体对称面。

这样，在任意竖直平面上，土的自重都不会产生剪应力，只有正应力存在。

因此，在均匀土体中，土中某点的自重应力将只与该点的深度有关。

（2）地基中自重应力的分布有什么特点？【答】自重应力在等重度的土中随深度呈直线分布，自重应力分布线的斜率是土的重度；自重应力在不同重度的成层土中呈折线分布，折点在土层分界线和地下水位线处；自重应力随深度的增加而增大。

（3）图1-7所示为某地基剖面图各土层的重度及地下水位，计算土中的自重应力并绘制自重应力分布图。

γ = 18.5 kN/m 黏土γ = 18 kN/m γ = 20 kN/m sat 细砂γ = 19 kN/m sat 黏土(按透水考虑)γ = 195 kN/m sat 砂砾2m 1m 1m 3m 2m 地下水位33333图1-7 某地基剖面图各土层的重度及地下水位【解】 第二层为细砂，地下水位以上的细砂不受浮力作用，而地下水位以下的受到浮力作用，其有效重度为333w sat 1m /kN 19.10kN/m 81.9kN/m 20=-=-='γγγ 第三层黏土按透水考虑，故认为黏土层受到水的浮力作用，其有效重度为333w sat 2m /kN 19.9kN/m 81.9kN/m 19=-=-='γγγ 第四层为砂砾，受到浮力作用，其有效重度为333w sat 3m /kN 69.9kN/m 81.9kN/m 5.19=-=-='γγγ 土中各点的自重应力计算如下：a 点：00c ===z z z γσ，b 点：，m 2=z kPa 37m 2kN/m 5.183c =⨯==z z γσc 点：，m 3=z kPa 55m 1kN/m 18kPa 3731c =⨯+==∑=n i i i z h γσd 点：，m 4=z kPa19.65m 1kN/m 19.10kPa 5531c =⨯+==∑=n i i i z h γσe 点：，m 7=z kPa76.92m 3kN/m 19.9kPa 19.6531c =⨯+==∑=n i i i z h γσf 点：，m 9=z kPa14.112m 2kN/m 69.9kPa 76.9231c =⨯+==∑=n i i i z h γσ该土层的自重应力分布如下图所示。