2.5时间与沉降的关系详解

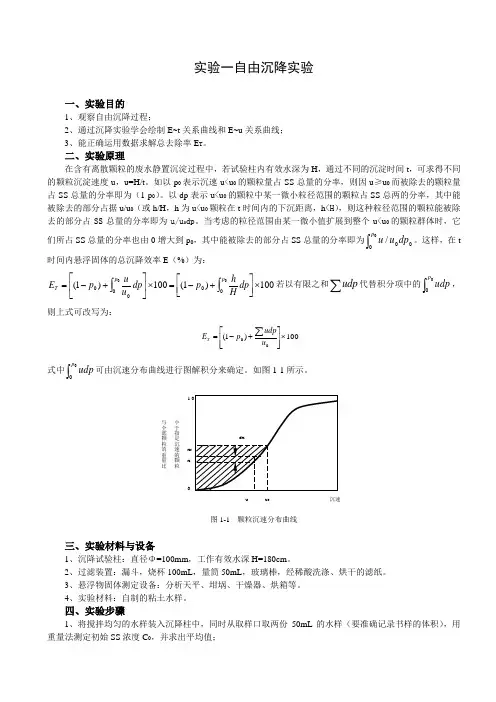
实验一自由沉降实验一、实验目的1、观察自由沉降过程；2、通过沉降实验学会绘制E~t 关系曲线和E~u 关系曲线；3、能正确运用数据求解总去除率E T 。

二、实验原理在含有离散颗粒的废水静置沉淀过程中，若试验柱内有效水深为H ，通过不同的沉淀时间t ，可求得不同的颗粒沉淀速度u ，u=H/t 。

如以p 0表示沉速u <u 0的颗粒量占SS 总量的分率，则因u ≥u 0而被除去的颗粒量占SS 总量的分率即为（1-p 0）。

以dp 表示u <u 0的颗粒中某一微小粒径范围的颗粒占SS 总两的分率，其中能被除去的部分占据u/u 0（或h/H ，h 为u <u 0颗粒在t 时间内的下沉距离，h <H ），则这种粒径范围的颗粒能被除去的部分占SS 总量的分率即为u/u 0dp 。

当考虑的粒径范围由某一微小值扩展到整个u <u 0的颗粒群体时，它们所占SS 总量的分率也由0增大到p 0，其中能被除去的部分占SS 总量的分率即为0000/dp u u p ⎰。

这样，在t时间内悬浮固体的总沉降效率E （%）为：100)1(100)1(0000000⨯⎥⎦⎤⎢⎣⎡+-=⨯⎥⎦⎤⎢⎣⎡+-=⎰⎰p p T dp H h p dp u u p E 若以有限之和∑udp 代替积分项中的⎰00p udp ，则上式可改写为：100)1(00⨯⎥⎥⎦⎤⎢⎢⎣⎡+-=∑u udp p E T式中⎰p udp 可由沉速分布曲线进行图解积分来确定。

如图1-1所示。

图1-1 颗粒沉速分布曲线三、实验材料与设备1、沉降试验柱：直径Φ=100mm ，工作有效水深H=180cm 。

2、过滤装置：漏斗，烧杯100mL ，量筒50mL ，玻璃棒，经稀酸洗涤、烘干的滤纸。

3、悬浮物固体测定设备：分析天平、坩埚、干燥器、烘箱等。

4、实验材料：自制的粘土水样。

四、实验步骤1、将搅拌均匀的水样装入沉降柱中，同时从取样口取两份50mL 的水样（要准确记录书样的体积），用重量法测定初始SS 浓度C 0，并求出平均值；小于指定沉速的颗粒与全部颗粒的重量比x 0 沉速u 0ux2、将柱内水位迅速调整到溢流口出，开始记时；3、当累计时间为5、10、20、30、45、60、90、120min时，从试验柱中部取样口取水2份，每份约50mL （准确记录体积）。

《北京大气干沉降及PM2.5中重金属和有机物污染及来源研究》篇一一、引言随着工业化和城市化的快速发展，大气污染问题日益突出，尤其是以北京为代表的大城市。

大气干沉降及PM2.5中的重金属和有机物污染成为当前环境科学研究的重要领域。

本研究以北京地区为研究对象，旨在深入探讨其大气干沉降特性以及PM2.5中重金属和有机物的污染程度和来源，为大气污染治理提供科学依据。

二、研究背景与意义北京作为我国的政治、文化中心，其大气环境质量关系到数百万市民的健康和生活质量。

近年来，PM2.5问题备受关注，其携带的重金属和有机物污染物对环境和人体健康造成严重威胁。

因此，对北京地区大气干沉降及PM2.5中重金属和有机物污染的研究，不仅有助于了解区域大气环境质量现状，还能为制定有效的污染控制措施提供科学依据。

三、研究方法本研究采用现场观测、实验室分析和模型模拟相结合的方法。

首先，在北京市内设置多个观测点，收集大气干沉降样品及PM2.5样品；其次，利用先进的检测仪器对样品中的重金属和有机物进行定量分析；最后，结合气象数据和模型模拟，分析污染物的来源和传输路径。

四、北京大气干沉降特性分析北京地区的大气干沉降主要包括颗粒物和气态污染物的沉降。

通过对观测数据的分析，发现干沉降中重金属元素如铅、锌、镉等有较高的浓度，而有机物主要来自工业排放、汽车尾气等。

干沉降的速率受气象条件、地形等因素影响，呈现出季节性和空间分布的不均匀性。

五、PM2.5中重金属和有机物污染分析PM2.5中的重金属和有机物主要来源于工业排放、交通尾气、燃煤等。

这些污染物经过复杂的大气化学反应后，以气溶胶的形式存在于空气中，对环境和人体健康造成危害。

通过实验室分析发现，北京地区PM2.5中的重金属和有机物浓度较高，尤其是某些重金属如铅、镉等超过了国家规定的标准。

六、污染来源解析通过模型模拟和数据分析，我们发现北京地区PM2.5中重金属和有机物的来源主要包括工业排放、交通尾气、燃煤等。

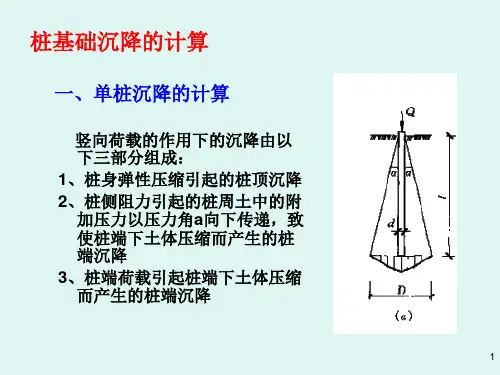
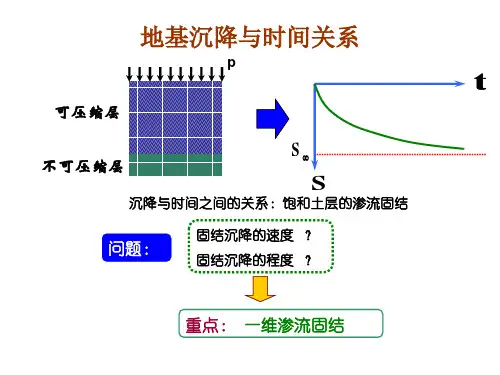
沉降与时间的关系曲线是工程地质和土木工程中的重要工具，它描述了地基或土体在荷载作用下的沉降量如何随时间变化。

这种关系对于预测土壤或地基的稳定性以及制定合理的设计和施工决策至关重要。

首先，我们需要理解沉降的概念。

沉降是指土壤或地基在受到外力作用后，其高度发生降低的现象。

这种现象通常是由于土壤中的水分被挤出，或者土壤颗粒之间的空隙被压缩所导致的。

沉降的程度通常用沉降量来表示，单位通常是毫米或厘米。

然后，我们来看看沉降与时间的关系。

在开始阶段，沉降速度通常会很快，随着时间的推移，沉降速度会逐渐减慢。

这是因为在开始阶段，土壤中的水分和空隙较多，容易发生变形；而在后期，土壤已经接近其固结状态，变形的空间较小。

因此，沉降与时间的关系通常呈现出先快后慢的趋势。

为了更直观地描述这种关系，我们可以绘制沉降与时间的关系曲线。

在这个曲线中，沉降量s为纵轴，时间t为横轴。

我们可以通过观测每次的沉降量，然后将这些数据点连接起来，形成一条曲线。

这条曲线就代表了沉降与时间的关系。

通过观察这条曲线，我们可以得出很多有用的信息。

例如，我们可以通过找到曲线的拐点来确定沉降的速度何时开始减慢；我们还可以通过比较不同时间的沉降量来评估土壤的稳定性；此外，我们还可以通过预测未来的沉降量来制定相应的设计和施工计划。

总的来说，沉降与时间的关系曲线是一种非常实用的工具，它可以帮助工程师更好地理解和控制土壤和地基的变形。

然而，要准确地绘制这条曲线，我们需要有精确的观测数据和深入的理论分析。

第四节 饱和粘性土地基沉降与时间的关系前面介绍的方法确定地基的沉降量，是指地基土在建筑荷载作用下达到压缩稳定后的沉降量，因而称为地基的最终沉降量。

然而，在工程实践中，常常需要预估建筑物完工及一般时间后的沉降量和达到某一沉降所需要的时间，这就要求解决沉降与时间的关系问题，下面简单介绍饱和土体依据渗流固结理论为基础解决地基沉降与时间的关系。

一、饱和土的有效应力原理用太沙基渗透固结模型很能说明问题。

当t ＝0时，u =σ，0='σ 当t ﹥0时，u +'=σσ，0≠'σ当t ＝∞时，σσ'=，u ＝0结论：u +'=σσ'，饱和土的渗透固结过程就是孔隙水压力向有效力应力转化的过程。

在渗透固结过程中，伴随着孔隙水压力逐渐消散，有效应力在逐渐增长，土的体积也就逐渐减小，强度随着提高。

二、饱和土的渗流固结整个模型（饱和土体）⎪⎩⎪⎨⎧→→→土的渗透性活塞小孔的大小孔隙水水固体颗粒骨架弹簧三、太沙基一维渗流固结理论（最简单的单向固结）——1925年太沙基提出 一．基本假设：将固结理论模型用于反映饱和粘性土的实际固结问题，其基本假设如下： 1．土层是均质的，饱和水的2．在固结过程中，土粒和孔隙水是不可压缩的； 3．土层仅在竖向产生排水固结（相当于有侧限条件）； 4．土层的渗透系数k 和压缩系数a 为常数；5．土层的压缩速率取决于自由水的排出速率，水的渗出符合达西定律； 6．外荷是一次瞬时施加的，且沿深度z 为均匀分布。

二．固结微分方程式的建立在饱和土体渗透固结过程中，土层内任一点的孔隙水应力),(t z u 所满足的微分方程式称为固结微分方程式。

在粘性土层中距顶面z 处取一微分单元，长度为dz ，土体初始孔隙比为e 1，设在固结过程中的某一时刻t ，从单元顶面流出的流量为q ＋dz zq∂∂则从底面流入的流量将为q 。

于是，在dt 时间内，微分单元被挤出的孔隙水量为：dzdt zqdt q dz z q q dQ )(])[(∂∂=-∂∂+= 设渗透固结过程中时间t 的孔隙比为e t ， 孔隙体积为：dz e e V tv 11+=在dt 时间内，微分单元的孔隙体积的变化量为：dzdte e dt dz e et dt t V dV ttt v v ∂∂+=+∂∂=∂∂=1111)1(由于土体中土粒，水是不可压缩的，故此时间内流经微分单元的水量变化应该等于微分单元孔隙体积的变化量，即：v dV dQ = 或 dzdt t e e dzdt z q t∂∂+=∂∂111)(即：te e z q t∂∂+=∂∂111 根据渗流满足达西定律的假设zu r k z h kki VA q w ∂∂=∂∂=== 式中：A 为微分单元在渗流方向上的载面积，A ＝1；i ：为水头梯度，zhi ∂∂=其中h 为侧压管水头高度 μ：为孔隙水压力， 0h r u w = 根据压缩曲线和有效应力原理，dpde a -= 而u p u z -=-=σσ' 所以：t ua t e t ∂∂=∂∂ 并令war e k Cv )1(1+= 则得t uzu Cv ∂∂=∂∂22此式即为饱和土体单向渗透固结微分方程式 。

关于沉降观测，这些你必须知道！导语随着工业与民用建筑业的发展，各种复杂而大型的工程建筑物日益增多，工程建筑物的兴建，改变了地面原有的状态，并且对于建筑物的地基施加了一定的压力，这就必然会引起地基及周围地层的变形。

为了保证建（构）筑物的正常使用寿命和建（构）筑物的安全性，并为以后的勘察设计施工提供可靠的资料及相应的沉降参数，建（构）筑物沉降观测的必要性和重要性愈加明显。

现行规范也规定，高层建筑物、高耸构筑物、重要古建筑物及连续生产设施基础、动力设备基础、滑坡监测等均要进行沉降观测。

特别在高层建筑物施工过程中，应用沉降观测加强过程监控，指导合理的施工工序，预防在施工过程中出现不均匀沉降，及时反馈信息，为勘察设计施工部门提供详尽的一手资料，避免因沉降原因造成建筑物主体结构的破坏或产生影响结构使用功能的裂缝，造成巨大的经济损失。

一规范中的相关规定《建筑变形测量规范JGJ8－2007》规定：（1）建筑物沉降观测应测定建筑物地基的沉降量、沉降差及沉降速度并计算基础倾斜、局部倾斜、相对弯曲及构件倾斜。

（2）沉降观测点的布置，应以能全面反映建筑物地基变形特征并结合地质情况及建筑结构特点确定。

点位宜选设在下列位置：１、建筑物的四角、大转角处及沿外墙每10～15m处或每隔2～3根柱基上。

２、高低层建筑物、新旧建筑物、纵横墙等交接处的两侧。

３、建筑物裂缝和沉降缝两侧、基础埋深相差悬殊外、人工地基与天然地基接壤处、不同结构的分界处及填挖方分界处。

４、宽度大于等于15m或小于15m而地质复杂以及膨胀土地区的建筑物，在承重内隔墙中部设内墙点，在室内陆面中心及四周设地面点。

５、邻近堆置重物处、受振动有显著影响的部位及基础下的暗浜（沟）处。

６、框架结构建筑物的每个或部分柱基上或沿纵横轴线设点。

７、片筏基础、箱形基础底板或接近基础的结构部分之四角处及其中部位置。

８、重型设备基础和动力设备基础的四角、基础型式或埋深改变处以及地质条件变化处两侧。

沉降的原理沉降是指土壤或地基在受到外部荷载作用下发生的垂直位移现象。

在建筑工程中，沉降是一个非常重要的问题，因为它会对建筑物的稳定性和安全性产生影响。

了解沉降的原理对于工程设计和施工具有重要意义。

沉降的原理可以从土壤力学的角度来解释。

土壤是由颗粒和孔隙水组成的多相体系，当外部荷载作用在土壤上时，土壤颗粒之间会发生相对位移，从而引起土壤的变形。

在这个过程中，孔隙水也会随着土壤的变形而发生流动，这就是沉降现象的基本原理。

沉降的原理可以用沉降计算公式来描述。

根据弹性理论和土壤力学的基本原理，可以得到沉降计算公式为：△h = (q × B)/(E × (1-μ^2))。

其中，△h为沉降量，q为荷载，B为地基宽度，E为土壤的弹性模量，μ为泊松比。

这个公式可以用来计算在给定荷载下地基的沉降量，为工程设计提供了重要的参考依据。

沉降的原理还与土壤的物理性质和力学性质密切相关。

土壤的类型、含水量、密实度、孔隙度等因素都会影响土壤的沉降特性。

例如，含水量高的粘性土壤在受到荷载作用后会发生较大的沉降，而砂土则因为颗粒间的摩擦作用而产生较小的沉降。

因此，在工程设计中需要对土壤的物理和力学性质进行充分的研究和分析，以准确预测土壤的沉降行为。

此外，沉降的原理还与建筑物的结构特性和荷载特性有关。

建筑物的结构刚度和荷载分布会影响地基土壤的受力状态，进而影响沉降的发生和发展。

因此，在建筑物的设计和施工中需要充分考虑建筑物的结构特性和荷载特性，以减小沉降对建筑物的影响。

综上所述，沉降的原理是一个复杂的土力学问题，涉及土壤的物理性质、力学性质、结构特性和荷载特性等多个方面。

了解沉降的原理对于工程设计和施工具有重要意义，可以为工程安全和稳定提供可靠的依据。

因此，在工程实践中需要对沉降的原理进行深入的研究和分析，以保证工程的质量和安全。

6.4.1 饱和土中的有效应力1、饱和土中的有效应力原理σσ’u非饱和土的有效应力原理的表达式饱和土的有效应力原理的表达式)- ( -w a a u u u χσσ+′=AA w＝χ总应力孔隙水压力有效应力σ —u—σ′—u+′=σσ研究意义§6.4 地基沉降与时间的关系z 地基最终沉降量相同，但沉降速率不同z 预测某时间地基的沉降量自重应力作用下的两种应力21h h sat w γγσ+=)(21h h u w +=γ)( 2121h h h h uw sat w ++=−=′γγγσσ－2)(h w sat γγ−=2h γ′=地面水面h 1h 2hA有效应力与地面上的水深无关H 2’σ’uσ1)向下渗流条件下σ′Δ2、土中水渗流时土中的有效应力H2H 1γ1γsat A地面抽水使地下水位下降,在土中产生向下的渗流,使有效应力增加,导致土层压密—渗流压密原地下水位现地下水位1)向下渗流条件下2、土中水渗流时土中的有效应力2)向上渗流条件H⋅=sat γσhH )h H (u w w w ΔγγΔγ+=+= )h H (H u w Δγγσσ+−⋅=−=′sat hH w w sat Δ−−=γγγ)(hH w Δ−′=γγ0=Δ−′=′h H w γγσwH h γγ′=Δwcr i γγ′=渗透压力砂层(承压水)粘土层γsatHΔhA9ｍ5ｍ3ｍσ’u (kPa)σ(kPa)ｚ1) 垂直方向总应力σ、孔隙水压力ｕ和有效应力σ’沿深度z 的分布【例题】解：uz u w w −=′⋅=⋅σσγγσ ｚ＝3×17=51(3×17)+(2×20)=91(3×17)十(2×20)+(4×19)=167０2×9.8＝19.66×9.8＝58.85171.4108.23、毛细水上升时的土中有效应力σ’uσｚ9ｍ5ｍ3ｍ2m 解：(2) 当地下水位以上1m 内为毛细饱和区时σ、ｕ、σ’沿深度z 的分布2×17=342×17+1×20=542×17+120+2×20=9494十4×19=170-9.82×9.8= 19.66×9.8=58.8111.2043.8 5474.4uz u w w −=′⋅=⋅σσγγσ ｚ＝【例题】6.4.2 一维固结理论1、饱和土渗流固结过程(3) 水的运动是层流，服从达西定律(6) 附加应力一次瞬时施加(5) 在渗流固结中，土的K和Es不变饱和土(2) 土的排水和压缩为竖直向的，即一维的(1) 土层均匀, 各向同性，完全饱和(4) 土颗粒和土中水都是不可压缩的(7) 土体的变形完全是孔隙水压力消散引起的基本假设2、太沙基一维固结理论在dt时间内流经微元体的水量变化：dzdtz q qdt dt dz z q q q ∂∂=−⎟⎠⎞⎜⎝⎛∂∂+=Δ根据达西定律，从而得dzdt zuγK q ∂∂−=Δdz zq q ∂∂+qzu γK w ∂∂−=KiA q =⎟⎠⎞⎜⎝⎛∂∂−=z h K 单向渗流固结微分方程推导wuh γ=在dt 时间内微元体的压缩量为dz e deV 11+=Δ()u σd a σd a de −=′=dt t u aadu ∂∂−=−=dzdtt ue a V ∂∂⋅+−=Δ11tue a z u γK w ∂∂+−=∂∂−1221△q =△Vtuz u a γe K w ∂∂=∂∂+221)(1tu z u C v∂∂=∂∂22——饱和土单向渗流固结微分方程v C ——土的固结系数，(cm 2/s, m 2/y r )根据初始条件和边界条件求微分方程的特解0 ,000000 00=≤≤∞==∂∂=∞<<==∞<<=≤≤=u H z t zuH z t u z t u H z t 时和时，和时，和时，和当σtu z u C v∂∂=∂∂22应用傅立叶级数，采用分离变量法求得特殊解如下(kPa)eH z m πsin mσπu T πm m z t ,z 41214−∞=⋅=∑m ——正奇整数（1，3，5，…）；e ——自然对数底；H ——最大排水距离，双面排水取(1/2)H ；T V ——时间因数。

《西安市大气颗粒物PM2.5污染特征及其与降水关系研究》篇一摘要本文旨在探讨西安市大气颗粒物PM2.5的污染特征及其与降水的相互关系。

通过收集和分析西安市近年的PM2.5浓度数据和气象数据，本文揭示了PM2.5污染的时空分布特征，并探讨了其与降水事件的关系。

本文的研究有助于加深对PM2.5污染特征的理解，并为城市环境治理提供科学依据。

一、引言随着工业化和城市化的快速发展，大气颗粒物污染问题日益突出，其中PM2.5（粒径小于或等于 2.5微米的颗粒物）由于其对人体健康和环境的危害性备受关注。

作为我国的重要城市之一，西安市的PM2.5污染问题尤为严重。

因此，研究西安市PM2.5的污染特征及其与降水的相互关系具有重要的现实意义。

二、研究区域与方法2.1 研究区域本研究以西安市为研究对象，该市位于中国中部，是陕西省的省会城市，人口密集，工业发达。

2.2 研究方法本研究采用的方法主要包括数据收集、统计分析及模型构建。

数据来源于西安市环保局提供的PM2.5浓度数据及气象数据。

通过统计分析，揭示PM2.5浓度的时空分布特征；通过构建模型，探讨PM2.5与降水事件的关系。

三、PM2.5污染特征分析3.1 空间分布特征分析结果显示，西安市的PM2.5浓度在空间上呈现出明显的差异。

城市中心及工业区的PM2.5浓度较高，而郊区及农村地区的浓度相对较低。

这主要与交通排放、工业生产及气象条件等因素有关。

3.2 时间变化特征时间上，PM2.5浓度在冬季和春季较高，夏季和秋季相对较低。

这主要受到供暖季的影响以及气象条件的变化。

此外，还发现PM2.5浓度在特定天气条件下（如静风、逆温等）有明显上升趋势。

四、PM2.5与降水的关系分析4.1 PM2.5与降水量统计关系通过对历史数据的分析发现，降水量对PM2.5浓度有显著影响。

在降水事件发生时，PM2.5浓度往往会有所降低。

这主要是由于降水过程能够有效地冲刷大气中的颗粒物，降低其浓度。

地基沉降计算任何建筑物都要建造在土层或岩石上面，土层受到建筑物的荷载作用后，就要产生压缩变形，当变形超过了允许值，将影响建筑物的使用功能。

或者当荷载较大超过了地基土的承载能力，将造成地基的破坏，丧失稳定性，从而导致整体的失稳。

为保证建筑物的安全，岩土体应同时满足两个基本要求：（1）土体应具有足够的强度，在荷载作用后，不致因失稳而破坏；（2）土体不能产生过大的变形而影响建筑物的安全与正常使用。

一般建筑荷载等级不大，大部分土体的强度与压缩性，容易满足上述要求。

在一些地区由于特定的地质条件，工程上常遇到软弱土体，对这种土体必须进行相应的处理，才能满足强度与变形的要求。

一、地基最终沉降量的计算地基最终沉降量是指地基在建筑物荷载作用下，最后的稳定沉降量。

计算地基最终沉降量的目的，在于确定建筑物最大沉降量、沉降差和倾斜，并控制在容许范围以内，以保证建筑物的安全和正常使用。

计算地基沉降量的方法有多种，如分层总和法、规范法及弹性理论法等。

一）分层总和法1、单向压缩基本公式1）计算原理及公式假定：（1）地基土受荷后不能发生侧向变形；（2）按基础底面中心点下附加应力计算土层分层的压缩量； （3）基础最终沉降量等于基础底面下压缩层（见后）范围内各土层分层压缩量的总和。

我们将基础底面下压缩层范围内的土层划分为若干分层，现分析第i 分层的压缩量的计算方法，参见（图5-1）。

在建筑物建造以前，第i 分层仅受到土的自重应力作用，在建筑物建造以后，该分层除受自重应力外，还受到建筑物荷载所产生的附加应力的作用。

如前所述，在一般情况下，土的自重应力产生的变形过程早已完结，而只有附加应力（新增加的）才会产生土层新的变形，从而使基础沉降。

由于假定土层受荷后不产生侧向变形，所以它的受力状态与压缩试验时土样一样，故第i 层的压缩量可按下式计算：S i =i i h ε∆ （5-1）其中iii i e e e 1211+-=∆ε，代入上式，得：S i =i iii h e e e 1211+- （5-2）则地基总沉降量： S=∑=ni i S 1=i iii h e e e ∑+-1211 （5-3）式中： S —地基最终沉降量；i e 1—第i 分层在建筑物建造前，在土的平均自重应力作用下的孔隙比；i e 2—第i 分层在建筑物建造后，在土的平均自重应力和平均附加应力作用下的孔隙比；h i —第i 分层的厚度，为了保证计算的精确性，一般取h i ≤0.4b （b 为基础宽度）； n —压缩层范围内土层分层数目。