第七章二阶电路重点要求:1. 理解二阶电路零输入响应过渡过程的三种情况;2. 了解二阶电路的阶跃响应和冲击响应。
3.学习数学中的拉普拉斯变换的定义、性质及反变换的方法;4.掌握用拉普拉斯变换求解电路的过渡过程的方法。
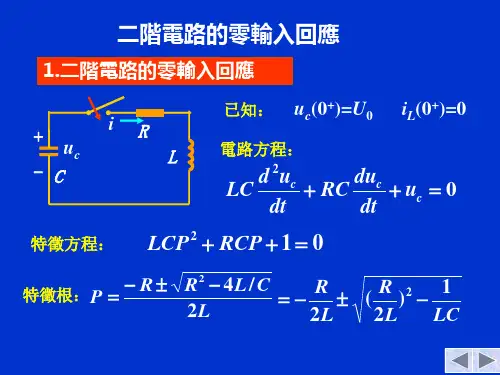
1§7-1 二阶电路的零输入响应二阶电路:由二阶微分方程描述的电路。
典型的二阶电路是RLC串联电路。
求全响应方法:1.经典法(时域分析法)全响应= 稳态分量(强制分量) + 暂态分量(自由分量)2.拉普拉斯变换法(频域分析法)2响应曲线:U 0u C , u L , i 0ωtiu Cu L§7-1 二阶电路的零输入响应220p ααω=−±−一. 问题的提出经典法解动态电路过渡过程存在的问题：对较复杂的电路，联立求解微分方程特别是定积分常数比较困难。
若激励不是直流或正弦交流时，特解不容易求得。
二. 拉氏变换法用积分变换的原理简化求解电路过渡过程时域电路解微分方程时域响应f(t)取拉斯变换复频域电路解代数方程复频域响应F(s)取拉斯反变换7.2 动态电路的复频域分析应用拉氏变换法进行电路分析称为电路的一种复频域分析方法，也叫运算法！是数学中的一种积分变换.优点：对复杂电路﹑无稳态情况﹑换路时出现强迫跃变等用拉氏变换法较经典法方便。
三. 拉普拉斯变换的定义设函数f(t)在0≤t ≤∞时有定义，则积分称为原函数f(t)的拉普拉斯变换（象函数）。
()dte tf s F st∫∞−−=0)(式中s=σ+ j ω----复频率。
单位：熟悉的变换:相量法⎩⎨⎧=∫∞+∞−)s (21)(ds e F j t f stj c j c π反变换正变换ZH1.象函数F (s)存在的条件：∞<∫∞−−dt et f st0)(说明：电路分析中的函数都能满足上述条件。
2. 在电路中积分的下限定义为“0-”, 更有实际意义(将奇异函数也包括在内)。
[][]⎩⎨⎧==−)( )()( )( S F t f t f S F 1简写正变换反变换在电路分析中通常直接查表得到。
四. 几个简单f(t)的象函数as dt dt e L ee e ta s stat at−===−−∞−∞∫∫−−1][.3)(00()()()()1][.100000====∫∫∫+−+−−−−∞dt t dt t dt t L e et ststδδδδ()()sdt dt t L eet stst1][.200===−∞−∞∫∫−−εεℒℒℒ说明：拉普拉斯变换将时域中的微分运算变成了复频域中算子s 与象函数的乘法运算。
)0(0)(),()]([−−==f t t f s F t f L 时的初值为在且若()()()()()()()）（−−∞−−∞∞−−∞−=+−=−−==∫∫∫−−−−0]00[)(][][0000f s sFdte tf s f dtes t f t f edtedtt dfdtt dfL stststst二﹑微分性质：证明：()())0(][−−=f s sF dtt df L 则∫∫−=vduuv udv 分部积分公式ℒℒℒ三﹑积分性质：说明：拉普拉斯变换将时域中的积分运算变成了复频域中算子s 与象函数的除法运算。
∫==ts F sdt t f L s F t f L 0)(1])([),()]([则有若()()()()()00,,0===−−∫h t f dtt dh dt t f t h t且则设()()()][0)]([][t h L s h t h L s dtt dh L ×=−×=−由微分性质有：()()()()s F st f L s dt t dh L s t h L 1][1][1][===∴∫=t s F sdt t f L 0)(1])([即有：ℒℒℒℒℒℒℒ四﹑延迟性质：0[()](),[()]()st L f t F s L f t t eF s −=−=若则有例5. 求矩形脉冲f(t)=A{ε(t)-ε(t-t 0)}的象函数。
解：()()()())1(11][][][)]([τττεετεεs s e sA e s A s A t L A t L A t t L A t f L −−−=⋅−⋅=−×−×=−−×=f(t)τtAℒℒℒℒ、n、、i p s s F k ip s i i L 321))((=−==122112121()()n n nn n n s F s s p s p s p p s p AAAAA−−+=++++−−−−−LL )(lim)(22s F n p s Anp S n −→=)]([lim )(21s F n dsdp s An p S n −→=1. 二重根情况:AA n 11−L L 其中系数的求法与前面相同。
()()kk S p k s p F s A ==−即有1,,2,1−=n k L L 具有重根若0=)(s D 22. n 重根情况:p s a s a s a s F nmm m )()(11−10−+⋅⋅⋅++=nnn n p s K p s K p s K p s K s F )()()()(111−11−12112111−+−+⋅⋅⋅+−+−=1=11−=pS nn s F p s K )]()[(1=11−1−=ps nn s F p s dsd K )]()([1=1222−1−21=ps n n s F p s dsd K )]()(1(−=⎟⎠⎞⎜⎝⎛+===→−S S s s ds d s F ds d s A()212)(lim 023023=⎟⎟⎠⎞⎜⎜⎝⎛−+===→S S s s s F s A5)1(2)]([!11lim 02322=⎟⎠⎞⎜⎝⎛−+=⋅==→S S s s ds d s F s dsd A例8)1(2!21)]([!21lim 0222322021=⎟⎟⎠⎞⎜⎜⎝⎛−+=⋅==→S S s s dsd s F s ds d A()32232322221212112581318)1(1)(ss s s s ss s s s s F AAAAA+++−+−−=+++−+−=()()()())58(38!1325838213t t e t tt te e t f ttt++++−=−++++−=∴−()()atn nen t a s −−−+!1)(11的原函数为查表得：相量形式KCL 、KVL 元件→复阻抗、复导纳相量形式电路模型U u Ii &&→→7.2.2运算电路I Z U&&=基尔霍夫定律的时域表示：∑=0(t)i ∑=0(t)u 基尔霍夫定律的相量表示：∑=0I &0=∑U &相量法：1.电路定律的运算形式（复频域形式）电路定律的运算形式：)()()()(s I t i s U t u →→元件→运算阻抗、运算导纳运算形式的KCL 、KVL运算形式电路模型)()()(s I s Z s U =∑=0)I(s 0)(=∑s U 运算法与相量法的基本思想类似：①把时间函数变换为对应的象函数②把微积分方程变换为以象函数为变量的线性代数方程目的：直接由复频域形式的电路定律和复频域形式的电路模型列写复频域电路方程。
二﹑欧姆定律的运算形式（复频域形式）1. R ﹑L ﹑C 三元件的运算电路①电阻的运算电路U(s)=RI(s)拉氏变换u(t)=Ri(t)u (t )i (t )R+-时域电路U (s )I (s)R+-运算电路②电感的运算电路i (t )u (t )L+-时域电路tt i Lt u d d )()(=拉氏变换)]0()([)(−−=i s sI L s U )0()()(−−=Li s sLI s U sL I (s )U (s)+-+-Li(0-)运算电路附加电源运算感抗②电容的运算电路拉氏变换()()su s I sc s U −+=01)(运算电路附加电源运算容抗时域电路i (t )u (t )C+-()()()∫−−+=tu dt t i ct u 001I (s )U (s)+-+-()s u −0sc12．R ﹑C ﹑L 串联电路的运算阻抗0)0(,0)0(≠−≠−CLu i 设()s I RsL +_()s U _+_+()−0L Li sC1()su C−0运算电路()su s I sC sL R s U C L Li −+−−++=0)0()()1()(()su Lis U s I s Z C L−−−+=0)0()()()(()t i LCR+_()t u 时域电路+u c(t)－()s I RsL +_()s U _+_+()−0L Li sC1()su C−0sCsL R s Z /1)(++=运算阻抗：()s Z s Y 1)(=运算导纳：()su Lis U s I s Z C L−−−+=0)0()()()(3. 运算形式的欧姆定律运算形式的欧姆定律三﹑独立电源及受控电源的运算电路独立电源的运算电路+－U(s)=A/s+－u(t)=Ai(t)=δ(t)I(s)=1四﹑运算电路模型时域电路中所有变量、激励源、受控源都用其象函数表示，电路元件都用运算阻抗（或运算导纳）及相应的附加电源表示，所得到的电路模型称为运算电路模型。
1. 电压、电流用象函数形式2. 元件用运算阻抗或运算导纳3.电容电压和电感电流初始值用附加电源表示VCR 运算形式)(:1=∑=bk ks I KCL 运算形式0)(:1=∑=bk ks U KVL 运算形式因而可将电阻电路中各种分析方法应用于运算电路中。
7.2.3 应用拉普拉斯变换法分析线性电路求解步骤：1. 求初始值:由换路前的电路求());0(0−−i L C u 和2.画运算电路:根据各元件的运算模型将换路后时域电路转化为运算电路;3.求频域解: 在运算电路中应用各种解题方法列代数方程解得象函数F(s);4.反变换得时域解: 将F(s)部分分式展开后求得原函数f(t)。
RL Us+_()t u C CS(t=0)()t i L 已知：R=40Ω, L=0.5H, C=50μF, Us=40V, ()Vu C 200=−求: 开关闭合后u c (t)的变化规律。
