【2019年整理】函数的单调性与极值3理
- 格式:ppt
- 大小:476.50 KB
- 文档页数:35
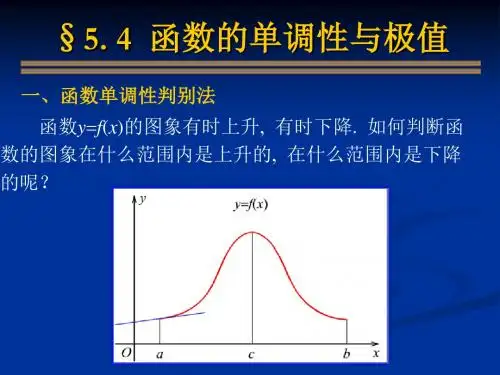





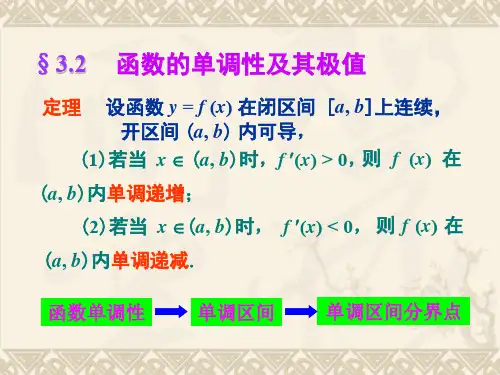




函数的单调性与极值函数)(x f y =单调性的考察,可用当21x x <时,比较)(1x f 与)(2x f 的大小来进行判定的.但判定)(1x f 与)(2x f 的大小并非是一件容易的事情.所以希望找到一种简单的判定方法.我们知道,如果函数)(x f y =在某区间上单调增加,其图形是一条沿x 轴正向上升的曲线,曲线上各点处的切线斜率为非负,即0)(≥'='x f y ;若单调减少,其图形是一条沿x 轴正向下降的曲线,曲线上各点处的切线斜率为非正,即0)(≤'='x f y ,如图3-2.可见,函数的单调性与导数的符号有着密切的联系.那么反之成立吗?定理1 设函数)(x f 在区间),(b a (1)如果在),(b a 内0)(>'x f ,那么)(x f 在),(b a 内单调增加; (2)如果在),(b a 内0)(<'x f ,那么)(x f 在),(b a 内单调减少.证明 (1)在),(b a 内任取两点21,x x ,且21x x <,根据拉格郎日中值定理,存在一点ξ(21x x <<ξ),使))(()()(1212x x f x f x f -'=-ξ (1)因为在区间),(b a 内有0)(>'x f ,则(1)式中的0)(>'ξf ,而012>-x x ,因此由(1)式知)()(12x f x f >,这就是说)(x f 在),(b a 内单调增加. 同理可证明结论(2)成立.有些可导函数在某区间内的个别点处导数等于零,但函数在该区间内仍是单调增加(或单调减少).如函数3x y =的导数23x y =',在0=x 时,0='y ,但它在区间),(+∞-∞内是单调增加.例1 判定函数13--=-x ey x的单调性.解 因为函数的定义域为),(+∞-∞,其导数为3--='-xe y ,所以在整个定义域内都有0<'y ,故函数13--=-x e y x 在定义域内单调减少.有时,函数在其整个定义域上不具有单调性,但在其各个部分区间上却具有单调性,如图3-3所示. 函数)(x f 在区间],[],,[21b x x a 上单调增加,而 在区间],[21x x 上单调减少,且从图3-3上容易看到,可导函数)(x f 在单调增加、减少的分界点处的导数为零,即0)()(21='='x f x f使导数等于零的点(即方程0)(='x f 的实根),叫做函数)(x f 的驻点.因此要确定可导函数)(x f 的单调区间,首先要求出驻点,然后用这些驻点将其定义域分成若干个区间,再在每个区间上判定函数的单调性.例2讨论函数)(x f x x x 2213123-+=的单调性 解 因为)1)(2(2)(2-+=-+='x x x x x f ,令0)(='x f ,得驻点1,221=-=x x .这两点将)(x f 的定义域),(+∞-∞分成三个部分:),1(),1,2(),2,(+∞---∞,下面用列表的形式来进行讨论,(表中“ ”表示单调增加,“ ”表示单调减少)根据上面的讨论可得:函数)(x f 在区间)2,(--∞和),1(+∞内单调增加,在区间()1,2-内单调减少. 另外,还需注意函数的不定义点,或是连续而不可导点也可能是单调区间的分界点. 例3 确定函数32x y =的单调区间. 解 函数的定义域为),(+∞-∞,而332x y =',显然当0=x 又函数没有驻点.但当0>x 时,有0>'y ,函数在区间),0(+∞内单调增加; 当0<x 时,有0<'y ,函数在区间)0,(-∞内单调减少. 二、函数的极值定义3.1 设函数)(x f 在),(0δx N 有定义,且对此邻域内任一点x )(0x x ≠均有)(x f )(0x f <,则称)(0x f 是函数)(x f 的一个极大值;如果对此邻域内任一点x )(0x x ≠均有)(x f )(0x f >,则称)(0x f 是函数)(x f 的一个极小值. 函数的极大值与极小值统称为函数的极值,使函数取得极值的点0x 称为极值点.从图3-5可知,关于函数的极值,应注意以下几点:(1) 函数的极大值和极小值是局部概念, 即如果)(0x f 是)(x f 的极值,只是对极值点0x 的左右近旁一个小范围来讲的.(2)函数在一个区间上可能会有几个极大值和几个 极小值,且其中的极大值未必比极小值要大. 如图3-5, 极大值)(1x f 就比极小值)(5x f 还要小.(3)函数的极值只能在区间内部取到.求极值的关键是找出极值点,从图3-5中看到,对可导函数来讲,在取得极值处,曲线的切线是水平的,即在极值点处函数的导数为零.但反之不成立.如0)(3='x f .定理2(极值存在的必要条件) 设函数)(x f 在点0x 处导数存在,且在0x 处取得极值,则函数)(x f 在0x 处的导数0)(0='x f ,即0x 是函数)(x f 的驻点.注意,定理3.5仅是极值存在的必要条件,而非充分条件.如函数3x y =,在0=x 处有00='=x y ,但00==x y不是极值.该定理说明可导函数的极值点必是驻点,而驻点却未必是极值点.对于一个连续函数,它的极值点还可能是使导数不存在的点.如)(x f ||x =,显然,)0(f '不存在. 但0=x 且是它的一个极小值点,在||)(x x f =图形上,)0,0(称为曲线的尖点.因此,连续函数有可能取得极值的点是驻点与尖点. 但问题是这些点满足什么条件才能为极值点,观察图3-5,得下面判定函数极值的一个充分条件.定理 3 (极值存在第一充分条件) 设函数)(x f 在点0x 连续,在),ˆ(0δx N 内可导(0x 可除外),当x 由小增大经过0x 时,如果:(1))(x f '的符号由正变负,则)(x f 在点0x 处取得极大值; (2))(x f '的符号由负变正,则)(x f 在点0x 处取得极小值; (3))(x f '的符号不变,则)(x f 在点0x 处取不到极值.证明 (1)由条件,)(x f 在点0x 左近旁单调增加,在点0x 右近旁单调减少,即当0x x <时,有)()(0x f x f <,当0x x >时,有)()(0x f x f <,因此)(x f 在点0x 处取到极大值.同理可证明结论(2)、(3).此外还可利用二阶导数来判定极值.定理4(极值存在的第二充分条件)设函数)(x f 在),(0δx N 内有二阶导数)(x f ''存在且连续,又0)(0='x f ,如果(1)0)(0<''x f ,则)(x f 在0x 处取得极大值;(2)0)(0>''x f ,则)(x f 在0x 处取得极小值.(证明从略) 例4 求函数322)4()(-=x x f 的极值.解 因为)2(434)(32±≠-='x x x x f , 令 0)(0='x f ,得驻点 0=x ,所以函数有驻点0=x ,尖点2±=x列表考察)(x f '的符号故当=x 0时,函数)(x f 有极大值316, 当=x 2±时,函数)(x f 有极小值0. 例5 求函数x x x f sin 23)(+=在区间]2,0[π内的及值 解 因为x x f cos 23)(+=',x x f sin 2)(-=''.令 0)(0='x f ,得驻点 67,6521ππ==x x 而01)65(<-=''πf ,所以=)65(πf 1635+π为极大值; 01)67(>=''πf ,所以1637)67(-=ππf 为极小值. 例6 求函数)(x f =1)1(32+-x 的极值.解 函数)(x f 的定义域为),(+∞-∞ 32)1(6)(-='x x x f 由0)(0='x f ,得驻点1,0,1321==-=x x x . 列表:故函数)(x f 在0=x 处有极小值0)0(=f ,而1,131=-=x x 不是极值点.三、函数的最值问题在实际生活中,常会遇到:在一定条件下,怎样使“产量最高”、“用料最省”、“成本最低”、“耗时最少”等问题.这一类问题在数学上可归结为函数的最大值、最小值.因为在闭区间],[b a 上连续的函数)(x f 一定存在最大值和最小值. 由于函数的最值可在区间内部取到,也可在区间的端点上取到,如果是在区间内部取到,那么这个最值一定是函数的极值,因此求)(x f 在区间],[b a 上的最值,可求出一切可能的极值点(驻点及尖点)和端点处的函数值,进行比较,其中最大者就是函数的最大值,最小者就是函数的最小值.例7 求函数6424+-=x x y 在区间]3,3[-上的最大值和最小值. 解 因为x x y 843-='令,0='y 得驻点 2,0,2321==-=x x x因此 51,6,232===±==±=x x x yyy而.经比较,得函数的最大值为51=y如果函数)(x f 在一个开区间内连续且有惟一的极值点0x ,则当)(0x f 为极大值时,)(0x f 就是)(x f 在该区间上的最大值;当)(0x f 为极小值时,)(0x f 就是)(x f 在开区间上的最小值(见图3-7).例8 求函数1)1()(32+-=x x f.解 由例6可知,0=x 是函数)(x f 极小值点,且在整个定义域中极值点是惟一的,故 函数的极小值就是函数的最小值,为0)0(=f ,不存在最大值.下面讨论求最值的应用题.在实际问题中,往往可以根据实际情况断定函数)(x f 在其定义区间内确有最值存在,而当可导函数)(x f 在这定义区间内又只有惟一的驻点0x ,则可断定)(x f 在点0x 处取到了相应的最值.例9 有一块长为a ,宽为a 83的长方形铁片,将它的四角各剪去一个 大小相同的小正方形,四边折起,做成一个无盖的长方盒,问截去的小正方形的边长为多少时,其容积最大.解 如图3-8,设小正方形的边长为x ,则其容积为x a ax x x a x a x x V 223834114)283)(2()(+-=--=, (a x 1630<<) )83)(121(128321112)(22a x a x a ax x x V --=+-='得驻点 a x 1211=,a x 832=(舍),所以a x 1211=是惟一的驻点,又该实际问题的最值一定存在,故当小正方形的边长为a x 1211=时,长方体的容积最大. 例10 设铁路边上离工厂C 最近的点A 距工厂20km ,铁路边上B 城距A 点200km ,现要在铁路线AB 上选定一点D 修筑一条公路,已知铁路与公路每吨千米的货运费之比为3:5,问D 选在何处时,才能使产品从工厂C 运到B 城的每吨货物的总运费最省?(图3-9)解 设D 点选在距离A 处x 千米,又设铁路与公路的每吨千米货运费分别为k k 5,3(k 为常数)则产品从C 处运到B 城的每吨总运费为BD k CD k y ⋅+⋅=35)200(340052x k x k -+= )2000(≤≤x因为,222400)40035(34005xx x k k xx ky ++-=-+='令0='y ,即240035x x +=,得15=x .将 k yx 68015==,与闭区间]200,0[端点处的函数值比较,由于k yx 7000==,k k yx 1000404005200>==,因此,当D 点选在距离A 点km 15处,这时每吨货物的总运费最省.习题1、 求下列函数的单调区间:(1)x xe y =; (2)7186223---=x x x y ; (3))1ln(+-=x x y ; (4)322)1()12(x x y --=. 2、 求下列函数的极值:(1)1156)(23+-+=x x x x f ; (2)4334)(x x x f -=;(3)32)1()(x x x f -=; (4))20(,cos sin )(π≤≤+=x x x x f . 3、 已知函数bx ax x x f ++=23)(在1=x 处有极值12-,试确定系数b a ,的值. 4、 求下列函数在给定区间上的最值: (1),62)(24+-=x x x f ]3,2[-; (2)4)1()(+=x x f , ),(+∞-∞.。