公开课 竞赛课课件根据三视图还原立体图形
- 格式:pptx
- 大小:3.08 MB
- 文档页数:51




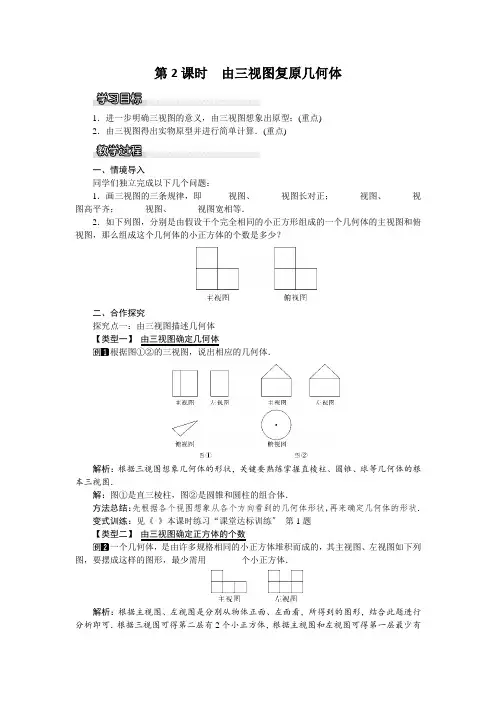
第2课时由三视图复原几何体1.进一步明确三视图的意义,由三视图想象出原型;(重点)2.由三视图得出实物原型并进行简单计算.(重点)一、情境导入同学们独立完成以下几个问题:1.画三视图的三条规律,即______视图、______视图长对正;______视图、______视图高平齐;______视图、______视图宽相等.2.如下列图,分别是由假设干个完全相同的小正方形组成的一个几何体的主视图和俯视图,那么组成这个几何体的小正方体的个数是多少?二、合作探究探究点一:由三视图描述几何体【类型一】由三视图确定几何体根据图①②的三视图,说出相应的几何体.解析:根据三视图想象几何体的形状,关键要熟练掌握直棱柱、圆锥、球等几何体的根本三视图.解:图①是直三棱柱,图②是圆锥和圆柱的组合体.方法总结:先根据各个视图想象从各个方向看到的几何体形状,再来确定几何体的形状.变式训练:见《》本课时练习“课堂达标训练〞第1题【类型二】由三视图确定正方体的个数一个几何体,是由许多规格相同的小正方体堆积而成的,其主视图、左视图如下列图,要摆成这样的图形,最少需用________个小正方体.解析:根据主视图、左视图是分别从物体正面、左面看,所得到的图形,结合此题进行分析即可.根据三视图可得第二层有2个小正方体,根据主视图和左视图可得第一层最少有4个小正方体,故最少需用7个小正方体.故答案为7.方法总结:由三视图判断几何体由多少个立方体组成时,先由俯视图判断底面的行列组成;再从主视图判断每列的高度(有几个立方体),并在俯视图中按照左、中、右的顺序用数字标出来;然后由左视图判断行的高度,在俯视图中按照上、中、下的顺序用数字标出来;最后把俯视图中的数字加起来.变式训练:见《 》本课时练习“课堂达标训练〞 第5题 探究点二:三视图的相关计算如图是某工件的三视图,其中圆的半径是10cm ,等腰三角形的高是30cm ,那么此工件的体积是( )A .1500πcm 3B .500πcm 3C .1000πcm 3D .2000πcm 3解析:由三视图可知该几何体是圆锥,底面半径和高.解:∵底面半径为10cm ,高为30cm.∴体积V =13π×102×30=1000π(cm 3).应选C.方法总结:依据三视图“长对正,高平齐,宽相等〞的原那么,正确识别几何体,再进行有关计算.变式训练:见《 》本课时练习“课堂达标训练〞第8题 三、板书设计本节课是在学习了简单几何体的三视图的根底上,反过来几何体的三视图想象出几何体,既是对三视图知识的完善,又是三视图知识的简单应用,培养了学生的空间想象能力,使学生初步体会到由平面图形到立体图形的转化也是一种数学方法.1.4 二次函数与一元二次方程的联系1.通过探索,理解二次函数与一元二次方程之间的联系,会用二次函数图象求一元二次方程的近似解;(重点)2.通过研究二次函数与一元二次方程的联系体会数形结合思想的应用.(难点)一、情境导入小唐画y =x 2-6x +c 的图象时,发现其顶点在x 轴上,请你帮小唐确定字母c 的值是多少?二、合作探究探究点一:二次函数与一元二次方程的联系【类型一】 二次函数图象与x 轴交点情况的判断以下函数的图象与x 轴只有一个交点的是( ) A .y =x 2+2x -3 B .y =x 2+2x +3 C .y =x 2-2x +3 D .y =x 2-2x +1解析:选项A 中b 2-4ac =22-4×1×(-3)=16>0,选项B 中b 2-4ac =22-4×1×3=-8<0,选项C 中b 2-4ac =(-2)2-4×1×3=-8<0,选项D 中b 2-4ac =(-2)2-4×1×1=0,所以选项D 的函数图象与x 轴只有一个交点.应选D.变式训练:见《 》本课时练习“课后稳固提升〞第1题【类型二】 利用函数图象与x 轴交点情况确定字母的取值范围(2021·武汉模拟)二次函数y =kx 2-6x +3的图象与x 轴有交点,那么k 的取值范围是( )A .k <3B .k <3且k ≠0C .k ≤3D .k ≤3且k ≠0解析:∵二次函数y =kx 2-6x +3的图象与x 轴有交点,∴方程kx 2-6x +3=0(k ≠0)有实数根,即Δ=36-12k ≥0,k ≤3.由于是二次函数,故k ≠0,那么k 的取值范围是k ≤3且k ≠0.应选D.方法总结:二次函数y =ax 2+bx +c ,当b 2-4ac >0时,图象与x 轴有两个交点;当b 2-4ac =0时,图象与x 轴有一个交点;当b 2-4ac <0时,图象与x 轴没有交点.变式训练:见《 》本课时练习“课堂达标训练〞第4题【类型三】利用抛物线与x 轴交点坐标确定一元二次方程的解(2021·苏州中考)假设二次函数y =x 2+bx 的图象的对称轴是经过点(2,0)且平行于y 轴的直线,那么关于x 的方程x 2+bx =5的解为( )A.⎩⎪⎨⎪⎧x 1=0,x 2=4B.⎩⎪⎨⎪⎧x 1=1,x 2=5C.⎩⎪⎨⎪⎧x 1=1,x 2=-5D.⎩⎪⎨⎪⎧x 1=-1,x 2=5解析:∵对称轴是经过点(2,0)且平行于y 轴的直线,∴-b2=2,解得b =-4.解方程x 2-4x =5,解得x 1=-1,x 2=5.应选D.方法总结:此题容易出错的地方是不知道二次函数的图象与一元二次方程的解的关系导致无法求解.变式训练:见《 》本课时练习“课堂达标训练〞第1题 探究点二:用二次函数的图象求一元二次方程的近似解利用二次函数的图象求一元二次方程-x 2+2x -3=-8的实数根(精确到0.1). 解析:对于y =-x 2+2x -3,当函数值为-8时,对应点的横坐标即为一元二次方程-x 2+2x -3=-8的实数根,故可通过作出函数图象来求方程的实数根.解:在平面直角坐标系内作出函数y =-x 2+2x -3的图象,如图.由图象可知方程-x 2+2x -3=-8的根是抛物线y =-x 2+2x -3与直线y =-8的交点的横坐标,左边的交点横坐标在-1与-2之间,另一个交点的横坐标在3与4之间.(1)先求在-2和-1之间的根,利用计算器进行探索:x - - - - - y-----因此x ≈-是方程的一个实数根. (2)另一个根可以类似地求出:x y-----x ≈是方程的另一个实数根.方法总结:用二次函数的图象求一元二次方程满足精确度的实数根的方法:(1)作出函数的图象,并由图象确定方程解的个数;(2)由图象与y =h 的交点的位置确定交点横坐标的取值范围;(3)利用计算器求方程的实数根.变式训练:见《 》本课时练习“课堂达标训练〞第8题 探究点三:二次函数与一元二次方程在运动轨迹中的应用某学校初三年级的一场篮球比赛中,如图,队员甲正在投篮,球出手时距地面209米,与篮框中心的水平距离为7米,当球出手后水平距离为4米时到达最大高度4米,设篮球运行轨迹为抛物线,篮框距地面3米.(1)建立如下列图的平面直角坐标系,问此球能否准确投中?(2)此时,假设对方队员乙在甲面前1米处跳起盖帽拦截,乙的最大摸高为米,那么他能否获得成功?解析:这是一个有趣的、贴近学生日常生活的应用题,由条件可得到出手点、最高点(顶点)和篮框的坐标,再由出手点、顶点的坐标可求出函数表达式;判断此球能否准确投中的关键就是判断代表篮框的点是否在抛物线上;判断盖帽拦截能否获得成功,就是比较当x =1时函数y 的值与最大摸高米的大小.解:(1)由条件可得到出手点、最高点和篮框的坐标分别为A (0,209),B (4,4),C (7,3),其中B 是抛物线的顶点.设二次函数关系式为y =a (x -h )2+k ,将点A 、B 的坐标代入,可得y =-19(x -4)2+4.将点C 的坐标代入上式,得左边=3,右边=-19(7-4)2+4=3,左边=右边,即点C在抛物线上.所以此球一定能投中;(2)将x =1代入函数关系式,得y =3.因为>3,所以盖帽能获得成功. 变式训练:见《 》本课时练习“课后稳固提升〞第7题 三、板书设计教学过程中,强调学生自主探索和合作交流,通过观察二次函数与x 轴的交点个数,讨论一元二次方程的根的情况,体会知识间的相互转化和相互联系.。





