第4单元 第18讲 直角三角形(解析版)
- 格式:doc
- 大小:2.07 MB
- 文档页数:25


2020-2021学年人教版四年级下册同步培优练习【第18讲:三角形的分类】一、我会选:1.下列选项的图形中,不能直接判断出三角形种类的是()A. B. C.2.有长度分别为3 cm、4 cm、5 cm、7 cm的小棒各一根,任选其中三根围成三角形,可以围成( )种不同形状的三角形。
A.3B.4C.53.一个直角三角形的三条边分别是3厘米、4厘米、5厘米,这个直角三角形互相垂直的两条边的长度分别是()。
A.3厘米和4厘米B.3厘米和5厘米C.4厘米和5厘米4.等腰三角形有()条边相等A.1B.2C.35.正三角形的三条边()A.不相等B.无法确定C.相等6.锐角三角形有()个锐角。
A.1B.2C.37.如图所示,张海将自己剪的一个三角形给损坏了,你能判断它是一个()三角形.A.锐角三角B.直角三角形C.无法准确判断8.一个三角形如果有两条边一样长,下面描述不正确的是( )。
A.一定也有两个角相等B.一定是一个等腰三角形C.一定是一个锐角三角形9.下面的关系图,( )是错误的。
A. B. C.二、我会判:10.等腰三角形都是锐角三角形。
()A.正确B.错误11.三条长度相等的线段一定能围成一个三角形。
()A.正确B.错误12.三角形按边分为等腰三角形和等边三角形。
()A.正确B.错误13.一个三角形不是锐角三角形,就是钝角三角形。
()A.正确B.错误14.用6 cm,6 cm,15 cm的三根小棒可以围成一个等腰三角形。
()A.正确B.错误三、我会填:15.三角形按照内角大小不同可以分成________三角形、________三角形和________三角形。
16.三角形按边的长短可以分为________三角形、________三角形和________三角形。
17.选一选,填一填锐角三角形有________;钝角三角形有________;直角三角形有________;等腰三角形有________;等边三角形有________.18.现有三种小棒,3cm、6cm、9cm,选一根6cm的小棒和两根________的小棒可以围城一个等腰三角形。



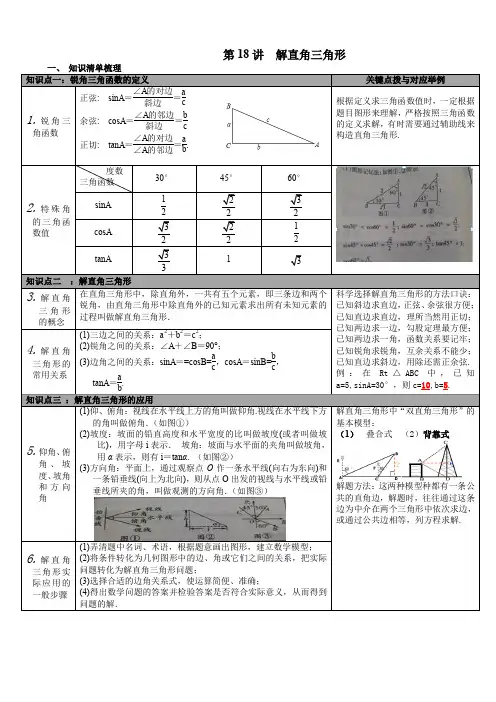


专题18直角三角形的核心知识点精讲1.了解直角三角形的概念;2.证明并掌握直角三角形的性质定理:直角三角形的两个锐角互余(无需证明);直角三角形斜边上的中线等于斜边的一半;3.掌握直角三角形的判定定理:有两个角互余的三角形是直角三角形;4.掌握勾股定理;会运用勾股定理解决简单问题;会用勾股定理的逆定理判定直角三角形;5.掌握直角三角形全等的判定定理:斜边和一组直角边对应相等的两个直角三角形全等;考点1:直角三角形的性质与判定考点2:勾股定理及逆定理(1)勾股定理:直角三角形两直角边的平方和等于斜边的平方如图:直角三角形ABC 的两直角边长分别为a b ,,斜边长为c ,那么222a b c .直角三角形性质1.两锐角之和等于90°2.斜边上的中线等于斜边的一半3.30°角所对的直角边等于斜边的一半1.若有一条直角边等于斜边的一半,则这条直角边所对的锐角等于30°(应用时需先证明)2.勾股定理:若直角三角形的两直角边分别为a ,b,斜边为c,则c b a 222 判定 1.有一个角为90°的三角形时直角三角形2.有两个角的和时90°的三角形是直角三角形1.一边上的中线等于这条边的一半的三角形是直角三角形2.勾股定理的逆定理:如果三角形的三边长分别为a,b,c 若满足,那么这个三角形为直角三角形。
c b a 222 面积公式,其中a 是底边常,hs 是底边上的高ch S 21ab 21(2)勾股定理的逆定理:如果三角形的三条边长a b c ,,,满足222a b c ,那么这个三角形是直角三角形.(3)勾股数:像15,8,17这样,能够成为直角三角形三条边长的三个正整数,称为勾股数。
勾股数满足两个条件:①满足勾股定理②三个正整数【题型1:直角三角形的性质与判定】【典例1】(2022•绍兴)如图,把一块三角板ABC 的直角顶点B 放在直线EF 上,∠C =30°,AC ∥EF ,则∠1=()A .30°B .45°C .60°D .75°1.(2022•岳阳)如图,已知l ∥AB ,CD ⊥l 于点D ,若∠C =40°,则∠1的度数是()A .30°B .40°C .50°D .60°2.(2023•贵州)5月26日,“2023中国国际大数据产业博览会”在贵阳开幕,在“自动化立体库”中有许多几何元素,其中有一个等腰三角形模型(示意图如图所示),它的顶角为120°,腰长为12m ,则底边上的高是()A .4mB .6mC .10mD .12m【题型2:勾股定理及逆定理】【典例2】(2023•恩施州)《九章算术》被称为人类科学史上应用数学的“算经之首”.书中记载:“今有户不知高、广,竿不知长短.横之不出四尺,从之不出二尺,邪之适出.问户高、广、邪各几何?”译文:今有门,不知其高宽;有竿,不知其长短,横放,竿比门宽长出4尺;竖放,竿比门高长出2尺;斜放,竿与门对角线恰好相等.问门高、宽和对角线的长各是多少(如图)?答:门高、宽和对角线的长分别是尺.1.(2023•天津)如图,在△ABC中,分别以点A和点C为圆心,大于的长为半径作弧(弧所在圆的半径都相等),两弧相交于M,N两点,直线MN分别与边BC,AC相交于点D,E,连接AD.若BD=DC,AE=4,AD=5,则AB的长为()A.9B.8C.7D.62.(2023•东营)一艘船由A港沿北偏东60°方向航行30km至B港,然后再沿北偏西30°方向航行40km 至C港,则A,C两港之间的距离为km.3.(2023•安徽)清初数学家梅文鼎在著作《平三角举要》中,对南宋数学家秦九韶提出的计算三角形面积的“三斜求积术”给出了一个完整的证明,证明过程中创造性地设计直角三角形,得出了一个结论:如图,AD是锐角△ABC的高,则BD=(BC+).当AB=7,BC=6,AC=5时,CD=.4.(2023•广安)如图,圆柱形玻璃杯的杯高为9cm,底面周长为16cm,在杯内壁离杯底4cm的点A处有一滴蜂蜜,此时,一只蚂蚁正好在杯外壁上,它在离杯上沿1cm,且与蜂蜜相对的点B处,则蚂蚁从外壁B处到内壁A处所走的最短路程为cm.(杯壁厚度不计)【题型3:勾股定理与弦图、拼图】【典例3】(2020•随州)勾股定理是人类最伟大的十个科学发现之一,西方国家称之为毕达哥拉斯定理.在我国古书《周髀算经》中就有“若勾三,股四,则弦五”的记载,我国汉代数学家赵爽为了证明勾股定理,创制了一幅“弦图”(如图1),后人称之为“赵爽弦图”,流传至今.(1)①请叙述勾股定理;②勾股定理的证明,人们已经找到了400多种方法,请从下列几种常见的证明方法中任选一种来证明该定理;(以下图形均满足证明勾股定理所需的条件)(2)①如图4、5、6,以直角三角形的三边为边或直径,分别向外部作正方形、半圆、等边三角形,这三个图形中面积关系满足S1+S2=S3的有个;②如图7所示,分别以直角三角形三边为直径作半圆,设图中两个月形图案(图中阴影部分)的面积分别为S1,S2,直角三角形面积为S3,请判断S1,S2,S3的关系并证明;(3)如果以正方形一边为斜边向外作直角三角形,再以该直角三角形的两直角边分别向外作正方形,重复这一过程就可以得到如图8所示的“勾股树”.在如图9所示的“勾股树”的某部分图形中,设大正方形M的边长为定值m,四个小正方形A,B,C,D的边长分别为a,b,c,d,已知∠1=∠2=∠3=∠α,则当∠α变化时,回答下列问题:(结果可用含m的式子表示)①a2+b2+c2+d2=;②b与c的关系为,a与d的关系为.1.(2022•湘潭)中国古代数学家赵爽在为《周髀算经》作注解时,用4个全等的直角三角形拼成正方形(如图),并用它证明了勾股定理,这个图被称为“弦图”.若“弦图”中小正方形面积与每个直角三角形面积均为1,α为直角三角形中的一个锐角,则tanα=()A.2B.C.D.2.(2022•永州)我国古代数学家赵爽创制了一幅“赵爽弦图”,极富创新意识地给出了勾股定理的证明.如图所示,“赵爽弦图”是由四个全等的直角三角形与中间的小正方形拼成的一个大正方形.若大正方形的面积是25,小正方形的面积是1,则AE=.一.选择题(共7小题)1.在Rt△ABC中,若一个锐角等于40°,则另一个锐角的度数为()A.40°B.45°C.50°D.60°2.如图,在△ABC中,∠ACB=90°,点D在AB上,沿CD折叠,使A点落在BC边上的E点,若∠B =26°,则∠CDE的度数为()A.52°B.71°C.72°D.81°3.如图,在△ABC中,∠C=90°,∠A=15°,点D是AC上一点,连接BD,∠DBC=60°,BC=2,则AD长是()A.4B.5C.6D.84.以2,3为直角边的直角三角形斜边长为()A.B.C.4D.55.下列各组数据是勾股数的是()A.,,B.4,5,6C.0.3,0.4,0.5D.9,40,416.如图,已知AB⊥BD,CD⊥BD,若用“HL”判定Rt△ABD和Rt△CDB全等,则需要添加的条件是()A.AD=CB B.∠A=∠C C.BD=DB D.AB=CD7.如图所示,已知在△ABC中,∠C=90°,AD=AC,DE⊥AB交BC于点E,若∠B=28°,则∠AEC =()A.28°B.59°C.60°D.62°二.填空题(共6小题)8.如图,在△ABC中,∠ACB=90°,∠A=40°,D为线段AB的中点,则∠BCD=°.9.我国古代数学著作《九章算术》记载了这样一个有趣的问题:“有一个水池,水面是边长为10尺的正方形,在水池中央有一根新生的芦苇,它高出水面1尺,如果将这根芦苇垂直拉向岸边,它的顶端刚好达到岸边的水面”,则水池的深度为尺.10.如图△ABC中,∠A:∠B=1:2,DE⊥AB于E,且∠FCD=75°,则∠D=.11.如图,在一个三角形的纸片(△ABC)中,∠C=90°,则图中∠1+∠2的度数为°.12.如图,在Rt△ACB中,∠ACB=90°,以AC为边向外作正方形ADEC,若图中阴影部分的面积为9c m2,BC=4cm,则AB=cm.13.如图,D为△ABC内一点,CD平分∠ACB,BD⊥CD,∠A=∠ABD,若BD=1,BC=3,则AC的长为.三.解答题(共4小题)14.如图,在△ABC中,D是BC的中点,DE⊥AB,DF⊥AC,垂足分别是E,F,且DE=DF.求证:Rt △BDE≌Rt△CDF.15.如图,已知∠ADC=90°,AD=8,CD=6,AB=26,BC=24.(1)证明:△ABC是直角三角形.(2)请求图中阴影部分的面积.16.如图1,荡秋千是中国古代北方少数民族创造的一种运动.有一天,小明在公园里游玩,如图2,他发现秋千静止时,踏板离地的垂直高度DE=1m,将它往前推送6m(水平距离BC=6m)时,秋千的踏板离地的垂直高度BF=CE=3m,秋千的绳索始终拉得很直,求绳索AD的长度?17.一架方梯长25米,如图,斜靠在一面墙上,梯子底端离墙7米,(1)这个梯子的顶端距地面有多高?(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?一.选择题(共5小题)1.如图,在Rt△ABC中,∠ACB=90°,∠A=30°,点D是AC上一点,将△ABD沿线段BD翻折,使得点A落在A'处,若∠A'BC=20°,则∠CBD=()A.5°B.10°C.15°D.20°2.如图,Rt△ABC中,∠C=90°,∠ABC=60°,以顶点B为圆心、适当长为半径作弧,在边BC、BA 上截取BE、BD;然后分别以点D、E为圆心、以大于DE的长为半径作弧,两弧在∠CBA内交于点F;作射线BF交AC于点G.若AC=6,P为边AB上一动点,则GP的最小值为()A.3B.2C.1D.无法确定3.如图,△ABC中,∠ACB=90°,∠CAB=60°,动点P在斜边AB所在的直线m上运动,连接PC,那点P在直线m上运动时,能使图中出现等腰三角形的点P的位置有()A.6个B.5个C.4个D.3个4.如图,线段OP=1,过点P作PP1⊥OP且PP1=1,连结OP1;过点P1作P1P2⊥OP1且P1P2=1,连结OP2;过点P2作P2P3⊥OP2且P2P3=1,连结OP3,则OP3的长为()A.1B.C.D.25.如图,以Rt△ABC的三条边作三个正三角形,则S1、S2、S3、S4的关系为()A.S1+S2+S3=S4B.S1+S2=S3+S4C.S1+S3=S2+S4D.不能确定二.填空题(共3小题)6.如图,在△ABC,∠ACB=90°,分别以三边为直径向上作三个半圆.若AB=5,AC=4,则阴影部分图形的面积为.7.如图,在一个长方形草坪ABCD上,放着一根长方体的木块.已知AD=12米,AB=8米,该木块的较长边与AD平行,横截面是边长为1米的正方形,一只蚂蚁从点A爬过木块到达C处需要走的最短路程是米.8.如图①,四个全等的直角三角形与一个小正方形,恰好拼成一个大正方形,这个图形是由我国汉代数学家赵爽在为《周髀算经》作注时给出的,人们称它为“赵爽弦图”.如果图①中的直角三角形的长直角边为7cm,短直角边为3cm,连结图②中四条线段得到如图③的新图案,则图③中阴影部分的周长为cm.三.解答题(共4小题)9.如图,在△ABC中,∠C=90°,∠A=30°,AB=4cm,动点P、Q同时从A、B两点出发,分别在A B、BC边上匀速移动,它们的速度分别为V P=2cm/s,V Q=1cm/s,当点P到达点B时,P、Q两点同时停止运动,设点P的运动时间为t s.(1)当t为何值时,△PBQ为等边三角形?(2)当t为何值时,△PBQ为直角三角形?10.如图,等腰直角三角板如图放置.直角顶点B在直线CD上,分别过点A、E作AC⊥直线CD于点C,ED⊥直线CD于点D.(1)求证:CD=AC+ED.(2)若设△ABC三边长分别为a、b、c,利用此图证明勾股定理.11.如图,铁路上A,B两点相距25km,C,D为两庄,DA⊥AB于A,CB⊥AB于B,已知DA=15km,C B=10km,现在要在铁路AB上建一个土特产品收购站E,使得C,D两村到E站的距离相等.问:(1)在离A站多少km处?(2)判定三角形DEC的形状.12.今年第6号台风“烟花”登陆我国沿海地区,风力强,累计降雨量大,影响范围大,有极强的破坏力.如图,台风“烟花”中心沿东西方向AB由A向B移动,已知点C为一海港,且点C与直线AB上的两点A、B的距离分别为AC=300km,BC=400km,又AB=500km,经测量,距离台风中心260km及以内的地区会受到影响.(1)海港C受台风影响吗?为什么?(2)若台风中心的移动速度为28千米/时,则台风影响该海港持续的时间有多长?1.(2023•株洲)一技术人员用刻度尺(单位:cm)测量某三角形部件的尺寸.如图所示,已知∠ACB=90°,点D为边AB的中点,点A、B对应的刻度为1、7,则CD=()A.3.5cm B.3cm C.4.5cm D.6cm2.(2022•永州)如图,在Rt△ABC中,∠ABC=90°,∠C=60°,点D为边AC的中点,BD=2,则BC 的长为()A.B.2C.2D.43.(2020•河北)如图是用三块正方形纸片以顶点相连的方式设计的“毕达哥拉斯”图案.现有五种正方形纸片,面积分别是1,2,3,4,5,选取其中三块(可重复选取)按如图的方式组成图案,使所围成的三角形是面积最大的直角三角形,则选取的三块纸片的面积分别是()A.1,4,5B.2,3,5C.3,4,5D.2,2,44.(2022•陕西)如图,是一个棱长为1的正方体纸盒.若一只蚂蚁要沿着正方体纸盒的表面,从顶点A爬到顶点B去觅食,则需要爬行的最短路程是()A.B.2C.D.35.(2023•攀枝花)如图,在△ABC中,∠A=40°,∠C=90°,线段AB的垂直平分线交AB于点D,交A C于点E,则∠EBC=.6.(2023•郴州)如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点M是AB的中点,求CM=.7.(2023•大连)如图,在平面直角坐标系中,点A,B的坐标分别为(1,0)和(0,2),连接AB,以点A 为圆心、AB的长为半径画弧,与x轴正半轴相交于点C,则点C的横坐标是.8.(2023•随州)如图,在Rt△ABC中,∠C=90°,AC=8,BC=6,D为AC上一点,若BD是∠ABC的角平分线,则AD=.9.(2023•扬州)我国汉代数学家赵爽证明勾股定理时创制了一幅“勾股圆方图”,后人称之为“赵爽弦图”,它是由4个全等的直角三角形和一个小正方形组成.如图,直角三角形的直角边长为a、b,斜边长为c,若b﹣a=4,c=20,则每个直角三角形的面积为.10.(2021•杭州)如图,在△ABC中,∠ABC的平分线BD交AC边于点D,AE⊥BC于点E.已知∠ABC =60°,∠C=45°.(1)求证:AB=BD;(2)若AE=3,求△ABC的面积.。

2023年中考数学一轮复习备考第18讲等腰三角形与直角三角形考点清单考点1 等腰三角形的性质与判定性质(1)两底角相等,即∠B=∠C(等边对等角);(2)两腰相等,即AB=AC;(3)是轴对称图形,有一条对称轴,即AD所在的直线;(4)“三线合一”(即顶角的①、底边上的中线和底边上的高互相重合)判定(1)两边相等的三角形是等腰三角形;(2)②相等的三角形是等腰三角形(等角对等边)周长、面积周长:C=a+2b;面积:S=③(其中a是底边长,b是腰长,h是底边上的高)【易错警示】等腰三角形中的分类讨论:(1)当顶角和底角不确定时,需要分类讨论,且需要用三角形内角和定理检验;(2)当腰长和底边长不确定时,需要分类讨论,且需要用三角形三边关系检验.考点2 等边三角形的性质与判定性质(1)等边三角形的三条边相等,即AB=BC=AC;(2)等边三角形的三个内角相等且每一个角都等于④,即∠B=∠C=∠BAC=60°;(3)等边三角形是轴对称图形,有⑤条对称轴;(4)等边三角形“三线合一”;(5)等边三角形的内心、外心重合判定(1)三条边都相等的三角形是等边三角形;(2)三个角都相等的三角形是等边三角形;(3)有一个角是⑥的等腰三角形是等边三角形周长、面积周长:C=3a;面积:S=12ah=34a2(h=32a)(其中a是边长,h是任一边上的高)考点3 直角三角形的性质与判定性质(1)两锐角之和等于90°,即∠A+∠B=90°;(2)斜边上的中线等于斜边的⑦;(3)30°角所对的直角边等于斜边的⑧;(4)勾股定理:如果直角三角形的两条直角边长分别为a,b,斜边长为c,那么⑨;【拓展】在直角三角形中,如果一条直角边长等于斜边长的一半,那么这条直角边所对的锐角等于⑩;外接圆半径R=c2,内切圆半径r=12(a+b-c)判定(1)有一个角为⑪的三角形是直角三角形;(2)有两个角互余的三角形是直角三角形;(3)勾股定理的逆定理:如果三角形的三边长a,b,c满足⑫,那么这个三角形是直角三角形;【拓展】一条边上的中线等于这条边的一半的三角形是直角三角形周长、面积周长:C=a+b+c;面积:S△ABC=12ab=12ch(其中a,b分别为两个直角边长,c为斜边长,h为斜边上的高)考点4 等腰直角三角形的性质与判定性质(1)两直角边相等,即AC=BC;(2)两锐角相等且都等于45°;(3)是轴对称图形,有一条对称轴,即CD所在的直线;(4)“三线合一”判定(1)顶角为⑬的等腰三角形是等腰直角三角形;(2)有两个角为⑭的三角形是等腰直角三角形;(3)有一个角为⑮的直角三角形是等腰直角三角形;(4)两直角边相等的直角三角形是等腰直角三角形周长、面积 周长:C =2a +c ;面积:S =12a 2=12ch =22ah (其中a 为直角边长,c 为斜边长,h 为斜边上的高)强 化 演 练基础练1.如图,在Rt △ABC 中,∠ACB =90°,AC =BC ,过点C 作 CD ⊥AB ,垂足为D ,E 为BC 的中点,AE 与CD 交于点F .若DF 的长为23,则AE 的长为( )A .2B .2C .5D .2 52.已知a ,b 是等腰三角形的两边长,且a ,b 满足2a -3b +5+(2a +3b -13)2=0,则此等腰三角形的周长为( )A .8B .6或8C .7D .7或83.如图,在等腰三角形ABC 中,AB =AC =5,BC =8,AD ⊥AC 交BC 于点D ,则AD 的值为( )A .125B .154C .5D .2034.如图,AD 是等边三角形ABC 的中线,AE =AD ,则∠EDC 的度数为( )A .30°B .20°C .25°D .15°5.如图是“人字形”钢架,其中斜梁AB =AC ,顶角∠BAC =120°,跨度BC =10 m ,AD 为支柱(即底边BC 上的中线),两根支撑架DE ⊥AB ,DF ⊥AC ,则DE +DF 等于( )A .10 mB .5 mC .2.5 mD .9.5 m6.如图,在△ABC 中,AB =BC ,由图中的尺规作图痕迹得到的射线BD 与AC 交于点E ,点F 为BC 的中点,连接EF .若BE =AC =2,则△CEF 的周长为( )A .3+1B .5+3C .5+1D .47.如图,在4×4的正方形网格中有两个格点A ,B ,连接AB ,在网格中再找一个格点C , 使得△ABC 是等腰直角三角形,满足条件的格点C 的个数是( )A .2B .3C .4D .58.如图,在△ABC 中AC =BC ,点D 和E 分别在AB 和AC 上,且AD =AE .连接DE ,过点A 作AH ⊥BC 于点H ,交DE 于点F .若∠C =40°,则∠AFE 的度数为( )A .60°B .65°C .75°D .80°9.如图,在△ABC 中,点O 是角平分线AD ,BE 的交点.若AB =AC =10,BC =12,则tan ∠OBD 的值是( )A .12B .2C .63D .6410.如图,在Rt △ABC 中,CD 为斜边AB 上的中线.若CD =2,则AB = .11.如图,在△ABC 中,AB =AC =2,P 是BC 上任意一点,PE ⊥AB 于点E ,PF ⊥AC 于点F .若S △ABC =1,则PE +PF = .12.如图,在Rt△ABC中,∠C=90°,AF=EF.若∠CFE=72°,则∠B=.13.如图,EA=EB=EC,∠AEB=70°,则∠ACB=°.14.如图,在Rt△ABC中,∠A=30°,DE垂直平分斜边AC,交AB于点D,E为垂足,连接CD.若BD=1,则AC的长是 .15.如图,在△ABC中,∠ABC的平分线BD交AC边于点D,AE⊥BC于点E.已知∠ABC=60°,∠C =45°.(1)求证:AB=BD;(2)若AE=3,求△ABC的面积.16.如图,在△ABC中,AD⊥BC,垂足为D,BD=CD,延长BC至点E,使得CE=CA,连接AE.(1)求证:∠B=∠ACB;(2)若AB=5,AD=4,求△ABE的周长和面积.强化练17.如图,在等边三角形ABC中,AB=10,E为AC的中点,点F,G为AB边上的动点,且FG=5,则EF+CG的最小值是()A.57 B.5 6 C.53+5 D.1518.如图,在△ABC中,AD和BE是高,∠ABE=45°,F是AB的中点,AD与FE,BE分别交于点G,H,∠CBE=∠BAD.有下列结论:①FD=FE;②AH=2CD;③BC·AD=2AE2;④S△ABC=4S△ADF.其中正确的有()A.1个B.2个C.3个D.4个提升练19.七巧板是大家熟悉的一种益智类玩具,用七巧板能拼出许多有趣的图案.小聪同学将一个直角边长为20 cm的等腰直角三角形纸板,切割七块,正好制成一副七巧板,则图中阴影部分的面积为cm2.20.如图,在△ABC中,AB=AC=6,∠BAC=120°,P是BC上的动点,Q是AC上的动点(Q不与A,C重合).(1)线段P A的最小值为;(2)当△ABP 为直角三角形,△PCQ 也为直角三角形时,CQ 的长度为 .参 考 答 案考点清单①两角 ②两角 ③12ah ④60° ⑤三 ⑥60° ⑦一半 ⑧一半 ⑨a 2+b 2=c 2 ⑩30° ⑪90° ⑫a 2+b 2=c 2 ⑬90° ⑭45° ⑮45°强化演练1. C2. D3. B4. D5. B6. C7. B8. C9. A 10. 4 11. 1 12. 54° 13. 35 14. 2 3 15. (1)证明:∵BD 平分∠ABC ,∠ABC =60°,∴∠DBC =12∠ABC =30°. ∵∠C =45°,∴∠ADB =∠DBC +∠C =75°,∠BAC =180°-∠ABC -∠C =75°,∴∠BAC =∠ADB ,∴AB =BD .(2)解:在Rt △ABE 中,∵∠ABC =60°,AE =3,∴BE =AE tan ∠ABC = 3. 在Rt △AEC 中,∵∠C =45°,AE =3,∴EC =AE tan C =3,∴BC =3+3,∴S △ABC =12BC ·AE =9+332.16. (1)证明:在△ADB 和△ADC 中,⎩⎪⎨⎪⎧AD =AD ,∠ADB =∠ADC ,BD =CD ,∴△ADB ≌△ADC (SAS),∴∠B =∠ACB .(2)解:在Rt △ADB 中,∵AB =5,AD =4,∴BD =AB 2-AD 2=52-42=3,∴BD =CD =3,AC =AB =CE =5,∴BE =2BD +CE =2×3+5=11,DE =CD +CE =8. 在Rt △ADE 中,由勾股定理,得AE =AD 2+DE 2=42+82=45,∴C △ABE =AB +BE +AE =5+11+45=16+45,S △ABE =12BE ·AD =12×11×4=22.17. A 18. D 19.25420. (1)3 (2)4.5或4或3。


直角三角形是特殊的三角形,本节主要讨论直角三角形全等的判定定理和性质,难点是直角三角形的性质及应用.综合性较强,会牵涉到辅助线的添加,连接中线,将散落的条件集中到直角三角形中进行求解.1、直角三角形全等的判定方法:(1)直角三角形是特殊的三角形,对于一般三角形全等的判定方法,直角三角形都适用;(2)直角三角形还有一个特殊的判定方法:有一条直角边和斜边对应相等的两个直角三角形全等(简记“H.L”).直角三角形的全等判定及性质知识结构模块一:直角三角形全等的判定知识精讲内容分析【例1】 如图,∠D =∠C =90°,请添加一个条件,使得△ABC ≌△BAD ,并在括号内写出判定的依据.(1)AD =__________(); (2)∠DAB =_________ ().【难度】★【答案】BC ,.H L ;CBA ,..A A S .【解析】(1)有一条直角边和斜边对应相等的两个直角三角形全等; (2)两角及其中一角的对边对应相等的两个三角形全等. 【总结】考查直角三角形全等判定及三角形全等判定定理.【例2】 已知:如图,EF ⊥AD ,BC ⊥AD ,AG =DH ,AF =DC ,那么图中全等的三角形共有______对. 【难度】★ 【答案】3对.【解析】AFG DCH ≌;ACB DFE ≌;EOG BOH ≌. 【总结】考查学生对全等三角形判定的灵活运用.【例3】 下列命题中,正确的个数是()①两条边分别相等的两个直角三角形全等; ②斜边和直角边对应相等的两个直角三角形全等; ③斜边相等的两个等腰直角三角形全等. A .3B .2C .1D .0【难度】★★ 【答案】B【解析】①错误;②、③正确.【总结】考查直角三角形全等的判定定理.例题解析BACDABCDEFGOH【例4】 已知:如图,AC ⊥BC ,AD ⊥BD ,AD =BC ,CE ⊥AB ,DF ⊥AB ,垂足分别是E 、F ,求证:CE =DF .【难度】★★ 【答案】见解析.【解析】AC ⊥BC ,AD ⊥BD ,90ACB BDA ∴∠=∠=︒在RT ACB 和RT BDA 中, AB BA BC AD =⎧⎨=⎩RT ACB ∴≌RT BDA (.H L )CAB DBA ∴∠=∠(全等三角形对应角相等),AC BD =(全等三角形对应边相等)CE ⊥AB ,DF ⊥AB 90AEC BFD ∴∠=∠=︒在RT AEC 和RT BFD 中AEC BFD CAB DBA AC BD ∠=∠⎧⎪∠=∠⎨⎪=⎩, RT AEC ∴≌RT BFD (..A A S )CE DF ∴=(全等三角形对应边相等)【总结】考查直角三角形全等判定及三角形全等判定定理的综合应用.【例5】 如图,已知:Rt △ABC 中,∠ACB 是直角,D 是AB 上一点,BD =BC ,过D 作AB的垂线交AC 于E ,求证:CD ⊥BE . 【难度】★★ 【答案】见解析.【解析】90ACB DE AB ∠=︒⊥,,90ECB EDB ∠∴∠==︒. 在RT BEC 和RT BED 中,BE BEBC BD =⎧⎨=⎩,RT BEC ∴≌RT BED (.H L ) EC ED ∴=(全等三角形对应边相等)E ∴在CD 的垂直平分线上(垂直平分线逆定理)又BC BD =(已知),B ∴也在CD 的垂直平分线上(垂直平分线逆定理) BE ∴垂直平分CD (两点确定一条直线),即CD ⊥BE .【总结】考查直角三角形斜边直角边判定的用法以及垂直平分线的性质定理的逆定理的应用.E ABCDF ABCDE【例6】 如图,△ABC 中,AB ⊥BC ,AD 平分∠BAC ,DF ⊥AC ,ED =CD .求证:AC =AE +2BE .【难度】★★ 【答案】见解析.【解析】AD 平分∠BAC ,且AB ⊥BC ,DF ⊥ACBD FD ∴=(角平分线性质定理)在RT BED 和RT FCD 中,ED CD BD FD =⎧⎨=⎩, RT BED ∴≌RT FCD (.H L )BE FC ∴=(全等三角形对应边相等)同理可证:RT ABD ≌RT AFD (.H L ),AB AF ∴=(全等三角形对应边相等)AC AF FC AB AE BE =+=+,, 2AC AE BE ∴=+.【总结】本题主要考查直角三角形全等判定与角平分线性质的综合应用.【例7】 如图1,点A 、E 、F 、C 在一条直线上,AE =CF ,过E 、F 分别作DE ⊥AC ,BF ⊥AC .若AB =CD ,(1)BD 与EF 有什么关系?为什么?(2)若变为图2所示位置,结论是否仍然成立?请说明理由. 【难度】★★【答案】(1)BD 与EF 互相平分; (2)成立.【解析】(1)提示:证 RT ABF ≌RT CDE (.H L ); RT DEG ≌RT BFG (..A A S )得:EG FG DG BG ==,(全等三角形对应边相等) (2)同理可证,结论成立.【总结】考查直角三角形全等的判定及全等三角形 的判定定理的应用.AB CD EFAB CD EF GA BCD EFG图2图1【例8】 在直角△ABC 中,AB =AC ,∠BAC =90°,直线l 为经过点A 的任一直线,BD ⊥l于点D ,CE ⊥l 于点E ,若BD >CE ,试问: (1) AD 与CE 的大小关系如何?请说明理由;(2) 线段BD 、DE 、CE 之间的数量关系如何?你能说明清楚吗?试一试. 【难度】★★★【答案】(1)AD CE =;(2)BD CE DE =+. 【解析】(1)90BAC ∠=︒,90BAD CAE ∴∠+∠=︒,BD l CE l ⊥⊥,, 90BDA AEC ∴∠=∠=︒, 90DBA BAD ∴∠+∠=︒, DBA EAC ∴∠=∠在RT ABD 和RT CAE 中,BDA AECAB CA DBA EAC ∠=∠⎧⎪=⎨⎪∠=∠⎩, RT ABD ∴≌RT CAE (..A S A ) AD CE ∴=(全等三角形对应边相等) (2)BD CE DE =+ AD CE =,又AE AD DE =+ ,AE CE DE ∴=+RT ABD ≌RT CAE , BD AE ∴=BD CE DE ∴=+.【总结】考查全等三角形的应用及线段间的等量代换.AB CD El【例9】 如图,在△ABC 中,AB =AC ,DE 是过点A 的直线,BD ⊥DE 于D ,CE ⊥DE 于E .(1) 若BC 在DE 的同侧(如图1),且AD =CE ,求证:AB ⊥AC .(2) 若BC 在DE 的两侧(如图2),其他的条件不变,问AB 与AC 仍垂直吗?若是,请予以证明,若不是,请说明理由.【难度】★★★ 【答案】见解析.【解析】(1)证明:BD ⊥DE ,CE ⊥DE90BDA AEC ∴∠=∠=︒.在RT BDA 和RT AEC 中,AB CA AD CE =⎧⎨=⎩, RT ABD ∴≌RT CAE (.H L ),DAB ECA ∴∠=∠.90AEC ∠=︒, 90CAE ECA ∴∠+∠=︒, 90CAE DAB ∴∠+∠=︒, 90BAC ∴∠=︒ ,∴AB ⊥AC .(2)AB ⊥AC .同理可证: RT ABD ≌RT CAE ,则可证90BAC ∠=︒,即AB ⊥AC .【总结】考查直角三角形全等的判定及同角的余角相等相结合.【例10】 如图,在△ABC 中,∠ACB =90°,CD 是斜边AB 上的高,在AB 上截取AE =AC ,过点E 作EF ∥CD 、交BC 边于点F ,EG 垂直BC 于点G ,求证:DE=EG . 【难度】★★★ 【答案】见解析. 【解析】联结CEAE =AC ,ACE AEC ∴∠=∠90ACB ∠=︒, 90ACE ECG ∴∠+∠=︒ CD AB ⊥, 90AEC ECD ∴∠+∠=︒ ECD ECG ∴∠=∠又CD AB ⊥,EG BC ⊥DE GE ∴=【总结】考查等边对等角及角平分线性质定理的综合运用.图1ABCDE图2ABCDE ABCD EFG2、 两个性质:(1) 直角三角形的两个锐角互余;(2) 在直角三角形中,斜边的中线等于斜边的一半.如果有直角三角形,作斜边的中线这条辅助线,可达到解决问题的目的.【例11】 如图,在△ABC 中,∠ACB =90°,CD ⊥AB 于D : (1)若∠B =55°,则∠A =________; (2)若∠B -∠A =10°,则∠B =_________;(3)图中与∠A 互余的角有_________,与∠A 相等的角有_________. 【难度】★★【答案】(1)35︒;(2)50︒;(3)B ∠、ACD ∠;BCD ∠.【解析】直角三角形的两个锐角互余,题目中有三个直角三角形ABC 、ACD 、BCD . 【总结】直角三角形性质1:直角三角形的两个锐角互余的运用.【例12】 如图,已知,四边形ABCD 中,∠ABC =∠ADC =90°,M 、N 分别是AC 、BD 中点.求证:MN ⊥BD . 【难度】★★ 【答案】见解析. 【解析】联结MD 、MB .90ABC ADC ∠=∠=︒,M 分别是AC 中点 1122BM AC DM AC ∴==,(直角三角形斜边上中线等于斜边的一半)BM DM ∴=, N 是BD 中点, MN BD ∴⊥(等腰三角形三线合一).【总结】考查直角三角形斜边中线性质及等腰三角形三线合一性质的综合运用.模块二:直角三角形的性质例题解析知识精讲ABCD ABC DMN【例13】 如图,在Rt △ABC 中,∠C =90°,AB 的中垂线交AB 于E 、AC 于D ,BD 、CE交于F ,设∠A =y ,∠DFC =x , (1)求证:∠CDB =∠CEB ; (2)用x 的代数式表示y . 【难度】★★【答案】(1)略;(2)1603y x =︒-.【解析】(1)90C ∠=︒ ,AB 的中垂线交AB 于E 12AE BE AB ∴==、12CE AB =(直角三角形斜边中线等于斜边一半)AE CE ∴=,A ACE ∴∠=∠,2CEB A ∴∠=∠.又AB 的中垂线交AB 于E , AD DB ∴=(垂直平分线的性质)A ABD ∴∠=∠,2CDB A ∴∠=∠, CDB CEB ∴=∠(2)A y DFC x ∠=∠=,,A ACE ∠=∠,A ABD ∠=∠ 又2CDB A ABD CDB y ∠=∠+∠∴∠=,ACE y ∠= 180ACE CDB DFC ∴∠+∠+∠=︒.即3180x y +=︒,1603y x ∴=︒-【总结】主要考查:直角三角形斜边中线的性质、线段垂直平分线的性质、三角形内角和性质的综合运用.【例14】 如图ABC ∆中,AD 是BC 边上的高,CF 是AB 边的中线,BF DC =,P 是CF中点. 求证:(1)DP FC ⊥;(2)2B BCF ∠=∠.【难度】★★ 【答案】略【解析】(1)联结DFAD 是BC 边上的高,CF 是AB 边的中线, 12BF AB ∴= ∵DF 是直角ABD 斜边上的中线, 12DF AB ∴=, BF DF ∴=. BF DC =, DC DF ∴=, 又P 是CF 中点, DP CF ∴⊥.(2)BF DF =, B BDF ∴∠=∠,DF DC =, BCF DFC ∴∠=∠.2BDF BCF DFC BCF ∠=∠+∠=∠, 2B BCF ∴∠=∠.【总结】考查等腰三角形的判定与性质,注意掌握直角三角形中,斜边中线等于斜边一半的定理应用.ABCDEAB CDPF【例15】 如图,AB ,CD 交于点O ,且BD=BO ,CA =CO ,E 、F 、M 分别是OD 、OA 、BC 的中点,求证:ME MF =.【难度】★★【答案】略 【解析】联结BE CF ,BD BO CA CO ==,,E 、F 分别是OD 、OA 的中点BE DO CF AO ∴⊥⊥,M 是BC 的中点1122EM BC FM BC ∴==,(直角三角形斜边上的中线等于斜边的一半)EM MF ∴=【总结】本题主要考查直角三角形的性质与等腰三角形性质的综合运用.【例16】 如图,在梯形ABCD 中,AD //BC ,M 、N 分别是AD 、BC 的中点,若∠B 与∠C 互余,则MN 与(BC -AD )的关系是什么? 【难度】★★ 【答案】()12MN BC AD =-. 【解析】过点M 分别作////ME AB MF DC ,,交BC 于点E 、FB MEFC MFE ∴∠=∠∠=∠,,∠B 与∠C 互余, 90MEF MFE ∴∠+∠=︒,90EMF ∴∠=︒,即MEF 为直角三角形.在梯形ABCD 中,AD //BC ,////ME AB MF DC ,,AM BE DM CF ∴==,, M 、N 分别是AD 、BC 的中点, AM DM BN CN ∴==,()BC AD BC BE CF EF ∴-=-+=,EN FN = 12MN EF ∴=, ()12MN BC AD ∴=-. 【总结】考查直角三角形斜边中线性质的应用.ABCDEFO M ABCDMN E F【例17】 如图,已知在钝角∆ABC 中,AC 、BC 边上的高分别是BE 、AD ,BE 、AD 的延长线交于点H ,点F 、G 分别是BH 、AC 的中点. (1)求证:∠FDG =90°;(2)连结FG ,试问∆FDG 能否为等腰直角三角形?若能,试确定∠ABC 的度数,并写出你的推理过程;若不能,请简要说明理由. 【难度】★★★ 【答案】见解析.【解析】(1)证明:AC 、BC 边上的高分别是BE 、AD ,又点F 、G 分别是BH 、AC 的中点,12DG CG AC ∴==,12DF BF BH ∴==(斜边中线等于斜边的一半) GDC GCD BCE ∴∠=∠=∠,DBF BDF ∴∠=∠ GDC BDF BCE DBF ∴∠+∠=∠+∠,又AE BH ⊥,90BCE DBF ∴∠+∠=︒90GDC BDF ∴∠+∠=︒,即90FDG ∠=︒(2)能,45ABC ∠=︒.若GDF 为直角等腰三角形,则GD FD =,AC BH ∴=, ACD ∴≌BHD (..A A S ),AD BD ∴=,45ABC ∴∠=︒. 【总结】主要考查对直角三角形性质的掌握,以及能否灵活的运用.BE FHD AGC【例18】 如图,等腰直角三角形ABC 中,∠ACB =90°,AD 为腰CB 上的中线,CE ⊥AD交AB 于E .求证:∠CDA =∠EDB . 【难度】★★ 【答案】见解析.【解析】过点C 作CH AB ⊥于点H ,交AD 于点F .等腰直角三角形ABC 中,90ACB ∠︒=, 45B ∴∠=︒.CH AB ⊥,45ACH BCH ∴∠=∠=︒, ACF BCH B ∴∠=∠=∠又CE AD ⊥, 12∴∠=∠. 在ACF 和CBE 中, 12ACF B AC CB ∠=∠⎧⎪=⎨⎪∠=∠⎩, ACF ∴≌CBE (..A S A ),CF BE ∴=.AD 为腰CB 上的中线,CD BD ∴=.在CFD 和BED 中, CF BE DCF B CD BD =⎧⎪∠=∠⎨⎪=⎩, CFD ∴≌BED (..S AS )CDF BDE ∴∠=∠, 即CDAEDB ∠∠=. 【总结】考查学生对辅助线的添加及全等三角形的构造能力.AB C DE1 2H F【例19】 如图,点A 、B 、C 在同一直线上,在直线AC 的同侧作△ABE 和△BCF ,连接AF 、CE ,取AF 、CE 的中点M 、N ,连接MB 、NB 、NM .(1) 若△ABE 和△FBC 是等腰直角三角形,且∠ABE =∠FBC =90°,如图1所示,则△MBN 是_____________三角形;(2) 若△ABE 和△FBC 中,BA =BE ,BC =BF ,且∠ABE =∠FBC =α,如图2所示,则△MBN 是_____________三角形,且∠MBN =_______;(3) 若(2)中的△ABE 绕点B 旋转一定的角度,如图3,其他的条件不变那么(2)中的结论是否成立?若成立,给出你的证明,若不成立,写出正确的结论并给出证明.【难度】★★★【答案】(1)等腰直角;(2)等腰,α;(3)结论仍然成立. 【解析】(1)易证ABF ≌EBC , AF EC ∴=,BM BN ∴=,∴AMB ≌ENB ,MBA NBE ∴∠=∠ 90MBA MBF ∠+∠=︒,90MBF NBE ∴∠+∠=︒即90MBN ∠=︒,MBN ∴为等腰直角三角形 (2)根据题意,可知ABF ≌EBC ,BM BN ∴= 即MBN 为等腰三角形,ABM EBN ∠=∠ ABE MBN α∴∠=∠=,MBN α∴∠=(3)∵ABF ≌EBC ,AF CE AFB ECB ∴=∠=∠, FM CN ∴=, MFB ∴≌NCB BM BN ∴=,MBF NBC ∠=∠MBN MBF FBN FBN NBC FBC α∴∠=∠+∠=∠+∠=∠=【总结】本题考查了图形旋转的性质,等腰三角形和 全等三角形的判定.掌握等腰三角形和全等三角形的性 质及判定并学会灵活运用是解题的关键.ABCMEFN图2A B CNEFM图1ABCEFNM图3【例20】 已知,如图,在△ABC 中,边AB 上的高CF 、边BC 上的高AD 与边CA 上的高BE 交于点H ,连接EF ,AH 和BC 的中点为N 、M . 求证:MN 是线段EF 的中垂线. 【难度】★★★ 【答案】见解析.【解析】连接FM 、EM 、FN 、EN∵︒=∠90BFC ,M 为BC 的中点, ∴BC FM 21=∵︒=∠90BEC ,M 为BC 的中点,∴BC EM 21=,∴ME FM =∵︒=∠90AFH ,N 为AH 的中点,∴AH FN 21= ∵︒=∠90AEH ,N 为AH 的中点,∴AH EN 21=, ∴EN FN =, ∵ME FM =,EN FN = ∴MN 是线段EF 的中垂线.【总结】考察直角三角形的性质和线段垂直平分线性质定理逆定理的综合运用.3、 推论:(1) 在直角三角形中,30°所对的直角边等于斜边的一半;(2) 在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°.模块三:直角三角形性质的推论知识精讲ABCDE FNHM【例21】 (1)△【例22】 △ABC 中,AB =AC =6,∠B =30°,则BC 边上的高AD =________;(2)△ABC 中,AB =AC ,AB 上的高CD =12AB ,则顶角∠BAC =_______. 【难度】★【答案】(1)3;(2)30︒或150︒.【解析】(1)在RT ABD 中,30B ∠=︒,则132AD AB ==; (2)要分两种情况考虑,△ABC 可能是锐角三角形,也可能是钝角三角形; 当△ABC 是锐角三角形时,30BAC ∠=︒; 当△ABC 是钝角三角形时,150BAC ∠=︒.【总结】考查直角三角形性质的两条推论的运用以及分类讨论思想.【例23】 如图,在矩形ABCD 中,AB =2BC ,在CD 上取一点E ,使AE =AB ,则∠EBC 的度数为__________. 【难度】★ 【答案】15︒.【解析】过点E 作EH AB ⊥,垂足为H ,则EH BC =. 又2AB BC =,AE AB =,2AE EH ∴=,30EAB ∴∠=︒75ABE ∴∠=︒,15EBC ∴∠=︒【总结】考查直角三角形性质的推论的运用:在直角三角形中,如果一条直角边等于斜边的一半,那么这条直角边所对的锐角等于30°例题解析A BCDEH【例24】 已知:如图,在△ABC 中,BA =BC ,∠B =120°,AB 的垂直平分线MN 交AC 于D ,求证:12AD DC =.【难度】★★ 【答案】见解析. 【解析】连接BD∵BA =BC ,∠B =120°, ∴︒=∠=∠30C A ∵AB 的垂直平分线MN 交AC 于D ,∴DB AD =, ∴︒=∠=∠30DBA A∵∠B =120°,∴︒=︒-︒=∠9030120DBC∵︒=∠30C ,︒=∠90DBC ,∴DC BD 21=∵DB AD =,∴DC AD 21=【总结】考察线段垂直平分线的性质和直角三角形性质的综合运用.【例25】 已知:如图,Rt △ABC 和Rt △ABD 中,DA =DB ,∠ADB =90°,BC =12AB , ∠ACB =90°,DE ⊥AB ,联结DC ,求∠EDC 的大小. 【难度】★★ 【答案】75°. 【解析】连接CE∵DA =DB ,DE ⊥AB ,∴EB AE =∵Rt △ABC ,BC =12AB ,∴︒=∠30CAB∵Rt △ABC ,EB AE =,∴CE AE =∴ACE CAB ∠=∠,∴︒=∠+∠=∠60ACE CAB CEB ∵DE ⊥AB ,∴︒=︒-︒=∠306090DEC ∵Rt △ABC 和Rt △ABD ,EB AE =∴AB CE AB DE 21,21==,∴CE DE =∵︒=∠30DEC ,∴︒=︒-︒=∠75230180EDC 【总结】考察线段垂直平分线的性质和直角三角形的性质和等腰三角形性质的综合运用.AB CDNM EDCBA【例26】 已知如图,在直角△ABC 中,∠ACB =90°,∠A =30°,D 为AB 上一点,且BD =14AB .求证:CD ⊥AB . 【难度】★★ 【答案】见解析【解析】取AB 的中点E ,连接CE∵AB BE 21=,BD =14AB ,∴BE BD =2,∴DB ED = ∵∠ACB =90°,∠A =30°,∴AB BC 21= ∵∠ACB =90°,EB AE =,∴AB CE 21=,∴CE BC = ∵CE BC =,DB ED =,∴CD ⊥AB .【总结】考察直角三角形的性质的应用及等腰三角形三线合一性质的运用.【例27】 已知等边△ABC 中,D 、E 分别是BC 、AC 上的点,且AE =CD ,AD 与BE 相交于点F ,过点B 作BG ⊥AD ,垂足为G , (1) 求FG :BF 的值;(2) 若D 、E 分别在BC 、CA 的延长线上,其他条件都不变,上述结论是否仍然成立,请说明理由.【难度】★★【答案】(1)1:2;(2)见解析.【解析】(1)∵BAE ACD ∠=∠,AE =CD ,AB =CA ,∴CAD ABE ≌△△,∴ABE CAD ∠=∠∵︒=∠+∠60BAF CAD ,∴︒=∠+∠60BAF ABE ∴︒=∠60BFG ,∴︒=∠30FBG∵BG ⊥AD ,∴BF FG 21=,即FG :BF=1:2;(2)若D 、E 分别在BC 、CA 的延长线上,其他条件都不变,也可以用同样的方法证 明出两个三角形全等,进而得到结论.【总结】考察直角三角形的性质的应用及利用三角形的外角性质求角的度数.A BCDEFGABCDE【例28】 在△ABC 中,已知∠A=60°,BE ⊥AC 于E ,CF ⊥AB 于F ,点D 是BC 中点. (1)如果AB=AC ,求证△DEF 为等边三角形;(2)如果AB≠AC ,试猜想△DEF 是不是等边三角形,若是,请加以证明,若不是,请说明理由;(3)如果CM =4,FM =5,求BE 的长度. 【难度】★★★【答案】(1)见解析;(2)是,理由见解析;(3)12.【解析】(1)∵BE ⊥AC ,点D 是BC 中点,∴BC DC DE 21==∵CF ⊥AB ,点D 是BC 中点,∴BC BF DF 21==,∴DF DE = ∵∠A =60°,AB =AC ,∴△ABC 是等边三角形,∴︒=∠=∠60ACB ABC ∵DC DE =,︒=∠60ACB ,∴△DEC 是等边三角形,∴︒=∠60EDC ∵DB DF =,︒=∠60ABC ,∴△BFD 是等边三角形,∴︒=∠60FDB ∴︒=︒-︒-︒=∠606060180FDE ∵DF DE =,∴△DEF 为等边三角形(2)∵BE ⊥AC ,点D 是BC 中点,∴BC DC DE 21== ∵CF ⊥AB ,点D 是BC 中点,∴BC BF DF 21==,∴DF DE = ∵∠A =60°,∴︒=∠+∠120ACB ABC , ∵DC DE =,∴ACB DEC ∠=∠ ∵DB DF =,∴ABC DFB ∠=∠, ∴180FDE FDB EDC ∠=︒-∠-∠()()180********ABC ACB =︒-︒-∠-︒-∠ ()218060ABC ACB =∠+∠-︒=︒ ∵DF DE =,∴△DEF 为等边三角形(3)∵∠A =60°,BE ⊥AC 于E ,CF ⊥AB ,∴︒=∠=∠30ECM FBM∴1122FM BM EM CM ==,∵CM =4,FM =5,∴102==BM EM ,, ∴12210=+=+=ME BM BE【总结】考察直角三角形性质及等边三角形性质的综合运用.ABCDE FM【例29】 已知∠MAN ,AC 平分∠MAN ,(1)在图1中,若∠MAN =120°,∠ABC =∠ADC =90°,求证:AB +AD =AC . (2)在图2中,若∠MAN =120°,∠ABC +∠ADC =180°,则(1)中的结论是否仍然成立?若成立,请给出证明;若不成立,请说明理由. 【难度】★★★ 【答案】见解析【解析】(1)∵∠MAN =120°,AC 平分∠MAN ,∴︒=∠=∠60CAB CAD∵∠ABC =∠ADC =90°,∴∠ACD =∠ACB =30°,∴AC AB 21=,AC AD 21=∴AC AC AC AD AB =+=+2121; (2)过C 作CE ⊥AM ,过C 作CF ⊥AN ,垂足分别为E 、F ∵AC 平分∠MAN ,CE ⊥AM ,CF ⊥AN , ∴CF CE =∵∠ABC +∠ADC =180°,∠MDC +∠ADC =180°, ∴∠EDC =∠ABC∵∠EDC =∠ABC ,CF CE =,CFB CED ∠=∠ ∴CBF CED ≌△△,∴BF ED =∴AF AE BF AF DE AE AB AD +=++-=+ ∵∠MAN =120°,AC 平分∠MAN , ∴︒=∠=∠60CAB CAD ∵∠ABC =∠ADC =90°, ∴∠ACE =∠ACF =30°, ∴AC AE 21=,AC AF 21=∴AC AC AC AD AB =+=+2121 【总结】考察角平分线的性质和直角三角形的性质的综合运用.ABCDMNNA BCD ME F【练习1】 下列条件不可以判定两个直角三角形全等的是().A 、两条直角边对应相等B 、斜边一个锐角对应相等C 、一条直角边和一条斜边对应相等D 、一条边和一个角对应相等 【难度】★ 【答案】D【解析】A 的理由是S A S ..;B 的理由是S A A ..,C 的理由是L H . 【总结】考察直角三角形全等的判定.【练习2】 如图在△ABC 中,∠ACB =90°,在AB 上截取AE =AC ,BD =BC ,则∠DCE =_________.【难度】★ 【答案】45°【解析】180DCE CDE CED ∠=︒-∠-∠180********B A︒-∠︒-∠=︒--452A B∠+∠==︒. 【总结】本题主要考查等边对等角及三角形内角和定理的综合运用.【练习3】 如图在△ABC 中,∠ACB =90°,CD ⊥AB 于点D ,∠A =30°,则AD =_____AB 【难度】★【答案】43.【解析】∵︒=∠+∠90ACD A ,︒=∠+∠90ACD BCD , ∴︒=∠=∠30A BCD∵︒=∠90ACB ,∠A =30°,∴AB BC 21=∵︒=∠90BDC ,︒=∠30BCD ,∴BC BD 21=,∴AB BD 41=,∴AB AD 43= 【总结】考察直角三角形的性质的运用.随堂检测ABCD【练习4】 如图,在直角△ABC 在,∠ACB =90°,AB =8cm ,D 为AB 的中点,DE ⊥AC 于E ,∠A =30°,求BC 、CD 和DE 的长.【难度】★★【答案】BC =4cm ,CD=4cm ,DE=2cm .【解析】∵∠ACB = 90°,AB = 8cm ,D 为AB 的中点,∠A =30°,∴421421====AB BC AB CD ,∵DE ⊥AC ,∠A =30°,∴221==AD DE . 【总结】考察直角三角形的性质的运用.【练习5】 如图,△ABC 中,AD ⊥BC 于点D ,BE ⊥AC 于点E ,交AD 于点H ,且AD=BD ,AC=BH ,连接CH .求证:∠ABC=∠BCH . 【难度】★★ 【答案】见解析【解析】∵ADC BDH ∠=∠90=,AC =BH ,BD AD =∴ACD BHD ≌△△, ∴DC DH = ∵AD ⊥BC , ∴︒=∠=∠45BCH CHD∵BD AD =,BC AD ⊥,∴︒=∠=∠45BAD ABC , ∴∠ABC =∠BCH .【总结】考察直角三角形全等的判定和性质的运用.【练习6】 如图,已知,在锐角三角形ABC 中,∠ABC =2∠C ,AD ⊥BC 于点D ,E 为AC的中点,ED 的延长线交AB 的延长线于点F ,求证:BF =BD . 【难度】★★ 【答案】见解析.【解析】∵AD ⊥BC ,E 为AC 的中点,∴AC EC DE 21==,∴EDC C ∠=∠∵BDF EDC ∠=∠,∴BDF C ∠=∠ ∵∠ABC =2∠C ,∴BDF ABC ∠=∠2∵F BDF ABC ∠+∠=∠,∴F BDF ∠=∠,∴BF =BD . 【总结】考察直角三角形的性质和三角形外角性质的综合运用.【练习7】 如图,在△ABC 中,BE ⊥AC 于点E ,CF ⊥AB 于点F ,D 是边BC 的中点,连接ABCDEAB CDEFABCDEHDF 、EF 、DE . (1)求证:ED =DF ;(2)若△DEF 是等边三角形,则△ABC 应满足什么条件? 【难度】★★ 【答案】见解析.【解析】(1)∵BE ⊥AC ,点D 是BC 中点,∴BC DC DE 21==∵CF ⊥AB ,点D 是BC 中点,∴BC BD DF 21==,∴DF DE =;(2)︒=∠60A 时,△DEF 是等边三角形. ∵BE ⊥AC ,点D 是BC 中点,∴BC DC DE 21== ∵CF ⊥AB ,点D 是BC 中点,∴BC BF DF 21==,∴DF DE =∵∠A =60°,∴︒=∠+∠120ACB ABC , ∵DC DE =,∴ACB DEC ∠=∠ ∵DB DF =,∴ABC DFB ∠=∠, ∴180FDE FDB EDC ∠=︒-∠-∠()()180********ABC ACB =︒-︒-∠-︒-∠ ()218060ABC ACB =∠+∠-︒=︒ ∵DF DE =, ∴△DEF 为等边三角形【总结】考察直角三角形的性质和等边三角形判定的综合运用.【练习8】 如图,AD ∥BC ,且BD ⊥CD ,BD = CD ,AC = BC .求证:AB = BO .【难度】★★ 【答案】见解析.【解析】过A 作AE ⊥BC 垂足为E ,过D 作DF ⊥BC ,垂足为F∵BD ⊥CD ,BD = CD ,DF ⊥BC ,∴BC DF 21=∵AE ⊥BC ,DF ⊥BC ,AD ∥BC , ∴四边形AEFD 是长方形,∴DF AE =∵BC DF 21=,DF AE =,AC = BC∴AC AE 21=,∴︒=∠30ACB ∵AC = BC ,∴︒=∠=∠75ABC BAO∵BD ⊥CD ,BD = CD ,∴︒=∠45DBC ,∴︒=∠30ABD ∵︒=∠75BAO ,∴︒=∠75AOB ∴AOB BAO ∠=∠,∴AB = BO【总结】考察直角三角形的性质和等腰三角形性质的应用.【练习9】 已知:如图在△ABC 中,AD 是BC 边上的高,CE 是AB 上的中线,DC =BE ,DG ⊥CE ,垂足为点G .求证:∠AEC =3∠DCE .【难度】★★ 【答案】见解析 【解析】联结ED∵AD 是BC 边上的高,CE 是AB 上的中线,∴AB BE ED 21== ∵DC =BE ,∴DC DE =,∴DEC DCE ∠=∠ ∴DCE DEC DCE EDB ∠=∠+∠=∠2∵ED BE =,∴EDB B ∠=∠,∴DCE B ∠=∠2 ∴DCE DCE B AEC ∠=∠+∠=∠3【总结】考察直角三角形的性质和等腰三角形的性质的综合应用.【练习10】 如图,在等边三角形ABC 中,D 、E 分别是BC 、AC 上的一点,且AE =CD ,ABDOCE FABCDEGAD 与BE 相交于点F ,CF ⊥BE . 求AF :BF 的值.【难度】★★★ 【答案】1:2.【解析】过B 作BK ⊥AD 的垂线,垂足为K∵AC AB =,ACD BAE ∠=∠,AE =CD , ∴CAD ABE ≌△△, ∴ABE DAC ∠=∠∴︒=∠+∠=∠+∠=∠60BAF DAC BAF ABE BFD ∵︒=∠60BFD ,BK ⊥AD ,∴︒=∠30FBK ,∴BF FK 21=∵CBF BAK ∠=∠,BFC AKB ∠=∠,BC AB = ∴BCF ABK ≌△△∴BF AK =,即BF FK AF =+∴BF BF AF =+21∴AF BF 2=,即AF :BF=1:2【总结】考察全等三角形的判定和性质以及直角三角形性质的综合运用.【练习11】 如图,在直角三角形ABC 中,∠BAC =90°,AB =AC ,以AB 为边向外作等边ABCDFE K三角形ABD ,AE ⊥BD 于点E ,AE 交CD 于点M . (1)线段DM 与线段BC 有怎样的数量关系?并证明;(2)若△ABC 于△ABD 在AB 的同侧,CD 的延长线与AE 的延长线交于点M ,请在图2 中画出△ABD 与点M ;线段DM 与BC 仍有(1)中的数量关系吗?并证明. 【难度】★★★ 【答案】见解析.【解析】(1)∵直角三角形ABC 中,∠BAC =90°,AB =AC ,等边三角形ABD ,∴︒=∠150CAD ,AC=AD∴()︒=∠-︒=∠1518021CAD ADC∵︒=∠60ADB ,∴︒=∠45CDB∵AE ⊥BD ,∴△DME 是等腰直角三角形 ∴DE DM 2=∵等边三角形ABD ,AE ⊥BD 于点E ∴DB DE 21=,∴DB DM 22= ∵直角三角形ABC 中,∠BAC =90°,AB =AC ,∴AB BC 2=∵AB DB =,∴DB BC 2= ∵DB DM 22=,∴DM BC 2= (2)成立.理由同(1)一样.【总结】本题综合性较强,一方面考察等腰直角三角形的性质 及等边三角形性质的综合运用,另一方面考查了勾股定理的 运用,教师可以选择性的讲解.课后作业ABCDME图1A BC图2【作业1】下列命题中,正确的有()个①腰长及底边上的高对应相等的两个等腰三角形全等 ②有一直角边和斜边对应相等的两个直角三角形全等 ③有两边和其中一边上的高对应相等的两个三角形全等 A .0B .1C .2D .3【难度】★ 【答案】C【解析】(1)(2)对,(3)错误,满足条件的三角形可以是锐角三角形也可以是钝角三角形. 【总结】考察三角形全等的判定方法.【作业2】(1)直角△ABC 中,∠C = 90°,CD ⊥AB ,点E 是AB 的中点,∠ACD =25°,则∠ECB =__________;(2)直角△ABC 中,∠C =90°,CD ⊥AB ,点E 是AB 的中点,∠DCE =10°,则∠B =______________. 【难度】★【答案】(1)25°;(2)40°.【解析】利用直角三角形斜边上的中线等于斜边的一半的角度之间的关系可得到答案.【总结】考察直角三角形的性质.【作业3】如图,ABC ∆中,AB AC =,DB DC =,DE AC ⊥,2AC AD =,8AB =,则AD =________,AE =____________.【难度】★★ 【答案】4;2.【解析】∵AB AC =,DB DC =,∴BC AD ⊥∵2AC AD =,∴︒=∠30C ,∴42121===AB AC AD∵DE AC ⊥,∴︒=∠=∠30B ADE ,∴221==AD AE . 【总结】考察等腰三角形的性质和直角三角形性质的综合运用.【作业4】(1)等腰三角形底角是75°,腰长为9,则此三角形的面积是_______;DABCEAB CD E(2)等腰三角形一腰上的高等于腰长的一半,则这个等腰三角形的顶角的度数是_____________. 【难度】★★ 【答案】(1)481;(2)30°或150°. 【解析】(1)∵等腰三角形底角是75°,∴顶角为30度,则腰上的高为29,则三角形的面 积为48129921=⨯⨯;(2)注意分锐角三角形和钝角三角形两种情况分类讨论.【总结】考察直角三角形的性质.注意等腰三角形分为锐角等腰三角形和钝角等腰三角形.【作业5】已知:AB ⊥BC ,DC ⊥BC ,点E 在BC 上,且AE =AD ,AB =BC ,求证:CE =CD . 【难度】★★ 【答案】见解析.【解析】过D 作DF ⊥AB ,垂足为F∵AB ⊥BC ,DC ⊥BC ,DF ⊥AB , ∴四边形BCDF 是长方形, ∴BC DF =,CD BF = ∵BC AB =,∴DF AB = ∵DF AB =,AE=AD , ∴EBA AFD ≌△△, ∴BE AF =∵BC AB =,∴BF CE = ∵CD BF =,∴CD CE =【总结】考察直角三角形全等的判定方法的运用.【作业6】已知:如图,△ABC 中,∠B =40°,∠C =20°,DA ⊥CA ,求证:CD=2AB .ABCDE F【难度】★★ 【答案】见解析【解析】取CD 的中点E ,联结AE∵DA ⊥CA ,ED CE =∴CD CE AE 21==∴︒=∠=∠20CAE C ∴︒=∠+∠=∠40CAE C AEB∵︒=∠40B ,∴B AEB ∠=∠,∴AB AE =∵CD AE 21=,∴CD AB 21=,即AB CD 2=【总结】考察等腰三角形的判定和直角三角形的性质的综合运用.【作业7】如图,已知:△ABC 中,AB =AC ,∠A=60°,BD =CD ,BE ∥AC ,DE ⊥BE ,求证:4BE=AC . 【难度】★★ 【答案】见解析. 【解析】连接AD∵AB =AC ,∠A=60°,∴△ABC 是等边三角形,∴BC =AC∵AB =AC ,BD =CD ,∴BC AD ⊥ ∵︒=∠=∠3021BAC DAC ,BC AD ⊥,∴AC DC 21=∵BD =CD ,∴AC BD 21=∵BE ∥AC ,∴︒=∠=∠60C DBE∵DE ⊥BE ,∴BD BE 21=∵AC BD 21=,∴AC BE 41=, 即4BE=AC .【总结】考察直角三角形的性质和等边三角形的性质的综合运用.【作业8】在等腰直角△ABC 中,D 是斜边AB 的中点,E 、F 分别在直线AC 、BC 上,ABCDEABCDE且AE =CF ,联结DE 、DF 、EF ,试判断△DEF 的形状,并加以证明. 【难度】★★【答案】等腰直角三角形.证明见解析. 【解析】等腰直角三角形.联结CD∵等腰直角△ABC 中,D 是斜边AB 的中点, ∴AB CD ⊥,︒=∠=∠=∠=∠45ACD BCD B A , DB AD CD ==∵DB CD =,ACD B ∠=∠,AE =CF ,∴FBD ECD ≌△△ ∴DF DE =,BDF CDE ∠=∠∵︒=∠+∠90BDF CDF ,∴︒=∠+∠90CDE CDF ,即︒=∠90EDF ∵DF DE =,∴△DEF 是等腰直角三角形.【总结】考察等腰直角三角形的性质及全等三角形性质的运用.【作业9】已知:如图,在四边形ABCD 中,∠ABC =∠ADC =90°,AC 、BD 相交于点O ,M 、N 分别为AC 、BD 的中点. (1)求证:MN ⊥BD ;(2)当∠BAC =15°,AC =10,OB =OM 时,求MN 的长. 【难度】★★ 【答案】见解析.【解析】(1)联结BM ,MD∵∠ABC =∠ADC =90°,M 分别为AC 的中点∴1122BM AC DM AC ==,, ∴MD BM =∵N 分别为BD 的中点, ∴MN ⊥BD ;(2)∵∠BAC =15°,AM BM =,∴︒=∠30BMC ∵OB =OM ,∴︒=∠=∠30MBO BMC∵MN ⊥BD ,∴BM MN 21=由(1)可得:521==AC BM ,∴25=MN 【总结】考察直角三角形的性质和等腰三角形性质的综合运用.【作业10】已知:等腰直角△ABC 中,O 是斜边AC 的中点,P 是斜边AC 上的一个动点,A BC D EFABC DM NOD 是线段BC 上的一点,且BP =PD ,过点D 作AC 边上的高DE ,求证:PE =BO . 【难度】★★★ 【答案】见解析.【解析】∵等腰直角△ABC 中,∴︒=∠45C∵O 是斜边AC 的中点,∴︒=∠45OBC ∴OBC C ∠=∠∵BP =PD ,∴PDB PBD ∠=∠∵C DPE PDB OBC PBO PBD ∠+∠=∠∠+∠=∠, ∴DPE PBO ∠=∠∵DPE PBO ∠=∠,POB PED ∠=∠,BP =PD , ∴PED BOP ≌△△ ∴PE =BO .【总结】考察等腰直角三角形的性质的应用.【作业11】如图1,已知点D 在AC 上,△ABC 和△ADE 都是等腰直角三角形,点M 为EC 的中点.(1)求证:△BMD 为等腰直角三角形;(2)将△ADE 绕点A 逆时针旋转45°,如图2所示,(1)中的结论是否仍然成立,请说明理由;(3)将△ADE 绕点A 逆时针旋转135°,(1)中的结论是否仍然成立,请说明理由.【难度】★★★ 【答案】见解析. 【解析】(1)联结DM∵︒=∠90ABC ,点M 为EC 的中点.∴EC BM 21=,BCM BME ∠=∠2∵︒=∠90EDC ,点M 为EC 的中点.∴EC DM 21=,DCM EMD ∠=∠2,∴DM BM =∴22BMD BME EMD BCM DCM ∠=∠+∠=∠+∠ ()2290BCM DCM BCD =∠+∠=∠=︒∴△BMD 为等腰直角三角形;(2)延长DM 与BC 交于点NABCDPEO图1 AB CDEMABCDE图2M N∵AB DE ⊥,AB CB ⊥∴BC DE ∥,∴MCN DEM ∠=∠ ∵NMC EMD ∠=∠,MC EM =∴CNM EDM ≌△△,∴MN DM =,CN ED = ∵ED AD =,∴CN AD = ∵BC AB =,∴BN BD =∵MN DM =,∴DM BM ⊥,DM BM = ∴△BMD 为等腰直角三角形;(3)过C 作CN ∥ED 交DM 的延长线于N ∵CN ∥ED ,∴MED MCN ∠=∠∵MED MCN ∠=∠,DME CMN ∠=∠,MC EM = ∴CNM EDM ≌△△,∴MN DM =,CN ED = ∵ED AD =,∴CN AD =∵BC AB =,BAD BCN ∠=∠,CN AD =∴BCN BAD ≌△△,∴BN BD =,CBN DBA ∠=∠∵︒=∠+∠90CBN ABN ,∴︒=∠+∠90DBA ABN ,即︒=∠90DBN ∵MN DM =,∴DM BM ⊥,DM BM = ∴△BMD 为等腰直角三角形.【总结】本题综合性较强,主要考察等腰直角三角形的性质和判定,在说理时注意认真分析,添加合适的辅助线.。
《中考数学总复习指导》第四单元三角形第18讲直角三角形一、考纲解读直角三角形也是一种特殊的三角形,直角三角形的有关概念是了解性知识,对于直角三角形我们需要会探索并掌握直角三角形的性质和一个三角形是直角三角形的条件并能体验勾股定理的探索过程,会运用勾股定理解决简单问题;会用勾股定理的逆定理判定直角三角形。
同时直角三角形的判定是我们证明线段互相垂直的主要方法之一,同时正确理解直角三角形的性质和判定,并利用这些性质来解决一些数学问题也是新课标给我们提出的具体要求。
二、命题规律1.三角形:本部分近几年,考查内容越来越综合,涉及的知识点主要有:直角三角形的性质(最广是勾股定理)。
预测2014年本部分内容考查仍旧以综合考查为主,直角三角形的性质为重点,单纯考查直角三角形知识可能性比较小。
三、知识梳理(一)直角三角形的性质1.勾股定理:如果直角三角形的两直角边长分别为a,b,斜边长为c,那么a2+b2=c2。
2. 直角三角形斜边上的中线等于斜边的一半。
3. 直角三角形中,30°角所对的直角边等于斜边的一半。
(二)直角三角形的判定1.在一个三角形中,有一个角是直角的三角形是直角三角形。
2.勾股定理逆定理:如果三角形三边长a,b,c满足a2+b2=c2。
,那么这个三角形是直角三角形。
3.在一个三角形中,如果一条边上的中线等于这条边的一半,那么这个三角形是直角三角形。
四、基础自测1.(2013•衢州)将一个有45°角的三角板的直角顶点放在一张宽为3cm的纸带边沿上.另一个顶点在纸带的另一边沿上,测得三角板的一边与纸带的一边所在的直线成30°角,如图,则三角板的最大边的长为()A.3cm B.6cm C..cm-=,则该直角三角2.(2013•巴中)若直角三角形的两直角边长为a、b40形的斜边长为_______________.3.(2013•鞍山)如图,D是△ABC 内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是.4.(2013•莆田)如图是一株美丽的勾股树,其中所有的四边形都是正方形,所有的三角形都是直角三角形,若正方形A、B、C、D的面积分别为2,5,1,2.则最大的正方形E的面积是.5.(2013•内江)已知,如图,△ABC和△ECD都是等腰直角三角形,∠AC B=∠DCE=90°,D为AB边上一点.求证:BD=AE.五、题型详解考点一:直角三角形的性质【例1】(2012•安徽)在一张直角三角形纸片的两直角边上各取一点,分别沿斜边中点与这两点的连线剪去两个三角形,剩下的部分是如图所示的直角梯形,其中三边长分别为2、4、3,则原直角三角形纸片的斜边长是()A.10B.C. 10或D.10或变式题:(2013•雅安)在平面直角坐标系中,已知点A0),B0),点C在坐标轴上,且AC+BC=6,写出满足条件的所有点C的坐标.考点二、直角三角形的判定【例2】(2013•包头)如图,点E是正方形ABCD内的一点,连接AE、BE、CE,将△ABE绕点B顺时针旋转90°到△CBE′的位置.若AE=1,BE=2,CE=3,则∠BE′C=度.变式题:(2013•东营)如图,圆柱形容器中,高为1.2m,底面周长为1m,在容器内壁..离容器底部0.3m的点B处有一蚊子,此时一只壁虎正好在容器外壁..的点A处,则壁虎捕捉蚊..,离容器上沿0.3m与蚊子相对子的最短距离为m(容器厚度忽略不计).六、课后练习基础巩固一、填空题1.(2013•梅州)如图,已知△ABC是腰长为1的等腰直角三形,以Rt△ABC的斜边AC为直角边,画第二个等腰Rt△ACD,再以Rt△ACD的斜边AD为直角边,画第三个等腰Rt△ADE,…,依此类推,则第2013个等腰直角三角形的斜边长是.2.(2013•哈尔滨)在△ABC中,AB=BC=1,∠ABC=450,以AB为一边作等腰直角三角形ABD,使∠ABD=900,连接CD,则线段CD的长为.思路分析:双解问题,画等腰直角三角形ABD,使∠ABD=900,分两种情况,点D与C在AB同侧, D与C在AB异侧,考虑要全面;, 解:当点D与C在AB同侧,BD=AB=,作CE⊥BD于由勾股定理,当点D与C在AB异侧,BD=AB=,∠BDC=1350,作DE⊥BC于E,BE=ED=2,EC=3,由勾股定理点拨:在几何题没有给出图形时,有的同学会忽略掉其中一些情况,故解决问题最好先画出图形,运用数形结合和分类讨论的数学思想进行解答,避免出现漏解.3.(2013•包头)如图,在三角形纸片ABC中,∠C=90°,AC=6,折叠该纸片,使点C落在AB边上的D 点处,折痕BE与AC交于点E,若AD=BD,则折痕BE的长为.4.(2013•陕西)如图,从点()02A ,发出的一束光,经x 轴反射,过点()43B ,,则这束光从点A 到点B 所经过路径的长为 .思路分析:由物理学内容及利用对称性,再结合相似三角形的知识(或者结合一次函数知识)都可以计算出答案。
5.如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是.二、选择题1.(2012•广西)已知三组数据:①2,3,4;②3,4,5;③12.分别以每组数据中的三个数为三角形的三边长,构成直角三角形的有()A.②B.①②C.①③D.②③2.(2013•绥化)如图,在Rt△ABC中,∠C=90°,,BC=1,D在AC上,将△ADB沿直线BD翻折后,点A落在点E处,如果AD⊥ED,那么△ABE的面积是()A.1 B.C.D.3.(2013•资阳)如图,点E在正方形ABCD内,满足∠AEB=90°,AE=6,BE=8,则阴影部分的面积是()A.48 B.60 C.76 D.804.(2013•雅安)如图,正方形ABCD中,点E、F分别在BC、CD上,△AEF是等边三角形,连接AC交EF于G,下列结论:①BE=DF,②∠DAF=15°,③AC垂直平分EF,④BE+DF=EF,⑤S△CEF=2S△ABE.其中正确结论有()个.A.2 B.3 C.4 D.5,三、解答题1.(2013•包头)如图,一根长米的木棒(AB),斜靠在与地面(OM)垂直的墙(ON)上,与地面的倾斜角(∠ABO)为60°.当木棒A端沿墙下滑至点A′时,B端沿地面向右滑行至点B′.(1)求OB的长;(2)当AA′=1米时,求BB′的长.2.(2013•烟台)已知,点P是直角三角形ABC斜边AB上一动点(不与A,B重合),分别过A,B向直线CP作垂线,垂足分别为E,F,Q为斜边AB的中点.(1)如图1,当点P与点Q重合时,AE与BF的位置关系是,QE与QF的数量关系式;(2)如图2,当点P在线段AB上不与点Q重合时,试判断QE与QF的数量关系,并给予证明;(3)如图3,当点P在线段BA(或AB)的延长线上时,此时(2)中的结论是否成立?请画出图形并给予证明.思路分析:(1)证△BFQ≌△AEQ即可;(2)证△FBQ≌△DAQ,推出QF=QD,根据直角三角形斜边上中线性质求出即可;(3)证△AEQ≌△BDQ,推出DQ=QE,根据直角三角形斜边上中线性质求出即可.∴△FBQ≌△DAQ(ASA),∴QF=QD,∵AE⊥CP,∴EQ是直角三角形DEF斜边上的中线,∴QE=QF=QD,即QE=QF.点拨:本题考查了全等三角形的性质和判定,直角三角形斜边上中线性质的应用,注意:①全等三角形的判定定理有SAS,ASA,AAS,SSS,②全等三角形的性质是:全等三角形的对应边相等,对应角相等.3.(2013•齐齐哈尔)已知等腰三角形ABC中,∠ACB=90°,点E在AC边的延长线上,且∠DEC=45°,点M、N分别是DE、AE的中点,连接MN交直线BE于点F.当点D在CB边上时,如图1所示,易证MF+FN=12BE(1)当点D在CB边上时,如图2所示,上述结论是否成立?若成立,请给与证明;若不成立,请写出你的猜想,并说明理由.(2)当点D在BC边的延长线上时,如图3所示,请直接写出你的结论.(不需要证明)解答:(1)答:不成立,猜想:FN ﹣MF=12BE ,理由如下:证明:如图2,连接AD ,∵M 、N 分别是DE 、AE 的中点,∴MN=12AD ,又∵在△ACD 与△BCE 中,AC BCACB BCE DC CE=⎧⎪∠=∠⎨⎪=⎩,∴△ACD ≌△BCE (SAS ),∴AD=BE ,∵MN=FN ﹣MF ,4.如图,在Rt△ABC中,∠C=90°,∠B=60°,点D是BC边上的点,CD=1,将△ABC沿直线AD翻折,使点C落在AB边上的点E处,若点P是直线AD上的动点,求△PEB的周长的最小值?即,5.(2013•吉林)图①、图②都是4×4的正方形网格,每个小正方形的顶点称为格点,每个小正方形的边长均为1.在每个网格中标注了5个格点.按下列要求画图:(1)在图①中以格点为顶点画一个等腰三角形,使其内部已标注的格点只有3个;(2)在图②中,以格点为顶点,画一个正方形,使其内部已标注的格点只有3个,且边长为无理数.能力提升1.(2013•宁波)如图,AE是半圆O的直径,弦,弦CD=DE=4,连结OB,OD,则图中两个阴影部分的面积和为.2.(2013•柳州)在△ABC中,∠BAC=90°,AB=3,AC=4.AD平分∠BAC交BC于D,则BD的长为()A.157B.125C.207D.215思路分析:根据勾股定理列式求出BC,再利用三角形的面积求出点A到BC上的高,根据角平分线上的点到角的两边的距离相等可得点D到AB、AC上的距离相等,然后利用三角形的面积求出点D到AB的长,再利用△ABD的面积列式计算即可得解.解:∵∠BAC=90°,AB=3,AC=4,∴5==,∴BC边上的高=12×3×4÷5=65,3.(2013•株洲)已知四边形ABCD是边长为2的菱形,∠BAD=60°,对角线AC与BD交于点O,过点O的直线EF交AD于点E,交BC于点F.(1)求证:△AOE≌△COF;(2)若∠EOD=30°,求CE的长.==,4.(2013•梅州)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.探究二:如图④,将△DEF的顶点D放在△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN 的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.设AM=x,则CN=x,AN=AC﹣BC﹣x.在Rt△AMN中,由勾股定理得:===.。