4-第四讲直角三角形和勾股定理.docx

中考数学复习必备教案 直角三角形与勾股定理知识点回顾知识点一：直角三角形的概念与性质1．有一个角是 的三角形叫做直角三角形； 2．直角三角形的两个锐角 ；3．直角三角形斜边上的中线等于 的一半.例1．（2009湖北省荆门市）如图1，Rt △ABC 中，∠ACB =90°，∠A =50°，将其折叠，使点A 落在边CB 上A ′处，折痕为CD ，则∠A ′DB = （ ）A 、40° B、30° C、20° D、10° 解：∵Rt △ABC 中，∠ACB =90°，∠A =50°， ∴∠B =90°－50°=40° 由折叠得∠DA ′C =∠A =50°， ∵∠DA ′C =∠B +∠A ′DB∴∠A ′DB =50°－40°=10°，选D.例2．若直角三角形斜边上的高和中线分别为10cm 、12cm ，则它的面积是 cm 2. 解：∵直角三角形斜边上的中线等于斜边的一半，∴直角三角形斜边的长为2×12=24cm. ∴直角三角形的面积是21×24×10=120cm 2.同步检测一：1．（2009年湖南省郴州市）如图2，桌面上平放着一块三角板和一把直尺，小明将三角板的直角顶点紧靠直尺的边缘，他发现无论是将三角板绕直角顶点旋转，还是将三角板沿直尺平移，∠1与∠2的和总是保持不变，那么∠1与∠2的和是_______度．2．如图3，Rt △ABC 中，∠B =90°，BD ⊥AC 于D ，点E 为AC 的中点，若BC =7，AB =24，则BE = ，BD = .A 'B DAC（图1）ABE D C（图3）21（图2）知识点二：勾股定理直角三角形 的平方和等于 的平方．例3．（2009年四川省宜宾市）已知：如图4，以Rt △ABC 的三边为斜边分别向外作等腰直角三角形．若斜边AB ＝3，则图中阴影部分的面积和为 ． 解：过点E 作ED ⊥AB 于点D ，可证得ED =21AB ， ∴ED AB S ABE ⨯⨯=∆21=41AB 2， 同理AHC S ∆=41AC 2，BFC S ∆=41BC 2， 从而图中阴影部分的面积和为41（AB 2+ AC 2+ BC 2） =41（AB 2+ AB 2）=29. 例4．（2009年湖南省衡阳市）如图5，矩形纸片ABCD 中，AB =4，AD =3，折叠纸片使AD 边与对角线BD 重合，折痕为DG ，则AG 的长为 （ ）A 、1B 、34 C 、23D 、2解：Rt △DAB 中，BD =54322=+， 设AG =x ，则BG=4－x由折叠得A ′D =AD =3，A ′G =AG =x ，∠DA ′G =∠A =90°， ∴A ′B =BD －A ′D =5－3=2，∠GA ′B =90°， 从而Rt △GA ′B 中，x 2+22=（4－x ）2. 解得x =23，选C. 同步检测二：3．如果直角三角形的两条边长分别是3和4，那么该直角三角形斜边上的中线等于 . 4．（2009年四川省达州市）如图6是一株美丽的勾股树， 其中所有的四边形都是正方形，所有的三角形都是直角 三角形．若正方形A 、B 、C 、D 的边长分别是3、5、 2、3，则最大正方形E 的面积是 （ ） A 、13 B 、26 C 、47 D 、94★5．（2009年黑龙江省哈尔滨市）若正方形ABCD 的边长为4，E 为BC 边上一点，BE ＝3，M 为线段AE 上一点，射线BM交正方形的一边于点F ，且BF ＝AE ，求BM 的长. （图5）AB CDA′G（图4）BHF EAC（图6）知识点三：直角三角形的判定方法1．根据定义：有一个角是 的三角形叫做直角三角形；2．勾股定理的逆定理：如果三角形的三边长a 、 b 、 c 有关系： ，那么这个三角形是直角三角形，且∠C =90°.例5．（2009年湖南省衡阳市）如图7，A 、B 、C 分别表示三个 村庄，AB ＝1000米，BC ＝600米，AC ＝800米，在社会主义 新农村建设中，为了丰富群众生活，拟建一个文化活动中心， 要求这三个村庄到活动中心的距离相等，则活动中心P 的位 置应在 （ ） A 、AB 中点 B 、BC 中点C 、AC 中点D 、∠C 的平分线与AB 的交点解：显然到A 、B 、C 三个村庄距离相等的点P 应该是AB 、BC 、AC 三边垂直平分线的交点. 又∵BC 2+AC 2=6002+8002=1000000；AB 2=10002=1000000 ∴BC 2+AC 2=AB 2， ∴∠ACB =90°,由于直角三角形三边垂直平分线的交点在斜边的中点处，从而活动中心P 的位置应在AB 的中点处，选A.例6．如图8，点P 是等边△ABC 内的一点，分别连接PA 、PB 、PC ，以BP 为边作∠PBQ =60°，且BQ =BP ，连接CQ .（1）观察并猜想AP 与CQ 之间的大小关系，并证明你的结论；（2）若PA ∶PB ∶PC =3∶4∶5，连接PQ ，试判断△PQC 的形状，并说明理由. （1）答：AP =CQ证：∵△ABC 为等边三角形 ∴AB =BC ，∠ABC =60° ∵∠PBQ =60° ∴∠ABC =∠PBQ ∴∠ABP =∠CBQ在△ABP 与△CBQ 中，⎪⎩⎪⎨⎧=∠=∠=BQ BP CBQ ABP CBAB∴△ABP ≌△CBQ （SAS ） ∴AP =CQ（2）答：△PQC 为直角三角形.理由是：设PA =3k ，则PB =4k ，PC =5k （k >0），CQ =AP =3k BAC（图7）ABP （图8）∵BQ =BP ，∠PBQ =60°∴△PBQ 为等边三角形（有一个角为60°的等腰三角形是等边三角形） ∴PQ =PB =4k又CQ 2=9k 2，PQ 2=16k 2，PC 2=25k 2， ∴CQ 2+PQ 2=PC 2∴△PQC 为直角三角形，且∠PQC =90°. 同步检测三：6、（2009年黑龙江省牡丹江市）如图9， △ABC 中，CD ⊥AB 于D ，下列条件中：①∠1=∠A ；②CDDBAD CD；③∠B +∠2=90°；④BC ∶AC ∶AB =3∶4∶5；⑤AC ×BD =AC ×CD ，一定能确定△ABC 为直角三角形的条件的个数是 （ ） A 、1B 、2C 、3D 、47、（2009年甘肃省定西市）如图10，△ACB 和△ECD 都是等腰直角三角形，∠ACB ＝∠ECD ＝90°，D 为AB 边上一点，求证：（1）△ACE ≌△BCD ；（2）AD 2+DB 2=DE 2.随堂检测：1．（2009年湖南省长沙市）如图11，等腰△ABC 中，AB =AC ，AD 是底边上的高，若AB =5cm ，BC =6cm ，则AD = cm ．2．(2009年上海市)如图12，在Rt △ABC 中，∠BAC =90°，AB =3， M 为边BC 上的点，联结AM ．如果将△ABM 沿直线AM 翻折后，点B 恰好落在边AC 的中点处，那么点M 到AC 的距离是 .3．（2009年贵州省安顺市）如图13，图甲是我国古代著名的“赵爽弦图”的示意图，它是AB CM（图12）（图10）EDBAC21DBAC（图9）（图11）AD CB（图13）CS 1S 2（图14）由四个全等的直角三角形围成的. 在Rt △ABC 中，若直角边AC ＝6，BC ＝6，将四个直角三角形中边长为6的直角边分别向外延长一倍，得到图乙所示的“数学风车”，则这个风车的外围周长（图乙中的实线）是______.4．（2009年浙江省湖州市）如图14，已知在Rt △ABC 中，∠ACB =Rt ∠，AB =4，分别以AC 、BC 为直径作半圆，面积分别记为S 1、S 2，则S 1+S 2的值等于 .5．（2009年湖北省恩施自治州）如图15，长方体的长为15，宽为10，高为20，点B 离点C的距离为5，一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ，需要爬行的最短距离是 （ ）A 、521B 、25C 、105+5D 、356．（2009年浙江省丽江市）如图16，已知△ABC 中，∠ABC ＝90°，AB ＝BC ，三角形的顶点在相互平行的三条直线l 1，l 2，l 3上，且l 1，l 2之间的距离为2 ， l 2，l 3之间的距离为3 ，则AC 的长是 （ ） A 、172 B 、52 C 、24 D 、77．（2009年新疆维吾尔自治区）如图17是用硬纸板做成的四个全等的直角三角形，两直角边长分别是a b ，，斜边长为c 和一个边长为c 的正方形，请你将它们拼成一个能证明勾股定理的图形．（1）画出拼成的这个图形的示意图． （2）证明勾股定理．8．（2009年湖北省恩施自治州）恩施州自然风光无限，特别是以“雄、奇、秀、幽、险”著称于世．如图18，著名的恩施大峡谷（A ）和世界级自然保护区星斗山（B ）位于笔直的沪渝高速公路X 同侧，AB =50km ，A 、B 到直线X 的距离分别为10km 和40km ，要在沪渝高速公路旁修建一服务区P ，向A 、B 两景区运送游客．小民设计了两种方案，图（1）是方案5201510CAB（图15）l 1l 2l 3ACB（图16）cba cba cba cbacc（图17）一的示意图（AP 与直线X 垂直，垂足为P ），P 到A 、B 的距离之和S 1=PA +PB ，图（2）是方案二的示意图（点A 关于直线X 的对称点是A ′，连接BA ′交直线X 于点P ），P 到A 、B 的距离之和S 2=PA +PB ．（1）求S 1、S 2，并比较它们的大小； （2）请你说明S 2=PA +PB 的值为最小；（3）拟建的恩施到张家界高速公路Y 与沪渝高速公路垂直，建立如图（3）所示的直角坐标系，B 到直线Y 的距离为30km ，请你在X 旁和Y 旁各修建一服务区P 、Q ，使P 、A 、B 、Q 组成的四边形的周长最小．并求出这个最小值．9．（2009年黑龙江省牡丹江市）有一块直角三角形的绿地，量得两直角边长分别为6m ，8m. 现在要将绿地扩充成等腰三角形，且扩充部分是以8m 为直角边的直角三角形，求扩充后等腰三角形绿地的周长. 10．（2009年湖北省咸宁市）问题背景：在△ABC 中，AB 、BC 、AC 三边的长分别为5、10、13，求这个三角形的面积．小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC （即△ABC 三个顶点都在小正方形的顶点处），如图19中的图①所示．这样不需求△ABC 的高，而借用网格就能计算出它的面积． （1）请你将△ABC 的面积直接填写在横线上：__________________ 思维拓展：（2）我们把上述求△ABC 面积的方法叫做构图法．．．．若△ABC 三边的长分别为5a 、a 22、a 17（a >0），请利用图19中的图②的正方形网格（每个小正方形的边长为a ）画出相应的△ABC ，并求出它的面积． 探索创新：（3）若△ABC 三边的长分别为2216n m +、2249n m +、222n m +（m >0，n >0，且m ≠n ），试运用构图法．．．求出这三角形的面积． （图18）BA P 图（1）YXBAQPO图（3）BAPXA '图（2） AB答案：知识点回顾的答案知识点一：直角；互为余角；斜边； 知识点二：两直角边；斜边； 知识点三：直角；a 2+b 2=c 2. 同步测试的答案 1．90°； 2．BE =225，BD =25168； 3．2或25； 4．A ； 5．（1）当点F 在DC 上时，如图1，先证△ABE ≌△BCF ，可得AE =BF =5，BE =CF =3，AE ⊥BF ，再由面积公式BE AB BM AE ⋅=⋅得BM =512.（2）当点F 在AD 上时，如图2，先证△ABE ≌△BAF ，可得BE =AF =3，∴AE =BF =5，连结EF ，证□ABEF ，∴BM =21BF =25. 6．C （提示：能确定△ABC 为直角三角形的有①②④，共3个） 7．证明:（1） ∵ ∠ACB =∠ECD =90°，∴∠ACB －∠ACD =∠ECD －∠ACD ， 即 ∠BCD =∠ACE ∵BC =AC ，DC =EC ， ∴△ACE ≌△BCD .（2）∵△ACB 是等腰直角三角形， ∴∠B =∠BAC =45°． ∵△ACE ≌△BCD ， ∴∠CAE =∠B =45°．∴∠DAE =∠CAE +∠BAC =45°+45°=90°． ∴Rt △DAE 中，AD 2+AE 2=DE 2. ∵△ACE ≌△BCD ∴ AE ＝DB ， ∴AD 2+DB 2=DE 2. A B F EDC M（图1）ABEC D M F（图2）（第5题答案图）随堂检测的答案：1．4cm ； 2．2； 3．76； 4．2π； 5．B ； 6．A 7．解：（1）如图，（2）证明：大正方形的面积表示为()2b a +，大正方形的面积也可表示为ab c 2142⨯+，∴()2b a +=ab c 2142⨯+，即ab c ab b a 22222+=++，∴222c b a =+，即直角三角形两直角边的平方和等于斜边的平方.8．解：（1）图18（1）中过B 作BC ⊥AP ，交PA 的延长线于点C ，则PC ＝40，又AP ＝10，∴AC ＝30.在Rt △ABC 中，AB ＝50 ，AC ＝30，∴BC ＝40 ，∴ BP ＝24022=+BC CP ， ∴S 1＝10240+；图18（2）中，过B 作BC ⊥AA ′，交A ′A 的延长线于点C ，则A ′C ＝50，又BC ＝40， ∴BA ′＝4110504022=+，由轴对称知：PA ＝PA ′，∴S 2＝BA ′＝4110， ∴S 1>S 2.（2）如 图18（2），在公路上任找一点M ，连接MA ，MB ，MA '，由轴对称知MA ＝MA ′，∴MB +MA ＝MB +MA ′>A ′B ，∴S 2＝BA ′为最小.（3）如图，过A 作关于X 轴的对称点A ′，过B 作关于Y 轴的对称点B ′，连接A ′B ′，交X 轴于点P ，交Y 轴于点Q ，则P ，Q 即为所求.过A ′、 B ′分别作X 轴、Y 轴的平行线交于点G ，A ′B ′＝5505010022=+， ∴所求四边形的周长为55050+.a bc a bcab cc b a（第7（1）题答案图）YB′BAQ9．解：设在Rt △ABC 中，∠ABC =90°，AB =8，BC =6. 由勾股定理有：AC =10. 扩充部分为Rt △ABD ，扩充成等腰△ACD ，应分以下三种情况： ①如图1，当AC =AD =10时，可求BD =CB =6，得△ACD 的周长为32m ；②如图2，当AC =CD =10时，可求BD =4，由勾股定理得：AD =45，得△ACD 的周长为（20+45）m ；③如图3，当AC 为底时，设AD =CD =x ，则BD =x －6，由勾股定理得：x =325，得△ACD 的周长为380m.10．（1）3.5；（2）如图②，构造△ABC ，使AB =5a ，BC =a 22，AC =a 17，∴△ABC 的面积为21×（2a +4a ）×2a －21×a ×2a －21×a ×4a =3a 2；（3）如图③，先构造长和宽分别为4n 、3m 的长方形网格，再构造△ABC ，使AC =2216n m +，BC =2249n m +，AB =222n m +，∴△ABC 的面积为3m ×4n －21×m ×4n －21×2n ×3m －21×2n ×2m =5mn .DC B ACB AD CBAD（图1）（图2）（图3）（第9题答案图）（第10题答案图）4n3mAC B （图②）（图③）。

初中数学试卷桑水出品《勾股定理》典型例题分析一、知识要点：1、勾股定理勾股定理：直角三角形两直角边的平方和等于斜边的平方。

也就是说：如果直角三角形的两直角边为a、b，斜边为c ，那么 a2 + b2= c2。

公式的变形：a2 = c2- b2， b2= c2-a2 。

2、勾股定理的逆定理如果三角形ABC的三边长分别是a，b，c，且满足a2 + b2= c2，那么三角形ABC 是直角三角形。

这个定理叫做勾股定理的逆定理.该定理在应用时，同学们要注意处理好如下几个要点：①已知的条件：某三角形的三条边的长度.②满足的条件：最大边的平方=最小边的平方+中间边的平方.③得到的结论：这个三角形是直角三角形，并且最大边的对角是直角.④如果不满足条件，就说明这个三角形不是直角三角形。

3、勾股数满足a2 + b2= c2的三个正整数，称为勾股数。

注意：①勾股数必须是正整数，不能是分数或小数。

②一组勾股数扩大相同的正整数倍后，仍是勾股数。

常见勾股数有：（3，4，5）(5，12，13) (6，8，10)(7，24，25)(8，15，17)(9，12，15)4、最短距离问题：主要运用的依据是两点之间线段最短。

二、考点剖析考点一：利用勾股定理求面积1、求阴影部分面积：（1）阴影部分是正方形；（2）阴影部分是长方形；（3）阴影部分是半圆．2. 如图，以Rt △ABC 的三边为直径分别向外作三个半圆，试探索三个半圆的面积之间的关系．3、如图所示，分别以直角三角形的三边向外作三个正三角形，其面积分别是S 1、S 2、S 3，则它们之间的关系是（ ）A. S 1- S 2= S 3B. S 1+ S 2= S 3C. S 2+S 3< S 1D. S 2- S 3=S 14、四边形ABCD 中，∠B=90°，AB=3，BC=4，CD=12，AD=13，求四边形ABCD 的面积。

5、在直线l 上依次摆放着七个正方形（如图4所示）。

京师蜀都学堂创新教材系列勾股定理（总复习）专题第讲时间：2014年月日老师：电话：一、兴趣导入（Topic-in）：专题简析：1、勾股定理：如果直角三角形两直角边分别为a，b，斜边为c，那么a2+b2=c2，即直角三角形两直角边的平方和等于斜边的平方。

2、勾股定理的逆定理：如果三角形的三边长a，b，c满足a2+b2=c2，即三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

（C为斜边最长，c＞a，c＞b ）注释：（1）勾股定理揭示了一个直角三角形三边之间的数量关系。

（2）勾股定理只适用于直角三角形，而不适用于锐角三角形和钝角三角形。

（3）理解勾股定理的一些变式： c2=a2+b2，a2=c2－b2， b2=c2－a23、图形解释：4、勾股数：满足a2+b2=c2的三个正整数成为勾股数.例如：（3，4，5），（6，8，10），（5，12，13），（7，24，25）注释：勾股数的每一项的整数倍的组合也是勾股数，例如（3，4，5）的二倍（6，8，10）同样也为勾股数。

二、知识讲解及例题分析(Teaching)：例1 已知两边求第三边:1．在△ABC中，∠C＝90°，a、b、c分别是∠A、∠B、∠C的对边①若a＝5，b＝12，则c＝________；②若c＝41，a＝40，则b＝________；③若∠A＝45°，a＝1．则b＝________，c＝________ ,a：b：c＝ .2. 在直角三角形中,若两直角边的长分别为1cm，2cm ，则斜边长为_____________．3. 已知直角三角形的两边长为3、2，则另一条边长是________________．4．如图，在△ABC中，AB=AC，∠BAC的角平分线交BC边于点D，AB=5，BC=6，则AD= 。

5. 如图∠B=∠ACD=90°, AD=13,CD=12, BC=3，则AB的长是多少?总结：在应用勾股定理进行计算时，一定要分清哪条是直角边哪条是斜边。

直角三角形和勾股定理一、直角三角形的定义与性质1.1 定义：在平面直角坐标系中，有一个角为直角（即90度），由两条直角边和一条斜边组成的三角形称为直角三角形。

1.2 性质：（1）直角三角形的两个锐角互余，即它们的和为90度。

（2）直角三角形的两个直角边互为邻边。

（3）直角三角形的斜边是直角边的非邻边。

（4）直角三角形的斜边长度大于任意一个直角边的长度。

（5）直角三角形的中线、高线、角平分线三线合一。

二、勾股定理的定义与证明2.1 定义：直角三角形中，两条直角边的平方和等于斜边的平方，即a^2 + b^2 = c^2，其中c为斜边长度，a和b为直角边长度。

2.2 证明：（1）几何法：通过画出直角三角形ABC，其中∠C为直角，AC为直角边，BC 为另一直角边，AB为斜边，利用平行线等知识进行证明。

（2）代数法：通过构造直角三角形ABC的相似三角形，利用相似三角形的性质进行证明。

三、勾股定理的应用3.1 直角三角形边长求解：已知直角三角形中，两个直角边的长度，可以通过勾股定理求出斜边的长度。

3.2 直角三角形面积求解：已知直角三角形中，两个直角边的长度，可以通过勾股定理求出三角形的面积。

3.3 逆定理：如果一个三角形的三边满足a^2 + b^2 = c^2，那么这个三角形是直角三角形。

四、与直角三角形和勾股定理相关的数学文化4.1 勾股定理的历史：勾股定理是古代中国数学家毕达哥拉斯发现的，被称为“勾三股四弦五”。

4.2 勾股定理的应用：在建筑、工程、物理学等领域有着广泛的应用。

以上是关于直角三角形和勾股定理的知识点介绍，希望对您有所帮助。

习题及方法：1.习题：已知直角三角形ABC中，∠C为直角，AB为斜边，AC=3，BC=4，求斜边AB的长度。

方法：根据勾股定理，AB^2 = AC^2 + BC2，代入已知数值，得AB2 = 3^2 + 4^2 = 9 + 16 = 25，所以AB = √25 = 5。

勾股定理【知识点】１．勾股定理（只适用于直角三角形）内容：直角三角形两直角边的平方和等于斜边的平方；表示方法：如果直角三角形的两直角边分别为a ，b ，斜边为c ，那么222a b c +=２.勾股定理的证明证明方法1：4EFGH S S S ∆+=正方形正方形ABCD ，2214()2ab b a c ⨯+-=，化简可证．证明方法2：四个直角三角形的面积与小正方形面积的和等于大正方形的面积．四个直角三角形的面积与小正方形面积的和为221422S ab c ab c =⨯+=+大正方形面积为222()2S a b a ab b =+=++ 所以222a b c +=证明方法3：1()()2S a b a b =+⋅+梯形，2112S 222ADE ABE S S ab c ∆∆=+=⋅+梯形，化简得证３.勾股定理的适用范围勾股定理揭示了直角三角形三条边之间所存在的数量关系，它只适用于直角三角形，对于锐角三角形和钝角三角形的三边就不具有这一特征，因而在应用勾股定理时，必须注明所考察的对象是直角三角形４.勾股定理的应用①已知直角三角形的任意两边长，求第三边在ABC ∆中，90C ∠=︒，则c，bacbaHG F EDCBAbacbac cabcab a bc cbaED CBA②可运用勾股定理解决一些实际问题③利用勾股定理作长为 n （n 为大于1的整数）的线段５.勾股定理的逆定理如果三角形三边长a ，b ，c 满足222a b c +=，那么这个三角形是直角三角形，其中c 为斜边 注意：①勾股定理的逆定理是判定一个三角形是否是直角三角形的一种重要方法，它通过“数转化为形”来确定三角形的可能形状，在运用这一定理时，可用两小边的平方和22a b +与较长边的平方2c 作比较：若222a b c +=时，以a ，b ，c 为三边的三角形是直角三角形； 若222a b c +<时，以a ，b ，c 为三边的三角形是钝角三角形； 若222a b c +>时，以a ，b ，c 为三边的三角形是锐角三角形；②定理中a ，b ，c 及222a b c +=只是一种表现形式，不可认为是唯一的，如若三角形三边长a ，b ，c 满足222a c b +=，那么以a ，b ，c 为三边的三角形是直角三角形，但是b 为斜边③勾股定理的逆定理在用问题描述时，不能说成：当斜边的平方等于两条直角边的平方和时，这个三角形是直角三角形６.勾股数①能够构成直角三角形的三边长的三个正整数称为勾股数，即222a b c +=中，a ，b ，c 为正整数时，称a ，b ，c 为一组勾股数②记住常见的勾股数可以提高解题速度，如3,4,5；6,8,10；5,12,13；7,24,25等 ③用含字母的代数式表示n 组勾股数： 221,2,1n n n -+（2,n ≥n 为正整数）； 2221,22,221n n n n n ++++（n 为正整数）2222,2,m n mn m n -+（,m n >m ，n 为正整数）考点例析考点1：已知直角三角形两边边长，求第三边边长1、如果直角三角形的两直角边长分别为1n 2-，2n （n>1），那么它的斜边长是（ ） A 、2nB 、n+1C 、n 2－1D 、1n 2+2、直角三角形的斜边比一直角边长2 cm ，另一直角边长为6 cm ，则它的斜边长 A 、4 cmB 、8 cmC 、10 cmD 、12 cm3、已知一个Rt △的两边长分别为3和4，则第三边长的平方是（ ） A 、25B 、14C 、7D 、7或254、在ABC ∆中，90C ∠=︒．⑴已知6AC =，8BC =．求AB 的长⑵已知17AB =，15AC =，求BC 的长考点2：已知直角三角形的一边以及另外两边的关系利用勾股定理求周长、面积等问题。

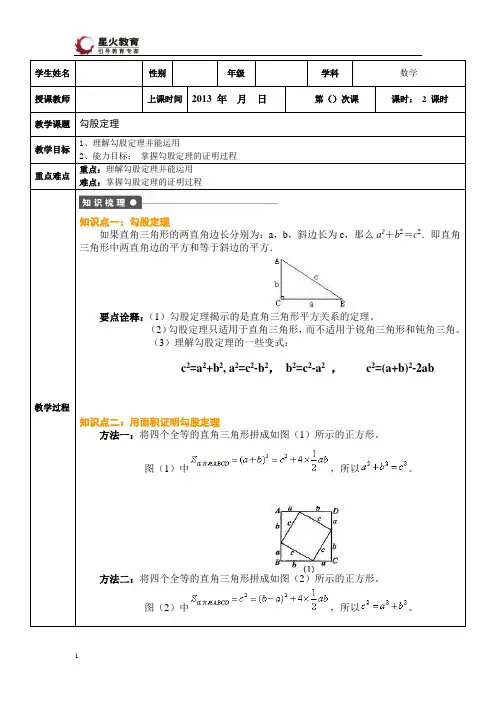
学生姓名性别年级学科数学授课教师上课时间2013 年月日第（）次课课时：2 课时教学课题勾股定理教学目标1、理解勾股定理并能运用2、能力目标：掌握勾股定理的证明过程重点难点重点：理解勾股定理并能运用难点：掌握勾股定理的证明过程教学过程知识点一：勾股定理如果直角三角形的两直角边长分别为：a，b，斜边长为c，那么a2＋b2＝c2．即直角三角形中两直角边的平方和等于斜边的平方．要点诠释：（1）勾股定理揭示的是直角三角形平方关系的定理。

（2）勾股定理只适用于直角三角形，而不适用于锐角三角形和钝角三角。

（3）理解勾股定理的一些变式：c2=a2+b2, a2=c2-b2，b2=c2-a2，c2=(a+b)2-2ab知识点二：用面积证明勾股定理方法一：将四个全等的直角三角形拼成如图（1）所示的正方形。

图（1）中，所以。

方法二：将四个全等的直角三角形拼成如图（2）所示的正方形。

图（2）中，所以。

知识点三：勾股定理的作用1．已知直角三角形的两条边长求第三边；2.已知直角三角形的一条边，求另两边的关系；3．用于证明平方关系的问题；4．利用勾股定理，作出长为的线段。

(3)在理解的基础上熟悉下列勾股数满足不定方程x2+y2=z2的三个正整数，称为勾股数（又称为高数或毕达哥拉斯数），显然，以x,y,z为三边长的三角形一定是直角三角形。

熟悉下列勾股数，对解题是会有帮助的：①3、4、5②5、12、13；③8、15、17；④7、24、25；⑤10、24、26；⑥9、40、41．如果(a,b,c)是勾股数，当t>0时，以at,bt,ct为三角形的三边长，此三角形必为直角三角形。

经典例题透析类型一：勾股定理的直接用法1、在Rt△ABC中，∠C=90°(1)已知a=6，c=10，求b，(2)已知a=40，b=9，求c；(3)已知c=25，b=15，求a.举一反三【变式】:如图∠B=∠ACD=90°, AD=13,CD=12, BC=3,则AB的长是多少?类型二：勾股定理的构造应用2、如图，已知：在中，，，. 求：BC的长.举一反三【变式1】如图，已知：，，于P. 求证：.【变式2】已知：如图，∠B=∠D=90°，∠A=60°，AB=4，CD=2。

勾股定理、一、勾股定理：1、勾股定理定义：如果直角三角形的两直角边长分别为a，b，斜边长为c，那么a2＋b2＝c2. 即直角三角形两直角边的平方和等于斜边的平方ABCabc弦股勾勾：直角三角形较短的直角边股：直角三角形较长的直角边弦：斜边勾股定理的逆定理：如果三角形的三边长a，b，c有下面关系：a2＋b2＝c2，那么这个三角形是直角三角形。

2. 勾股数：满足a2＋b2＝c2的三个正整数叫做勾股数（注意：若a，b，c、为勾股数，那么ka，kb，kc同样也是勾股数组。

）*附：常见勾股数：3,4,5； 6,8,10； 9,12,15； 5,12,133. 判断直角三角形：如果三角形的三边长a、b、c满足a2+b2=c2 ，那么这个三角形是直角三角形。

（经典直角三角形：勾三、股四、弦五）其他方法：（1）有一个角为90°的三角形是直角三角形。

（2）有两个角互余的三角形是直角三角形。

用它判断三角形是否为直角三角形的一般步骤是：（1）确定最大边（不妨设为c）；（2）若c2＝a2＋b2，则△ABC是以∠C为直角的三角形；若a2＋b2＜c2，则此三角形为钝角三角形（其中c为最大边）；若a2＋b2＞c2，则此三角形为锐角三角形（其中c为最大边）4.注意：（1）直角三角形斜边上的中线等于斜边的一半（2）在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

（3）在直角三角形中，如果一条直角边等于斜边的一半，那么这条直角边所对的角等于30°。

5. 勾股定理的作用：（1）已知直角三角形的两边求第三边。

（2）已知直角三角形的一边，求另两边的关系。

（3）用于证明线段平方关系的问题。

（4）利用勾股定理，作出长为n的线段（一）结合三角形：1.已知∆ABC 的三边a 、b 、c 满足0)()(22=-+-c b b a ，则∆ABC 为 三角形2.在∆ABC 中，若2a =（b +c ）（b -c ），则∆ABC 是 三角形，且∠ ︒90 3.在∆ABC 中，AB=13，AC=15，高AD=12，则BC 的长为1.已知2512-++-y x x 与25102+-z z 互为相反数，试判断以x 、y 、z 为三边的三角形的形状。

勾股定理(基础)学习目标1．掌握勾股定理的内容，了解勾股定理的多种证明方法，体验数形结合的思想；2．能够运用勾股定理求解三角形中相关的边长（只限于常用的数）；3．通过对勾股定理的探索解决简单的实际问题，进一步运用方程思想解决问题．要点梳理要点一、勾股定理直角三角形两条直角边的平方和等于斜边的平方．如果直角三角形的两直角边长分别为，斜边长为，那么．要点诠释：（1）勾股定理揭示了一个直角三角形三边之间的数量关系．（2）利用勾股定理，当设定一条直角边长为未知数后，根据题目已知的线段长可以建立方程求解，这样就将数与形有机地结合起来，达到了解决问题的目的．（3）理解勾股定理的一些变式：，，．要点二、勾股定理的证明方法一：将四个全等的直角三角形拼成如图（1）所示的正方形．图（1）中，所以．方法二：将四个全等的直角三角形拼成如图（2）所示的正方形．图（2）中，所以．方法三：如图（3）所示，将两个直角三角形拼成直角梯形．，所以．要点三、勾股定理的作用1．已知直角三角形的任意两条边长，求第三边；2．用于解决带有平方关系的证明问题；3．与勾股定理有关的面积计算；4．勾股定理在实际生活中的应用．典型例题类型一、勾股定理的直接应用1、在△ABC中，∠C＝90°，∠A、∠B、∠C的对边分别为、、．（1）若＝5，＝12，求；（2）若＝26，＝24，求．【变式】在△ABC中，∠C＝90°，∠A、∠B、∠C的对边分别为、、．（1）已知＝6，＝10，求；（2）已知，＝32，求、．类型二、与勾股定理有关的证明2、如图所示，在Rt△ABC中，∠C＝90°，AM是中线，MN⊥AB，垂足为N，试说明．【变式】如图，在△ABC中，∠C＝90°，D为BC边的中点，DE⊥AB于E，则AE2-BE2等于（）A．AC2 B．BD2C．BC2 D．DE2类型三、与勾股定理有关的线段长3、如图，长方形纸片ABCD中，已知AD＝8，折叠纸片使AB边与对角线AC重合，点B 落在点F 处，折痕为AE，且EF＝3，则AB的长为（）A．3 B．4 C．5 D．6类型四、与勾股定理有关的面积计算4、如图，直线l上有三个正方形a，b，c，若a，c的面积分别为5和11，则b的面积为（）A．6 B．5 C．11 D．16类型五、利用勾股定理解决实际问题5、一圆形饭盒，底面半径为8，高为12，若往里面放双筷子（精细不计），那么筷子最长不超过多少，可正好盖上盒盖？巩固练习一．选择题1．在△ABC中，AB＝12，AC＝9，BC＝15，则△ABC的面积等于（）A．108 B．90C．180D．542．若直角三角形的三边长分别为2，4，，则的值可能有( )A．1个 B．2个 C．3个 D．4个3．小明想知道学校旗杆的高度，他发现旗杆上的绳子垂到地面还多1米,当他把绳子的下端拉开5米后，发现下端刚好接触地面，则旗杆的高是( )A．12米 B．10米 C．8米 D．6米4．Rt△ABC中，斜边BC＝2，则的值为( )A．8 B．4 C．6 D．无法计算5．如图，△ABC中，AB＝AC＝10，BD是AC边上的高线，DC＝2，则BD等于( )A．4 B．6 C．8 D．56．如图，Rt△ABC中，∠C＝90°，若AB＝15，则正方形ADEC和正方形BCFG的面积和为( )A．150B．200 C．225 D．无法计算二．填空题7．甲、乙两人同时从同一地点出发，已知甲往东走了4，乙往南走了3，此时甲、乙两人相距____．8．如图，有一块长方形花圃，有少数人为了避开拐角走“捷径”，在花圃内走出了一条“路”，他们仅仅少走了______米路，却踩伤了花草．9．如图是一个外轮廓为矩形的机器零件平面示意图，根据图中的尺寸（单位：mm），计算两圆孔中心A和B的距离为mm．10．如图，有两棵树，一棵高8，另一棵高2，两树相距8，一只小鸟从一棵树的树梢飞到另一棵树的树梢，至少要飞______．11．如图，直线经过正方形ABCD的顶点B，点A、C到直线的距离分别是6、8，则正方形的边长是______．12．如图，王大爷准备建一个蔬菜大棚，棚宽2．4m，高3．2m，长15m，棚的斜面用塑料薄膜遮盖，不计墙的厚度，请计算阳光透过的最大面积是 m2．三．解答题13．如图四边形ABCD的周长为42，AB＝AD＝12，∠A＝60°，∠D＝150°，求BC的长．14．已知在三角形ABC中，∠C＝90°，AD平分∠BAC交BC于D，CD＝3，BD＝5，求AC 的长．勾股定理逆定理(基础)学习目标1．理解勾股定理的逆定理，并能与勾股定理相区别；2. 能运用勾股定理的逆定理判断一个三角形是否是直角三角形；3. 理解勾股数的含义；4. 通过探索直角三角形的判定条件的过程，培养动手操作能力和逻辑推理能力.要点梳理要点一、勾股定理的逆定理如果三角形的三条边长，满足，那么这个三角形是直角三角形.要点诠释：（1）勾股定理的逆定理的作用是判定某一个三角形是否是直角三角形.（2）勾股定理的逆定理是把“数”转为“形”，是通过计算来判定一个三角形是否为直角三角形.要点二、如何判定一个三角形是否是直角三角形（1）首先确定最大边（如）.（2）验证与是否具有相等关系.若，则△ABC是∠C＝90°的直角三角形；若，则△ABC不是直角三角形.要点诠释：当时，此三角形为钝角三角形；当时，此三角形为锐角三角形，其中为三角形的最大边.要点三、勾股数满足不定方程的三个正整数，称为勾股数（又称为高数或毕达哥拉斯数），显然，以为三边长的三角形一定是直角三角形.熟悉下列勾股数，对解题会很有帮助：①3、4、5；②5、12、13；③8、15、17；④7、24、25；⑤9、40、41……如果是勾股数，当为正整数时，以为三角形的三边长，此三角形必为直角三角形.要点诠释：（1）（是自然数）是直角三角形的三条边长；（2）（是自然数）是直角三角形的三条边长；（3）（是自然数）是直角三角形的三条边长；典型例题类型一、勾股定理的逆定理1、判断由线段组成的三角形是不是直角三角形．（1）＝7，＝24，＝25；（2）＝，＝1，＝；（3），，()；【变式】一个三角形的三边之比是3:4:5 则这个三角形三边上的高之比是（）A．20:15:12 B．3:4:5 C．5:4:3 D．10:8:2类型二、勾股定理逆定理的应用例3、已知：为的三边且满足，试判断的形状.例：4、“远航”号、“海天”号轮船同时离开港口，各自沿一固定方向航行“远航”号每小时航行16海里，“海天”号每小时航行12海里，它们离开港口一个半小时后相距30海里，如果知道“远航”号沿东北方向航行，能知道“海天”号沿哪个方向航行吗？巩固练习一.选择题1．在三边分别为下列长度的三角形中，不是直角三角形的是（）．A. 9，12，15 B．3，4，5 C．1.4，4.8,5 D．4，7，52. 如图，在单位正方形组成的网格图中标有AB、CD、EF、GH四条线段，其中能构成一个直角三角形三边的线段是（）．A．CD、EF、GH B．AB、EF、GH C．AB、CF、EF D．GH、AB、CD3. 下列说法：（1）在△ABC中，若a2+b2≠c2，则△ABC不是直角三角形；（2）若△ABC 是直角三角形，∠C=90°，则a2+b2=c2；（3）在△ABC中，若a2+b2=c2，则∠C=90°；（4）直角三角形的两条直角边的长分别为5和12，则斜边上的高为．其中说法正确的有（）．A．4个B．3个C．2个D．1个4．下面各选项给出的是三角形中各边的长度的平方比，其中不是直角三角形的是( )．A．1∶1∶2 B．1∶3∶4C．9∶25∶26 D．25∶144∶1695．已知三角形的三边长为(其中)，则此三角形( )．A．一定是等边三角形 B．一定是等腰三角形C．一定是直角三角形 D．形状无法确定6．三角形的三边长分别为、、（都是正整数），则这个三角形是（）．A．直角三角形 B．钝角三角形 C．锐角三角形 D．不能确定二.填空题7．若一个三角形的三边长分别为6，8，10，则这个三角形中最短边上的高为______．8．已知两条线段的长分别为11和60，当第三条线段的长为时，这3条线段能组成一个直角三角形（要求三边长均为整数）．9. 已知,则由此为边的三角形是三角形.10．在△ABC中，若其三条边的长度分别为9、12、15，则以两个这样的三角形所拼成的四边形的面积是_____．11．若一个三角形的三边之比为5：12：13，且周长为60，则它的面积为．12．如图，AB＝5，AC＝3，BC边上的中线AD＝2，则△ABC的面积为______．三.解答题13．已知：如图，在正方形ABCD中，F为DC的中点，E为CB的四等分点且CE＝，求证：AF⊥FE．14．观察下列各式：，，，，…，你有没有发现其中的规律?请用含的代数式表示此规律并证明，再根据规律写出接下来的式子．15．在B港有甲、乙两艘渔船，若甲船沿北偏东60°方向以每小时8海里的速度前进，乙船沿南偏东某个角度以每小时15海里的速度前进，2小时后，甲船到M岛，乙船到P岛，两岛相距34海里，你知道乙船是沿哪个方向航行的吗?。

直角三角形与勾股定理【复习目标】1．掌握直角三角形的边、角之间所存在的关系，掌握勾股定理以及逆定理。

2．熟练应用直角三角形的勾股定理和逆定理来解决实际问题． 3．掌握直角三角形常用的判定方法。

【直击考点】1．若 a 、b 、c 是Rt △ABC 的三边， 90=∠C ，则a 2＋b 2＝ 。

c 2 2．若 a 、b 、c 是△ABC 的三边，且a 2＋b 2＝c 2，则∠C= 。

90° 3．如图,三个正方形中的两个的面积S 1＝25，S 2＝144，则另一个的面积S 3为________． 1694．直角三角形斜边上的中线等于斜边的一半 ；三角形中一条边上的中线等于这条边的一半，那么这条边所对的角是直角 。

5．直角三角形中，30°的角所对的边等于斜边的一半 ；一直角边等于斜边的一半，这条直角边所对的角等于 30 度。

【名题点拔】考点1 “双垂图”中的计算问题例1 已知：在Rt △ABC 中，∠C=90°，CD ⊥BC 于D ，∠A=60°，CD=3，求线段AB 的长。

点拨：本题是“双垂图”的计算题，“双垂图”是中考重要的考点，对图形及性质应熟练掌握，能够灵活应用。

“双垂图”中有：3个直角三角形， 6条线段，4个锐角。

知道其中的任意两条线段，或一条线段和一个锐角，总可以求出其余的线段。

欲求AB ，可由AB=BD+CD ，分别在两个三角形中利用勾股定理和特殊角，求出BD=3和AD=1。

或欲求AB ，可由22BC AC AB +=，分别在两个三角形中利用勾股定理和特殊角，CD求出AC=2和BC=23。

因此AB=4。

考点2 勾股定理在轴对称问题中的应用例2 如图，有一个直角三角形纸片，两直角边AC =6c m ，BC =8c m ，现将直角边AC 沿直线AD 折叠，使它落在斜边AB 上，且与AE 重合，求CD 的长。

点拨：设CD =x ，在Rt △BDE 中使用勾股定理列方程即可。