第四讲-立体几何题型归类总结
- 格式:docx
- 大小:495.74 KB
- 文档页数:17

2024年高考数学立体几何知识点总结立体几何是数学中的一个重要分支,也是高考数学中的重要内容之一。
在高考中,立体几何的知识点主要包括空间几何、立体图形的面积与体积等方面。
下面是对2024年高考数学立体几何知识点的总结,供考生参考。
一、空间几何1. 空间几何中的点、线、面的概念和性质。
点是没有长度、宽度和高度的,只有位置的大小,用字母表示。
线是由一组无限多个点构成的集合,用两个点的字母表示。
面是由无限多条线构成的,这些线共面且没有相交或平行关系。
2. 空间几何中的垂直、平行等概念和性质。
两条线在同一平面内,如果相交角为90°,则称两线垂直。
两条线没有相交关系,称两线平行。
3. 点到直线的距离的计算。
点到直线的距离等于该点在直线上的正交投影点的距离。
二、立体图形的面积与体积1. 立体图形的分类和性质。
立体图形包括球体、圆柱体、圆锥体、棱柱体、棱锥体等。
各种立体图形具有不同的性质,如球体表面上每一点到球心的距离都相等。
2. 立体图形的面积计算。
(1)球体的表面积计算公式:S = 4πr²,其中r为球的半径。
(2)圆柱体的侧面积计算公式:S = 2πrh。
(3)圆柱体的全面积计算公式:S = 2πrh + 2πr²。
(4)圆锥体的侧面积计算公式:S = πrl,其中r为圆锥底面半径,l为斜高。
(5)棱柱体的侧面积计算公式:S = ph,其中p为棱柱底面周长,h为高。
3. 立体图形的体积计算。
(1)球体的体积计算公式:V = 4/3πr³,其中r为球的半径。
(2)圆柱体的体积计算公式:V = πr²h。
(3)圆锥体的体积计算公式:V = 1/3πr²h。
(4)棱柱体的体积计算公式:V = ph。
(5)棱锥体的体积计算公式:V = 1/3Bh,其中B为底面积,h 为高。
三、立体几何的一般理论1. 点、线、面的位置关系。
在空间中,点、线、面可以相互相交、平行、垂直等。

立体几何的知识点总结篇1:高中立体几何知识点总结高中立体几何知识点总结1.棱柱、棱锥、棱(圆)台的本质特征⑴棱柱:①有两个互相平行的面(即底面平行且全等),②其余各面(即侧面)每相邻两个面的公共边都互相平行(即侧棱都平行且相等)。
⑵棱锥:①有一个面(即底面)是多边形,②其余各面(即侧面)是有一个公共顶点的三角形。
⑶棱台:①每条侧棱延长后交于同一点,②两底面是平行且相似的多边形。
⑷圆台:①平行于底面的截面都是圆,②过轴的截面都是全等的等腰梯形,③母线长都相等,每条母线延长后都与轴交于同一点。
2.圆柱、圆锥、圆台的展开图、表面积和体积的计算公式3.线线平行常用方法总结(1)定义:在同一平面内没有公共点的两条直线是平行直线。
(2)公理:在空间中平行于同一条直线的两条直线互相平行。
(3)线面平行的性质:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线就和两平面的交线平行。
么两直线平行。
(5)面面平行的性质:若两个平行平面同时与第三个平面相交,那么两条交线平行。
4.线面平行的判定方法。
(1)定义:直线和平面没有公共点。
(2)判定定理:若不在平面内的一条直线和平面内的一条直线平行,那么这条直线和这个平面平行。
(3)面面平行的性质:两个平面平行,其中一个平面内的任何一条直线必平行于另一个平面。
(4)线面垂直的性质:平面外于已知平面的垂线垂直的直线平行于已知平面。
5.判定两平面平行的方法。
(1)依定义采用反证法;(2)利用判定定理:如果一个平面内有两条相交直线平行于另一个平面,那么这两个平面平行。
(3)利用判定定理的推论:如果一个平面内有两条相交直线平行于另一个平面内的两条直线,则这两平面平行。
(4)垂直于同一条直线的两个平面平行。
(5)平行于同一个平面的两个平面平行。
6.证明线线垂直的方法(1)利用定义。
条直线垂直于这个平面的任何一条直线。
7.证明线面垂直的方法(1)线面垂直的定义。
立体几何专题复习1.棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱底面为正方形2. 棱锥棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
★正棱锥——如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥。
3.球球的性质:①球心与截面圆心的连线垂直于截面;★②r =d 、球的半径为R 、截面的半径为r )★球与多面体的组合体:球与正四面体,球与长方体,球与正方体等的内接与外切.注:球的有关问题转化为圆的问题解决. 球面积、体积公式:2344,3S R V R ππ==球球(其中R 为球的半径)俯视图11_________________.第1题2.若某空间几何体的三视图如图2所示,则该几何体的体积是________________.第2题 第3题3.一个几何体的三视图如图3所示,则这个几何体的体积为 .侧(左)视图 正(主)视图4.若某几何体的三视图(单位:cm )如图4所示,则此几何体的体积是 .第4题 第5题5.如图5是一个几何体的三视图,若它的体积是 a .6.已知某个几何体的三视图如图6,根据图中标出的尺寸(单位:cm ),可得这个几何体的体积是 .7.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是 3cm 8.设某几何体的三视图如图8(尺寸的长度单位为m ),则该几何体的体积为_________m 3。
3俯视图正视图侧视图俯视图俯视图正(主)视图侧(左)视图第7题 第8题9.一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个圆,那么这个几何体的侧面积为_________________.图910.一个三棱柱的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如图10所示(单位cm ),则该三棱柱的表面积为_____________.图1011.如图11所示,一个空间几何体的主视图和左视图都是边长为1的正方形,俯视图是一个直径为1的圆,那么这个几何体的全面积为_____________.图图11 图12 图1312. 如图12,一个空间几何体的主视图和左视图都是边长为1的正三角形,俯视图是一个圆,那么几何体的侧面积为_____________.13.已知某几何体的俯视图是如图13所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其表面积是_____________.14.如果一个几何体的三视图如图14所示(单位长度: cm ), 则此几何体的表面积是_____________.图14正视图俯视图15.一个棱锥的三视图如图,则该棱锥的全面积(单位:2cm )_____________.正视图 左视图 俯视图1. 正方体1111ABCD-A B C D ,1AA =2,E 为棱1CC 的中点. (Ⅰ) 求证:11B D AE ⊥; (Ⅱ) 求证://AC 平面1B DE ; (Ⅲ)求三棱锥A-BDE 的体积.2. 已知正方体1111ABCD A B C D -,O 是底ABCD 对角线的交点.求证:(1) C 1O ∥面11AB D ;(2)1AC ⊥面11AB D .3.如图,PA ⊥矩形ABCD 所在平面,M 、N 分别是AB 和PC 的中点.AD 11A E CD 1ODBA C 1B 1A 1C(Ⅰ)求证:MN ∥平面PAD ; (Ⅱ)求证:MN CD ⊥;(Ⅲ)若45PDA ∠=,求证:MN ⊥平面PCD .4. 如图(1),ABCD 为非直角梯形,点E ,F 分别为上下底AB ,CD 上的动点,且EF CD ⊥。


立体几何大题题型总结
立体几何大题包括以下几种题型:
1. 体积计算题:给定一个几何体的形状和尺寸,求其体积。
2. 表面积计算题:给定一个几何体的形状和尺寸,求其表面积。
3. 三视图综合题:给定一个几何体的三视图,通过推理和计算求出其体积和表面积。
4. 截面综合题:给定一个几何体的各个截面的形状和尺寸,通过推理和计算求出其体积和表面积。
5. 相似几何体综合题:给定多个几何体的形状和尺寸,在它们之间应用相似性质,求出它们各自的体积和表面积。
6. 空间几何关系题:给定多个几何体之间的位置关系,例如相切、相交、包含等,求出它们各自的体积和表面积。
7. 作图求解题:通过构造一些几何形状,例如放射形、圆锥、圆台等,求出特定几何体的体积和表面积。
8. 混合几何体综合题:将以上多种题型进行综合,考查学生的综合运用能力。

高中立体几何知识点总结高中立体几何知识点总结高中立体几何知识点总结1三角函数。
注意归一公式、诱导公式的正确性数列题。
1.证明一个数列是等差(等比)数列时,最后下结论时要写上以谁为首项,谁为公差(公比)的等差(等比)数列;2.最后一问证明不等式成立时,如果一端是常数,另一端是含有n的式子时,一般考虑用放缩法;如果两端都是含n的式子,一般考虑数学归纳法(用数学归纳法时,当n=k+1时,一定利用上n=k时的假设,否则不正确。
利用上假设后,如何把当前的式子转化到目标式子,一般进行适当的放缩,这一点是有难度的。
简洁的方法是,用当前的式子减去目标式子,看符号,得到目标式子,下结论时一定写上综上:由①②得证;3.证明不等式时,有时构造函数,利用函数单调性很简单立体几何题1.证明线面位置关系,一般不需要去建系,更简单;2.求异面直线所成的角、线面角、二面角、存在性问题、几何体的高、表面积、体积等问题时,要建系;3.注意向量所成的角的余弦值(范围)与所求角的余弦值(范围)的关系。
概率问题。
1.搞清随机试验包含的所有基本事件和所求事件包含的基本事件的个数;2.搞清是什么概率模型,套用哪个公式;3.记准均值、方差、标准差公式;4.求概率时,正难则反(根据p1+p2+...+pn=1);5.注意计数时利用列举、树图等基本方法;6.注意放回抽样,不放回抽样; 高中立体几何知识点总结2平面通常用一个平行四边形来表示。
平面常用希腊字母α、β、γ…或拉丁字母M、N、P来表示,也可用表示平行四边形的两个相对顶点字母表示,如平面AC。
在立体几何中,大写字母A,B,C,…表示点,小写字母,a,b,c,…l,m,n,…表示直线,且把直线和平面看成点的集合,因而能借用集合论中的符号表示它们之间的关系,例如:a) A∈l—点A在直线l上;Aα—点A不在平面α内;b) lα—直线l在平面α内;c) aα—直线a不在平面α内;d) l∩m=A—直线l与直线m相交于A点;e) α∩l=A—平面α与直线l交于A点;f) α∩β=l—平面α与平面β相交于直线l。

立体几何归类总结一、异面直线所成的角:平移线段法是求异面直线所成角的常用方法,其基本思路是通过平移直线,把异面直线的问题化归为共面直线问题来解决,具体步骤如下:(1)平移:平移异面直线中的一条或两条,作出异面直线所成的角; (2)认定:证明作出的角就是所求异面直线所成的角; (3)计算:求该角的值,常利用解三角形;(4)取舍:由异面直线所成的角的取值范围是0,2π⎛⎤⎥⎝⎦,当所作的角为钝角时,应取它的补角作为两条异面直线所成的角.二、直线和平面所成的角求直线与平面所成的角的一般步骤:(1)利用面面垂直的性质定理,得到线面垂直,进而确定线面角的垂足,明确斜线在平面内的射影,即可确定线面角;(2)在构成线面角的直角三角形中,可利用等体积法求解垂线段的长度h ,从而不必作出线面角,则线面角θ满足sin hl θ=(l 为斜线段长),进而可求得线面角; (3)通过建系,利用坐标系向量求解:直线与平面所成的角(射影角,也是夹角,[0.]2πϑ∈),m n ,是平面法向量sin |cos a |=b θ=,三、二面角的平面角角的棱的垂线,两条垂线确定的平面和二面角的棱垂直,由此可得二面角的平面角.(1)利用面面垂直的性质定理,得到线面垂直,进而确定线面角的垂足,明确斜线在平面内的射影,即可确定线面角;(2)在构成线面角的直角三角形中,可利用等体积法求解垂线段的长度h ,从而不必作出线面角,则线面角θ满足sin hlθ=(l 为斜线段长),进而可求得线面角;(3)建立空间直角坐标系,利用向量法求解,设a 为直线l 的方向向量,n 为平面的法向量,则线面角θ的正弦值为sin cos ,a n θ=<>.【题型一】异面直线所成的角1: 平移直线法(中位线)【例1】如图∶已知A 是BCD △所在平面外一点,AD BC =,E 、F 分别是AB 、CD 的中点,若异面直线AD 与BC 所成角的大小为θ,AD 与EF 所成角的大小为_______________.【例2】如图,在四棱锥P ABCD -中,PA ⊥平面ABCD ,四边形ABCD 为菱形,60ABC ∠=且PA AB E =,为AP 的中点,则异面直线PC 与DE 所成的角的余弦值为( )A B C D 【例3】空间四边形ABCD 的对角线10AC =,6BD =,M ,N 分别为AB ,CD 的中点,7MN =,则异面直线AC 和BD 所成的角等于( )A .30°B .60°C .90°D .120°【例4】在我国古代数学名著《九章算术》中,将四个面都为直角三角形的四面体称为鳖臑,在鳖臑 ABCD 中,AB ⊥平面BCD ,且AB =BC =CD ,则异面直线AC 与BD 所成角为( )A .30°B .45°C .60°D .90°【题型二】异面直线所成的角2:平行四边形、梯形等【例1】已知六棱锥P ﹣ABCDEF 的底面是正六边形,PA ⊥平面ABC ,PA =2AB ,则异面直线CD 与PB 所成的角的余弦值为( )A B C D【例2】已知圆柱的母线长为2ABCD 为其轴截面,若点E 为上底面圆弧AB 的中点,则异面直线DE 与AB 所成的角为( )A .4πB .6πC .512πD .3π【例3】如图,在正方体1111ABCD A B C D -中,E ,F ,G ,H 分别为1AA ,AB ,1BB ,11B C 的中点,则异面直线EF 与GH 所成的角等于( )A .45︒B .60︒C .90︒D .120︒【例4】正方体1111ABCD A B C D -中,已知E 为1CC 的中点,那么异面直线1BC 与AE 所成的角等于( ) A .30 B .45︒ C .60︒ D .90︒【题型三】异面直线所成的角3:垂直【例1】如图,在三棱柱111ABC A B C -中,CA CB =,1AB AA =,1π3BAA ∠=,那么异面直线AB 与1A C 所成的角为A .6πB .π4C .π3D .π2【例2】在如图所示的正方体中,M ,N 分别为棱BC 和DD 1的中点,则异面直线AN 和B 1M 所成的角为( )A .30°B .45°C .90°D .60°【例3】菱形ABCD 的对角线AC 、BD 的交点为O ,P 是菱形所在平面外一点,PO ⊥平面ABCD ,则异面直线AC 与PD 所成角大小为______.【例4】若异面直线a ,b 所成的角为3π,且直线c a ⊥,则异面直线b ,c 所成角的范围是______.【题型四】 异面直线所成角的范围与最值(难点)【例1】如图,点M N 、分别是正四面体ABCD 棱AB CD 、上的点,设BM x =,直线MN 与直线BC 所成的角为θ,则( )A .当2ND CN =时,θ随着x 的增大而增大B .当2ND CN =时,θ随着x 的增大而减小C .当2CN ND =时,θ随着x 的增大而减小 D .当2CN ND =时,θ随着x 的增大而增大【例2】已知菱形ABCD ,60DAB ∠=︒,E 为边AB 上的点(不包括A B ,),将ABD △沿对角线BD 翻折,在翻折过程中,记直线BD 与CE 所成角的最小值为α,最大值为β( ) A .αβ,均与E 位置有关B .α与E 位置有关,β与E 位置无关C .α与E 位置无关,β与E 位置有关D .αβ,均与E 位置无关【例3】在正方体1111ABCD A B C D -中,已知,,E F G 分别为111,,CD D D A B 的中点,P 为平面11CDD C 内任一点,设异面直线GF 与PE 所成的角为α,则cos α的最大值为( )A .13BCD .1【例4】已知圆柱12O O 的底面半径和母线长均为1,A ,B 分别为圆2O 、圆1O 上的点,若2AB =,则异面直线1O B ,2O A 所成的角为( )A .6π B .3πC .23π D .56π【题型五】 异面直线所成角:综合【例1】在正方体ABCD ﹣A 1B 1C 1D 1中,过点C 做直线l ,使得直线l 与直线BA 1和B 1D 1所成的角均为70,则这样的直线l ( )A .不存在B .2条C .4条D .无数条【例2】在正方体1111ABCD A B C D -的所有面对角线中,所在直线与直线1A B 互为异面直线且所成角为60︒的面对角线的条数为( ) A .2 B .4 C .6 D .8【例3】1111ABCD A B C D -是棱长为1的正方体,一个质点从A 出发沿正方体的面对角线运动,每走完一条面对角线称“走完一段”,质点的运动规则如下:运动第i 段与第2i +所在直线必须是异面直线(其中i 是正整数).问质点走完的第2021段与第1段所在的直线所成的角是( )A .0°B .30°C .60°D .90°【例4】已知异面直线a 、b 所成角为80︒,P 为空间一定点,则过P 点且与a 、b 所成角都是50︒的直线有且仅有( )条. A .2 B .3 C .4D .6【题型六】 直线和平面所成的角1:垂线法【例1】在空间,若60AOB AOC ∠=∠=︒,90BOC ∠=°,直线OA 与平面OBC 所成的角为θ,则cos θ=( )A B C .12D .13【例2】正四面体ABCD 中,直线AB 与平面BCD 所成的角的正弦值是( )A B .14C D【例3】如图,已知正方体1111ABCD A B C D -,直线1A B 与平面11A B CD 所成的角为( )A .30B .45︒C .60︒D .90︒【例4】已知正四棱柱1111ABCD A B C D -,设直线1AB 与平面11ACC A 所成的角为α,直线1CD 与直线11A C 所成的角为β,则( ) A .2βα= B .2αβ=C .αβ=D .2παβ+=【题型七】直线和平面所成 的角2:垂面法【例1】如图,在三棱锥P ABC -中,平面PAB ⊥平面,2ABC PA PB AB ===,,AB BC BC ⊥=线PC 与平面ABC 所成的角是( )A .30︒B .45︒C .60︒D .90︒【例2】正三棱柱ABC -A 1B 1C 1的底面边长为2,侧棱长为则直线1B A 与平面11BB C C 所成的角为( )A .3πB .6πC .512πD .4π【例3】如图,在正三棱柱111ABC A B C -中,底面边长为2,侧棱长为3,则直线1BB 与平面11AB C 所成的角为________.【例4】已知四棱锥P ABCD -底面是边长为2的正方形,PA ⊥平面ABCD ,且2PA =,则直线PB 与平面PCD 所成的角大小为__________.【题型八】直线和平面所成 的角3:体积法(距离法)【例1】如图,在直三棱柱111ABC A B C -中,1AB BC ==,120ABC ∠=︒.M 为11A C 的中点,则直线BM 与平面11ABB A 所成的角为( )A .15°B .30°C .45°D .60°【例2】在正方体''''ABCD A B C D -中,直线'BC 与平面'A BD 所成的角的余弦值等于A B C D【例3】已知长方体1111ABCD A B C D -中,1112AA AB AD ===,,1AA 与平面1A BD 所成的角为______.【例4】直线l 与平面α所成的角为6π,且AB 是直线l 上两点,线段AB 在平面α内的射影长为3,则AB =___________.【题型九】线面角中的范围与最值【例1】在正方体1111ABCD A B C D -中,点O 为线段BD 的中点,设点P 在直线1CC 上,直线OP 与平面1A BD 所成的角为α,则sin α的取值范围是A .⎤⎥⎣⎦B .⎤⎥⎣⎦C .⎣⎦D .⎣⎦【例2】若直线l 与平面α所成的角为3π,直线a 在平面α内,则直线l 与直线a 所成的角的取值范围是( )A .0,3π⎡⎤⎢⎥⎣⎦B .,62ππ⎡⎤⎢⎥⎣⎦ C .,32ππ⎡⎤⎢⎥⎣⎦ D .,63ππ⎡⎤⎢⎥⎣⎦【例3】在正方体1111ABCD A B C D -中,点P 在线段11C D 上,若直线1B P 与平面11BC D 所成的角为θ,则tan θ的取值范围是( )A .⎣⎦B .⎡⎣C .11,32⎡⎤⎢⎥⎣⎦D .⎤⎥⎣⎦【例4】直线l 与平面α所成的角为π3,则直线l 与平面α内直线所成角的最小值是________.【题型十】线面角:综合【例1】如图所示,在正方体1AC 中,2AB =,1111AC B D E =,直线AC 与直线DE 所成的角为α,直线DE 与平面11BCC B 所成的角为β,则()cos αβ-=__________.【例2】直线l 与平面α所成的角是45°,若直线l 在α内的射影与α内的直线m 所成的角是45°,则l 与m 所成的角是( ) A .30° B .45°C .60°D .90°【例3】若直线l 与平面α所成的角为3π,直线a 在平面α内,且与直线l 异面,则直线l 与直线a 所成角的取值范围是( )A .0,3π⎡⎤⎢⎥⎣⎦B .,62ππ⎡⎤⎢⎥⎣⎦C .,63ππ⎡⎤⎢⎥⎣⎦D .,32ππ⎡⎤⎢⎥⎣⎦【例4】如图,在长方体1111ABCD A B C D -中,11AD AA ==,2AB =,点E 在棱AB 上,若直线1DD 与平面1D EC 所成的角为4π,则AE =__________.【题型十一】定义法求二面角的平面角【例1】自二面角内任意一点分别向两个面引垂线,则两垂线所成的角与二面角的平面角的关系是( ) A .相等 B .互补 C .互余 D .相等或互补【例2】如图,菱形ABCD 的边长为60BCD ∠=︒,将BCD △沿对角线BD 折起,使得二面角C BD A '--的平面角的余弦值是13,则C B '与平面ABD 所成角的正弦值是( )A B C D【例3】在三棱锥P -ABC 中,P A =PB =AC =CB =AB =2,PC =3,则二面角P -AB -C 的大小为( ) A .30° B .60° C .90° D .120°【例4】在四棱锥P ABCD -中,底面ABCD 是矩形,PA ⊥底面ABCD ,且PA AB =,AD =,则二面角P CD B --的大小为( ) A .30° B .45° C .60°D .75°【题型十二】二面角内的角度【例1】从空间一点P 向二面角l αβ--的两个面α、β分别作垂线PE 、PF ,E ,F 为垂足,若二面角l αβ--的大小为60°,则⊥EPF 的大小为( )A .60°B .120°C .60°或120°D .不确定【例2】如图,在ABC 中,AB AC =,3A π∠=,P 为底边BC 上的动点,BP BC λ=,102λ<<,沿折痕AP把ABC 折成直二面角B AP C '--,则B AC '∠的余弦值的取值范围为( )A .⎛ ⎝⎭B .12⎛ ⎝⎭C .13,24⎛⎫ ⎪⎝⎭D .10,2⎛⎫⎪⎝⎭【例3】如图,圆锥AO 中,B 、C 是圆O 上的不同两点,若30OAB ∠=,且二面角B AO C --所成平面角为60,动点P 在线段AB 上,则CP 与平面AOB 所成角的正切值的最大值为( )A .2 BC D .1【例4】已知E ,F 分别是矩形ABCD 边AD ,BC 的中点,沿EF 将矩形ABCD 翻折成大小为α的二面角.在动点P 从点E 沿线段EF 运动到点F 的过程中,记二面角B AP C --的大小为θ,则( ) A .当90α<︒时,sin θ先增大后减小 B .当90α<︒时,sin θ先减小后增大 C .当90α>时,sin θ先增大后减小 D .当90α>时,sin θ先减小后增大【题型十三】二面角内的距离【例1】如图,在大小为60︒的二面角A EF D --中,四边形ABFE ,四边形CDEF 都是边长为1的正方形,则B ,D 两点间的距离是( )AB .2C .1 D【例2】在三棱锥A -BCD 中,ABC 和BCD △均为边长为2的等边三角形,若AB CD ⊥,则二面角A -BC -D 的余弦值为( )A B C .13D【例3】120°的二面角的棱上有A ,B 两点,直线AC ,BD 分别在这个二面角的两个半平面内,且都垂直于AB .已知2AB =,3AC =,4BD =,则CD 的长为( )A B C D【例4】如下图,面α与面β所成二面角的大小为3π,且A ,B 为其棱上两点.直线AC ,BD 分别在这个二面角的两个半平面中,且都垂直于AB ,已知AB =2AC =,4BD =,则CD =( )AB C D .【题型十四】综合角度:比大小(难点)【例1】在正方体1111ABCD A B C D -中,M 是线段1A C (不含端点)上的点,记直线M B 与直线11A B 成角为α,直线MC 与平面ABC 所成角为β,二面角M BC A --的平面角为γ,则( )A .βγα<<B .αβγ<<C .βαγ<<D .γαβ<<【例2】已知矩形ABCD ,M 是边AD 上一点,沿BM 翻折ABM ,使得平面ABM ⊥平面BCDM ,记二面角A BC D --的大小为α,二面角A DM C --的大小为β,则( )A .αβ<B .αβ>C .2παβ+< D .2παβ+>【例3】四棱锥P ABCD -的各棱长均相等,M 是AB 上的动点(不包括端点),点N 在线段AD 上且满足2AN ND =,分别记二面角P MN C --,P AB C ,P MD C --的平面角为,,αβγ,则( ) A .βαγ>> B .βγα>>C .γβα>>D .γαβ>>【例4】已知等边ABC ,点,E F 分别是边,AB AC 上的动点,且满足EF BC ∥,将AEF 沿着EF 翻折至P 点处,如图所示,记二面角P EF B --的平面角为α,二面角P FC B --的平面角为β,直线PF 与平面EFCB 所成角为γ,则( )A .αβγ≥≥B .αγβ≥≥C .βαγ≥≥D .βγα≥≥1.在长方体1111ABCD A B C D -中,1AB BC ==,1AA =1AD 与1BB 所成角为( )A .6πB .3πC .4πD .2π2.若二面角l αβ--的平面角为θ,异面直线a ,b 满足a α⊂,b β⊂,且a l ⊥,b l ⊥,则异面直线a ,b 所成的角为( ).A .θB .πθ-C .2θπ-D .θ或πθ-3..已知正三棱锥A BCD -中,BC =,E 是CD 的中点,则异面直线BE 与AD 所成角为( ) A .30° B .45° C .60° D .90°4.在直三棱柱111ABC A B C -中,12AB AA ==,1BC =,AB BC ⊥,点D 是侧棱1BB 的中点,则异面直线1C D 与直线1AB 所成的角大小为( )A .6πB .4πC .3πD .2π5.两条异面直线,a b 所成的角为60,在直线,a b 上分别取点,A E 和点,B F ,使AB a ⊥,且AB b ⊥.已知6,8,14AE BF EF ===,则线段AB 的长为( )A .20或12B .12或C .D .206..已知两条异面直线a ,b 所成角为60°,在直线a 上取点C ,E .在直线b 上取点D ,F ,使CD a ⊥,且CD b ⊥.已知1CE DF CD ===,则线段EF 的长为______.7..在正方体1111ABCD A B C D -中,设直线1BD 与直线AD 所成的角为α,直线1BD 与平面11CDD C 所成的角为β,则αβ+=( )A .4πB .3πC .2πD .23π8.如图,正四棱锥P ABCD -的体积为2,底面积为6,E 为侧棱PC 的中点,则直线BE 与平面PAC 所成的角为_______.9.在正方体1111ABCD A B C D -中,若存在平面α,使每条棱所在的直线与平面α所成的角都相等,则各棱所在的直线与此平面所成角的正切值为_______.10.过正方体1111ABCD A B C D -的顶点A 作平面α,使正方形ABCD 、正方形11ABB A 、正方形11ADD A 所在平面与平面α所成的二面角的平面角相等,则这样的平面α可以作( )A .1个B .2个C .3个D .4个11.如图,已知二面角l αβ--平面角的大小为3π,其棱l 上有A 、B 两点,AC 、BD 分别在这个二面角的两个半平面内,且都与AB 垂直.已知1AB =,2==AC BD ,则CD =( )A .5B .13C D11.已知矩形 ABCD ,1AB =,BC =沿对角线AC 将ABC 折起,若二面角B AC D --的余弦值为13-,则B 与D 之间距离为( )A.1 BC D12.已知在正方体1111ABCD A B C D -中,点E 为棱BC 的中点,直线l 在平面1111D C B A 内.若二面角A l E --的平面角为θ,则cos θ的最小值为( )A B .1121 C D .3513.已知在正四棱锥P ABCD -中,2AB =,3PA =,侧棱与底面所成角为α,侧面与底面所成角为β,二面角A PB C --的平面角为θ,则下列说法正确的是( ) A .βαθ<< B .αθβ<< C .2cos cos 0θβ+= D .2cos cos 0θα+=。

高考数学立体几何题型大全总结1. 三角锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
2. 三棱锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
3. 四棱锥的体积公式
体积公式:V=1/3∗S∗h
其中,S为底面积,h为高。
4. 圆锥的体积公式
体积公式:V=1/3∗π∗r2∗h
其中,r为圆锥的半径,h为圆锥的高。
5. 球的体积公式
体积公式:V=4/3∗π∗r3
其中,r为球的半径。
6. 圆柱的体积公式
体积公式:V=π∗r2∗h
其中,r为圆柱的半径,h为圆柱的高。
7. 圆台的体积公式
体积公式:V=1/3∗π∗h∗(r12+r22+r1r2)
其中,r1,r2为底面半径,h为圆台高。
8. 空间向量的共线与垂直判定公式
共线判定公式:
如果两个向量a,b共线,则有a=kb,其中k为一个实数。
垂直判定公式:
如果两个向量a,b垂直,则有a·b=0,其中“·”表示向量的数量积。
9. 空间向量的平面垂直判定公式
若向量a与平面P垂直,则a在平面P上的投影为零向量。
10. 空间向量的平面共面判定公式
若向量a和向量b在同一平面上,则a和b的向量积c在该平面内。
11. 空间中两直线相交的条件
两直线相交的条件是它们至少有一个公共点,并且既不平行也不重合。

高考数学立体几何题型全归纳一、空间几何体的结构特征1. 一个三棱柱的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如下(单位cm),则该三棱柱的表面积为()正视图:是一个矩形,长为2,高为√(3);侧视图:是一个矩形,长为2,高为1;俯视图:是一个正三角形,边长为2。
解析:底面正三角形的边长a = 2,底面积S_{底}=(√(3))/(4)a^2=(√(3))/(4)×2^2=√(3)。
侧棱长h = 1,三个侧面的面积S_{侧}=3×2×1 = 6。
所以表面积S=2S_{底}+S_{侧}=2√(3)+6。
2. 若某几何体的三视图(单位:cm)如图所示,则此几何体的体积是()正视图:是一个梯形,上底为1,下底为2,高为2;侧视图:是一个矩形,长为2,宽为1;俯视图:是一个矩形,长为2,宽为1。
解析:该几何体是一个四棱台。
上底面积S_{1}=1×1 = 1,下底面积S_{2}=2×2=4,高h = 2。
根据四棱台体积公式V=(1)/(3)h(S_{1}+S_{2}+√(S_{1)S_{2}})=(1)/(3)×2×(1 + 4+√(1×4))=(14)/(3)二、空间几何体的表面积与体积3. 已知球的直径SC = 4,A,B是该球球面上的两点,AB=√(3),∠ ASC=∠BSC = 30^∘,则棱锥S - ABC的体积为()解析:设球心为O,因为SC是球的直径,∠ ASC=∠ BSC = 30^∘所以SA=SB = 2√(3),AO = BO=√(3)又AB=√(3),所以 AOB是等边三角形,S_{ AOB}=(√(3))/(4)×(√(3))^2=(3√(3))/(4)V_{S - ABC}=V_{S - AOB}+V_{C - AOB}=(1)/(3)× S_{ AOB}×(SO + CO)=(1)/(3)×(3√(3))/(4)×2=√(3)4. 一个正方体被一个平面截去一部分后,剩余部分的三视图如图,则截去部分体积与剩余部分体积的比值为()正视图:是一个正方形,右上角缺了一个等腰直角三角形;侧视图:是一个正方形,右上角缺了一个等腰直角三角形;俯视图:是一个正方形,右上角缺了一个小正方形。

立体几何解答题最全归纳总结【题型归纳目录】题型一:非常规空间几何体为载体题型二:立体几何存在性问题题型三:立体几何折叠问题题型四:立体几何作图问题题型五:立体几何建系繁琐问题题型六:两角相等(构造全等)的立体几何问题题型七:利用传统方法找几何关系建系题型八:空间中的点不好求题型九:创新定义【典例例题】题型一:非常规空间几何体为载体例1.如图,P 为圆锥的顶点,O 为圆锥底面的圆心,圆锥的底面直径AB =4,母线PH =22,M 是PB 的中点,四边形OBCH 为正方形.(1)设平面POH ∩平面PBC =l ,证明:l ∥BC ;(2)设D 为OH 的中点,N 是线段CD 上的一个点,当MN 与平面PAB所成角最大时,求MN 的长.【解析】(1)因为四边形OBCH 为正方形,∴BC ∥OH ,∵BC ⊄平面POH ,OH ⊂平面POH ,∴BC ∥平面POH .∵BC ⊂平面PBC ,平面POH ∩平面PBC =l ,∴l ∥BC .(2)∵圆锥的母线长为22,AB =4,∴OB =2,OP =2,以O 为原点,OP 所在的直线为z 轴,建立如图所示的空间直角坐标系,则P 0,0,2 ,B 0,2,0 ,D 1,0,0 C 2,2,0 ,M 0,1,1 ,设DN =λDC =λ,2λ,0 0≤λ≤1 ,ON =OD +DN =1+λ,2λ,0 ,MN =ON -OM =1+λ,2λ-1,-1 ,OD =1,0,0 为平面PAB 的一个法向量,设MN 与平面PAB 所成的角为θ,则sin θ=1+λ,2λ-1,-1 ⋅1,0,0 1+λ 2+2λ-1 2+1 =1+λ5λ2-2λ+3,令1+λ=t ∈1,2 ,则sin θ=t 5t 2-12t +10=15-12t +101t 2=1101t -35 2+75所以当1t =35时,即λ=23时,sin θ最大,亦θ最大,此时MN =53,13,-1 ,所以MN =MN =53 2+13 2+-1 2=353.例2.如图所示,圆锥的底面半径为4,侧面积为162π,线段AB 为圆锥底面⊙O 的直径,C 在线段AB 上,且BC =3CA ,点D 是以BC 为直径的圆上一动点;(1)当CD =CO 时,证明:平面PAD ⊥平面POD(2)当三棱锥P -BCD 的体积最大时,求二面角B -PD -A 的余弦值.【解析】(1)∵PO 垂直于圆锥的底面,∴PO ⊥AD ,当CD =CO 时,CD =OC =AC ,∴AD ⊥OD ,又OD ∩PO =O ,∴AD ⊥平面POD ,又AD ⊂平面PAD ,∴平面PAD ⊥平面POD ;(2)由题可知OA =OB =4,4π⋅PB =162π,∴PB =42,∴PO =4,当三棱锥P -BCD 的体积最大时,△DBC 的面积最大,此时D 为BC的中点,如图,建立空间直角坐标系O -xyz ,则A (0,-4,0),B (0,4,0),P (0,0,4),D 3,1,0 ,∴BP =0,-4,4 ,PD =3,1,-4 ,AP =(0,4,4),设平面PAD 的法向量为n 1 =(a ,b ,c ),则n 1 ⋅AP =0n 1 ⋅PD =0 ,即4b +4c =03a +b -4c =0,令a =5,则b =-3,c =3,∴n 1 =(5,-3,3),设平面PBD 的法向量n 2 =x ,y ,z ,则n 2 ⋅BP =0n 2 ⋅PD =0 ,即-4y +4z =03x +y -4z =0,令x =1,则y =1,z =1,∴n 2 =1,1,1 ,则cos n 1 ,n 2 =n 1 ⋅n 2 n 1 n 2 =5-3+33×52+-3 2+32=5129129,∴二面角B -PD -A 的余弦值为-5129129.例3.如图,圆锥PO 的母线长为6,△ABC 是⊙O 的内接三角形,平面PAC ⊥平面PBC .BC =23,∠ABC =60°.(1)证明:PA ⊥PC ;(2)设点Q 满足OQ =λOP ,其中λ∈0,1 ,且二面角O -QB -C 的大小为60°,求λ的值.【解析】(1)∵PA =PB =PC =6,BC =23,PB 2+PC 2=BC 2,∴PB ⊥PC∵平面PAC ⊥平面PBC 且平面PAC ∩平面PBC =PC ,PB ⊂平面PBC ,PB ⊥PC ,∴PB ⊥平面PAC ,又PA ⊂平面PAC ,∴PB ⊥PA ,∴AB =PA 2+PB 2=23,∴∠ABC =60°,∴△ABC 是正三角形,AC =23,∵PA 2+PC 2=AC 2∴PA ⊥PC ;(2)在平面ABC 内作OM ⊥OB 交BC 于M ,以O 为坐标原点,OM ,OB ,OP 所在直线分别为x 轴,y 轴,z 轴,建立空间直角坐标系O -xyz 如图所示:易知OB =OC =2,OP =PB 2-OB 2=2,所以B 2,0,0 ,P 0,0,2 ,C -1,3,0 ,Q 0,0,2λ ,QB =2,0,-2λ ,BC =-3,3,0 ,设平面OBC 的法向量n 1 =x ,y ,z ,依题意n 1 ⋅QB =0n 1 ⋅CB =0 ,即2x -2λz =0-3x +3y =0 ,不妨令y =3λ,得n 1 =λ,3λ,2 ,易知平面OQB 的法向量n 2 =0,1,0 ,由λ∈0,1 可知cos n 1 ,n 2 =n 1 ⋅n 2 n 1 ⋅n 2=cos60°,即3λλ2+(3λ)2+2 2=12,解得λ=12例4.如图,D 为圆锥的顶点,O 为圆锥底面的圆心,AB 为底面直径,C 为底面圆周上一点,DA =AC =BC =2,四边形DOAE 为矩形,点F 在BC 上,且DF ⎳平面EAC .(1)请判断点F 的位置并说明理由;(2)平面DFO 将多面体DBCAE 分成两部分,求体积较大部分几何体的体积.【解析】(1)点F 是BC 的中点,取BC 的中点F ,连接OF ,DF ,因为O 为AB 的中点,所以OF ⎳AC ,又AC ⊂平面AEC ,OF ⊄平面AEC ,所以OF ⎳平面AEC ,由四边形DOAE 为矩形,所以DO ⎳AE ,又AE ⊂平面AEC ,OD ⊄平面AEC ,所以OD ⎳平面AEC ,因为DO ∩OF =O ,DO ,OF ⊂平面DOF ,所以平面DOF ⎳平面AEC ,因为DF ⊂平面DOF ,所以DF ⎳平面AEC ,(2)由(1)知点F 是BC 的中点,因为DA =AC =BC =2,所以AB =AC 2+BC 2=22,所以OA =OC =OB =2,且OC ⊥AB ,所以OD =AD 2-OA 2=2,所以三棱锥D -BOF 的体积V D -BOF =13S △BOF ⋅DO =13×12×2×22×2=26;又三棱锥D -BOC 的体积V D -BOC =13S △BOC ⋅DO =13×12×2×2×2=23,所以四棱锥C -DOAE 的体积V C -DOAE =13S DOAE ×2=13×2 2×2=223,所以几何体DBCAE 的体积V DBCAE =V D -BCO +V C -DOAE =2,所以体积较大部分几何体的体积为V DBCAE -V D -BOF =2-26=526;例5.如图,在直角△POA 中,PO ⊥OA ,PO =2OA ,将△POA 绕边PO 旋转到△POB 的位置,使∠AOB =90°,得到圆锥的一部分,点C 为AB 的中点.(1)求证:PC ⊥AB ;(2)设直线PC 与平面PAB 所成的角为φ,求sin φ.【解析】(1)证明:由题意知:PO ⊥OA ,PO ⊥OB ,OA ∩OC =0∴PO ⊥平面AOB ,又∵AB ⊂平面AOB ,所以PO ⊥AB .又点C 为AB 的中点,所以OC ⊥AB ,PO ∩OC =0,所以AB ⊥平面POC ,又∵PC ⊂平面POC ,所以PC ⊥AB .(2)以O 为原点,OA ,OB ,OP 的方向分别作为x ,y ,z 轴的正方向建立如图所示的空间直角坐标系,设OA =2,则A 2,0,0 ,B 0,2,0 ,P 0,0,4 ,C 2,2,0 ,所以AB =-2,2,0 ,AP =-2,0,4 ,PC =2,2,-4 .设平面PAB 的法向量为n =a ,b ,c ,则n ⋅AB =-2a +2b =0,n ⋅AP =-2a +4c =0, 取c =1,则a =b =2可得平面PAB 的一个法向量为n =2,2,1 ,所以sin φ=cos n ,PC =n ⋅PC n PC =42-465=210-5 15.例6.如图,四边形ABCD 为圆柱O 1O 2的轴截面,EF 是该圆柱的一条母线,EF =2EA ,G 是AD 的中点.(1)证明:AF ⊥平面EBG ;(2)若BE =3EA ,求二面角E -BG -A 的正弦值.【解析】(1)由已知EF ⊥平面ABE ,BE ⊂平面ABE ,所以EF ⊥BE ,因为AB 是圆O 1的直径,所以AE ⊥BE ,因为AE ∩FE =E ,所以BE ⊥平面AFE ,AF ⊂平面AFE ,故BE ⊥AF ,因为EF =2EA =2AG ,所以EA =2AG ,易知:Rt △AEG ∼Rt △EFA ,所以∠GEA +∠EAF =90°,从而AF ⊥EG ,又BE ∩EG =E ,所以AF ⊥平面EBG .(2)以E 为坐标原点,EA 为x 轴正方向,EA 为单位向量,建立如图所示的空间直角坐标系E -xyz ,则AB =2,BE =3,EF =2,从而A 1,0,0 ,B 0,3,0 ,D 1,0,2 ,F 0,0,2 ,AB =-1,3,0 ,AD =0,0,2 ,设n =x ,y ,z 位平面BGA 的法向量,则{n ⋅AB =0n ⋅AD =0⇒{-x +3y =02z =0⇒{x =3y =1z =0,所以n =3,1,0 ,由(1)知:平面BEG 的法向量为AF =-1,0,2 ,因为cos n ,AF =n ⋅AF n ⋅AF=-12,所以二面角E -BG -A 的正弦值为32.例7.例7.如图,几何体是圆柱的一部分,它是由矩形ABCD (及其内部)以AB 边所在直线为旋转轴旋转120°得到的,G 是DF的中点.(1)设P 是CE 上的一点,且AP ⊥BE ,求证BP ⊥BE ;(2)当AB =3,AD =2时,求二面角E -AG -C 的大小.【解析】(1)因为AP ⊥BE ,AB ⊥BE ,AB ,AP ⊂平面ABP ,AB ∩AP =A ,所以BE ⊥平面ABP ,又BP ⊂平面ABP ,所以BP ⊥BE .(2)以B 为坐标原点,分别以BE ,BP ,BA 所在的直线为x ,y ,z 轴,建立如图所示的空间直角坐标系.由题意得A (0,0,3),E (2,0,0),G (1,3,3),C (-1,3,0),故AE =(2,0,-3),AG =(1,3,0),CG =(2,0,3).设m =x 1,y 1,z 1 是平面AEG 的一个法向量,由m ·AE =0m ·AG =0 可得2x 1-3z 1=0,x 1+3y 1=0.取z 1=2,可得平面AEG 的一个法向量m =(3,-3,2).设n =x 2,y 2,z 2 是平面ACG 的一个法向量,由n ·AG =0n ·CG =0,可得x 2+3y 2=0,2x 2+3z 2=0. 取z 2=-2,可得平面ACG 的一个法向量n =(3,-3,-2).所以cos ‹m ,n ›=m ⋅n |m |⋅|n |=12, 因为<m ,n >∈[0,π],故所求的角为60°.例8.如图,四边形ABCD 是一个半圆柱的轴截面,E ,F 分别是弧DC ,AB 上的一点,EF ∥AD ,点H 为线段AD 的中点,且AB =AD =4,∠FAB =30°,点G 为线段CE 上一动点.(1)试确定点G 的位置,使DG ⎳平面CFH ,并给予证明;(2)求二面角C -HF -E 的大小.【解析】(1)当点G 为CE 的中点时,DG ∥平面CFH .证明:取CF 得中点M ,连接HM ,MG .∵G ,M 分别为CE 与CF 的中点,∴GM ∥EF ,且GM =12EF =12AD ,又H 为AD 的中点,且AD ∥EF ,AD =EF ,∴GM ∥DH ,GM =DH .四边形GMHD 是平行四边形,∴HM ∥DG又HM ⊂平面CFH ,DG ⊄平面CFH∴DG ∥平面CFH(2)由题意知,AB 是半圆柱底面圆的一条直径,∴AF ⊥BF .∴AF =AB cos30°=23,BF =AB sin30°=2.由EF ∥AD ,AD ⊥底面ABF ,得EF ⊥底面ABF .∴EF ⊥AF ,EF ⊥BF .以点F 为原点建立如图所示的空间直角坐标系,则F (0,0,0),B (0,2,0),C (0,2,4),H (23,0,2)FH =(23,0,2),FC =(0,2,4)设平面CFH 的一个法向量为n =(x ,y ,z )所以n ⋅FH =23x +2z =0n ⋅FC =2y +4z =0则令z =1则y =-2,x =-33即n =-33,-2,1由BF ⊥AF ,BF ⊥FE ,AF ∩FE =F .得BF ⊥平面EFH ∴平面EFH 的一个法向量为FB =(0,2,0)设二面角C -HF -E 所成的角为θ∈0,π2则cos θ=∣cos ‹n ,FB ›=|n ⋅FB ||n ||FB |=0×-33 +(-2)×2+1×02×13+4+1=32 ∴二面角C -HF -E 所成的角为π6.例9.坐落于武汉市江汉区的汉口东正教堂是中国南方唯一的拜占庭式建筑,象征着中西文化的有机融合.拜占庭建筑创造了将穹顶支承于独立方柱上的结构方法和与之相呼应的集中式建筑形制,其主体部分由一圆柱与其上方一半球所构成,如图所示.其中O 是下底面圆心,A ,B ,C 是⊙O 上三点,A 1,B 1,C 1是上底面对应的三点.且A ,O ,C 共线,AC ⊥OB ,C 1E =EC ,B 1F =13FB ,AE 与OF 所成角的余弦值为36565.(1)若E 到平面A 1BC 的距离为233,求⊙O 的半径.(2)在(1)的条件下,已知P 为半球面上的动点,且AP =210,求P 点轨迹在球面上围成的面积.【解析】(1)如图,取BB 1,CE 上的点N ,M .连接OM ,OF ,FM .过N 作NH ⊥A 1B 于H ,则OM ∥AE ,由题意知cos ∠FOM =36565,设⊙O 的半径为r ,AA 1=h ,由勾股定理知OF =r 2+916h 2,OM =r 2+116h 2,FM =2r 2+14h 2,由余弦定理知cos ∠FOM =OF 2+OM 2-FM 22×OF ×OM.代入解得h =2r ,因为EN ∥BC ,EN ⊄面A 1BC ,所以EN ∥面A 1BC ,故N 到面A 1BC 的距离是233,因为BC ⊥AB ,BC ⊥AA 1,AA 1∩AB =A ,所以BC ⊥面A 1AB ,BC ⊥NH ,因为NH ⊥BC ,NH ⊥A 1B ,A 1B ∩BC =B ,所以NH ⊥面A 1BC ,NH =233,而sin ∠A 1BB 1=NH BN =A 1B 1A 1B ,即233×h 2=2r 2r 2+h 2,解得r =2,h =4,即⊙O 的半径为2.(2)设上底面圆心为O 1,则O 1P =2,O 1O 2与O 1P 的夹角为θ,所以|AP |=|AO 1 +O 1P |=20+4+85cos θ=210,解得cos θ=255,过P 作PO 2⊥AO 1于O 2,则O 2P =O 1P ⋅sin θ=255,所以点P 的轨迹是以O 2为圆心,以255为半径的圆,因此可作出几何体被面AOA 1所截得到的截面,如图所示.设弧A 1C 1旋转一周所得到的曲面面积为S 1,弧PP 得到的为S 2,则S 2S 1=1-cos θS 1=12×4πr2 ,因此S 2=2πr 2(1-cos θ)=8π1-255 .因此P 点轨迹在球面上围成的面积为8π1-255.例10.如图,ABCD 为圆柱OO 的轴截面,EF 是圆柱上异于AD ,BC 的母线.(1)证明:BE ⊥平面DEF ;(2)若AB =BC =6,当三棱锥B -DEF 的体积最大时,求二面角B -DF -E 的正弦值.【解析】(1)证明:如图,连接AE ,由题意知AB 为⊙O 的直径,所以AE ⊥BE .因为AD ,EF 是圆柱的母线,所以AD ∥EF 且AD =EF ,所以四边形AEFD 是平行四边形.所以AE ⎳DF ,所以BE ⊥DF .因为EF 是圆柱的母线,所以EF ⊥平面ABE ,又因为BE ⊂平面ABE ,所以EF ⊥BE .又因为DF ∩EF =F ,DF 、EF ⊂平面DEF ,所以BE ⊥平面DEF .(2)由(1)知BE 是三棱锥B -DEF 底面DEF 上的高,由(1)知EF ⊥AE ,AE ∥DF ,所以EF ⊥DF ,即底面三角形DEF 是直角三角形.设DF =AE =x ,BE =y ,则在Rt △ABE 中有:x 2+y 2=6,所以V B -DEF =13S △DEF ⋅BE =13⋅12x ⋅6⋅y =66xy ≤66⋅x 2+y 22=62,当且仅当x =y =3时等号成立,即点E ,F 分别是AB ,CD的中点时,三棱锥B -DEF 的体积最大,(另等积转化法:V B -DEF =V D -BEF =V D -BCF =V B -CDF =13S △CDF⋅BC 易得当F 与CD 距离最远时取到最大值,此时E 、F 分别为AB 、CD 中点)下面求二面角B -DF -E 的正弦值:法一:由(1)得BE ⊥平面DEF ,因为DF ⊂平面DEF ,所以BE ⊥DF .又因为EF ⊥DF ,EF ∩BE =E ,所以DF ⊥平面BEF .因为BF ⊂平面BEF ,所以BF ⊥DF ,所以∠BFE 是二面角B -DF -E 的平面角,由(1)知△BEF 为直角三角形,则BF =(3)2+(6)2=3.故sin ∠BFE =BE BF=33,所以二面角B -DF -E 的正弦值为33.法二:由(1)知EA ,EB ,EF 两两相互垂直,如图,以点E 为原点,EA ,EB ,EF 所在直线为x ,y ,z 轴建立空间直角坐标系E -xyz ,则B (0,3,0),D (3,0,6),E (0,0,0),F (0,0,6).由(1)知BE ⊥平面DEF ,故平面DEF 的法向量可取为EB =(0,3,0).设平面BDF 的法向量为n =(x ,y ,z ),由DF =(-3,0,0),BF =(0,-3,6),得n ⋅DF =0n ⋅BF =0 ,即-3x =0-3y +6z =0,即x =0y =2z ,取z =1,得n =(0,2,1).设二面角B -DF -E 的平面角为θ,|cos θ|=∣cos n ,EB =|n ⋅EB ||n |⋅|EB |=2×33×3=63,所以二面角B -DF -E 的正弦值为33例11.如图,O 1,O 分别是圆台上、下底的圆心,AB 为圆O 的直径,以OB 为直径在底面内作圆E ,C 为圆O 的直径AB 所对弧的中点,连接BC 交圆E 于点D ,AA 1,BB 1,CC 1为圆台的母线,AB =2A 1B 1=8.(1)证明;C 1D ⎳平面OBB 1O 1;(2)若二面角C 1-BC -O 为π3,求O 1D 与平面AC 1D 所成角的正弦值.【解析】(1)连接DE ,O1E ,C 为圆O 的直径AB 所对弧的中点,所以△BOC 为等腰直角三角形,即∠OBD =45°,又D 在圆E 上,故△BED 为等腰直角三角形,所以DE ⎳OC 且DE =12OC ,又CC 1是母线且O 1C 1=12OC ,则O 1C 1⎳OC ,故DE ⎳O 1C 1且DE =O 1C 1,则DEO 1C 1为平行四边形,所以EO 1⎳DC 1,而EO 1⊂面OBB 1O 1,DC 1⊄面OBB 1O 1,故C 1D ⎳平面OBB 1O 1.(2)由题设及(1)知:O 1O 、OB 、OC 两两垂直,构建如下图示的空间直角坐标系,过C 1作C 1F ⎳O 1O ,则F 为OC 的中点,再过F 作FG ⎳OD ,连接C 1G ,由O 1O ⊥圆O ,即C 1F ⊥圆O ,BC ⊂圆O ,则C 1F ⊥BC ,又OD⊥BC ,则FG ⊥BC ,故二面角C 1-BC -O 的平面角为∠FGC 1=π3,而FG =12OD =24OB =2,所以O 1O =C 1F =FG tan π3=6.则A (0,-4,0),D (2,2,0),C 1(2,0,6),O 1(0,0,6),所以AD =(2,6,0),C 1D =(0,2,-6),O 1D =(2,2,-6),若m =(x ,y ,z )为面AC 1D 的一个法向量,则m ⋅AD =2x +6y =0m ⋅C 1D =2y -6z =0,令y =6,则m =(-36,6,2),|cos <m ,O 1D >|=6614×8=32128,故O 1D 与平面AC 1D 所成角的正弦值32128.例12.某市在滨海文化中心有滨海科技馆,其建筑有鲜明的后工业风格,如图所示,截取其中一部分抽象出长方体和圆台组合,如图所示,长方体ABCD -A 1B 1C 1D 1中,AB =4,AD =AA 1=2,圆台下底圆心O 为AB 的中点,直径为2,圆与直线AB 交于E ,F ,圆台上底的圆心O 1在A 1B 1上,直径为1.(1)求A 1C 与平面A 1ED 所成角的正弦值;(2)圆台上底圆周上是否存在一点P 使得FP ⊥AC 1,若存在,求点P 到直线A 1B 1的距离,若不存在则说明理由.【解析】(1)(1)由长方体ABCD -A 1B 1C 1D 1可知,以D 为原点,DA 为x 轴,DC 为y 轴,DD 1为z 轴,建立空间直角坐标系如图所示,则A 12,0,2 ,C 0,4,0 ,E 2,1,0 ,D 0,0,0 .所以A 1C =(-2,4,-2),DA 1 =(2,0,2),DE =(2,1,0).设平面A 1ED 的一个法向量为n=(x ,y ,z ),则有n .DA=0n .DE =0 ,即2x +2z =02x +y =0 ,令x =1,则y =-2,z =-1,故n=(1,-2,-1),所以|cos <A 1C ,n >|=|AC ⋅n||AC ||n |=|-2-8+2|4+16+4⋅1+4+1=23,故A 1C 与平面A 1ED 所成角的正弦值为23;(2)由(1)可知,A 2,0,0 ,C 10,4,2 ,所以AC 1=(-2,4,2),假设存在这样的点P ,设P x ,y ,2 ,由题意可知(x -2)2+(y -2)2=14,所以FP =(x -2,y -3,2),因为FP ⊥AC 1,则有FP ⋅AC 1 =-2(x -2)+4(y-3)+4=0,所以x =2y -2,又(x -2)2+(y -2)2=14,所以5y 2-20y +794=0,解得x =2-55y =2-510(舍),x =2+55y =2+510,所以当P 2+55,2+510,2 时,FP ⊥AC 1,此时点P 到直线A 1B 1的距离为55.题型二:立体几何存在性问题例13.如图,三棱锥P -ABC 中,PA ⊥平面ABC ,PA =1,AB =1,AC =2,∠BAC =60°.(1)求三棱锥A -PBC 的体积;(2)在线段PC 上是否存在一点M ,使得BM ⊥AC ?若存在,求MCPM的值,若不存在,请说明理由.【解析】(1)因为AB =1,AC =2,∠BAC =60°,所以S △ABC =12⋅AB ⋅AC ⋅sin60°=32.由PA ⊥平面ABC 知:PA 是三棱锥P -ABC 的高,又PA =1,所以三棱锥A -PBC 的体积V A -PBC =V P -ABC =13⋅S △ABC ⋅PA =36.(2)在线段PC 上存在一点M ,使得BM ⊥AC ,此时MCPM =3.如图,在平面PAC 内,过M 作MN ⎳PA 交AC 于N,连接BN ,BM .由PA ⊥平面ABC ,AC ⊂平面ABC ,故PA ⊥AC ,所以MN ⊥AC .由MN ⎳PA 知:AN NC =PM MC=13,则AN =12,在△ABN 中,BN 2=AB 2+AN 2-2AB ⋅AN cos ∠BAC =12+12 2-2×1×12×12=34,所以AN 2+BN 2=AB 2,即AC ⊥BN .由于BN ∩MN =N 且BN ,MN ⊂面MB N ,故AC ⊥平面MB N .又BM ⊂平面MB N ,所以AC ⊥BM .例14.已知四棱锥P -ABCD 中,底面ABCD 是矩形,且AD =2AB ,△PAD 是正三角形,CD ⊥平面PAD ,E 、F 、G 、O 分别是PC 、PD 、BC 、AD 的中点.(1)求平面EFG 与平面ABCD 所成的锐二面角的大小;(2)线段PA 上是否存在点M ,使得直线GM 与平面EFG 所成角的大小为π6,若存在,求出PMPA的值;若不存在,说明理由.【解析】(1)因为△PAD 是正三角形,O 为AD 的中点,所以,PO ⊥AD ,因为CD ⊥平面PAD ,PO ⊂平面PAD ,∴PO ⊥CD ,∵AD ∩CD =D ,∴PO ⊥平面ABCD ,因为AD ⎳BC 且AD =BC ,O 、G 分别为AD 、BC 的中点,所以,AO ⎳BG 且AO =BG ,所以,四边形ABGO 为平行四边形,所以,OG ⎳AB ,∵AB ⊥AD ,则OG ⊥AD ,以点O 为坐标原点,OA 、OG 、OP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,设AB =2,则AD =4,A 2,0,0 、G 0,2,0 、D -2,0,0 、C -2,2,0 、P 0,0,23 、E -1,1,3 、F -1,0,3 ,EF=0,-1,0 ,EG =1,1,-3 ,设平面EFG 的法向量为n=x ,y ,z ,则n ⋅EF=-y =0n ⋅EG=x +y -3z =0 ,取x =3,可得n =3,0,1 ,易知平面ABCD 的一个法向量为m=0,0,1 ,所以,cos <m ,n >=m ⋅nm ⋅n=12,因此,平面EFG 与平面ABCD 所成的锐二面角为π3.(2)假设线段PA 上是否存在点M ,使得直线GM 与平面EFG 所成角的大小为π6,设PM=λPA =λ2,0,-23 =2λ,0,-23λ ,其中0≤λ≤1,GM =GP +PM=0,-2,23 +2λ,0,-23λ =2λ,-2,23-23λ ,由题意可得cos <n ,GM > =n ⋅GM n ⋅GM =2324λ2+4+121-λ 2=12,整理可得4λ2-6λ+1=0,因为0≤λ≤1,解得λ=3-54.因此,在线段PA 上是否存在点M ,使得直线GM 与平面EFG 所成角的大小为π6,且PM PA=3-54.例15.已知三棱柱ABC -A 1B 1C 1中,∠ACB =90°,A 1B ⊥AC 1,AC =AA 1=4,BC =2.(1)求证:平面A 1ACC 1⊥平面ABC ;(2)若∠A 1AC =60°,在线段AC 上是否存在一点P ,使二面角B -A 1P -C 的平面角的余弦值为34若存在,确定点P 的位置;若不存在,说明理由.【解析】(1)由AC =AA 1知:四边形AA 1C 1C 为菱形.连接A 1C ,则A 1C ⊥AC 1,又A 1B ⊥AC 1且A 1C ∩A 1B =A 1,∴AC 1⊥平面A 1CB ,BC ⊂平面A 1CB ,则AC 1⊥BC ;又∠ACB =90°,即BC ⊥AC ,而AC ∩AC 1=A ,∴BC ⊥平面A 1ACC 1,而BC ⊂平面ABC ,∴平面A 1ACC 1⊥平面ABC .(2)以C 为坐标原点,射线CA 、CB 为x 、y 轴的正向,平面A 1ACC 1上过C 且垂直于AC 的直线为z 轴,建立如图所示的空间直角坐标系.∵AC =AA 1=4,BC =2,∠A 1AC =60°,∴C 0,0,0 ,B 0,2,0 ,A 4,0,0 ,A 12,0,23 .设在线段AC 上存在一点P ,满足AP =λAC0≤λ≤1 ,使二面角B -A 1P -C 的余弦值为34,则AP =-4λ,0,0 ,所以BP =BA +AP=4,-2,0 +-4λ,0,0 =4-4λ,-2,0 ,A 1P =A 1A +AP=2-4λ,0,-23 .设平面BA 1P 的一个法向量为m=x 1,y 1,z 1 ,由m ⋅BP=4-4λ x 1-2y 1=0m ⋅A 1P =2-4λ x 1-23z 1=0,取x 1=1,得m=1,2-2λ,1-2λ3;平面A 1PC 的一个法向量为n=0,1,0 .由cos m ,n =m ⋅n m ⋅n =2-2λ 1+2-2λ 2+1-2λ23×1=34,解得λ=43或λ=34.因为0≤λ≤1,则λ=34.故在线段AC 上存在一点P ,满足AP =34AC ,使二面角B -A 1P -C 的平面角的余弦值为34.例16.如图,在四棱锥P -ABCD 中,PA ⊥平面ABCD ,AD ⎳BC ,AD ⊥CD ,且AD =CD ,BC =2CD ,PA =2AD .(1)证明:AB ⊥PC ;(2)在线段PD 上是否存在一点M ,使得二面角M -AC -D 的余弦值为1717,若存在,求BM 与PC 所成角的余弦值;若不存在,请说明理由.【解析】(1)证明:连接AC ,设AD =CD =1,因为AD ⊥CD ,则AC =AD 2+CD 2=2,且△ACD 为等腰直角三角形,因为AD ⎳BC ,则∠ACB =∠CAD =45∘,因为BC =2CD =2,由余弦定理可得AB 2=AC 2+BC 2-2AC ⋅BC cos45∘=2,所以,AC 2+AB 2=BC 2,则AB ⊥AC ,∵PA ⊥平面ABCD ,AB ⊂平面ABCD ,∴AB ⊥PA ,∵PA ∩AC =A ,∴AB ⊥平面PAC ,∵PC ⊂平面PAC ,∴AB ⊥PC .(2)因为PA ⊥平面ABCD ,AB ⊥AC ,以点A 为坐标原点,AB 、AC 、AP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,设AD =CD =1,则A 0,0,0 、B 2,0,0 、C 0,2,0 、D -22,22,0 、P 0,0,2 ,设PM =λPD =-22λ,22λ,-2λ ,其中0≤λ≤1,则AM =AP +PM=-22λ,22λ,2-2λ ,AC =0,2,0 ,设平面ACM 的法向量为m=x ,y ,z ,则m ⋅AC=2y =0m ⋅AM =-22λx +22y +2-2λ z =0,取x =2-2λ,可得m =2-2λ,0,λ ,易知平面ACD 的一个法向量为n=0,0,1 ,由题意可得cos <m ,n > =m ⋅n m ⋅n =λ41-λ 2+λ2=1717,因为0≤λ≤1,解得λ=13,此时,AM =-26,26,223 ,BM =BA +AM =-726,26,223 ,PC =0,2,-2 ,所以,cos <BM ,PC >=BM ⋅PCBM ⋅PC =-1333×2=-3322,因此,在线段PD 上是否存在一点M ,使得二面角M -AC -D 的余弦值为1717,且BM 与PC 所成角的余弦值为3322.例17.如图,△ABC 是边长为6的正三角形,点E ,F ,N 分别在边AB ,AC ,BC 上,且AE =AF =BN =4,M 为BC 边的中点,AM 交EF 于点O ,沿EF 将三角形AEF 折到DEF 的位置,使DM =15.(1)证明:平面DEF ⊥平面BEFC ;(2)试探究在线段DM 上是否存在点P ,使二面角P -EN -B 的大小为60°?若存在,求出DPPM的值;若不存在,请说明理由.【解析】(1)在△DOM 中,易得DO =23,OM =3,DM =15,由DM 2=DO 2+OM 2,得DO ⊥OM ,又∵AE =AF =4,AB =AC =6,∴EF ⎳BC ,又M 为BC 中点,∴AM ⊥BC ,∴DO ⊥EF ,因为EF ∩OM =O ,EF ,OM ⊂平面EBCF ,∴DO ⊥平面EBCF ,又DO ⊂平面DEF ,所以平面DEF ⊥平面BEFC ;(2)由(1)DO ⊥平面EBCF ,以O 为原点,以OE ,OM ,OD为x ,y ,z 的正方向建立空间直角坐标系O -xyz ,D (0,0,23),M (0,3,0),E (2,0,0),N (-1,3,0)∴DM =(0,3,-23),ED =(-2,0,23),由(1)得平面ENB 的法向量为n=(0,0,1),设平面ENP 的法向量为m=(x ,y ,z ),DP =λDM (0≤λ≤1),所以DP =(0,3λ,-23λ),所以EP =ED +DP =(-2,3λ,23-23λ).由题得,所以EN =(-3,3,0),所以m ⋅EN=-3x +3y =0m ⋅EP =-2x +3λy +(23-23λ)z =0,所以m =1,3,2-3λ23-23λ,因为二面角P -EN -B 的大小为60°,所以12=2-3λ23-23λ1+3+2-3λ23-23λ2,解之得λ=2(舍去)或λ=67.此时DP =67DM ,所以DP PM=6.例18.图1是直角梯形ABCD ,AB ⎳CD ,∠D =90∘,AB =2,DC =3,AD =3,CE =2ED,以BE 为折痕将△BCE 折起,使点C 到达C 1的位置,且AC 1=6,如图2.(1)求证:平面BC 1E ⊥平面ABED ;(2)在棱DC 1上是否存在点P ,使得C 1到平面PBE 的距离为62?若存在,求出二面角P -BE -A 的大小;若不存在,说明理由.【解析】(1)在图1中取CE 中点F ,连接BF ,AE ,∵CE =2ED ,CD =3,AB =2,∴CF =1,EF =1,∵DF =AB =2,DF ⎳AB ,∠D =90∘,∴四边形ABFD 为矩形,∴BF ⊥CD ,∴BE =BC =3+1=2,又CE =2,∴△BCE 为等边三角形;又AE =3+1=2,∴△ABE 为等边三角形;在图2中,取BE 中点G ,连接AG ,C 1G ,∵△C 1BE ,△ABE 为等边三角形,∴C 1G ⊥BE ,AG ⊥BE ,∴C 1G =AG =3,又AC 1=6,∴AG 2+C 1G 2=AC 21,∴C 1G ⊥AG ,又AG ∩BE =G ,AG ,BE ⊂平面ABED ,∴C 1G ⊥平面ABED ,∵C 1G ⊂平面BC 1E ,∴平面BC 1E ⊥平面ABED .(2)以G 为坐标原点,GA ,GB ,GC 1正方向为x ,y ,z 轴,可建立如图所示空间直角坐标系,则B 0,1,0 ,E 0,-1,0 ,A 3,0,0 ,C 10,0,3 ,D 32,-32,0,∴DC 1 =-32,32,3 ,EB =0,2,0 ,EC 1 =0,1,3 ,设棱DC 1上存在点P x ,y ,z 且DP=λDC 1 0≤λ≤1 满足题意,即x -32=-32λy +32=32λz =3λ,解得:x =32-32λy =32λ-32z =3λ,即P 32-32λ,32λ-32,3λ,则EP =32-32λ,32λ+12,3λ ,设平面PBE 的法向量n=a ,b ,c ,则EP ⋅n =32-32λ a +32λ+12 b +3λc =0EB ⋅n =2b =0,令a =2,则b =0c =1-λλ,∴n =2,0,1-λλ,∴C 1到平面PBE 的距离为d =EC 1 ⋅nn=3-3λλ4+1-λλ2=62,解得:λ=13,∴n=2,0,2 ,又平面ABE 的一个法向量m=0,0,1 ,∴cos <m ,n >=m ⋅nm ⋅n=222=22,又二面角P -BE -A 为锐二面角,∴二面角P -BE -A 的大小为π4.例19.如图所示,在四棱柱ABCD -A 1B 1C 1D 1中,侧棱A 1A ⊥底面ABCD ,AB ⊥AC ,AB =1,AC =AA 1=2,AD =CD =5,E 为棱AA 1上的点,且AE =12.(1)求证:BE ⊥平面ACB 1;(2)求二面角D 1-AC -B 1的余弦值;(3)在棱A 1B 1上是否存在点F ,使得直线DF ∥平面ACB 1?若存在,求A 1F 的长;若不存在,请说明理由.【解析】(1)∵A 1A ⊥底面ABCD ,AC ⊂平面ABCD ∴A 1A ⊥AC又AB ⊥AC ,A 1A ∩AB =A ,AA 1,AB ⊂平面ABB 1A 1,∴AC ⊥平面ABB 1A 1∵BE ⊂平面ABB 1A 1,∴AC ⊥BE ∵AE AB =12=ABBB 1,∠EAB =∠ABB 1=90∘,∴∠ABE =∠AB 1B∵∠BAB 1+∠AB 1B =90∘,∴∠BAB 1+∠ABE =90∘,∴BE ⊥AB 1,又AC ∩AB 1=A ,AC ,AB 1⊂平面ACB 1,∴BE ⊥平面ACB 1(2)如图,以A 为原点建立空间直角坐标系A -xyz ,依题意可得A (0,0,0),B (0,1,0),C (2,0,0),D (1,-2,0),D1(1,-2,2),E 0,0,12,由(1)知,EB =0,1,-12为平面ACB 1的一个法向量.设n=x ,y ,z 为平面ACD 1的一个法向量.因为AD 1 =(1,-2,2),AC =(2,0,0),所以n ⋅AD 1=0n ⋅AC =0 ,即:x -2y +2z =02x =0 ,不妨设z =1,可得n=(0,1,1).因此cos n ,EB =n ⋅EB n ⋅EB =1010由图可知二面角D 1-AC -B 1为锐角,所以二面角D 1-AC -B 1的余弦值为1010.(3)假设存在满足题意的点F ,设A 1F =a (a >0),则由(2)得F (0,a ,2),DF=(-1,a +2,2).由题意可知DF ⋅EB=a +2-1=0,解得a =-1(舍去),即直线DF 的方向向量与平面ACB 1的法向量不可能垂直.所以,在棱A 1B 1上不存在点F ,使得直线DF ∥平面ACB 1.例20.如图,在五面体ABCDE 中,已知AC ⊥BD ,AC ⊥BC ,ED ⎳AC ,且AC =BC =2ED =2,DC =DB =3.(1)求证:平面ABE ⊥与平面ABC ;(2)线段BC 上是否存在一点F ,使得平面AEF 与平面ABE 夹角余弦值的绝对值等于54343,若存在,求BFBC的值;若不存在,说明理由.【解析】(1)证明:∵AC ⊥BD ,AC ⊥BC ,BC ∩BD =B ,∴AC ⊥平面BCD ,∵AC ⊂平面ABC ,∴平面ABC ⊥平面BCD ,取BC 的中点O ,AB 的中点H ,连接OD 、OH 、EH ,∵BD =CD ,∴DO ⊥BC ,又DO ⊂平面BCD ,平面ABC ⊥平面BCD ,平面BCD ∩平面ABC =BC ,∴DO ⊥平面ABC ,又OH ⎳AC ,OH =12AC ,DE ⎳AC ,DE =12AC ,所以,OH ⎳DE 且OH =DE ,∴四边形OHED 为平行四边形,∴EH ⎳OD ,∵DO ⊥面ABC ,则EH ⊥平面ABC ,又∵EH ⊂面ABE ,所以,平面ABE ⊥平面ABC .(2)因为AC ⊥BC ,OH ⎳AC ,则OH ⊥BC ,因为OD ⊥平面ABC ,以点O 为坐标原点,OH 、OB 、OD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系,则A 2,-1,0 、B 0,1,0 、C 0,-1,0 、E 1,0,2 、H 1,0,0 ,HE=0,0,2 ,AB =-2,2,0 ,设平面ABE 的法向量为m=x 1,y 1,z 1 ,则m ⋅HE=2z 1=0m ⋅AB=-2x 1+2y 1=0 ,取x 1=1,可得m=1,1,0 ,设在线段BC 上存在点F 0,t ,0 -1≤t ≤1 ,使得平面AEF 与平面ABE 夹角的余弦值等于54343,设平面AEF 的法向量为n=x 2,y 2,z 2 ,AF =-2,t +1,0 ,AE =-1,1,2 ,由n ⋅AF=-2x 2+t +1 y 2=0n ⋅AE =-x 2+y 2+2z 2=0 ,取x 2=2t +1 ,可得n =2t +1 ,22,t -1 ,由题意可得cos <m ,n> =m ⋅n m ⋅n =2t +32⋅3t 2+2t +11=54343,整理可得2t 2-13t -7=0,解得:t =-12或t =7(舍),∴F 0,-12,0 ,则BF =32,∴BF BC =34,综上所述:在线段BC 上存在点F ,满足BF BC=34,使得平面AEF 与平面ABE 夹角的余弦值等于54343.题型三:立体几何折叠问题例21.如图1,在边上为4的菱形ABCD 中,∠DAB =60°,点M ,N 分别是边BC ,CD 的中点,AC ∩BD =O 1,AC ∩MN =G .沿MN 将△CMN 翻折到△PMN 的位置,连接PA ,PB ,PD ,得到如图2所示的五棱锥P -ABMND .(1)在翻折过程中是否总有平面PBD ⊥平面PAG ?证明你的结论;(2)当四棱锥P -MNDB 体积最大时,求直线PB 和平面MNDB 所成角的正弦值;(3)在(2)的条件下,在线段PA 上是否存在一点Q ,使得二面角Q -MN -P 余弦值的绝对值为1010若存在,试确定点Q 的位置;若不存在,请说明理由.【解析】(1)在翻折过程中总有平面PBD ⊥平面PAG ,证明如下:∵点M ,N 分别是边CD ,CB 的中点,又∠DAB =60°,∴BD ∥MN ,且△PMN 是等边三角形,∵G 是MN 的中点,∴MN ⊥PG ,∵菱形ABCD 的对角线互相垂直,∴BD ⊥AC ,∴MN ⊥AC ,∵AC ∩PG =G ,AC ⊂平面PAG ,PG ⊂平面PAG ,∴MN ⊥平面PAG ,∴BD ⊥平面PAG ,∵BD ⊂平面PBD ,∴平面PBD ⊥平面PAG .(2)由题意知,四边形MNDB 为等腰梯形,且DB =4,MN =2,O 1G =3,所以等腰梯形MNDB 的面积S =2+4 ×32=33,要使得四棱锥P -MNDB 体积最大,只要点P 到平面MNDB 的距离最大即可,∴当PG ⊥平面MNDB 时,点P 到平面MNDB 的距离的最大值为3,此时四棱锥P -MNDB 体积的最大值为V =13×33×3=3,直线PB 和平面MNDB 所成角的为∠PBG ,连接BG ,在直角三角形△PBG 中,PG =3,BG =7,由勾股定理得:PB =PG 2+BG 2=10.sin ∠PBG =PGPB=310=3010.(3)假设符合题意的点Q 存在.以G 为坐标原点,GA ,GM ,GP 所在直线分别为x 轴、y 轴、z 轴,建立如图所示空间直角坐标系,则A 33,0,0 ,M 0,1,0 ,N 0,-1,0 ,P 0,0,3 ,由(2)知,AG ⊥PG ,又AG ⊥MN ,且MN ∩PG =G ,MN ⊂平面PMN ,PG ⊂平面PMN ,AG ⊥平面PMN ,故平面PMN 的一个法向量为n 1=1,0,0 ,设AQ =λAP(0≤λ≤1),∵AP=-33,0,3 ,AQ=-33λ,0,3λ ,故331-λ ,0,3λ ,∴NM=0,2,0 ,QM =33λ-1 ,1,-3λ ,平面QMN 的一个法向量为n 2=x 2,y 2,z 2 ,则n 2 ⋅NM =0,n 2 ⋅QM=0,即2y 2=0,33λ-1 x 2+y 2-3λz 2=0,令z 2=1,所以y 2=0,x 2=λ3λ-1n 2 =13λ-1 ,0,1=13λ-1λ,0,3λ-1 ,则平面QMN 的一个法向量n=λ,0,3λ-1 ,设二面角Q -MN -P 的平面角为θ,则cos θ =n ⋅n 1 n n 1 =λλ2+9λ-1 2=1010,解得:λ=12,故符合题意的点Q 存在且Q 为线段PA 的中点.例22.如图,在等腰直角三角形PAD 中,∠A =90°,AD =8,AB =3,B 、C 分别是PA 、PD 上的点,且AD ⎳BC ,M 、N 分别为BP 、CD 的中点,现将△BCP 沿BC 折起,得到四棱锥P -ABCD ,连接MN .(1)证明:MN ⎳平面PAD ;(2)在翻折的过程中,当PA =4时,求二面角B -PC -D 的余弦值.【解析】(1)在四棱锥P -ABCD 中,取AB 的中点E ,连接EM ,EN .因为M ,N 分别为BP ,CD 的中点,AD ⎳BC ,所以ME ⎳PA ,EN ⎳AD ,又PA ⊂平面PAD ,ME ⊄平面PAD ,所以ME ⎳平面PAD ,同理可得,EN ⎳平面PAD ,又ME ∩EN =E ,ME ,EN ⊂平面MNE ,所以平面MNE ⎳平面PAD ,因为MN ⊂MNC 平面MNE ,所以MN ⎳平面PAD .(2)因为在等腰直角三角形PAD 中,∠A =90°,AD ⎳BC ,所以BC ⊥PA ,在四棱锥P -ABCD 中,BC ⊥PB ,BC ⊥AB ,因为AD ⎳BC ,则AD ⊥PB ,AD ⊥AB ,又PB ∩AB =B ,PB ,AB ⊂平面PAB ,所以AD ⊥平面PAB ,又PA ⊂平面PAB ,所以PA ⊥AD ,因为AD =8,AB =3,PA =4,AD ⎳BC ,则PB =5,BC =5,所以AB 2+PA 2=PB 2,故PA ⊥AB ,所以以点A 为坐标原点,分别以AB ,AD ,AP 所在方向为x 轴,y 轴,z 轴建立如图所示的空间直角坐标系A -xyz ,如图所示,A (0,0,0),B (3,0,0),C (3,5,0),P 0,0,4 ,D 0,8,0 ,所以PB =(3,0,-4),PC =(3,5,-4),PD =(0,8,-4),设m =(x 1,y 1,z 1)为平面PBC 的一个法向量,则m ⋅PB =0m ⋅PC =0,即3x 1-4z 1=03x 1+5y 1-4z 1=0 ,令x 1=4,则y 1=0,z 1=2,m =(4,0,3),设n =(x 2,y 2,z 2)为平面PCD 的一个法向量,则m ⋅PD =0m ⋅PC =0 ,即8y 2-4z 2=03x 2+5y 2-4z 2=0,令y 2=1,则x 2=1,z 2=2,n =(1,1,2),设二面角B -PC -D 所成角为α,则cos α=-cos m ,n =-m ⋅n m ⋅n =-4×1+0×1+2×3 42+02+32×12+12+22=-105×6=-63.因为二面角B -PC -D 的余弦值为-63.例23.如图1,在平面四边形PDCB 中,PD ∥BC ,BA ⊥PD ,PA =AB =BC =2,AD =1.将△PAB 沿BA 翻折到△SAB 的位置,使得平面SAB ⊥平面ABCD ,如图2所示.(1)设平面SDC 与平面SAB 的交线为l ,求证:BC ⊥l ;(2)点Q 在线段SC 上(点Q 不与端点重合),平面QBD 与平面BCD 夹角的余弦值为66,求线段BQ 的长.【解析】(1)依题意,AD ⊥AB ,因为PD ∥BC ,所以BC ⊥AB ,由于平面SAB ⊥平面ABCD ,且交线为AB ,BC ⊂平面ABCD ,所以BC ⊥平面SAB ,因为l 是平面SDC 与平面SAB 的交线,所以l ⊂平面SAB ,故BC ⊥l .(2)由上可知,AD ⊥平面SAB ,所以AD ⊥SA ,由题意可知SA ⊥AB ,AD ⊥AB ,以点A 为坐标原点,分别以AD ,AB ,AS 所在直线为x ,y ,z 轴建立空间直角坐标系,则A 0,0,0 ,B 0,2,0 ,C 2,2,0 ,D 1,0,0 ,S 0,0,2 ,BD =1,-2,0 ,SC =2,2,-2 ,设SQ =λSC 0<λ<1 ,则Q 2λ,2λ,2-2λ ,BQ =2λ,2λ-2,2-2λ ,设n =x ,y ,z 是平面QBD 的一个法向量,则n ⋅BD =x -2y =0n ⋅BQ =2λx +2λ-1 y +21-λ z =0,令x =2,可得n =2,1,1-3λ1-λ由于m =0,0,1 是平面CBD 的一个法向量,依题意,二面角Q -BD -C 的余弦值为66,所以cos m ,n =m ⋅n m ⋅n =1-3λ1-λ 1×4+1+1-3λ1-λ2=66,解得λ=12∈0,1 ,此时BQ =1,-1,1 ,BQ =3,即线段BQ 的长为3.例24.如图,在平面五边形PABCD 中,△PAD 为正三角形,AD ∥BC ,∠DAB =90°且AD =AB =2BC =2.将△PAD 沿AD 翻折成如图所示的四棱锥P -ABCD ,使得PC =7.F ,Q 分别为AB ,CE 的中点.(1)求证:FQ ∥平面PAD ;(2)若DE PE=12,求平面EFC 与平面PAD 夹角的余弦值.【解析】(1)(1)证明:取DC 的中点M ,连接MF ,MQ .则MQPD ,MFDA .因为MQ ⊄面PAD ,ME ⊄面PAD ,所以,MQ ∥面PAD ,MF ∥面PAD ,因为MQ ∩ME =M ,所以,面MQF 面PAD ,因为FQ ⊂面MQF ,所以FQ ∥面PAD .(2)(2)取AD 的中点O ,连接OP ,OC ,因为△PAD 为正三角形,AD =2,所以OP ⊥AD 且OP =3,在直角梯形ABCD 中,AD ∥BC ,∠DAB =90°,AB =2BC =2,所以,OC ⊥AD 且OC =2,又因为PC =7,所以在△POC 中,OP 2+OC 2=PC 2,即OP ⊥OC ,所以,以O 为坐标原点,分别以OD ,OC ,OP 的方向为x ,y ,z 轴的正向,建立如图所示的空间直角坐标系,则D 1,0,0,C 0,2,0 ,F -1,1,0 ,P 0,0,3 ,DP =-1,0,3 .因为DE PE=12,即DE =13DP =-13,0,33 ,λ>0,所以,E 23,0,33,所以EC =-23,2,-33 ,EF =-53,1,-33.设n =x 1,y 1,z 1 为平面EFC 的一个法向量,则n ⋅EC =0n ⋅EF =0 ,即-23x 1+2y 1-33z 1=0-53x 1+y 1-33z 1=0,取n =3,-3,-83 .又平面PAD 的一个法向量m =0,1,0 ,设平面EFC 与平面PAD 夹角为α,cos α=n ⋅m n ⋅m =39+9+192=21070.例25.如图,在平行四边形ABCD 中,AB =3,AD =2,∠A =60°,E ,F 分别为线段AB ,CD 上的点,且BE =2AE ,DF =FC ,现将△ADE 沿DE 翻折至△A 1DE 的位置,连接A 1B ,A 1C .(1)若点G 为线段A 1B 上一点,且A 1G =3GB ,求证:FG ⎳平面A 1DE ;(2)当三棱锥C -A 1DE 的体积达到最大时,求二面角B -A 1C -D 的正弦值.【解析】(1)在A 1E 上取一点M ,使A 1M =3ME ,连接DM ,MG ,因为A 1G =3GB ,EB =2AE ,所以MG ∥EB ,MG =34EB =34×23AB =12AB ,因为平行四边形ABCD 中,AB =CD ,AB ∥CD ,F 为CD 的中点,所以DF =12CD =12AB ,所以DF =MG ,DF ∥MG ,所以四边形DMGF 为平行四边形,所以FG ∥DM ,因为FG ⊄平面A 1DE ,DM ⊂平面A 1DE ,所以FG ∥平面A 1DE ,(2)当平面A 1DE ⊥平面DEC 时,三棱锥C -A 1DE 的体积最大,△ADE 中,∠A =60°,AD =2,AE =1,则DE 2=AD 2+AE 2-2AD ⋅AE cos A =4+1-2×2×1×12=3,所以DE 2+AE 2=AD 2,所以∠AED =90°,所以A 1E ⊥DE ,因为平面A 1DE ⊥平面DEC ,平面A 1DE ∩平面DEC =DE ,所以A 1E ⊥平面DEC ,因为BE ⊂平面DEC ,所以A 1E ⊥BE ,所以A 1E ,BE ,DE 两两垂直,所以以E 为原点,EB ,ED ,EA 1所在的直线分别为x ,y ,z 轴建立空间直角坐标系,如图所示,则D (0,3,0),A 1(0,0,1),B (2,0,0),C (3,3,0),所以DC =(3,0,0),DA 1 =(0,-3,1),BC =(1,3,0),CA 1 =(-3,-3,1),设平面A 1CD 的法向量为n =(x ,y ,z ),则n ⋅DA 1 =-3y +z =0n ⋅CA 1 =-3x -3y +z =0,令y =1,则n =(0,1,3),设平面A 1BC 的法向量为m =(a ,b ,c ),则m ⋅BC =a +3b =0m ⋅CA 1 =-3a -3b +c =0,令b =1,则m =(-3,1,-23),所以cos m ,n =m ⋅n m n=1-62×4=-58,所以二面角B -A 1C -D 的正弦值为1--58 2=398例26.如图1,四边形ABCD 是边长为2的正方形,四边形ABEF 是等腰梯形,AB =BE =12EF ,现将正方形ABCD 沿AB 翻折,使CD 与C D 重合,得到如图2所示的几何体,其中D E =4.(1)证明:AF ⊥平面AD E ;(2)求二面角D -AE -C 的余弦值.【解析】(1)证明:易得AD =AF =2,EF =D E =4,所以AE =23,则AD 2+AE 2=D E 2=EF 2,∴AD ⊥AE ,AE ⊥AF .又AD ⊥AB ,且AB ∩AE =A ,AB ,AE ⊂平面ABEF ,∴AD ⊥平面ABEF .∵AF ⊂平面ABEF ,∴AF ⊥AD .∵AE ∩AD =A ,AE ⊂平面AD E ,AD ⊂平面AD E ,∴AF ⊥平面AD E .(2)由(1)知AD ⊥平面ABEF ,则以A 为坐标原点,AB ,AD 所在直线分别为y ,z 轴,平面ABEF 内过点A 且垂直于AB 的直线为x 轴,建立如图所示的空间直角坐标系,则A 0,0,0 ,E 3,3,0 ,F 3,-1,0 ,C 0,2,2 ,∴AF =3,-1,0 ,AE =3,3,0 ,AC =00,2,2 .设平面AEC 的一个法向量为m =x ,y ,z ,则m ⋅AE =0m ⋅AC =0 ,得3x +3y =0,2y +2z =0,令x =3,则m =3,-1,1 .由(1)知,平面AED 的一个法向量为AF =3,-1,0 .∴cos AF ,m =AF ⋅m AF m=255.易知二面角D -AE -C 为锐二面角,∴二面角D -AE -C 的余弦值为255.例27.如图,在梯形ABCD 中,AD ∥BC ,AB =BC =2,AD =4,现将△ABC 所在平面沿对角线AC 翻折,使点B 翻折至点E ,且成直二面角E -AC -D .(1)证明:平面EDC ⊥平面EAC ;(2)若直线DE 与平面EAC 所成角的余弦值为12,求二面角D -EA -C 的余弦值.【解析】(1)证明:取AD 中点M ,连接CM ,由题意可得AM =2,AM 平行且等于BC ,∴四边形ABCM 为平行四边形,∵AM =MD =CM =2,∴△ACD 为直角三角形,即AC ⊥CD ,∵直二面角E -AC -D ,CD ⊂平面ACD ,∴平面EAC ⊥平面ACD ,平面EAC ∩平面ACD =AC ,∴CD ⊥平面EAC ,CD ⊂平面ECD ,∴平面ECD ⊥平面EAC .(2)由(1)可得DC ⊥平面EAC ,∴∠DEC 为直线DE 与平面EAC 所成角,∴cos ∠DEC =12,∴∠DEC =60°.在Rt △ECD 中,∵CE =2,∴CD =23,ED =4,在Rt △ACD 中,AC =2,∴△ABC 、△AEC 为等边三角形,以AC 中点O 为坐标原点,以OC ,OM ,OE 所在直线分别为x ,y ,z 轴建立如图所示的空间直角坐标系,A (-1,0,0),C (1,0,0),E (0,0,3),D (1,23,0),平面EAC 为xOz 平面,则其法向量为v =(0,1,0),在平面AED 内,设其法向量为u =(x ,y ,z ),AD =(2,23,0),AE =(1,0,3),则AD ⋅u =0AE ⋅u =0 ,即2x +23y =0x +3z =0,令x =3,则y =-1,z =-1,∴u =(3,-1,-1),设二面角D -EA -C 的平面角为θ,∴cos ‹u ,v ›=u ⋅v |u ||v |=-55,由图可知二面角D -EA -C 为锐角,∴cos θ=55.例28.如图1,在△ABC 中,∠ACB =90°,DE 是△ABC 的中位线,沿DE 将△ADE 进行翻折,使得△ACE 是等边三角形(如图2),记AB 的中点为F .(1)证明:DF ⊥平面ABC .(2)若AE =2,二面角D -AC -E 为π6,求直线AB 与平面ACD 所成角的正弦值.【解析】(1)如图,取AC 中点G ,连接FG 和EG ,由已知得DE ∥BC ,且DE =12BC .因为F ,G 分别为AB ,AC 的中点,所以FG ∥BC ,且FG =12BC 所以DE ∥FG ,且DE =FG .所以四边形DEGF 是平行四边形.所以EG ∥DF .因为翻折的BC ⊥AC ,易知DE ⊥AC .所以翻折后DE ⊥EA ,DE ⊥EC .又因为EA ∩EC =E ,EA ,EC ⊂平面AEC ,所以DE ⊥平面AEC .因为DE ∥BC ,所以BC ⊥平面AEC .因为EG ⊂平面AEC ,所以EG ⊥BC .因为△ACE 是等边三角形,点G 是AC 中点,所以EG ⊥AC又因为AC ∩BC =C ,AC ,BC ⊂平面ABC .所以EG ⊥平面ABC .。

高中数学立体几何知识点归纳总结一、立体几何知识点归纳 第一章 空间几何体(一)空间几何体的结构特征(1)多面体——由若干个平面多边形围成的几何体.围成多面体的各个多边形叫叫做多面体的面,相邻两个面的公共边叫做多面体的棱,棱与棱的公共点叫做顶点。
旋转体——把一个平面图形绕它所在平面内的一条定直线旋转形成的封闭几何体。
其中,这条定直线称为旋转体的轴。
(2)柱,锥,台,球的结构特征 1.棱柱1.1棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
1.2相关棱柱几何体系列(棱柱、斜棱柱、直棱柱、正棱柱)的关系:①⎧⎪⎧−−−−−→⎨⎪−−−−−→⎨⎪⎪⎩底面是正多形棱垂直于底面斜棱柱棱柱正棱柱直棱柱其他棱柱 底面为矩形侧棱与底面边长相等1.3①侧棱都相等,侧面是平行四边形;②两个底面与平行于底面的截面是全等的多边形; ③过不相邻的两条侧棱的截面是平行四边形;④直棱柱的侧棱长与高相等,侧面与对角面是矩形。
1.4长方体的性质:①长方体一条对角线长的平方等于一个顶点上三条棱的平方和;【如图】222211AC AB AD AA =++②(了解)长方体的一条对角线1AC 与过顶点A 的三条棱所成的角分别是αβγ,,,那么222cos cos cos 1αβγ++=,222sin sin sin 2αβγ++=;③(了解)长方体的一条对角线1AC 与过顶点A 的相邻三个面所成的角分别是αβγ,,,则222cos cos cos 2αβγ++=,222sin sin sin 1αβγ++=.1.5侧面展开图:正n 棱柱的侧面展开图是由n 个全等矩形组成的以底面周长和侧棱长为邻边的矩形.1.6面积、体积公式:2S c hS c h S S h=⋅=⋅+=⋅直棱柱侧直棱柱全底棱柱底,V (其中c 为底面周长,h为棱柱的高) 2.圆柱2.1圆柱——以矩形的一边所在的直线为旋转轴,其余各边旋转而形成的曲面所围成的几何体叫圆柱. 2.2圆柱的性质:上、下底及平行于底面的截面都是等圆;过轴的截面(轴截面)是全等的矩形. 2.3侧面展开图:圆柱的侧面展开图是以底面周长和母线长为邻边的矩形. 2.4面积、体积公式:S 圆柱侧=2rh π;S 圆柱全=222rh r ππ+,V 圆柱=S 底h=2r h π(其中r 为底面半径,h 为圆柱高) 3.棱锥3.1棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
立体几何截面、外接球、动点归类目录题型一:动点:恒平行题型二:动点:恒垂直题型三:动点:球截面题型四:动点;定角题型五:外接球:线面垂直型题型六:外接球:垂面型题型七:外接球:两线定心法题型八:外接球:二面角型题型九:外接球:最值范围型题型十:外接球:动点与翻折题型十一:动点型最短距离和题型十二:动点:内切球题型十三:多选题综合应用:二面角型几何体题型十四:多选题综合应用:翻折型题型十五:多选题综合应用:正方体表面动点型题型十六:多选题综合应用:两部分体积比型题型一:动点:恒平行线面恒平行,过线做面,需要找它们和第三个面的交线互相平行,借助好“第三个面的交线平行“这个性质,可以解决线面恒平行题型的截面问题1在四棱锥P-ABCD中,PA⊥平面ABCD,且PA=AC=2AB=2AD=4,CD⊥AD,CB⊥AB,G为PC的中点,过AG的平面α与棱PB、PD分别交于点E、F.若EF∥平面ABCD,则截面AEGF的面积为.【答案】865【分析】由题知AC =2AB +2AD ,则PA =23PB +23PD -13PC ①,再根据E 、F 、G 三点共面得PA=xPE +yPF +zPG ,其中x +y +z =1.设PE =λPB 0<λ<1 ,PF =λPD ,从而可求PA =λxPB +λyPD +z 2PC ,与①对比即可求出λ,从而可求EF 的长度;再证明BD 垂直平面PAC ,EF ∥BD ,从而得AG ⊥EF ,根据S 截面AEGF =12AG ⋅EF 即可得答案.【详解】∵AC =2AB =2AD ,CD ⊥AD ,CB ⊥AB ,∴∠DAC =∠BAC =60°,则根据向量加法法则易知,AC =2AB +2AD ,即PC -PA =2PB -PA +2PD -PA ,则PA =23PB +23PD -13PC .根据共面向量定理的推论知,PA =xPE +yPF +zPG,其中x +y +z =1.连接BD ,∵EF ∥平面ABCD ,EF ⊂平面PBD ,平面PBD ∩平面ABCD =BD ,∴EF ∥BD ,设PE =λPB 0<λ<1 ,则PF =λPD ,又G 为PC 的中点,∴PA =xPE +yPF +zPG =λxPB +λyPD+z 2PC ,则λx =λy =23,z 2=-13,解得λ=45,AB =2,BD =2×AB sin60°=23,则EF =45BD =835.连接AG ,∵PA =AC =4,G 为PC 的中点,故AG =12PC =22.易知BD ⊥AC ,BD ⊥PA ,AC ∩PA =A ,故BD ⊥平面PAC ,又AG ⊂平面PAC ,∴BD ⊥AG ,∴AG ⊥EF ,因此S 截面AEGF =12AG ⋅EF=12×22×835=865.故答案为:865.解法二:连接BD ,设AC 与BD 交于点K ,连接AG 、PK ,设AG 与PK 交于点L ,由题易得BD ∥EF ,则PL PK =PE PB =EFBD ,作KN ∥AG 交PC 于N ,易知CK =3AK ,则CN =3GN ,从而PG =4GN ,故EF BD =PL PK =PG PN=45,即EF =45BD =835.以下解法同上故答案为:865.2在三棱锥ABCD 中,对棱AB =CD =5,AD =BC =13,AC =BD =10,当平面α与三棱锥ABCD 的某组对棱均平行时,则三棱锥ABCD 被平面α所截得的截面面积最大值为.【答案】3【分析】每组对棱棱长相等,所以可以把三棱锥ABCD 放入长方体中,设长宽高分别为x ,y ,z ,求出x ,y ,z ,由线面平行得线线平行,证明当E ,F ,G ,H 是所在棱中点时面积最大,按截面与哪对棱平行分类讨论求得截面面积的最大值.【详解】因为每组对棱棱长相等,所以可以把三棱锥ABCD 放入长方体中,设长宽高分别为x ,y ,z ,则x 2+y 2=5,x 2+z 2=10,y 2+z 2=13,则x =1,y =2,z =3.当平面α与三棱锥ABCD 的对棱AB ,CD 均平行时,截而为四边形EFGH ,AB ⎳FG ⎳EH ,CD ⎳EF ⎳HG ,设AE AC =t (0<t <1),则EF CD =AE AC=t ,EF =tCD ,同理EH =(1-t )AB ,∠HEF (或其补角)是异面直线AB ,CD 所成的角,S EFGH =EF ⋅EH sin ∠HEF =t (1-t )AB ⋅CD sin ∠HEF ,其中AB ⋅CD sin ∠HEF 为定值,t (1-t )=-t 2+t =-t -12 2+14,t =12时,t (1-t )取得最大值,即截面EFGH 面积最大,此时E ,F ,G ,H是所在棱中点,由长方体性知最大面积为长方体上下底面面积的一半12xy =1,同样地,当平面a 与三棱锥ABCD 的对棱AC ,BD 均平行时,截面最大面积为12xz =32;当平面α与三棱锥ABCD 的对棱AD ,BC 均平行时,截面最大面积为12yz =3.故答案为:3.3(山西省怀仁市2022届高三下学期一模数学试)在四棱锥P -ABCD 中,底面ABCD 是边长为22的正方形,P 在底面的射影为正方形的中心O ,PO =4,Q 点为AO 中点.点T 为该四棱锥表面上一个动点,满足PA ,BD 都平行于过QT 的四棱锥的截面,则动点T 的轨迹围成的多边形的面积为()A.55B.554C.354D.552【答案】D【分析】首先取AD 的中点E ,PD 的中点F ,PO 的中点R ,PB 的中点N ,连接QR 延长交PC 与点M ,连接EFMNG ,证明平面EFMNG 即为所求的截面,再证明四边形EFNG 是矩形,RM ⊥FN ,矩形面积加三角形面积之和即为所求.【详解】取AD 的中点E ,PD 的中点F ,PO 的中点R ,PB 的中点N ,连接QR 延长交PC 与点M ,连接EFMNG ,因为底面ABCD 是边长为22的正方形,所以对角线AC =BD =4,AO =2,因为在底面的射影为正方形的中心,可得PO ⊥面ABCD ,因为AO ⊂面ABCD ,所以PO ⊥AO ,因为PO =4,AO =2,所以PA =22+42=25,因为E 、F 为AD 、PD 的中点,所以EF =12PA =5,且EF ⎳PA ,因为PA ⊄平面EFMG ,EF ⊂平面EFMG ,所以PA ⎳平面EFMG ,同理BD ⎳平面EFMG ,所以平面EFMG 即为所求截面.又因为平面APC ∩平面EFMG =QM ,PA ⊂平面APC ,所以QM ⎳AP ,因为Q 为AO 的中点,可得QC =34AC ,所以QM =34AP ,QR =12AP ,RM =QM -QR =14AP =52,因为N 、F 为PB 、PD 的中点,所以FN ⎳BD ,FN =12BD ,所以FN ⎳EG ,FN =EG ,所以四边形EFNG 是平行四边形,因为EG ⊥PO ,EG ⊥AC ,PO ∩AC =O ,所以EG ⊥平面APC ,因为QM ⊂平面APC ,可得EG ⊥QM ,所以EG ⊥GN ,所以四边形EFNG 是矩形,所以动点T 的轨迹围成的多边形的面积为5×2+12×2×52=552.故选:D题型二:动点:恒垂直恒垂直型截面,可以借助投影解决,投影型,需要利用”三垂线定理及其逆定理“这个性质转化寻找。
第四讲-立体几何题型归类总结高中数学-立体几何第四讲立体几何题型归类总结一、考点分析基本图形1.棱柱——有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
斜棱柱底面是正多边形的棱柱正棱柱直棱柱其他棱柱2.棱锥——有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
正棱锥——如果有一个棱锥的底面是正多边形,并且顶点在底面的垂线上,这样的棱锥叫做正棱锥。
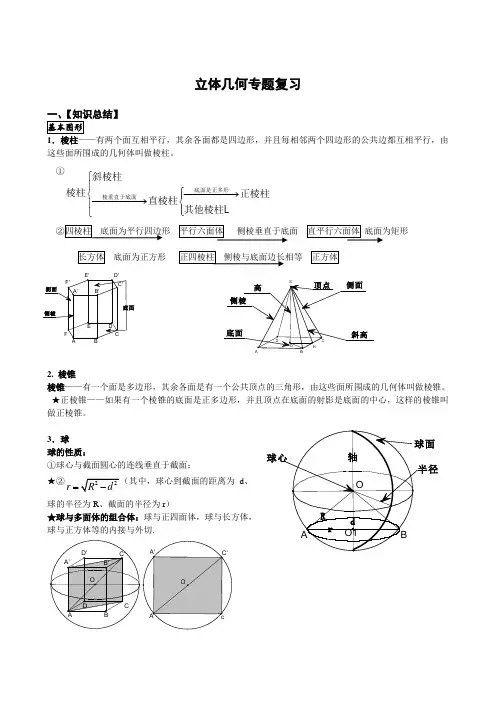
3.球球的性质:球心与截面圆心的连线垂直于截面;r=R2-d2(其中,球心到截面的距离为d、球的半径为R、截面的半径为r)球与多面体的组合体:球与正四面体、长方体、正方体等的内接与外切。
注:球的有关问题转化为圆的问题解决。
球面积、体积公式:S球=4πR,V球=4/3πR³(其中R为球的半径)二、平行垂直基础知识网络平行与垂直关系可互相转化平行关系a⊥α,b⊥α⇒a//ba⊥α,a//b⇒b⊥αa⊥α,a⊥β⇒α//βα//β,a⊥α⇒a⊥βα//β,γ⊥α⇒γ⊥β垂直关系线线平行判定线线垂直性质判定性质判定面面垂直定义面面垂直线面平行面面平行线面垂直异面直线所成的角,线面角,二面角的求法1.求异面直线所成的角θ∈(0°,90°):解题步骤:找(作):利用平移法找出异面直线所成的角;(1)可固定一条直线平移另一条与其相交;(2)可将两条一面直线同时平移至某一特殊位置。
常用中位线平移法证:证明所找(作)的角就是异面直线所成的角(或其补角)。
常需要证明线线平行;计算:通过解三角形,求出异面直线所成的角;2求直线与平面所成的角度$\theta\in[0^\circ,90^\circ]$:关键在于找到“两足”:垂足和斜足。
解题步骤:1.找到斜线与其在平面内的射影的夹角(注意三垂线定理的应用);2.证明所找到的角度就是直线与平面所成的角度(或其补角)(常常需要证明线面垂直);3.通过解直角三角形,计算线面角度。
立体几何解答题常考模型归纳总结 高考立体几何解答题常考模型主要包括柱体、锥体、球体、旋转体、多面体等。
这些模型常涉及体积、表面积的计算,截面问题,以及与其他几何体的组合或相交问题。
此外,空间位置关系,如平行、垂直的判断与证明,也是常考内容。
空间角的计算,包括异面直线所成的角、直线与平面所成的角、二面角等,同样是高考立体几何的重要考点。
最后,空间距离的计算,如点到平面的距离、两平行平面间的距离等,也是解答题中常见的考查点。
掌握这些模型的基本性质和解题方法,对于提高高考立体几何的解题能力至关重要。
题型一:非常规空间几何体为载体【典例1-1】(2024·河南濮阳·模拟预测)如图,侧面11BCC B 水平放置的正三棱台11111,24ABC A B C AB A B -==(1)求证:1AA ^平面11BCC B ;(2)求直线AB 和平面1ACB 所成角的正弦值.【典例1-2】(2024·云南昆明·三模)如图,在三棱台111ABC A B C -中,上、下底面是边长分别为2和4的正三角形,1AA ^平面ABC ,设平面11AB C I 平面=ABC l ,点,E F 分别在直线l 和直线1BB 上,且满足EF l ^,1EF BB ^.(1)证明:^EF 平面11BCC B ;(2)若直线EF 和平面ABC 【变式1-1】(2024·天津和平·二模)如图,三棱台111ABC A B C -中,ABC V 为等边三角形,1124AB A B ==,1AA ^平面ABC ,点M ,N ,D 分别为AB ,AC ,BC 的中点,11A B AC ^.(1)证明:1CC ∥平面1A MN ;(2)求直线1A D 与平面1A MN 所成角的正弦值;(3)求点D 到平面1A MN 的距离.【变式1-2】(2024·河南周口·模拟预测)如图,平行六面体1111ABCD A B C D -中,底面ABCD 与平面11ABC D 都是边长为2的菱形,11120BCD BC D °Ð=Ð=,侧面11BCC B(1)求平行六面体1111ABCD A B C D -的体积;(2)求平面11BCC B 与平面11CDD C 的夹角的余弦值.题型二:立体几何存在与探索性问题【典例2-1】如图1,ABC V 是边长为3的等边三角形,点,D E 分别在线段,AC AB 上,且1,2AE AD ==,沿DE 将ADE V 翻折到PDE △的位置,使得PB 2.(1)求证:平面PDE ^平面BCDE ;(2)在线段PB 上是否存在点M ,使得//EM 平面PCD ,若存在,求出PM MB的值;若不存在,请说明理由.【典例2-2】(2024·广东·一模)如图所示,四边形ABCD 是圆柱底面的内接四边形,AC 是圆柱的底面直径,PC 是圆柱的母线,E 是AC 与BD 的交点,608AB AD BAD AC Ð===o ,,.(1)记圆柱的体积为1V ,四棱锥P ABCD -的体积为 2V ,求 12V V ;(2)设点F 在线段AP 上,且存在一个正整数k ,使得PA kPF PC kCE ==,,若已知平面FCD 与平面PCDk 的值.【变式2-1】在ABC V 中,90ABC Ð=°,6AB BC ==,D 为边AB 上一点,2AD =,E 为AC 上一点,//DE BC ,将ADE V 沿DE 翻折,使A 到A ¢处,90DA B ¢Ð=°.(1)证明:A B ¢^平面A DE ¢;(2)若射线DE 上存在点M ,使l =uuuu r uuu r DM DE ,且MC 与平面A EC ¢所成角的正弦值为15,求λ.【变式2-2】(2024·甘肃张掖·模拟预测)如图,在四棱锥P ABCD -中,底面四边形ABCD为菱形,且60,DAB PAD Ð=o V 是边长为2的等边三角形,且平面PAD ^平面,ABCD O 为AD 中点.(1)求证:OB ^平面PAD ;(2)在线段PC 上是否存在点M ,使二面角M BO C --的大小为60o ,若存在,求PM PC的值,若不存在,请说明理由.题型三:立体几何折叠问题【典例3-1】(2024·湖北武汉·模拟预测)如图1,在矩形ABCD 中,2AB =,BC =ABD △沿矩形的对角线BD 进行翻折,得到如图2所示的三棱锥A BCD -,且AB CD ^.(1)求翻折后线段AC 的长;(2)点M 满足2AM MD =uuuu r uuuu r ,求CM 与平面ABD 所成角的正弦值.【典例3-2】(2024·山东·模拟预测)如图,在菱形ABCD 中,60BAD Ð=°,E 是AD 的中点,将ABE V沿直线BE 翻折使点A 到达点1A 的位置,F 为线段1AC 的中点.(1)求证:DF ∥平面1A BE ;(2)若平面1A BE ^平面BCDE ,求直线1A E 与平面1A BC 所成角的大小.【变式3-1】(2024·河南驻马店·二模)在如图①所示的平面图形中,四边形ACDE 为菱形,现沿AC 进行翻折,使得AB ^平面ACDE ,过点E 作//EF AB ,且12EF AB =,连接,,FD FB BD ,所得图形如图②所示,其中G 为线段BD 的中点,连接FG .(1)求证:FG ^平面ABD ;(2)若2AC AD ==,直线FG 与平面BCD ,求AB 的值.【变式3-2】在等腰梯形ABCD 中,//AB CD ,2AB =,2AD BC ==,60DAB Ð=°,M 为AB 中点,将AMD V ,BMC △沿MD ,MC 翻折,使A ,B 重合于点E ,得到三棱锥M CDE -.(1)求ME 与平面CDE 所成角的大小;(2)求二面角M DE C --的余弦值.题型四:立体几何作图问题【典例4-1】(2024·河南信阳·模拟预测)长方体1111ABCD A B C D -中,123,2AB AA AD CE ED ===uuu r uuu r .(1)过E 、B 作一个截面,使得该截面平分长方体的表面积和体积.写出作图过程及其理由.(2)记(1)中截面为a ,若a 与(1)中过D 点的长方体的三个表面成二面角分别为,,q j w ,求222cos cos cos q j w ++的值.【典例4-2】(2024·高三·河北承德·期中)如图,在四棱锥P ABCD -中,底面ABCD 是正方形,,,O E F 分别是,,BD PA BC 的中点.(1)证明://OE 平面PBC ;(2)若平面a 经过点,,F D E ,且与棱PB 交于点H .请作图画出H 在棱PB 上的位置,并求出PH HB的值.【变式4-1】(2024·辽宁大连·一模)如图多面体ABCDEF 中,面FAB ^面ABCD ,FAB V 为等边三角形,四边形ABCD 为正方形,EF BC ∥,且334EF BC ==,H ,G 分别为CE ,CD 的中点.(1)证明:BF AD ^;(2)求平面BCEF 与平面FGH 所成角的余弦值;(3)作平面FHG 与平面ABCD 的交线,记该交线与直线AD 交点为P ,写出AP AD的值(不需要说明理由,保留作图痕迹).【变式4-2】如图,已知底面为平行四边形的四棱锥P ABCD -中,平面MNGH 与直线PB 和直线AC 平行,点E 为PD 的中点,点F 在CD 上,且:1:2DF FC =.(1)求证:四边形MNGH 是平行四边形;(2)求作过EF 作四棱锥P ABCD -的截面,使PB 与截面平行(写出作图过程,不要求证明).截面的定义:用一个平面去截一个几何体,平面与几何体的表面的交线围成的平面图形.【变式4-3】(2024·北京·三模)四棱锥P ABCD -中,底面ABCD 是边长为2的菱形,23DAB p Ð=.AC BD O =I ,且^PO 平面ABCD ,PO =,点,F G 分别是线段.PB PD 上的中点,E 在PA 上.且3PA PE =.(Ⅰ)求证://BD 平面EFG ;(Ⅱ)求直线AB 与平面EFG 的成角的正弦值;(Ⅲ)请画出平面EFG 与四棱锥的表面的交线,并写出作图的步骤.题型五:立体几何建系繁琐问题【典例5-1】(2024·山东淄博·二模)已知直角梯形ABCD ,90ADC Ð=°,//AB CD ,2AB CD AD ===M 为对角线AC 与BD 的交点.现以AC 为折痕把ADC V 折起,使点D 到达点P 的位置,点Q 为PB 的中点,如图所示:(1)证明:AC ^平面PBM ;(2)求三棱锥P ACQ -体积的最大值;(3)当三棱锥P ACQ -的体积最大时,求直线AB 与平面PBC 所成角的正弦值.【典例5-2】(2024·贵州黔东南·二模)如图,在四棱台1111ABCD A B C D -中,O 为AC 的中点,1111122AA A C C C AC ====.(1)证明:1//OC 平面11AA D D ;(2)若平面ABCD ^平面11ACC A ,AB BC ^,当四棱锥11B AA C C -的体积最大时,求1CC 与平面11AA B B 夹角的正弦值.【变式5-1】(2024·重庆·三模)如图所示的几何体是一个半圆柱和一个三棱锥的组合体.11,BB CC 是半圆柱的母线,1,O O 分别是底面直径BC 和11B C 的中点,11114,2,BC B C BB CC A ====是半圆O 上一动点,1A 是半圆1O 上的动点,1AA 是圆柱的母线,延长1A A 至P 点使得A 为1A P 的中点,连接PB ,PC 构成三棱锥P ABC -.(1)证明:1AC BA ^;(2)当三棱锥P ABC -的体积最大时,求平面1ABA 与平面1BA C 的夹角.【变式5-2】已知平面四边形ABCD ,2AB AD ==,60BAD Ð=°,30BCD Ð=°,现将ABD D 沿BD 边折起,使得平面ABD ^平面BCD ,此时AD CD ^,点P 为线段AD 的中点.(1)求证:BP ^平面ACD ;(2)若M 为CD 的中点①求MP 与平面BPC 所成角的正弦值;②求二面角P BM D --的平面角的余弦值.题型六:两角相等(构造全等)的立体几何问题【典例6-1】(2024·河南·模拟预测)如图,在三棱锥A BCD -中,ABC V 是等边三角形,90BAD BCD Ð=Ð=°,点P 是AC 的中点,连接,BP DP .(1)证明:平面ACD ^平面BDP ;(2)若BD =,且二面角A BD C --为120°,求直线AD 与平面BCD 所成角的正弦值.【典例6-2】(2024·广西桂林·二模)如图,四棱锥F ABCD -中,底面ABCD 为边长是2的正方形,E ,G 分别是CD ,AF 的中点,4AF =,FAE BAE Ð=Ð,且二面角F AE B --的大小为90°.(1) 求证:AE BG ^;(2) 求二面角B AF E --的余弦值.【变式6-1】(2024·安徽合肥·模拟预测)如图,四棱锥E ABCD -中,四边形ABCD 是边长为2的菱形,45DAE BAE °Ð=Ð=,60DAB Ð=°.(1)证明:平面ADE ^平面ABE ;(2)当直线DE 与平面ABE 所成的角为30°时,求平面DCE 与平面ABE 所成锐二面角的余弦值.【变式6-2】(2024·辽宁沈阳·模拟预测)如图,四棱锥E ABCD -中,四边形ABCD 是边长为2的菱形45DAE BAE Ð=Ð=°,60DAB Ð=°(1)证明:平面ADE ^平面ABE ;(2)当平面DCE 与平面ABE DE 与平面ABE 所成角正弦值.题型七:利用传统方法找几何关系建系【典例7-1】(2024·江苏南京·二模)如图,//AD BC ,AD AB ^,点E 、F 在平面ABCD 的同侧,//CF AE ,1AD =,2AB BC ==,平面ACFE ^平面ABCD ,EA EC ==(1)求证://BF 平面ADE ;(2)若直线EC 与平面FBD ,求线段CF 的长.【典例7-2】斜三棱柱ABC -A 1B 1C 1上,侧面AA 1C 1C ⊥平面ABC ,侧面AA 1C 1C 是菱形,∠A 1AC =60°,A 1C =AC AB =2,为BB 1的中点.(1)求二面角C -A 1D -C 1的余弦值;(2)记△ABC 的外接圆上有一动点P ,若二面角P -AA 1-C 与二面角C -A 1D -C 1相等,求AP 的长.【变式7-1】如图,已知四棱锥P ABCE -中,PA ^平面ABCE ,平面PAB ^平面PBC ,且1AB =,2BC =,BE =,点A 在平面PCE 内的射影恰为PCE V 的重心G .(1)证明:BC AB ^;(2)求直线CG 与平面PBC 所成角的正弦值.【变式7-2】如图所示,圆锥的高2PO =,底面圆O 的半径为R ,延长直径AB 到点C ,使得BC R =,分别过点A ,C 作底面圆O 的切线,两切线相交于点E ,点D 是切线CE 与圆O 的切点.(1)证明:平面PDE ^平面POD ;(2)若直线PE 与平面PBD ,求点A 到平面PED 的距离.题型八:空间中的点不好求【典例8-1】(2024·山东日照·三模)在五面体ABCDEF 中,CD ADE ^平面,EF ADE ^平面.(1)求证:AB CD ∥;(2)若222AB AD EF ===,3CD =,90ADE Ð=°,点D 到平面ABFE A BC F --的余弦值.【典例8-2】(2024·全国·校联考模拟预测)已知三棱锥ABCD ,D 在面ABC 上的投影为O ,O 恰好为△ABC 的外心.4AC AB ==,2BC =.(1)证明:BC ⊥AD ;(2)E 为AD 上靠近A 的四等分点,若三棱锥A-BCD 的体积为1,求二面角E CO B --的余弦值.【变式8-1】(2024·河南·校联考模拟预测)如图,在四棱锥P ABCD -中,AB BC ==AD CD AC ===E ,F 分别为AC ,CD 的中点,点G 在PF 上,且G 为三角形PCD 的重心.(1)证明://GE 平面PBC ;(2)若PA PC =,PA CD ^,四棱锥P ABCD -的体积为GE 与平面PCD 所成角的正弦值.【变式8-2】(2024·湖北武汉·华中师大一附中校考模拟预测)如图,平行六面体1111ABCD A B C D -中,点P 在对角线1BD 上,AC BD O =I ,平面ACP ∥平面11AC D .(1)求证:O ,P ,1B 三点共线;(2)若四边形ABCD 是边长为2的菱形,11π3BAD BAA DAA =ÐÐ==Ð,13AA =,求二面角P AB C --大小的余弦值.【变式8-3】(2024·全国·模拟预测)已知菱形ABCD 中,1AB BD ==,四边形BDEF 为正方形,满足2π3ABF Ð=,连接AE ,AF ,CE ,CF .(1)证明:CF AE ^;(2)求直线AE 与平面BDEF 所成角的正弦值.题型九:数学文化与新定义问题【典例9-1】(2024·高三·山东青岛·期中)某校积极开展社团活动,在一次社团活动过程中,一个数学兴趣小组发现《九章算术》中提到了“刍薨”这个五面体,于是他们仿照该模型设计了一道数学探究题,如图1,E 、F 、G 分别是边长为4的正方形的三边AB CD AD 、、的中点,先沿着虚线段FG 将等腰直角三角形FDG 裁掉,再将剩下的五边形ABCFG 沿着线段EF 折起,连接AB CG 、就得到了一个“刍甍” (如图2)。
立体几何知识归纳+典型例题+方法总结一、知识归纳1.平面平面的基本性质:掌握三个公理及推论,会说明共点、共线、共面问题.(1)证明点共线的问题,一般转化为证明这些点是某两个平面的公共点(依据:由点在线上,线在面内,推出点在面内),这样可根据公理2证明这些点都在这两个平面的公共直线上.(2)证明共点问题,一般是先证明两条直线交于一点,再证明这点在第三条直线上,而这一点是两个平面的公共点,这第三条直线是这两个平面的交线.(3)证共面问题一般先根据一部分条件确定一个平面,然后再证明其余的也在这个平面内,或者用同一法证明两平面重合.2. 空间直线(1)空间直线位置关系三种:相交、平行、异面. 相交直线:共面有且仅有一个公共点;平行直线:共面没有公共点;异面直线:不同在任一平面内,无公共点(2)平行公理:平行于同一条直线的两条直线互相平行.等角定理:如果一个角的两边和另一个角的两边分别平行并且方向相同,那么这两个角相等(如右图).(直线与直线所成角]90,0[︒︒∈θ)(向量与向量所成角])180,0[οο∈θ推论:如果两条相交直线和另两条相交直线分别平行,那么这两组直线所成锐角(或直角)相等.(3)两异面直线的距离:公垂线段的长度.空间两条直线垂直的情况:相交(共面)垂直和异面垂直.[注]:21,l l 是异面直线,则过21,l l 外一点P ,过点P 且与21,l l 都平行平面有一个或没有,但与21,l l 距离相等的点在同一平面内. (1L 或2L 在这个做出的平面内不能叫1L 与2L 平行的平面)3. 直线与平面平行、直线与平面垂直(1)空间直线与平面位置分三种:相交、平行、在平面内.(2)直线与平面平行判定定理:如果平面外一条直线和这个平面内一条直线平行,那么这条直线和这个平面平行.(“线线平行⇒线面平行”)(3)直线和平面平行性质定理:如果一条直线和一个平面平行,经过这条直线的平面和这个平面相交,那么这条直线和交线平行.(“线面平行⇒线线平行”)(4)直线与平面垂直是指直线与平面任何一条直线垂直,过一点有且只有一条直线和一个平面垂直,过一点有且只有一个平面和一条直线垂直. 若PA⊥α,a ⊥AO ,得a ⊥PO (三垂线定理),三垂线定理的逆定理亦成立.直线与平面垂直的判定定理一:如果一条直线和一个平面内的两条相PO A a交直线都垂直,那么这两条直线垂直于这个平面.(“线线垂直⇒线面垂直”)直线与平面垂直的判定定理二:如果平行线中一条直线垂直于一个平面,那么另一条也垂直于这个平面.性质:如果两条直线同垂直于一个平面,那么这两条直线平行.(5)a.垂线段和斜线段长定理:从平面外一点..向这个平面所引的垂线段和斜线段中,①射影相等的两条斜线段相等,射影较长的斜线段较长;②相等的斜线段的射影相等,较长的斜线段射影较长;③垂线段比任何一条斜线段短.b.射影定理推论:如果一个角所在平面外一点到角的两边的距离相等,那么这点在平面内的射影在这个角的平分线上.4. 平面平行与平面垂直(1)空间两个平面的位置关系:相交、平行.(2)平面平行判定定理:如果一个平面内有两条相交直线都平行于另一个平面,那么这两个平面平行.(“线面平行⇒面面平行”)推论:垂直于同一条直线的两个平面互相平行;平行于同一平面的两个平面平行.[注]:一平面内的任一直线平行于另一平面.(3)两个平面平行的性质定理:如果两个平面平行同时和第三个平面相交,那么它们交线平行.(“面面平行⇒线线平行”)(4两个平面垂直判定一:两个平面所成的二面角是直二面角,则两个平面垂直.两个平面垂直判定二:如果一条直线与一个平面垂直,那么经过这条直线的平面垂直于这个平面.(“线面垂直⇒面面垂直”)注:如果两个二面角的平面分别对应互相垂直,则两个二面角没有什么关系.(5)两个平面垂直性质定理:如果两个平面垂直,那么在一个平面内垂直于它们交线的直线也垂直于另一个平面.推论:如果两个相交平面都垂直于第三平面,则它们交线垂直于第三平面.简证:如图,在平面内过O 作OA 、OB 分别垂直于21,l l ,因为ααββ⊥⊂⊥⊂OB PM OA PM ,,,则OB PM OA PM ⊥⊥,.所以结论成立 b.最小角定理的应用(∠PBN 为最小角) 简记为:成角比交线夹角一半大,且又比交线夹角补角一半长,一定有4条.成角比交线夹角一半大,又比交线夹角补角小,一定有2条.成角比交线夹角一半大,又与交线夹角相等,一定有3条或者2条. 成角比交线夹角一半小,又与交线夹角一半小,一定有1条或者没有.5. 棱柱. 棱锥(1)棱柱a.①直棱柱侧面积:Ch S =(C 为底面周长,h 是高)该公式是利用直棱柱的侧面展开图为矩形得出的.②斜棱住侧面积:l C S 1=(1C 是斜棱柱直截面周长,l 是斜棱柱的侧棱长)该公式是利用斜棱柱的侧面展开图为平行四边形得出的.b.{四棱柱}⊃{平行六面体}⊃{直平行六面体}⊃{长方体}⊃{正四棱PαβθM A B O柱}⊃{正方体}.{直四棱柱}I {平行六面体}={直平行六面体}.c.棱柱具有的性质:①棱柱的各个侧面都是平行四边形,所有的侧棱都相等;直棱柱的各.个侧面都是矩形.......;正棱柱的各个侧面都是全等的矩形...... ②棱柱的两个底面与平行于底面的截面是对应边互相平行的全等..多边形.③过棱柱不相邻的两条侧棱的截面都是平行四边形.d.平行六面体:定理一:平行六面体的对角线交于一点.............,并且在交点处互相平分. [注]:四棱柱的对角线不一定相交于一点.定理二:长方体的一条对角线长的平方等于一个顶点上三条棱长的平方和.推论一:长方体一条对角线与同一个顶点的三条棱所成的角为γβα,,,则 1cos cos cos 222=++γβα.推论二:长方体一条对角线与同一个顶点的三各侧面所成的角为γβα,,,则2cos cos cos 222=++γβα. (2)棱锥:棱锥是一个面为多边形,其余各面是有一个公共顶点的三角形.[注]:①一个三棱锥四个面可以都为直角三角形.②一个棱柱可以分成等体积的三个三棱锥;所以棱柱棱柱3V S h V ==. a.①正棱锥定义:底面是正多边形;顶点在底面的射影为底面正多边形的中心.[注]:i. 正四棱锥的各个侧面都是全等的等腰三角形.(不是等边三角形)ii. 正四面体是各棱相等,而正三棱锥是底面为正三角形,侧棱与底棱不一定相等iii. 正棱锥定义的推论:若一个棱锥的各个侧面都是全等的等腰三角形(即侧棱相等);底面为正多边形. ②正棱锥的侧面积:'Ch 21S =(底面周长为C ,斜高为'h ) ③棱锥的侧面积与底面积的射影公式:αcos 底侧S S =(侧面与底面成的二面角为α) 附:以知c ⊥l ,b a =⋅αcos ,α为二面角b l a --.则l a S ⋅=211①,b l S ⋅=212②,b a =⋅αcos ③ ⇒①②③得αcos 底侧S S =.注:S 为任意多边形的面积(可分别求多个三角形面积和的方法). b.棱锥具有的性质:①正棱锥各侧棱相等,各侧面都是全等的等腰三角形,各等腰三角形底边上的高相等(它叫做正棱锥的斜高).②正棱锥的高、斜高和斜高在底面内的射影组成一个直角三角形,正棱锥的高、侧棱、侧棱在底面内的射影也组成一个直角三角形.c.特殊棱锥的顶点在底面的射影位置:①棱锥的侧棱长均相等,则顶点在底面上的射影为底面多边形的外心. ②棱锥的侧棱与底面所成的角均相等,则顶点在底面上的射影为底面多边形的外心. ③棱锥的各侧面与底面所成角均相等,则顶点在底面上的射影为底面l abc多边形内心.④棱锥的顶点到底面各边距离相等,则顶点在底面上的射影为底面多边形内心.⑤三棱锥有两组对棱垂直,则顶点在底面的射影为三角形垂心.⑥三棱锥的三条侧棱两两垂直,则顶点在底面上的射影为三角形的垂心.⑦每个四面体都有外接球,球心0是各条棱的中垂面的交点,此点到各顶点的距离等于球半径;⑧每个四面体都有内切球,球心I 是四面体各个二面角的平分面的交点,到各面的距离等于半径.(3)球:a.球的截面是一个圆面.①球的表面积公式:24R S π=.②球的体积公式:334R V π=. b.纬度、经度:①纬度:地球上一点P 的纬度是指经过P 点的球半径与赤道面所成的角的度数.②经度:地球上B A ,两点的经度差,是指分别经过这两点的经线与地轴所确定的二个半平面的二面角的度数,特别地,当经过点A 的经线是本初子午线时,这个二面角的度数就是B 点的经度.附:①圆柱体积:h r V 2π=(r 为半径,h 为高) ②圆锥体积:h r V 231π=(r 为半径,h 为高) ③锥体体积:Sh V 31=(S 为底面积,h 为高)(1). ①内切球:当四面体为正四面体时,设边长为a ,a h 36=,243a S =底,243a S =侧,得R a R a a a ⋅⋅+⋅=⋅2224331433643a a a R 46342334/42=⋅==⇒. 注:球内切于四面体:h S R S 313R S 31V 底底侧ACD B ⋅=⋅+⋅⋅⋅=-. ②外接球:球外接于正四面体,可如图建立关系式.6. 空间向量(1)a.共线向量:共线向量亦称平行向量,指空间向量的有向线段所在直线互相平行或重合.b.共线向量定理:对空间任意两个向量)0(≠a , ∥的充要条件是存在实数λ(具有唯一性),使b a λ=.c.共面向量:若向量a 使之平行于平面α或a 在α内,则a 与α的关系是平行,记作∥α.d.①共面向量定理:如果两个向量b a ,不共线,则向量与向量b a ,共面的充要条件是存在实数对x 、y 使y x +=.②空间任一点...O .和不共线三点......A .、.B .、.C .,则)1(=++++=z y x OC z OB y OA x OP 是PABC 四点共面的充要条件. (简证:→+==++--=AC z AB y AP OC z OB y OA z y OP )1(P 、A 、B 、C 四点共面)注:①②是证明四点共面的常用方法.(2)空间向量基本定理:如果三个向量....c b a ,,不共面...,那么对空间任一向量P ,存在一个唯一的有序实数组x 、y 、z ,使c z b y a x p ++=.推论:设O 、A 、B 、C 是不共面的四点,则对空间任一点P , 都存在唯一的有序实数组x 、y 、z 使 z y x ++=(这里隐含x+y+z≠1). O BDO R注:设四面体ABCD 的三条棱,,,,d AD c AC b AB ===其中Q 是△BCD 的重心, 则向量)(31c b a AQ ++=用MQ AM AQ +=即证.对空间任一点O 和不共线的三点A 、B 、C ,满足OP xOA yOB zOC =++u u u r u u u r u u u r u u u r , 则四点P 、A 、B 、C 是共面⇔1x y z ++=(3)a.空间向量的坐标:空间直角坐标系的x 轴是横轴(对应为横坐标),y 轴是纵轴(对应为纵坐标),z 轴是竖轴(对应为竖坐标). ①令=(a 1,a 2,a 3),),,(321b b b =,则),,(332211b a b a b a b a ±±±=+,))(,,(321R a a a a ∈=λλλλλ,332211b a b a b a b a ++=⋅ ,a ∥)(,,332211Rb a b a b a b ∈===⇔λλλλ332211b a b a b a ==⇔ 0332211=++⇔⊥b a b a b a .222321a a a ++==(向量模与向量之间的转化:a a =⇒•=空间两个向量的夹角公式232221232221332211||||,cos b b b a a a b a b a b a b a b a b a ++⋅++++=⋅•>=<ρρρρρρ(a =123(,,)a a a ,b =123(,,)b b b ). ②空间两点的距离公式:212212212)()()(z z y y x x d -+-+-=.b.法向量:若向量a 所在直线垂直于平面α,则称这个向量垂直于平面α,记作α⊥a ,如果α⊥a 那么向量a 叫做平面α的法向量.c.向量的常用方法:①利用法向量求点到面的距离定理:如图,设n 是平面α的法向量,AB 是平面α的一条射线,其中α∈A ,则点B 到平面α||n . ②异面直线间的距离d = (12,l l 是两异面直线,其公垂向量为n r ,C D 、分别是12,l l 上任一点,d 为12,l l 间的距离).③直线AB 与平面所成角的正弦值sin ||||AB m AB m β⋅=u u u r u r u u u r u r (m u r 为平面α的法向量). ④利用法向量求二面角的平面角定理:设21,n n 分别是二面角βα--l 中平面βα,的法向量,则21,n n 所成的角就是所求二面角的平面角或其补角大小(21,n n 方向相同,则为补角,21,n 反方,则为其夹角).d.证直线和平面平行定理:已知直线⊄a 平面α,α∈∈D C a B A ,,,,且C 、D 、E 三点不共线,则a ∥α的充要条件是存在有序实数对μλ,使μλ+=.(常设μλ+=求解μλ,若μλ,存在即证毕,若μλ,不存在,则直线AB 与平面相交).AB二、经典例题考点一 空间向量及其运算1. 已知,,A B C 三点不共线,对平面外任一点,满足条件122555OP OA OB OC =++u u u r u u u r u u u r u u u r , 试判断:点P 与,,A B C 是否一定共面?解析:要判断点P 与,,A B C 是否一定共面,即是要判断是否存在有序实数对,x y 使AP xAB y AC =+u u u r u u u r u u u r 或对空间任一点O ,有OP OA x AB y AC =++u u u r u u u r u u u r u u u r .答案:由题意:522OP OA OB OC =++u u u r u u u r u u u r u u u r ,∴()2()2()OP OA OB OP OC OP -=-+-u u u r u u u r u u u r u u u r u u u r u u u r ,∴22AP PB PC =+u u u r u u u r u u u r ,即22PA PB PC =--u u u r u u u r u u u r ,所以,点P 与,,A B C 共面.点评:在用共面向量定理及其推论的充要条件进行向量共面判断的时候,首先要选择恰当的充要条件形式,然后对照形式将已知条件进行转化运算.2.如图,已知矩形ABCD 和矩形ADEF 所在平面互相垂直,点M ,N 分别在对角线BD ,AE 上,且13BM BD =,13AN AE =.求证://MN 平面CDE .解析:要证明//MN 平面CDE ,只要证明向量NM u u u u r 可以用平面CDE 内的两个不共线的向量DE u u u r 和DC u u u r 线性表示. 答案:证明:如图,因为M 在BD 上,且13BM BD =, 所以111333MB DB DA AB ==+u u u r u u u r u u u r u u u r .同理1133AN AD DE =+u u u r u u u r u u u r , 又CD BA AB ==-u u u r u u u r u u u r ,所以MN MB BA AN =++u u u u r u u u r u u u r u u u r 1111()()3333DA AB BA AD DE =++++u u u r u u u r u u u r u u u r u u u r 2133BA DE =+u u u r u u u r 2133CD DE =+u u u r u u u r . 又CD uuu r 与DE u u u r 不共线,根据共面向量定理,可知MN u u u u r ,CD uuu r ,DE u u u r 共面.由于MN 不在平面CDE 内,所以//MN 平面CDE .点评:空间任意的两向量都是共面的.与空间的任两条直线不一定共面要区别开.考点二 证明空间线面平行与垂直3. 如图, 在直三棱柱ABC -A 1B 1C 1中,AC =3,BC =4,AA 1=4,点D 是AB 的中点, (I )求证:AC ⊥BC 1; (II )求证:AC 1//平面CDB 1;解析:(1)证明线线垂直方法有两类:一是通过三垂线定理或逆定理证明,二是通过线面垂直来证明线线垂直;(2)证明线面平行也有两类:一是通过线线平行得到线面平行,二是通过面面平行得到线面平行. 答案:解法一:(I )直三棱柱ABC -A 1B 1C 1,底面三边长AC =3,BC =4AB =5,∴ AC ⊥BC ,且BC 1在平面ABC 内的射影为BC ,∴ AC ⊥BC 1; (II )设CB 1与C 1B 的交点为E ,连结DE ,∵ D 是AB 的中点,E 是BC 1的中点,∴ DE//AC 1,∵ DE ⊂平面C D B 1,AC 1⊄平面C D B 1,∴ AC 1//平面C D B 1;解法二:∵直三棱柱ABC -A 1B 1C 1底面三边长AC =3,BC =4,AB =5,∴AC 、BC 、C 1C 两两垂直,如图,以C 为坐标原点,直线CA 、CB 、C 1C 分别为x 轴、y轴、z 轴,建立空间直角坐标系,则C (0,0,0),A (3,0,0),C 1(0,0,4),B (0,4,0),B 1(0,4,4),D (23,2,0) (1)∵AC =(-3,0,0),1BC =(0,-4,0),∴AC •1BC =0,∴AC ⊥BC 1. (2)设CB 1与C 1B 的交战为E ,则E (0,2,2).∵DE =(-23,0,2),1AC =(-3,0,4),∴121AC DE =,∴DE ∥AC 1.A B C A B C E x yz4. 如图所示,四棱锥P —ABCD 中,AB ⊥AD ,CD ⊥AD ,PA ⊥底面ABCD ,PA=AD=CD=2AB=2,M 为PC 的中点.(1)求证:BM ∥平面PAD ;(2)在侧面PAD 内找一点N ,使MN ⊥平面PBD ;(3)求直线PC 与平面PBD 所成角的正弦.解析:本小题考查直线与平面平行,直线与平面垂直,二面角等基础知识,考查空间想象能力和推理论证能力.答案:(1)ΘM 是PC 的中点,取PD 的中点E ,则 ME CD 21,又AB CD 21 ∴四边形ABME 为平行四边形∴BM ∥EA ,PAD BM 平面⊄,PAD EA 平面⊂∴BM ∥PAD 平面(2)以A 为原点,以AB 、AD 、AP 所在直线为x 轴、y 轴、z 轴建立空间直角坐标系,如图,则())0,0,1B ,()0,2,2C ,()0,2,0D ,()2,0,0P ,()1,1,1M ,()1,1,0E在平面PAD 内设()z y N ,,0,()1,1,1---=→--z y MN ,()2,0,1-=→--PB ,()0,2,1-=→--DB 由→--→--⊥PB MN ∴0221=+--=⋅→--→--z PB MN ∴21=z由→--→--⊥DB MN ∴0221=+--=⋅→--→--y DB MN ∴21=y∴⎪⎭⎫ ⎝⎛21,21,0N ∴N 是AE 的中点,此时BD MN P 平面⊥(3)设直线PC 与平面PBD 所成的角为θ()2,2,2-=→--PC ,⎪⎭⎫ ⎝⎛---=→--21,21,1MN ,设→--→--MN PC ,为α 3226322cos -=⋅-=⋅=→--→--→--→--MN PC MNPC α 32cos sin =-=αθ 故直线PC 与平面PBD 所成角的正弦为32解法二: (1)ΘM 是PC 的中点,取PD 的中点E ,则ME CD 21,又AB CD 21 ∴四边形ABME 为平行四边形∴BM ∥EA ,PAD BM 平面⊄PAD EA 平面⊂∴BM ∥PAD 平面(2)由(1)知ABME 为平行四边形ABCD PA 底面⊥∴AB PA ⊥,又AD AB ⊥∴PAD AB 平面⊥ 同理PAD CD 平面⊥,PAD 平面⊂AE∴A E A B ⊥ ∴AB ME 为矩形 CD ∥ME ,PD CD ⊥,又A E PD ⊥ ∴PD ⊥ME ∴ABME 平面⊥PD PBD PD 平面⊂∴ABME PBD 平面平面⊥ 作EB ⊥MF 故PBD 平面⊥MFMF 交AE 于N ,在矩形ABME 内,1==ME AB ,2=AE∴32=MF ,22=NE N 为AE 的中点 ∴当点N 为AE 的中点时,BD MN P 平面⊥(3)由(2)知MF 为点M 到平面PBD 的距离,MPF ∠为直线PC 与平面PBD 所成的角,设为θ,32sin ==MP MF θ ∴直线PC 与平面PBD 所成的角的正弦值为32点评:(1)证明线面平行只需证明直线与平面内一条直线平行即可;(2)求斜线与平面所成的角只需在斜线上找一点作已知平面的垂线,斜线和射影所成的角,即为所求角;(3)证明线面垂直只需证此直线与平面内两条相交直线垂直变可.这些从证法中都能十分明显地体现出来考点三 求空间图形中的角与距离根据定义找出或作出所求的角与距离,然后通过解三角形等方法求值,注意“作、证、算”的有机统一.解题时注意各种角的范围:异面直线所成角的范围是0°<θ≤90°,其方法是平移法和补形法;直线与平面所成角的范围是0°≤θ≤90°,其解法是作垂线、找射影;二面角0°≤θ≤180°,其方法是:①定义法;②三垂线定理及其逆定理;③垂面法 另外也可借助空间向量求这三种角的大小.5. 如图,四棱锥P ABCD -中,侧面PDC 是边长为2的正三角形,且与底面垂直,底面ABCD 是60ADC ∠=o 的菱形,M 为PB 的中点.(Ⅰ)求PA 与底面ABCD 所成角的大小;(Ⅱ)求证:PA ⊥平面CDM ;(Ⅲ)求二面角D MC B --的余弦值.解析:求线面角关键是作垂线,找射影,求异面直线所成的角采用平 移法 求二面角的大小也可应用面积射影法,比较好的方法是向量法答案:(I)取DC 的中点O ,由ΔPDC 是正三角形,有PO ⊥DC . 又∵平面PDC ⊥底面ABCD ,∴PO ⊥平面ABCD 于O .连结OA ,则OA 是PA 在底面上的射影.∴∠PAO 就是PA 与底面所成角.∵∠ADC =60°,由已知ΔPCD 和ΔACD 是全等的正三角形,从而求得OA =OP =3∴∠PAO =45°.∴PA 与底面ABCD 可成角的大小为45°.(II)由底面ABCD 为菱形且∠ADC =60°,DC =2,DO =1,有OA ⊥DC . 建立空间直角坐标系如图, 则(3,0,0),(0,0,3),(0,1,0)A P D -, (3,2,0),(0,1,0)B C .由M 为PB 中点,∴33(1,M . ∴33((3,0,3),DM PA ==u u u u r u u u r (0,2,0)DC =u u u r . ∴333203)0PA DM ⋅=⨯-=u u u r u u u u r ,03200(3)0PA DC ⋅=⨯+⨯-=u u u r u u u r .∴PA ⊥DM ,PA ⊥DC . ∴PA ⊥平面DMC .(III)33(),(3,1,0)CM CB ==u u u u r u u u r .令平面BMC 的法向量(,,)n x y z =r , 则0n CM ⋅=u u u u r r ,从而x +z =0; ……①, 0n CB ⋅=u u u r r 30x y +=. ……②由①、②,取x =−1,则3,1y z =. ∴可取(3,1)n=-r . 由(II)知平面CDM 的法向量可取(3,0,3)PA =u u u r , ∴2310cos ,||||56n PA n PA n PA ⋅-<>=⋅u u u r r u u u r r u u u r r 10法二:(Ⅰ)方法同上(Ⅱ)取AP 的中点N ,连接MN ,由(Ⅰ)知,在菱形ABCD 中,由于60ADC ∠=o ,则AO CD ⊥,又PO CD ⊥,则CD APO ⊥平面,即CD PA ⊥,又在PAB ∆中,中位线//MN 12AB ,1//2CO AB ,则//MN CO , 则四边形OCMN 为Y ,所以//MC ON ,在APO ∆中,AO PO =,则ON AP ⊥,故AP MC ⊥而MC CD C =I ,则PA MCD ⊥平面(Ⅲ)由(Ⅱ)知MC PAB ⊥平面,则NMB ∠为二面角D MC B --的平面角, 在Rt PAB ∆中,易得PA=PB ===,cos AB PBA PB ∠===,cos cos()5NMB PBA π∠=-∠=-故,所求二面角的余弦值为5-点评:本题主要考查异面直线所成的角、线面角及二面角的一般求法,综合性较强 用平移法求异面直线所成的角,利用三垂线定理求作二面角的平面角,是常用的方法.6. 如图,在长方体1111ABCD A B C D -中,11,2,AD AA AB ===点E 在线段AB 上. (Ⅰ)求异面直线1D E 与1A D 所成的角;(Ⅱ)若二面角1D EC D --的大小为45︒,求点B 到平面1D EC 的距离.解析:本题涉及立体几何线面关系的有关知识, 本题实质上求角度和距离,在求此类问题中,要将这些量归结到三角形中,最好是直角三角形,这样有利1D A B CD E 1A 1B 1C于问题的解决,此外用向量也是一种比较好的方法.答案:解法一:(Ⅰ)连结1AD .由已知,11AA D D 是正方形,有11AD A D ⊥.∵AB ⊥平面11AA D D ,∴1AD 是1D E 在平面11AA D D 内的射影.根据三垂线定理,11AD D E ⊥得,则异面直线1D E 与1A D 所成的角为90︒. 作DF CE ⊥,垂足为F ,连结1D F ,则1CE D F ⊥所以1DFD ∠为二面角1D EC D --的平面角,145DFD ∠=︒.于是111,DF DD D F ==易得Rt Rt BCE CDF ∆≅∆,所以2CE CD ==,又1BC =,所以BE =. 设点B 到平面1D EC 的距离为h .∵1,B CED D BCE V V --=即1111113232CE D F h BE BC DD ⋅⋅⋅=⋅⋅⋅,∴11CE D F h BE BC DD ⋅⋅=⋅⋅,即=,∴4h =.故点B 到平面1D EC 解法二:分别以1,,DA DB DD 为x 轴、y 轴、z 轴,建立空间直角坐标系.(Ⅰ)由1(1,0,1)A ,得1(1,0,1)DA =u u u u r设(1,,0)E a ,又1(0,0,1)D ,则1(1,,1)D E a =-u u u u r .∵111010DA D E ⋅=+-=u u u u r u u u u r ∴11DA D E ⊥u u u u r u u u u r则异面直线1D E 与1A D 所成的角为90︒.(Ⅱ)(0,0,1)=m 为面DEC 的法向量,设(,,)x y z =n 为面1CED 的法向量,则(,,)x y z =n|||cos ,|cos 45||||2⋅<>===︒=m n m n m n ∴222z x y =+. ①由(0,2,0)C ,得1(0,2,1)DC =-u u u u r ,则1D C ⊥u u u u r n ,即10DC ⋅=u u u u r n ∴20y z -= ② 由①、②,可取(3,1,2)=n 又(1,0,0)CB =u u u r ,所以点B 到平面1D EC 的距离||36422CB d ⋅===u u u r n |n |. 点评:立体几何的内容就是空间的判断、推理、证明、角度和距离、面积与体积的计算,这是立体几何的重点内容,本题实质上求角度和距离,在求此类问题中,尽量要将这些量归结于三角形中,最好是直角三角形,这样计算起来,比较简单,此外用向量也是一种比较好的方法,不过建系一定要恰当,这样坐标才比较容易写出来.考点四 探索性问题7. 如图所示:边长为2的正方形ABFC 和高为2的直角梯形ADEF 所在的平面互相垂直且DE=2,ED//AF 且∠DAF =90°.(1)求BD 和面BEF 所成的角的余弦;(2)线段EF 上是否存在点P 使过P 、A 、C 三点的平面和直线DB 垂直,若存在,求EP 与PF 的比值;若不存在,说明理由.解析:1.先假设存在,再去推理,下结论: 2.运用推理证明计算得出结论,或先利用条件特例得出结论,然后再根据条件给出证明或计算. 答案:(1)因为AC 、AD 、AB 两两垂直,建立如图坐标系,则B (2,0,0),D (0,0,2),E (1,1,2),F (2,2,0), 则)0,2,0(),2,1,1(),0,0,2(=-==BF BE DB设平面BEF 的法向量x z y x n -=则),,,(0,02==++y z y ,则可取)0,1,2(=n ,∴向量)1,0,2(=n DB 和所成角的余弦为1010)2(21220222222=-++-+⋅. 即BD 和面BEF 所成的角的余弦1010. (2)假设线段EF 上存在点P 使过P 、A 、C 三点的平面和直线DB 垂直,不妨设EP 与PF 的比值为m ,则P 点坐标为),12,121,121(m m m m m +++++ 则向量=),12,121,121(m m m m m +++++,向量=CP ),12,11,121(mm m m ++-++ 所以21,012)2(12101212==+-++++++m m m m m m 所以. 点评:本题考查了线线关系,线面关系及其相关计算,本题采用探索式、开放式设问方式,对学生灵活运用知识解题提出了较高要求.8. 如图,在三棱锥V ABC -中,VC ABC ⊥底面,AC BC ⊥,D 是AB 的中点,且AC BC a ==,π02VDC θθ⎛⎫=<< ⎪⎝⎭∠.(I )求证:平面VAB ⊥平面VCD ;(II )试确定角θ的值,使得直线BC 与平面VAB 所成的角为π6. 解析:本例可利用综合法证明求解,也可用向量法求解.答案:解法1:(Ⅰ)AC BC a ==∵,ACB ∴△是等腰三角形,又D 是AB 的中点,CD AB ⊥∴,又VC ⊥底面ABC .VC AB ⊥∴.于是AB ⊥平面VCD .又AB ⊂平面VAB ,∴平面VAB ⊥平面VCD .(Ⅱ) 过点C 在平面VCD 内作CH VD ⊥于H ,则由(Ⅰ)知CD ⊥平面VAB . 连接BH ,于是CBH ∠就是直线BC 与平面VAB 所成的角. 依题意π6CBH ∠=,所以在CHD Rt △中,sin 2CH a θ=; 在BHC Rt △中,πsin 62a CH a ==,sin θ=∴. π02θ<<∵,π4θ=∴. 故当π4θ=时,直线BC 与平面VAB 所成的角为π6.解法2:(Ⅰ)以CA CB CV ,,所在的直线分别为x 轴、y 轴、z 轴,建立如图所示的空间直角坐标系,则(000)(00)(00)000tan 222a a C A a B a D V a θ⎛⎫⎛⎫⎪ ⎪ ⎪⎝⎭⎝⎭,,,,,,,,,,,,,,,于是,tan 222a a VD θ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,,,022a a CD ⎛⎫= ⎪⎝⎭u u u r ,,,(0)AB a a =-u u u r ,,. 从而2211(0)0002222a a ABCD a a a a ⎛⎫=-=-++= ⎪⎝⎭u u u r u u u r ,,,,··,即AB CD ⊥.同理2211(0)tan 02222a a AB VD a a a a θ⎛⎫=-=-++ ⎪ ⎪⎝⎭u u u r u u u r ,,,,··即AB VD ⊥.又CD VD D =I ,AB ⊥∴平面VCD . 又AB ⊂平面VAB .∴平面VAB ⊥平面VCD .(Ⅱ)设平面VAB 的一个法向量为()x y z =,,n ,则由00AB VD ==u u u r,··nn .得0tan 0222ax ay a a x y θ-+=⎧⎪⎨+-=⎪⎩,.可取(11)θ=n ,又(00)BC a =-u u u r,,,于是πsin 62BC BC θ===u u u r u u u r n n ··,即sin 2θ=π02θ<<∵,π4θ∴=. 故交π4θ=时,直线BC 与平面VAB 所成的角为π6.解法3:(Ⅰ)以点D 为原点,以DC DB ,所在的直线分别为x 轴、y 轴,建立如图所示的空间直角坐标系,则(000)000000222D A a B a C a ⎛⎫⎛⎫⎛⎫-- ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭,,,,,,,,,,,,0tan 22V a θ⎛⎫- ⎪ ⎪⎝⎭,,,于是0tan 22DV a a θ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,,,002DC ⎛⎫=- ⎪ ⎪⎝⎭u u u r ,,,(00)AB =u u u r ,.从而(00)AB DC =u u u r u u u r ,·0002a ⎛⎫-= ⎪ ⎪⎝⎭,,·,即AB DC ⊥.同理(00)0tan 0AB DV θ⎛⎫== ⎪ ⎪⎝⎭u u u r u u u r ,,·,即AB DV ⊥. 又DC DV D =I , AB ⊥∴平面VCD . 又AB ⊂平面VAB , ∴平面VAB ⊥平面VCD .(Ⅱ)设平面VAB 的一个法向量为()x y z =,,n ,则由00AB DV ==u u u r u u u r ,··n n ,得2022tan 022ay ax az θ⎧=⎪⎨-+=⎪⎩,. 可取(tan 01)n θ=,,,又220BC a a ⎛⎫=-- ⎪ ⎪⎝⎭u u u r ,,, 于是22tan π22sin sin 61tan a BC BC a θθθ===+u u u r u u u r n n ···, 即πππsin 0224θθθ=<<,,∵∴=. 故角π4θ=时, 即直线BC 与平面VAB 所成角为π6.点评:证明两平面垂直一般用面面垂直的判定定理,求线面角一是找线在平面上的射影在直角三角形中求解,但运用更多的是建空间直角坐标系,利用向量法求解考点五 折叠、展开问题9.已知正方形ABCD E 、F 分别是AB 、CD 的中点,将ADE V 沿DE 折起,如图所示,记二面角A DE C --的大小为(0)θθπ<<(I) 证明//BF 平面ADE ;(II)若ACD V 为正三角形,试判断点A 在平面BCDE 内的射影G 是否在直线EF 上,证明你的结论,并求角θ的余弦值分析:充分发挥空间想像能力,重点抓住不变的位置和数量关系,借助模型图形得出结论,并给出证明.解: (I)证明:EF 分别为正方形ABCD 得边AB 、CD 的中点,ADBCVxyAEB CF DG∴EB//FD,且EB=FD,∴四边形EBFD 为平行四边形∴BF//ED.,EF AED BF AED ⊂⊄Q 平面而平面,∴//BF 平面ADE(II)如右图,点A 在平面BCDE 内的射影G 在直线EF 上,过点A 作AG 垂直于平面BCDE,垂足为G,连结GC,GDQ ∆ACD 为正三角形,∴AC=AD. ∴CG=GD. Q G在CD 的垂直平分线上, ∴点A 在平面BCDE 内的射影G 在直线EF 上,过G 作GH 垂直于ED 于H,连结AH,则AH DE ⊥,所以AHD ∠为二面角A-DE-C 的平面角 即G AH θ∠=.设原正方体的边长为2a,连结AF,在折后图的∆AEF中,EF=2AE=2a,即∆AEF 为直角三角形, AG EF AE AF ⋅=⋅.2AG a ∴=在Rt ∆ADE 中, AH DE AE AD ⋅=⋅AH ∴=.GH ∴=,1cos 4GH AH θ== 点评:在平面图形翻折成空间图形的这类折叠问题中,一般来说,位于同一平面内的几何元素相对位置和数量关系不变:位于两个不同平面内的元素,位置和数量关系要发生变化,翻折问题常用的添辅助线的方法是作棱的垂线.关键要抓不变的量.考点六 球体与多面体的组合问题10.设棱锥M-ABCD 的底面是正方形,且MA =MD ,MA ⊥AB ,如果ΔAMD 的面积为1,试求能够放入这个棱锥的最大球的半径.分析:关键是找出球心所在的三角形,求出内切圆半径. 解: ∵AB ⊥AD ,AB ⊥MA , ∴AB ⊥平面MAD ,由此,面MAD ⊥面AC.记E 是AD 的中点,从而ME ⊥AD. ∴ME ⊥平面AC ,ME ⊥EF.设球O 是与平面MAD 、平面AC 、平面MBC 都相切的球. 不妨设O ∈平面MEF ,于是O 是ΔMEF 的内心. 设球O 的半径为r ,则r =MFEM EF S MEF++△2设AD =EF =a,∵S ΔAMD =1. ∴ME =a 2.MF =22)2(aa +, r =22)2(22aa a a +++≤2222+=2-1. 当且仅当a =a2,即a =2时,等号成立.∴当AD =ME =2时,满足条件的球最大半径为2-1.点评:涉及球与棱柱、棱锥的切接问题时一般过球心及多面体中的特殊点或线作截面,把空间问题化归为平面问题,再利用平面几何知识寻找几何体中元素间的关系.注意多边形内切圆半径与面积和周长间的关系;多面体内切球半径与体积和表面积间的关系. 三、方法总结1.位置关系:(1)两条异面直线相互垂直证明方法:○1证明两条异面直线所成角为90º;○2证明两条异面直线的方向量相互垂直.(2)直线和平面相互平行证明方法:○1证明直线和这个平面内的一条直线相互平行;○2证明这条直线的方向向量和这个平面内的一个向量相互平行;○3证明这条直线的方向向量和这个平面的法向量相互垂直.(3)直线和平面垂直证明方法:○1证明直线和平面内两条相交直线都垂直,○2证明直线的方向量与这个平面内不共线的两个向量都垂直;○3证明直线的方向量与这个平面的法向量相互平行.(4)平面和平面相互垂直证明方法:○1证明这两个平面所成二面角的平面角为90º;○2证明一个平面内的一条直线垂直于另外一个平面;○3证明两个平面的法向量相互垂直.2.求距离:求距离的重点在点到平面的距离,直线到平面的距离和两个平面的距离可以转化成点到平面的距离,一个点到平面的距离也可以转化成另外一个点到这个平面的距离.(1)两条异面直线的距离。
立体几何题型及解题方法总结1. 立体几何题型啊,那可是个神奇的领域!有求各种立体图形体积的题型,就像求一个装满水的古怪形状瓶子能装多少水一样。
比如说正方体,正方体的体积公式就是边长的立方。
要是有个正方体边长是3厘米,那它的体积就是3×3×3 = 27立方厘米,简单吧!这类型的题就像是数糖果,一个一个数清楚就行。
2. 还有求立体图形表面积的题型呢。
这就好比给一个形状奇怪的礼物包装纸,得算出需要多少纸才能把它包起来。
像长方体,表面积就是六个面的面积之和。
假如一个长方体长4厘米、宽3厘米、高2厘米,那表面积就是2×(4×3 + 4×2 + 3×2) = 52平方厘米。
哎呀,可别小瞧这表面积,有时候算错一点就像给礼物包了个破纸一样难看。
3. 立体几何里关于线面关系的题型也不少。
这就像在一个迷宫里找路,线和面的关系复杂得很。
比如说直线和平面平行的判定,就像在一个方方正正的房间里,一根直直的杆子和地面平行,只要杆子和地面内的一条直线平行就行。
像有个三棱柱,一条棱和底面的一条棱平行,那这条棱就和底面平行啦,是不是很有趣呢?4. 线面垂直的题型也很重要哦。
这就像是建房子时的柱子和地面的关系,必须垂直才稳当。
判断一条直线和一个平面垂直,就看这条直线是不是和平面内两条相交直线都垂直。
就像搭帐篷,中间那根杆子要和地面上交叉的两根绳子都垂直,帐篷才能稳稳地立起来。
比如一个正四棱锥,它的高就和底面垂直,因为高和底面两条相交的对角线都垂直呢。
5. 面面平行的题型有点像照镜子。
两个平面就像两面镜子,要想平行,得看一个平面内的两条相交直线和另一个平面内的两条相交直线分别平行。
就像有两个一样的盒子,一个盒子里面两条交叉的边和另一个盒子里面对应的两条交叉边平行,那这两个盒子的面就是平行的关系。
想象一下,如果两个平行的黑板,是不是很有画面感?6. 面面垂直的题型就像是打开的书页。
、考点分析基本图形1 •棱柱一一有两个面互相平行,其余各面都是四边形,并且每相邻两个四边形的公共边都互相平行,由这些面所围成的几何体叫做棱柱。
斜棱柱①棱柱棱垂直于底面古严壯底面是正多形正棱柱★夂其他棱柱卅②四棱柱I底面为平行四边形I平行六面体I侧棱垂直于底面[直平行六面体I底面为矩形2. 棱锥棱锥一一有一个面是多边形,其余各面是有一个公共顶点的三角形,由这些面所围成的几何体叫做棱锥。
★正棱锥一一如果有一个棱锥的底面是正多边形,并且顶点在底面的射影是底面的中心,这样的棱锥叫做正棱锥注:球的有关问题转化为圆的问题解决第四讲立体几何题型归类总结长方体底面为正方形正四棱柱侧棱与底面边长相等正方体侧棱底面顶点侧面斜高3.球球的性质:①球心与截面圆心的连线垂直于截面;球心球面半径★②r R2 d2(其中,球心到截面的距离为d、球的半径为R、截面的半径为r)★球与多面体的组合体:球与正四面体,球与长方体,球与正方体等的内接与外切.O1球面积、体积公式: -R3(其中R为球的半径)3平行垂直基础知识网络★★★1 •求异面直线所成的角0 ,90 :解题步骤:一找(作):利用平移法找岀异面直线所成的角;(1)可固定一条直线平移另一条与其相交;(2)可将两条一面直线同时平移至某一特殊位置。
常用中位线平移法二证:证明所找(作)的角就是异面直线所成的角(或其补角)。
常需要证明线线平行;三计算:通过解三角形,求岀异面直线所成的角;2求直线与平面所成的角0 ,90 :关键找“两足”:垂足与斜足解题步骤:一找:找(作)岀斜线与其在平面内的射影的夹角(注意三垂线定理的应用);二证:证明所找(作)的角就是直线与平面所成的角(或其补角)(常需证明线面垂直);三计算:常通过解直角三角形,求岀线面角。
3求二面角的平面角0,解题步骤:一找:根据二面角的平面角的定义,找(作)出二面角的平面角;二证:证明所找(作)的平面角就是二面角的平面角(常用定义法,三垂线法,垂面法);三计算:通过解三角形,求出二面角的平面角。
二、典型例题 考点一:三视图2.若某空间几何体的三视图如图 ____________________ 2所示,则该几何体的体积是3.—个几何体的三视图如图 ____________________ 3所示,则这个几何体的体积为4. 若某几何体的三视图(单位:cm )如图4所示,则此几何体的体积是 _______________ .俯视图俯视图3*正视图左视图第4题第5题5•如图5是一个几何体的三视图,若它的体积是3 3,则a7.若某几何体的三视图(单位:cm )如图所示,则此几何体的体积是8.设某几何体的三视图如图8 (尺寸的长度单位为m,则该几何体的体积为3cmm10. 一个三棱柱的底面是正三角形,侧棱垂直于底面,它的三视图及其尺寸如图图1011.如图11所示,一个空间几何体的主视图和左视图都是边长为体的全面积为_______________ .左视图12.如图12,一个空间几何体的主视图和左视图都是边长为图131的正三角形,俯视图是一个圆,那么几何体的侧面积为第7题9 •一个空间几何体的主视图和左视图都是边长为1的正方形, 俯视图是一个圆, 那么这个几何体的侧面积为10所示(单位cm),则该三棱柱的表面积为1的正方形,俯视图是一个直径为1的圆,那么这个几何正视图13.已知某几何体的俯视图是如图13所示的边长为2的正方形,主视图与左视图是边长为2的正三角形,则其表面积是2cm ) .图1516•图16是一个几何体的三视图,根据图中数据,可得该几何体的表面积是17.如图17, —个空间几何体的主视图、左视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为 这个几何体的体积为 ________________ .18.若一个底面为正三角形、侧棱与底面垂直的棱柱的三视图如图14.如果一个几何体的三视图如图 14所示(单位长度:cm ). 则此几何体的表面积是—2 f厶 □ □主视图主视團正视图俯视图左视图 1,那么9-3-14所示,则这个棱柱的体积为9-3-7,则该棱锥的全面积(单位:图18 考点二—体积、表面积、距离、角—注:1-6体积表面积7-11异面直线所成角12-15线面甭1. __________________________________________________________________________ 将一个边长为a的正方体,切成27个全等的小正方体,则表面积增加了_____________________________________________________ .2. 在正方体的八个顶点中,有四个恰好是正四面体的顶点,则正方体的表面积与此正四面体的表面积的比值为________________3. 设正六棱锥的底面边长为___________________________ 1,侧棱长为J5,那么它的体积为.14•正棱锥的高和底面边长都缩小原来的一,则它的体积是原来的________________ .25•已知圆锥的母线长为8,底面周长为6n,则它的体积是______________________ .6. ___________________________________________________________ 平行六面体AG的体积为30,则四面体AB1CD1的体积等于__________________________________________________________ .7. __________________________________________________________________________________________ 如图7,在正方体ABCD ABCiD中,E,F分别是A D i , GD中点,求异面直线AB与EF所成角的角____________________________ .8.如图8所示,已知正四棱锥S —ABCD侧棱长为■■ 2,底面边长为.3,E是SA的中点,则异面直线BE与SC所成角9.正方体ABCD A BCD'中,异面直线CD和BC'所成的角的度数是________________________的大小为/;:/-----10 •如图9-1-3,在长方体ABCD ABGD1中,已知AB.3BC,BC CC1,则异面直线AA与BC1所成的角是曰,异面直线AB与CD1所成的角的度[X ______________ [? -e 数是图1311. 如图9-1-4,在空间四边形ABCD中,AC BD AC BD,E,F分别是AB、CD的中点,则EF与AC所成角的大小为______________ .12. 正方体AC1中,AB|与平面ABC1D1所成的角为___________________ .13 .如图13在正三棱柱ABC ARG 中, AB AA,则直线CB!与平面AARB所成角的正弦值为 __________________________________ ,14.如图9-3-6,在正方体ABCD —A1B1C1D1中,对角线BD1与平面ABCD所成图9-3-6图9-3-1图715. 如图9-3-1,已知ABC为等腰直角三角形,P为空间一点,且AC BC 5 2, PC AC,PC BC,PC 5,AB的中点为M,则PM与平面ABC所成的角为16. 如图7,正方体ABCD - A1B1C1D1的棱长为1,O是底面A1B1C1D1的中心,贝u O到平面AB C1D1的距离为17. 一平面截一球得到直径是6cm的圆面,球心到这个平面的距离是18•长方体ABCD AB1C1D1的8个顶点在同一个球面上,且AB=2 AD=. 3,AA1 1,则顶点A、B间的球面距离__B10D的角的正切值为4cm,则该球的体积是/I是__________________ .19. 已知点A,B,C,D 在同一个球面上,AB 平面BCD,BC CD,若AB 6, AC 2 13, AD 8,则B,C两点间的球面距离是_______________ .20. 在正方体ABCD —A i B i C i D i中,M为DD 1的中点,0为底面ABCD的中心,P为棱A i B i上任意一点,则直线0P与直线AM所成的角是____________________ .21 .△ABC的顶点B在平面a内,A、C在a的同一侧,AB、BC与a所成的角分别是30 °和45 °,若AB=3 , BC= 4、2,AC=5,则AC与a所成的角为___________ .22 .矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折成一个直二面角B - AC- D,则四面体ABCD的外接球的体积为________________ .23•已知点A,B,C,D在同一个球面上,AB 平面BCD, BC CD,若AB 6, AC 2、i3, AD 8,则B,C两点间的球面距离是______________ .24 •正三棱锥的一个侧面的面积与底面积之比为2: 3,则这个三棱锥的侧面和底面所成二面角的度数为_____________ .25.已知S,代B,C是球0表面上的点,SA 平面ABC,AB BC,SA AB i,BC J2,则球O表面积等于 _________________ .3226•已知正方体的八个顶点都在球面上,且球的体积为—,则正方体的棱长为_______________ .327. 一个四面体的所有棱长都为42,四个顶点在同一球面上,则此球的表面积为_________________ .1.正方体ABCD-A 1B1C1D i,AA i=2,E为棱CC i 的中点.(I)求证:B i D i AE ;(n)求证:AC// 平面B i DE ;(山)求三棱锥A-BDE的体积.2.已知正方体ABCD A 1B 1C 1D 1,O 是底ABCD 对角线的交点.求证:(1 ) C i O //面ABQ ; (2)AC 面AB 1D 1 .图(2)3•如图,PA 矩形ABCD 所在平面,M 、N 分别是AB 和PC 的中点. (I ) (U ) 求证:求证: MN MN //平面PAD ;CD ;(山)PDA 45,求证:MN 平面PCD .4. 如图(1),ABCD 为非直角梯形,点E ,F 分别为上下底AB , 起,得到图(2)(1)若折起后形成的空间图形满足 DF BC ,求证:ADCD 上的动点,且 EF CD 。
现将梯形AEFD 沿EF 折CF ;(2)若折起后形成的空间图形满足A, B,C, D 四点共面,求证:图(1)5.如图,在五面体 ABCDEF 中,FA 平面ABCD,CDAD//BC//FE , AB AD , M 为EC 的中点,1N 为AE 的中点,AF=AB=BC=FE= AD2(I) 证明平面AMD 平面CDE;(II) 证明BN //平面CDE ;6. 在四棱锥P-ABCD中侧面PCD是正三角形,且与底面ABCD垂直,已知菱形ABCD中/ ADC = 60 M是PA的中点,0是DC中点.(1)求证:0M //平面PCB ;(2)求证:PA丄CD ;(3)求证:平面FAB丄平面COM .7. 如图,在四棱锥P—ABCD中,底面ABCD是正方形,侧棱PD丄底面ABCD , PD=DC , E是PC的中点,作EF丄PB交PB于点F.(1)证明PA//平面EDB ; (2)证明PB丄平面EFD8. 正四棱柱ABCD-A i B i C i D i的底面边长是3,侧棱长是3,点E,F分别在BB i,DD i 上,且AE 丄A i B,AF 丄A i D .(1)求证:A i C 丄面AEF ; ⑵求二面角A-EF-B 的大小; ⑶点B i 到面AEF 的距离.考点五异面直线所成的角,线面角,二面角1. 如图,四棱锥P — ABCD 的底面ABCD 为正方形,PD 丄底面ABCD , PD=AD.求证:(1)平面PAC 丄平面PBD ; (2)求PC 与平面PBD 所成的角;2. 如图所示,已知正四棱锥 S — ABCD 则棱长为..2,底面边长为 3 , E 是SA 的中点,则异面直线 BE 与SC 所成角的大小3. 正六棱柱 ABCDEF - A i B i C i D i E i F i 底面边长为4.若正四棱锥的底面边长为 2 ■. 3 cm ,体积为4cm 3,则它的侧面与底面所成的二面角的大小是(3)若PA AB AC a ,求三棱锥E -ACD 的体积;5.如图,在底面为平行四边形的四棱锥 AB P -ABCD 中, >AC , PA 平面ABCD ,且PA = AB ,点E 是PD 的中点.(1)求证:AC PB ;( 2)求证:PB// 平面AEC ; (4)求二面角 E -AC - D 的大小.E i D 与BC i 所成的角是1 .已知直线I、m平面a、B,且I丄a, m B,给出下列四个命题:(1 )a//B,_则I丄m(2)若1丄m则a//B(3 )若a丄B ,_则I // m(4 )若1 // m,则a 丄B其中正确的是2. m、n是空间两条不同直线,、是空间两条不同平面,下面有四个命题①m , n1,1| m n;② m n,,m③m n,| n ;④m ,m n,其中真命题的编号是(写岀所有真命题的编号)。