安庆市高三模拟考试(三模).docx

安庆市高三下学期语文第三次模拟考试试卷姓名:________ 班级:________ 成绩:________一、选择题 (共3题；共8分)1. （4分）(2017·德州模拟) 阅读下面的文字，完成问题。

在我们的日常语言中，真、善、美这三个词常常是相题并论的。

仔细寻思后不难发现，自然的根本性质是真，人生的根本意义为善，艺术的根本价值在于美。

如此看来，真、善、美之间似乎并没有直接的联系，但是在审美的意义上，自然于潜移默化中感发和（涤荡/激荡）着人的情性与思绪，也安顿和抚慰着人的心灵；人则通过审美的思维方式达到______的合谐境界。

可以说，一片自然山水就是一个人诗意栖居的心灵寓所与精神家园。

更为重要的是，每个人的人生都是一道（独特/独到）的风景，具有审美价值，而且整个审美活动的出发点和落脚点就在于（关照/观照）人的生存境况，并努力成就自由完美的人生，使人生得以丰富地展开。

那么，审美人生的具体内容是什么呢？在我看来，审美意义上的人生，一方面是指主体以自然的感性生命为基础，又不滞于感性生命，由切身感悟和内省体验而达到与宇宙精神合一的体道境界；另一方面，主体还以人的社会特质为基础，又不滞于人的社会特质，从心灵中获得精神自由的境界。

这种体道的境界与精神自由的境界在审美思维方式上的贯通合一，即审美的人生境界，这是对现实人生的积极______。

（1）文中划线字的注音和划线词语的字形，都正确的一项是（）A . 抚（fǔ）合谐B . 寓（yù）相题并论C . 栖（xī）思绪D . 省（xǐng）贯通合一（2）依次选用文中括号中的词语，最恰当的一项是（）A . 涤荡独到观照B . 激荡独特观照C . 涤荡独特关照D . 激荡独到关照（3）在文中两处横线上依次填入词句，衔接最恰当的一项是（）A . 物我统一，情景交融提升、拓展与超越B . 物我统一，情景交融拓展、提升与超越C . 情景交融、物我统一拓展、提升与超越D . 情景交融、物我统一提升、拓展与超越。

安徽省安庆市高三数学第三次模拟考试卷理（扫描版）2013年安庆市高三模拟考试（三模） 数学试题（理科）参考答案及评分标准一、选择题 题号 1 2 3 4 5 67 8 9 10 选项 B A C C DD C C A C1．解析：∵i i i i8)2()1()11(366=-=-=+，故选B 。

2．解析：x x x x g 2cos )22sin(]3)12(2sin[)(=+=++=πππ，故选A 。

3．解析：3lg lg lg 963=++a a a ⇒10101063363963=⇒=⇒=a a a a a ，∴10026111==a a a ，故选C 。

4．解析：当 x 为直线， y 、 z 为平面时，x 可能在平面y ；故A 错； 当 x 、 y 、 z 为平面时，x ， y 可能相交； 当 x 、 y 为直线， z 为平面时， x ∥ y 当 x 、 y 、 z 为直线时，x ， y 可能相交也可能异面； 故选C 。

5．解析：由100111≤<⇒≥-⇒≥x xx x ，100)1ln(<≤⇒≤-x x ， 故选D 。

6．解析：4(4x tt y t=⎧⎪⎨=⎪⎩为参数），03=+-⇒y x ，ρθ=⇒2)2(22=-+y x ，∴圆心到直线的距离为2223<-=d故选D 。

7．解析：∵021=⋅PF PF ，∴21PF PF ⊥，不妨设点P 在右支上，∴22121222212||||2||||4||||b PF PF aPF PF c PF PF =⇒⎩⎨⎧=-=+，∴221||||2121b PF PF S F PF ==∆，故选C 。

8．解析：由12123)(23++-=x x x x f 2133)('2+-=⇒x x x f21036)(''=⇒=-=⇒x x x f ，∴1)21(=f ，∴)(x f 的对称中心为)1,21(，∴2)()1(=+-x f x f ，∴2013)20142013()20142()20141(=+++f f f ，故选C 9．解析：74cos72cos 7cos πππ⋅⋅=S 817sin878sin 7sin 274cos 72cos 7cos 7sin233-==⋅⋅=πππππππ，故选A 。

2024届安徽省安庆市高三下学期三模考试全真演练物理试题一、单项选择题（本题包含8小题，每小题4分，共32分。

在每小题给出的四个选项中，只有一项是符合题目要求的）(共8题)第(1)题如图甲所示，光滑的绝缘水平桌面上静止着一松软的不可伸长的带电绳，总电荷量为（q>0），绳上的电荷和绳的质量都均匀分布，绳的两端分别固定在M、N两点的绝缘钉上，绳NP段的长度为总长度的。

若在空间中加上垂直于M、N连线且与桌面平行的匀强电场，电场强度大小为E，带电绳静止时如图乙所示，此时绳上P点的张力大小为，则此时处于M点的绝缘钉受到的绳的拉力大小为（ ）A．B．C．D．qE第(2)题伽利略曾设计如图所示的一个实验，将摆球拉至M点放开，摆球会达到同一水平高度上的N点．如果在E或F处钉子，摆球将沿不同的圆弧达到同一高度的对应点；反过来，如果让摆球从这些点下落，它同样会达到原水平高度上的M点．这个实验可以说明，物体由静止开始沿不同倾角的光滑斜面（或弧线）下滑时，其末速度的大小A．只与斜面的倾角有关B．只与斜面的长度有关C．只与下滑的高度有关D．只与物体的质量有关第(3)题如图所示，理想变压器输入电压保持不变，副线圈接有两个灯泡和一个定值电阻R，电流表、电压表均为理想电表。

开关S原来是断开的，现将开关S闭合，则（）A．电流表的示数减小B．电压表的示数增大C．原线圈输入功率减小D．电阻R消耗的电功率增大第(4)题均匀带电的球壳在球外空间产生的电场等效于电荷集中于球心处的点电荷产生的电场。

如图所示，在绝缘球球面上均匀分布正电荷，总电荷量为q；在剩余球面AB上均匀分布负电荷，总电荷量是。

球半径为R，球心为O，CD为球面的对称轴，在轴线上有M、N两点，且，。

已知球面在M点的场强大小为E，静电力常量为k，则N点的场强大小为（ ）A．E B．2E C．D．第(5)题在如图所示的四种电场中，分别标记有a、b两点。

其中a、b两点电场强度大小相等、方向相反的是（ ）A．甲图中与点电荷等距的a、b两点B．乙图中两等量异种电荷连线的中垂线上与连线等距的a、b两点C．丙图中两等量同种电荷连线的中垂线上与连线等距的a、b两点D．丁图中非匀强电场中的a、b两点第(6)题如图，A、B两点分别位于大、小轮的边缘上，C点位于大轮半径的中点，大轮的半径是小轮半径的2倍，它们之间靠摩擦传动，接触面不打滑。

2023届安徽省安庆市一中高三三模理综生物试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．双歧杆菌和乳酸菌是人和动物肠道菌群的重要组成成员，它们能抑制有害细菌的生长。

下列有关说法正确的是（）A．细胞壁是乳酸菌和双歧杆菌的系统边界B．拟核是乳酸菌和双歧杆菌的遗传控制中心C．乳酸菌代谢产生的CO2能调节肠道的pHD．肠道中的乳酸菌和双歧杆菌构成一个群落2．人类癌细胞和正常细胞一样，每条染色体的两端都有一段特殊序列的DNA—蛋白质复合体，称为端粒。

细胞每分裂一次，端粒就会缩短一截。

一旦端粒缩短到一定程度，细胞就会进入衰老状态进而死亡，但癌细胞却可以无限增殖，成为“不死细胞”。

人类癌细胞和正常细胞一样，能够进行有氧呼吸，但癌细胞在氧气充足时，也主要依赖无氧呼吸产生ATP，这一现象称为“瓦堡效应”。

下列相关说法错误的是（）A．正常细胞通常会随着分裂次数的增多而衰老B．癌细胞中可能存在特殊结构能够及时修复端粒C．癌细胞在增殖过程中核糖体和线粒体活动增强D．癌症患者的肿瘤组织区域内可检测到大量乳酸3．下列关于“噬菌体侵染大肠杆菌的实验”的叙述，正确的是（）A．用同时含有32P和35S的噬菌体侵染大肠杆菌B．搅拌是为了使大肠杆菌体内的噬菌体释放出来C．噬菌体在自身RNA聚合酶作用下转录出RNAD．离心是为了沉淀培养液中被侵染的大肠杆菌4．甲型流感病毒表面有血凝素（HA）和神经氨酸酶（NA）等蛋白，HA分为H1~H18等亚型，NA分为N1~N11等亚型，HA和NA可以随机组合，宿主有人、猪及禽类等。

甲型流感病毒的表面抗原经常发生微小变异，从而能够逃避体内免疫系统的识别。

下列相关说法错误的是（）A．不同地区流行的甲型流感病毒可能不同B．甲型流感病毒的清除需要细胞免疫参与C．一个B细胞可接受多种甲型流感病毒刺激D．接种甲型流感疫苗后仍可感染甲型流感病毒5．研究者以拟南芥根段作为组织培养材料，探讨了激素诱导愈伤组织分化生芽的机制。

安庆2022届高三第三次模拟考试文科数学（答案在最后）本试卷总分150分，考试时间120分钟注意事项：1.答卷前，考试务必将自己的姓名､准考证号填写在答题卡上.2.回答选择题时，选出每小题答案后，用铅笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号.回答非选择题时，将答案写在答题卡上，写在本试卷上无效.3.考试结束后，将本试卷和答题卡一并交回.第Ⅰ卷一､选择题：本小题12小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}=|1A x x ≥，1=|32B y y ⎧⎫≤<⎨⎬⎩⎭那么A B = （）A.1,12⎡⎫⎪⎢⎣⎭ B.(]1,3 C.1,32⎛⎫ ⎪⎝⎭D.[)1,3【答案】D 【解析】【分析】集合A 和集合B 都是数集，由交集运算和区间的表示易得D 选项正确【详解】{}=|1A x x ≥ ，1B=|32y y ⎧⎫≤<⎨⎬⎩⎭{}=|13A B x x ∴⋂≤<，该集合用区间表示为[)1,3.故选：D.2.若复数1i z =+，则下列说法正确的是（）A.复数z 的虚部为iB.z 在复平面对应点位于第一象限C.复数i z -为纯虚数D.i z =【答案】B 【解析】【分析】A 选项，根据实数概念得到z 的虚部为1；B 选项，写出复数对应点的坐标，得到其所在象限；C选项，计算得到i z -为实数；D 选项，计算出i 1i z =-+=D 错误.【详解】A 选项，复数z 的虚部为1，A 错误；B 选项，z 在复平面对应点坐标为()1,1，故z 在复平面对应点位于第一象限，B 正确；C 选项，复数i 1i i 1z -=+-=，故i z -为实数，C 错误；D 选项，()2i 11i i i i i z ===-+=+=+，D 错误.故选：B 3.命题:sin 0p θ≠是()2πZ k k θ≠∈的充要条件；命题q ：函数sin y x =在,22ππx ⎡⎤∈-⎢⎥⎣⎦不是单调函数，则下列命题是真命题的是（）A.p q ∧B.()()p q ⌝∧⌝ C.()p q⌝∨ D.()p q ∨⌝【答案】C 【解析】【分析】先得到p 为假命题，q 为真命题，进而对四个选项一一判断.【详解】sin 0θ≠，解得()11πZ k k θ≠∈，由于()()11πZ 2πZ k k k k θθ≠∈⇒≠∈，但()2πZ k k θ≠∈⇒()11πZ k k θ≠∈，故:sin 0p θ≠不是()2πZ k k θ≠∈的充要条件，p 为假命题，由于()()sin sin f x x x f x -=-==，故sin y x =在,22ππx ⎡⎤∈-⎢⎥⎣⎦上为偶函数，故sin y x =在,22ππx ⎡⎤∈-⎢⎥⎣⎦上不单调，q 为真命题，则p q ∧为假命题，A 错误；()()p q ⌝∧⌝为假命题，B 错误；()p q ⌝∨为真命题，C 正确；()p q ∨⌝为假命题，D 错误.故选：C4.2022年4月23日是第27个世界读书日，以引导全民阅读为出发点，弘扬中华优秀文化，传承中华悠久文明，我校高一年级部举行了“培养阅读习惯，分享智慧人生”为主题的读书竞赛活动.如图所示的茎叶图是甲､乙两个代表队各7名队员参加此次竞赛的成绩，乙队成绩的众数为81m +，则下列关于这两个代表队成绩的叙述中，其中错误的是（）A.甲队的众数大于乙队的众数B.甲队的中位数大于乙队的中位数C.甲队的平均数小于乙队的平均数D.甲队的方差小于乙队的方差【答案】D 【解析】【分析】由茎叶图中数据通过计算可得甲队的众数、中位数均大于乙队,甲队的平均数小于乙队的平均数，根据数据波动情况可判断甲队的方差大于乙队的方差.【详解】根据茎叶图可知，甲队的众数为85，乙队的众数为84，所以甲队的众数大于乙队的众数，A 正确；易知甲队的中位数为85，乙队的中位数为84，所以甲队的中位数大于乙队的中位数，B 正确；乙队的众数为84，所以8184m +=，即3m =，甲队的平均数为()17081848585859383.37++++++≈，乙队的平均数为()17984848486879385.37++++++≈，所以甲队的平均数小于乙队的平均数，C 正确；由茎叶图中的数据分步可知，甲队数据偏离平均数的波动性更大，而乙队数据相对比较稳定，因此甲队的方差大于乙队的方差，即D 错误.故选：D5.已知直平行六面体1111ABCD A B C D -中，12,60AA AB BC BAD ===∠=︒，则直线1BC 与DB 所成角的余弦值为（）A.4B.12C.14D.0【答案】A 【解析】【分析】作出辅助线，建立空间直角坐标系，写出点的坐标，求出直线1BC 与DB 所成角的余弦值.【详解】取AB 的中点F ，连接DF ，因为2,60AB BC BAD ︒==∠=，所以2AB AD ==，故ABD △为等边三角形，故DF ⊥AB ，所以DF ⊥CD ，又平行六面体1111ABCD A B C D -为直平行六面体，故以D 为坐标原点，1,,DF DC DD 所在直线分别为,,x y z 轴，建立空间直角坐标系，则())()10,0,0,,0,2,2D BC ，设直线1BC 与DB 所成角的大小为θ，则111cos cos ,4BC DB BC DB BC DBθ⋅=====⋅.1BC 与DB 所成角的余弦值为4.故选：A 6.若1cos 64x π⎛⎫-= ⎪⎝⎭，则sin 26x π⎛⎫+= ⎪⎝⎭（）A.158B.78C.158-D.78-【答案】D 【解析】【分析】利用诱导公式和二倍角公式化简，即sin 2sin 2cos 26626x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫+=-+=- ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦22cos 16x π⎛⎫=-- ⎪⎝⎭，代值计算即可【详解】解：因为1cos 64x π⎛⎫-= ⎪⎝⎭，所以sin 2sin 2cos 26626x x x ππππ⎡⎤⎛⎫⎛⎫⎛⎫+=-+=- ⎪ ⎪ ⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦22cos 16x π⎛⎫=-- ⎪⎝⎭21214⎛⎫=⨯- ⎪⎝⎭78=-．故选：D ．7.某地为方便群众接种新冠疫苗，开设了A ，B ，C ，D 四个接种点，每位接种者可去任一个接种点接种．若甲，乙两人去接种新冠疫苗，则两人不在同一接种点接种疫苗的概率为（）A.12B.23C.34 D.14【答案】C 【解析】【分析】根据题意列出甲，乙两人去A ，B ，C ，D 四个接种点接种新冠疫苗的所有选择，然后再求出甲，乙两人不在同一个接种点接种的情况有多少种，从而可求出概率.【详解】甲，乙两人去A ，B ，C ，D 四个接种点接种新冠疫苗的所有选择共有16种，分别为：AA ，AB ，AC ，AD ，BA ，BB ，BC ，BD ，CA ，CB ，CC ，CD ，DA ，DB ，DC ，DD ；其中两人不在同一个接种点接种的情况有12种，从而有123164P ==.故选：C ．8.设变量x ，y 满足约束条件211y x y x y ≤⎧⎪+≥⎨⎪-≤⎩，则目标函数313+⎛⎫= ⎪⎝⎭x y z 的最大值为（）A.1113⎛⎫ ⎪⎝⎭B.313⎛⎫ ⎪⎝⎭C.3D.4【答案】C 【解析】【分析】作出变量x，y满足约束条件211yx yx y≤⎧⎪+≥⎨⎪-≤⎩可行域，然后将求313+⎛⎫= ⎪⎝⎭x yz的最大值，转化为求u＝3x＋y的最小值求解．【详解】变量x，y满足约束条件211yx yx y≤⎧⎪+≥⎨⎪-≤⎩可行域如图所示阴影部分:目标函数313+⎛⎫= ⎪⎝⎭x yz，设u＝3x＋y，欲求313+⎛⎫= ⎪⎝⎭x yz的最大值，等价于求u＝3x＋y的最小值．u＝3x＋y可化为y＝－3x＋u，平移直线y＝－3x，当直线y＝－3x＋u经过点B(－1，2)时，纵截距u取得最小值u min＝3×(－1)＋2＝－1，所以313+⎛⎫= ⎪⎝⎭x yz的最大值1133z-⎛⎫==⎪⎝⎭，故选：C.9.正项等比数列{}n a中，3122a a a=+，若2116m na a a=，则41m n+的最小值等于（）A.1B.35 C.136 D.32【答案】D【解析】【分析】设出等比数列的公比，得到方程，求出公比2q=，从而求出6m n+=，再利用基本不等式“1”的妙用求出最小值.【详解】设{}n a的公比为q，则21112a q a a q=+，因为10a>，所以220q q--=，解得2q=或1-（舍去），11222111122216m n m nm na a a a a a--+-=⋅⋅⋅=⋅=，故24m n+-=，即6m n+=，()4114114134156662n mm nm n m n m n⎛⎛⎫⎛⎫+=++=++≥+=⎪ ⎪⎝⎭⎝⎭⎝，当且仅当4n mm n =，即4,2m n ==时，等号成立，故41m n +的最小值等于32故选：D10.已知定义在R 上的函数()(),1f x f x +是偶函数，()2f x +是奇函数，则()2022f 的值为（）A.0B.1C.2D.3【答案】A 【解析】【分析】根据已知条件可知()f x 关于点()2,0中心对称，结合偶函数定义可推导得到()f x 的周期，根据周期性和奇偶性可得()()202202=f f =.【详解】()1f x+Q 为偶函数，()()1=1f x f x ∴+-()f x \的图像关于1x =对称，()()2f x f x ∴+=-；()2f x + 是奇函数，()()+22f x f x ∴-=-+，可知()f x 关于点()2,0中心对称，()()22f f ∴=-()20f ∴=，()()()()42,2,f x f x f x f x ∴+=-+∴+=-()()()()()42,f x f x f x f x ∴+=-+=--=()f x \是周期为4的周期函数，()()()20224505+220f f f ∴=⨯==.故选：A.11.已知双曲线2222:1(0,0)x y C a b a b-=>>的左、右焦点坐标分别为12,F F ，过1F 作圆222x y a +=的切线交C 的右支于A 点.若122F F F A =，则C 的离心率为（）A.B.3C.53D.【答案】C 【解析】【分析】作1OD F A ⊥垂足为D ，由题意12cos bAF F c∠=，在12F F A △中，由余弦定理得222112212112cos 2F A F F F AAF F F A F F +-∠=⋅，化简得223250c ac a +-=，即可得解.【详解】作1OD F A ⊥垂足为D ，由题意OD a =，1OF c =，则1F D b ==，∴12cos b AF F c∠=，122F F F A =，∴22F A c =，122F A a c =+，在12F F A △中，()()222211221211222cos 222222a c F A F F F Aa c AF F F A F F a c c c++-+∠===⋅+⋅，∴2a c bc c+=，结合222b c a =-可得223250c ac a +-=，∴23250e e +-=，由1e >可得53e =.故选：C.【点睛】本题考查了双曲线离心率的求解，考查了运算能力，属于中档题.12.当1a <时，已知()f x ax a =-，()()21xg x x e =-，若存在唯一的整数0x ，使得()()00g x f x <成立，则a 的取值范围是（）A.3[,1)2e -B.33[,)24e -C.33[,)2e 4D.3[,1)2e【答案】D 【解析】【分析】根据题设条件，问题转化为存在唯一整数0x 使得点00(,())x g x 在直线y ax a =-的下方，对()g x 求导并探讨其图象及性质，再作出()g x 图象及直线y ax a =-，结合图形即可得解.【详解】由题意知，存在唯一整数0x 使得点00(,())x g x 在直线y ax a =-的下方，()()21x g x e x '=+，12x <-时()0g x '<，12x >-时()0g x '>，即()g x 在1(,]2-∞-上递减，在1[,)2-+∞上递增，min 1()(2g x g =-=，直线y ax a =-恒过定点()1,0且斜率为a ，1a <，如图：又(0)1g =-，(1)g e =，(0)1,(1)0f a f =->-=，于是有(0)(0),(1)(1)g f g f <>，符合题意的唯一整数为0，观察图形得，3(1)(1)2g f a e-≥-⇔-≥-，即32a e ≥，从而得312a e ≤<，所以a 的取值范围是3[,1)2e故选：D第Ⅱ卷二､填空题：本大题共4小题，每小题5分，共20分.13.设A 、B 为曲线C ：24x y =上两点，A 与B 的横坐标之和为4，则直线AB 的斜率______．【答案】1【解析】【分析】先设()11,A x y 、()22,B x y ，将A 、B 两点坐标代入抛物线方程，两式作差整理，即可得出直线AB 的斜率.【详解】设()11,A x y 、()22,B x y ，因为A 、B 为曲线C ：24x y =上两点，所以21122244x y x y ⎧=⎪⎪⎨⎪=⎪⎩，则()()2212121212444x x x x x x y y -+-=-=，又A 与B 的横坐标之和为4，即124x x +=，因此直线AB 的斜率为12121214AB y yx x k x x -+===-.故答案为：1.14.已知单位向量21,e e 的夹角为1212π,,43a e eb e e λ=+=- ，若a b ⊥ ，则实数λ=___________.【答案】27-【解析】【分析】利用向量数量积公式可得112402a b λλ⋅=-+-=，即可解出实数λ的值.【详解】根据题意可得121== e e ，且1212π1cos 32e e e e ⋅=⋅= ；由a b ⊥ 可得0a b ⋅= ，即()()212121121222144240241e e e e e e e e e e λλλλλ=-⋅+⋅+-=-+=-- ，解得27λ=-.故答案为：27-15.函数()π2πcos 21,33f x x x x ⎛⎫⎡⎤=+-∈-⎪⎢⎥⎣⎦⎝⎭的取值范围是___________.【答案】198⎡-⎢⎣【解析】【分析】先化简()f x ，再根据余弦函数和二次函数的性质求解即可.【详解】()2cos 212cos 11f x x x x x =+-=-+-22cos 2x x =+-，因为π2π,33x ⎡⎤∈-⎢⎥⎣⎦，1cos ,12x ⎡⎤∈-⎢⎥⎣⎦，令cos t x =，1,12t ⎡⎤∈-⎢⎥⎣⎦，所以()222f t t =+-，对称轴为224t =-=-⨯，因为()f t 在1,24t ⎡∈--⎢⎣⎦上单调递减，在14t ⎡⎤∈-⎢⎥⎣⎦上单调递增，所以()2min19224448f t f ⎛⎛⎛=-=⨯-+--=- ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，()()max 122f t f ==+=所以函数()π2πcos 21,33f x x x x ⎛⎫⎡⎤=+-∈- ⎪⎢⎥⎣⎦⎝⎭的取值范围是198⎡-⎢⎣.故答案为：198⎡-⎢⎣.16.在三棱锥-P ABC 中，ABC 是边长为2的正三角形，,,PA PB PC E F ==分别是,PA AB 的中点，且CE EF ⊥，则三棱锥-P ABC 外接球的表面积为___________.【答案】6π【解析】【分析】作出辅助线，证明出,,PA PB PC 两两垂直，将三棱锥外接球转化为以,,PA PB PC 为长，宽，高的长方体的外接球，进而求出外接球半径和表面积.【详解】取AC 的中点N ，连接,PN BN ，因为ABC 是边长为2的正三角形，PA PC =，所以,PN AC BN AC ⊥⊥，因为PN BN N Ç=，,PN BN ⊂平面BPN ，所以AC ⊥平面BPN ，因为BP ⊂平面BPN ，所以AC ⊥BP ，因为,E F 分别是,PA AB 的中点，所以EF 是ABP 的中位线，故//EF PB ，因为CE EF ⊥，所以CE PB ⊥，因为,CE AC ⊂平面PAC ，CE AC C = ，所以PB ⊥平面PAC ，因为,PA PC ⊂平面PAC ，所以PB ⊥PA ，PB ⊥PC ，因为2AB BC ==，PA PB PC ==，由勾股定理得PA PB PC ===因为2AC =，所以222PA PC AC +=，由勾股定理逆定理可得PA ⊥PC ，所以,,PA PB PC 两两垂直，故棱锥-P ABC 外接球即为以,,PA PB PC 为长，宽，高的长方体的外接球，设外接球半径为R ，则2R ==，解得2R =，则三棱锥-P ABC 外接球的表面积为24π6πR =.故答案为：6π三､解答题：本大题70分.解答应写出文字说明､证明过程或演算步骤，第17-21题为必考题，每个试题考生都必须作答.第22､23题为选考题，考生根据要求作答.（一）必考题：60分.17.△ABC 中，内角A 、B 、C 的对边分别为a 、b 、c ，D 是AC 的中点，已知平面向量m 、n满足()sin sin ,sin sin m A B B C =-- ，(),n a b c =+ ，m n ⊥ ．（1）求A ；（2）若BD =，2b c +=ABC 的面积．【答案】（1）3A π=（2）2【解析】【分析】（1）先利用正弦定理角化边得到222b c a bc +-=，再借助余弦定理即可求出A ；（2）先利用余弦定理得到224212c b bc +-=，再化简为()22612b c bc +-=，即可求出6bc =，再利用三角形面积公式求解即可.【小问1详解】∵()sin sin ,sin sin m A B B C =-- ，(),n a b c =+ ，m n ⊥ ，∴()()()sin sin sin sin 0A B a b B C c -++-=．∴()()()0a b a b b c c -++-=，即222b c a bc +-=．∴2221cos 22b c a A bc +-==．∵0A π<<，∴3A π=．【小问2详解】在△ABD 中，由BD =，3A π=和余弦定理，得2222232cos BD AB AD AB AD A AB AD AB AD ==+-⋅=+-⋅．∵D 是AC 的中点，∴2b AD =∴22322b b c c ⎛⎫+-⨯= ⎪⎝⎭，化简得224212c b bc +-=，即()22612b c bc +-=．∵2b c +=∴(2612bc -=，解得6bc =．∴11333sin sin 22342ABC S bc A bc π==== ．∴△ABC 的面积为332．18.如图，O 是圆锥底面圆的圆心，AB 是圆O 的直径，PAB 为直角三角形，C 是底面圆周上异于,A B的任一点，D 是线段AC 的中点，E 为母线PA 上的一点，且2PE EA =.（1）证明：平面POD ⊥平面PAC ；（2）若2AC BC ==，求三棱锥P ODE -的体积.【答案】（1）证明见解析；（2【解析】【分析】（1）由圆锥的性质可知，PO ⊥底面圆，再根据线面垂直的性质得出AC PO ⊥，由AB 为直径得出AC BC ⊥，再根据中位线的性质得出OD AC ⊥，最后利用面面垂直的判定定理，即可证明平面POD ⊥平面PAC ；（2）在PD 上取点F ，使得2PF FD =，连接EF ，结合题意可知//EF AC ，从而有EF ⊥平面POD ，得出EF 为三棱锥E POD -的高，最后利用等体积法和三棱锥的体积公式，即可求出三棱锥P ODE -的体积.【小问1详解】证明：由圆锥的性质可知，PO ⊥底面圆，又AC 在底面圆O 上，所以AC PO ⊥，又因为C 在圆O 上，AB 为直径，所以AC BC ⊥，又点O D ，分别为AB AC ，的中点，所以//OD BC ，所以OD AC ⊥，又OD PO O = ，且OD PO ⊂，平面POD ，所以AC ⊥平面POD ，又AC ⊂平面PAC ，所以平面POD ⊥平面PAC .【小问2详解】解：由题可知，2AC BC ==，则12AD AC ==，如图，在PD 上取点F ，使得2PF FD =，连接EF ，由题知2PE EA =，所以//EF AC ，所以22333EF AD ==，又因为AC ⊥平面POD ，所以EF ⊥平面POD ，所以EF 为三棱锥E POD -的高，又232AC BC ==，，所以224AB AC BC =+=，又因为PAB 为等腰直角三角形，所以122PO AB ==，又PO OD ⊥，所以11··21122POD S PO OD ==⨯⨯= ，而11233··13339P ODE E POD POD V V EF S --===⨯⨯= ，所以三棱锥P ODE -2319.安庆某农场主拥有两个面积都是220亩的农场——加盟“生态农场”与“智慧农场”，种植的都是西瓜，西瓜根据品相和质量大小分为优级西瓜､一级西瓜､残次西瓜三个等级.农场主随机抽取了两个农场的西瓜各100千克，得到如下数据：“生态农场”优级西瓜和一级西瓜共95千克，两个农场的残次西瓜一共20千克，优级西瓜数目如下：“生态农场”20千克，“智慧农场”25千克.（1）根据所提供的数据，完成下列22⨯列联表，并判断是否有95%的把握认为残次西瓜率与农场有关？农场非残次西瓜残次西瓜总计生态农场智慧农场总计（2）种植西瓜的成本为0.5元/千克，且西瓜价格如下表：等级优级西瓜一级西瓜残次西瓜价格（元/千克） 2.5 1.50.5-（无害化处理费用）①以样本的频率作为概率，请分别计算两个农场每千克西瓜的平均利润；②由于农场主精力有限，决定售卖其中的一个农场，请你根据以上数据帮他做出决策.（假设两个农场的产量相同）参考公式：()()()()22()n ad bc K a b c d a c b d -=++++，其中n a b c d =+++.附表：()20P K k ≥0.1000.0500.0100.0010k 2.7063.841 6.63510.828【答案】（1）答案见解析（2）答案见解析【解析】【分析】（1）根据题目中提供数据即可完成表格，代入计算可得2 5.56 3.841K ≈>，即可得出结论；（2）①分别计算出两农场三种等级的西瓜不同利润盈利的频率，再由期望值公式即可求得结果；②根据两农场每千克西瓜的平均利润的大小可知，售卖利润较低的即可.【小问1详解】根据题意完成22⨯列联表如下：农场非残次西瓜残次西瓜总计生态农场955100智慧农场8515100总计18020200所以可得22200(9515855) 5.56 3.84110010018020K ⨯-⨯=≈⨯⨯⨯>，参考附表可知有95%的把握认为残次西瓜率与农场有关.【小问2详解】①对于“生态农场”，抽到优级西瓜即盈利2元的频率为0.2，抽到一级西瓜即盈利1元的频率为0.75，盈利1-元的频率为0.05；所以“生态农场”农场每千克西瓜的平均利润为20.210.7510.05 1.1⨯+⨯-⨯=（元）；对于“智慧农场”，抽到优级西瓜即盈利2元的频率为0.25，抽到一级西瓜即盈利1元的频率为0.6，盈利1-元的频率为0.15；所以“智慧农场”农场每千克西瓜的平均利润为20.2510.610.150.95⨯+⨯-⨯=（元）；②由于两个农场的产量相同，所以“生态农场”的利润更大，应该售卖“智慧农场”.20.已知椭圆2222:1(0)x y C a b a b +=>>过点()(),0,0,A a B b --两点，椭圆的离心率为32，O 为坐标原点，且1OAB S = .（1）求椭圆C 的方程；（2）设P 为椭圆C 上第一象限内任意一点，直线PA 与y 轴交于点M ，直线PB 与x 轴交于点N ，求证：四边形ABNM 的面积为定值.【答案】（1）2214x y +=（2）证明见解析【解析】【分析】（1）根据离心率和1OAB S = 可解得224,1a b ==，可写出椭圆C 的方程；（2）设()00,P x y 分别求出直线PA ，PB 的方程并解出,M N 的坐标，可得四边形ABNM 的面积122S AN BM =⋅=.【小问1详解】根据题意可知32c e a ==，又112OAB b S a == ，即可得2ab =，结合222a b c =+，解得2224,1,3a b c ===；即椭圆C 的方程为2214x y +=.【小问2详解】证明：由（1）可知()()2,0,0,1A B --，如下图所示：设()00,P x y ，且000,0x y >>；易知直线PA 的斜率002PA y k x =+，所以PA 的直线方程为()0022y y x x =++；同理直线PB 的斜率001PB y k x +=，所以PB 的直线方程为0011y y x x +=-；由题意解得000020,,,021y x M N x y ⎛⎫⎛⎫ ⎪ ⎪++⎝⎭⎝⎭；所以可得000022,112x y AN BM y x =+=+++，四边形ABNM 的面积()()()()2220000000000000000002224448411212212221222x y x y x y x y x y S AN BM y x x y x y x y ++⎛⎫⎛⎫+++++=⋅=++== ⎪⎪+++++++⎝⎭⎝⎭又220014x y +=，可得220044x y +=，故()()()()220000000000000000000000000042244484444842222222222x y x y x y x y x y x y x y S x y x y x y x y x y x y ++++++++++++====+++++++++，即四边形ABNM 的面积为定值.21.已知函数()x f x e x a =--，对于x ∀∈R ，()0f x ≥恒成立.（1）求实数a 的取值范围；（2）证明：当4 0,x π⎡⎤∈⎢⎥⎣⎦时，cos tan +≤x x x e .【答案】（1）(],1-∞；（2）证明见解析.【解析】【分析】（1）利用参数分离法可知x a e x ≤-，构造函数()xg x e x =-，即()min a g x ≤，利用导数研究函数的最小值即可得解；（2）由（1）得1x e x ≥+恒成立，将不等式的证明转化为证cos tan 1x x x ++≤，构造函数()cos tan 1h x x x x =+--，即证()max 0h x ≤，利用导数研究函数的单调性及最值即可.【详解】（1）由0x e x a --≥恒成立，得x a e x ≤-对x ∀∈R 恒成立.令()x g x e x =-，()1xg x e '=-，令()0g x '=，得0x =当0x >，()0g x '>，()g x 单调递增；当0x <，()0g x '<，()g x 单调减，所以()()min 01g x g ==.故所求实数a 的取值范围为(],1-∞.（2）证明：由（1）得1x e x ≥+恒成立，要证cos tan +≤x x x e ，只需证cos tan 1x x x ++≤即可.令()cos tan 1h x x x x =+--，()()()22222sin sin cos sin sin sin 11sin 1.cos cos cos x x x x x x h x x x x x-+-'=-+-==令()2sin sin 1F x x x =+-，易知()F x 在0,4⎡⎤⎢⎥⎣⎦π单调递增，且()00F <，04⎛⎫> ⎪⎝⎭F π，故存在00,4x π⎛⎫∈ ⎪⎝⎭，使得()00F x =.当[)00,x x ∈时，()0F x <，()0h x '≤，()h x 单调递减；当0,4⎛⎤∈ ⎥⎝⎦x x π时，()0F x >，()0h x '>，()h x 单调递增，又()00h =，0424h ππ⎛⎫=-<⎪⎝⎭，()()max 00h x h ==.故当0,4x π⎡⎤∈⎢⎥⎣⎦时，cos tan +≤x x x e .【点睛】方法点睛：本题考查绝对值不等式的恒成立问题，不等式恒成立问题常见方法：①分离参数()a f x ≥恒成立(()max a f x ≥即可)或()a f x ≤恒成立（()min a f x ≤即可）；②数形结合(()y f x =图像在()y g x =上方即可)；③讨论最值()min 0f x ≥或()max 0f x ≤恒成立.（二）选考题：共10分.请考生在第22､23题中任选一题作答.如果多做，则按所做的第一题计分.22.在直角坐标系xOy 中，直线l 的参数方程为315415x t y t ⎧=+⎪⎪⎨⎪=+⎪⎩（t 为参数），以坐标原点为极点，x 轴的正半轴为极轴建立极坐标系，曲线C 的极坐标方程为2221sin ρθ=+，点P的极坐标为4π⎫⎪⎭.（1）求C 的直角坐标方程和P 的直角坐标；（2）设l 与C 交于A ，B 两点，线段AB 的中点为M ，求PM .【答案】（1）2212x y +=，()1,1（2）5541PM =【解析】【分析】（1）利用互化公式把曲线C 化成直角坐标方程，把点P 的极坐标化成直角坐标；（2）把直线l 的参数方程的标准形式代入曲线C 的直角坐标方程，根据韦达定理以及参数t 的几何意义可得．【详解】（1）由ρ2221sin θ=+得ρ2+ρ2sin 2θ＝2，将ρ2＝x 2+y 2，y ＝ρsinθ代入上式并整理得曲线C 的直角坐标方程为22x +y 2＝1，设点P 的直角坐标为（x ，y ），因为P，4π），所以x ＝ρcosθ=cos 4π=1，y ＝ρsinθ=4π=1，所以点P 的直角坐标为（1，1）．（2）将315415x t y t ⎧=+⎪⎪⎨⎪=+⎪⎩代入22x +y 2＝1，并整理得41t 2+110t +25＝0，因为△＝1102﹣4×41×25＝8000＞0，故可设方程的两根为t 1，t 2，则t 1，t 2为A ，B 对应的参数，且t 1+t 211041=-，依题意，点M 对应的参数为122t t +，所以|PM |＝|122t t +|5541=．【点睛】本题考查了简单曲线的极坐标方程，属中档题．23.已知函数()2429a b a b f x x x +++=+++-.（1）求证：()5f x ≥；（2）若0,0,1a b a b >>+=，证明：2211252a b a b ⎛⎫⎛⎫+++≥ ⎪ ⎪⎝⎭⎝⎭.【答案】（1）证明见解析（2）证明见解析【解析】【分析】（1）利用绝对值三角不等式与二次函数的性质计算可得；（2）利用基本不等式证明即可.【小问1详解】因为()2429a b a b f x x x +++=+++-()()22429429a b a b a b a b x x ++++++++--=≥-+，当且仅当()()20429a b a b x x ++++-≤+时取等号，又2429a b a b +++-+()22255a b +-+=≥，当且仅当22a b +=，即1a b +=时取等号，所以()5f x ≥.【小问2详解】因为0a >，0b >，且1a b +=，又因为222x y xy +≥，当且仅当x y =时取等号，所以()222222x yx y xy +≥++，即()()2222x y x y +≥+，所以()2222x y x y ++≥，当且仅当x y =时取等号，所以22222111111111222a b a b a b a b a b ab ab ⎛⎫+++ ⎪+⎛⎫⎛⎫⎛⎫⎛⎫⎝⎭+++≥=+=+ ⎪ ⎪⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭，又因为2124a bab+⎛⎫<≤=⎪⎝⎭，当且仅当12a b==时取等号，。

2021年安庆市高三模拟考试（三模）语文试题本试卷分为第Ⅰ卷（阅读题）和第Ⅱ卷（表达题）两部分，第Ⅰ卷第1页至7页，第Ⅱ卷第8页至10页。

全卷满分150分，考试时间150分钟。

第Ⅰ卷（阅读题共66分）一、（9分）阅读下面的文字，完成1～3题。

文化与代沟①关于年轻一代和年长一代在行为方式、生活态度、价值观方面的差异、对立和冲突，即所谓代沟问题。

二战后它就引起了文化人类学家的留意。

杰弗里·戈若在1948年出版的《美国人：一项国民争辩》中就曾争辩过代际脱节现象，但对“代沟”问题作了最具说服力的阐释的却是米德1970年出版的《文化与承诺：一项有关代沟问题的争辩》。

②《文化与承诺》出版于欧美60年月青年运动刚刚退潮之际。

米德提出，纷呈于当今世界的代与代之间的冲突和冲突既不能归咎于两代人在社会地位和政治观念方面的差异，更不能归咎于两代人在生物学和心理学方面的差异，而首先导源于文化传递方面的差异。

从文化传递的方式动身，米德将整个人类文化划分为三种基本类型：前喻文化、并喻文化和后喻文化。

这三种文化模式是米德创设其代沟思想的理论基石。

③前喻文化，即老年文化，其特点是晚辈主要向长辈学习，这是一切传统社会的基本特征。

在传统社会中，由于进展格外缓慢，阅历就有了举足轻重的作用，而阅历丰富的老者自然就成了整个社会公认的行为楷模。

在这种以前喻方式为特征的文化传递过程中，年长一代传喻给年轻一代的不仅是基本的生存技能，还包括他们对生活的理解、公认的生活方式和简拙的是非观念。

这种前喻型文化从根本上来说排解了变革的可能，当然也就排解了年轻一代对年长一代的生活予以反叛的可能，因此，在前喻文化中是不存在代沟现象的。

④并喻文化，是一种过渡性质的文化，它肇始于前喻文化崩溃之际，比如移民运动、科学进展、战斗失败等缘由。

由于从前文化的中断，前辈无法再向晚辈供应符合新的环境和时代要求的全新的行为模式，晚辈就只能以在新的环境中捷足先登的同伴为自己仿效的楷模，这就产生了文化传递的并喻方式。

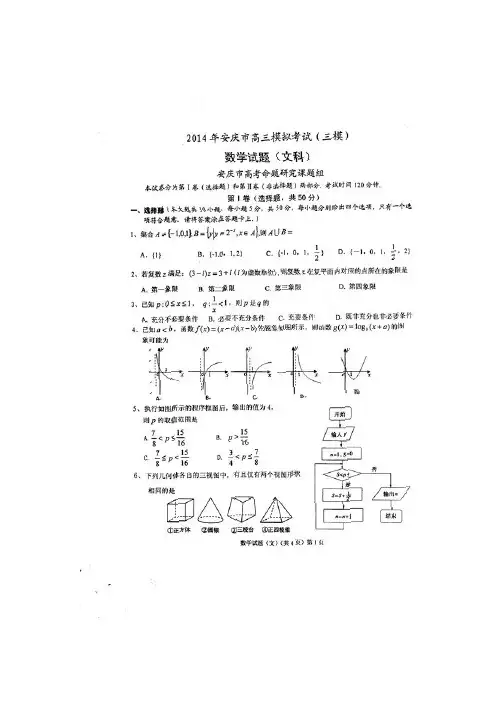
D3、解析：由11<x知1>x 或0<x ，故选D. 4、解析：由图可知b a <<<10，故函数)(xg 单调递增，排除A,D ，结合a 的范围选B. 9、解析：将向量投影到,上，即过点P 作AC AB ,的平行线，分别交AB AC ,于点.,E D 由系数,5152的几何意义知，2,51=AC AD AB AE 于是,252=⋅=∆∆AC AD AB AE S S ABC ADE 又APE ADEP ADE S S S ∆∆==21 数学试题参考答案（文）（共6页）第1页所以.252=∆∆ABC APE S S 而,51==∆∆AB AE S S ABP APE 所以.52=∆∆ABC ABP S S 故选C. 10、解析：采用特殊值法，令直线为2=y ，则2||||==CD AB ，于是4||||=⋅CD AB ，选A.15、解析：圆心O 到直线l 的距离为13||c ，当113||<c 即1313<<-c 时，圆O 上有四个不同点到直线l 的距离为1；当13±=c 时，圆O 上恰有三个不同点到直线l 的距离为1；当3913<<c 或1339-<<-c 时，圆O 上恰有两个不同点到直线l 的距离为1；当39±=c 时，圆O 上只有一个点到直线l 的距离为1.故①②⑤正确.三、解答题(本大题共6小题，共75分.解答应写出文字说明，证明过程或演算步骤)16、（本题满分12分）解：（Ⅰ）由已知，根据正弦定理得22(2)(2)a b c b c b c =+++即222a b c bc =++ 由余弦定理得 2222cos a b c bc A =+-故 1cos 2A =-，∴∈),,0(πA A= 32π ……6分 （Ⅱ）由（Ⅰ）知23)21(sin 2sin 2sin 21sin 22cos )(22+--=+-=+=x x x x x x f数学试题参考答案（文）（共6页）第2页因为R x ∈，所以[]sin 1,1x ∈-，因此，当1sin 2x =时，)(x f 有最大值32. 当1sin -=x 时，)(x f 有最小值-3，所以所求函数)(x f 的值域是33,2⎡⎤-⎢⎥⎣⎦. ……………………12分11(,),A B 12(,),A B 21(,),A B 22(,),A B 31(,),A B 12(,),B B 32(,),A B 11(,),B C 21(,),B C 共9种．所以其中第4组的2位同学为12,B B 至少有一位同学入选的概率为93155= . ……12分两式相减得01)1()2(1=+----n n a n a n ，于是01)1(1=+--+n n na a n两式相减得n n n a a a 211=+-+（2≥n ）。

安徽省安庆市2021-2022学年高三下学期第三次模拟检测语文试题本试卷总分150分，考试时间150分钟（答案在最后）考生注意事项：1．答题前，务必在试题卷规定的地方填写自己的姓名、座位号，并认真核对答题卡上所粘贴的条形码中座位号与本人座位号是否一致。

2．答选择题时，每小题选出答案后，用2B铅笔把答题卡上对应题目的答案标号涂黑。

3．答非选择题时，必须使用0.5毫米的黑色墨水签字笔在答题卡上书写，必须在题号所指示的答题区域作答。

一、现代文阅读（36分）（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成下列小题。

春秋时期，孔子通过总结和反思夏、商、周三代的文化遗产，继承并发展了古老的“礼”观念，赋予其新的思想内涵，创造性地建立起一套以“礼”为核心价值观念的儒家思想体系。

“礼”既是一种社会政治理想，又是一种伦理道德规范。

它通过对人们思想行为的引导、制约和规范，来维护社会的安定和发展。

在孔子的思想体系中，“仁”与“礼”均处于非常重要的地位。

从《礼记》看来，“礼”是高于“仁”的。

《礼记·曲礼》云：“道德仁义，非礼不成”。

由此可见，连“仁”也是以“礼”为依据的。

中国古代政治是以“礼”为基础的政治。

“礼”与中国古代政治理念、政治行为和政治制度，都有着密不可分的联系。

我国古代社会的宗法制度、爵位制度、土地制度及其他各种政治制度，在古代都属于“礼”的范畴。

“礼”与法制也有密切关系。

“法”源于“礼”，是从“礼”中衍生出来的，《管子·枢言》云：“法出于礼。

”“礼”被赋予了强制力便是“法”。

“礼”是一种社会道德教化工具，“法”是一种事后的惩罚措施。

“礼”和“法”都是人们的行为规范，“礼”依靠道德教化的方式引导人们别贵贱、序尊卑；而“法”则依靠强制力使人们共同遵守礼的有关规范。

在中国古代国家治理模式中，“礼”与“法”紧密地结合在一起，对社会秩序发挥着调节、约束的功能。

许多统治者和政治家还往往以“礼”为依据，进行制度建设或改革。

2023-2024学年安徽省安庆市高考三模数学模拟试题一、单选题1．设集合{}2,0,1,2,{2A B xx =-=≤-∣或2}x >，则()R A B ⋂=ð（）A ．{}2-B ．{}1C ．2,0,1-D ．{}0,1,2【正确答案】D【分析】根据集合的运算求解.【详解】由{2B xx =≤-∣或2}x >得：R {22}B x x =-<≤∣ð，而{}2,0,1,2A =-，所以(){}R 0,1,2A B = ð.故选:D.2．复数20232i z =-+的共轭复数z =（）A ．2i +B ．2i-+C ．2i--D ．2i-【正确答案】B【分析】根据虚数单位i 的性质求复数z ，再根据共轭复数的概念分析判断.【详解】因为()2023202032i 2i i 2i z =-+=-+⋅=--，所以2i z =-+.故选：B.3．已知两个非零向量a ，b 满足3a b = ，()a b b +⊥ ，则cos ,a b 〈〉= （）A ．12B ．12-C ．13D ．13-【正确答案】D【分析】根据向量的数量积运算律和夹角公式求解.【详解】因为()a b b +⊥，所以()0a b b +⋅= ，所以20a b b ⋅+= ，所以2a b b ⋅=- ，221cos ,33b b a b a b a b a b b b--⋅〈〉====-⋅⋅⋅，故选:D.4．在等比数列{}n a 中，2345674,16a a a a a a ==，则8910a a a =（）A ．4B ．8C ．32D ．64【正确答案】D【分析】根据等比数列的性质求解即可.【详解】由2345674,16a a a a a a ==可得33364,16a a ==，又2639a a a =，故633639a a a =，则239164a =，解得3964a =，即891064a a a =.故选：D5．陀螺起源于我国，最早出土的石制陀螺是在山西夏县发现的新石器时代遗址.如图所示的是一个陀螺立体结构图.已知，底面圆的直径12cm AB =，圆柱体部分的高6cm BC =，圆锥体部分的高4cm CD =，则这个陀螺的表面积（单位：2cm ）是（）A ．(144π+B ．(144π+C ．(108π+D ．(108π+【正确答案】C【分析】根据圆柱与圆锥的表面积公式求解.【详解】由题意可得圆锥体的母线长为l =，所以圆锥体的侧面积为112π2⋅⋅=，圆柱体的侧面积为12π672π⨯=，圆柱的底面面积为2π636π⨯=，所以此陀螺的表面积为()()272π36π108cm ++=+，故选：C.6．在ABC 中，角A ､B ､C 的对边分别为a ､b ､c ，已知ABC 的面积为4，b =4，8BA AC ⋅=，则a =（）A B ．C ．D 【正确答案】C【分析】由题中的两个等式解得A 与c 的值，再由余弦定理解得a 的值.【详解】∵4b =，||||cos()cos 8BA AC BA AC A bc A π⋅=-=-= ，1=sin 42ABC S bc A =△∴cos 2c A =-①，sin 2c A =②，∴由①②得tan 1A =-，∵(0,)A π∈∴3=4A π∴c =∴22232cos 16824404a b c bc A π=+-=+-⨯⨯=，∴a =故选：C.7．在高三复习经验交流会上，共有3位女同学和6位男同学进行发言.现用抽签的方式决定发言顺序，事件()19,k A k k ≤≤∈N 表示“第k 位发言的是女同学”，则()82P A A =∣（）A ．14B ．712C ．16D ．13【正确答案】A【分析】根据条件概率公式计算即可.【详解】由题意，()27378299A A 61A 7212P A A ===，()1838299A A 1A 3P A ==所以()()()828221112143P A A P A A P A ===∣，故选：A8．已知函数2()e 2ln ax f x x x ax =--+，若()0f x >恒成立，则实数a 的取值范围为（）A ．1,e ⎛⎫+∞ ⎪⎝⎭B ．(1,)+∞C ．2,e ⎛⎫+∞ ⎪⎝⎭D ．(e,)+∞【正确答案】C【分析】依题意可得22ln e 2ln e 2ln ax x ax x x x +>+=+，进而可得2ln xa x>在()0,x ∈+∞上恒成立，构造函数2ln ()xh x x=，利用导数研究函数的单调性以及最值，即可求出参数的取值范围.【详解】()0f x >等价于22ln e 2ln e 2ln ax x ax x x x +>+=+．令函数()e x g x x =+，则()e 10x g x '=+>，故()g x 是增函数．2ln e e 2ln ax x ax x +>+等价于2ln (0)ax x x >>，即2ln xa x>．令函数2ln ()xh x x =，则222ln ()x h x x -'=．当(0,e)x ∈时，()0h x '>，()h x 单调递增：当(e,)x ∈+∞时，()0h x '<，()h x 单调递减．max 2()(e)eh x h ==.故实数a 的取值范围为2,e ⎛⎫+∞ ⎪⎝⎭．故选：C.二、多选题9．函数()()sin f x A x ωϕ=+（其中0,0,2A πωϕ>><）的图像如图所示，则下列说法正确的是（）A ．函数()f x 的最小正周期是2πB ．3πϕ=C ．为了得到()cos 23g x x π⎛⎫=+ ⎪⎝⎭的图像，只需将()f x 的图像向左平移2π个单位长度D ．为了得到()cos 23g x x π⎛⎫=+ ⎪⎝⎭的图像，只需将()f x 的图像向左平移4π个单位长度【正确答案】BD【分析】根据函数图像结合三角函数性质，根据周期，初相判断A,B 选项，根据平移判断C,D 选项即可.【详解】对A ，由图可知，1A =，最小正周期T 满足7πππ41234T =-=，所以πT =，所以函数()f x 的最小正周期是π，故A 错误；对B ，2π2πω==，即()()sin 2f x x ϕ=+，将7π12x =代入可得7π3π22π,122k k ϕ⨯+=+∈Z ，得π2π3k ϕ=+，又π2ϕ<，所以π3ϕ=，故B 正确；对C ，由上述结论可知()πsin 23f x x ⎛⎫=+ ⎪⎝⎭，为了得到()πππ5πcos 2sin 2sin233212g x x x x ⎡⎤⎛⎫⎛⎫⎛⎫=+=++=+ ⎪ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎝⎭⎣⎦，应将函数()f x 向左平移π4个单位长度.故C 错误，D 正确.故选：BD.10．若甲组样本数据1x ，2x ，…，n x （数据各不相同）的平均数为2，方差为4，乙组样本数据13x a +，23x a +，…，3n x a +的平均数为4，则下列说法正确的是（）A ．a 的值为-2B ．乙组样本数据的方差为36C ．两组样本数据的样本中位数一定相同D ．两组样本数据的样本极差不同【正确答案】ABD【分析】结合平均数、方差、中位数、极差的概念以及平均数的和差倍分性质，及一组数据同时乘一个数，同时加一个数对方差的影响，逐项分析即可求出结果.【详解】由题意可知：324a ⨯+=，故2a =-，故A 正确；乙组样本数据方差为9436⨯=，故B 正确；设甲组样本数据的中位数为i x ，则乙组样本数据的中位数为32i x -，所以两组样本数据的样本中位数不一定相同，故C 错误；甲组数据的极差为max min x x -，则甲组数据的极差为()()()max min max min 32323x x x x ---=-，所以两组样本数据的样本极差不同，故D 正确；故选：ABD.11．如图，已知四边形,ABCD BCD 是以BD 为斜边的等腰直角三角形，ABD △为等边三角形，2BD =，将ABD △沿对角线BD 翻折到PBD △在翻折的过程中，下列结论中正确的是（）A ．BD PC⊥B ．DP 与BC 可能垂直C ．四面体PBCD 33D ．直线DP 与平面BCD 所成角的最大值是45 【正确答案】ABC【分析】由折叠平面的变与不变性，对于A ，取BD 中点M ，可得BD ⊥面PMC ，A 选项可判断；对于B ，假设DP 与BC 垂直，则BC ⊥面PCD ，再根据题目所给长度即可判断；对于C ，当面PBD ⊥面BCD 时，此时四面体PBCD 的体积的最大,计算最大体积即可;对于D ，当面PBD ⊥面BCD 时，此时直线DP 与平面BCD 所成角最大，判断即可.【详解】对于A ，如图所示，取BD 的中点M ，连接,PM CM ，BCD △是以BD 为斜边的等腰直角三角形，BD CM ∴⊥，ABD △为等边三角形，BD PM ∴⊥，又,,PM CM M PM CM =⊂ 面PMC ，BD ∴⊥面PMC ，又PC ⊂面PMC ，BD PC ∴⊥，故A 正确.对于B ，假设DP BC ⊥，又,,,BC CD CD DP P CD DP ⊥=⊂ 面PCD ，BC ∴⊥面PCD ，又PC ⊂面PMC ，BC PC ∴⊥，又2,2PB BC ==331PC ⎡⎤∈⎣⎦，当2PC =222BC PC PB +=，故DP 与BC 可能垂直，故B 正确.对于D ，当面PBD ⊥面BCD 时，面PBD 面BCD =BD ，,BD PM PM ⊥⊂平面PBD ，此时PM ⊥面,BCD PDB ∠即为直线DP 与平面BCD 所成角，此时60PDB ∠= ，故D 错误.对于C ，易知当面PBD ⊥面BCD 时，此时四面体PBCD 的体积最大，此时的体积为：1113323BCDV SPM ⎛=⋅=⨯= ⎝，故C 正确.故选：ABC.12．已知数列{}n a 满足328a =，()()1122nn n a n a n --⎡⎤=+≥⎢⎥⎣⎦，*n ∈N ，数列{}n b 的前n 项和为n S ，且()()222212221log log n n n n n b a a a a +-+=⋅-⋅，则下列说法正确的是（）A ．4221a a =B ．1216a a ⋅=C ．数列212n n a a -⎧⎫⎨⎬⎩⎭为单调递增的等差数列D ．满足不等式50n S ->的正整数n 的最小值为63【正确答案】ABD【分析】由328a =和递推公式()112nn n a n a --⎡⎤=+⎢⎥⎣⎦→28a =→12a =，4168a =→A 选项正确，B 选项正确；()()1122n n n a n a n --⎡⎤=+≥⎢⎥⎣⎦→()112nn n a n a --=+→()212212222n n n a n n a --=+=+为单调递增的等差数列→C 选项不正确；22log 1n n b n +=+→22log 52n n S +=>→62n >→D 选项正确【详解】因为328a =，所以()313222328a a a -=⋅+=，所以28a =，则()21211228a a a -=⋅+=，解得12a =，()4143324168a a a -=⋅+=，所以4221a a =，1216a a ⋅=，所以A 选项正确，B 选项正确；因为()()1122n n n a n a n --⎡⎤=+≥⎢⎥⎣⎦，所以()()1122n n n a n n a --=+≥，所以()212212222n n n a n n a --=+=+，又*n ∈N ，所以22221232222n n n n a a n n a a ----=+-=，*n ∈N 所以221n n a a -⎧⎫⎨⎬⎩⎭为单调递增的等差数列，则数列212n n a a -⎧⎫⎨⎬⎩⎭不是单调递增的等差数列，所以C 选项不正确；()221222122224n n n a n n a +-++=++=+，则()()2221222212221222212log log log log 1n n n n n n n n n a a n b a a a a a a n +-+-++⋅+=-⋅==+，222222341234122log log log log log log 52312312n n n n n n S n n n n +++++⎛⎫=++++=⨯⨯⨯⨯=> ⎪++⎝⎭ ，解得62n >，又*n ∈N ，所以正整数n 的最小值为63，所以D 选项正确．故选：ABD ．数列问题，常常需要由递推公式求出通项公式，方法有累加法，累乘法，构造法等，要根据数列特征选择不同的方法.三、填空题13．已知某地最近10天每天的最高气温（单位：C ）分别为10,9,13,15,17,16,18,17,20,12，则这10天平均气温的80%分位数为___________C .【正确答案】17.5【分析】根据百分位数的定义求解.【详解】这10天的平均气温的数据按照从小到大的顺序排列为：9,10,12,13,15,16,17,17,18,20,1080%8,⨯= ∴这10天平均气温的80%分位数为171817.5C 2+= .故17.5.14．已知7sin cos 5αα+=，则tan α=________.【正确答案】43或34【分析】利用平方关系式和商数关系式转换求解即可得tan α的值.【详解】解：将7sin cos 5αα+=两边平方得4912sin cos 25αα+=，所以12sin cos 25αα=，所以22sin cos 12sin cos 25αααα=+分式上下同除2cos α得：2tan 12tan 125αα=+整理得：212tan 25tan 120αα-+=，解得：4tan 3α=或3tan 4α=故答案为:43或34.15．已知非负数,x y 满足1x y +=，则1912x y +++的最小值是___________.【正确答案】4【分析】根据题意124x y +++=，再构造等式利用基本不等式求解即可.【详解】由1x y +=，可得()19119124,1212412x y x y x y x y ⎛⎫+++=+=++++ ⎪++++⎝⎭()911219412x y x y ⎛⎫++=+++ ⎪++⎝⎭11044⎛ ≥+= ⎝，当且仅当()231y x +=+，即0,1x y ==时取等号.故416．抛物线22(0)x pyp =>上一点)(1)A m m >到抛物线准线的距离为134，点A 关于y 轴的对称点为B ，O 为坐标原点，OAB ∆的内切圆与OA 切于点E ，点F 为内切圆上任意一点，则•OE OF的取值范围为__________．【正确答案】[3【详解】因为点)A m 在抛物线上，所以3322pm m p=⇒=，点A 到准线的距离为313224p p +=，解得12p =或6p =．当6p =时，114m =<，故6p =舍去，所以抛物线方程为2x y=，∴3)(3)A B ，，所以OAB 是正三角形，边长为22(2)1x y +-=，如图所示，∴32E ⎫⎪⎪⎝⎭，．设点(cos 2sin )F θθ+，（θ为参数），则3π·cos 33226OE OF θθθ⎛⎫=++=++ ⎪⎝⎭，∴·[33OE OF ∈ ．本题主要考查抛物线性质的运用，参数方程的运用，三角函数的两角和公式合一变形求最值，属于难题，对于这类题目，首先利用已知条件得到抛物线的方程，进而可得到OAB ∆为等边三角形和内切圆的方程，进而得到点E 的坐标，可利用内切圆的方程设出点F 含参数的坐标，进而得到π·336OE OF θ⎛⎫=++ ⎪⎝⎭ ，从而得到其取值范围，因此正确求出内切圆的方程是解题的关键.四、解答题17．已知函数()21cos 3cos 2f x x x x =+⋅-.(1)求函数()f x 的单调递增区间；(2)求()f x 在区间［0，2π］上的最值.【正确答案】(1),36k k ππππ⎡⎤-+⎢⎥⎣⎦（k ∈Z ）(2)最大值为1，最小值为-12.【分析】（1）由三角函数降幂公式与二倍角公式，根据辅助角公式，化简函数为单角三角函数，根据正弦函数的单调性，可得答案；（2）利用整体思想，根据正弦函数的图象性质，可得答案.【详解】（1）()f x =1cos23131cos2sin 2222226x x x x x π+⎛⎫+-=+=+ ⎪⎝⎭.因为y ＝sin x 的单调递增区间为2,222k k ππππ⎡⎤-+⎢⎥⎣⎦（k ∈Z ），令22,2622x k k πππππ⎡⎤+∈-+⎢⎥⎣⎦（k ∈Z ），得,36x k k ππππ⎡⎤∈-+⎢⎥⎣⎦（k ∈Z ）.所以()f x 的单调递增区间为,36k k ππππ⎡⎤-+⎢⎥⎣⎦（k ∈Z ）.（2）因为x ∈［0，2π］，所以2x ＋7,666πππ⎡⎤∈⎢⎥⎣⎦.当2x ＋6π=2π，即x ＝6π时，()f x 最大值为1，当2x ＋6π=76π，即x ＝2π时，()f x 最小值为-12.18．设数列{}n a 的前n 项和n S 满足12n n S a a =-，且1a ，21a -33a -成等比数列.(1)求数列{}n a 的通项公式；(2)设12n n b a ⎧⎫+⎨⎬⎩⎭是首项为1，公差为2的等差数列，求数列{}n b 的通项公式与前n 项和n T .【正确答案】(1)12n n a -=(2)()2212n n b n =--，21222n n T n +=-+【分析】（1）先根据1n n n a S S -=-得到12n n a a -=，利用1a ，21a -33a -成等比数列，可得11a =，可判断数列{}n a 是首项为1，公比为2的等比数列，即可得12n n a -=.（2）由12n n a -=得()2212n n b n =--，利用分组求和法可得.【详解】（1）由已知12n n S a a =-，有()11222n n n n n a S S a a n --=-=-≥，即()122n n a a n -=≥，从而212a a =，32124a a a ==，又因为1a ，21a -33a -成等比数列，即()()221313a a a -=-，所以()()21112143a a a -=-，解得11a =，所以，数列{}n a 是首项为1，公比为2的等比数列，故12n n a -=.（2）因为12n n b a ⎧⎫+⎨⎬⎩⎭是首项为1，公差为2的等差数列，所以()11212n n b a n +=+-，所以数列{}n b 的通项公式为()2212nn b n =--，()()1221321222nn T n ⎡⎤=+++--+++⎣⎦ ()()2121212212nn n -⎡⎤+-⎣⎦=--21222n n +=-+.19．如图,四棱锥P ABCD -中,PA ⊥底面,,ABCD AD BC N ∥为PB 的中点.(1)若点M 在AD 上,32,4AM MD AD BC ==,证明:MN 平面PCD ;(2)若4,5,6PA AB AC AD BC =====,求二面角D AC N --的余弦值.【正确答案】(1)证明见解析(2)【分析】（1）取PC 中点F ,连接,NF DF ,根据已知条件证明四边形NFDM 是平行四边形,即可证明;（2）取BC 中点Q ,根据条件可以证明AQ AD ⊥,所以,,AQ AD AP 所在直线分别为x 轴,y 轴,z 轴建立空间直角坐标系,分别求出平面ACN 的法向量和平面ACD 的法向量,再利用公式求解即可.【详解】（1）如图所示:取PC 中点F ,连接,NF DF ,因为2MD AM =,所以23MD AD =,又34AD BC =,所以12MD BC =,因为AD BC ∥,所以MD BC ∥,又因为N 为PB 的中点,所以NF BC ∥且12NF BC =,即有NF MD ∥且NF MD =,所以四边形NFDM 是平行四边形,所以MN DF ∥,又因为MN ⊄平面,PCD DF ⊂平面PCD ，所以MN平面PCD .（2）连接NC ,因为5AB AC ==,所以ABC 为等腰三角形,取BC 中点Q ,连接AQ ,则有AQ BC ⊥,又因为AD BC ∥,所以AQ AD ⊥,又因为PA ⊥底面ABCD ,如图,以,,AQ AD AP 所在直线分别为x 轴,y 轴,z 轴建立空间坐标系,因为4,5,6PA AB AC AD BC =====,则有()()()30,0,0,0,5,0,4,3,0,2,,22A D C N ⎛⎫- ⎪⎝⎭,所以()32,,2,4,3,02AN AC ⎛⎫=-= ⎪⎝⎭,设平面ACN 的法向量为(),,n x y z =r,则有43032202x y x y z +=⎧⎪⎨-+=⎪⎩,则()3,4,6n =-- ,因为PA ⊥底面ABCD ,取平面ACD 的法向量()0,0,1m =,设二面角D AC N --的大小为(θθ为钝角),则有cos cos ,m n m n m n θ⋅===-⋅,即二面角D AC N --的余弦值为61-.20．已知双曲线2222:1x y E a b -=的焦距为4，以原点为圆心，实半轴长为半径的圆和直线0x y -=相切．(1)求双曲线E 的方程；(2)已知点F 为双曲线E 的左焦点，试问在x 轴上是否存在一定点M ，过点M 任意作一条直线l 交双曲线E 于P ，Q 两点，使FP FQ ⋅为定值？若存在，求出此定值和所有的定点M 的坐标；若不存在，请说明理由．【正确答案】(1)22:13x E y -=(2)存在，定值为1，()3M -【分析】(1)利用点到直线的距离公式求得a 的只，再根据焦距，求得b 即可求解；(2)假设存在满足条件的点M ，先在直线垂直于y 轴时，求得定值，再结合根与系数的关系，分析验证直线不垂直于y 轴时，求得此定值的情况，从而得出结论.【详解】（1）原点到直线0x y -=的距离d ==，∴2,c a ==1b ∴=，∴双曲线E 的方程为22:13x E y -=；（2）假设存在点(,0)M m 满足条件，①当直线l 方程为0y =时，则())(),,2,0P Q F -，∴())2,02,01FP FQ ⋅=⋅=；②当直线l 方程不是0y =时，可设直线:l x ty m =+，(t ≠代入22:13x E y -=整理得()(2223230t y mty m t -++-=≠，*由0∆>得223m t +>，设方程*的两个根为1y ，2y ，满足212122223,33mt m y y y y t t -+=-=--，∴()()11222,2,FP FQ ty m y ty m y ⋅=++⋅++()()()()221212122t y y t m y y m =++++++222212153t m m t ---=-，当且仅当2212153m m ++=时，FP FQ ⋅为定值1，解得3m =-，3m =-不满足对任意t 贡0∆>，∴不合题意，舍去．而且3m =-满足0∆>；综上得：过定点()3M -任意作一条直线l 交双曲线E 于P ，Q 两点，使FP FQ ⋅为定值1．21．某校组织“青春心向党，喜迎二十大”主题知识竞赛，每题答对得3分，答错得1分，已知小明答对每道题的概率是12，且每次回答问题是相互独立的.(1)记小明答3题累计得分为X ，求X 的分布列和数学期望；(2)若小明连续答题获得的分数的平均值大于2分，即可获得优秀奖.现有答2n 和22n +道题两种选择，要想获奖概率最大，小明应该如何选择？请说明理由.【正确答案】(1)分布列见解析，数学期望：6(2)小明选择答22n +道题时，获奖的概率更大，理由见解析【分析】（1）由X 的取值为3，5，7，9，再利用独立重复试验求得概率，然后列出分布列进而求得数学期望；（2）分别求出小明选择答2n 道题与22n +道题获得优秀奖的概率，再进行比较即可.【详解】（1）由题意知()303113C 28P X ⎛⎫==⨯= ⎪⎝⎭，()2131135C 228P X ⎛⎫==⨯⨯= ⎪⎝⎭，()2231137C 228P X ⎛⎫==⨯⨯= ⎪⎝⎭，()333119C 28P X ⎛⎫==⨯= ⎪⎝⎭，所以X 的分布列为X3579P18383818()1331357968888E X =⨯+⨯+⨯+⨯=；（2）由题意可知甲同学答一题得3分的概率为12，得1分的概率为12，若选择答2n 道题，此时要能获得优秀奖，则需2n 次游戏的总得分大于4n ，设答2n 道题中，得3分的题数为m ，则()324m n m n +->，则m n >，易知12,2m B n ⎛⎫~ ⎪⎝⎭，故此时获优秀奖的概率：11222122122211111()C C C 22222n n n n nn n n n nn P P m n +-+-++⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫=>=⨯⨯+⨯⨯++⨯ ⎪⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭，()21222221CCC2nn n n nnn++⎛⎫=+++⨯ ⎪⎝⎭，()()2201222222222C 11111C C C C 2C 1222222nnn n n n n nn n n n n n ⎛⎫⎛⎫⎛⎫=+++-⨯=-⨯=- ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭，同理可以求出当选择答22n +道题，获优秀奖的概率为122222C 1122n n n P +++⎛⎫=- ⎪⎝⎭，因为()()()()()()()()()2222112222222!C 4!!214C 4(1)2122!C C 22212121!1!n n nn n n n n n n n n n n n n n n n n n +++++++====>++++⎡⎤⎡⎤++⎣⎦⎣⎦，所以1222222C C 22n n n n n n +++>，则12P P <，所以小明选择答22n +道题时，获奖的概率更大.22．已知函数()()ln 1f x x =+，()2g x ax x =+.(1)当1x >-时，()()f x g x ≤，求实数a 的取值范围；(2)已知*n ∈N ，证明.111sin sin sin ln2122n n n+++<++ 【正确答案】(1)0a ≥(2)证明见解析【分析】（1）证明出()ln 1x x ≤+，在0a ≥时，可得出()2ln 1x ax x +≤+，在a<0时，010x a=->，分析可知()()00f x g x >，综合可得出实数a 的取值范围；（2）由（1）变形可得()1ln 11x x x ≥->，令111t x =-，可得出()()1ln ln 11t t t t--≥>，可得出()()1ln ln 1n k n k n k≤+-+-+，{}0,1,2,,k n ∈ ，证明出()sin 0x x x <>，可得出()()1sinln ln 1n k n k n k<+-+-+，{}0,1,2,,k n ∈ ，利用不等式的基本性质可证得结论成立.【详解】（1）解：令()()()ln 11h x x x x =+->-，则()1111x h x x x '=-=-++，当10x -<<时，()0h x '>，则函数()h x 在()1,0-上单调递增，当0x >时，()0h x '<，则函数()h x 在()0,∞+上单调递减，所以，()()max 00h x h ==，即()ln 1x x ≤+，所以，当0a ≥时，()2ln 1x x ax x +≤≤+，即()()f x g x ≤，当a<0时，取010x a=->，由于()0ln 1ln10x +>=，而2200110ax x a a a⎛⎫+=⋅--= ⎪⎝⎭，得()2000ln 1x ax x +>+，故()()00f x g x >，不合乎题意.综上所述，0a ≥.（2）证明：当0a =时，由（1）可得()ln 1x x ≤+，则ln 1≤-x x ，可得11ln1x x ≤-，即1ln 1x x -≤-，即()1ln 11x x x≥->，令111t x =-，所以，1t x t =-，所以，1ln1t t t ≥-，即()()1ln ln 11t t t t --≥>，所以，()()1ln ln 1n k n k n k≤+-+-+，{}0,1,2,,k n ∈ ，令()()sin 0g x x x x =->，则()1cos 0g x x '=-≥，且()g x '不恒为零，所以，函数()g x 在()0,∞+上单调递增，故()()00g x g >=，则()sin 0x x x <>，所以，()()11sin ln ln 1n k n k n k n k<≤+-+-++，{}0,1,2,,k n ∈ ，所以，111sinsin sin 122n n n+++++()()()()()ln 1ln ln 2ln 1ln 2ln 21n n n n n n <+-++-+++--⎡⎤⎡⎤⎡⎤⎣⎦⎣⎦⎣⎦()2ln 2ln lnln 2nn n n=-==.方法点睛：利用导数证明不等式问题，方法如下：（1）直接构造函数法：证明不等式()()f x g x >（或()()f x g x <）转化为证明()()0f x g x ->（或()()0f x g x -<），进而构造辅助函数()()()h x f x g x =-；（2）适当放缩构造法：一是根据已知条件适当放缩；二是利用常见放缩结论；（3）构造“形似”函数，稍作变形再构造，对原不等式同解变形，根据相似结构构造辅助函数.。

数学试题（文科）参考答案xyo AB Ck 一、选择题（本大题共10小题，每小题5分，共50分，每小题分别给出四个选项，只有一个选项符合题意.）题号 1 2 3 4 5 6 7 8 9 10 答案CBDBAACDCD1、解析：i m m z z )38(21221-++=⋅.由038=-m 得，.38=m 选C. 2、解析：y a x 12=,准线方程为ay 41-=. 选B. 3、解析:易知函数x x x f cos 4)(2+=为偶函数,故排除A,C.又10cos )0(==f ,故排除B,选择D. 4、解析：本题主要考查等比数列的性质、累乘求积法.因为11211a a a a a a n n n ++=⋅⋅⋅==，所以,)()(11121321+++=⋅⋅⋅n n n n a a a a a a a即,)(111223221n n n n a a a a a a a ++=⋅⋅⋅ 故=⋅⋅⋅⋅⋅⋅+13221111n n a a a a a a nn a a )(111+⋅.选B. 5、解析：12,3a i ==.选A. 6、解析： )(.31)(,62)(,82)(,83)(A P D P C P B P A P ====＞)()(D P C P =＞)(B P ∴ 选择游戏盘A 中奖的机会最大．7、解析：显然.0>k 联立⎩⎨⎧=-+=012y x k x 解得)21,(kk B -. 过点)21,(k k B -时，直线kz x k y +-=1在y 轴上的截距最小，即kz最小，所以,221-=-⋅+kk k 解得.4=k 过点)4,4(C 时,y x z 4+=取最大值20. 选C.8、解析：显然，EFGH 是平行四边形.取BD 的中点P ，则,,BD CP BD AP ⊥⊥所以BD ⊥平面APC ，BD .AC ⊥所以EFGH 是矩形.选D.9、解析：作正反两个方面的推理.充分性：当0a =时，()f x 在)0,(-∞内单减; 当0a <，)0,(-∞∈x 时，x ax x f --=2)(，()f x 在（-∞，0）内单减.所以0a ≤是()f x 在)0,(-∞内单减的充分条件.数学试题（文科）参考答案（共5页）第1页必要性：当0a =时，x x f -=)(在)0,(-∞内单减；当0a < 时，()f x 在)0,(-∞内单减；当0a > 时，()f x 在)0.21(),1,(a a ---∞内单减，在)21,1(aa --内单增. 所以0a ≤是()f x 在)0,(-∞内单减的必要条件. 正确答案是C.10、解析; )1,0()(log )(≠>+=c c t c x h x c ，1>c 或10<<c ，)(x h 都是R 上的增函数，∴⎪⎪⎩⎪⎪⎨⎧==2)(2)(bb h a a h ，即2,2)(log x x xc c t c x t c =+=+有两不等实根，令)0(2>=m m c x ∴2m m t -=有两不等正根，结合图象知410<<t .选D. 二、填空题：（本大题共5小题，每小题5分，共25分.） 11、900π 12、3 13、12114、6 15、①②③④ 11、解析：，，，圆柱侧下底面半球πππ600100200===S S S ∴π900=表S12、解析： ,3,6==y x 代入ˆybx a =+得1318=a ，∴3=y 13、解析：因为,sin 3sin 3sin 2C B A ==所以.2:32:331:31:21::==c b a 设,2,32,3k c k b k a ===则.1213221294cos 222=⨯⨯-+=k k k k k B 14、解析：)2(26)(''f x x f +=，令2=x ，则12)2('-=f ，∴6)5('=f 15、解析:对①，,3252222=-=⋅++=+b a b a ba 3=+b a .①正确.对②，=AD =+)(21AC AB )(21→→++b a k ，②正确.对③，若A ∠为直角，则,0=⋅AC AB 0152=-+-k k ，.2215±=k ③正确. 对④，当→→+b k a 与→→+b a k 不反向时，=+⋅+→→→→)()(b a k b k a 222)1(→→→→+⋅++b k b a k a k=k +k k 4120cos 21)1(02+⨯⨯⨯+152-+-=k k .由题意得，0152<-+-k k , ∴2215-<k 或k 2215+>.数学试题（文科）参考答案（共5页）第2页当→→+b k a 与→→+b a k 反向时，仍有)()(→→→→+⋅+b a k b k a 0<.此时设→a +→b k =λ(k →a +→b ) (λ<0)，显然→a 、→b 不共线. ∴,1,,1±==∴==λλλk k k 取.1-==λk 所以2215-<k 且1-≠k 或k 2215+>.④正确. 对⑤，当→→+b k a 与→→+b a k 不同向时，0152>-+-k k ⇒2215-＜k ＜2215+.当→→+b k a 与→→+b a k 同向时，取.1==λk 所以2215-＜k ＜2215+且.1≠k ⑤错误.三、解答题(本大题共6小题，共75分.解答应写出文字说明，证明过程或演算步骤) 16．（本小题满分12分） 解析: （Ⅰ）)32sin()4cos()4sin(32)(πππ+-+⋅+=x x x x f3sin 2sin 22π⎛⎫=++ ⎪⎝⎭x x 2sin 23π⎛⎫=+ ⎪⎝⎭x 22ππ∴==T . …………6分(2)由已知得，()2sin 2443g x f x x πππ⎡⎤⎛⎫⎛⎫=+=++ ⎪ ⎪⎢⎥⎝⎭⎝⎭⎣⎦2sin 2=2cos(2)233x x πππ⎛⎫=+++ ⎪⎝⎭ 0,2π⎡⎤∈⎢⎥⎣⎦x ，42,333x πππ⎡⎤∴+∈⎢⎥⎣⎦， 故当ππ=+32x ，即3π=x 时，2)3()(min -==πg x g .当233x ππ+=，即0x =时，.1)0()(max ==g x g ………… 12分17．（本小题满分12分） 解析：（Ⅰ）5019=P ………………2分 （Ⅱ）设这7名学生为a,b,c,d,e,A,B(大写为男生)，则从中抽取两名学生的所有情况是：ab,ac,ad,ae,aA,aB,bc,bd,be,bA, bB,cd,ce,cA,cB,de,dA,dB,eA,eB,AB 共21种情况，其中含一名男生的有10种情况，∴.2110=P …………………8分 （Ⅲ）根据828.10538.1125252624)761918(50))()()(()(222>≈⨯⨯⨯⨯-⨯⨯=++++-=d b c a d c b a bc ad n K ∴我们有99.9%把握认为“学生的学习积极性与对待班级工作的态度”有关系. ……12分数学试题（文科）参考答案（共5页）第3页18．（本小题满分12分）解析：（Ⅰ）过点B 作EF BM ⊥于M ，连DM ∵平面BEF ⊥底面CDEF ,且2==BF BE ,∴M 为等腰直角三角形底边EF 的中点，易知 CDEF BM 底面⊥, CDEF AD 底面⊥,BM ⇒//AD ,又∵1==BM AD ,∴四边形ADMB 为平行四边形，即AB//DM,⊄AB CDEF 底面CDEF DM 底面⊂∴CDEF AB 平面// …… 6分（Ⅱ） ∵d S V V ADC ADC B BCD A ∙==∆--31（d 为三棱锥B-ADC 高）∵ADC DE AD DE DC DE 平面⊥⇒⊥⊥,又∵平面BEF ⊥底面CDEF ，EF DE ⊥BEF DE 平面⊥⇒ BEF 平面⇒//平面ADC1==ED d ,12121=⨯⨯=∆ADC S ,∴3131=∙=∆-d S V ADC BCD A …… 12分19．（本小题满分13分）解析：(Ⅰ) bx ax x x f ++=2ln )(的定义域为),0(+∞，.12)(b xax x f ++=' ∵图象在点))1(,1(f 处的切线平行于x 轴，∴012)1(=++='b a f ，12--=a b ，.)1)(12(1212)(x x ax a x ax x f --=--+=' 当1=a 时，令.1,21,0)1)(12()(21===--='x x x x x x f当210<<x 时，0)(>'x f ，)(x f 单调增；121<<x 时，0)(<'x f ，)(x f 单调减；1>x 时，0)(>'x f ，)(x f 单调增.∴)(x f 的极大值为2ln 45)21(--=f ，)(x f 的极小值为2)1(-=f . …6分 （Ⅱ）由(Ⅰ)知: .)1)(12(1212)(xx ax a x ax x f --=--+='∴0≤a 时， )1,0(∈x 时，0)(>'x f ，)(x f 单调增，),1(+∞∈x 时，0)(<'x f ，)(x f 单调减；210<<a 时,)1,0(∈x 时，0)(>'x f ，)(x f 单调增，)21,1(ax ∈时，0)(<'x f ，)(x f 单调减， ),21(+∞∈ax 时，0)(>'x f ，)(x f 单调增；21=a 时，),0(+∞∈x 时，0)(>'x f ，)(x f 单调增； 21>a 时，)21,0(a x ∈时，0)(>'x f ，)(x f 单调增，)1,21(a x ∈时，0)(<'x f ，)(x f 单调减，),1(+∞∈x 时，0)(>'x f ，)(x f 单调增.………13分数学试题（文科）参考答案（共5页）第4页20．（本小题满分13分） 解析：（Ⅰ）213113121131131113111-+⋅=-⇒+⋅=⇒+=+++n n n n n n n a a a a a a a ).211(312111-⋅=-⇒+n n a a ……3分 又11=a ，所以.212112111=-=-⇒a ∴数列⎭⎬⎫⎩⎨⎧-211n a 是以12为首项，31为公比的等比数列．…… 6分（Ⅱ）由（Ⅰ）知，,31)211(21111-⋅-=-n n a a ,21312111+⋅=-n n a 所以n na n n n +=-132.…… 8分 令 12333321-++++=n n n T .则n n n nn T 33132313112+-+++=- .∴两式相减得, n n n n T 331313131132132-+++++=- , 即.3432491-⋅+-=n n n T …… 11分 故=++++=n T S n n 21.343249222)1(343249121--⋅+-++=++⋅+-n n n n n n n n . ………13分21．（本小题满分13分）解析：（Ⅰ）因为1F ),0,3(-),0,3(2F 且点)2,3(P 在椭圆E 上，所以.3,6)02()33()02()33(22222==-+-+-++=a a因此.639222=-=-=c a b 故椭圆E 的方程为.16922=+y x …… 5分 （Ⅱ）因为,22=a c 所以c a 2=.设t B F =1（0>t ），则t AB t AF 4,31==. 在21F AF ∆中，)32(322)32(9)32(32)2()32()3(cos 222222t a t a t a t t a t c t a t A -⨯⨯--+=-⨯⨯--+=—————————— 新学期 新成绩 新目标 新方向 ——————————桑水 在2ABF ∆中，)32(42)2()32(16)32(42)2()32()4(cos 222222t a t t a t a t t a t t a t a t A -⨯⨯---+=-⨯⨯---+= ……10分 所以=-⨯⨯--+)32(322)32(9222t a t a t a t )32(42)2()32(16222t a t t a t a t -⨯⨯---+，整理得，.3,32t a a at == 于是,4,5,3212t AB t BF AF t AF ====,90=∠A 故2AF AB ⊥. ………..13分 数学试题（文科）参考答案（共5页）第5页。