2018届高中数学人教B版(理科) 双曲线 单元测试 Word版 含答案

．双曲线的几何性质
学习目标.了解双曲线的几何性质，如范围、对称性、顶点、渐近线和离心率等.能用双曲线的简单性质解决一些简单问题.能区别椭圆与双曲线的性质．
知识点一双曲线的几何性质
类比椭圆的几何性质，结合图象得到双曲线的几何性质如下表：
标准方程
－＝
(＞，＞) －＝
(＞，＞) 图形
性质
范围
对称性
对称轴：
对称中心：
对称轴： 对称中心： 顶点坐标
渐近线
＝± ＝± 离心率
＝，∈(，＋∞)
知识点二双曲线的离心率
思考如何求双曲线的渐近线方程？
思考椭圆中，椭圆的离心率可以刻画椭圆的扁平程度，在双曲线中，双曲线的“张口”大小是图象的一个重要特征，怎样描述双曲线的“张口”大小呢？
梳理双曲线的半焦距与实半轴的比叫做双曲线的，其取值范围是．越大，双曲线的开口．
类型一已知双曲线的标准方程求其简单性质
例求双曲线－＝－的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程
反思与感悟由双曲线的方程研究几何性质的解题步骤
()把双曲线方程化为标准形式是解决本题的关键．
()由标准方程确定焦点位置，确定，的值．
()由＝＋求出值，从而写出双曲线的几何性质．
跟踪训练求双曲线－＝的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程．。

【2015,2016】1.【2016新课标2文数】设F 为抛物线C ：y 2=4x 的焦点，曲线y =kx（k >0）与C 交于点P ，PF ⊥x 轴，则k =（A ）12 （B ）1 （C ）32（D ）2 【答案】D 【解析】【考点】 抛物线的性质，反比例函数的性质【名师点睛】抛物线方程有四种形式，注意焦点的位置. 对于函数y =kx(0)k ≠，当0k >时，在(,0)-∞，(0,)+∞上是减函数，当0k <时，在(,0)-∞，(0,)+∞上是增函数.2. 【2016新课标2文数】(本小题满分12分)已知A 是椭圆E ：22143x y +=的左顶点，斜率为()0k k >的直线交E 于A ，M 两点，点N 在E 上，MA NA ⊥.(Ⅰ)当AM AN =时，求AMN △的面积(Ⅱ) 当2AM AN =2k <<. 【答案】（Ⅰ）14449；（Ⅱ）详见解析. 【解析】试题分析：（Ⅰ）先求直线AM 的方程，再求点M 的纵坐标，最后求AMN ∆的面积；（Ⅱ）设()11,M x y ，将直线AM 的方程与椭圆方程组成方程组，消去y ，用k 表示1x ，从而表示||AM ，同理用k 表示||AN ，再由2AM AN =求k 的取值范围.试题解析：（Ⅰ）设11(,)M x y ，则由题意知10y >.由已知及椭圆的对称性知，直线AM 的倾斜角为π4. 又(2,0)A -，因此直线AM 的方程为2y x =+.将2x y =-代入22143x y +=得27120y y -=.解得0y =或127y =，所以1127y =. 因此AMN ∆的面积11212144227749AMN S ∆=⨯⨯⨯=.【考点】椭圆的性质，直线与椭圆的位置关系【名师点睛】对于直线与椭圆的位置关系问题，通常将直线方程与椭圆方程联立进行求解，注意计算的准确性.3.【2015新课标2文数】已知双曲线过点(,且渐近线方程为12y x =±,则该双曲线的标准方程为 ．【答案】2214x y -=【解析】试题分析：根据双曲线渐近线方程为12y x =±,可设双曲线的方程为224x y m -= ,把(代入224x y m -=得1m =.所以双曲线的方程为2214x y -=.【考点定位】本题主要考查双曲线几何性质及计算能力.【名师点睛】本题是求双曲线的标准方程,若设标准形式,需先判断焦点是在x 轴上,还是在y 轴上,而此题解法通过设共渐近线的双曲线的方程,就不需要判断双曲线焦点是在x 轴上,还是在y 轴上.一般的结论是：以()0,0by x a b a=±>>为渐近线的双曲线的方程可设为()22220x y m m a b -=≠. 4. 【2015新课标2文数】（本小题满分12分）已知椭圆()2222:10x y C a b a b+=>> 的离心率为2,点(在C 上. （I ）求C 的方程；（II ）直线l 不经过原点O ,且不平行于坐标轴,l 与C 有两个交点A ,B ,线段AB 中点为M ,证明：直线OM 的斜率与直线l 的斜率乘积为定值.【答案】（I ）2222184x y +=（II ）见试题解析【解析】试题解析：解：（I ）由题意有22421,2a a b=+= 解得228,4a b ==,所以椭圆C 的方程为2222184x y +=. （II ）设直线():0,0l y kx b k b =+≠≠,()()()1122,,,,,M M A x y B x y M x y ,把y kx b =+代入2222184x y += 得()222214280.k x kbx b +++-=故12222,,22121M M M x x kb bx y kx b k k +-===+=++ 于是直线OM 的斜率1,2M OM M y k x k==- 即12OM k k ⋅=-,所以直线OM 的斜率与直线l 的斜率乘积为定值.【考点定位】本题主要考查椭圆方程、直线与椭圆及计算能力、逻辑推理能力.【名师点睛】本题第一问求椭圆方程的关键是列出关于22,a b 的两个方程,通过解方程组求出22,a b ,解决此类问题要重视方程思想的应用；第二问是证明问题,解析几何中的证明问题通常有以下几类：证明点共线或直线过定点；证明垂直；证明定值问题.一．基础题组1. 【2013课标全国Ⅱ，文5】设椭圆C ：2222=1x y a b+(a ＞b ＞0)的左、右焦点分别为F 1，F 2，P 是C 上的点，PF 2⊥F 1F 2，∠PF 1F 2＝30°，则C 的离心率为( )．AB ．13C ．12 D【答案】：D∴32a x ==，∴c e a === 2. 【2012全国新课标，文4】设F 1，F 2是椭圆E ：22221x y a b+=(a ＞b ＞0)的左、右焦点，P为直线32ax =上一点，△F 2PF 1是底角为30°的等腰三角形，则E 的离心率为( ) A ．12 B ．23 C ．34 D ．45【答案】C3. 【2010全国新课标，文5】中心在原点，焦点在x 轴上的双曲线的一条渐近线经过点(4，－2)，则它的离心率为( )22【答案】：D【解析】b a ＝24＝12e 4. 【2006全国2，文5】已知ABC ∆的顶点B 、C 在椭圆2213x y +=上，顶点A 是椭圆的一个焦点，且椭圆的另外一个焦点在BC 边上，则ABC ∆的周长是( )（A ） （B ）6 （C ） （D ）12 【答案】C【解析】由椭圆的定义椭圆上一点到两焦点的距离之和等于长轴长2a ，可得△ABC 的周长为4a =，所以选C.5. 【2005全国2，文5】抛物线24x y =上一点A 的纵坐标为4，则点A 与抛物线焦点的距离为（ ）(A) 2 (B) 3 (C) 4 (D) 5【答案】D【解析】由题意知(4,4)A ±，抛物线的焦点坐标为(0,1)，所以点A 5=.6. 【2005全国2，文6】双曲线22149x y -=的渐近线方程是（ ）(A) 23y x =±(B) 49y x =±(C) 32y x =±(D) 94y x =±【答案】C【解析】由题意知：2,3a b ==，∴双曲线22149x y -=的渐近线方程是32y x =±.7. 【2014全国2，文20】（本小题满分12分）设12,F F 分别是椭圆22221(0)x y a b a b +=>>的左右焦点，M 是C 上一点且2MF 与x 轴垂直，直线1MF 与C 的另一个交点为N .（Ⅰ）若直线MN 的斜率为34，求C 的离心率； （Ⅱ）若直线MN 在y 轴上的截距为2，且1||5||MN F N ，求,a b . 【答案】见解析8. 【2013课标全国Ⅱ，文20】(本小题满分12分)在平面直角坐标系xOy 中，已知圆P在x 轴上截得线段长为y 轴上截得线段长为 (1)求圆心P 的轨迹方程；(2)若P 点到直线y ＝x 的距离为2，求圆P 的方程． 【答案】见解析9. 【2010全国新课标，文20】设F 1、F 2分别是椭圆E ：x 2＋22y b＝1(0＜b ＜1)的左、右焦点，过F 1的直线l 与E 相交于A ，B 两点，且|AF 2|，|AB|，|BF 2|成等差数列． (1)求|AB|；(2)若直线l 的斜率为1，求b 的值．【解析】：(1)由椭圆定义知|AF 2|＋|AB |＋|BF 2|＝4， 又2|AB |＝|AF 2|＋|BF 2|，得|AB |＝43.(2)l 的方程为y ＝x ＋c ，其中c .10. 【2005全国3，文22】 (本小题满分14分)设),(),,(2211y x B y x A 两点在抛物线22x y =上，l 是AB 的垂直平分线， （Ⅰ）当且仅当21x x +取何值时，直线l 经过抛物线的焦点F ？证明你的结论； （Ⅱ）当3,121-==x x 时，求直线l 的方程.【解析】：（Ⅰ）∵抛物线22x y =，即41,22=∴=p y x ， ∴焦点为1(0,)8F ………………………………………………………1分（1）直线l 的斜率不存在时，显然有021=+x x ………………………………3分 （2）直线l 的斜率存在时，设为k ，截距为b 即直线l ：y=kx+b 由已知得：12121212221k bk y y x x y y ⎧++⎪=⋅+⎪⎨-⎪=-⎪-⎩……………5分2212122212122212222k b k x x x x x x x x ⎧++=⋅+⎪⎪⇒⎨-⎪=-⎪-⎩22121212212k b k x x x x x x +⎧+=⋅+⎪⎪⇒⎨⎪+=-⎪⎩……………7分 2212104b x x ⇒+=-+≥14b ⇒≥即l 的斜率存在时，不可能经过焦点1(0,)8F ……………………………………8分 所以当且仅当12x x +=0时，直线l 经过抛物线的焦点F …………………………9分二．能力题组1. 【2014全国2，文10】设F 为抛物线2:=3C y x 的焦点，过F 且倾斜角为30︒的直线交C 于A ,B 两点，则 AB =（ ）（A）3（B ）6 （C ）12 （D）【答案】C【解析】由题意，得3(,0)4F ．又因为0k tan 303==，故直线AB 的方程为3y )4=-，与抛物线2=3y x 联立，得21616890x x -+=，设1122(x ,y ),(x ,y )A B ，由抛物线定义得，12x x AB p =++=168312162+=，选C ． 2. 【2013课标全国Ⅱ，文10】设抛物线C ：y 2＝4x 的焦点为F ，直线l 过F 且与C 交于A ，B 两点．若|AF |＝3|BF |，则l 的方程为( )．A ．y ＝x －1或y ＝－x ＋1B ．y 1)x -或y ＝1)x -C ．y ＝(1)3x -或y ＝1)3x --D ．y ＝1)2x -或y ＝1)2x -- 【答案】：C3. 【2012全国新课标，文10】等轴双曲线C 的中心在原点，焦点在x 轴上，C 与抛物线y 2＝16x 的准线交于A ，B 两点，||AB C 的实轴长为( )A B ． C ．4 D ．8 【答案】 C4. 【2006全国2，文9】已知双曲线22221x y a b-=的一条渐近线方程为43y x =，则双曲线的离心率为( ) （A ）53 （B ）43 （C ）54 （D ）32【答案】A5. 【2005全国3，文9】已知双曲线1222=-y x 的焦点为F 1、F 2，点M 在双曲线上且120,MF MF ⋅=则点M 到x 轴的距离为（ ）A ．43B ．53CD【答案】C【解析】∵点M 在双曲线上，∴12||||||22MF MF a -==，12||2F F c ==，又∵120MF MF ∙=，∴12MF F ∆为直角三角形，∴2221212||||||12MF MF F F +==，∴12||||4MFMF =， 设点M 到x 轴的距离为d ，∵120MF MF ∙= ，∴12MFMF ⊥，∴12121211||||||22MF F S MF MF F F d ∆==∙，∴1212||||||MF MF d F F ===. 6. 【2012全国新课标，文20】设抛物线C ：x 2＝2py (p ＞0)的焦点为F ，准线为l ，A 为C上一点，已知以F 为圆心，FA 为半径的圆F 交l 于B ，D 两点．(1)若∠BFD ＝90°，△ABD 的面积为p 的值及圆F 的方程；(2)若A ，B ，F 三点在同一直线m 上，直线n 与m 平行，且n 与C 只有一个公共点，求坐标原点到m ，n 距离的比值． 【答案】见解析(2)因为A ，B ，F 三点在同一直线m 上， 所以AB 为圆F 的直径，∠ADB ＝90°. 由抛物线定义知|AD |＝|FA |＝12|AB |，所以∠ABD ＝30°，m 的斜率为3或3-.当m n ：y ＋b ，代入x 2＝2py ，得x 2px －2pb ＝0.由于n 与C 只有一个公共点，故∆＝43p 2＋8pb ＝0， 解得6p b =-. 因为m 的截距12p b =，1||3||b b =，所以坐标原点到m ，n 距离的比值为3.当m 的斜率为3时，由图形对称性可知，坐标原点到m ，n 距离的比值为3. 三．拔高题组1. 【2010全国2，文12】已知椭圆C ：22x a ＋22y b ＝1(a ＞b ＞0)的离心率为2，过右焦点F 且斜率为k (k ＞0)的直线与C 相交于A 、B 两点，若AF ＝3FB，则k 等于( )A ．．2 【答案】：B∴|AM |＝|AA 1|－|MA 1|＝|AA 1|－|BB 1|＝2FBe，而|AB |＝|AF |＋|FB |＝4|FB |，在Rt△BAM 中，cos∠BAM ＝AM AB＝24FBe FB ＝12e∴sin ∠BAMk ＝tan ∠BAM2. 【2007全国2，文11】已知椭圆的长轴长是短轴长的2倍,则椭圆的离心率为( )(A) 13(B)33 (C)21 (D)23 【答案】：D3. 【2007全国2，文12】设F 1,F 2分别是双曲线1922=-y x 的左右焦点，若点P 在双曲线上,且120PF PF ∙= ，则12||PF PF +=( )(A)10(B)102(C)5 (D) 52【答案】：B【解析】∵120PF PF ∙= ，∴12PFPF ⊥，∴221212||||4(19)40PF PF F F +==+=，∴12||PF PF +=4. 【2006全国2，文11】过点（－1，0）作抛物线21y x x =++的切线，则其中一条切线为( )（A ）220x y ++= （B ）330x y -+= （C ）10x y ++= （D ）10x y -+= 【答案】D 【解析】5. 【2005全国3，文10】设椭圆的两个焦点分别为F1、、F 2，过F 2作椭圆长轴的垂线交椭圆于点P ，若△F 1PF 2为等腰直角三角形，则椭圆的离心率是（ ）AC．2D1【答案】D6. 【2010全国2，文15】已知抛物线C ：y 2＝2px (p ＞0)的准线为l ，过M (1,0)的直线与l 相交于点A ，与C 的一个交点为B ，若AM ＝MB，则p ＝________. 【答案】：2 【解析】：l ：x ＝－2p，过M (1,0)yx －1)，联立得21)p x y x ⎧=-⎪⎨⎪=-⎩解得23(1)2p x p y ⎧=-⎪⎪⎨⎪=+⎪⎩∴A (－2p2p ＋1))．又∵AM ＝MB ，∴M 点为AB 的中点．∴B 点坐标为(2p ＋22p＋1))．将B (2p ＋22p ＋1))代入y 2＝2px (p ＞0)，得3(2p ＋1)2＝2p (2p ＋2)，解得p ＝2或p ＝－6(舍)．7. ）【2010全国2，文22】已知斜率为1的直线l 与双曲线C ：22x a－22y b ＝1(a ＞0，b ＞0)相交于B 、D 两点，且BD 的中点为M (1,3)． (1)求C 的离心率；(2)设C 的右顶点为A ，右焦点为F ，|DF |·|BF |＝17，证明过A 、B 、D 三点的圆与x 轴相切．(2)由①②知，C 的方程为3x 2－y 2＝3a 2，A (a,0)，F (2a,0)，x 1＋x 2＝2，x 1·x 2＝－2432a +＜0，故不妨设x 1≤－a ，x 2≥a .|BF |a －2x 1，|FD |2x 2－a .|BF |·|FD |＝(a －2x 1)(2x 2－a ) ＝－4x 1x 2＋2a (x 1＋x 2)－a 2＝5a 2＋4a ＋8. 又|BF |·|FD |＝17， 故5a 2＋4a ＋8＝17， 解得a ＝1或a ＝－95(舍去)．故|BD |x 1－x 2| 6.连结MA ，则由A (1,0)，M (1,3)知|MA |＝3，从而MA ＝MB ＝MD ，且MA ⊥x 轴，因此以M 为圆心，MA 为半径的圆经过A 、B 、D 三点，且在点A 处与x 轴相切． 所以过A 、B 、D 三点的圆与x 轴相切． 8. 【2006全国2，文22】（本小题满分１２分） 已知抛物线24x y =的焦点为F ，A 、B 是抛物线上的两动点，且(0).AF FB λλ=>过A 、B两点分别作抛物线的切线，设其交点为M 。

[高考基础题型得分练]1．双曲线x 2－my 2＝1的实轴长是虚轴长的2倍，则m ＝( ) A.14 B.12 C ．2 D ．4答案：D解析：双曲线的方程可化为x 2－y21m＝1，∴实轴长为2，虚轴长为21m ，∴2＝2×21m ，解得m ＝4.2．已知双曲线C 的渐近线方程为y ＝±2x ，且经过点(2,2)，则C 的方程为( )A.x 23－y 212＝1 B.x 212－y 23＝1 C.y 23－x 212＝1 D.y 212－x 23＝1答案：A解析：由题意，设双曲线C 的方程为y 24－x 2＝λ(λ≠0)，因为双曲线C 过点(2,2)，则224－22＝λ，解得λ＝－3，所以双曲线C 的方程为y 24－x 2＝－3，即x 23－y212＝1.3．[2017·吉林长春模拟]已知F 1，F 2是双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的两个焦点，以F 1F 2为直径的圆与双曲线的一个交点是P ，且△F 1PF 2的三条边长成等差数列，则此双曲线的离心率是( )A. 2B. 3 C ．2 D ．5答案：D解析：不妨设点P 位于第一象限，F 1为左焦点，|PF 2|＝m －d ，|PF 1|＝m ，|F 1F 2|＝m ＋d ，其中m ＞d ＞0，则有(m －d )2＋m 2＝(m ＋d )2，解得m ＝4d ，故双曲线的离心率 e ＝|F 1F 2||PF 1|－|PF 2|＝5.4．若双曲线x 2＋y 2m ＝1的一条渐近线的倾斜角α∈⎝ ⎛⎭⎪⎫0，π3，则m 的取值范围是( )A ．(－3,0)B ．(－3，0)C ．(0,3) D.⎝ ⎛⎭⎪⎫－33，0答案：A解析：由题意可知m <0，双曲线的标准方程为x 2－y 2－m＝1，经过第一、三象限的渐近线方程为y ＝－mx ，因为其倾斜角α∈⎝⎛⎭⎪⎫0，π3，所以－m ＝tan α∈(0，3)，故m ∈(－3,0)．5．[2017·河南郑州模拟]已知双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的右焦点为F ，过F 作斜率为－1的直线交双曲线的渐近线于点P ，点P 在第一象限，O 为坐标原点，若△OFP 的面积为a 2＋b 28，则该双曲线的离心率为( )A.53B.73C.103D.153答案：C解析：如图所示，由 k PF ＝－1，得∠PFO ＝π4， 由 k OP ＝tan ∠POF ＝ba ，得 sin ∠POF ＝b a 2＋b 2＝bc ，cos ∠POF ＝a a 2＋b2＝ac ，所以sin ∠OPF ＝sin ⎝ ⎛⎭⎪⎫∠POF ＋π4＝b c ×22＋a c ×22＝a ＋b2c.又∵S △OPF ＝12c ·|PF |·22＝a 2＋b 28＝c 28，得|PF |＝c22，由正弦定理，得a ＋b 2c c ＝b cc 22，整理得a ＝3b ，又a 2＋b 2＝c 2，故e ＝103.6．[2015·新课标全国卷Ⅰ]已知M (x 0，y 0)是双曲线C ：x 22－y 2＝1上的一点，F 1，F 2是C 的两个焦点．若MF 1→·MF 2→＜0，则y 0的取值范围是( )A.⎝ ⎛⎭⎪⎫－33，33B.⎝ ⎛⎭⎪⎫－36，36C.⎝⎛⎭⎪⎫－223，223 D.⎝⎛⎭⎪⎫－233，233 答案：A解析：由题意知，a ＝2，b ＝1，c ＝3， ∴ F 1(－3，0)，F 2(3，0)，∴ MF 1→＝(－3－x 0，－y 0)，MF 2→＝(3－x 0，－y 0)． ∵ MF 1→·MF 2→＜0，∴ (－3－x 0)(3－x 0)＋y 20＜0， 即x 20－3＋y 20＜0.∵ 点M (x 0，y 0)在双曲线上，∴ x 202－y 20＝1，即x 20＝2＋2y 20， ∴ 2＋2y 20－3＋y 20＜0，∴ －33＜y 0＜33.故选A.7．已知F 为双曲线C ：x 29－y 216＝1的左焦点，P ，Q 为C 上的点．若PQ 的长等于虚轴长的2倍，点A (5,0)在线段PQ 上，则△PQF 的周长为________．答案：44解析：由x 29－y 216＝1，得a ＝3，b ＝4，c ＝5. ∴|PQ |＝4b ＝16>2a .又∵A (5,0)在线段PQ 上， ∴P ，Q 在双曲线的右支上， 且PQ 所在直线过双曲线的右焦点，由双曲线定义知，⎩⎪⎨⎪⎧|PF |－|P A |＝2a ＝6，|QF |－|QA |＝2a ＝6，∴|PF |＋|QF |＝28.∴△PQF 的周长是|PF |＋|QF |＋|PQ |＝28＋16＝44.8．已知F 1，F 2是双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的两焦点，以线段F 1F 2为边作正三角形MF 1F 2，若边MF 1的中点P 在双曲线上，则双曲线的离心率是________．答案：3＋1解析：因为MF 1的中点P 在双曲线上，|PF 2|－|PF 1|＝2a ，△MF 1F 2为正三角形，边长都是2c ，所以3c －c ＝2a ，所以e ＝c a ＝23－1＝3＋1.9．过双曲线C ：x 2a 2－y 2b 2＝1(a >0，b >0)的右焦点作一条与其渐近线平行的直线，交C 于点P .若点P 的横坐标为2a ，则C 的离心率为________．答案：2＋3解析：如图，F 1，F 2为双曲线C 的左，右焦点，将点P 的横坐标2a 代入x 2a 2－y 2b 2＝1中，得y 2＝3b 2， 不妨令点P 的坐标为(2a ，－3b )， 此时kPF 2＝3bc －2a ＝ba ，得到c ＝(2＋3)a ，即双曲线C 的离心率e ＝ca ＝2＋ 3.10．[2017·江南十校联考]已知双曲线的中心在原点，焦点F 1，F 2在坐标轴上，离心率为2，且过点P (4，－10)．(1)求双曲线的方程；(2)若点M (3，m )在双曲线上，求证：MF 1→·MF 2→＝0. (1)解：∵e ＝2，∴可设双曲线的方程为x 2－y 2＝λ(λ≠0)． ∵双曲线过点(4，－10)， ∴16－10＝λ，即λ＝6. ∴双曲线的方程为x 2－y 2＝6.(2)证明：证法一：由(1)可知，a ＝b ＝6， ∴c ＝23，∴F 1(－23，0)，F 2(23，0)， ∴kMF 1＝m 3＋23，kMF 2＝m 3－23，kMF 1·kMF 2＝m 29－12＝－m 23.∵点M (3，m )在双曲线上， ∴9－m 2＝6，m 2＝3， 故kMF 1·kMF 2＝－1， ∴MF 1⊥MF 2.∴MF 1→·MF 2→＝0.证法二：由(1)可知，a ＝b ＝6，∴c ＝23， ∴F 1(－23，0)，F 2(23，0)，MF 1→＝(－23－3，－m )，MF 2→＝(23－3，－m )， ∴MF 1→·MF 2→＝(3＋23)×(3－23)＋m 2＝－3＋m 2， ∵点M (3,0)在双曲线上， ∴9－m 2＝6，即m 2－3＝0， ∴MF 1→·MF 2→＝0.[冲刺名校能力提升练]1．如图，F 1，F 2是椭圆C 1：x 24＋y 2＝1与双曲线C 2的公共焦点，A ，B 分别是C 1，C 2在第二、四象限的公共点．若四边形AF 1BF 2为矩形，则C 2的离心率是( )A. 2B. 3C.32D.62答案：D解析：|F1F2|＝2 3.设双曲线的方程为x2a2－y2b2＝1(a＞0，b＞0)．∵|AF2|＋|AF1|＝4，|AF2|－|AF1|＝2a，∴|AF2|＝2＋a，|AF1|＝2－a.在Rt△F1AF2中，∠F1AF2＝90°，∴|AF1|2＋|AF2|2＝|F1F2|2，即(2－a)2＋(2＋a)2＝(23)2，∴a＝2，∴e＝ca＝32＝62.故选D.2.[2017·广西柳州、北海、钦州三市联考]已知双曲线x2a2－y2b2＝1(a>0，b>0)与抛物线y2＝8x有一个公共的焦点F，且两曲线的一个交点为P，若|PF|＝5，则双曲线的渐近线方程为()A．x±2y＝0 B．2x±y＝0C．x±3y＝0 D.3x±y＝0答案：D解析：抛物线y2＝8x的焦点坐标为(2,0)，准线方程为直线x＝－2，∵双曲线x2a2－y2b2＝1(a＞0，b＞0)与抛物线y2＝8x有一个公共的焦点F，则双曲线的半焦距c＝2，∴a2＋b2＝4，①又∵|PF|＝5，∴点P的横坐标为3，代入抛物线y2＝8x得y＝±26，则P(3，±26)，∵点P在双曲线上，则有9a2－24b2＝1，②联立①②，解得a＝1，b＝3，∴双曲线x2a2－y2b2＝1的渐近线方程为y＝±3x.3．[2017·山西太原二模]已知F1，F2分别是双曲线x2a2－y2b2＝1(a>0，b>0)的左、右焦点，过F1的直线l与双曲线的左、右两支分别交于点A，B，若|AB|＝|AF2|，∠F1AF2＝90°，则双曲线的离心率为()A.6＋32 B.6＋ 3C.5＋222 D.5＋2 2答案：B解析：∵|AB|＝|AF2|，∠F1AF2＝90°，∴|BF2|＝2|AF2|.又由双曲线的定义知，|BF1|－|BF2|＝2a，∴|AF1|＋|AB|－2|AF2|＝2a，即|AF1|＋(1－2)·|AF2|＝2a.又|AF2|－|AF1|＝2a，∴|AF2|＝2(2＋2)a，|AF1|＝2(1＋2)a. 在Rt△AF1F2中，|AF1|2＋|AF2|2＝|F1F2|2，即[2(2＋2)a]2＋[2(1＋2)a]2＝(2c)2，∴c2a2＝9＋62，∴e＝9＋62＝6＋ 3.故选B.4．设直线x－3y＋m＝0(m≠0)与双曲线x2a2－y2b2＝1(a＞0，b＞0)的两条渐近线分别交于点A，B.若点P(m,0)满足|P A|＝|PB|，则该双曲线的离心率是________．答案：52解析：由⎩⎨⎧x －3y ＋m ＝0，y ＝ba x ，得点A 的坐标为⎝ ⎛⎭⎪⎫am 3b －a ，bm 3b －a ，由⎩⎨⎧x －3y ＋m ＝0，y ＝－b a x ，得点B 的坐标为⎝⎛⎭⎪⎫－am 3b ＋a ，bm 3b ＋a ， 则AB 的中点C 的坐标为⎝ ⎛⎭⎪⎫a 2m 9b 2－a 2，3b 2m 9b 2－a 2，而k AB ＝13，由|P A |＝|PB |，可得AB 的中点C 与点P 连线的斜率为－3， 即k CP ＝3b 2m 9b 2－a 2a 2m 9b 2－a 2－m＝－3，化简得⎝ ⎛⎭⎪⎫b a 2＝14，所以双曲线的离心率e ＝1＋⎝ ⎛⎭⎪⎫b a 2＝1＋14＝52.5．[2017·甘肃兰州诊断]已知曲线C ：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的一条渐近线的方程为y ＝3x ，右焦点F 到直线x ＝a 2c 的距离为32.(1)求双曲线C 的方程；(2)斜率为1且在y 轴上的截距大于0的直线l 与双曲线C 相交于B ，D 两点，已知A (1,0)，若DF →·BF →＝1，证明：过A ，B ，D 三点的圆与x 轴相切．(1)解：依题意有b a ＝3，c －a 2c ＝32，∵a 2＋b 2＝c 2，∴c ＝2a ，∴a ＝1，c ＝2，∴b 2＝3，∴双曲线C 的方程为x 2－y 23＝1.(2)证明：设直线l 的方程为y ＝x ＋m (m ＞0)，B (x 1，x 1＋m )，D (x 2，x 2＋m )，BD 的中点为M ，由⎩⎨⎧ y ＝x ＋m ，x 2－y 23＝1，得2x 2－2mx －m 2－3＝0，∴x 1＋x 2＝m ，x 1x 2＝－m 2＋32，又DF →·BF →＝1，即(2－x 1)(2－x 2)＋(x 1＋m )(x 2＋m )＝1，∴m ＝0(舍去)或m ＝2，∴x 1＋x 2＝2，x 1x 2＝－72，点M 的横坐标为x 1＋x 22＝1，∵DA →·BA →＝(1－x 1)(1－x 2)＋(x 1＋2)(x 2＋2)＝5＋2x 1x 2＋x 1＋x 2＝5－7＋2＝0，∴AD ⊥AB ，∴过A ，B ，D 三点的圆以点M 为圆心，BD 为直径，∵点M 的横坐标为1，∴MA ⊥ x 轴．∴过A ，B ，D 三点的圆与x 轴相切．6．已知中心在原点的双曲线C 的右焦点为(2,0)，实轴长为2 3.(1)求双曲线C 的方程；(2)若直线l ：y ＝kx ＋2与双曲线C 左支交于A ，B 两点，求k 的取值范围；(3)在(2)的条件下，线段AB 的垂直平分线l 0与y 轴交于M (0，m )，求m 的取值范围．解：(1)设双曲线C 的方程为x 2a 2－y 2b 2＝1(a >0，b >0)．由已知，得a ＝3，c ＝2，再由a 2＋b 2＝c 2，得b 2＝1，∴双曲线C 的方程为x 23－y 2＝1.(2)设A (x A ，y A )，B (x B ，y B )，将y ＝kx ＋2代入x 23－y 2＝1，得(1－3k 2)x 2－62kx －9＝0.由题意知，⎩⎪⎨⎪⎧ 1－3k 2≠0，Δ＝36(1－k 2)>0，x A ＋x B ＝62k 1－3k 2<0，x A x B ＝－91－3k 2>0，解得33<k <1.此时，l 与双曲线左支有两个交点．故k 的取值范围为⎝ ⎛⎭⎪⎫33，1. (3)由(2)，得x A ＋x B ＝62k 1－3k 2， ∴y A ＋y B ＝(kx A ＋2)＋(kx B ＋2)＝k (x A ＋x B )＋22＝221－3k 2. ∴AB 的中点P 的坐标为⎝ ⎛⎭⎪⎫32k 1－3k 2，21－3k 2. 设直线l 0的方程为y ＝－1k x ＋m ，将点P 的坐标代入直线l 0的方程，得m ＝421－3k 2. ∵33<k <1，∴－2<1－3k 2<0.∴m <－2 2.∴m 的取值范围为(－∞，－22)．。

2018年普通高等学校招生全国统一考试理科数学注意事项:1 •答卷前，考生务必将自己的姓名、考生号等填写在答题卡和试卷指定位置上。

2•回答选择题时，选出每小题答案后，用铅笔把答题卡对应题目的答案标号涂黑。

如需改动，用橡皮 擦干净后，再选涂其它答案标号。

回答非选择题时，将答案写在答题卡上。

写在本试卷上无效。

3 •考试结束后，将本试卷和答题卡一并交回。

一、选择题：本题共 12小题，每小题5分，共60分。

在每小题给出的四个选项中，只有一项是符合题目 要求的。

1 —i1 .设 z 二——2i ，则 | z| =1 +i1lA . 0B .C . 1D ••- 222.已知集合 A ={x x 2 —x —2 >0}，则 e R A =A. {x —1c x c 2}B . {x —1^x^2}C . 1x|x ：：：-1U1x|x 2?D . Cx|x^-1iu 「x|x_2l3 .某地区经过一年的新农村建设，农村的经济收入增加了一倍，实现翻番，为更好地了解该地区农村的经 济收入变化情况，统计了该地区新农村建设前后农村的经济收入构成比例，得到如下饼图：建设前经济收入构成比例则下面结论中不正确的是 A .新农村建设后，种植收入减少B. 新农村建设后，其他收入增加了一倍以上C. 新农村建设后，养殖收入增加了一倍绝密★启用前建设后经济收入构成比例C . P 2=P 3D . P 1 = P 2+P 3D •新农村建设后，养殖收入与第三产业收入的总和超过了经济收入的一半 4 .设S n 为等差数列 玄1的前n 项和，若3S^ = S 2 S 4， a i=2，则氏口A . -12B . -10C . 10D . 125.设函数f (x) = x 3 (a -1)x 2 ax ，若f(x)为奇函数，则曲线、二f (x)在点(0,0)处的切线方程为6.在厶ABC 中，AD 为BC 边上的中线，E 为AD 的中点，贝V EB =9.已知函数f(x)=*e ，X 兰°’ g(x)= f(x)+x+a .若g (x )存在2个零点，贝y a 的取值范围是Jn x , x >0,10 .下图来自古希腊数学家希波克拉底所研究的几何图形.此图由三个半圆构成，三个半圆的直径分别为直角三角形 ABC 的斜边BC ,直角边AB , AC . A ABC 的三边所围成的区域记为 I ，黑色部分记为II , 其余部分记为III .在整个图形中随机取一点，此点取自 1,11 , III 的概率分别记为P 1, P 2, P 3,则B . y - -xC . y =2x3 1 T A . —AB -一 AC4 41 3T B . —AB- —AC 4 4 31 T C . -ABAC 4 41 3 T D . — AB — AC 4 47.某圆柱的高为 2,底面周长为16,其三视图如图.圆柱表面上的点M 在正视图上的对应点为 A ，圆柱 表面上的点N 在左视图上的对应点为 B ，则在此圆柱侧面上，从M 到N 的路径中，最短路径的长度为A . 2 .172.5设抛物线 2C : y =4x 的焦点为F ,2过点(-,0 )且斜率为一 3的直线与C 交于M , N 两点，则7M FN =A . [ - , 0)B . [0 , +8)C . [ - , +8)D . [1 , +8)A . P1=P2B . P1=P3C . P2=P3D . P1 = P2+P3211.已知双曲线C：— -y2 =1 , O为坐标原点，F为C的右焦点，过F的直线与C的两条渐近线的交点3分别为M、N.若厶OMN为直角三角形，则|MN|=3 A .-2 B . 3C. 2「3D. 412.已知正方体的棱长为 1 ,每条棱所在直线与平面a所成的角相等，则a截此正方体所得截面面积的最大值为A . 31B.二C. 口 D . -J4342、填空题：本题共4小题，每小题5分，共20分。

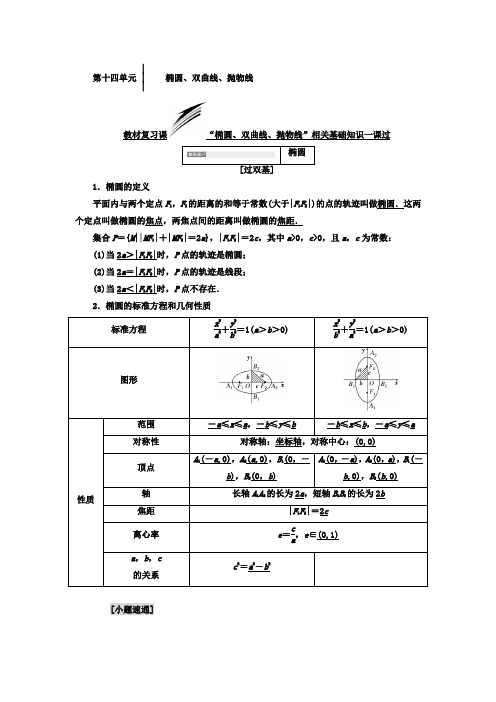
第十四单元 ⎪⎪⎪椭圆、双曲线、抛物线教材复习课“椭圆、双曲线、抛物线”相关基础知识一课过1．椭圆的定义平面内与两个定点F 1，F 2的距离的和等于常数(大于|F 1F 2|)的点的轨迹叫做椭圆．这两个定点叫做椭圆的焦点，两焦点间的距离叫做椭圆的焦距．集合P ＝{M ||MF 1|＋|MF 2|＝2a }，|F 1F 2|＝2c ，其中a >0，c >0，且a ，c 为常数： (1)当2a ＞|F 1F 2|时，P 点的轨迹是椭圆； (2)当2a ＝|F 1F 2|时，P 点的轨迹是线段； (3)当2a ＜|F 1F 2|时，P 点不存在． 2．椭圆的标准方程和几何性质[小题速通]1．设P 是椭圆x 225＋y 216＝1上的点，若F 1，F 2是椭圆的两个焦点，则|PF 1|＋|PF 2|等于( )A ．4B ．5C ．8D ．10解析：选D 由椭圆的定义知：|PF 1|＋|PF 2|＝2×5＝10.2．(2016·天津红桥一模)已知椭圆C 的焦点在y 轴上，焦距等于4，离心率为22，则椭圆C 的标准方程是( )A.x 216＋y 212＝1 B.x 212＋y 216＝1 C.x 24＋y 28＝1 D.x 28＋y 24＝1 解析：选 C 由题意可得2c ＝4，故c ＝2，又e ＝2a ＝22，解得a ＝22，故b ＝()222－22＝2，因为焦点在y 轴上，故选C.3．(2017·临沂一中模拟)设椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为F 1，F 2，P是C 上的点，PF 2⊥F 1F 2，∠PF 1F 2＝30°，则C 的离心率为( )A.36B.13C.12D.33解析：选D 在Rt △PF 2F 1中，令|PF 2|＝1，因为∠PF 1F 2＝30°，所以|PF 1|＝2，|F 1F 2|＝ 3.故e ＝2c 2a ＝|F 1F 2||PF 1|＋|PF 2|＝33.故选D.4．若焦点在x 轴上的椭圆x 22＋y 2m ＝1的离心率为12，则m ＝________.解析：因为焦点在x 轴上，所以0＜m ＜2，所以a 2＝2，b 2＝m ，c 2＝a 2－b 2＝2－m .椭圆的离心率为e ＝12，所以e 2＝14＝c 2a 2＝2－m 2，解得m ＝32.答案：32[清易错]1．椭圆的定义中易忽视2a ＞|F 1F 2|这一条件，当2a ＝|F 1F 2|其轨迹为线段F 1F 2，当2a ＜|F 1F 2|不存在轨迹．2．求椭圆的标准方程时易忽视判断焦点的位置，而直接设方程为x 2a 2＋y 2b2＝1(a ＞b ＞0)．1．若直线x －2y ＋2＝0经过椭圆的一个焦点和一个顶点，则该椭圆的标准方程为( ) A.x 25＋y 2＝1 B.x 24＋y 25＝1 C.x 25＋y 2＝1或x 24＋y 25＝1 D ．以上答案都不对解析：选C 直线与坐标轴的交点为(0,1)，(－2,0)， 由题意知当焦点在x 轴上时，c ＝2，b ＝1， ∴a 2＝5，所求椭圆的标准方程为x 25＋y 2＝1.当焦点在y 轴上时，b ＝2，c ＝1， ∴a 2＝5，所求椭圆标准方程为y 25＋x 24＝1.2．已知椭圆x 29＋y 24－k ＝1的离心率为45，则k 的值为( )A ．－21B ．21C ．－1925或21 D.1925或－21解析：选D 当9＞4－k ＞0，即4＞k ＞－5时，a ＝3，c 2＝9－(4－k )＝5＋k ，∴5＋k 3＝45，解得k ＝1925. 当9＜4－k ，即k ＜－5时，a ＝4－k ，c 2＝－k －5， ∴－k －54－k＝45，解得k ＝－21，所以k 的值为1925或－21. 双曲线1．双曲线的定义平面内与两个定点F 1，F 2的距离的差的绝对值等于常数(小于|F 1F 2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的焦点，两焦点间的距离叫做双曲线的焦距．集合P ＝{M |||MF 1|－|MF 2||＝2a }，|F 1F 2|＝2c ，其中a ，c 为常数且a >0，c >0. (1)当2a <|F 1F 2|时，P 点的轨迹是双曲线； (2)当2a ＝|F 1F 2|时，P 点的轨迹是两条射线； (3)当2a >|F 1F 2|时，P 点不存在． 2．标准方程(1)中心在坐标原点，焦点在x 轴上的双曲线的标准方程为x 2a 2－y 2b 2＝1(a >0，b >0)；(2)中心在坐标原点，焦点在y 轴上的双曲线的标准方程为y 2a 2－x 2b2＝1(a >0，b >0)．3．双曲线的性质[小题速通]1．(2017·邢台摸底)双曲线x 2－4y 2＝－1的渐近线方程为( ) A ．x ±2y ＝0 B ．y ±2x ＝0 C ．x ±4y ＝0D ．y ±4x ＝0解析：选A 依题意，题中的双曲线即y 214－x 2＝1，因此其渐近线方程是y 214－x 2＝0，即x ±2y＝0，选A.2．(2017·江南十校联考)已知双曲线的焦距为23，离心率为3，则双曲线的标准方程是( )A ．x 2－y 22＝1 B.x 24－y 28＝1C ．x 2－y 22＝1或y 2－x 22＝1 D.y 22－x 2＝1解析：选C 因为双曲线的焦距为23，所以2c ＝23，c ＝3，因为双曲线的离心率为3，所以c a＝3，a ＝1，因为a 2＋b 2＝c 2，所以b 2＝2，由题意无法判断焦点的位置，故有两个标准方程，故选C.3．(2016·甘肃张掖一诊)如图，F 1，F 2分别是双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的左、右焦点，过F 1的直线l 与双曲线的左、右两支分别交于点B ，A .若△ABF 2为等边三角形，则双曲线的离心率为( )A.7 B ．4 C.233D. 3解析：选 A 依题意得|AB |＝|AF 2|＝|BF 2|，结合双曲线的定义可得|BF 1|＝2a ，|BF 2|＝4a ，|F 1F 2|＝2c ，根据等边三角形，可知∠F 1BF 2＝120°，应用余弦定理，可得4a 2＋16a 2＋2×2a ×4a ×12＝4c 2，整理得c a＝7，故选A.4．已知F 为双曲线C ：x 29－y 216＝1的左焦点，P ，Q 为C 上的点．若PQ 的长等于虚轴长的2倍，点A (5,0)在线段PQ 上，则△PQF 的周长为________．解析：由题意得，|FP |－|PA |＝6，|FQ |－|QA |＝6，两式相加，利用双曲线的定义得|FP |＋|FQ |＝28，所以△PQF 的周长为|FP |＋|FQ |＋|PQ |＝44.答案：44[清易错]1．双曲线的定义中易忽视2a ＜|F 1F 2|这一条件．若2a ＝|F 1F 2|，则轨迹是以F 1，F 2为端点的两条射线，若2a ＞|F 1F 2|，则轨迹不存在．2．注意区分双曲线中的a ，b ，c 大小关系与椭圆中的a ，b ，c 关系，在椭圆中a 2＝b 2＋c 2，而在双曲线中c 2＝a 2＋b 2.3．易忽视渐近线的斜率与双曲线的焦点位置关系．当焦点在x 轴上，渐近线斜率为±ba，当焦点在y 轴上，渐近线斜率为±a b.1．双曲线x 236－m 2－y 2m2＝1(0＜m ＜3)的焦距为( )A ．6B ．12C ．36D ．236－2m 2解析：选B c 2＝36－m 2＋m 2＝36，∴c ＝6.双曲线的焦距为12. 2．双曲线x 24－y 212＝1的焦点到渐近线的距离为( )A ．2 3B ．2 C. 3D ．1解析：选A 由题意知双曲线的渐近线方程为y ＝±3x ，焦点为(±4,0)，故焦点到渐近线的距离d ＝2 3.1．抛物线的定义平面内与一个定点F 和一条定直线l (l 不经过点F )的距离相等的点的轨迹叫做抛物线．点F 叫做抛物线的焦点，直线l 叫做抛物线的准线．2．抛物线的标准方程与几何性质[小题速通]1．已知抛物线y 2＝2px (p ＞0)的准线经过点(－1,1)，则该抛物线焦点坐标为( ) A ．(－1,0) B ．(1,0) C ．(0，－1)D ．(0,1)解析：选B 抛物线y 2＝2px (p ＞0)的准线为x ＝－p 2且过点(－1,1)，故－p2＝－1，解得p ＝2.所以抛物线的焦点坐标为(1,0)．2．若抛物线y ＝4x 2上的一点M 到焦点的距离为1，则点M 的纵坐标是( ) A.1716B.1516C.78D ．0解析：选B M 到准线的距离等于M 到焦点的距离，又准线方程为y ＝－116，设M (x ，y )，则y ＋116＝1，∴y ＝1516.3．已知抛物线C ：y 2＝x 的焦点为F ，A (x 0，y 0)是C 上一点，|AF |＝54x 0，则x 0＝( )A ．4B ．2C ．1D ．8解析：选C 由y 2＝x ，得2p ＝1，即p ＝12，因此焦点F ⎝ ⎛⎭⎪⎫14，0，准线方程为l ：x ＝－14.设A 点到准线的距离为d ，由抛物线的定义可知d ＝|AF |，从而x 0＋14＝54x 0，解得x 0＝1，故选C.4．(2017·唐山模拟)已知抛物线的焦点F (a,0)(a ＜0)，则抛物线的标准方程是( ) A ．y 2＝2ax B ．y 2＝4ax C ．y 2＝－2axD ．y 2＝－4ax解析：选B 以F (a,0)为焦点的抛物线的标准方程为y 2＝4ax .[清易错]1．抛物线的定义中易忽视“定点不在定直线上”这一条件，当定点在定直线上时，动点的轨迹是过定点且与直线垂直的直线．2．抛物线标准方程中参数p 易忽视只有p ＞0，才能证明其几何意义是焦点F 到准线l 的距离，否则无几何意义．1．抛物线y ＝ax 2的准线方程是y ＝1，则a 的值为( ) A.14B ．－14C ．4D ．－4解析：选B 由题意知抛物线的标准方程为x 2＝1a y ，所以准线方程y ＝－14a ＝1，解得a＝－14.2．动圆过点(1,0)，且与直线x ＝－1相切，则动圆的圆心的轨迹方程为________． 解析：设动圆的圆心坐标为(x ，y )，则圆心到点(1,0)的距离与到直线x ＝－1的距离相等，根据抛物线的定义易知动圆的圆心的轨迹方程为y 2＝4x .答案：y 2＝4x[过双基]1．直线与圆锥曲线的位置关系判断直线l 与圆锥曲线C 的位置关系时，通常将直线l 的方程Ax ＋By ＋C ＝0(A ，B 不同时为0)代入圆锥曲线C 的方程F (x ，y )＝0，消去y (也可以消去x )得到一个关于变量x (或变量y )的一元方程．即⎩⎪⎨⎪⎧Ax ＋By ＋C ＝0，F x ，y ＝0，消去y ，得ax 2＋bx ＋c ＝0.(1)当a ≠0时，设一元二次方程ax 2＋bx ＋c ＝0的判别式为Δ，则Δ>0⇔直线与圆锥曲线C 相交；Δ＝0⇔直线与圆锥曲线C 相切； Δ<0⇔直线与圆锥曲线C 相离．(2)当a ＝0，b ≠0时，即得到一个一次方程，则直线l 与圆锥曲线C 相交，且只有一个交点，此时，若C 为双曲线，则直线l 与双曲线的渐近线的位置关系是平行；若C 为抛物线，则直线l 与抛物线的对称轴的位置关系是平行或重合．2．圆锥曲线的弦长设斜率为k (k ≠0)的直线l 与圆锥曲线C 相交于A ，B 两点，A (x 1，y 1)，B (x 2，y 2)，则 |AB |＝1＋k 2|x 1－x 2| ＝1＋k 2·x 1＋x 22－4x 1x 2＝1＋1k 2·|y 1－y 2|＝1＋1k2·y 1＋y 22－4y 1y 2.[小题速通]1．直线y ＝kx －k ＋1与椭圆x 29＋y 24＝1的位置关系为( )A ．相交B ．相切C ．相离D ．不确定解析：选A 直线y ＝kx －k ＋1＝k (x －1)＋1恒过定点(1,1)，又点(1,1)在椭圆内部，故直线与椭圆相交．2．(2017·福州质检)抛物线C 的顶点为原点，焦点在x 轴上，直线x －y ＝0与抛物线C 交于A ，B 两点，若P (1,1)为线段AB 的中点，则抛物线C 的方程为( )A ．y ＝2x 2B ．y 2＝2x C ．x 2＝2yD ．y 2＝－2x解析：选B 设A (x 1，y 1)，B (x 2，y 2)，抛物线方程为y2＝2px ，则⎩⎪⎨⎪⎧y 21＝2px 1，y 22＝2px 2两式相减可得2p ＝y 1－y 2x 1－x 2×(y 1＋y 2)＝k AB ×2＝2，即可得p ＝1， ∴抛物线C 的方程为y 2＝2x .3．设双曲线x 29－y 216＝1的右顶点为A ，右焦点为F .过点F 平行于双曲线的一条渐近线的直线与双曲线交于点B ，则△AFB 的面积为________．解析：c ＝5，设过点F 平行于一条渐近线的直线方程为y ＝43(x －5)，即4x －3y －20＝0，联立直线与双曲线方程，求得y B ＝－3215，则S ＝12×(5－3)×3215＝3215.答案：3215[清易错]1．直线与双曲线交于一点时，易误认为直线与双曲线相切，事实上不一定相切，当直线与双曲线的渐近线平行时，直线与双曲线相交于一点．2．直线与抛物线交于一点时，除直线与抛物线相切外易忽视直线与对称轴平行时也相交于一点．1．过点(0,1)作直线，使它与抛物线y 2＝4x 仅有一个公共点，这样的直线有( ) A ．1条 B ．2条 C ．3条D ．4条解析：选C 结合图形分析可知，满足题意的直线共有3条：直线x ＝0，过点(0,1)且平行于x 轴的直线以及过点(0,1)且与抛物线相切的直线(非直线x ＝0)．2．直线y ＝b a x ＋3与双曲线x 2a 2－y 2b2＝1的交点个数是( )A ．1B ．2C ．1或2D ．0解析：选A 因为直线y ＝ba x ＋3与双曲线的渐近线y ＝b ax 平行，所以它与双曲线只有1个交点．[双基过关检测] 一、选择题1．以x 轴为对称轴，原点为顶点的抛物线上的一点P (1，m )到焦点的距离为3，则抛物线的方程是( )A ．y ＝4x 2B ．y ＝8x 2C ．y 2＝4xD ．y 2＝8x解析：选D 设抛物线的方程为y 2＝2px ，则由抛物线的定义知1＋p2＝3，即p ＝4，所以抛物线方程为y 2＝8x .2．(2017·济南第一中学检测)抛物线y ＝4x 2的焦点坐标是( )A.⎝ ⎛⎭⎪⎫116，0 B ．(1,0) C.⎝ ⎛⎭⎪⎫0，116 D ．(0,1)解析：选C 抛物线的标准方程为x 2＝14y ，则p ＝18，所以焦点坐标是⎝ ⎛⎭⎪⎫0，116.3．(2017·贵州七校联考)已知双曲线x 2＋my 2＝1的虚轴长是实轴长的两倍，则实数m 的值是( )A ．4B ．－14C.14D ．－4解析：选B 由双曲线的方程知a ＝1，b ＝－1m ，又b ＝2a ，所以－1m＝2，解得m ＝－14，故选B.4．已知椭圆x 225＋y 2m2＝1(m ＞0)的左焦点为F 1(－4,0)，则m ＝( )A ．2B ．3C ．4D ．9解析：选B 由左焦点为F 1(－4,0)知c ＝4.又a ＝5， ∴25－m 2＝16，解得m ＝3或－3.又m ＞0，故m ＝3.5．(2016·甘肃张掖一诊)过抛物线y 2＝4x 的焦点的直线l 交抛物线于P (x 1，y 1)，Q (x 2，y 2)两点，如果x 1＋x 2＝6，则|PQ |＝( )A ．9B ．8C ．7D ．6解析：选B 抛物线y 2＝4x 的焦点为F (1,0)，准线方程为x ＝－1.根据题意可得，|PQ |＝|PF |＋|QF |＝x 1＋1＋x 2＋1＝x 1＋x 2＋2＝8.故选B.6．已知椭圆C ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点为F 1，F 2，离心率为33，过F 2的直线l交C 于A ，B 两点，若△AF 1B 的周长为43，则C 的方程为( )A.x 23＋y 22＝1B.x 23＋y 2＝1 C.x 212＋y 28＝1 D.x 212＋y 24＝1 解析：选A 由椭圆的性质知|AF 1|＋|AF 2|＝2a ，|BF 1|＋|BF 2|＝2a ，又∵△AF 1B 的周长＝|AF 1|＋|AF 2|＋|BF 1|＋|BF 2|＝43，∴a ＝ 3.又e ＝33，∴c ＝1.∴b 2＝a 2－c 2＝2，∴椭圆的方程为x 23＋y 22＝1，故选A.7．椭圆ax 2＋by 2＝1与直线y ＝1－x 交于A ，B 两点，过原点与线段AB 中点的直线的斜率为32，则ab ＝( ) A.32 B.233 C.932D.2327解析：选A 设A (x 1，y 1)，B (x 2，y 2)，AB 的中点M (x 0，y 0)，结合题意，由点差法得，y 2－y 1x 2－x 1＝－a b ·x 1＋x 2y 1＋y 2＝－a b ·x 0y 0＝－a b ·23＝－1，∴a b ＝32. 8．已知双曲线x 212－y 24＝1的右焦点为F ，若过点F 的直线与双曲线的右支有且只有一个交点，则此直线斜率的取值范围是( )A.⎝ ⎛⎭⎪⎫－33，33 B.()－3，3C.⎣⎢⎡⎦⎥⎤－33，33 D.[]－3，3解析：选 C 由题意知F (4,0)，双曲线的两条渐近线方程为y ＝±33x .当过点F 的直线与渐近线平行时，满足与右支只有一个交点，画出图象，数形结合可知应选C.二、填空题9．(2016·北京高考)已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的一条渐近线为2x ＋y ＝0，一个焦点为(5，0)，则a ＝________，b ＝________.解析：因为双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的一条渐近线为2x ＋y ＝0，即y ＝－2x ，所以b a＝2.①又双曲线的一个焦点为(5，0)，所以a 2＋b 2＝5.② 由①②得a ＝1，b ＝2. 答案：1 210．(2016·山东高考)已知双曲线E ：x 2a 2－y 2b2＝1(a ＞0，b ＞0)，若矩形ABCD 的四个顶点在E 上，AB ，CD 的中点为E 的两个焦点，且2|AB |＝3|BC |，则E 的离心率是________．解析：如图，由题意知|AB |＝2b2a，|BC |＝2c .又2|AB |＝3|BC |， ∴2×2b2a＝3×2c ，即2b 2＝3ac ，∴2(c 2－a 2)＝3ac ，两边同除以a 2并整理得2e 2－3e －2＝0，解得e ＝2(负值舍去)． 答案：211．已知点P 是椭圆x 25＋y 24＝1上y 轴右侧的一点，且以点P 及焦点F 1，F 2为顶点的三角形的面积等于1，则点P 的坐标为________．解析：设P (x ，y )，由题意知c 2＝a 2－b 2＝5－4＝1，所以c ＝1，则F 1(－1,0)，F 2(1,0)，由题意可得点P 到x 轴的距离为1，所以y ＝±1，把y ＝±1代入x 25＋y 24＝1，得x ＝±152，又x ＞0，所以x ＝152，∴P 点坐标为⎝ ⎛⎭⎪⎫152，1或⎝ ⎛⎭⎪⎫152，－1. 答案：⎝⎛⎭⎪⎫152，1或⎝ ⎛⎭⎪⎫152，－1 12．(2017·西安中学模拟)如图，过抛物线y ＝14x 2的焦点F 的直线l 与抛物线和圆x2＋(y －1)2＝1交于A ，B ，C ，D 四点，则AB ―→·DC ―→＝________.解析：不妨设直线AB 的方程为y ＝1，联立⎩⎪⎨⎪⎧y ＝1，y ＝14x 2，解得x ＝±2，则A (－2,1)，D (2,1)，因为B (－1,1)，C (1,1)，所以AB ―→＝(1,0)，DC ―→＝(－1,0)，所以AB ―→·DC ―→＝－1.答案：－1 三、解答题13．(2017·揭阳一中期末)已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率为22，右焦点为F (1,0)．(1)求椭圆E 的标准方程；(2)设点O 为坐标原点，过点F 作直线l 与椭圆E 交于M ，N 两点，若OM ⊥ON ，求直线l 的方程．解：(1)依题意可得⎩⎪⎨⎪⎧1a ＝22，a 2＝b 2＋1，解得a ＝2，b ＝1，所以椭圆E 的标准方程为x 22＋y 2＝1.(2)设M (x 1，y 1)，N (x 2，y 2)， ①当MN 垂直于x 轴时，直线l 的方程为x ＝1，不符合题意；②当MN 不垂直于x 轴时， 设直线l 的方程为y ＝k (x －1)．联立得方程组⎩⎪⎨⎪⎧x 22＋y 2＝1，y ＝k x －，消去y ，整理得(1＋2k 2)x 2－4k 2x ＋2(k 2－1)＝0， 所以x 1＋x 2＝4k21＋2k2，x 1x 2＝k 2－1＋2k2. 所以y 1y 2＝k 2[x 1x 2－(x 1＋x 2)＋1]＝－k21＋2k 2.因为OM ⊥ON ， 所以OM ―→·ON ―→＝0，所以x 1x 2＋y 1y 2＝k 2－21＋2k2＝0，所以k ＝±2，即直线l 的方程为y ＝±2(x －1)．14.已知点F 为抛物线E ：y 2＝2px (p >0)的焦点，点A (2，m )在抛物线E 上，且|AF |＝3.(1)求抛物线E 的方程；(2)已知点G (－1,0)，延长AF 交抛物线E 于点B ，证明：以点F 为圆心且与直线GA 相切的圆，必与直线GB 相切．解：(1)由抛物线的定义得|AF |＝2＋p2.因为|AF |＝3，即2＋p2＝3，解得p ＝2，所以抛物线E 的方程为y 2＝4x .(2)因为点A (2，m )在抛物线E ：y 2＝4x 上， 所以m ＝±2 2.由抛物线的对称性，不妨设A (2,22)．由A (2,22)，F (1,0)可得直线AF 的方程为y ＝22(x －1)． 由⎩⎨⎧y ＝22x －，y 2＝4x ，得2x 2－5x ＋2＝0， 解得x ＝2或x ＝12，从而B ⎝ ⎛⎭⎪⎫12，－2. 又G (－1,0)， 所以k GA ＝22－02－－＝223，k GB ＝－2－012－－＝－223，所以k GA ＋k GB ＝0，从而∠AGF ＝∠BGF ，这表明点F 到直线GA ，GB 的距离相等，故以F 为圆心且与直线GA 相切的圆必与直线GB 相切．高考研究课(一)————————————————————————————————————— 椭圆命题3角度——求方程、研性质、判关系————————————————————————————————————— [全国卷5年命题分析][典例] (1)若椭圆C ：9＋2＝1的焦点为F 1，F 2，点P 在椭圆C 上，且|PF 1|＝4，则∠F 1PF 2＝( )A.π6 B.π3 C.2π3D.5π6(2)(2017·大庆模拟)如图，已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)，其中左焦点为F (－25，0)，P 为C 上一点，满足|OP |＝|OF |，且|PF |＝4，则椭圆C 的方程为( )A.x 225＋y 25＝1 B.x 236＋y 216＝1C.x 230＋y 210＝1 D.x 245＋y 225＝1 [解析] (1)由题意得a ＝3，c ＝7，则|PF 2|＝2. 在△F 2PF 1中，由余弦定理可得 cos ∠F 2PF 1＝42＋22－722×4×2＝－12.又∵∠F 2PF 1∈(0，π)，∴∠F 2PF 1＝2π3.(2)设椭圆的焦距为2c ，右焦点为F 1，连接PF 1，如图所示． 由F (－25，0)，得c ＝2 5. 由|OP |＝|OF |＝|OF 1|， 知PF 1⊥PF .在Rt △PF 1F 中，由勾股定理， 得|PF 1|＝|F 1F |2－|PF |2＝()452－42＝8.由椭圆定义，得|PF 1|＋|PF |＝2a ＝4＋8＝12， 从而a ＝6，得a 2＝36，于是b 2＝a 2－c 2＝36－(25)2＝16， 所以椭圆C 的方程为x 236＋y 216＝1.[答案] (1)C (2)B [方法技巧]求椭圆标准方程的基本方法是待定系数法，具体过程是先定形，再定量，即首先确定焦点所在位置，然后再根据条件建立关于a ，b 的方程组．如果焦点位置不确定，可把椭圆方程设为mx 2＋ny 2＝1(m >0，n >0，m ≠n )的形式．[即时演练]1．(2016·西安质检)已知中心在原点的椭圆C 的右焦点为F (1,0)，离心率等于12，则椭圆C 的方程是( )A.x 23＋y 24＝1B.x 24＋y 23＝1 C.x 24＋y 23＝1 D.x 24＋y 2＝1解析：选C 依题意，所求椭圆的焦点位于x 轴上，且c ＝1，e ＝c a ＝12⇒a ＝2，b 2＝a2－c 2＝3，因此椭圆C 的方程是x 24＋y 23＝1.2．已知F 1，F 2是椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的两个焦点，P 为椭圆C 上的一点，且PF 1―→⊥PF 2―→.若△PF 1F 2的面积为9，则b ＝________.解析：设|PF 1|＝r 1，|PF 2|＝r 2，则⎩⎪⎨⎪⎧r 1＋r 2＝2a ，r 21＋r 22＝4c 2，∴2r 1r 2＝(r 1＋r 2)2－(r 21＋r 22)＝4a 2－4c 2＝4b 2， 又∵S △PF 1F 2＝12r 1r 2＝b 2＝9，∴b ＝3.答案：3[典例] (1)(2017·兰州一模)已知椭圆a 2＋b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，点P 在椭圆上，O 为坐标原点，若|OP |＝12|F 1F 2|，且|PF 1||PF 2|＝a 2，则该椭圆的离心率为( )A.34B.32C.22D.12(2)如图，椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，过F 2的直线交椭圆于P ，Q 两点，且PQ ⊥PF 1.①若|PF 1|＝2＋2，|PF 2|＝2－2，求椭圆的标准方程； ②若|PQ |＝λ|PF 1|，且34≤λ＜43，求椭圆离心率e 的取值范围．[解析] (1)由|OP |＝12|F 1F 2|，且|PF 1||PF 2|＝a 2，可得点P 是椭圆的短轴端点，即P (0，±b )，故b ＝12×2c ＝c ，故a ＝2c ，即c a ＝22，故选C. 答案：C(2)①由椭圆的定义，2a ＝|PF 1|＋|PF 2|＝(2＋2)＋(2－2)＝4，故a ＝2.设椭圆的半焦距为c ，由已知PF 1⊥PF 2， 因此2c ＝|F 1F 2|＝|PF 1|2＋|PF 2|2＝＋22＋－22＝23，即c ＝3，从而b ＝a 2－c 2＝1. 故所求椭圆的标准方程为x 24＋y 2＝1.②如图，由PF 1⊥PQ ， |PQ |＝λ|PF 1|， 得|QF 1|＝|PF 1|2＋|PQ |2＝1＋λ2|PF 1|.由椭圆的定义，|PF 1|＋|PF 2|＝2a ，|QF 1|＋|QF 2|＝2a ，进而|PF 1|＋|PQ |＋|QF 1|＝4a . 于是(1＋λ＋1＋λ2)|PF 1|＝4a ， 解得PF 1＝4a 1＋λ＋1＋λ2，故|PF 2|＝2a －|PF 1|＝2aλ＋1＋λ2－1＋λ＋1＋λ2.由勾股定理得|PF 1|2＋|PF 2|2＝|F 1F 2|2＝(2c )2＝4c 2，从而⎝ ⎛⎭⎪⎫4a 1＋λ＋1＋λ22＋⎣⎢⎡⎦⎥⎤2a λ＋1＋λ2－1＋λ＋1＋λ22＝4c 2， 两边除以4a 2，得4＋λ＋1＋λ22＋λ＋1＋λ2－2＋λ＋1＋λ22＝e 2.若记t ＝1＋λ＋1＋λ2， 则上式变成e 2＝4＋t －2t 2＝8⎝ ⎛⎭⎪⎫1t －142＋12. 由34≤λ＜43，并注意到t ＝1＋λ＋1＋λ2关于λ单调递增，得3≤t ＜4，即14＜1t ≤13. 进而12＜e 2≤59，即22＜e ≤53.[方法技巧]椭圆几何性质的应用技巧(1)与椭圆几何性质有关的问题要结合图形进行分析，即使画不出图形，思考时也要联想到一个图形．(2)椭圆的范围或最值问题常常涉及一些不等式．例如，－a ≤x ≤a ，－b ≤y ≤b,0＜e ＜1，在求椭圆相关量的范围时，要注意应用这些不等关系．[即时演练]1．设椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点为 F 1，F 2，过F 2 作x 轴的垂线与C 相交于A ，B 两点，F 1B 与y 轴交于点D ，若AD ⊥F 1B ，则椭圆C 的离心率等于________．解析：由题意知F 1(－c,0)，F 2(c,0)，其中c ＝a 2－b 2，因为过F 2且与x 轴垂直的直线为x ＝c ，由椭圆的对称性可设它与椭圆的交点为A ⎝ ⎛⎭⎪⎫c ，b 2a ，B ⎝ ⎛⎭⎪⎫c ，－b 2a .因为AB 平行于y 轴，且|F 1O |＝|OF 2|，所以|F 1D |＝|DB |，即D 为线段F 1B 的中点，所以点D 的坐标为⎝⎛⎭⎪⎫0，－b 22a ，又AD ⊥F 1B ，所以k AD ·kF 1B ＝－1，即b 2a －⎝ ⎛⎭⎪⎫－b 22a c －0×－b 2a －0c －－c＝－1，整理得3b 2＝2ac ，所以3(a 2－c 2)＝2ac ，又e ＝c a，0<e <1，所以3e 2＋2e －3＝0，解得e ＝33(e ＝－3舍去)． 答案：332．(2017·安徽黄山质检)已知椭圆C ：x 2a 2＋y 2b2＝1(a >b >0)的左、右焦点分别为 F 1，F 2，点P 为椭圆C 与y 轴的交点，若以F 1，F 2，P 三点为顶点的等腰三角形一定不可能为钝角三角形，则椭圆C 的离心率的取值范围是________．解析：∵点P 为椭圆C 与y 轴的交点，以F 1，F 2，P 三点为顶点的等腰三角形一定不可能为钝角三角形，即∠F 1PF 2≤90°，∴tan ∠OPF 2≤1，∴cb≤1，c ≤b ，c 2≤a 2－c 2，∴0＜e ≤22. 答案：⎝ ⎛⎦⎥⎤0，22[典例] (2016·四川高考)已知椭圆E ：a 2＋b2＝1(a ＞b ＞0)的一个焦点与短轴的两个端点是正三角形的三个顶点，点P ⎝⎛⎭⎪⎫3，12在椭圆E 上． (1)求椭圆E 的方程；(2)设不过原点O 且斜率为12的直线l 与椭圆E 交于不同的两点A ，B ，线段AB 的中点为M ，直线OM 与椭圆E 交于C ，D ，证明：|MA |·|MB |＝|MC |·|MD |.[解] (1)由已知，a ＝2b ，又椭圆x 2a 2＋y 2b 2＝1过点P ⎝ ⎛⎭⎪⎫3，12， 故34b 2＋14b2＝1，解得b 2＝1. 所以椭圆E 的方程是x 24＋y 2＝1.(2)证明：设直线l 的方程为y ＝12x ＋m (m ≠0)，A (x 1，y 1)，B (x 2，y 2)．联立方程组⎩⎪⎨⎪⎧x 24＋y 2＝1，y ＝12x ＋m ，得x 2＋2mx ＋2m 2－2＝0，由Δ＝4(2－m 2)＞0，解得－2＜m ＜ 2. 由根与系数的关系得x 1＋x 2＝－2m ，x 1x 2＝2m 2－2，所以M 点坐标为⎝⎛⎭⎪⎫－m ，m 2，直线OM 的方程为y ＝－12x .由方程组⎩⎪⎨⎪⎧x 24＋y 2＝1，y ＝－12x ，得C ⎝ ⎛⎭⎪⎫－2，22，D ⎝⎛⎭⎪⎫2，－22. 所以|MC |·|MD |＝52(－m ＋2)·52(2＋m ) ＝54(2－m 2)． 又|MA |·|MB |＝14|AB |2＝14[(x 1－x 2)2＋(y 1－y 2)2]＝516[(x 1＋x 2)2－4x 1x 2]＝516[4m 2－4(2m 2－2)] ＝54(2－m 2)， 所以|MA |·|MB |＝|MC |·|MD |. [方法技巧](1)解决直线与椭圆的位置关系的相关问题，其常规思路是先把直线方程与椭圆方程联立，消元、化简，然后应用根与系数的关系建立方程，解决相关问题．涉及弦中点的问题常常用“点差法”解决往往会更简单．(2)设直线与椭圆的交点坐标为A (x 1，y 1)，B (x 2，y 2)，则|AB |＝＋k 2[x 1＋x 22－4x 1x 2]＝⎝ ⎛⎭⎪⎫1＋1k 2[y 1＋y 22－4y 1y 2](k 为直线斜率)．[提醒] 利用公式计算直线被椭圆截得的弦长是在方程有解的情况下进行的，不要忽略判别式．[即时演练]1．若对任意k ∈R ，直线y －kx －1＝0与椭圆x 22＋y 2m＝1恒有公共点，则实数m 的取值范围是( )A ．(1,2]B ．[1,2)C ．[1,2)∪(2，＋∞)D ．[1，＋∞)解析：选C 联立直线与椭圆的方程，消去y 得(2k 2＋m )x 2＋4kx ＋2－2m ＝0，因为直线与椭圆恒有公共点，所以Δ＝16k 2－4(2k 2＋m )(2－2m )≥0，即2k 2＋m －1≥0恒成立，因为k ∈R ，所以k 2≥0，则m －1≥0，所以m ≥1，又m ≠2，所以实数m 的取值范围是[1,2)∪(2，＋∞)．2．(2017·辽宁质检)已知离心率为63的椭圆x 2a 2＋y2b 2＝1(a ＞b ＞0)的一个焦点为F ，过F且与x 轴垂直的直线与椭圆交于A ，B 两点，|AB |＝233.(1)求此椭圆的方程；(2)已知直线y ＝kx ＋2与椭圆交于C ，D 两点，若以线段CD 为直径的圆过点E (－1,0)，求k 的值．解：(1)设焦距为2c ， ∵e ＝c a ＝63，a 2＝b 2＋c 2， ∴b a ＝33， 由|AB |＝233，易知b 2a ＝33，∴b ＝1，a ＝3， ∴椭圆的方程为x 23＋y 2＝1.(2)将y ＝kx ＋2代入椭圆方程， 得(1＋3k 2)x 2＋12kx ＋9＝0，又直线与椭圆有两个交点，所以Δ＝(12k )2－36(1＋3k 2)＞0，解得k 2＞1. 设C (x 1，y 1)，D (x 2，y 2)，则x 1＋x 2＝－12k 1＋3k 2，x 1x 2＝91＋3k 2，若以CD 为直径的圆过E 点，则EC ―→·ED ―→＝0，即(x 1＋1)(x 2＋1)＋y 1y 2＝0， 而y 1y 2＝(kx 1＋2)(kx 2＋2)＝k 2x 1x 2＋2k (x 1＋x 2)＋4， 则(x 1＋1)(x 2＋1)＋y 1y 2＝(k 2＋1)x 1x 2＋(2k ＋1)(x 1＋x 2)＋5＝k 2＋1＋3k 2－12k k ＋1＋3k2＋5＝0，解得k ＝76，满足k 2＞1.1．(2016·全国乙卷)直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为( )A.13B.12C.23D.34解析：选B 不妨设直线l 经过椭圆的一个顶点B (0，b )和一个焦点F (c,0)，则直线l 的方程为x c ＋y b＝1，即bx ＋cy －bc ＝0.由题意知|－bc |b 2＋c 2＝14×2b ，解得c a ＝12，即e ＝12.故选B.2．(2016·全国甲卷)已知A 是椭圆E ：x 24＋y 23＝1的左顶点，斜率为k (k ＞0)的直线交E 于A ，M 两点，点N 在E 上，MA ⊥NA .(1)当|AM |＝|AN |时，求△AMN 的面积； (2)当2|AM |＝|AN |时，证明：3＜k ＜2. 解：(1)设M (x 1，y 1)，则由题意知y 1＞0.由已知及椭圆的对称性知，直线AM 的倾斜角为π4.又A (－2,0)，因此直线AM 的方程为y ＝x ＋2.将x ＝y －2代入x 24＋y 23＝1得7y 2－12y ＝0.解得y ＝0或y ＝127，所以y 1＝127.因此△AMN 的面积S △AMN ＝2×12×127×127＝14449.(2)证明：设直线AM 的方程为y ＝k (x ＋2)(k ＞0)， 代入x 24＋y 23＝1得(3＋4k 2)x 2＋16k 2x ＋16k 2－12＝0.由x 1·(－2)＝16k 2－123＋4k2，得x 1＝－4k23＋4k2，故|AM |＝|x 1＋2|1＋k 2＝121＋k23＋4k 2.由题意，设直线AN 的方程为y ＝－1k(x ＋2)，故同理可得|AN |＝12k 1＋k23k 2＋4. 由2|AM |＝|AN |，得23＋4k 2＝k3k 2＋4， 即4k 3－6k 2＋3k －8＝0.设f (t )＝4t 3－6t 2＋3t －8，则k 是f (t )的零点．f ′(t )＝12t 2－12t ＋3＝3(2t －1)2≥0，所以f (t )在(0，＋∞)上单调递增．又f (3)＝153－26＜0，f (2)＝6＞0，因此f (t )在(0，＋∞)上有唯一的零点，且零点k 在(3，2)内，所以3＜k ＜2.3．(2015·全国卷Ⅱ)已知椭圆C ：9x 2＋y 2＝m 2(m >0)，直线l 不过原点O 且不平行于坐标轴，l 与C 有两个交点A ，B ，线段AB 的中点为M .(1)证明：直线OM 的斜率与l 的斜率的乘积为定值；(2)若l 过点⎝ ⎛⎭⎪⎫m3，m ，延长线段OM 与C 交于点P ，四边形OAPB 能否为平行四边形？若能，求此时l 的斜率；若不能，说明理由．解：(1)证明：设直线l ：y ＝kx ＋b (k ≠0，b ≠0)，A (x 1，y 1)，B (x 2，y 2)，M (x M ，y M )．将y ＝kx ＋b 代入9x 2＋y 2＝m 2， 得(k 2＋9)x 2＋2kbx ＋b 2－m 2＝0， 故x M ＝x 1＋x 22＝－kb k 2＋9，y M ＝kx M ＋b ＝9bk 2＋9. 于是直线OM 的斜率k OM ＝y M x M＝－9k，即k OM ·k ＝－9.所以直线OM 的斜率与l 的斜率的乘积为定值． (2)四边形OAPB 能为平行四边形．因为直线l 过点⎝ ⎛⎭⎪⎫m3，m ，所以l 不过原点且与C 有两个交点的充要条件是k >0，k ≠3.由(1)得OM 的方程为y ＝－9kx .设点P 的横坐标为x P . 由⎩⎪⎨⎪⎧y ＝－9k x ，9x 2＋y 2＝m 2，得x 2P ＝k 2m 29k 2＋81，即x P ＝±km3k 2＋9. 将点⎝ ⎛⎭⎪⎫m3，m 的坐标代入直线l 的方程得b ＝m－k 3，因此x M ＝k k －mk 2＋.四边形OAPB 为平行四边形，当且仅当线段AB 与线段OP 互相平分，即x P ＝2x M . 于是±km 3k 2＋9＝2×k k －mk 2＋，解得k 1＝4－7，k 2＝4＋7. 因为k i >0，k i ≠3，i ＝1,2，所以当直线l 的斜率为4－7或4＋7时， 四边形OAPB 为平行四边形． [高考达标检测] 一、选择题1．如果x 2＋ky 2＝2表示焦点在y 轴上的椭圆，那么实数k 的取值范围是( ) A ．(0,1) B ．(0,2) C ．(1，＋∞)D ．(0，＋∞)解析：选A x 2＋ky 2＝2转化为椭圆的标准方程，得x 22＋y 22k＝1，∵x 2＋ky 2＝2表示焦点在y 轴上的椭圆，∴2k＞2，解得0＜k ＜1.∴实数k 的取值范围是(0,1)．故选A.2．(2017·济南质检)已知焦点在x 轴上的椭圆的离心率为12，且它的长轴长等于圆C ：x 2＋y 2－2x －15＝0的半径，则椭圆的标准方程是( )A.x 24＋y 23＝1B.x 216＋y 212＝1 C.x 24＋y 2＝1 D.x 216＋y 24＝1 解析：选A 由x 2＋y 2－2x －15＝0， 知r ＝4＝2a ，所以a ＝2.又e ＝c a ＝12，所以c ＝1，则b 2＝a 2－c 2＝3. 因此椭圆的标准方程为x 24＋y 23＝1.3．设F 1，F 2是椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点，P 为直线x ＝3a2上一点，△F 2PF 1是底角为30°的等腰三角形，则E 的离心率为( )A.12 B.23 C.34D.45解析：选C 由题意可得|PF 2|＝|F 1F 2|，所以2⎝ ⎛⎭⎪⎫32a －c ＝2c ， 所以3a ＝4c ，所以e ＝34.4．(2017·厦门模拟)椭圆E ：x 2a 2＋y 23＝1(a ＞0)的右焦点为F ，直线y ＝x ＋m 与椭圆E交于A ，B 两点，若△FAB 周长的最大值是8，则m 的值等于( )A ．0B ．1 C. 3D ．2解析：选B 设椭圆的左焦点为F ′，则△FAB 的周长为AF ＋BF ＋AB ≤AF ＋BF ＋AF ′＋BF ′＝4a ＝8，所以a ＝2，当直线AB 过焦点F ′(－1,0)时，△FAB 的周长取得最大值，所以0＝－1＋m ，所以m ＝1.故选B.5．已知椭圆C ：x 24＋y 23＝1的左、右焦点分别为F 1，F 2，椭圆C 上点A 满足AF 2⊥F 1F 2.若点P 是椭圆C 上的动点，则F 1P ―→·F 2A ―→的最大值为( )A.32B.332 C.94D.154解析：选 B 设向量F 1P ―→，F 2A ―→的夹角为θ.由条件知|AF 2|＝b 2a ＝32，则F 1P ―→·F 2A ―→＝32|F 1P |―→cos θ，于是F 1P ―→·F 2A ―→要取得最大值，只需F 1P ―→在向量F 2A ―→上的投影值最大，易知此时点P 在椭圆短轴的上顶点，所以F 1P ―→·F 2A ―→＝32|F 1P |―→cos θ≤332，即F 1P ―→·F 2A ―→的最大值为332.6．从椭圆x 2a 2＋y 2b2＝1(a >b >0)上一点P 向x 轴作垂线，垂足恰为左焦点F 1，A 是椭圆与x轴正半轴的交点，B 是椭圆与y 轴正半轴的交点，且AB ∥OP (O 是坐标原点)，则该椭圆的离心率是( )A.24B.12C.22D.32解析：选C 由题意可设P (－c ，y 0)(c 为半焦距)，k OP ＝－y 0c ，k AB ＝－b a，由于OP ∥AB ，∴－y 0c ＝－b a ，y 0＝bc a ，把P ⎝⎛⎭⎪⎫－c ，bc a 代入椭圆方程得－c 2a 2＋⎝ ⎛⎭⎪⎫bc a 2b 2＝1，即⎝ ⎛⎭⎪⎫c a 2＝12，∴e ＝ca ＝22.选C. 二、填空题7．若F 1，F 2分别是椭圆E ：x 2＋y 2b2＝1(0<b <1)的左、右焦点，过点F 1的直线交椭圆E于A ，B 两点．若|AF 1|＝3|F 1B |，AF 2⊥x 轴，则椭圆E 的方程为________________．解析：设点A 在点B 上方，F 1(－c,0)，F 2(c,0)，其中c ＝1－b 2，则可设A (c ，b 2)，B (x 0，y 0)，由|AF 1|＝3|F 1B |，可得AF 1―→＝3F 1B ―→，故⎩⎪⎨⎪⎧－2c ＝x 0＋c ，－b 2＝3y 0，即⎩⎪⎨⎪⎧x 0＝－53c ，y 0＝－13b 2，代入椭圆方程可得－b 29＋19b 2＝1， 解得b 2＝23，故椭圆方程为x 2＋3y22＝1.答案：x 2＋3y22＝18．已知椭圆的方程是x 2＋2y 2－4＝0，则以M (1,1)为中点的弦所在直线方程是______． 解析：设过M (1,1)点的方程为y ＝kx ＋b ， 则有k ＋b ＝1，即b ＝1－k ，即y ＝kx ＋(1－k )，联立方程组⎩⎪⎨⎪⎧x 2＋2y 2－4＝0，y ＝kx ＋－k ，则有(1＋2k 2)x 2＋(4k －4k 2)x ＋(2k 2－4k －2)＝0，所以x 1＋x 22＝12·4k 2－4k1＋2k2＝1，解得k ＝－12，故b ＝32，所以y ＝－12x ＋32，即x ＋2y －3＝0.答案：x ＋2y －3＝09．如图，椭圆的中心在坐标原点O ，顶点分别是A 1，A 2，B 1，B 2，焦点分别为F 1，F 2，延长B 1F 2与A 2B 2交于P 点，若∠B 1PA 2为钝角，则此椭圆的离心率的取值范围为________．解析：设椭圆的方程为x 2a 2＋y 2b2＝1(a ＞b ＞0)，∠B 1PA 2为钝角可转化为B 2A 2―→，F 2B 1―→所夹的角为钝角，则(a ，－b )·(－c ，－b )＜0，得b 2＜ac ，即a 2－c 2＜ac ，故⎝ ⎛⎭⎪⎫c a2＋c a－1＞0，即e 2＋e －1＞0，e ＞5－12或e ＜－5－12，又0＜e ＜1，∴5－12＜e ＜1.答案：⎝⎛⎭⎪⎫5－12，1三、解答题10．(2016·洛阳一模)设椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)过点(0,4)，离心率为35.(1)求C 的方程；(2)求过点(3,0)且斜率为45的直线被C 所截线段的中点坐标．解：(1)将(0,4)代入C 的方程得16b 2＝1，∴b ＝4，由e ＝c a ＝35，得a 2－b 2a 2＝925，即1－16a 2＝925，∴a ＝5，∴C 的方程为x 225＋y 216＝1.(2)过点(3,0)且斜率为45的直线方程为y ＝45(x －3)，设直线与椭圆C 的交点为A (x 1，y 1)，B (x 2，y 2)，线段AB 的中点为M (x 0，y 0)． 将直线方程y ＝45(x －3)代入椭圆C 的方程，得x 225＋x －225＝1，即x 2－3x －8＝0，由根与系数的关系得x 1＋x 2＝3， ∴x 0＝x 1＋x 22＝32， y 0＝y 1＋y 22＝25(x 1＋x 2－6)＝－65，即线段AB 的中点坐标为⎝ ⎛⎭⎪⎫32，－65.11．(2017·广州五校联考)已知椭圆E ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的离心率e ＝22，且经过点(6，1)，O 为坐标原点．(1)求椭圆E 的标准方程；(2)圆O 是以椭圆E 的长轴为直径的圆，M 是直线x ＝－4在x 轴上方的一点，过M 作圆O 的两条切线，切点分别为P ，Q ，当∠PMQ ＝60°时，求直线PQ 的方程．解：(1)由题意可得e ＝c a ＝22， ∵椭圆E 经过点(6，1)，∴6a 2＋1b2＝1，又a 2－b 2＝c 2，解得a ＝22，b ＝2， ∴椭圆E 的标准方程为x 28＋y 24＝1.(2)连接OM ，OP ，OQ ，OM 与PQ 交于点A ， 依题意可设M (－4，m )．由圆的切线性质及∠PMQ ＝60°，可知△OPM 为直角三角形且∠OMP ＝30°， ∵|OP |＝22，∴|OM |＝42， ∴－2＋m 2＝42，又m ＞0，解得m ＝4，∴M (－4,4)， ∴直线OM 的斜率k OM ＝－1， 由MP ＝MQ ，OP ＝OQ 可得OM ⊥PQ ， ∴直线PQ 的斜率k PQ ＝1， 设直线PQ 的方程为y ＝x ＋n ， ∵∠OMP ＝30°，∴∠POM ＝60°， ∵∠OPA ＝30°，由|OP |＝22知|OA |＝2，即点O 到直线PQ 的距离为2， ∴|n |12＋－2＝2，解得n ＝±2(舍去负值)，∴直线PQ 的方程为x －y ＋2＝0.12.如图，在平面直角坐标系xOy 中，椭圆x 2a 2＋y 2b2＝1(a ＞b ＞0)的离心率为22，过椭圆右焦点F 作两条互相垂直的弦AB 与CD .当直线AB 的斜率为0时，|AB |＋|CD |＝3 2.(1)求椭圆的方程；(2)求以A ，B ，C ，D 为顶点的四边形的面积的取值范围． 解：(1)由题意知，e ＝c a ＝22，则a ＝2c ，b ＝c . 当直线AB 的斜率为0时，|AB |＋|CD |＝2a ＋2b2a＝22c ＋2c ＝32，∴c ＝1.∴椭圆的方程为x 22＋y 2＝1.(2)①当直线AB 与直线CD 中有一条的斜率为0时，另一条的斜率不存在． 由题意知S 四边形＝12|AB |·|CD |＝12×22×2＝2.②当两条直线的斜率均存在且不为0时， 设A (x 1，y 1)，B (x 2，y 2)，直线AB 的方程为y ＝k (x －1)，则直线CD 的方程为y ＝－1k(x －1)．将直线AB 的方程代入椭圆方程，并整理得 (1＋2k 2)x 2－4k 2x ＋2k 2－2＝0， ∴x 1＋x 2＝4k21＋2k 2，x 1x 2＝2k 2－21＋2k2，∴|AB |＝k 2＋1|x 1－x 2| ＝k 2＋1·22k 2＋11＋2k2＝22k 2＋1＋2k2.同理，|CD |＝22⎝ ⎛⎭⎪⎫1k 2＋11＋2k 2＝22k 2＋k 2＋2.∴S 四边形＝12·|AB |·|CD |＝12·22k 2＋1＋2k 2·22k 2＋k 2＋2＝k 2＋22k 4＋2＋5k2＝4⎝⎛⎭⎪⎫k ＋1k 22⎝ ⎛⎭⎪⎫k ＋1k 2＋1＝2－22⎝ ⎛⎭⎪⎫k ＋1k 2＋1. ∵2⎝⎛⎭⎪⎫k ＋1k 2＋1≥2⎝⎛⎭⎪⎫2k ·1k 2＋1＝9， 当且仅当k ＝±1时取等号，∴S 四边形∈⎣⎢⎡⎭⎪⎫169，2. 综合①与②可知，S 四边形∈⎣⎢⎡⎦⎥⎤169，2.高考研究课(二)————————————————————————————————————— 双曲线命题3角度——用定义、求方程、研性质—————————————————————————————————————[全国卷5年命题分析][典例] (1)设F 1，F 2是双曲线x 2－24＝1的两个焦点，P 是双曲线上的一点，且|PF 1|＝43|PF 2|，则△PF 1F 2的面积等于( ) A ．4 2 B ．8 3 C ．24D ．48(2)已知双曲线C ：x 2a 2－y 2b2＝1(a >0，b >0)的焦距为10，点P (2,1)在C 的一条渐近线上，则C 的方程为( )A.x 220－y 25＝1 B.x 25－y 220＝180202080[解析] (1)由双曲线定义||PF 1|－|PF 2||＝2， 又|PF 1|＝43|PF 2|，∴|PF 1|＝8，|PF 2|＝6， 又|F 1F 2|＝2c ＝10，∴|PF 1|2＋|PF 2|2＝|F 1F 2|2，△PF 1F 2为直角三角形．△PF 1F 2的面积S ＝12×6×8＝24.(2)依题意⎩⎪⎨⎪⎧a 2＋b 2＝25，1＝ba×2，解得⎩⎪⎨⎪⎧a 2＝20，b 2＝5，∴双曲线C 的方程为x 220－y 25＝1.[答案] (1)C (2)A [方法技巧]双曲线定义及标准方程问题求解中的2个注意点(1)应用双曲线的定义需注意的问题：在双曲线的定义中要注意双曲线上的点(动点)具备的几何条件，即“到两定点(焦点)的距离之差的绝对值为一常数，且该常数必须小于两定点的距离”．若定义中的“绝对值”去掉，点的轨迹是双曲线的一支．同时注意定义的转化应用．(2)求双曲线方程时一是标准形式判断；二是注意a ，b ，c 的关系易错易混． [即时演练]1．若双曲线x 24－y 212＝1的左焦点为F ，点P 是双曲线右支上的动点，A (1,4)，则|PF |＋|PA |的最小值是( )A ．8B ．9C ．10D ．12解析：选B 由题意知，双曲线x 24－y 212＝1的左焦点F 的坐标为(－4,0)，设双曲线的右焦点为B ，则B (4,0)，由双曲线的定义知，|PF |＋|PA |＝4＋|PB |＋|PA |≥4＋|AB |＝4＋－2＋－2＝4＋5＝9，当且仅当A ，P ，B 三点共线且P 在A ，B 之间时取等号．2．(2016·天津高考)已知双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的焦距为25，且双曲线的一条渐近线与直线2x ＋y ＝0垂直，则双曲线的方程为( )。

班级 姓名 学号 分数（测试时间：120分钟 满分：150分）一、选择题（共12小题，每题5分，共60分）1. 双曲线122=-y x 右支上一点Ｐ（a, b ）到直线l ：y = x 的距离2=d 则a+b=（ ） A ．–12 B ．21 C ．21或21- D ．２或–2【答案】B 【解析】试题分析：由题意可知221a b -=，解方程组可得12a b +=考点：双曲线方程及点到直线的距离2. 已知抛物线x y C 8:2=的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若FP ＝4FQ ，则||QF ＝ A ．27 B ．25C ．3D ．2 【答案】C 【解析】考点：抛物线的定义．3. 椭圆的左、右焦点分别为、，则椭圆上满足的点（ ）A ．有2个B ．有4个C ．不一定存在D ．一定不存在【答案】D 【解析】试题分析：点P 为椭圆上任一动点，当点P 是短轴端点时，可求得，,即为锐角．同时可知，当点P 在此位置时，最大，所以不存在点P 使，故选D ．考点：存在性问题．4. 已知抛物线C ：x y 82=的焦点为F ，准线为l ，P 是l 上一点，Q 是直线PF 与C 的一个交点，若QF PF 3=，则QF =（ ） A ．25 B ．38C ．3D ．6 【答案】B 【解析】考点：直线与抛物线的位置关系及抛物线定义的应用。

5. 过抛物线24y x =的焦点作两条垂直的弦,AB CD ,则11AB CD+=（ ） A ．2 B ．4 C ．12 D ．14【答案】D 【解析】试题分析：由抛物线24y x =，可知24p =，设1l 的倾斜角为θ，则2l 的倾斜角为2πθ-，过焦点的弦222222,sin cos sin ()2p p pAB CD πθθθ===-，所以2211sin cos 1224AB CD p p θθ+=+=，故选D. 考点：抛物线的标准方程及其简单的几何性质.6. 【2018山西两校联考】已知双曲线()222210,0x y a b a b-=>>，则其渐近线与圆()22214x a y a -+=的位置关系是（ ） A. 相交 B. 相切 C. 相离 D. 不确定 【答案】C7. 已知P 为抛物线24y x =上一个动点，Q 为圆()2241x y +-=上一个动点，那么点P 到点Q 的距离与点P 到抛物线的准线距离之和的最小值是（ ）A．1- B．2- C1- D2- 【答案】C 【解析】试题分析：由抛物线定义可知，点P 到准线的距离可转化为到焦点F 的距离，即求PQ PF+的最小值即可，又因为1PQ PC ≥-，所以111PQ PF PC PF FC +≥-+≥-=-，故选C ．考点：1．抛物线和定义与几何性质；2．数形结合与求最值．学科￥网8. 【2018黑龙江海林中学联考】已知双曲线22221(0,0)x y a b a b-=>>，若存在过右焦点F的直线与双曲线交于A ， B 两点，且3AF BF =，则双曲线离心率的最小值为（ ）A.B. C. 2 D.【答案】C【解析】因为过右焦点的直线与双曲线C 相交于A 、B 两点，且3AF BF =，故直线与双曲线相交只能交于左右两只，即A 在左支，B 在右支，设()11,A x y ， ()22,B x y ，右焦点(),0F c ，因为3AF BF =，所以()123c x c x -=- ， 2132x x c -= ，由于12,x a x a ≤-≥，所以12,33x a x a -≥≥ ，故2134x x a -≥，即24,2,cc a a≥≥ 即2e ≥ ，选C.【点睛】求双曲线的离心率或离心率的取值范围问题是高考常见问题，求离心率只需寻求一个关于,,a b c 的等量关系，求离心率的取值范围只需列出一个关于,,a b c 的不等关系，进而求出离心率的值或离心率的取值范围，求范围时还要注意曲线的离心率的范围，如双曲线的离心率的范围要大于1 。

椭圆、双曲线、抛物线的基本问题【考点梳理】1.圆锥曲线的定义(1)椭圆：|MF 1|＋|MF 2|＝2a (2a ＞|F 1F 2|)；(2)双曲线：||MF 1|－|MF 2||＝2a (2a ＜|F 1F 2|)；(3)抛物线：|MF |＝d (d 为M 点到准线的距离).2.圆锥曲线的标准方程(1)椭圆：x 2a 2＋y 2b 2＝1(a ＞b ＞0)(焦点在x 轴上)或y 2a 2＋x 2b 2＝1(a ＞b ＞0)(焦点在y 轴上)；(2)双曲线：x 2a 2－y 2b 2＝1(a ＞0，b ＞0)(焦点在x 轴上)或y 2a 2－x 2b 2＝1(a ＞0，b ＞0)(焦点在y 轴上)；(3)抛物线：y 2＝2px ，y 2＝－2px ，x 2＝2py ，x 2＝－2py (p ＞0).3.圆锥曲线的重要性质(1)椭圆、双曲线中a ，b ，c 之间的关系①在椭圆中：a 2＝b 2＋c 2；离心率为e ＝c a ＝1－b 2a 2.②在双曲线中：c 2＝a 2＋b 2；离心率为e ＝c a ＝1＋b 2a 2. (2)双曲线的渐近线方程与焦点坐标①双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的渐近线方程为y ＝±b a x ；焦点坐标F 1(－c ，0)，F 2(c ，0).②双曲线y 2a 2－x 2b 2＝1(a >0，b >0)的渐近线方程为y ＝±a b x ，焦点坐标F 1(0，－c )，F 2(0，c ).(3)抛物线的焦点坐标与准线方程①抛物线y 2＝2px (p >0)的焦点F ⎝ ⎛⎭⎪⎫p 2，0，准线方程x ＝－p 2. ②抛物线x 2＝2py (p >0)的焦点F ⎝ ⎛⎭⎪⎫0，p 2，准线方程y ＝－p 2. 4.弦长问题(1)直线与圆锥曲线相交的弦长设而不求，利用根与系数的关系，进行整体代入.即当斜率为k ，直线与圆锥曲线交于A (x 1，y 1)，B (x 2，y 2)时，|AB |＝1＋k 2|x 1－x 2|＝1＋k 2（x 1＋x 2）2－4x 1x 2.(2)过抛物线焦点的弦长抛物线y 2＝2px (p >0)过焦点F 的弦AB ，若A (x 1，y 1)，B (x 2，y 2)，则x 1x 2＝p 24，y 1y 2＝－p 2，弦长|AB |＝x 1＋x 2＋p .【题型突破】题型一、圆锥曲线的定义及标准方程【例1】(1)已知P 是抛物线y 2＝4x 上的一个动点，Q 是圆(x －3)2＋(y －1)2＝1上的一个动点，N (1，0)是一个定点，则|PQ |＋|PN |的最小值为( )A.3B.4C.5D.2＋1 (2)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的左焦点为F ，离心率为 2.若经过F 和P (0，4)两点的直线平行于双曲线的一条渐近线，则双曲线的方程为( ) A.x 24－y 24＝1B.x 28－y 28＝1C.x 24－y 28＝1D.x 28－y 24＝1【答案】(1)A (2)B【解析】(1)由抛物线方程y 2＝4x ，可得抛物线的焦点F (1，0)，又N (1，0)，所以N 与F 重合.过圆(x －3)2＋(y －1)2＝1的圆心M 作抛物线准线的垂线MH ，交圆于Q ，交抛物线于P ，则|PQ |＋|PN |的最小值等于|MH |－1＝3.(2)由e ＝2知a ＝b ，且c ＝2a .∴双曲线渐近线方程为y ＝±x .又k PF ＝4－00＋c ＝4c＝1，∴c ＝4，则a 2＝b 2＝c 22＝8. 故双曲线方程为x 28－y 28＝1.【类题通法】1.凡涉及抛物线上的点到焦点距离，一般运用定义转化为到准线的距离处理.如本例充分运用抛物线定义实施转化，使解答简捷、明快.2.求解圆锥曲线的标准方程的方法是“先定型，后计算”.所谓“定型”，就是指确定类型，所谓“计算”，就是指利用待定系数法求出方程中的a 2，b 2，p 的值，最后代入写出椭圆、双曲线、抛物线的标准方程.【对点训练】(1)已知双曲线x 2a 2－y 2b 2＝1(a >0，b >0)的焦距为25，且双曲线的一条渐近线与直线2x ＋y ＝0垂直，则双曲线的方程为( )A.x 24－y 2＝1B.x 2－y 24＝1C.3x 220－3y 25＝1D.3x 25－3y 220＝1(2)已知椭圆x 24＋y 22＝1的两个焦点是F 1，F 2，点P 在该椭圆上，若|PF 1|－|PF 2|＝2，则△PF 1F 2的面积是________.【答案】(1)A (2) 2【解析】(1)依题意得b a ＝12，①又a 2＋b 2＝c 2＝5，②联立①②得a ＝2，b ＝1.∴所求双曲线的方程为x 24－y 2＝1.(2)由椭圆的方程可知a ＝2，c ＝2，且|PF 1|＋|PF 2|＝2a ＝4，又|PF 1|－|PF 2|＝2，所以|PF 1|＝3，|PF 2|＝1.又|F 1F 2|＝2c ＝22，所以有|PF 1|2＝|PF 2|2＋|F 1F 2|2，即△PF 1F 2为直角三角形，且∠PF 2F 1为直角，所以S △PF 1F 2＝12|F 1F 2||PF 2|＝12×22×1＝ 2.题型二、圆锥曲线的几何性质【例2】(1)直线l 经过椭圆的一个顶点和一个焦点，若椭圆中心到l 的距离为其短轴长的14，则该椭圆的离心率为( )A.13B.12C.23D.34(2)在平面直角坐标系xOy 中，双曲线x 2a 2－y 2b 2＝1(a ＞0，b ＞0)的右支与焦点为F 的抛物线x 2＝2py (p ＞0)交于A ，B 两点，若|AF |＋|BF |＝4|OF |，则该双曲线的渐近线方程为________.【答案】(1)B (2)y ＝±22x【解析】(1)不妨设椭圆的方程为x 2a 2＋y 2b 2＝1(a >b >0)，右焦点F (c ，0)，则直线l 的方程为x c ＋y b ＝1，即bx ＋cy －bc ＝0. 由题意|－bc |b 2＋c2＝12b ，且a 2＝b 2＋c 2， 得b 2c 2＝14b 2a 2，所以e ＝c a ＝12.(2)设A (x 1，y 1)，B (x 2，y 2)，联立方程：⎩⎪⎨⎪⎧x 2a 2－y 2b 2＝1，x 2＝2py ，消去x 得a 2y 2－2pb 2y ＋a 2b 2＝0， 由根与系数的关系得y 1＋y 2＝2b 2a 2p ，又∵|AF |＋|BF |＝4|OF |，∴y 1＋p 2＋y 2＋p 2＝4×p 2，即y 1＋y 2＝p ，∴2b 2a 2p ＝p ，即b 2a 2＝12⇒b a ＝22.∴双曲线渐近线方程为y ＝±22x .。

9．6 双曲线1．双曲线的定义(1)定义：平面内与两个定点F1，F2的距离的差的________等于常数2a(2a______|F1F2|)的点的轨迹叫做双曲线．这两个定点叫做双曲线的________，两焦点间的距离叫做双曲线的________．※(2)另一种定义方式(见人教A版教材选修2-1 P59例5)：平面内动点M到定点F的距离和它到定直线l的距离之比等于常数e(e>1)的轨迹叫做双曲线．定点F叫做双曲线的一个焦点，定直线l叫做双曲线的一条准线，常数e叫做双曲线的________．(3)实轴和虚轴相等的双曲线叫做_________．“离心率e＝2”是“双曲线为等轴双曲线”的______条件，且等轴双曲线两条渐近线互相______．一般可设其方程为x2-y2＝λ(λ≠0)．2．双曲线的标准方程及几何性质自查自纠1．(1)绝对值＜焦点焦距(2)离心率(3)等轴双曲线充要垂直2．(2)x2a2-y2b2＝1(a＞0，b＞0)(5)A1(0，-a)，A2(0，a)(7)F1(-c，0)，F2(c，0) (9)e＝ca(e＞1)(10)y＝±bax(2015·广东)已知双曲线C：x2a2-y2b2＝1的离心率e＝54，且其右焦点为F2(5，0)，则双曲线C的方程为( )A.x24-y23＝1 B.x29-y216＝1C.x216-y29＝1 D.x23-y24＝1解：c＝5，e＝ca＝5a＝54，得a＝4，b2＝c2-a2＝52-42＝9，双曲线方程为x216-y29＝1.故选C.(2015·福建)若双曲线x29-y216＝1的左、右焦点分别为F1，F2，点P在双曲线E上，且|PF1|＝3，则|PF2|(( (解：设双曲线方程为x 2a 2-y 2b2＝1(a >0，在双曲线的右支上，如图，AB ＝BM 轴于H ，则∠MBH ＝60，3a )．将点M 的坐标代入双曲线a ＝b ，所以e ＝ca＝·南昌调研)已知F 1，F 2是双曲线的两个焦点，P 是C 上一点，若F 2最小内角的大小为的渐近线方程是( )0 B ．x ±0D ．2x ±解：由题意，不妨设|PF |>|PF |，则根据双曲线＝AE ＝1，则AD ＝BE ，双曲线实轴长为23，2a ′＝3-1，所以＝ 3.故填3. )过双曲线x 2-y 23＝轴垂直的直线，交该双曲线的两条渐近线于为坐标原点，动直线分别在第一、四象限试探究：是否存在总与直线E？若存在，求出双曲线程；若不存在，说明理由．因为双曲线E的渐近线分别为。

专题三三角函数及解三角形第1讲三角函数图象与性质、三角恒等变换(限时:45分钟)【选题明细表】知识点、方法题号同角三角函数关系式、诱导公式1,7三角恒等变换2,6,9三角函数图象与性质3,5,8,11综合应用4,10一、选择题1.(2017·河南天一大联考)若cos(-α)=,则cos(π-2α)等于( B )(A)(B)-(C)(D)-解析:cos(π-2α)=2cos2(-α)-1=-.故选B.2.(2017·云南民族中学三模)已知sin 2α=,则tan α+等于( A )(A)(B) (C) (D)4解析:由sin 2α=2sin αcos α=,可得sin αcos α=,所以tan α+=+==.故选A.3.(2017·成都实验外国语学校二诊)已知函数f(x)=sin2x+cos2x-,若将其图象向左平移(>0)个单位后所得的图象关于原点对称,则的最小值为( C )(A) (B) (C) (D)解析:函数f(x)=sin 2x+cos2x-=sin 2x+cos 2x=sin(2x+),将其图象向左平移(>0)个单位后,可得y=sin(2x+2+)的图象,若该函数图象关于原点对称,则2+=kπ,k∈Z,故的最小值为.故选C.4.(2017·云南昆明一模)已知常数ω>0,f(x)=-1+2sin ωx cos ωx+2cos2ωx图象的对称中心到对称轴的距离的最小值为,若f(x0)=,≤x0≤,则cos 2x0等于( D )(A)(B)(C)(D)解析:f(x)=-1+2sin ωxcos ωx+2cos2ωx,sin 2ωx+cos 2ωx=2sin(2ωx+)因为对称中心到对称轴的距离的最小值为,所以T=π.由T==π,可得ω=1.f(x0)=,即2sin(2x0+)=,因为≤x0≤,所以≤2x0+≤,又sin(2x0+)=>0,所以cos(2x0+)=-.那么cos 2x0=cos(2x0+-)=cos(2x0+)cos+sin(2x0+)sin=. 故选D.5. (2017·青海西宁二模)函数y=cos(ωx+)(ω>0,0<<π)为奇函数,其部分图象如图所示,A,B分别为最高点与最低点,且|AB|=2,则该函数图象的一条对称轴方程为( D )(A)x= (B)x=。

2018届高考数学双曲线总复习测试题（附答案）5 c 第三节双曲线一、填空题1 (x23=1，∴a=6，b=3，∵2a=26＞4，∴点P到另一焦点的距离为26+43 3 解析设AB=2c，则BD=c，AD=3c，所以椭圆与双曲线的离心率分别是23+1与23-1，所以倒数和为3+12+3-12=34 2-x29=1 解析设所求双曲线方程为2-x29= ( 0)，将点(3，2)代入得2-99= ，解得 =1，∴这条双曲线的方程是2-x29=15 3215 解析双曲线右顶点为A(3,0)，右焦点为F(5,0)，双曲线一条渐近线的斜率是43，直线FB的方程是=43(x-5)，与双曲线方程联立解得点B的纵坐标为-3215，故△AFB的面积为12 AF |B|=12 2 3215=32156 (8， 33) 解析由题意可知点P只能在双曲线的右支上，根据双曲线的第二定义得点P到右准线的距离为6e=6 45=245，又右准线的方程为x=165，所以点P的横坐标为245+165=8，代入双曲线方程解得纵坐标为 33，所以点P的坐标是(8， 33)．7 4 解析由题意可知aba2+b2=14c+1，得14c2+c=ab≤a2+b22=12c2，解得c≥4，即c的最小值为48 5+12 解析由题意可知AB=c，AF=a+c，BF=b2+c2，∵AB⊥BF，∴AB2+BF2=AF2，∴c2+b2+c2=(a+c)2，化简得b2=ac，∴c2-a2=ac，两边同时除以a2得e2-e-1=0，解得e=1 52，又e＞1，∴e=1+529 因为动圆P过点N，所以PN是圆P的半径，又因为动圆P与圆外切，所以P=PN+22，即P-PN=22(小于4)，故点P的轨迹是以，N为焦点，实轴长为22的双曲线的左支．。