当前位置：文档之家 › 三棱锥的外接球

三棱锥的外接球

  • 格式：ppt
  • 大小：1.75 MB
  • 文档页数：19

下载文档原格式

  / 19

合集下载

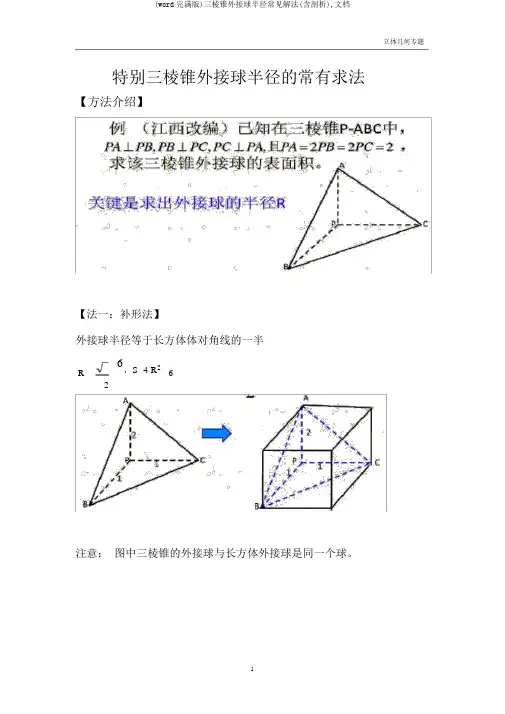
(word完整版)三棱锥外接球半径常见解法(含解析),文档

(word完整版)三棱锥外接球半径常见解法(含解析),文档

特别三棱锥外接球半径的常有求法【方法介绍】
【法一：补形法】
外接球半径等于长方体体对角线的一半
R
6
，S 4 R26 2
注意：图中三棱锥的外接球与长方体外接球是同一个球。

【法二：轴截面法】
1、搜寻底面△ PBC的外心；
2、过底面的外心作底面的垂线；
3、外接球的球心必在该垂线上，利用轴截面计算出球心的地址。

【法三：向量法】
设外接球的球心坐标为：O ( x, y, z) .由 OP OA OB OC 可得：
【方法总结】
三棱锥外接球半径的常见解法：
1、补形法；
2、轴截面法；
3、向量法 .
【练习坚固】
【参照答案】
练习 1【补形法】【轴截面法】
练习 2【补形法】【轴截面法】
练习 3【补形法】
练习 4【轴截面法】。

正三棱锥外接球半径求法

正三棱锥外接球半径求法

正三棱锥外接球半径求法今天咱们来唠唠正三棱锥外接球半径的求法。

这可是个很有趣的数学小知识呢！一、什么是正三棱锥。

正三棱锥呢，就是底面是正三角形，然后从底面的中心向顶点引一条垂线，这个顶点在底面上的射影就是底面正三角形的中心。

它的四个面可都是全等的等腰三角形哦。

这就像一个超级稳定的小金字塔一样，特别神奇。

二、外接球的概念。

那外接球是啥呢？就是这个正三棱锥在一个球里面，这个球刚刚好把正三棱锥给包起来，这个球就叫做正三棱锥的外接球。

就好像给这个正三棱锥穿上了一个圆圆的大外套，这个外套的半径就是我们要找的外接球半径啦。

三、求外接球半径的方法。

1. 补形法。

这是一个很巧妙的方法哦。

咱们可以把正三棱锥补成一个正方体或者是直三棱柱。

比如说补成正方体的时候，正三棱锥的外接球其实就是这个正方体的外接球。

为啥能这么补呢？这就像是把零散的小零件组合成一个大的整体，然后利用这个大整体的性质来求我们想要的东西。

如果正三棱锥的棱长是a，补成正方体后，正方体的棱长设为x，我们可以通过一些几何关系找到它们之间的联系，然后根据正方体的外接球半径公式R = 棱长×√3/2（这里的棱长就是正方体的棱长x），再把x用a表示出来，就能求出正三棱锥外接球的半径啦。

2. 直接法。

这个方法就比较直接啦。

我们要先找到正三棱锥底面三角形的中心O₁，然后连接顶点和这个中心得到一条线，设正三棱锥的高为h，底面正三角形的边长为a。

底面正三角形中心到底面顶点的距离可以根据正三角形的性质求出来，是√3a/3。

然后我们设外接球的球心为O，球心O可能在正三棱锥的内部或者外部。

根据勾股定理，在直角三角形OO₁A（A是底面三角形的一个顶点）中，OA就是外接球的半径R，我们可以得到一个等式：R²=(h - R)²+(√3a/3)²（当球心在正三棱锥内部的时候）或者R²=(R - h)²+(√3a/3)²（当球心在正三棱锥外部的时候），然后解这个方程就可以求出外接球的半径R啦。

侧棱相等的三棱锥外接球半径公式

侧棱相等的三棱锥外接球半径公式

侧棱相等的三棱锥外接球半径公式侧棱相等的三棱锥外接球半径公式指的是一个三棱锥如果满足其侧棱长度相等，那么该三棱锥外接球的半径可以由以下公式计算得出：
R=s√2/3，
其中R为三棱锥外接球的半径，s为三棱锥的侧棱长度。

这个公式的推导过程比较复杂，需要用到三角函数和向量的知识。

简单来说，侧棱相等的三棱锥外接球半径公式的基本思想是，将该三棱锥的每条侧棱的中点连接起来，得到四个相互垂直的向量，然后根据这四个向量计算出三棱锥外接球的半径。

由于三棱锥的侧棱长度相等，所以可以简化计算，得到以上公式。

这个公式在几何学中具有重要的应用价值，可以用来求解侧棱相等的三棱锥相关问题。

三棱锥外接球的半径常见解法-锥形外接圆半径

三棱锥外接球的半径常见解法-锥形外接圆半径

C
y
x2
y
（0,1,0）解得：
2 z2 x1
x2 ,y
1
( ,
y z
1)2 1
z
2
22
所以 R=|OP|= 6 2
方法介绍
三棱锥的外接球半径的常见解法:
1、补形法 2、轴截面法 3、向量法
练习巩固
练习1（陕西，2010）如图，在三棱锥P-ABC
中，PA 平面ABC,CB PB,CB AB,且PA 2AB 2BC 2 ，
y
R 5
（B 2,0,0） x
轴截面法 活学活用，开阔思维
学习小结
三棱锥的外接球半径的常见解法:
1、补形法 2、轴截面法 3、向量法
练习1
PP2AA NhomakorabeaC
B
1
C
1
B
R= 6 , V 4 R3 6
2
3
练习1
P
O
D
A
C
B
OA=OB=OC=OP
R= 1 CP 6 , V 4 R3 6
22
（A 0,0,0）
C（-1，3,0）
y
R 5
（B 2,0,0） x
轴截面法 活学活用，开阔思维
练习巩固
练习4 如图，已知三棱锥P-ABC中，PA⊥底
面ABC，PA=AB=AC=2，∠BAC=120。，求其外
接球的半径。
z P（0,0,2）
球心坐标（1, 3,1）
（A 0,0,0）
C（-1，3,0）
3
练习2
D
A
D
A
C
C
B
R= 6 , 4
B
S 4 R2 3

对棱相等的三棱锥外接球半径公式

对棱相等的三棱锥外接球半径公式

对棱相等的三棱锥外接球半径公式对于棱相等的三棱锥，我们可以利用其几何特征来推导其外接球的半径公式。

首先，我们先来了解一下什么是外接球。

外接球是指能够同时接触到三棱锥的每一个顶点的球形体，它是一个球心位于三棱锥外部并和三棱锥顶点连成的线段相切。

要推导外接球的半径公式，我们可以利用欧拉公式来解决。

欧拉公式是指，对于所有的凸多面体，其顶点数、棱数和面数满足以下关系：顶点数+面数=棱数+2现在我们来考虑一个有n个棱边的三棱锥。

根据三棱锥的定义，它有n+1个顶点（其中一个顶点是顶点，其余n个顶点是底面的顶点）。

同时，它有n个面（一个是底面，其余n-1个是三角面）。

由于三棱锥的每个面都是一个三角形，所以它共有3n个棱边（每个三角形有3个边）。

将这些数据代入欧拉公式中，我们可以得到：n+1+n=3n+2化简得：2n+1=3n+2n=1这意味着棱相等的三棱锥只有一个边，也就是说它是一个等边三角形。

在等边三角形中，每个角度都是60度。

接下来，我们来推导等边三角形的外接球半径公式。

为了方便推导，我们假设等边三角形的边长为a。

根据三角形的性质，我们可以知道等边三角形的高等于边长的一半乘以根号3（即h=(a√3)/2）。

外接球的半径可以通过等边三角形的高来计算。

根据立体几何的知识，我们可以知道外接球的半径r等于等边三角形的高的三分之二（即r=(a√3)/3）。

将等边三角形的边长a代入到外接球半径公式中，我们可以得到：r=(a√3)/3所以，棱相等的三棱锥的外接球半径公式就是r=(a√3)/3综上所述，对棱相等的三棱锥来说，其外接球半径公式是r=(a√3)/3，其中a代表等边三角形的边长。

三棱锥外接球半径常见解法含答案解析

三棱锥外接球半径常见解法含答案解析

三棱锥外接球半径常见解法含答案解析
Document serial number【NL89WT-NY98YT-NC8CB-NNUUT-NUT108】
特殊三棱锥外接球半径的常见求法
【法一：补形法】
外接球半径等于长方体体对角线的一半
注意：图中三棱锥的外接球与长方体外接球是同一个球。

【法二：轴截面法】
1、 寻找底面△PBC 的外心；
2、 过底面的外心作底面的垂线；
外接球的球心必在该垂线上，利用轴截面计算出球心的
3、 位置。

【法三：向量法】
设外接球的球心坐标为：),,(z y x O .由→
→→→===OC OB OA OP 可得：
【练习巩固】
【参考答案】
练习1【补形法】
【轴截面法】
练习2【补形法】
【轴截面法】
练习3【补形法】。

正三棱锥的外接球半径万能公式

正三棱锥的外接球半径万能公式1. 引言说到几何，很多人可能会皱起眉头，觉得那是个复杂的数学领域。

其实，正三棱锥可不是那么高深莫测的东西。

它就像一个长得像三角形的冰淇淋，底下是个正三角形，顶上则有个尖尖的顶点。

这种形状在生活中可不少见，比如你喜欢的那些建筑模型，或者就是你朋友家里装饰的小摆件。

今天，我们就要深入探讨一下正三棱锥的外接球半径，顺便带你领略一下其中的乐趣。

2. 正三棱锥的基本概念2.1 什么是正三棱锥？正三棱锥，顾名思义，就是底面是个正三角形，上面再加个顶点的立体图形。

想象一下，三个边相等的三角形，站在一个小高台上，嘿，就是它了。

它的每一条边都那么对称，真的很养眼呢！你可以把它想象成一座小山，三个小溪在山脚下汇聚。

2.2 外接球的定义说到外接球，可能有人会一头雾水。

简单来说，外接球就是那个能把整个正三棱锥包裹起来的球，就像我们包饺子一样，饺子皮包着馅。

而这个球的半径，就是我们要计算的重点。

就像捏饺子一样，得掌握好这个“半径”，才能包得又美又好吃。

3. 外接球半径公式的来历3.1 公式的推导这里来点干货！外接球半径公式其实是通过一些简单的几何关系推导出来的。

如果你知道正三棱锥的底边长和高，就能轻松算出外接球的半径。

我们用一个小公式来概括：R = (a√6) / 6，其中R是外接球半径，a是底边长。

简单吧？这就像是在计算你心中最爱的冰淇淋球的半径，给你甜蜜的享受。

3.2 公式的应用有了这个公式，我们就能用它解决各种实际问题。

比如，假设你想设计一个新型的房屋，或者给孩子的玩具设计一个外形，都会用到这个半径。

它甚至能帮助你在建筑中找到更好的空间利用方式。

想象一下，你的设计变成现实，成为了一个时尚的聚会场所，绝对让人眼前一亮。

4. 总结总之，正三棱锥的外接球半径并没有你想象中的那么复杂，它其实就像是生活中的一部分。

只要你掌握了这个简单的公式，数学将不再是个冷冰冰的怪物，而是个充满乐趣的好伙伴。

无论是在课堂上，还是在设计中，这个知识都能让你受益匪浅。

三棱锥的外接球


要点、难点：
要点：三棱锥旳外接球旳还原措施；外接球半径旳求法. 难点：“切割”和“整体与局部”思想旳了解.
复习回 顾
文档仅供参考，如有不当之处，请联系改正。
1.球旳表面积和体积公式（半径为 r ）：
（1）球旳表面积公式：S 4r 2
r
（2）球旳体积公式： V 4 r3
3
2.长方体与正方体旳体对角线：
BAC 120,则此球的表面积等于 B
A. 52
9
B.20
C.8
D. 52
3
R d
r复习回 顾Fra bibliotek文档仅供参考，如有不当之处，请联系改正。
类型四：平面截球旳三棱锥外接球问题 措施：设球心到截面旳距离为 d ，球旳半径为 R，截面圆旳半径为 r ，则有 R2 d 2 r 2.
例5 一个空间几何体的三视图如图所示，则该几何体的外接球的表面积
为 4
正视图
1
俯视图
1
侧视图
1
1
P
A
A D
B C
解：把正四面体补充成一个正方体，如图所示，
已知正四面体的棱长为1，由勾股定理可得：
正方体的棱长为 2 ， 2
外接球的半径r 3a2 6 ， 24
所以，外接球的表面积为S 4r 2 3 .
2
课堂探 究
文档仅供参考，如有不当之处，请联系改正。
类型一：正四面体旳外接球问题
措施：把正四面体补充成正方体.
（1）长方体旳体对角线： l a2 b2 c2 （2）正方体旳体对角线： l 3a2
3.三视图旳投影规律：
c b
a
长对正，高平齐，宽相等.
课堂探 究
文档仅供参考，如有不当之处，请联系改正。

对棱相等的三棱锥外接球半径公式

对棱相等的三棱锥外接球半径公式对于棱相等的三棱锥，我们可以利用其几何性质来推导其外接球半径的公式。

在推导之前，我们需要先了解一些基本概念。

首先，我们需要知道什么是三棱锥的外接球。

外接球是指能够同时与三棱锥的四个顶点相切的球。

在这个球的表面上，四个顶点和球心之间的距离是相等的。

然后，我们需要明白什么是棱相等的三棱锥。

棱相等的三棱锥是指三条棱的长度都相等的三棱锥。

也就是说，三棱锥的底面是一个等边三角形，顶点到底面三个顶点的距离也相等。

接下来，我们开始推导外接球半径的公式。

假设三棱锥的底面边长为a，棱长为l，外接球半径为R。

首先，我们考虑三棱锥的高h与外接球半径R之间的关系。

由于底面是等边三角形，我们可以通过勾股定理计算底面的高。

设底面边长的一半为s，那么根据勾股定理有：h²=a²-s²接下来，我们需要计算底面边长的一半s。

由于底面是等边三角形，可以用等边三角形的高的公式来计算：s=a√3/2将这个结果代入到h²=a²-s²中，可以得到：h²=a²-(a√3/2)²=a²-3a²/4=a²/4因此，三棱锥的高为h=a/2接着，我们考虑外接球的半径R与三棱锥的高h之间的关系。

根据勾股定理，我们可以知道三棱锥的高、半径和斜高（即顶点到底面边的距离）构成一个直角三角形。

设斜高为d，那么有：R²=h²+d²根据勾股定理，我们可以知道斜高d的长度为底面边长a的一半。

即d=a/2将这个结果和前面推导的h=a/2代入到R²=h²+d²中，可以得到：R²=(a/2)²+(a/2)²=(a²/4)+(a²/4)=a²/2因此，三棱锥外接球的半径R为R=√(a²/2)=a/√2综上所述，我们得到了棱相等的三棱锥外接球半径的公式：R=a/√2这个公式表明，对于棱相等的三棱锥，其外接球的半径等于底面边长的一半除以√2这个公式的推导基于一些假设和简化，仅适用于棱相等的三棱锥。

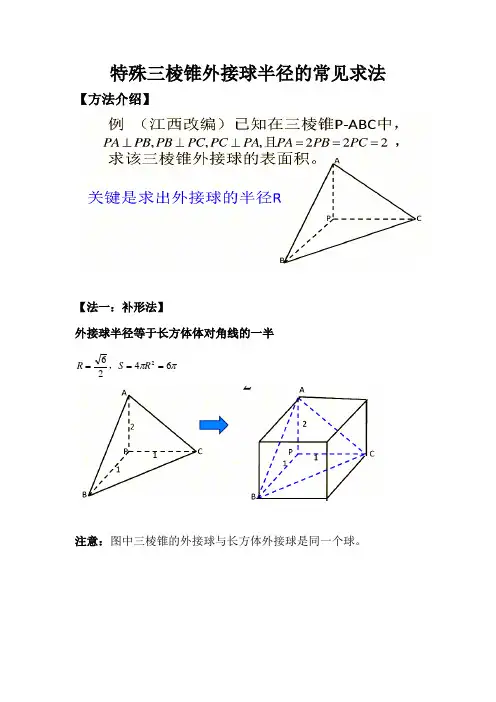
三棱锥外接球半径常见解法

特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一：补形法】
外接球半径等于长方体体对角线的一半
ππ642
6
2===
R S R ，
注意：图中三棱锥的外接球与长方体外接球是同一个球。

【法二：轴截面法】
1、 寻找底面△PBC 的外心；
2、 过底面的外心作底面的垂线；
3、 外接球的球心必在该垂线上，利用轴截面计算出球心的位置。

【法三：向量法】
设外接球的球心坐标为：),,(z y x O .由→
→
→
→
===OC OB OA OP 可得：
【方法总结】
三棱锥外接球半径的常见解法：
1、 补形法；
2、轴截面法；
3、向量法.
【练习巩固】
【参考答案】
练习1 【补形法】【轴截面法】
【轴截面法】
练习3 【补形法】。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2
c a
b
3.三视图的投影规律：
长对正，高平齐，宽相等.
课堂探 究
问题1：长方体或正方体的体对角线和体心与它的外接球有什么关 系？
答： （1）体对角线等于外接球的直径；
（2）体心和球心重合.
问题2：边长为2的正方体的外接球的表面积为多少？
解：体对角线 l 3a2 12 2 3
则外接球的半径 r 3
球的体积为
D
6 8
C
D P（A）
C A E B E
课堂探 究
类型二：三垂直的四面体的外接球问题
方法：把该四面体补充成正方体或者长方体.
三棱锥P ABC中，侧棱AB, AC, AP两两垂直， ABC, ACP, APB的
面积分别为
P
2 3 6 ， ， ，则该三棱锥外接球的 表面积为 2 2 2
6
A C
B
课堂探 究
类型三：双垂直的四面体的外接球问题
方法：把该四面体补充成正方体或者长方体.
三棱锥P ABC中，PA 平面ABC，AC CB, AC CB 1 ，PA 3,
则该三棱锥的外接球的 表面积为
P
5
A B
C
课堂探 究
类型三：双垂直四面体的外接球问题
方法：把该四面体补充成正方体或者长方体.
如下图所示，在正三棱 锥P ABC中，E、F分别是PA, AB的中点， CEF 90 , 若AB 2, 则该三棱锥的外接球的 表面积为 4
P E
A F C
B
直三棱柱ABC A1B1C1的各顶点都在同一球面 上，若AB AC AA 1 2
BAC 120 , 则此球的表面积等于 B
方法：设球心到截面的距离为 d ，球的半径为 R，截面圆的半径为
r ，则有
R2 d 2 r 2 .
一个空间几何体的三视 图如图所示，则该几何 体的外接球的表面积
为
16 3
P
正视图
3
侧视图 O
1
俯视图
1
1
A
B O1 C
课堂探 究
类型四：平面截球的三棱锥外接球问题
方法：设球心到截面的距离为 d ，球的半径为 R，截面圆的半径为
1.球的表面积公式和体积公式：
（1）球的表面积公式： S 4r 2 4 （2）球的体积公式： V r 3 3
2.四种类型的三棱锥的外接球问题求解：
类型一：正四面体的外接球问题 类型二：三垂直的四面体的外接球问题 类型三：双垂直的四面体的外接球问题 类型四：平面截球的三棱锥外接球问题
课堂探 究
d
R
r
复习回 顾
类型四：平面截球的三棱锥外接球问题
方法：设球心到截面的距离为 d ，球的半径为 R，截面圆的半径为
r ，则有
R2 d 2 r 2 .
一个空间几何体的三视 图如图所示，则该几何 体的外接球的表面积
为
4
P 正视图
1 1 1 1
侧视图
俯视图
A B
O
C
复习回 顾
类型四：平面截球的三棱锥外接球问题
52 9
B.20 C .8
A.
D.
52 3
重点、难点：
重点：三棱锥的外接球的还原方法；外接球半径的求法. 难点：“切割”和“整体与局部”思想的理解.
复习回 顾 1.球的表面积和体积公式（半径为 r ）：
（1）球的表面积公式： S 4r 2 4 （2）球的体积公式： V r 3 3
r
2.长方体与正方体的体对角线：
（1）长方体的体对角线： l a 2 b2 c 2 （2）正方体的体对角线： l 3a
方法：设球心到截面的距离为 d ，球的半径为 R，截面圆的半径为
r ，则有
R2 d 2 r 2 .
三个半径均为 3的球O1, O2 , O3与半径为 1 的球I两两外切，则以 O1, O2 , O3和I为四个顶点的三棱锥外 接球的半径为
I
4
O2 O1 O4 O O3 O O1
O4
课堂小 结
B
（3）正四面体的对棱互相 垂直. 能在正方体中切割出一 个正四面体，如图所示 .
C
课堂探 究
问题5：棱长为 1的正四面体的外接球的表面积为多少？
A D
解：把正四面体补充成 一个正方体，如图所示 ， 已知正四面体的棱长为 1，由勾股定理可得：
B
C
2 正方体的棱长为 ， 2 3a 2 6 外接球的半径 r ， 2 4
所以，外接球的表面积 为S 4r 2 12
课堂探 究
问题3：假如一个正方体的8个顶点都在同一个球的球面上，那么 任意选出4个顶点，这4个顶点还在该球的球面上吗？
A D
答： 在
B
C
问题4：正四面体有什么特征？在正方体中能否切割出一个正 四面体？
A D
（ 1 ）正四面体的所有棱长 都相等； 答： （2）正四面体的四个面都 是全等的等边三角形 .
高考总复习之专题突破
§专题复习：三棱锥习导 航
学习目标：
（1）知识与技能目标：通过本节复习，能够熟悉的掌握三棱 锥的外接球的表面积和体积的求法. （2）过程与方法目标：在探究三棱锥的外接球的过程中，体 会“切割”、“化归”及“局部和整体”的思想.
（3）情感、态度与价值观目标：通过本节复习,培养数形结合 的思想，抽象概括能力及创新意识.
如图是一个空间几何体 的三视图，则该几何体 的外接球的表面积为
8
正视图 2
侧视图
1 2 1
俯视图 P
2
2
A B
C
复习回 顾
类型四：平面截球的三棱锥外接球问题
方法：平面截球的截面是圆，设球心到截面的距离为 d ，球的半径为 R ，截面 圆的半径为 r ，则有 R 2 d 2 r 2 . 注：（1）圆的直径所对的圆周角等于90°； （2）直角三角形斜边上的中线等于斜边的一半； （3）等边三角形三线合一，重心是中线的三等分点.
所以，外接球的表面积 为S 4r 2
3 . 2
课堂探 究
类型一：正四面体的外接球问题
方法：把正四面体补充成正方体.
在等腰梯形 ABCD中，AB 2CD 2，DAB 60 , E为AB的中点，将 ADE
与BEC分别沿ED, EC向上折起，使 A, B重合于点P，则三棱锥 P DCE的外接
r ，则有
R2 d 2 r 2 .
如图所示的三棱锥 D ABC的四个顶点均在球 O的球面上， ABC
和DBC所在的平面互相垂直， AB 3，AC 3, BC CD BD 2 3,
则球O的表面积为
16
D
O C O1 B
A
课堂探 究
类型四：平面截球的三棱锥外接球问题