均值和极差图使用说明

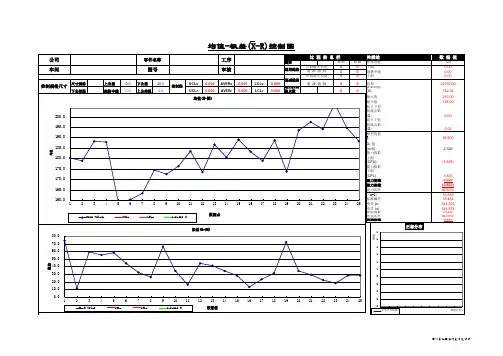
均值-极差控制图（x-R）X匀值：是通过每组样本的平均值得出的,然后把每组的平均值相加除以组数,得到总的平均值.R 匀值：是通过每组两个极端值得到的,就是每组的最⼤值-最⼩值,等于每组的极差,再通过每组的极差值来计算总的极差平均值平均极差分布及控制图常数表2 ⽤EXCEL软件绘均值⼀极差控制图(rR图)2．1 绘图⽅法2．1．1 EXCEL软件的作⽤随着计算机技术的不断发展，尤其是计算速度的不断加快，使其在办公领域得以充分应⽤。

⼀些软件不但能制表，还能绘图，使质量管理⼯作也上了⼀个新⽔平。

近来，笔者尝试⽤EXCEL 绘均值⼀极差控制图( R 图)，以使质量管理⼯作更⽅便、更快捷。

2．1．2 应⽤⽰例现以齿条总⾼为例，⽤EXCEL软件绘a-R 图。

设共有25组数据，样本⼤⼩为5，其操作过程如下。

2．1．2．1 打开EXCEL软件中的⼀个⼯作薄，选择其中⼀个⼯作表。

2．1．2．2 在第1⾏输⼊表头。

2．1_2．3 在第l列单元格输⼊样本编号：选定要填充的第1个单元格A2，输⼊1，A3格输⼊2，选择A2、A3格将⿏标移到A3格右下⾓的填充柄上，当⿏标指针变成⼩⿊⼗字时，按⿏标左键在要填充的区域上拖动(即从A4到A26)，松开⿏标左键，填充⾃动完成。

2．1．2．4 在第2列单元格输⼊标准值：选定单元格B2，输⼊2．8，将⿏标移到B2格右下⾓的填充柄上，当⿏标指针变成⼩⿊⼗字时，按⿏标左键在B3到B26格上拖动，松开⿏标左键填充⾃动完成。

2．1．2．5 将收集到的数据输⼊表中。

2．1．2．6 计算均值：选定H2，选“常⽤”⼯具栏中的“粘贴函数”(即⼚ )，出现“粘贴函数”对话框，在函数分类栏中选“常⽤函数”，在函数名栏中选“AV—ERAGE”，点“确定”，在“Number1”栏中输⼊“C2：G2”，点“确定”，即求得⼀个均值，选定H2格，点常⽤⼯具栏中的“复制”，再选定H3到H26，选“常⽤”⼯具栏中的“粘贴”，即求出其余24个均值。

控制图1控制图——过程控制的工具。

用来表示一个过程特性的图象。

它有两个基本用途：①用来判断过程是否一直受统计控制。

②用来帮助过程保持受控状态。

2控制图的构成：：上控制线：中心线下控制线取样时间①收集：收集数据并画在图上。

②控制：根据过程数据计算试验控制线识别变差特殊原因并采取措施。

③分析及改进：确定普通变差的大小，并采取减少它的措施。

重复三个阶段，从而不断改进过程。

3控制图的益处：①供正在进行过程控制的操作者使用。

②有助于过程在质量上和成本上能持续地、可预见的保持下去。

③使过程达到：——更高的质量。

——更低的单件成本。

——更高的有效能力。

④为讨论过程的性能提供共同的语言。

⑤区分变差的特殊原因和普通原因，作为采取局部措施或对系统采取措施的指南。

第二章计量型数据控制图第一节均值和极差图参见“均值和极差控制图”1．收集数据1．1子组大小：一般为4-5件（连续生产的产品的组合）。

各子组样本应一样。

选择原则：一子组各样本间出现的变差的机会小。

子组内变差主要由普通原因造成。

1．2子组频率：应在适当时间收集足够的子组，能反映潜在的变化。

过程处于稳定，频率可减少。

（每班两次、每小时一次或其他频率）。

1．3子组组数：≧25个。

总单值≧100个。

2．控制图及记录原始数据：①X图绘在R图的上方。

下面再接一个数据栏。

②X和R值为纵坐标，时间为横坐标。

③数据栏应包括：每个读数空间、读数、和、均值、极差以及日期/时间或其他识别子组的代码的空间等。

3．计算均值（X）和极差（R）：X=( X1+X2+…+X n)/n R=X MAX﹣X MINX1,X2,…X n——测量值。

n——子组容量。

4．控制图刻度；①对X图：坐标刻度最大值-最小值≧2（X max–X min）②对R图：坐标刻度最大值≧2R max5．计算控制限：①平均极差（R）及过程平均值（X）R=（R1+R+2…+R K）/K（1X2+…+X K）/KK——子组的数量。

平均值和极差法(Xbar & R)是一种可同时对测量系统提供重复性和再现性的估计值的研究方法。

与单独的极差法不同，该方法允许将测量系统的变差分解成两个独立的部分：重复性和再现性，但不能确定它们两者的相互作用。

同时，基于评估者与零件/量具交互作用产生的变差也没有计入分析中。

进行研究尽管评价者的人数、测量次数及零件数量均可能会不同，但下面的讨论呈现进行研究的最佳情况。

参见图B6中的GRR数据表，详细的程序如下：1) 取得一个能代表过程变差实际或预期范围的样本，为n> 10个零件44的样本。

2) 给评价者编号为A、B、C等，并将零件从1到n进行编号，但零件编号不要让评价者看到。

3) 对量具进行校准，如果这是正常测量系统程序中的一部分的话。

让评价者A以随机顺序45测量n个零件，并将结果记录在第1行。

4) 让评价者B和C依次测量这些一样的n个零件,不要让他们知道别人的读值，然后将结果分别的记录在第6行和第11行。

5) 用不同的随机测量顺序重复以上循环，并将数据记录在第2、7和12行：注意将数据记录在适当的栏位中，例如：如果首先被测量的是零件7，然后将数据记录在标有零件7的字段中。

如果需要进行三次测量，则重复以上循环，并将数据记录在第3、8和13行中。

6) 当测量大型零件或不可能同时获得数个零件时，第4步到第5步将变更成以下顺序:让评价者A测量第一个零件并将读值记录在第1行；让评价者B测量第一个零件并将读值记录在第6行；让评价者C测量第一个零件并将读值记录在第11行。

让评价者A重新测量第一个零件并将读值记录在第2行；评价者B重新测量第一个零件并将读值记录在第7行；评价者C重复测量第一个零件并将读值记录在第12行。

如果需要进行三次测量，则重复以上循环，并将数值记录在第3、8和13行中。

7) 如果评价者处于不同的班次，可以使用一个替代的方法。

让评价者A 测量所有10个零件，并将读值记录在第1行；然后让评价者A按照不同的顺序重新测量，并把读值记录在第2行和第3行。

质量控制图的绘制及使用[2,5,7]根据误差为正态分布的原理，在统计学上X±1S占正态曲线下面积的%，以此作为上辅助限和下辅助限；X±2S占总面积的%，以此作为上警戒限和下警戒限；X±3S占总面积的%，以此作为控制图的上控制限和下控制限（图）；超过3倍S的概率总共只占%，以乃属于小概率事件，亦即同一总体中出现如此大偏差的概率极小，可以认为它不是这个总体中的一个随机样品，这个结论具有%的把握是正确的。

既然不能作为同一总体中的一个随机组成者，而在分析测试中是用同一分析方法，在相同条件下所测得的同一个样品（例如空白试验）的检测值，则必然发生了某种影响较大因素的作用，从而有根据否定这一测定值。

图质量控制图图中质量控制图的形式与正态曲线形式完全相同，即将正态曲线向逆时针方向旋转了90度，以正态曲线的中心m被X所代替，作为理想的预期测定值；将%概率保证的置信区间作为目标值（即上、下辅助限之间的区域）；以%概率保证的置信区间作为可接受范围（即上、下警戒限之间的区域）；将上、下警戒限至上、下控制限的区间作为可能存在“失控”倾向，应进行检查并采取相应的校正措施；在上、下控制限以外，则表示测定过程已失去控制，应立即停止检测，待查明原因加以纠正后对该批样品全部重新测定。

对于质量控制检查样品和实验室控制样品的控制图，是把算术平均值作为中心值统计。

最初控制限制是用平均值的百分数表示，通常系列测定算术平均值±10%。

然而，最少进行7个测定值后才能建立统计控制限度。

警戒限度设在来自平均数(X)±2Sx (标准误，来自质量控制样品的95%）；控制限度设在离平均数(X)±3 Sx应包含质量控制样品的%）。

质量控制样品数据的5%将落在警戒限外面，如果两个连续测定值落在警戒限外面被认为是“失控”状态(Taylor, 1987)。

由于%的数据应该落在X±3Sx以内，控制限外面的点是最可能失控的，矫正活动是有根据的。

1目的与适用范围1.1 目的了解过程变差，识别过程的受控状态。

1.2 适用范围适用于计量型数据。

2工作要求2.1收集数据使用该控制图所收集的数据要求以样本容量恒定的子组的形式报出的。

每个子组通常包括2～5件连续的产品，并周期性的抽取子组（例如：每一小时抽取5件）。

2.1.1选择子组的大小、频率和数据2.1.1.1子组大小确定“合理子组”是决定控制图的效果和效率的关键，选择子组时应注意：a）应使得一个子组内在该单元中的各样本之间出现变差的机会小；b）子组一般由2～5件连续的产品组成。

2.1.1.2 子组频率确定子组收集的频率，其目的是检查经过一段时间后过程的变化，因此：a）应在适当的时间收集足够的子组，这样子组才能反映潜在的变化（如：换班、操作人员的变更、材料批次的不同）。

b）子组间的间隔时间可随着过程的稳定状态，进行调整（增加或减少）。

2.1.1.3 子组数的大小应遵循以下2个原则：a）所有子组包括的样本总数达100个以上；b）子组数一般为25组。

2.2 数据收集2.2.1 按照一定的频次定期的收集数据（如1次/4小时、1次/班等）。

并将每次收集数据的日期和时间记录在控制图中的“日期/时间”栏目中。

2.2.2 每次收集的检验样本（即子组）的容量（如同种零件的数量）要求相等（每次2～5件），并将样本的特性进行测量，并将测量的数据记录在控制图的“读数”栏目中。

2.2.3“X”栏目中。

计算每个子组中数据的极差，R”栏目中。

上式中X1、X2…为子组内的每个测量值，n为子组的样本容量。

2.2.4 选择控制图的刻度a）对于均值图，坐标上的刻度值的最大和最小值之差应至少为子组均值（X）的最大值和最小值之差的2倍；b）对于极差图，坐标上刻度值应为最低值0开始到最大值之间的差值为初始研究阶段所遇到的最大极差（R）的2倍。

2.2.5 计算每个子组的均值（X）和极差（R）在均值图（X图）和极差图（R图）上所对应的刻度值和抽样时间交叉的地方描点，并将点与点之间用直线连接起来。

控制图（均值图）培训讲义在经济飞速发展的今天，为了企业的发展、事业的昌盛，我们必须致力于持续改进，我们必须寻找更有效的方法来生产产品提供服务，这些产品和服务必须不断地在价值上待以改进和提高，我们必须重视内部以及外部的顾客，并将顾客满意作为企业主要的目标。

为达到这一目标，我们公司的每一位员工都必须确保不断改进以及使用更有效的方法。

下面给大家描述一种最有效的控制图统计方法，可以使改进更加明确、有效。

一、所使用符号的介绍：CP（理想值）稳定的过程能力指数CPK（实测值）稳定的过程能力指数CPU上限的能力指数CPL下限的能力指数PP（理想值）性能指数PPK（实测值）性能指数PPU上限性能PPL下限性能USL工程规范上限LSL工程规范下限X均埴R极差T公差范围S样本标准差D2值估计值二、控制图的结构：收集数据控制图是从对某个特性或过程特征的测量发展而来的。

这些测量值构成了描述过程分布特性（控制）统计量（例如：均值、中位数、极差、标准差、单值）。

测量数据取自于过程流的单个样品。

按子组的形式收集样本，它可以是由一个零件或多个零件组成。

通常，一个较大的子组使得更容易发现微小的过程变化。

建立一个抽样计划为了控制图的有效性，抽样计划应该定义“合理子组”。

合理子组是选择样本以使得在一个子组内出现特殊原因变差的机会最小，而在子组间出现特殊原因变差的机会最大。

要记住的关键一条是当开发一个抽样计划时，要将子组间的变差和子组内的变差进行比较。

连续取样而形成的子组，使过程改变的机会最小并且子组内的变差也应该最小。

抽样的频率将取决于子组间过程改变的时机。

子组内的变差代表短时间18内的零件间的变差，子组间出现的任何大的变差则表明过程发生变化，应该进行调查并采取适当的措施。

子组容量——所研究的过程的类型决定了如何定义子组容量。

按照前面的阐述，较大的子组使得容易探测出较小的过程变化。

负责的团队必须确定适当的子组容量。

如果预期的过程变化相对小，则应该有较大的子组容量。

均值极差图(X-R图‎)分析极差图R‎1、受控制的过程的极‎差UCLRLCL‎★存在特殊原因变差‎2、不受控制的过程的‎极差(有超过控制限的‎点)UCLRLCL解释：超出极差上‎控制限的点通常说明存‎在下列情况的一种或几‎种：●控制限计算错误‎或描点时描错；●零件‎间的变化性或分布的宽‎度已经增大（即变坏）‎，这种增大可以发生在‎某个时间点上，也可能‎是整个趋势的一部分；‎●测量系统变化（如不‎同的检具或检验员）；‎●测量系统没有适当的‎分辨力。

有一点位于‎控制限之下（样本容量‎大于等于7的情况），‎说明存在下列情况的一‎种或几种：●控制限或‎描点错误；●分布的宽‎度变小（即变好）；●‎测量系统已改变（包括‎数据编辑或变换）。

‎★链——有下‎列现象之一表明过程已‎改变或出现种趋势：●‎连续7点位于平均值的‎一侧；●连续7点上升‎或下降。

‎(存在高于和低于极差‎均值的两种链)UCLRLCL4、不受‎控制的过程的极差(‎存在长的上升链)UCLRLCL解释：‎高于平均极差的链或‎上升链说明存在下列情‎况的一种或全部：●输‎出值的分布宽度增加，‎其原因可能是无规律的‎（如设备工作异常或固‎定松动）或是由于过程‎中的某个要素变化（如‎材料变化），是常见问‎题，需纠正；●测量系‎统变化（如不同的检具‎或检验员）；低于平‎均极差的链或下降链说‎明存在下列情况的一种‎或全部：●输出值的分‎布宽度减小，这常常是‎一个好状态，应研究以‎便推广应用和改进过程‎；●测量系统改变，这‎会掩盖过程的真实性的‎变化。

★其它明显的‎非随机的图形5、不‎受控制的过程的极差‎(点离极差均值太近)‎UCLRLCL‎(点离控制‎限太近)解释：各点与‎极差均值R 的距离：一‎般地，大约2/3的描‎点应落在控制限的中间‎1/3的区域内，1/‎3的描点应落在其外的‎2/3的区域内。

a ‎）如果显著多于2/3‎以上的描点落在离极差‎均值R 很近之处（超过‎90％的点落在控制限‎1/3的区域内），说‎明存在下列情况的一种‎或全部： ● 控制限计算‎错误或描点时描错； ● ‎过程或取样方法被分层‎；每个子组系统化包含‎了从两个或多个具有完‎全不同的过程均值的过‎程流的测量值（如用几‎根测量轴每一轴测一个‎数）； ● 数据已经过编‎辑。

均值和极差图（X-R）一、收集数据以样本容量恒定的子组形式报告，子组通常包括2-5件连续的产品，并周性期的抽取子组。

注：应制定一个收集数据的计划，将其作为收集、记录及描图的依据。

1. 选择子组大小，频率和数据a)子组大小：一般为5件连续的产品，仅代表单一刀具/冲头/过程流等。

（注：数据仅代表单一刀具、冲头、模具等生产出来的零件，即一个单一的生产流。

）b)子组频率：在适当的时间内收集足够的数据，这样子组才能反映潜在的变化，这些变化原因可能是换班/操作人员更换/材料批次不同等原因引起。

对正在生产的产品进行监测的子组频率可以是每班2次，或一小时一次等。

c)子组数：子组越多，变差越有机会出现。

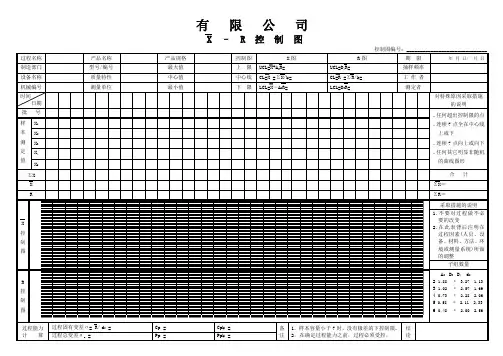
一般为25组，首次使用管制图选用35 组数据，以便调整。

2. 建立控制图及记录原始数据（见下图）3. 计算每个子组的均值（X）和极差R对每个子组计算：X=（X1+X2+…+Xn）/ nR=Xmax-Xmin式中： X1 ，X2 • • • •为子组内的每个测量值。

n 表示子组的样本容量4. 选择控制图的刻度4-1两个控制图的纵坐标分别用于 X 和 R 的测量值。

4-2刻度选择：对于X 图，坐标上的刻度值的最大值与最小值的差应至少为子组均值（X）的最大值与最小值的差的2倍，对于R图坐标上的刻度值的最大值与最小值的差应为初始阶段所遇到的最大极差（R）的2倍。

注：一个有用的建议是将 R 图的刻度值设置为 X 图刻度值的2倍。

（例如：平均值图上1个刻度代表0.01英寸，则在极差图上1个刻度代表0.02英寸）5. 将均值和极差画到控制图上5-1 X 图和 R 图上的点描好后及时用直线联接，浏览各点是否合理，有无很高或很低的点，并检查计算及画图是否正确。

5-2 确保所画的X 和R点在纵向是对应的。

注：对于还没有计算控制限的初期操作的控制图上应清楚地注明“初始研究”字样。

二、计算控制限首先计算极差的控制限，再计算均值的控制限。

1.计算平均极差（R）及过程均值（X）R=（R1+R2+…+Rk）/ k（K表示子组数量）X =（X1+X2+…+Xk）/ k2.计算控制限计算控制限是为了显示仅存在变差的普通原因时子组的均值和极差的变化和范围。

excel2020怎么制作平均值-极差控制图
excel2010制作平均值-极差控制图的步骤:
点击打开excel。

输入数据，及需要计算的项目(极差、平均极差、UCL、LCL等)。

用MAX()-MIN()函数和复制拖动，计算20天数据每天(组)的极差值。

用AVERAGE函数计算“总平均值”，范围从$B$2到$U$6，然后拷贝直到U9单元。

用AVERAGE函数计算“平均极差”值，范围从$B$8到$U$8，然后拷贝直到U10单元。

计算控制图上控制限UCL=总平均值+A2×平均极差、LCL=总评均值-A2*平均极差、CL=平均值、极差UCL=平均极差*A4、极差LCL=平均极差*A3
点击工具栏中“图表向导”按钮，在弹出的对话框中选择“折线图”后，按完成退出。

得到平均值控制图。

同理可得,极差控制图。

平均值-极差控制图如下。

计量值控制图之均值-极差控制图
摘要：在处理一个计量值的控制图时，我们要控制的是这个质量特性的均值和变异数,其中包括均值控制图跟极差控制图,简称为X-R控制图.
均值-极差控制图
1.在处理一个计量值的控制图时，我们要控制的是这个质量特性的均值和变异数:
●要控制平均数，通常是使用均值控制图;
●而控制过程的分散或变异则使用极差控制图称R控制图;
2.同时维持过程均值和过程变异在控制状态下是很重要的
3.最常用、最基本的控制图
●用于控制对象为长度、重量、强度、厚度、时间等计量值;
●由用于描述均值变化的均值图和反映过程波动的极差控制图组成;
4.计算均值控制图与极差控制图的上下控制界限公式:
式中：A2 ，D3，D4 ——是由样本大小n确定的系数，可由下表查得。

当n≤6时，D3为负值，而R值为非负，此时LCL实质不存在。

此时，可令LCL=0作为下控制线。

均值控制图
主要用于诊断过程均值的异常波动:
极差R控制图
●均值控制图是对过程均值变化的诊断
●如果过程波动随时间变化是不稳定的
●那么在均值控制图上从不稳定过程中计算出的控制线，就不能反映只有随机
因素作用产生的过程波动
●因此对均值控制图的解释就会出现误导
●只有在稳定的过程中才可以构造控制图实施过程的诊断
●判断过程稳定需要用R控制图
计量值控制图主要用于长度、重量、时间、强度、成份等以计量值来管理工程的控制图，利用统计手法，设定控制均值X和极差R的界限，同时利用统计手法判定导致工程质量变异是随机原因，还是异常原因的图表。

均值-极差控制图是常用于SPC统计过程控制分析中,它们常用的两种控制图分析图表.。