热力学一般关系
- 格式:doc
- 大小:1.00 MB
- 文档页数:36

第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如内能U、熵S)及其为某一研究方便而设的组合函数(如焓H、自由能F、自由焓G等)许多都是不可测量,必须将它们与可测量(如压力p、体积V、温度T等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式 全微分性质+基本热力学关系式6.1 状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
设函数),(y x f z =具有全微分性质dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= (6-1) 则必然有(1) 互易关系令式(6-1)中),(y x M x z y=⎪⎪⎭⎫ ⎝⎛∂∂, ),(y x N y z x =⎪⎪⎭⎫ ⎝⎛∂∂ 则 y x x N y M ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ (6-2)互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(6-1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂z xz y dy y z dx x z则 xy z y z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂y z x z x x y y z (6-3)此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
结果也很容易记忆,只需将三个变量依上、下、外次序,即))()((xzy yxz zyx 循环就行了。



第二部分工质的热力性质热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如能U、熵S)及其为某一研究方便而设的组合函数(如焓H、自由能F、自由焓G等)许多都是不可测量,必须将它们与可测量(如压力p、体积V、温度T等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式全微分性质+基本热力学关系式6.1状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理设函数z f (x,y)具有全微分性质则必然有(1)互易关系令式(6-1 )中N(x,y)(6-2)互易关系与…dz 0等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2)循环关系当保持z不变,即dz0时,由式(6-1),得zdx z zdy z 0dz dx dyx(6-1 ) M (x, y)故有 此式的功能是:若能直接求得两个偏导数,便可确定第三个 偏导数。
结果也很容易记忆,只需将三个变量依上、下、外 次序,即(zyx)(yxz)(xzy)循环就行了。
(3)变换关系两边同除以dx ,得立变量时,函数z(x,)对x 的偏导数。
上面的关系可用于它们 之间的变换。
这一关系式对于热力学公式的推导十分重要。
(4)链式关系按照函数求导法则,可有下述关系:式中: x y 是函数z (x,y)对x 的偏导数;:是以O')为独xxyy x x(6-3 ) 将式(6-1 )用于某第四个变量 不变的情况,可有dzz —dx z —dyz_z z y(6-4)(6-5 )(6-5a )这是在同一参数(如y)保持不变时,一些参数(z,x,,)循环求导所得偏导数间的关系。


第6章 热力学一般关系式和实际气体的性质6-1 一个容积为23.3m 3的刚性容器内装有1000kg 温度为360℃水蒸气,试分别采用下述方式计算容器内的压力:1) 理想气体状态方程; 2) 范德瓦尔方程; 3) R-K 方程;4) 通用压缩因子图;4)查附录,水蒸气的临界参数为:K T cr 3.647=,bar p cr 9.220=,Z Pakg m K K kg J Z p v T ZR p p p cr g cr r 5682.0109.220/0233.015.633/9.461153=×××⋅×=×==978.03.64715.633===K K T T T crr 查通用压缩因子图6-3,作直线r p Z 76.1=与978.0=r T 线相交,得82.0=r p则bar MPa p p p cr r 1819.22082.0=×== 5)查水蒸气图表,得bar p 02.100=6-2 试分别采用下述方式计算20MPa 、400℃时水蒸气的比体积: 1) 理想气体状态方程; 2) 范德瓦尔方程; 3) R-K 方程;()b V V T b V m m m +−5.05.05.022−⎟⎟⎠⎜⎜⎝−+−pT V pT b p V p m m m mm m V V V ⎟⎠⎞⎜⎝⎛×−+×××−××−⇒5.02626315.67320059.14202111.010*******.015.6733.8314102015.6733.8314 067320002111.059.1425.0=××−()000058.002748.00004456.0005907.0279839.023=−−+−×−⇒m m m V V V000058.002112.0279839.023=−×+×−⇒m m m V V Vkmol m V m /1807.03=⇒ 则kg m V v m /01003.002.18/3==⇒4)查附录,水蒸气的临界参数为:K T cr 3.647=,bar p cr 9.220=,905.09.220200===cr r p pp()()()∫∫∫⎟⎠⎞⎜⎝⎛−−+−⎟⎟⎠⎞⎜⎜⎝⎛−=−−21212122221221v v v v v v g dv v a dv b v b b v d b v T R ()()⎟⎟⎠⎞⎜⎜⎝⎛−−⎟⎟⎠⎞⎜⎜⎝⎛−−−+⎟⎟⎠⎞⎜⎜⎝⎛−−=1212212211211ln 21v v a b v b v b b v b v T R g 6-4 Berthelot 状态方程可以表示为:2mm TV ab V RT p −−=,试利用临界点的特性即0=⎟⎟⎠⎞⎜⎜⎝⎛∂∂cr T m V p 、022=⎟⎟⎠⎞⎜⎜⎝⎛∂∂crT m V p 推出:cr cr p T R a 326427=,cr cr p RT b 83= 解:()0232=+−−=⎟⎟⎠⎞⎜⎜⎝⎛∂∂m cr m cr T m V T a b V RT V p cr()322m cr m cr V T ab V RT =−⇒ (1) ()0624322=−−=⎟⎟⎞⎜⎜⎛∂∂cr V T a b V RT V p ()433cr V T a b V RT =−⇒ (2)()22T R b v T p g v−−=⎟⎠⎞⎜⎝⎛∂∂()()v C T R b v p g 22+−=⇒ 由于以上两式是同一方程,必然有()()021==v C T C ,即()TR b v p g 2−=6-6 在一个大气压下,水的密度在约4℃时达到最大值,为此,在该压力下,我们可以方便地得到哪个温度点的()T p s ∂∂/的值?是3℃,4℃还是5℃?解:由麦克斯韦关系式p TT v p s ⎟⎠⎞⎜⎝⎛∂∂−=⎟⎟⎠⎞⎜⎜⎝⎛∂∂,可知在一个大气压的定压条件下,4℃时有0=⎟⎠⎞⎜⎝⎛∂∂T v 。


热力学一般关系本章提要及安排本章提要:1.工质的平衡热力性质是指工质状态参数间的函数关系,特别以可测参数为独立变量的热力学能、焓、熵函数在工程应用中尤为重要。
2.对热力学状态函数的研究通常从它们的偏微商着手。
在常用状态函数的偏微商中,有的是可以通过实验测定的,常将它们定义为各种热系数;有的则不能用实验的方法得出。
3.工质在准平衡变化中的热力学基本定律表达式同时也表达了热力学状态函数之间的基本关系,又称基本热力学关系式。
通过勒让德变换,基本热力学关系可以用不同的组合参数表达。
基本热力学关系的一阶偏微商和二阶混合偏微商给出状态函数偏微商之间的一般关系。
当然,与热力学基本定律一样这些一般关系对任何工质都是适用的。
4.按照基本热力学关系,可以用可测的状态参数和热系数来表达不能通过实验直接得出的偏微商,从而将各常用状态函数的全微分式用可测的参数及免系数表达出来。
这样,就为在实验测定数据的基础上得出工质的状态函数开辟了道路。
5.在工质热力性质研究中,并非所有热系数都是必需沤过实验测定的,应用热系数间的一般关系可以由少虽测得的热系数得到所需的其它热系数。
这样,可以大大减少研究中的实验工作量.同时减小由于有限的实验精确度带来的误差。
6.依据本章所导出的一般关系式,应用所讲述的推导方法,还可导得工程中需用的各种函数关系。
7.本章所导出的一般关系式只适用于简单可压缩系统。
本章要求:1.了解热力学一般关系的内容及其在工质热力性质研究中的地位和作用;2.掌握导出热力学一般关系的思路和推导方法;3.熟悉简单可压缩工质基本的和常用的热力学一般关系。
学习建议:本章学习时间建议共2学时:1.常用状态函数的偏微商;基本热力学关系; 1学时2.热力学能、焓和熵的微分式;热系数之间的一般关系; 1学时4.1 常用状态函数的偏微商本节知识点:状态方程的偏微商热力学能函数的偏微商焓函数的偏微商熵函数的偏微商本节参考图片:麦克斯韦汤姆逊汤姆逊实验本节疑问解答:思考题4.1.1 思考题4.1.2 思考题4.1.3本节基本概念:定温压缩系数压力的温度系数绝热压缩系数比定容热容比定压热容绝热节流系数工程中常用的状态函数有状态方程 F(p ,v ,T )=0,和以可测参数为独立变量的热力学能、焓、熵函数,通常热力学能函数u(T ,v ),焓函数h(T ,p),和熵函数s(T ,v),s(T ,p)的导得较为方便。
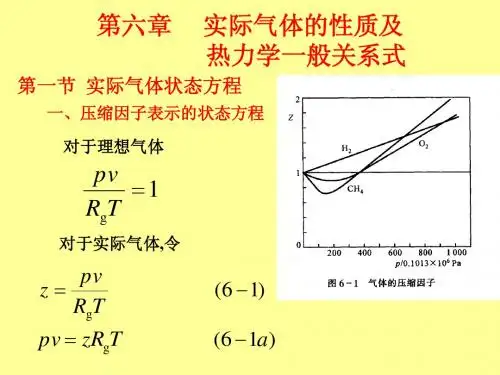
第六章实际气体的性质及热力学一般关系一、目的及要求:了解实际气体与理想气体之间差异产生的原因,掌握利用范德瓦尔方程表征实际气体的状态方程;掌握利用通用压缩因子图求解实际气体的状态参数,了解实际气体的热力学能、焓、熵等参数的表达式。
二、内容:6.1理想气体与实际气体的区别6.2范德瓦尔议程及R-K方程6.3对应态原理与通用压缩因子图6.4维里方程、麦克斯韦关系和热系数6.5热力学能、焓、熵及比热容的一般关系三、重点及难点:6.1了解热力学一般关系式及如何由可测量参数求不可测量参数;由易测量参数求不易测量参数。
6.2了解如何根据热力学理论来指导实验和整理实验数据,以减少实验次数,节省人力和物力。
6.3了解常用的实际气体状态方程,掌握范德瓦尔方程及R-K方程(包括其各项的物理意义)。
6.4掌握对比态原理,会计算对比参数并能利用通用压缩因子图进行实际气体的计算。
四、主要外语词汇:real gas五、本章节采用多媒体课件六、复习思考题及作业:思考题:1、实际气体性质与理想气体差异产生的原因是什么?在什么条件下才可以把实际气体作为理想气体处理?2、压缩因子Z的物理意义怎么理解?能否将Z当作常数处理?3、范德瓦尔方程的精度不高,但在实际气体状态方程的研究中范德瓦尔方程的地位却很高,为什么?4、什么叫做对应态原理?为什么引入对应态原理?什么是比参数?作业:6-2,6-4,6-5第六章实际气体的性质及热力学一般关系式分析工质的热力过程和热力循环时,需要确定工质的各种热力参数的数值,常用的热力参数中,只有p、v、T和c p等少数几种状态参数可由实验测定,而u、h、s等值是无法测量的,它们的值必须根据可测参数的值,按照一定的热力学关系加以确定。
在本章中,主要讨论了依据热力学第一和第二定律,运用数学工具导出的这些参数间的适用于任何工质的热力学一般关系式。
由于这些关系式常以微分或微商的形式表示,故又称之为微分关系式。
在此基础上还讨论了实际气体的性质及其参数计算。
第二部分工质的热力性质六热力学函数的一般关系式由热力学基本定律引出的一些基本热力学状态函数(如内能U、熵S)及其为某一研究方便而设的组合函数(如焓H、自由能F、自由焓G等)许多都是不可测量,必须将它们与可测量(如压力p、体积V、温度T等)联系起来,否则我们将得不到实际的结果,解决不了诸如上一章讲的最大功计算等一些具体的问题。
这就需要发展热力学的数学理论以将热力学基本定律应用到各种具体问题中去。
热力学函数一般关系式 全微分性质+基本热力学关系式状态函数的数学特性对于状态参数,当我们强调它们与独立变量的函数关系时,常称它们为状态函数。
从数学上说,状态函数必定具有全微分性质。
这一数学特性十分重要,利用它可导出一系列很有实用价值的热力学关系式。
下面我们扼要介绍全微分的一些基本定理。
设函数),(y x f z =具有全微分性质 dy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= (6-1) 则必然有(1) 互易关系令式(6-1)中 ),(y x M x z y =⎪⎪⎭⎫ ⎝⎛∂∂, ),(y x N y z x=⎪⎪⎭⎫ ⎝⎛∂∂ 则 yx x N y M ⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ (6-2) 互易关系与⎰=0dz 等价。
它不仅是全微分的必要条件,而且是充分条件。
因此,可反过来检验某一物理量是否具有全微分。
(2) 循环关系当保持z 不变,即0=dz 时,由式(6-1),得0=⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂z xz y dy y z dx x z则 xy z y z x z x y ⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 故有 1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂y z xz x x y y z (6-3) 此式的功能是:若能直接求得两个偏导数,便可确定第三个偏导数。
结果也很容易记忆,只需将三个变量依上、下、外次序,即))()((xzy yxz zyx 循环就行了。
(3) 变换关系将式(6-1)用于某第四个变量ω不变的情况,可有ωωωdy y z dx x z dz xy ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= 两边同除以ωdx ,得ωω⎪⎭⎫ ⎝⎛∂∂⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂x y y z x z x z x y (6-4) 式中:yx z ⎪⎭⎫ ⎝⎛∂∂是函数),(y x z 对x 的偏导数;ω⎪⎭⎫ ⎝⎛∂∂x z 是以),(ωx 为独立变量时,函数),(ωx z 对x 的偏导数。
上面的关系可用于它们之间的变换。
这一关系式对于热力学公式的推导十分重要。
(4) 链式关系按照函数求导法则,可有下述关系:1=⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂yy z x x z (6-5) 1=⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂yy y z x x z ωω (6-5a ) 这是在同一参数(如y )保持不变时,一些参数),,,(Λωx z 循环求导所得偏导数间的关系。
若将关系式中每个偏导数视为链的一环,则链式关系的环数可随所涉及参数的个数而增减。
以上这些关系式都是针对二元函数的,即以具有两个独立状态参数的简单系统为背景。
但对具有两个以上独立参数的系统即多元状态函数,其也有推广价值。
例题6-1 已知理想气体状态方程为RT pv =,试检验v 是否有全微分。
解 由状态方程得 pRT v =,故有 dp p v dT T v dv Tp ⎪⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂=dp pRT dT p R 2-=于是 p R p T M =),(, 2),(p RT p T N -= 而2p R p R p p M T T -=⎪⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂22p R p RT T T N p -=⎪⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ 二者相等,可见v 有全微分,即其为状态函数。
基本热力学关系式6.2.1 基本热力学关系式为简单计,以下推导全部采用比参数。
由热力学第一定律,得w du q δδ+= (3-18d )对简单可压缩系统,若过程可逆,则pdv w =δ,故pdv du q +=δ而由热力学第二定律Tds q =δ (4-14b )二式联立,最后得pdv Tds du -= (6-6)式(6-6)表达了热力学基本定律对系统状态参数变化的限制,是导出其它热力学关系式的基本依据,称为基本热力学关系式。
需要指出的是:虽然式(6-6)是从可逆变化推导而来,但因为du 是状态函数的变化,它只与变化前后的状态有关,而与实际过程的可逆与否无关,所以对于不可逆变化仍然适用。
但若作为能量平衡方程,它只适用于可逆过程。
由焓的定义 pv u h += 得vdp pdv du pv d du dh ++=+=)(将式(6-6)代入上式,可得vdp Tds dh += (6-7)同样,由自由能的定义 Ts u f -= 可得pdv sdT df--= (6-8)由自由焓的定义 Ts h g -= 可得vdp sdT dg+-=(6-9)以上式(6-7)~(6-9)为基本热力学关系式用组合参数表达的形式,故式(6-6)~(6-9)可统称为基本热力学关系式。
6.2.2 特性函数基本热力学关系式(6-6)~(6-9)分别为以特定参数为独立变量的状态函数),(v s u 、),(p s h 、),(v T f 、),(p T g 的全微分表达式。
这些函数有一个很重要的性质,就是它们的偏导数各给出一个状态函数。
对于函数),(v s u ,将其全微分解析式dv v u ds s u du sv ⎪⎭⎫ ⎝⎛∂∂+⎪⎭⎫ ⎝⎛∂∂= 与式(6-6)作对比,即得 T s u v=⎪⎭⎫ ⎝⎛∂∂ (6-10) p v u s-=⎪⎭⎫ ⎝⎛∂∂ (6-11) 同样,由于式(6-7)是函数),(p s h 的全微分,则有 T s h p=⎪⎭⎫ ⎝⎛∂∂ (6-12) v p h s=⎪⎪⎭⎫ ⎝⎛∂∂ (6-13) 式(6-8)是函数),(v T f 的全微分,有s T f v-=⎪⎭⎫ ⎝⎛∂∂ (6-14) p v f T-=⎪⎭⎫ ⎝⎛∂∂ (6-15) 式(6-9)是函数),(p T g 的全微分,有 s T g p-=⎪⎭⎫ ⎝⎛∂∂ (6-16) v p g T=⎪⎪⎭⎫ ⎝⎛∂∂ (6-17) 正因为如此,只需知道上述函数中的任意一个函数,就可确定出所有的状态函数。
如已知),(v T f ,则由式(6-14)可得),(v T s ;由式(6-15)可得),(v T p 即状态方程;由自由能的定义Ts u f -=可得vT f T f v T u ⎪⎭⎫ ⎝⎛∂∂-=),( 由焓的定义pv u h +=可得v v f T f T f v T h Tv ⎪⎭⎫ ⎝⎛∂∂-⎪⎭⎫ ⎝⎛∂∂-=),( 由自由焓的定义pv f Ts h g +=-=可得v v f f v T g T⎪⎭⎫ ⎝⎛∂∂-=),(由此可见,若状态函数的独立参数选择适当,则可由这个函数及其偏导数得到所有的状态函数,从而将工质的平衡性质完全确定。
这样的函数称为特性函数。
特性函数包含了系统平衡状态的所有信息,它的自变量是特定的。
一经变换虽然还是状态函数,但由于信息丢失而不再是特性函数了,这一点需特别注意。
除了上面已给出的),(v s u 、),(p s h 、),(v T f 、),(p T g 这四个特性函数,还可通过基本热力学关系式寻找其它的特性函数。
如将式(6-6)写成 dv T pdu T ds +=1(6-18)则可知 ),(v u s 也是特性函数;将式(6-7)写成dp Tv dh T ds -=1 (6-19) 则可知 ),(p h s 也是特性函数,等等。
特性函数为联系各热力学函数的枢纽。
在许多实际问题中,常采用v T ,或p T ,这些可测量作独立变量,所以),(v T f 和),(p T g 是两个最重要的特性函数。
6.2.3 麦克斯韦关系由于基本热力学关系式(6-6)~(6-9)是各特性函数的全微分表达式,故可对它们应用互易关系式(6-2),因此可得vs s p v T ⎪⎭⎫ ⎝⎛∂∂-=⎪⎭⎫ ⎝⎛∂∂ (6-20) p s s v p T ⎪⎭⎫ ⎝⎛∂∂=⎪⎪⎭⎫ ⎝⎛∂∂ (6-21) vT T p v s ⎪⎭⎫ ⎝⎛∂∂=⎪⎭⎫ ⎝⎛∂∂ (6-22) p TT v p s ⎪⎭⎫ ⎝⎛∂∂-=⎪⎪⎭⎫ ⎝⎛∂∂ (6-23) 这四个关系式称为麦克斯韦关系。
借助它们可将包含不可测量熵s 的关系式代换成用可测量p 、v 、T 表达的关系式。
热系数状态函数的某些偏导数具有明确的物理意义,能表征工质的一定的热力性质,且可由实验测定,因而成为研究工质热力性质的重要数据,称为热系数。
常用的热系数有:热膨胀系数、定温压缩系数、绝热压缩系数、压力温度系数、定容比热、定压比热和绝热节流系数等。
1. 热膨胀系数pp T v v ⎪⎭⎫ ⎝⎛∂∂≡1α (6-24) 热膨胀系数表征物质在定压下的体积随温度变化的性质,单位为1-K 。
2. 定温压缩系数 TT p v v ⎪⎪⎭⎫ ⎝⎛∂∂-≡1κ (6-25) 定温压缩系数表征物质在恒定温度下的体积随压力变化的性质。
由于所有物质的Tp v ⎪⎪⎭⎫ ⎝⎛∂∂均为负值,故在定义式中引入负号,而使T κ为正值。
其单位为1-Pa 。
3. 压力温度系数 vv T p p ⎪⎭⎫ ⎝⎛∂∂≡1β (6-26) 压力温度系数表征物质在定容下的压力随温度变化的性质,单位为1-K 。
由微分的循环关系式(6-3),有1-=⎪⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂⎪⎭⎫ ⎝⎛∂∂Tp v p v v T T p 因而,上面的三个热系数之间有如下关系v T p p βκα= (6-27)显然,如果有了工质的状态方程,就可计算出这三个热系数。
反之,如果由实验测出这些热系数数据,就可积分得到状态方程式。
4. 绝热压缩系数ss p v v ⎪⎪⎭⎫ ⎝⎛∂∂-≡1κ (6-28) 绝热压缩系数表征工质在可逆绝热(定熵)变化中体积随压力变化的性质,单位为1-Pa 。
5. 定容比热 vv dT q c ⎪⎪⎭⎫ ⎝⎛≡δ (6-29) 定容比热表征物质在定容下的吸收热量的能力,单位为)/(K kg kJ ⋅。
根据热力学第一定律解析式w du q δδ+= (3-18d ) 对简单可压缩系统,定容下的体积功0=w δ,故du q =δ,因而vv T u c ⎪⎭⎫ ⎝⎛∂∂= (6-30)6. 定压比热pp dT q c ⎪⎭⎫ ⎝⎛≡δ (6-31) 定压比热表征物质在定压下的吸收热量的能力,单位为)/(K kg kJ ⋅。