热力学基本公式的导出关系概念图

2023课件热力学定律与能量守恒定律图文•热力学第一定律•热力学第二定律•能量的转化与守恒定律•热力学定律与能量守恒的相互关系目•实例分析•总结录01热力学第一定律1定义与内容23热力学第一定律的定义是能量守恒定律在热现象中的表现。

它表明，在封闭系统中，能量不能创造也不能消失，只能从一种形式转换成另一种形式。

热力学第一定律的内容是能量平衡方程，即Q=ΔU。

热力学第一定律的数学表达式是Q=ΔU+W，其中Q为传热热量，ΔU为系统内能的增量，W为系统对外做的功。

Q表示热力学系统吸收的热量，ΔU表示系统的内能增量，W 表示系统对外做的功。

数学表达式与符号热力学第一定律适用于封闭系统中涉及热现象的各种物理过程，如传热、相变、化学反应等。

对于开放系统，如气体膨胀对外做功或液体蒸发等过程，需要引入其他形式的能量转化，如电磁能、化学能等。

适用范围02热力学第二定律热力学第二定律的定义热力学第二定律是关于热现象的宏观自然过程具有方向性的原理，也就是说，热现象不可能自发地使物质的全部或一部分从低温状态向高温状态转化。

热力学第二定律的内容热力学第二定律规定了热力学过程中熵增加的方向，即熵增加原理。

在任何自然过程中，一个孤立系统的总熵不会减少，即系统的熵增加原理。

定义与内容热力学第二定律可以用数学公式表示为 dS≥0，其中S为熵，dS为微分符号，表示微分运算。

数学表达式热力学第二定律的符号为“≥”，表示在孤立系统中，系统的熵增加的方向是朝着熵增加的方向进行的。

符号数学表达式与符号适用范围01热力学第二定律适用于封闭系统，即系统与外界没有物质交换和能量交换。

02热力学第二定律适用于宏观自然过程，而不是微观粒子运动。

03热力学第二定律适用于孤立系统，即系统与外界没有相互作用。

03能量的转化与守恒定律定义能量守恒定律是指，在孤立系统中，能量既不会创生也不会消失，而只会从一种形式转变为另一种形式，从一个物体传递给另一个物体，能量的总玳保持不变。

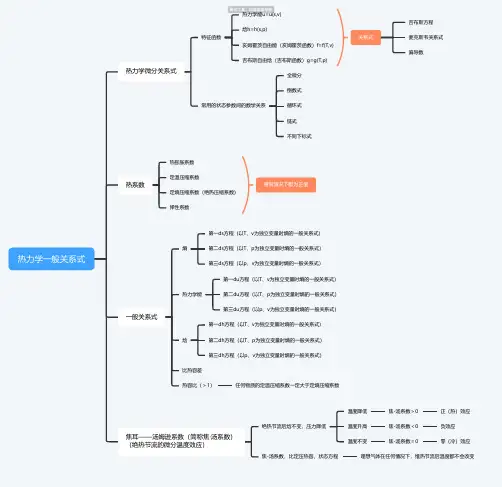
热力学一般关系式热力学微分关系式
特征函数
热力学能u=u(s,v)
焓h=h(s,p)
亥姆霍茨自由能（亥姆霍茨函数）f=f(T,v)
吉布斯自由焓（吉布斯函数）g=g(T,p)
关系式
吉布斯方程
麦克斯韦关系式
偏导数
常用的状态参数间的数学关系
全微分
倒数式
循环式
链式
不同下标式
热系数
热膨胀系数
定温压缩系数
定熵压缩系数（绝热压缩系数）
弹性系数
通常情况下都为正值
一般关系式
熵
第一ds方程（以T、v为独立变量时熵的一般关系式）
第二ds方程（以T、p为独立变量时熵的一般关系式）
第三ds方程（以p、v为独立变量时熵的一般关系式）
热力学能
第一du方程（以T、v为独立变量时熵的一般关系式）
第二du方程（以T、p为独立变量时熵的一般关系式）
第三du方程（以p、v为独立变量时熵的一般关系式）
焓
第一dh方程（以T、v为独立变量时熵的一般关系式）
第二dh方程（以T、p为独立变量时熵的一般关系式）
第三dh方程（以p、v为独立变量时熵的一般关系式）
比热容差
热容比（＞1）任何物质的定温压缩系数一定大于定熵压缩系数
焦耳——汤姆逊系数（简称焦·汤系数）
（绝热节流的微分温度效应）
绝热节流后焓不变，压力降低
温度降低焦-汤系数＞0正（热）效应
温度升高焦-汤系数＜0负效应
温度不变焦-汤系数＝0零（冷）效应
焦-汤系数、比定压热容、状态方程理想气体在任何情况下，维热节流后温度都不会改变。

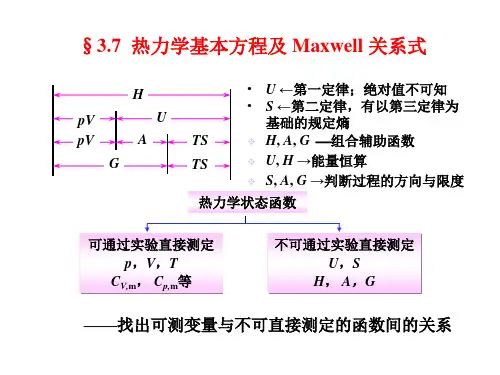
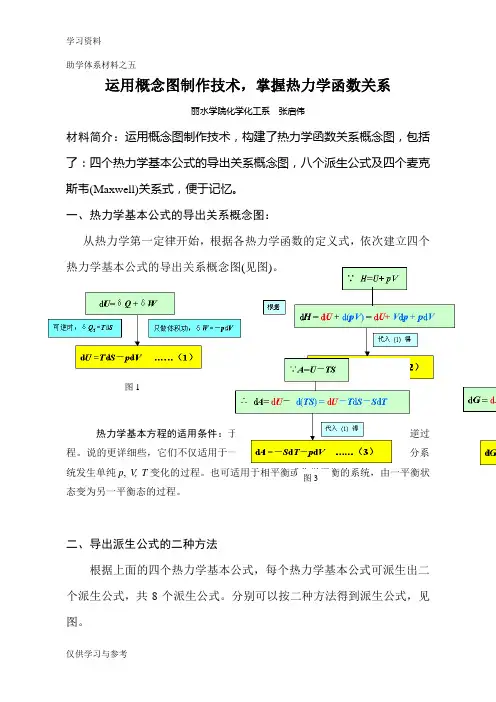
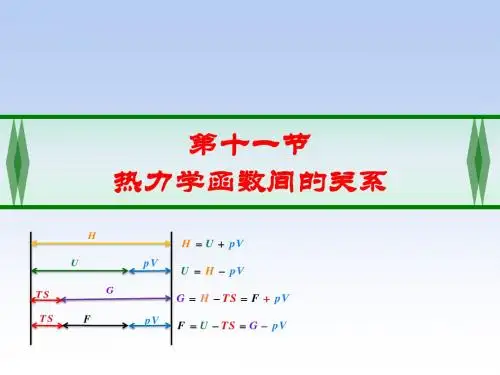
图1助学体系材料之五运用概念图制作技术，掌握热力学函数关系丽水学院化学化工系 张启伟材料简介：运用概念图制作技术，构建了热力学函数关系概念图，包括了：四个热力学基本公式的导出关系概念图，八个派生公式及四个麦克斯韦(Maxwell)关系式，便于记忆。

一、热力学基本公式的导出关系概念图：从热力学第一定律开始，根据各热力学函数的定义式，依次建立四个热力学基本公式的导出关系概念图(见图)。

热力学基本方程的适用条件：于封闭的热力学平衡系统所进行的一切可逆过程。

说的更详细些，它们不仅适用于一定量的单相纯物质，或组成恒定的多组分系统发生单纯p , V , T 变化的过程。

也可适用于相平衡或化学平衡的系统，由一平衡状态变为另一平衡态的过程。

二、导出派生公式的二种方法根据上面的四个热力学基本公式，每个热力学基本公式可派生出二个派生公式，共8个派生公式。

分别可以按二种方法得到派生公式，见图。

图2图3派生公式汇总表如下：2 d H = T d S + V d p等压(∂H/∂S)p=T等熵(∂H/∂p)S=V3 d A =－S d T－p d V 等容(∂A/∂T)V=－S等温(∂A/∂V)T=－p4 d G=－S d T+ V d p 等压(∂G/∂T)p=－S 等温(∂G/∂p)T=V注：同色偏微分的相同关系。

归纳为四组：T = (∂U/∂S)V = (∂H/∂S)p；p =－(∂U/∂V)S =－(∂A/∂V)TV= (∂H/∂p)S= (∂G/∂p)TS=－(∂A/∂T)V =－(∂G/∂T)p在学习过程中，一是要注意不同偏微分的相互替代关系；二是要注意难测或难得的偏微分可用一个简单的状态函数取代的关系。

三、麦克斯韦(Maxwell)关系式导出关系概念图同样以四个热力学基本公式为基础，每个基本公式可导出一个Maxwell关系式。

导出的数学模式概念图如下(见图)：按此求Maxwell 关系通式概念图，可分别写出四个热力学基本公式的Maxwell 关系式。

热量守恒定律思维导图(功能关系)概述热量守恒定律是热力学中的基本原理之一，表明在一个封闭系统内，热量的总量是不会改变的。

根据这一定律，热量可以从一个物体流向另一个物体，但总体上保持不变。

热量的转移热量可以通过三种方式进行转移：1. 对流：通过流体（液体或气体）的运动传递热量，如空气的对流传热。

2. 辐射：通过电磁波的传播传递热量，如太阳辐射热。

3. 导热：通过物质的接触传递热量，如金属导热。

热量守恒定律的应用热量守恒定律在工程和科学研究中具有广泛的应用。

以下是一些常见的应用场景：1. 热力学系统：在热力学系统分析中，热量守恒定律是基本原理之一，用于计算热量的输入和输出。

2. 能源转换：热量守恒定律可以用于分析能量的转换过程，如热能转换为机械能的热发动机。

3. 热传导计算：在材料研究和工程设计中，可以使用热量守恒定律来计算材料中的热传导过程。

4. 热交换器设计：在热交换器的设计中，热量守恒定律用于确定热量的输入和输出，以实现高效的换热。

热量守恒定律的限制热量守恒定律虽然在封闭系统中成立，但在开放系统和过程中存在一些限制和特殊情况：1. 开放系统：在开放系统中，物质可以进出系统，因此热量守恒定律需要结合物质守恒定律进行分析。

2. 相变过程：在物质相变过程中，热量守恒定律需要考虑物质潜热的吸放热效应。

3. 化学反应：在化学反应中，热量守恒定律需要考虑化学反应的吸放热效应。

总结热量守恒定律是热力学中的基本原理，用于描述封闭系统内热量的转移和守恒。

它在工程和科学研究中具有广泛的应用，但在开放系统和特殊情况下存在一些限制和特性需要考虑。

图1助学体系材料之五运用概念图制作技术，掌握热力学函数关系丽水学院化学化工系 张启伟材料简介：运用概念图制作技术，构建了热力学函数关系概念图，包括了：四个热力学基本公式的导出关系概念图，八个派生公式及四个麦克斯韦(Maxwell)关系式，便于记忆。

一、热力学基本公式的导出关系概念图：从热力学第一定律开始，根据各热力学函数的定义式，依次建立四个热力学基本公式的导出关系概念图(见图)。

热力学基本方程的适用条件：于封闭的热力学平衡系统所进行的一切可逆过程。

说的更详细些，它们不仅适用于一定量的单相纯物质，或组成恒定的多组分系统发生单纯p , V, T 变化的过程。

也可适用于相平衡或化学平衡的系统，由一平衡状态变为另一平衡态的过程。

二、导出派生公式的二种方法根据上面的四个热力学基本公式，每个热力学基本公式可派生出二个派生公式，共8个派生公式。

分别可以按二种方法得到派生公式，见图。

图2图3派生公式汇总表如下：等熵(∂U /∂V )S =－p 2d H = T d S + V d p等压 (∂H /∂S )p =T 等熵 (∂H /∂p )S =V 3 d A =－S d T －p d V等容 (∂A /∂T )V =－S 等温 (∂A /∂V )T =－p 4d G =－S d T + V d p等压 (∂G /∂T )p =－S 等温(∂G /∂p )T =V注：同色偏微分的相同关系。

归纳为四组：T = (∂U /∂S )V = (∂H /∂S )p ；p =－(∂U /∂V )S =－(∂A /∂V )T V = (∂H /∂p )S = (∂G /∂p )T S =－(∂A /∂T )V =－(∂G /∂T )p在学习过程中，一是要注意不同偏微分的相互替代关系；二是要注意难测或难得的偏微分可用一个简单的状态函数取代的关系。

三、麦克斯韦(Maxwell)关系式导出关系概念图同样以四个热力学基本公式为基础，每个基本公式可导出一个Maxwell 关系式。

第五节热力学图解大气的热力状态和热力过程，以及在热力过程中各种物理量的变化等，可以从理论上通过数学公式进行计算，但不直观。

热力学图解简单、直观，是把常用的热力学公式预先给定各种可能的参数作成图表；热力学图解不仅能用于分析研究，更适合于日常气象业务工作。

虽然精度没有理论公式计算高，但可获得直观认识。

公式法适用于理论研究，精度要求高的业务工作。

常用的热力学图解有T-lnp图、温熵图等.选热力学图表的结构应满足以下要求：1、为了便于在热力学图上反映系统作功和能量的变化，要求图上过程曲线所围的面积大小能代表功和能量的多少。

2、它的坐标最好是能实测到的气象要素或是其简单的函数。

3、图上的主要线条尽可能为直线或近似为直线。

4、图上各组线条之间的夹角尽可能大，以便准确读数。

一般绝热图上的基本线条有等温线、等压线、干绝热线、湿绝热线以及饱和比湿线。

我国普遍采用温度-对数压力图（T-lnp图），也叫埃玛图。

一、T-lnp图的结构1、坐标系,ln x T y p==−优点：1）气压向上减小，与实际大气相同；2）相差K 倍的等压线间的距离相等，1000-200hpa = 250-50hpa；2、基本线条等温线、等压线、等θ线（干绝热线）、等q s 线（等饱和比湿线）、等Θse 线（假绝热线）。

假绝热线（绿色虚线）气块沿干绝热线上升到凝结高度后，再沿湿绝热线上升，直到水汽全部凝结，再沿干绝热线下降到1000hpa时的温度，即假相当位温Θse。

q s q s二、T-lnp图的应用1、点绘层结曲线大气层结——一个地区上空大气温度和湿度的垂直分布p166.72、作气块绝热变化过程的状态曲线状态曲线——空气块上升下降过程中状态（温度）的变化，是未饱和湿空气先沿干绝热线上升至凝结高度，然后沿湿绝热线上升所构成的曲线。

3、求各温湿特征量1）位温2）饱和比湿q, 实际比湿qs3) 相对比湿f4)抬升凝结高度LCL5) 假相当位温θse3)相对湿度f:q/qs*100%, 例f=9.9/16.4=60%4)抬升凝结高度LCL过(T,p)的等θ线与过(Td ,p)的等qs线的交点所在高度(有时用气压值表示),例：Zc=893hpa5) 假相当位温θse（绿色虚线）过抬升凝结高度的等θse线的数值；例：p=1010hpa,t=22度，td =14度，θse=52度qsqs6）假湿球位温θsw 和假湿球温度T sw （150页)a) Θsw ：空气由状态（p , t , t d )按干绝热上升到凝结高度后，再沿湿绝热线下降到1000hpa时所具有的温度。