热力学函数基本关系式53页PPT
- 格式:ppt
- 大小:4.22 MB
- 文档页数:39





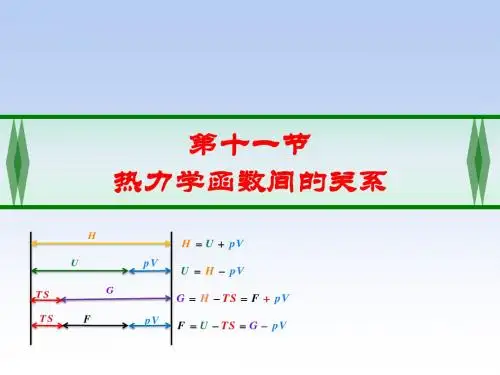





至今讨论中常应用的八个热力学函数--p、V、T、U、H、S、A、G。
其中 U 和 S 分别由热力学第一定律和第二定律导出;H、A、G 则由定义得来。
而 U、H、A、G 为具有能量量纲的函数。
这些热力学函数间通过一定关系式相互联系着。
基本热力学关系式共有十一个(以下分别用公式左边括弧中的数字标明)。
从这十一个基本关系式出发,可以导出许多其它衍生关系式,它们表示出各不同物理量间的相互关系,利用它们可以帮助我们由易于直接测量的物理量出发以计算难于直接测量的物理量的数值。
由定义可得如下三个关系式:(1) (3-136)(2) (3-137)(3) (3-138)又由热力学第一定律、第二定律联合公式,在无非膨胀功条件下:将它和式(3-136)、(3-137)、(3-138)联系起来:即可得以下四个一组被称为恒组成均相封闭系统的热力学基本方程。
又称 Gibbs 方程。
(4) (3-139)(5) (3-140)(6) (3-141)(7) (3-142)这四个基本方程均不受可逆过程的限制,因为 U、H、A、G 等随着相应两个独立的状态函数变化而变化,因而与变化的具体途径(可逆或不可逆)无关,自然亦可用于不可逆过程。
公式虽然是四个,但式(5)、(6)、(7)实际上是基本公式(4)在不同条件下的表示形式。
根据全微分定义可有如下关系:(3-143)(3-144)(3-145)(3-146)式(3-139)与式(3-143)对比、式(3-140)与式(3-144)对比、式(3-141)与式(3-145)对比、式(3-142)与式(3-146)对比,可得如下关系(或称"对应系数式"):(3-147)(3-148)(3-149)和 (3-150)如分别将尤拉(Euler)定则:应用于热力学基本方程(4)、(5)、(6)、(7)可得如下四式:(8) (3-151)(9) (3-152)(10) (3-153)(11) (3-154)这四式常称为"麦克斯威关系式"。