9热力学基本方程

写出四个热力学基本方程
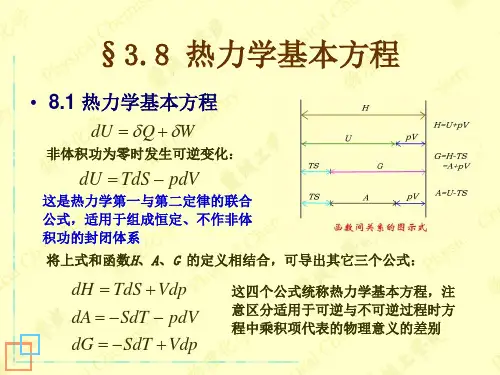
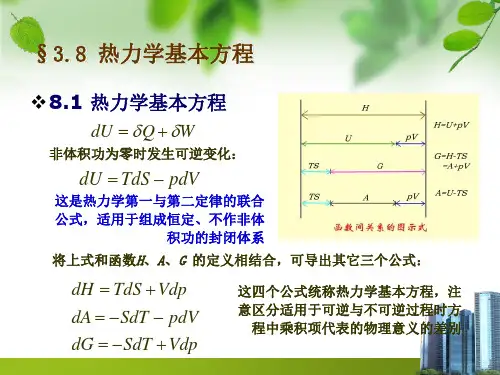
1.热力学的四个基本公式：dU=TdS-PdV；dH=TdS+VdP；
dF=-SdT-PdV；dG=-SdT+VdP。

热力学是从宏观角度研究物质的热运动性质及其规律的学科。

属于物理学的分支，它与统计物理学分别构成了热学理论的宏观和微观两个方面。

热力学定律，是描述物理学中热学规律的定律，包括热力学第零定律、热力学第一定律、热力学第二定律和热力学第三定律。

其中热力学第零定律又称为热平衡定律，这是因为热力学第一、第二定律发现后才认识到这一规律的重要性；热力学第一定律是能量守恒与转换定律在热现象中的应用；热力学第二定律有多种表述，也叫熵增加原理。

热力学第一定律也就是能量守恒定律。

自从焦耳以无以辩驳的精确实验结果证明机械能、电能、内能之间的转化满足守恒关系之后，人们就认为能量守恒定律是自然界的一个普遍的基本规律。

热力学第二定律的每一种表述，都揭示了大量分子参与的宏观过程的方向性，使人们认识到自然界中进行的涉及热现象的宏观过程都具有方向性。

2.热力学第二定律的英文解释是熵是趋向于总体增大,比如
1L90度水(A)和1L10度水(B)融合,不会是A的温度增加而 B的温度减小，因为如此的话，总体的熵减小。

如果A 温度降但B温度升高一点，其总体的熵增加。

热力学第三
定律通常表述为绝对零度时，所有纯物质的完美晶体的熵值为零。

或者绝对零度（T=0K即-273.15℃）不可达到。

R.H.否勒和 E.A.古根海姆还提出热力学第三定律的另一种表述形式：任何系统都不能通过有限的步骤使自身温度降低到0K，称为0K不能达到原理。

热力学计算公式整理热力学是研究物质的热与能的转化关系的学科，是广泛应用于化学、物理、工程等领域的重要理论基础。

在热力学计算中，有一系列公式被广泛应用于热力学参数的计算和分析。

1.热力学基本方程：对于一个热力学系统，其内部能量U可以由其热力学状态变量来表示，常用的基本方程有：U=TS-PV+μN其中，U为内部能量，T为温度，S为熵，P为压力，V为体积，μ为化学势，N为摩尔数。

2.热力学函数的计算：(1)焓（H）的计算公式：H=U+PV其中，H为焓，U为内部能量，P为压力，V为体积。

(2)外界对系统做的功（W）计算公式：W=-∫PdV其中，W为功，P为压力，V为体积，积分为从初态到末态的过程。

(3)熵（S）的计算公式：dS=dQ/T其中，S为熵，dS为熵的微分，dQ为系统的热量变化，T为温度。

(4) Helmholtz自由能（A）的计算公式：A=U-TS其中，A为Helmholtz自由能，U为内部能量，T为温度，S为熵。

(5) Gibbs自由能（G）的计算公式：G=U-TS+PV其中，G为Gibbs自由能，U为内部能量，T为温度，S为熵，P为压力，V为体积。

3.热力学热力学参数的计算：(1)热容的计算公式：Cv=(∂U/∂T)V其中，Cv为定容热容，∂U/∂T为导数，V为体积。

Cp=(∂H/∂T)P其中，Cp为定压热容，∂H/∂T为导数，P为压力。

(2)趋近于绝对零度时的熵变ΔS的计算公式：ΔS = Cvln(T2/T1) + Rln(V2/V1)其中，ΔS为熵的变化，Cv为定容热容，T2和T1为温度的变化，R 为气体常数，V2和V1为体积的变化。

(3)等温过程中的吸热计算公式：q=ΔH=nCpΔT其中，q为吸热，ΔH为焓的变化，n为物质的摩尔数，Cp为定压热容，ΔT为温度的变化。

(4)等温过程中的做功计算公式：w=-ΔG=PΔV其中，w为做功，ΔG为Gibbs自由能的变化，P为压力，ΔV为体积的变化。

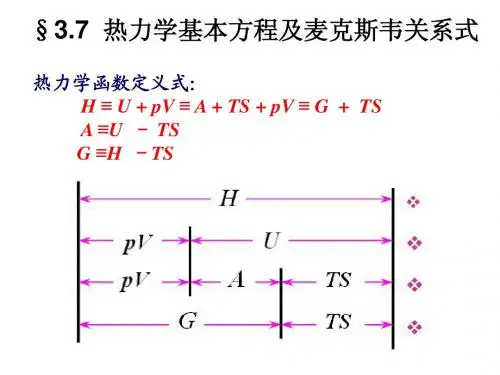
热力学方法和计算到此为止，我们已经学习了八个热力学状态函数：p、V、T、U、H、S、A、G。

这八个状态函数中p、V、T、U、S有着明确的物理意义，而H、A、G是定义出来的状态函数，并没有明确的物理意义。

这八个状态函数可以构成许许多多热力学函数关系式一、热力学基本方程在非体积功为0的条件下，单组分单相封闭系统经过一个始态到达末态，根据热力学第一定律有。

dU=δQ r+δW r=δQ+δW式子中，δQ r和δW r是可逆过程的热和功，δQ和δW是不可逆过程的热和功。

在非体积功为0的条件下，对于单组分单相封闭系统的可逆过程有δQ r=TdS δW r=−pdV带入后可得到一项重要的公式:dU=TdS−pdV这项式子称为热力学第一定律和第二定律的联合表达式，适用于单相单组分封闭系统可逆过程与不可逆过程。

由焓的定义H=U+pV,两端同时微分得到dH=dU+pdV+Vdp再将dU=TdS−pdV带入上式，得到dH=TdS+Vdp由亥姆霍兹函数的定义A=U−TS，两端同时取微分得到dA=dU−TdS−SdT再将dU=TdS−pdV带入上式，得到dA=−SdT−pdV由吉布斯函数的定义G=H−TS,两端同时微分得到dG=dH−TdS−SdT再将dH=TdS+Vdp带入上式，得到dG=−SdT+Vdp这四个关系式，叫做封闭系统的热力学基本关系式，地位相当重要，务必准确推导和记忆。

严格地讲，这四个关系式只适用于封闭系统中无非体积功的可逆过程，但是我们知道一切实际过程都是不可逆过程，所以我们也可以将这四个关系式用到不可逆过程中，尽管有一些误差，但是完全可以忽略。

为了避免理解过于麻烦，咱不解释误差的来源。

二、对应系数关系式由此我们可以将U、（S，p）、A=A（T，V）、G=G（T，p），根据全微分的性质，可以得到dU=(ðUðS)VdS+(ðUðV)SdV dH=(ðHðS)pdS+(ðHðp)SdpdA=(ðAðT)VdT+(ðAðV)TdV dG=(ðGðT)pdT+(ðGðp)Tdp将上面四个全微分式，对应到四个基本表达式中，我们可以得到T =(ðU ðS )V =(ðH ðS )p p =−(ðU ðV )S =−(ðA ðV )TV =(ðH ðp )S =(ðG ðp )T S =−(ðA ðT)V =−(ðG ðT )p三、麦克斯韦关系式在数学上dz =Mdx +Ndy 是一个全微分的充要条件为(ðM ðy )x =(ðNðx )y我们再一次调出四个热力学基本关系式dU =TdS −pdV dH =TdS +Vdp dA =−SdT −pdV dG =−SdT+Vdp来导出麦克斯韦关系式：(ðS ðV )T =(ðp ðT )V (ðS ðp )T =−(ðVðT )p麦克斯韦关系式的意义在于：它能将不能直接测量出来的物理量（如：熵S ），换成可以直接测量出来的物理量（如T 、V 、p ），或者由状态方程求得的物理量。

热力学基本方程热力学是一门描述物理系统中能量、势能和熵之间关系的学科。

它的基本方程，也就是“热力学基本方程”，定义了这些量之间的联系。

热力学基本方程可以用来描述物质在不同物理状态和条件下的变化。

热力学基本方程是一个多元方程，由热力学定律组成：第一定律是能量守恒定律；第二定律是熵守恒定律；第三定律是势能守恒定律。

第一定律：热力学的第一定律宣称，在任何物理过程中，能量守恒，即能量不会消失，也不会出现。

由于能量守恒，物质在不同状态间的变化都会有特定的方法。

第二定律：热力学的第二定律宣称，由于能量不能在未受外力作用的情况下自发地流向热源或冷池，因此，熵在受外力作用的情况下不会减少，而是会增大。

第三定律：热力学的第三定律宣称，势能可以变化，而它的变化与系统的熵有关，当熵增加时，势能也会增加。

这三定律构成了热力学基本方程，用于说明物质在不同物理状态下的变化。

它解释了物质在不同状态间的转换和质量变化，以及在这些转换中的能量的流动方式。

此外，热力学基本方程还可以用来描述物质处于不同环境中的变化，如汽化、液化、固化等，也可以用来解释物质在受外力作用时的表现。

热力学基本方程的应用也非常广泛，它可以用来表示物理和化学反应的能量改变，也可以用来描述物质运动规律，还可以用来计算化学反应产物的分子量、活性能和自由能。

由于热力学基本方程具有如此强大的表达能力，它被广泛应用于热力学的各个分支中，包括绝热热力学，热压热力学，绝热变动热力学，精确热力学，化学动力学，流体力学，量子力学，共性热力学等。

热力学基本方程是一种强有力的理论，它引发了新的科学发现，让物理学和化学学者们有机会探索全新的物理和化学现象，为科学知识的发展做出了巨大贡献。

从上面可以看出，热力学基本方程是一个强大的热力学定律，它可以用来说明物质在不同状态、环境的变化，也可以描述物质的运动规律，为物理学和化学学的研究作出了巨大贡献。

它的应用也非常广泛，它也被用于各个热力学分支，被广泛应用于物理和化学反应的研究中。