平面问题的有限元分析算例
- 格式:doc
- 大小:282.50 KB
- 文档页数:2

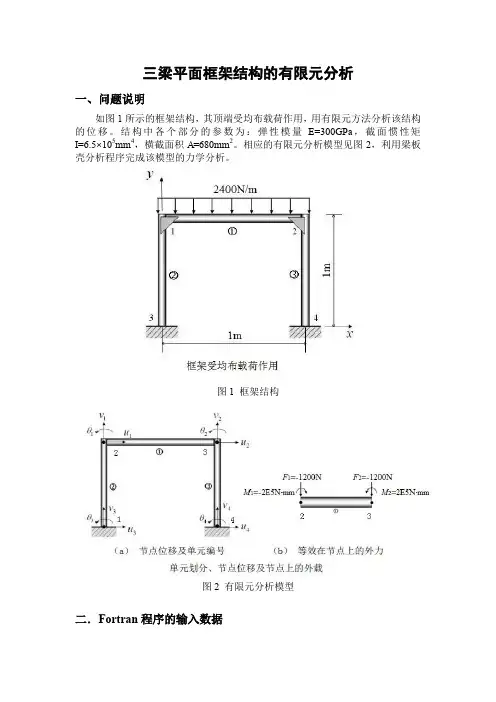
三梁平面框架结构的有限元分析一、问题说明如图1所示的框架结构,其顶端受均布载荷作用,用有限元方法分析该结构的位移。
结构中各个部分的参数为:弹性模量E=300GPa,截面惯性矩I=6.5×105mm4,横截面积A=680mm2。
相应的有限元分析模型见图2,利用梁板壳分析程序完成该模型的力学分析。
图1框架结构图2有限元分析模型二.Fortran程序的输入数据(1)Facile.11 4 3 6 0 12 42 1 11 1 11 3 51 2 2 3 3 40 0 0 0 1000 01000 1000 0 1000 0 0(2)Facile.2111 211 1111 0 0 0 1 03E5 1.6E5680 6.5E5 6.5E5 6.5E50 0(3)Facile.312 41 02 03 04 05 06 0 19 0 20 0 21 0 22 023 0 24 08 -1200 12 -200000 14 -1200 18 200000输出的数据文件为:Facile7和Facile8,其中各节点位移结果在文件Facile8中。
三.计算结果各节点的位移计算结果见表1。
四.Ansys分析结果Ansys计算结果如下图所示,图3为节点x方向的位移云图,图4为节点y 方向的位移云图,图5为节点转角云图。
图3 节点x方向的位移图4 节点y方向的位移图5 节点转角各节点的位移值见表2。
五.结果对比通过对比表1和表2中的数据可以发现,Fortran程序与Ansys分析的结果十分接近。

三梁平面框架结构的有限元分析针对如图1所示的框架结构,其顶端受均布力作用,用有限元方法分析该结构的位移。
结构中各个截面的参数都为:E=3.0 10 Pa,I =6.5 10〃m,2A =6.8 10 m,生成相应的有限元分析模型。
在ANSY平台上,完成相应的力学分析。
416~N nt3000N② ③144mI ------------------------------------------------------------------------------------------ |图1框架结构受一均布力作用ANSYS军答:对该问题进行有限元分析的过程如下。
(1)进入ANSYS设定工作目录和工作文件)程序—An sys —ANSYS In teractive —Worki ng directory (设置工作目录)—Initial jobname(设置工作文件名):beam3 —Run —OK(2)设置计算类型ANSYS Main Menu: Preferences , —Structural —OK(3)选择单元类型ANSYS Main Me nu: Preprocessor —Eleme nt Type —Add/Edit/Delete , —Add, —beam 2node188 —OK (返回到Element Types 窗口)—CloseCross-sectional area:6.8e-4 (梁的横截面积)—OK —Close八 Library of Element Types Library of Element TypesElement type referenc ■亡 number(4)定义材料参数ANSYS Mai n Me nu: Preprocessor — Material Props — Material Models —Structural — Lin ear — Elastic — Isotropic: EX:3e11 ( 弹性模量)—OKANSYS Main Menu: Preprocessor — Real Constants , — Add/Edit/Delete —Add — Type 1 Beam3 — OK — Real Constant Set No: 1 ( 第 1 号实常数),Ry finite 戟『気2 node 1882 node 188Canttl—鼠标点击该窗口右上角的“ ”来关闭该窗口。

一、平面3节点三角形单元分析的算例如图所示为一矩形薄平板,在右端部受集中力F=10000N 作用,材料常数为:弹性模量1E 二1 107 Pa 、泊松比,板的厚度为t 二0.1m ,试按平面应力问题计算各个节点位3移及支座反力。
閹4-^20右瑞部受集中力作用的平面问题(高深梁)解:(1) 结构的离散化与编号形单元。
载荷F 按静力等效原则向节点 1节点2移置等效。
约束的支反力列阵: R =「0 0 0 0 R X 3 &3 R x4 Ry 4T其中(R X 3, R y3)和(R x4,R y4)分别为节点3和节点4的两个方向的支反力。
(2)各个单元的描述当两个单元取图示中的局部编码(i,j,m)时,其单元刚度矩阵完全相同,即a=X j y m —X m y j , b i=y j —y m , C i=X j —X m a j =X m y i -xy m , b j =y m -y i , c^x^X i a m =X j y m —X m y j , b m =y i —y j , c^x^X j对该结构进行离散,单元编号及节点编号如图4-20(b)所示,即有二个3节点三角 节点位移列阵:q - g v u 2 v 2U 3 V 3 U 4 V 4 r1-^b r b s 十 ---- C r C s2 1 - J亠 -------- b r C s 2^C r b s十丁农I1 - J GG 2brbs"b r C sk iik ⑴,(2)k jjkmma)制赳描述 b)冇限元分折模型节点外载列阵:k ijk jmk mj1 00132I23-12T1I3023434323220042一』—112427433212d413L 333T(3)建立整体刚度方程按单元的位移自由度所对应的位置进行组装可以得到整体刚度矩阵,成k二k⑴k⑵具体写出单元刚度矩阵的各个子块在总刚度矩阵中的对应位置如下该组装过程可以写代入整体刚度方程Kq =P中,有(5)支反力的计算将所求得的节点位移式代入总刚度方程中,可求得支反力如下9Et/ 2 4 、 “(-U i ——V i + — V 2) = —2 F 32 3 3 9Et 2 1 4(U v U 2)»0.07F 32 3 3 3 9Et 2 (-U 2 V 2) =2F32 3 9Et 2 1 (u 2 v 2) = 1.07F7 亍474 3 n — 3-1—3斗1 3 q21-4一 一 □0 33 3 34 r74 "q—0 □-13 3 7亍31341-4 033 33 I2 4 "7'4"-1 7 0亍T7亍r 141 32— —□=-4 33J3 3 i hi BW-Wa-ivKaH4q7 4 0 □ -1——-—33 3 331 2413■^= -^^a--433373 J9Z732(4) 边界条件的处理及刚度方程求解该问题的位移边界条件为 U 3 = 0,V 3 二 0, U 4 二 0,V4 -0 将其代入上式中,划去已知节点位移对应的第5行至第8行(列),有13由上式可求出节点位移如下[U i w u 2 v 2]Et131.88 -8.99-1.50 -8.42 TR X 4 R y432 3 3、MATLAB —平面3节点三角形单元分析的算例(Triangle2D3Node)解:(1)结构的离散化与编号将结构离散为二个3节点三角形单元,单元编号及节点编号如图4-20(b)所示。




《有限元剖析与应用》详尽例题试题 1:图示无穷长刚性地基上的三角形大坝,受齐顶的水压力作用,试用三节点常单元和六节点三角形单元对坝体进行有限元剖析,并对以下几种计算方案进行比较:1)分别采纳同样单元数目的三节点常应变单元和六节点三角形单元计算;2)分别采纳不一样数目的三节点常应变单元计算;3)入选常应变三角单元时,分别采纳不一样区分方案计算。
一.问题描绘及数学建模无穷长的刚性地基上的三角形大坝受齐顶的水压作用可看作一个平面问题,简化为平面三角形受力问题,把无穷长的地基看着平面三角形的底边受固定支座拘束的作用,受力面的受力简化为受均布载荷的作用。
二.建模及计算过程1.分别采纳同样单元数目的三节点常应变单元和六节点三角形单元计算下边简述三节点常应变单元有限元建模过程(其余种类的建模过程近似):进入 ANSYS【开始】→【程序】→ANSYS → ANSYS Product Launcher → change the working directory→ Job Name: shiti1 → Run设置计算种类ANSYS Main Menu: Preferences → select Structural→ OK元型元是三节点常应变单元,能够用 4 节点退化表示。
ANSYS Main Menu: Preprocessor→ Element Type→ Add/Edit/Delete→ Add→ select Solid Quad 4 node 42 →OK (back to Element Types window)→Options ⋯→ select K3: Plane Strain →OK→ Close (the Element Type window)定资料参数资料,可找的参数并在有限元中定,此中性模量E=210Gpa,泊松比 v=。
ANSYS Main Menu : Preprocessor → Material Props → Material Models→ Structural→ Linear→Elastic → Isotropic→ input EX:, PRXY:→ OK生成几何模型生成特点点ANSYS Main Menu: Preprocessor→Modeling→ Create→Keypoints→ In Active CS→挨次入四个点的坐:input:1(0,0),2(3,0),3(6,0),4(3,5),5(0,10),6(0,5) → OK生成体截面ANSYS Main Menu: Preprocessor→Modeling→ Create→ Areas→ Arbitrary→ Through KPS→挨次接1,2,6;2,3,4;2,4,6;4,5,6 三个特点点→ OK网格区分ANSYS Main Menu : Preprocessor→ Meshing→ Mesh Tool→ (Size Controls) Global: Set→ input NDIV: 1→ OK → (back to the mesh tool window)Mesh: Areas, Shape: Tri, Free → Mesh → Pick All (in Picking Menu) → Close( the Mesh Tool window)模型施加束分下底和直的施加x 和 y 方向的束ANSYS Main Menu: Solution→ Define Loads→ Apply→ Structural→ Displacement→ On lines →底→OK → select:ALL DOF → OK斜施加x 方向的散布荷ANSYS 命令菜: Parameters→ Functions→ Define/Edit→ 1)在下方的下拉列表框内x ,作置的量;2) 在Result窗口中出{X},写入所施加的荷函数:1000*{X} ;3) File>Save(文件展名:func)→返回:Parameters→ Functions→ Read from file:将需要的.func文件翻开,任一个参数名,它表示随之将施加的荷→ OK→ ANSYS Main Menu: Solution→ Define Loads→ Apply→Structural→ Pressure→ On Lines→拾取斜;OK→在下拉列表框中,:Existing table (来自用定的量)→ OK →需要的荷参数名→OK剖析算ANSYS Main Menu: Solution→Solve→ Current LS→OK(to close the solve Current Load Step window)→OK果示确立目前数据最后步的数据ANSYS Main Menu: General Postproc→ Read Result→ Last Set看在外力作用下的形ANSYS Main Menu: General Postproc→ Plot Results → Deformed Shape→select Def + Undeformed→ OK看点位移散布状况Contour Plot→ Nodal Solu⋯→ select: DOF solution→Displacement vctor sum→ Def + Undeformed→OK看点力散布状况Contour Plot→ Nodal Solu⋯→ select: Stress→ XY shear stress→Def + Undeformed → OK退出系ANSYS Utility Menu: File→ Exit ⋯→ Save Everything→ OK三.结果剖析三节点常应变单元( 6 个节点, 4 个单元)几何模型图变形图,节点位移图,节点应力争,节点应变图六节点常应变单元( 6个节点, 4个单元)几何模型图变形图,节点位移图,节点应力争,节点应变图分别采纳同样单元数目的三节点常应变单元和六节点三角形单元计算结果比较单元区分方案变形大小应力大小应变大小值的比较剖析三节点三角形DMX:DMX:DMX: 1.最大变形值小;单元SMX:SMN:2778SMN: 2.最大应力值小;SMX:8749SMX: 3.最大应变值小。


第二章 弹性力学平面问题有限单元法§2-1 三角形单元(triangular Element)三角形单元是有限元分析中的常见单元形式之一,它的优点是:①对边界形状的适应性较好,②单刚形式及其推导比较简单,故首先介绍之。
一、结点位移和结点力列阵设右图为从某一结构中取出的一典型三角形单元。
在平面应力问题中,单元的每个结点上有沿x 、y 两个方向的力和位移,单元的结点位移列阵规定为: 相应结点力列阵为: (式2-1-1)二、单元位移函数和形状函数前已述及,有限单元法是一种近似方法,在单元分析中,首先要求假定(构造)一组在单元内有定义的位移函数作为近似计算的基础。
即以结点位移为已知量,假定一个能表示单元内部(包括边界)任意点位移变化规律的函数。
构造位移函数的方法是:以结点(i,j,m)为定点。
以位移(u i ,v i ,…u m v m )为定点上的函数值,利用普通的函数插值法构造出一个单元位移函数。
在平面应力问题中,有u,v 两个方向的位移,若假定单元位移函数是线性的,则可表示成:(,)123u u x y x y ααα==++546(,)v v x y x y ααα==++ (2-1-2)a{}⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧=⎪⎪⎪⎪⎭⎪⎪⎪⎪⎬⎫⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧=m j i m ed d d d m j j i v u v u v u i {}ii j j m X Y X (2-1-1)Y X Y iej m m F F F F ⎧⎫⎪⎪⎪⎪⎧⎫⎪⎪⎪⎪⎪⎪==⎨⎬⎨⎬⎪⎪⎪⎪⎩⎭⎪⎪⎪⎪⎪⎪⎩⎭式中的6个待定常数α1 ,…, α6 可由已知的6个结点位移分量(3个结点的坐标)确定。
将3个结点坐标(x i,y i ),(x j,y j ),(x m,y m )代入上式得如下两组线性方程:123i i i u x y ααα=++123j j j u x y ααα=++ (a)123m m m u x y ααα=++和546i i i v x y ααα=++546j j j v x y ααα=++ (b)546m m m v x y ααα=++利用线性代数中解方程组的克来姆法则,由(a)可解出待定常数1α 、2α 、3α :11A Aα=22A Aα=33A Aα=式中行列式:1i i i j j j m m m u x y A u x y u x y =2111i i j j m mu y A u y u y =3111i i j jm mx u A x u x u =2111i i j j m mAx y A x y x y ==A 为△ijm 的面积,只要A 不为0,则可由上式解出:11()2m m i ij j a u a u a u A α=++ 21()2m m i ij j bu b u b u A α=++ (C )31()2m mi i j j c u c u c u A α=++式中:m m i j j a x y x y =- m m j i i a x y x y =- m i j j i a x y x y =-m i j b y y =- m j i b y y =- m i j b y y =- (d )m i j c x x =- m j i c x x =- m j i c x x =-为了书写方便,可将上式记为:m m i j i a x y x y =-m ij by y =- (,,)i j mm i jc x x =-(,,)i j m表示按顺序调换下标,即代表采用i,j,m 作轮换的方式便可得到(d)式。
有限元平面问题三角形实例有限元法是一种常用的计算方法,可以用来解决各种工程问题。
其中,有限元平面问题是有限元法的一种应用,常用于分析三角形结构。
在有限元平面问题中,我们通常会将结构划分成许多小的单元,每个单元由节点和单元刚度矩阵组成。
而三角形结构则是有限元平面问题中常用的一种单元形状。
三角形结构的特点是简单而且易于处理,因此广泛应用于各种领域,如土木工程、机械工程、航空航天等。
下面我们就以一个实际的例子来说明如何应用有限元平面问题分析三角形结构。
假设我们要分析一个三角形钢板在受力作用下的变形情况。
首先,我们需要将钢板划分为许多小的三角形单元。
每个单元由三个节点组成,节点之间通过边连接。
在有限元分析中,我们需要对每个单元进行网格划分,并确定节点的坐标和边的长度。
然后,通过求解节点的位移和应力分布,可以得到钢板在受力作用下的变形情况。
具体来说,我们可以通过求解线性方程组来得到节点的位移。
而节点的应力则可以通过应变-位移关系来计算。
通过这种方式,我们可以得到钢板在受力作用下各个节点的位移和应力分布情况。
有限元平面问题的分析结果可以帮助我们了解结构的强度和刚度情况,为设计和优化提供依据。
例如,在钢板的设计中,我们可以通过有限元分析来确定合适的材料和尺寸,以满足结构的强度和刚度要求。
除了钢板,有限元平面问题还可以应用于其他类型的三角形结构。
例如,在土木工程中,我们可以使用有限元分析来分析三角形桥梁或者三角形支撑结构的变形和应力分布情况。
有限元平面问题是一种常用的分析方法,可以应用于各种三角形结构的分析。
通过对节点的位移和应力分布的求解,我们可以得到结构在受力作用下的变形情况。
这对于工程设计和优化至关重要,可以帮助我们提高结构的强度和刚度,确保其安全可靠。
梁问题1、一个长6m的工字截面梁,截面高0.42m,截面面积0.0072m2,截面惯性矩2.108e-4m4,材料弹性模量为3e11Pa, 泊松比0.3.两端简支,跨中受100N的集中力,试用有限元计算梁中点的挠度定义单元类型:Beam3;(分10份)定义材料弹性模量Ex=3e11和泊松比0.3;定义实常数:梁的截面积0.0072,惯性矩2.108e-4,高度0.42m2、一个长10m的方形截面梁,截面边长5mm,截面面积2.5e-4m2,截面惯性矩5.2e-7m4,材料弹性模量为3e11Pa, 泊松比0.3.两端简支,跨中受100N的集中力,试用有限元计算梁中点的挠度定义单元类型:Beam3;(分10或20份)定义材料弹性模量Ex=2e11和泊松比0.3;定义实常数:梁的截面积2.5e-4,惯性矩5.2e-7,高度0.05m3、一悬臂梁长10m,截面高0.1m,截面宽0.05m,材料弹性模量为2e11Pa, 泊松比0.3.在集中力P=10000N作用下求该梁A点处的挠度。
平面刚架问题1、建立如图所示的平面刚架结构;(建立节点和单元)2、定义单元类型:Beam33、定义材料弹性模量Ex=2e11和泊松比0.34、定义实常数:梁的截面积0.03,惯性矩2.5e-5,高度0.1m5、定义约束6 、施加载荷7 、进行求解8 、观察变形图、列出节点位移值2、一平面刚架右端固定,如图所示,已知组成刚架的各梁除梁长外,其余几何特性相同。
试以静力来分析各节点的位移。
横截面积:0.0072m 2横截高度:0.42m惯性矩:0.000218m 4 弹性模量:2.06e11n/m2泊松比0.3P x =100N200NP x =100N。