下载文档原格式
时间序列-小波分析时间序列（Time Series ）是地学研究中经常遇到的问题。
在时间序列研究中，时域和频域是常用的两种基本形式。
其中，时域分析具有时间定位能力，但无法得到关于时间序列变化的更多信息；频域分析（如Fourier 变换）虽具有准确的频率定位功能，但仅适合平稳时间序列分析。
然而，地学中许多现象（如河川径流、地震波、暴雨、洪水等）随时间的变化往往受到多种因素的综合影响，大都属于非平稳序列，它们不但具有趋势性、周期性等特征，还存在随机性、突变性以及“多时间尺度”结构，具有多层次演变规律。
对于这类非平稳时间序列的研究，通常需要某一频段对应的时间信息，或某一时段的频域信息。
显然，时域分析和频域分析对此均无能为力。
20世纪80年代初，由Morlet 提出的一种具有时-频多分辨功能的小波分析（Wavelet Analysis ）为更好的研究时间序列问题提供了可能，它能清晰的揭示出隐藏在时间序列中的多种变化周期，充分反映系统在不同时间尺度中的变化趋势，并能对系统未来发展趋势进行定性估计。
目前，小波分析理论已在信号处理、图像压缩、模式识别、数值分析和大气科学等众多的非线性科学领域内得到了广泛的应。
在时间序列研究中，小波分析主要用于时间序列的消噪和滤波，信息量系数和分形维数的计算，突变点的监测和周期成分的识别以及多时间尺度的分析等。
一、小波分析基本原理1. 小波函数小波分析的基本思想是用一簇小波函数系来表示或逼近某一信号或函数。
因此，小波函数是小波分析的关键，它是指具有震荡性、能够迅速衰减到零的一类函数，即小波函数)R (L )t (2∈ψ且满足：⎰+∞∞-=0dt )t (ψ （1）式中，)t (ψ为基小波函数，它可通过尺度的伸缩和时间轴上的平移构成一簇函数系：)abt (a)t (2/1b ,a -=-ψψ 其中，0a R,b a,≠∈ （2） 式中，)t (b ,a ψ为子小波；a 为尺度因子，反映小波的周期长度；b 为平移因子，反应时间上的平移。
时间序列的小波分析时间序列（Time Series ）是地学研究中经常遇到的问题。
在时间序列研究中，时域和频域是常用的两种基本形式。
其中，时域分析具有时间定位能力，但无法得到关于时间序列变化的更多信息；频域分析（如Fourier 变换）虽具有准确的频率定位功能，但仅适合平稳时间序列分析。
然而，地学中许多现象（如河川径流、地震波、暴雨、洪水等）随时间的变化往往受到多种因素的综合影响，大都属于非平稳序列，它们不但具有趋势性、周期性等特征，还存在随机性、突变性以及“多时间尺度”结构，具有多层次演变规律。
对于这类非平稳时间序列的研究，通常需要某一频段对应的时间信息，或某一时段的频域信息。
显然，时域分析和频域分析对此均无能为力。
20世纪80年代初，由Morlet 提出的一种具有时-频多分辨功能的小波分析（Wavelet Analysis ）为更好的研究时间序列问题提供了可能，它能清晰的揭示出隐藏在时间序列中的多种变化周期，充分反映系统在不同时间尺度中的变化趋势，并能对系统未来发展趋势进行定性估计。
目前，小波分析理论已在信号处理、图像压缩、模式识别、数值分析和大气科学等众多的非线性科学领域内得到了广泛的应。
在时间序列研究中，小波分析主要用于时间序列的消噪和滤波，信息量系数和分形维数的计算，突变点的监测和周期成分的识别以及多时间尺度的分析等。
一、小波分析基本原理1. 小波函数小波分析的基本思想是用一簇小波函数系来表示或逼近某一信号或函数。
因此，小波函数是小波分析的关键，它是指具有震荡性、能够迅速衰减到零的一类函数，即小波函数)R (L )t (2∈ψ且满足：⎰+∞∞-=0dt )t (ψ （1）式中，)t (ψ为基小波函数，它可通过尺度的伸缩和时间轴上的平移构成一簇函数系：)abt (a)t (2/1b ,a -=-ψψ 其中，0a R,b a,≠∈ （2）式中，)t (b ,a ψ为子小波；a 为尺度因子，反映小波的周期长度；b 为平移因子，反应时间上的平移。
奇异谱分析-CAL-FENGHAI.-(YICAI)-Company One1奇异谱分析奇异谱分析是近年来兴起的一种研究非线性时间序列数据的强大的方法。
它根据所观测到的时间序列构造出轨迹矩阵，并对轨迹矩阵进行分解、重构，从而提取出代表原时间序列不同成分的信号。
如长期趋势信号、周期信号、噪声信号等，从而对时间序列的结构进行分析，并可进一步预测。
奇异谱分析(SSA)方法最早由colebrook于1978年首先在海洋学研究中提出并使用。
Fracrich用一维时间序列在延迟相空间中做EOF展开，再通过显著性检验研究确定有意义的特征成分的个数，据此估计气候吸引子的维数。
这个工作被认为是SSA在气象学中的最早应用。
Hassani将这种方法引人到社会问题研究中来，并用其预测了美国交通事故的月时间序列数据。
N.Golyandina给出了奇异谱分析的扩展形式一多通道奇异谱分析的算法，并由Hossein Hassani用来对英镑/美元汇率进行了分析预测，取得了较好的效果。
奇异谱分析的基本思想是，将所观测到的一维时间序列数据：Y(T)=(y(1),⋯,y(T))转化为其轨迹矩阵：其中，m为选取的窗口长度，n=T-m+1，计算X.T*X并对其进行奇异值分解（SVD），从而得到其m个特征值：λ1≥λ2≥⋯≥λm≥0，及其相应的特征向量将每一个特征值所代表的信号进行分析组合，重构出新的时间序列。
奇异谱分析过程可分成嵌人、SVD分解、分组、重构四个步骤，接下来我们详细地介绍具体算法。
1）嵌入选择适当的窗口长度：m(2≤m≤T)，将所观测到的一维金融时间序列数据转化为多维序列：X1,...Xn,(Xi=(yi,...,yi+m−1),n=T−m+1)，得到轨迹矩阵：X=[X1,...,Xn]=(xij)n,mi,j=1。
这里m的选取不宜超过整个数据长度的1/3，如可根据事先经验大致确定数据的周期特征，则m的选取最好为周期的整数倍。
奇异谱分析奇异谱分析是近年来兴起的一种研究非线性时间序列数据的强大的方法。
它根据所观测到的时间序列构造出轨迹矩阵，并对轨迹矩阵进行分解、重构，从而提取出代表原时间序列不同成分的信号。
如长期趋势信号、周期信号、噪声信号等，从而对时间序列的结构进行分析，并可进一步预测。
奇异谱分析(SSA)方法最早由colebrook于1978年首先在海洋学研究中提出并使用。
Fracrich用一维时间序列在延迟相空间中做EOF展开，再通过显著性检验研究确定有意义的特征成分的个数，据此估计气候吸引子的维数。
这个工作被认为是SSA在气象学中的最早应用。
Hassani将这种方法引人到社会问题研究中来，并用其预测了美国交通事故的月时间序列数据。
给出了奇异谱分析的扩展形式一多通道奇异谱分析的算法，并由Hossein Hassani 用来对英镑/美元汇率进行了分析预测，取得了较好的效果。
奇异谱分析的基本思想是，将所观测到的一维时间序列数据：Y(T)=(y(1),⋯,y(T))转化为其轨迹矩阵：其中，m为选取的窗口长度，n=T-m+1，计算*X并对其进行奇异值分解（SVD），从而得到其m个特征值：λ1≥λ2≥⋯≥λm≥0，及其相应的特征向量将每一个特征值所代表的信号进行分析组合，重构出新的时间序列。
奇异谱分析过程可分成嵌人、SVD分解、分组、重构四个步骤，接下来我们详细地介绍具体算法。
1）嵌入选择适当的窗口长度：m(2≤m≤T)，将所观测到的一维金融时间序列数据转化为多维序列：X1,...Xn,(Xi=(yi,...,yi+m−1),n=T−m+1)，得到轨迹矩阵：X=[X1,...,Xn]=(xij)n,mi,j=1。
这里m的选取不宜超过整个数据长度的1/3，如可根据事先经验大致确定数据的周期特征，则m的选取最好为周期的整数倍。
2) svd分解（奇异值分解）V是n*n的正交阵，U是m*m的正交阵，Σ是m*n的对角阵。
首先，我们将一个矩阵A的转置 * A，将会得到一个方阵，我们用这个方阵求特征值可以得到：这里得到的v，就是我们上面的右奇异向量。
时间序列-小波分析时间序列（Time Series ）是地学研究中经常遇到的问题。
在时间序列研究中，时域和频域是常用的两种基本形式。
其中，时域分析具有时间定位能力，但无法得到关于时间序列变化的更多信息；频域分析（如Fourier 变换）虽具有准确的频率定位功能，但仅适合平稳时间序列分析。
然而，地学中许多现象（如河川径流、地震波、暴雨、洪水等）随时间的变化往往受到多种因素的综合影响，大都属于非平稳序列，它们不但具有趋势性、周期性等特征，还存在随机性、突变性以及“多时间尺度”结构，具有多层次演变规律。
对于这类非平稳时间序列的研究，通常需要某一频段对应的时间信息，或某一时段的频域信息。
显然，时域分析和频域分析对此均无能为力。
20世纪80年代初，由Morlet 提出的一种具有时-频多分辨功能的小波分析（Wavelet Analysis ）为更好的研究时间序列问题提供了可能，它能清晰的揭示出隐藏在时间序列中的多种变化周期，充分反映系统在不同时间尺度中的变化趋势，并能对系统未来发展趋势进行定性估计。
目前，小波分析理论已在信号处理、图像压缩、模式识别、数值分析和大气科学等众多的非线性科学领域内得到了广泛的应。
在时间序列研究中，小波分析主要用于时间序列的消噪和滤波，信息量系数和分形维数的计算，突变点的监测和周期成分的识别以及多时间尺度的分析等。
一、小波分析基本原理1. 小波函数小波分析的基本思想是用一簇小波函数系来表示或逼近某一信号或函数。
因此，小波函数是小波分析的关键，它是指具有震荡性、能够迅速衰减到零的一类函数，即小波函数)R (L )t (2∈ψ且满足：⎰+∞∞-=0dt )t (ψ （1）式中，)t (ψ为基小波函数，它可通过尺度的伸缩和时间轴上的平移构成一簇函数系：)abt (a)t (2/1b ,a -=-ψψ 其中，0a R,b a,≠∈ （2） 式中，)t (b ,a ψ为子小波；a 为尺度因子，反映小波的周期长度；b 为平移因子，反应时间上的平移。
太阳黑子的多项式趋势-自回归-条件异方差模型一、引言太阳黑子是太阳表面上的一种特殊现象，它是太阳活动的指示物之一。
科学家们长期以来对太阳黑子的产生规律和变化趋势进行研究，希望通过对太阳黑子的分析，可以更好地理解太阳活动的变化和预测太阳活动的未来走势。
本文将从太阳黑子的多项式趋势出发，结合自回归和条件异方差模型，对太阳黑子的变化趋势进行深入分析。
二、太阳黑子的多项式趋势1. 太阳黑子是太阳表面的一种磁活动现象，它的产生与太阳的磁活动周期密切相关。
科学家们通过长期的观测和数据分析，发现太阳黑子的数量呈现出一定的周期性变化。
在研究中，常常会使用多项式趋势拟合模型来描述太阳黑子的数量随时间变化的趋势。
多项式趋势模型可以帮助科学家们更好地理解太阳黑子的长期变化规律。
2. 太阳黑子的多项式趋势分析是建立在大量观测数据的基础之上的，通过对太阳黑子数量随时间变化的数据进行拟合分析，可以得到太阳黑子的长期趋势。
多项式趋势模型可以帮助科学家们预测太阳黑子未来的变化趋势，为太阳活动的预测提供重要的参考依据。
三、自回归模型在太阳黑子研究中的应用1. 自回归模型是一种描述时间序列数据的重要工具，它可以帮助科学家们更好地理解时间序列数据的内在规律。
在太阳黑子研究中，自回归模型被广泛应用于对太阳黑子数量随时间变化的数据进行建模和分析。
2. 自回归模型可以帮助科学家们找出太阳黑子数量之间的相关性和因果关系，从而揭示太阳黑子的变化规律。
通过对太阳黑子数量时间序列数据的自回归建模分析，可以得到太阳黑子数量未来的变化趋势，并进行预测。
四、条件异方差模型在太阳黑子研究中的应用1. 条件异方差模型是一种描述时间序列数据波动性的重要方法，它可以帮助科学家们更好地理解时间序列数据的波动规律。
在太阳黑子研究中，条件异方差模型被广泛应用于对太阳黑子数量随时间变化的数据进行建模和分析。
2. 条件异方差模型可以帮助科学家们发现太阳黑子数量波动的规律性和特征，并进行预测。
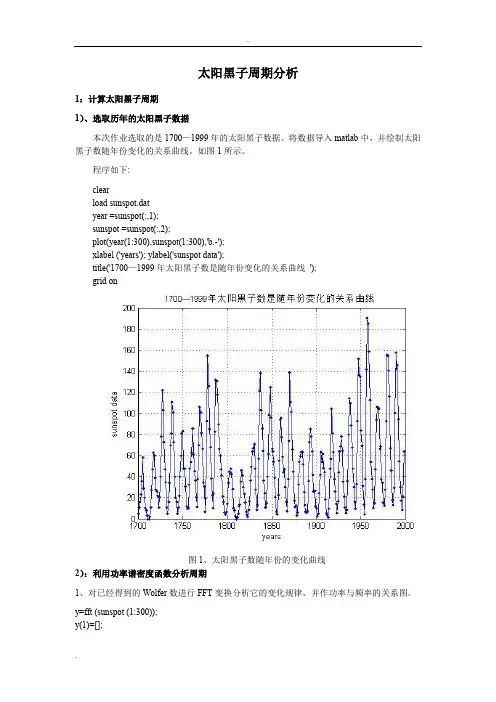
太阳黑子周期分析1：计算太阳黑子周期1）、选取历年的太阳黑子数据本次作业选取的是1700—1999年的太阳黑子数据。
将数据导入matlab中，并绘制太阳黑子数随年份变化的关系曲线。
如图1所示。
程序如下:clearload sunspot.datyear =sunspot(:,1);sunspot =sunspot(:,2);plot(year(1:300),sunspot(1:300),'b.-');xlabel ('years'); ylabel('sunspot data');title('1700—1999年太阳黑子数是随年份变化的关系曲线');grid on图1、太阳黑子数随年份的变化曲线2）：利用功率谱密度函数分析周期1、对已经得到的Wolfer数进行FFT变换分析它的变化规律，并作功率与频率的关系图。
y=fft (sunspot (1:300));y(1)=[];n=length(y);power =abs(y(1:n/2)).^2;q=1/2;f= (1:n/2)/(n/2)*q;plot(f, power);xlabel('周期/年');title('周期图');运行结果如图2所示。
图2、太阳黑子的功率谱为了清楚起见，取功率和频率的前50个分量作它的周期图，程序如下: plot(f(1:50),power(1:50));xlabel('频率');运行结果如图3所示。
图3、功率和频率的前50个分量的周期图2、确定太阳黑子的活动周期，画出功率与周期的关系图。
程序如下：T=1./f;plot (T, power);axis ([0 50 0 7e+6]); %X轴范围是0-50，Y轴范围是0-7*10^6xlabel ('周期');ylabel('功率');grid on%在功率与周期的关系图上标出功率的最高点，该位置对应的周期即为太阳黑子活动的周期。
太阳黑子数的小波包-小波网络混沌时序预测
潘玉民;张晓宇;张全柱
【期刊名称】《计算机科学》
【年(卷),期】2013(040)006
【摘要】太阳黑子是表征太阳活动的重要现象,影响地球、人体乃至生命环境.针对影响太阳黑子的因子难以确定的问题,引入小波包和混沌相空间重构子序列揭示太阳黑子时间序列的动力学及物理规律.该方法采用小波包分解原始时间序列,用混沌相空间重构恢复影响因子,并采用小波神经网络预测子序列,再经小波包重构获得太阳黑子的最终预测结果.其中小波神经网络采用自行开发的工具箱,其具有方便、收敛速度快、数据吞吐量大、预测精度高以及实用性强等特点,对推广小波神经网络应用具有重要作用,并为太阳黑子数的预测提供了一条新途径.
【总页数】6页(P260-264,267)
【作者】潘玉民;张晓宇;张全柱
【作者单位】华北科技学院信息与控制技术研究所北京101601;华北科技学院信息与控制技术研究所北京101601;华北科技学院信息与控制技术研究所北京101601
【正文语种】中文
【中图分类】TP18
【相关文献】
1.基于尺度UKF小波网络的混沌时间序列预测 [J], 赵鲲鹏;丛伟;赵亮
2.小波网络在带噪声的混沌时间序列预测中的研究 [J], 陈晓云;牛国鹏;吴本昌
3.基于小波网络的非线性经济时序预测模型 [J], 方先明;唐德善
4.基于Mexican Hat小波网络的时序预测 [J], 魏浩
5.基于混沌理论的太阳黑子数时间序列预测 [J], 伍友利;董福安;李世飞
因版权原因，仅展示原文概要，查看原文内容请购买。
第32卷第6期2007年11月测绘科学Science of Surveying and M app ingVol 132No 16Nov 1作者简介:徐克红(19822),女,山东泰安人,辽宁工程技术大学与中国测绘科学研究院联合培养硕士研究生,主要研究方向为卫星轨道确定。
E 2mail:xukehong0719@1631com 收稿日期:2007206228太阳黑子数时间序列的奇异谱分析和小波分析徐克红①②,程鹏飞①,文汉江①(①中国测绘科学研究院,北京 100039;②辽宁工程技术大学,辽宁阜新 123000)【摘 要】本文对小波变换和奇异谱分析方法进行了简要介绍,对离散小波的分解和重构、奇异谱分析的重构进行了详细阐述。
结合太阳黑子数1749年至2007年3月期间的月平均值时间序列进行了小波变换的分解和重构及SS A 方法的重构,提取了其主要的周期特性,并对两种分析方法进行了比较。
【关键词】小波分析;离散小波的分解与重构;奇异谱分析;太阳黑子数【中图分类号】P228 【文献标识码】A 【文章编号】100922307(2007)06200352041 引言太阳黑子是太阳光球上经常出现的阴暗斑点,是太阳活动的羁绊标志,是反映太阳辐射变化的重要指标,一般用太阳黑子数表示。
太阳黑子数反映了太阳活动强弱的变化,对地球的影响很大,诸如地磁变化、大气运动、气候异常、海洋变化等,都和太阳黑子数变化有着不同程度的关系。
因此研究太阳黑子数的变化有利于深入了解它对卫星轨道、定位等方面的影响。
对太阳黑子数变化的研究已有很多,韩延本,韩刚用小波分析的方法对太阳黑子数变化进行研究,验证了小波分析方法的可行性,并得到太阳黑子数变化包含多种周期分量的结论。
郝立生,李新,李月英利用Morlet 小波变换对太阳活动变化进行了研究,得到太阳活动存在141和106a 的变化周期。
小波变换的概念是1984年法国地球物理学家J 1Morlte 在分析处理地球物理勘探资料时提出来的。
其数学基础是19世纪的傅里叶变换,其后理论物理学家A 1Gr oss man 采用平移和伸缩不变性建立了小波变换的理论体系。
1989年S 1Mallat 提出了多分辨率分析概念,统一了在此之前的各种构造小波的方法,特别是提出了二进小波变换的快速算法,使得小波变换完全走向实用性[8]。
奇异谱分析(SS A )是对一维的时间序列进行分析的主成分分析方法。
该方法适用于从短噪声时间序列中提取信息。
SS A 在时空域中,通过将序列分解成元素行为模式的方法,将含在延迟坐标相空间的信息拆开,通过使用数据适应滤波器来帮助将时间序列分开为统计的独立成分,这些成分可以当作趋势、振动或噪声来进行分类。
本文选用太阳黑子数月平均值,采用小波变换和奇异谱分析的方法对该时间序列进行分析,同时对两种分析方法进行比较。
2 奇异谱分析主成分分析(PCA,Princi pal Component Analysis ),也称为经验正交函数(E OF,E mp irical O rthogonal Functi on ),可以由多维的时间序列中获取时间序列的主要成分,是常用的多元统计分析方法之一,主要将多个彼此相关的指标变换为少数几个彼此独立的综合指标即主成分,并要求主成分能反映原始数据的几乎全部信息,其中,常用于对一维的时间序列进行分析的方法称为奇异谱分析(SS A,Sin 2gular s pectru m analysis )。
奇异谱方法(SS A )是一种特别适合于研究周期振荡行为的分析方法,它是从时间序列的动力重构出发,并与经验正交函数相联系的一种统计技术,是E OF 分解的一特殊应用。
分解的空间结构与时间尺度密切相关,可以较好地从含噪声的有限尺度时间序列中提取信息,目前已应用于多种时间序列的分析中。
SS A 的具体操作过程是,将一个样本量为n 的时间序列按给定嵌套空间维数(即窗口长度)构造一资料矩阵。
当这一个资料矩阵计算出明显成对的特征值,且相应的E OF 几乎是周期性或正交时,通常就对应着信号中的振荡行为,可见SS A 在数学上相应于E OF 在延滞坐标上的表达。
对给定的X 1,X 2,…,X n 的时间序列,给定嵌套维数M ,M <N /2,建立时滞矩阵:X =x 1x 2…x N -M +1x 2x 3…x N -M +2…………x m x M +1…x N(1) (1)式的滞后自协方差是一个M ×M 的矩阵:S =s (0)s (1)…s (M -1)s (1)s (0)…s (M -2)…………s (M -1)s (M -2)…s (0)(2) S 为对称阵且主对角线为同一常数,称为Toep litz 矩阵,其特征值为:λ1≥λ2≥…≥λm ≥0,(3)λ1≥λ2≥…≥λm ≥0,(4) (4)式即为序列{x i }的奇异谱,称对X 的奇异值运算为奇异谱分析。
最大的特征值对应的特征向量看为第一阶模式,第二大的特征值对应的特征向量看为第二阶模式,依次类推。
第一阶模式代表了信号的最大变化趋势,第二阶模式代表了与第一阶模式无关的剩余信号量的最大变化趋势,依此类推。
在实际分析过程中,通常只选取前面的低阶模式进行分析。
计算出S 的特征值λk 和相应的特征向量,序列的SS A 展开为:x i+j =∑Mk =1aikE kj (5) 式中,i =1,2,…N 2M +1;j =1,2,…M 。
E kj 为时间E OF,记为T 2E OF,a ik 为时间主分量,记为T 2PC:a ik =∑Mj =1x i+j E kj ,(6) SS A 最重要的应用是重建成分RC (Reconstructi on )。
由第k 个的T 2E OF 和T 2PC 重建x i 的成分记为x k i ,公式为xk i=1i∑ij =1aij ,kE kj ,1≤i ≤M -1;1M∑Mj =1aij ,kE kj ,M ≤i ≤N -M +1;1N -i +1∑Mj =i-n +maij ,kE kj ,N -M +2≤i ≤N 1(7) 截取前k 个占比重大的成分近似表示原序列,x i =∑kk =1xik,i =1,2,…,N (8) 同时也可对各分量进行重建,用于对原信号的分析。
SS A 可以提取具有显著振荡行为的信号分量,并可选择若干有意义的分量进行序列重建。
其中低频信号的重建分量,显示了原始序列的主要演变特征。
3 小波分析311 小波分析小波分析是目前分析时间序列的有效工具,它可以获取时间序列的时间—频率特征,该分析方法是一种窗口大小(即窗口面积)固定但其形状可改变,时间窗和频率窗都可以改变的时频局域化分析方法,即在低频部分具有较高的频率分辨率和较低的时间分辨率,在高频部分具有较高的时间分辨率和较低的频率分辨率,所以被誉为数学显微镜。
正是这种特性,使小波变换具有对信号的自适应性。
将基本小波函数ψ(t )做位移τ后,再在不同尺度a 下与待分析信号x (t )做内积得到x (t )的小波变换:W T x (a,τ)=1a∫+∞-∞x (t )ψ3(t -τa)d t a >0(9) 式中,ψ3(t -τa )是ψ(t -τa)的逆变换。
小波变换将时间函数投影到二维的时间—尺度相平面上,提供了信号随时间变化的频谱特征,这对提取信号的某些本质特征创造了有利条件。
312 离散小波分解与重构离散小波变换定义(D iscrete W avelet Transf or m,简称DW T )为:W T f (a j 0,k τ0)=∫f (t )ψ3a j 0,k τ0(t )d t j =0,1,2,…,k ∈Z (10) 在多分辨率分析理论的基础上,1988年S 1Mallat 提出了离散小波分解与重构的快速算法,称为Mallat 算法[9]。
Mallat 分解算法使采样信号通过离散小波变换得到原始信号的低频系数和高频系数,然后保留高频部分,对低频系数进行再次的离散小波变换,由此一直下去,直至符合实际的要求。
重构算法正好与此过程相反。
见图1、图2。
其中,x 为原始信号,c N 为分解后的第N 层低频系数,d N为分解后的第N 层高频系数。
Lo_D 为小波分解低频滤波器,H i_D 为小波分解高频滤波器,Lo_R 为小波重构低频滤波器,H i_R 为小波重构高频滤波器。
4 太阳黑子数时间序列的奇异谱分析与小波分析人类对太阳的活动做了长期的观测,记录了太阳黑子数随时间变化的资料,这些资料记录了每天的、每月的和每年的太阳黑子数,而在实际应用中,它的月均值、月滑值和年均值才有较大的实用意义。
目前被认为较系统的太阳黑子相对数月值的时间序列起始于1749年,采用1749年22007年4月太阳黑子数时间序列,时间间隔为一个月,共3100个数据。
所有数据均来源于比利时皇家天文台(SI D C )[1]。
411 奇异谱分析(SSA)对太阳黑子数进行奇异谱分析,分别取窗口长度M 为100和150,单位为月。
首先,将M 取不同值时,所得的特征向量取前8个,将其变化曲线画出,见图3、图4。
由图可见,曲线呈现出十分明显的周期。
图3 成对特征向量(M =100)横坐标为:窗口长度(单位:月) 纵坐标为:特征向量图4 成对特征向量(M =150)图3和图4分别为窗口宽度取100和150时太阳黑子数SS A 的特征向量所表示的倾向或准周期信号的型态变化特征。
图3中a 图的1与2特征向量代表了倾向的变化特点,图3中b 、d 中各自两特征向量的形态变化均有些差别,其周期长度也有差别。
图4中的a 图同样代表了变化的倾向,而c 、d 中各自两特征向量的形态变化却很相似,周期长度也差别不大。
图3与图4相比,周期特性更明显,反映了1014a 的周期。
由于所取窗口长度度的限制,所以无法反映更长的周期特性。
然后,对前3阶的各分量进行了重构,并画出其对应的功率谱图,结果见图5和图6。
其中,M =100时,各模式所占比重为:第一阶模式,38166%;第二阶模式,63测绘科学 第32卷 31186%;第三阶模式,14134%;同理,取M =150时,所占比重为:第一阶模式,34186%;第二阶模式,28101%;第三阶模式,16176%。
图5 奇异谱分析(M =100)图6 奇异谱分析(M =150)由以上两图,各分量重构的结果所侧重细节差异很大,由所得功率谱图可见,所反映的主要周期是一致得,如两图中b 和d,均反应了1014a 的主周期,与准11a 的周期相一致。
两图中的f,与以上所反映的周期不同,为9216a 周期。
最后,分别对M =100,和M =150的前3阶模式进行重构,并与原始信号进行比较,并画出其功率普图,结果见图7和8。
