2003年全国初中数学竞赛天津赛区

2003年全国初中数学竞赛
嘉兴市评奖结果公告
2003年全国初中数学竞赛于2003年4月6日举行。

嘉兴市由嘉兴市教育局教研室、嘉兴市教育学会中学数学分会、嘉兴市数学会联合组织，共有6270名学生参加了本次竞赛，经成绩评定，确定嘉兴市团体优胜奖15名，个人一等奖68名、二等奖124名、三等奖127名。

现将结果公布如下：
团体优胜：
海盐县武原中学平湖市东湖中学
嘉兴三中求是实验中学
邵逸夫中学秀洲现代实验学校
嘉善泗洲中学桐乡六中
嘉兴市洪波中学嘉善四中
嘉兴秀中分校嘉善一中
海宁一中海盐县元通中学
海盐县实验中学
个人获奖：
一等奖
二等奖
嘉兴市教育局教研室嘉兴市教育学会中学数学分会
嘉兴市数学会
2003年5月8日。

5 EC 1 2 18 1 2 18第 4 期25 2003年全国初中数学竞赛天津赛区初赛一、选择题(每小题5 分,共30 分)(2003 - 03 - 23)AD 将△ABC 分成2 个等腰三角形. 则满足上述条件1. 化简2 4 + 2 3 - 21 - 12 3 为( ) .(A) 5 - 4 3 (B) 4 3 - 1 (C) 5 (D) 12.在凸八边形的所有内角中, 钝角至少有( ) 个.(A) 3 (B) 5 (C) 7 (D) 83.如图1 ,用3 个边长为1 的正方形组成一个对称图形,则能将其完全覆盖的圆的的不同形状(相似的认为是同一形状) 的△ABC 最多有个.三、解答题(每小题20 分,共60 分)12.有18 支足球队进行单循环赛,每个参赛队同其他各队都进行一场比赛. 假设比赛的结果没有平局,如果用a i和b i分别表示第i ( i = 1 ,2 ,3 , , 18) 支球队在整个赛程中胜与负的局数,求证:最小半径为( ) . a2+ a2+ + a2= b2+ b2+ + b2.(A) 2 (B) 5213.如图2 , PA 、PB 与⊙O 切于A 、B(C) 54 (D)5 17 图116两点, PC 是任意一条割线,且交⊙O于4.已知A 、B 为平面上的 2 个定点,且AB =5. 若点A 、B 到直线l 的距离分别等于2 、3 ,则满足条件的直线l 共有( ) 条.(A) 2 (B) 3 (C) 4 (D) 无数5.已知x 、y 、z 为3 个非负实数,且满足3 x + 2 y + z = 5 , x + y - z = 2. 若s = 2 x + y - z , 则s 的最大值与最小值的和为( ) .(A) 5 (B) 23 (C) 27 (D) 354 4 46. 使得2 n ( n + 1) ( n + 2) ( n + 3) + 12 可表示为2 个正整数平方和的自然数n ( ) .(A)不存在(B) 有1 个(C) 有2 个(D) 有无数个二、填空题(每小题6 分,共30 分)7.某编辑用0～9 这10 个数字给一本书的各页标上页码. 若共写了636 个数字, 则该书有点E、C , 交AB 于点AC2AD 图2D. 求证:BC2=BD.14. 已知函数y = ( a + 2) x2- 2 ( a2- 1) x + 1 ,其中自变量x 为正整数, a 也是正整数. 求x 为何值时,函数值最小.参考答案一、1. (C) .2. (B) .因为一个凸多边形的外角至多有 3 个钝角,故其内角中最多有 3 个锐角,所以凸八边形的内角中至少有 5 个钝角.3. (D) .如图 3 得a2+ 1 = r2,页.8.设△ABC 的面积是1 , D 是边BC 上一点,且(2 - a) 2 +122= r2.BD= 1. 若在边AC 上取一点E ,使四边形ABDE 的解得a =13, r =5 17. 图3DC 2 16 16面积为4,则A E的值为.9.已知二次函数y = ax2+ bx + c ,一次函数y =k24. (B) .以点A 、B 为圆心,半径分别为2 、3 的两圆的公切线的条数,即为所求.5. (A) .k ( x - 1) - 4 . 若它们的图像对于任意的实数k 都只有一个公共点,则二次函数的解析式为. x = s - 2 ≥0 ,10.已知α、β是方程x2α4 + 3β的值为. - x - 1 = 0 的两个根. 则3 x + 2 y + z = 5 ,由x + y - z = 2 ,2 x + y - z = s得y = 5 -4s31≥0 ,11.△ABC 中,有一内角为36°,过顶点A 的直线z = 1 - 3 s ≥0.26 中等数学。

1991年全国初中数学联合竞赛决赛试题第一试一、选择题本题共有8个小题，每小题都给出了（A ）、（B ）（C ）、（D ）四个答案结论，其中只有一个是正确的．请把正确结论的代表字母写在题后的圆括号内．１． 设等式y a a x a y a a x a ---=-+-)()(在实数范围内成立，其中a ，x ，y 是两两不同的实数，则22223yxy x y xy x +--+的值是 （A ）3 ； （B ）31； （C ）2； （D ）35． 答（ ）２． 如图，AB ‖EF ‖CD ，已知AB =20，CD =80，BC =100，那么EF 的值是（A ） 10； （B ）12；（C ） 16； （D ）18．答（ ）３． 方程012=--x x 的解是（A ）251±； （B ）251±-； （C ）251±或251±-； （D ）251±-±． 答（ ）４．已知：)19911991(2111n n x --=（n 是自然数）．那么n x x )1(2+-，的值是（Ａ）11991-； （Ｂ）11991--；（Ｃ）1991)1(n -； （Ｄ）11991)1(--n ．答（ ）５． 若M n 1210099321=⨯⨯⨯⨯⨯ ，其中Ｍ为自然数，n 为使得等式成立的最大的自然数，则Ｍ（Ａ）能被２整除，但不能被３整除；（Ｂ）能被３整除，但不能被２整除；（Ｃ）能被４整除，但不能被３整除；（Ｄ）不能被３整除，也不能被２整除．答（ ）６． 若a ，c ，d 是整数，b 是正整数，且满足c b a =+，d c b =+，a d c =+，那么 d c b a +++的最大值是（Ａ）1-；（Ｂ）5-；（Ｃ）0；（Ｄ）１．答（ ）７． 如图，正方形OPQR 内接于ΔABC ．已知ΔAOR 、ΔBOP 和ΔCRQ 的面积分别是11=S ，32=S 和13=S ，那么，正方形OPQR 的边长是 （Ａ）2；（Ｂ）3；（Ｃ）2 ；（Ｄ）3．答（ ）８． 在锐角ΔABC 中，1=AC ，c AB =， 60=∠A ，ΔABC 的外接圆半径R ≤1，则 （Ａ）21< c < 2 ； （Ｂ）0< c ≤21； 答（ ）（C ）c > 2； （D ）c = 2．答（ ）二、填空题１．Ｅ是平行四边形ABCD 中BC 边的中点，AE 交对角线BD 于G ，如果ΔBEG 的面积是１，则平行四边形ABCD 的面积是 ． ２．已知关于x 的一元二次方程02=++c bx ax 没有实数解．甲由于看错了二次项系数，误求得两根为２和４；乙由于看错了某一项系数的符号，误求得两根为－１和４，那么，=+ac b 32 ．3．设m ，n ，p ，q 为非负数，且对一切x >０，qpn m x x x x )1(1)1(+=-+恒成立，则 =++q p n m 22)2( ．４．四边形ABCD 中，∠ ABC 135=，∠BCD 120=，AB 6=，BC 35-=，CD = 6，则AD = ．第二试x + y ， x － y ， x y ， yx 四个数中的三个又相同的数值，求出所有具有这样性质的数对（x , y ）．二、ΔABC中，AB＜AC＜BC，D点在BC上，E点在BA的延长线上，且BD＝BE＝AC，ΔBDE的外接圆与ΔABC的外接圆交于F点（如图）．求证：BF＝AF＋CF三、将正方形ABCD分割为2n个相等的小方格（n是自然数），把相对的顶点A，C染成红色，把B，D染成蓝色，其他交点任意染成红、蓝两色中的一种颜色．证明：恰有三个顶点同色的小方格的数目必是偶数．1992年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.满足1=+-ab b a 的非负整数),(b a 的个数是(A)1; (B)2; (C)3; (D)4.2.若0x 是一元二次方程)0(02≠=++a c bx ax 的根,则判别式ac b 42-=∆与平方式20)2(b ax M +=的关系是(A)∆>M (B)∆=M (C)∆>M ; (D)不确定.3.若01132=+-x x ,则44-+x x 的个位数字是(A)1; (B)3; (C)5; (D)7.答( )4.在半径为1的圆中有一内接多边形,若它的边长皆大于1且小于2,则这个多边形的边数必为(A)7; (B)6; (C)5; (D)4.答( )5.如图,正比例函数)0(>==a ax y x y 和的图像与反比例函数)0(>=k xk y 的图像分别相交于A 点和C 点.若AOB Rt ∆和COD ∆的面积分别为S 1和S 2,则S 1与S 2的关系是 (A)21S S > (B)21S S =(C)21S S < (D)不确定 答( )6.在一个由88⨯个方格组成的边长为8的正方形棋盘内放一个半径为4的圆,若把圆周经过的所有小方格的圆内部分的面积之和记为1S ,把圆周经过的所有小方格的圆内部分的面积之和记为2S ,则21S S 的整数部分是 (A)0; (B)1; (C)2; (D)3.答( )7.如图,在等腰梯形ABCD 中, AB //CD , AB=2CD ,︒=∠60A ,又E 是底边AB 上一点,且FE=FB=AC , FA=AB .则AE :EB 等于(A)1:2 (B)1:3(C)2:5 (D)3:10答( )8.设9321,,,,x x x x ⋅⋅⋅均为正整数,且921x x x <⋅⋅⋅<<,220921=+⋅⋅⋅++x x x ,则当54321x x x x x ++++的值最大时,19x x -的最小值是(A)8; (B)9; (C)10; (D)11.答( )二.填空题1.若一等腰三角形的底边上的高等于18cm ,腰上的中线等15cm ,则这个等腰三角形的面积等于________________.2.若0≠x ,则x x x x 44211+-++的最大值是__________.3.在ABC ∆中,B A C ∠∠=∠和,90 的平分线相交于P 点，又AB PE ⊥于E 点，若3,2==AC BC ，则=⋅EB AE .4.若b a ,都是正实数，且0111=+--b a b a ，则=+33)()(ba ab . 第二试一、设等腰三角形的一腰与底边的长分别是方程062=+-a x x 的两根，当这样的三角形只有一个时，求a 的取值范围.二、如图，在ABC ∆中，D AC AB ,=是底边BC 上一点，E 是线段AD 上一点，且A CED BED ∠=∠=∠2.求证：CD BD 2=.三、某个信封上的两个邮政编码M 和N 均由0，1，2，3，5，6这六个不同数字组成，现有四个编码如下：A ：320651B ：105263C ：612305D ：316250已知编码A 、B 、C 、D 各恰有两个数字的位置与M 和N 相同.D 恰有三个数字的位置与M 和N 相同.试求：M 和N.1993年全国初中数学联合竞赛决赛试题第一试一.选择题本题共有8个小题,每小题都给出了(A), (B), (C), (D)四个结论,其中只有一个是正确的.请把正确结论的代表字母写在题后的圆括号内.1.多项式1612+-x x 除以12-x 的余式是(A)1; (B)-1; (C)1-x ; (D)1+x ;2.对于命题Ⅰ.内角相等的圆内接五边形是正五边形.Ⅱ.内角相等的圆内接四边形是正四边形,以下四个结论中正确的是(A )Ⅰ,Ⅱ都对 (B )Ⅰ对,Ⅱ错 (C )Ⅰ错,Ⅱ对. (D )Ⅰ,Ⅱ都错.3.设x 是实数,11++-=x x y .下列四个结论:Ⅰ.y 没有最小值;Ⅱ.只有一个x 使y 取到最小值;Ⅲ.有有限多个x (不止一个)使y 取到最大值;Ⅳ.有无穷多个x 使y 取到最小值.其中正确的是(A )Ⅰ (B )Ⅱ (C )Ⅲ (D )Ⅳ4.实数54321,,,,x x x x x 满足方程组⎪⎪⎪⎩⎪⎪⎪⎨⎧=++=++=++=++=++.;;;;52154154354324321321a x x x a x x x a x x x a x x x a x x x其中54321,,,,a a a a a 是实常数,且54321a a a a a >>>>,则54321,,,,x x x x x 的大小顺序是(A)54321x x x x x >>>>; (B )53124x x x x x >>>>;(C )52413x x x x x >>>>; (D )24135x x x x x >>>>.5.不等式73)1(12+<-<-x x x 的整数解的个解(A )等于4 (B )小于4 (C )大于5 (D )等于56.在ABC ∆中,BC AO O A =∠,,是垂心是钝角,则)cos(OCB OBC ∠+∠的值是 (A)22- (B)22 (C)23 (D)21-. 答( )7.锐角三角ABC 的三边是a , b , c ,它的外心到三边的距离分别为m , n ,p ,那么m :n :p 等于 (A)c b a 1:1:1; (B)c b a :: (C)C B A cos :cos :cos (D)C B A sin :sin :sin .答( )8.13333)919294(3-+-可以化简成 (A))12(333+; (B))12(333- (C)123- (D)123+答( )二.填空题1. 当x 变化时,分式15632212++++x x x x 的最小值是___________. 2.放有小球的1993个盒子从左到右排成一行,如果最左面的盒里有7个小球,且每四个相邻的盒里共有30个小球,那么最右面的盒里有__________个小球.3.若方程k x x =--)4)(1(22有四个非零实根,且它们在数轴上对应的四个点等距排列,则k =____________.4.锐角三角形ABC 中,︒=∠30A .以BC 边为直径作圆,与AB , AC分别交于D , E ,连接DE , 把三角形ABC 分成三角形ADE 与四边形BDEC ,设它们的面积分别为S 1, S 2,则S 1:S 2=___________. 第二试一.设H 是等腰三角形ABC 垂心,在底边BC 保持不变的情况下让顶点A 至底边BC 的距离变小,这时乘积HBC ABC S S ∆∆⋅的值变小,变大,还是不变?证明你的结论.二.ABC ∆中, BC =5, AC =12, AB =13, 在边AB ,AC 上分别取点D , E , 使线段DE 将ABC ∆分成面积相等的两部分.试求这样的线段DE 的最小长度.三.已知方程0022=++=++b cx x c bx x 及分别各有两个整数根21,x x 及21,x x '',且,021>x x 021>''x x . (1)求证:;0,0,0,02121<'<'<<x x x x (2)求证:1-b ≤c ≤1+b ; (3)求c b ,所有可能的值.1994年全国初中数学联赛试题第一试(4月3日上午8：30—9：30)考生注意：本试共两道大题，满分80分.一、选择题（本题满分48分，每小题6分）本题共有8个小题都给出了A，B、C，D，四个结论，其中只有一个是正确的，请把你认为正确结论的代表字母写在题后答案中的圆括号内，每小题选对得6分；不选、选错或选出的代表字母超过一个（不论是否写在圆括号内），一律得0分.〔答〕( )2．设a,b,c是不全相等的任意实数，若x=a2-bc,y=b2-ca,z=c2-ab,则x,y,zA．都不小于0B．都不大于0C．至少有一个小0于D．至少有一个大于0〔答〕( )3．如图1所示，半圆O的直径在梯形ABCD的底边AB上，且与其余三边BC，CD，DA相切，若BC=2，DA=3，则AB的长A．等于4B．等于5C．等于6D．不能确定〔答〕( )A．1 B．-1 C．22001D．-22001〔答〕( )5．若平行直线EF，MN与相交直线AB，CD相交成如图2所示的图形，则共得同旁内角A．4对B．8对C．12对D．16对〔答〕( )〔答〕( )7．设锐角三角形ABC的三条高AD，BE，CF相交于H。

【数学竞赛】2003年全国初中数学联赛试卷第一试（4月13日上午8:30—9:30）一、选择题（本题满分42分，每小题7分）1.A .5-B .1C .5D .1[答]（ ）2.在凸10边形的所有内角中，锐角的个数最多是A .0B .1C .3D .5[答]（ ）3.若函数()0y kx k =>与函数1y x=的图象相交于A ，C 两点，AB 垂直x 轴于B ，则△ABC 的面积为 A .1 B .2 C .k D .2k[答]（ ）4.满足等式2003的正整数对()x y ，的个数是A .1B .2C .3D .4[答]（ ）5.设△ABC 的面积为1，D 是边AB 上一点，且13AD AB =．若在边AC 上取一点E ，使四边形DECB 的面积为34，则CE EA的值为 A .12 B .13 C .14 D .15[答]（ ）6.如图，在□ABCD 中，过A ，B ，C 三点的圆交AD 于E ，且与CD 相切．若AB =4，BE =5，则DE 的长为A .3B .4C .154D .165[答]（ ） D CA B E二、填空题（本题满分28分，每小题7分）1.抛物线2y ax bx c =++与x 轴交于A ，B 两点，与y 轴交于点C ．若△ABC 是直角三角形，则ac =__________．2.设m 是整数，且方程2320x mx +-=的两根都大于95-而小于37，则m =____________． 3.如图，'AA ，'BB 分别是∠EAB ，∠DBC 的平分线．若''AA BB AB ==，则∠BAC 的度数为_____________．4.已知正整数a ，b 之差为120，它们的最小公倍数是其最大公约数的105倍，那么a ，b 中较大的数是_________．2003年全国初中数学联合竞赛试卷第二试（A ）（4月13日上午10:00—11:30）考生注意：本试三大题，第一题20分，第二、三题各25分，全卷满分70分．一、（本题满分20分）试求出这样的四位数，它的前两位数字与后两位数字分别组成的二位数之和的平方，恰好等于这个四位数．二、（本题满分25分）。

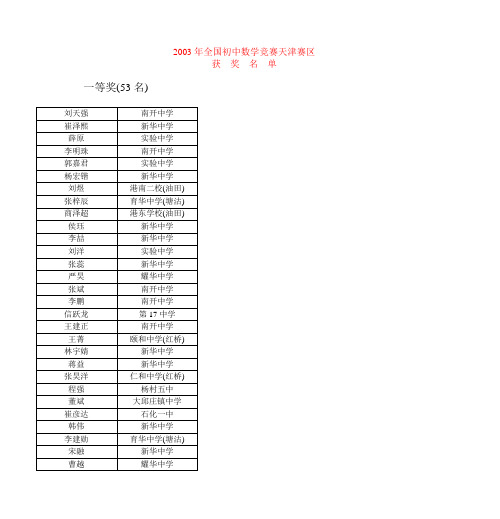
G F EDCB AOD CBA2003年“TRULY ®信利杯”全国初中数学联赛天津赛区复赛试卷1．若4x －3y －6z = 0，x +2y －7z = 0 (xyz≠0)，则代数式222222103225z y x z y x ---+的值等于 ( )． (A)12-(B)192-(C)15- (D)13-2．在本埠投寄平信，每封信质量不超过20g时付邮费0.80元，超过20g 而不超过40g 时付邮费1.60元，依次类推，每增加20g 需增加邮费0.80元（信的质量在100g 以内）． 如果某人所寄一封信的质量为72.5g ，那么他应付邮费 ( )．(A)2.4元 (B)2.8元(C) 3元 (D) 3.2元 3．如右图所示，∠A +∠B +∠C +∠D +∠E +∠F +∠G的值等于（ ）．(A) 360° (B) 450° (C) 540° (D) 720° 4．四条线段的长分别为9，5，x ，1（其中x 为正实数），用它们拼成两个直角三角形，且AB 与CD 是其中的两条线段（如右图），则x可取值的个数为（ ）．(A) 2个 (B) 3个 (C) 4个 (D) 6个5．某校九年级两个毕业班的学生和教师共100人一起在台阶上拍毕业照留 念，摄影师要将其排列成前多后少的梯形队阵（排数≥3），且要求各行的人数必须是连续的自然数，这样才能使后一排的人均站在前一排两人间的空当处，那么，满足上述要求的排法的方案有( )．(A) 1种 (B) 2种(C) 4种 (D) 0种6．已知31+=x ，那么2111242x x x +-+--的值等于 ． 7．若实数x ，y ，z 满足41=+yx ，11=+z y ，371=+x z ，则xyz 的值为 ．8．观察下列图形：① ② ③ ④根据图①、②、③的规律，图④中三角形的个数为 ． 9． 如右图所示，已知电线杆AB 直立于地面上，它的影子恰好照在土坡的坡面CD 和地面BC 上，如果CD 与地面成45º，∠A = 60º，CD = 4m ，BC =()2264-m ，则电线杆AB 的长为_______m ． 10．已知二次函数c bx ax y ++=2（其中a 是正整数）的图象经过点A （－1，4）与点B （2，1），并且与x 轴有两个不同的交点，则 b + c 的最大值为 ．三、解答题（本大题共4题，每小题15分，满分60分）如图所示，已知AB 是⊙O 的直径，BC 是⊙O 的切线，OC 平行于弦AD ，过点D 作DE ⊥AB 于点E ，连结AC ，与DE 交于点P ．问EP 与PD 是否相等？证明你的结论．某人租用一辆汽车由A 城前往B 城，沿途可能经过的城市以及通过两城市之间所需的时间（单位：小时）如图所示．若汽车行驶的平均速度为 80千米/小时，而汽车每行驶1千米需要的平均费用为1.2元．试指出此人从A 城出发到B 城的最短路线（要有推理过程），并求出所需费用最少为多少元？10111859712131761514FGO HBE DC APE DCB A OABCD已知：△ABC 中，∠ACB =90°．(1) 如图所示，当点D 在斜边AB 上（不含端点）时，求证：ABBDAD BC BD CD -=-222；(2)当点D 与点A 重合时，第(1)小题中的等式是否成立？请说明理由； (3)当点D 在BA 的延长线上时，第(1)小题中的等式是否成立？请说明理由．已知实数a ，b ，c 满足：a +b +c =2，abc =4. (1)求a ，b ，c 中的最大者的最小值； (2)求a b c ++的最小值.答案：1.答案：D ．由⎩⎨⎧=-+=--,072,0634z y x z y x 解得⎩⎨⎧==.2,3z y z x 代入，得原式=1310121818451043924295222222-=---+=-⨯-⨯-⨯+⨯z z z z z z ． 2. 答案：D ．因为20×3<72．5<20×4，所以根据题意，可知需付邮费0.8×4=3．2（元）． 3. 答案：C ．如图所示，∠B +∠BMN +∠E +∠G =360°， ∠FNM +∠F +∠A +∠C =360°，而∠BMN +∠FNM =∠D ＋180°，所以∠A +∠B +∠C +∠D +∠E +∠F +∠G =540°． 4. 答案：D ．显然AB 是四条线段中最长的，故AB =9或AB =x ． （1）若AB =9，当CD =x 时，222)51(9++=x ，53=x ；当CD =5时，222)1(59++=x ，1142-=x ； 当CD =1时，222)5(19++=x ，554-=x ．（2）若AB =x ，当CD =9时，222)51(9++=x ，133=x ；当CD =5时，222)91(5++=x ，55=x ； 当CD =1时，222)95(1++=x ，197=x ．5. 答案：B ．设最后一排有k 个人，共有n 排，那么从后往前各排的人数分别为k ，k +1，k +2，…，k +（n －1），由题意可知1002)1(=-+n n kn ，即()[]20012=-+n k n ．因为k ，n 都是正整数，且n ≥3，所以n <2k +（n －1），且n 与2k +（n －1）的奇偶性不同． 将200分解质因数，可知n =5或n =8． 当n =5时，k =18；当n =8时，k =9． 共有两种不同方案．6. 答案：23-． 4341442141212222--=-+--=---++x x x x x x将31+=x代入，可得其值为23-． 7. 答案：1．因为34371137137111114--+=---+=-+=-+=+=x x x xx x z z x z x y x ， 所以37)34()34(4-+-=-x x x x ，091242=+-x x ，0)32(2=-x ，故23=x ．从而 353237137=-=-=x z ， 5253111=-=-=z y ． 于是1355223=⨯⨯=xyz ．8. 答案：161．根据图中①、②、③的规律，可知图④中三角形的个数为1+4+3×4+432⨯+433⨯=1+4+12+36+108=161（个）．9. 答案：26．如图，延长AD 交地面于E ，过D 作DF ⊥CE 于F ． 因为∠DCF =45°，∠A =60°，CD =4（m ）， 所以CF =DF =22（m ），EF =DF tan60°=62（m ）． 因为3330tan == BE AB ， 所以2633)22642262(33=⨯-++=⨯=BE AB （m ）． 10. 答案：－4．G FE D CB ANM由于二次函数的图象过点A （－1，4），点B （2，1），所以⎩⎨⎧=++=+-,124,4c b a c b a解得⎩⎨⎧-=--=.23,1a c a b 因为二次函数图象与x 轴有两个不同的交点，所以42>-=∆ac b ，0)23(4)1(2>----a a a ，即0)1)(19(>--a a ， 由于a 是正整数，故1>a ，所以a ≥2．又因为b +c =－3a +2≤－4，且当a =2，b =－3，c =－1时，满足题意，故b +c 的最大值为－4．11. 解：DP =PE ． 证明如下：因为AB 是⊙O 的直径，BC 是切线，所以AB ⊥BC ． 由Rt △AEP ∽Rt △ABC ，得ABAEBC EP = ． ① ……（6分） 又AD ∥OC ，所以∠DAE=∠COB ，于是 Rt △AED ∽Rt △OBC ． 故ABAEAB AE OB AE BC ED 221===． ② ……（12分） 由①，②得 ED =2EP ． 所以 DP =PE ． ……（15分） 12. 解：从A 城出发到达B 城的路线分成如下两类： （1） 从A 城出发到达B 城，经过O 城．因为从A 城到O 城所需最短时间为26小时，从O 城到B 城所需最短时间为22小时． 所以，此类路线所需 最短时间为26+22=48（小时）． ……（5分）（2） 从A 城出发到达B 城，不经过O 城． 这时从A 城到达B 城，必定经过C ，D ，E 城或F ，G ，H 城，所需时间至少为49小时． ……（10分）综上，从A 城到达B 城所需的最短时间为48 小时，所走的路线为A →F →O →E →B ． ……（12分）所需的费用最少为80×48×1.2=4608（元）． ……（14分）答：此人从A 城到B 城最短路线是A →F →O →E →B ，所需的费用最少为4608元． ……（15分）13. 解：（1）作DE ⊥BC ，垂足为E ． 由勾股定理, 得.)()()(22222222BC BE CE BE CE DE BE DE CE BD CD -=-=+-+=-所以，BC BEBC CE BC BE CE BCBD CD -=-=-222． 因为DE ∥AC ，所以ABBD BC BE AB AD BC CE ==,．故AB BDAD AB BD AB AD BCBD CD -=-=-222． ……（10分） （2）当点D 与点A 重合时，第（1）小题中的等式仍然成立．此时有AD，BD=AB．所以122222222-=-=-=-BCBCBCABACBCBDCD，1-=-=ABAB．从而第（1）小题中的等式成立．……（13分）（3）当点D在BA的延长线上时，第（1）小题中的等式不成立．作DE⊥BC，交BC的延长线于点E，则222222CD BD CE BEBC BC--=21,CE BE CEBC BC+=-=--而1-=-=-ABABABBDAD,所以ABBDADBCBDCD-≠-222．……（15分）〖说明〗第（3）小题只要回答等式不成立即可（不成立的理由表述不甚清者不扣分）．14. 解：（1）不妨设a是a，b，c中的最大者，即a≥b，a≥c，由题设知a>0，且2b c a+=-，abc4=.于是b，c是一元二次方程04)2(2=+--axax的两实根，aa44)2(2⨯--=∆≥0，164423-+-aaa≥0，)4)(4(2-+aa≥0．所以a≥4．……（8分）又当a=4，b=c=-1时，满足题意. 故a，b，c中最大者的最小值为4.（2）因为abc>0，所以a，b，c为全大于0或一正二负.①若a，b，c均大于0，则由（1）知，a，b，c中的最大者不小于4，这与a+b+c=2矛盾.②若a，b，c为一正二负，设a>0，b<0，c<0，则22)2(-=--=--=++aaacbacba，由（1）知a≥4，故2a -2≥6，当a=4，b=c=-1时，满足题设条件且使得不等式等号成立.故cba++的最小值为AB DD。

2003年全国初中数学联合竞赛决赛一、选择题（每小题7分，共42分） 1. 221217223－＋－＝_________.A 5－42 B42－1 C5 D12. 在凸10边形的所有内角中，锐角的个数最多是_________个。

A0 B1 C3 D53.若函数y ＝kx(k ＞0)与函数y ＝x －1的图象相交于A 、C 两点，AB 垂直x 轴于B ，则△ABC 的面积为_________.A1 B2 Ck Dk 24.满足等式x 2003xy 2003y 2003x y x y ＋－－＋＝2003的正整数对的个数是 ___A1 B2 C3 D45、设△ABC 的面积为1，D 是边AB 上一点，且AD ∶AB ＝1∶3。

若在边AC 上取一点E ，使四边形DECB 的面积为43，则EAEC的值为＿＿。

A 21B 31C 41 D 516.如图，在平行四边形ABCD 中，过A 、B 、C 三点的圆交AD 于E ，且与CD 相切，若AB ＝4，BE ＝5，则ED 的长为＿＿。

A3 B4 C 415 D 516BCD AE二、填空题（每小题7分，共28分）1.抛物线y ＝ax ＋bx ＋c 与x 轴交于A ，B 两点，与y 轴交于点C 。

若△ABC 是直角三角形，则ac ＝_________.2.设m 是整数，且方程3x 2＋mx －2=0的两根都大于－59而小于73，则m=_______。

3.如图，AA 1、BB 1分别是∠EAB 、∠DBC 的平分线，若AA 1＝BB 1＝AB ，则∠BAC 的度数为_________.4.已知正整数a 、b 之差为120，它们的最小公倍数是其最大公约数的105倍，那么a 、b 中较大的数是_________.三.（本题满分20分）在△ABC 中，D 为AB 的中点，分别延长CA 、CB 到点E 、F ，使DE ＝DF ；过E ，F 分别作CA 、CB 的垂线，相交于P ，设线段PA 、PB 的中点分别为M 、N 。