卵形曲线

卡西尼卵形线二级结论概述卡西尼卵形线是指由卡西尼椭圆函数描述的一个曲线，其形状类似于椭圆，却有一端延伸得更加细长，如同一个鸟巢的形状。

该曲线的特殊性质引起了科学家的极大兴趣，并且在多个研究领域中发现了相关的二级结论。

本文将对卡西尼卵形线的二级结论进行全面、详细、完整的探讨。

卡西尼椭圆曲线的定义卡西尼椭圆曲线的数学表达式为：(x^2 + y^2)^2 = a^2 * (x^2 - y^2)其中，(x, y)为曲线上任意一点的坐标，a为常数。

卡西尼椭圆曲线具有一个特殊的性质，即曲线上任意一点到两个焦点的距离的乘积等于常数的平方：PF1 * PF2 = a^2卡西尼卵形线的性质卡西尼卵形线具有以下几个重要性质：1.中点切线平行于传方向曲线：卡西尼卵形线的中点切线与焦线的夹角等于传方向曲线与焦线的夹角。

2.对角线交点处切线垂直于传方向曲线：卡西尼卵形线的对角线交点处的切线与传方向曲线垂直。

3.曲线外端点处切线过焦点：卡西尼卵形线的曲线外端点处的切线经过焦点，即焦点是曲线上所有切线的一个公共点。

卡西尼卵形线的二级结论二级结论一：焦点与极限在卡西尼卵形线上，焦点有以下重要性质：1.焦点是曲线的对称中心：任意取曲线上一点P和其对称点P’，则P和P’到焦点的距离之积相等。

2.焦点与曲线的对称轴上有垂直关系：曲线的对称轴与曲线上任意一点到焦点的距离的乘积为常数。

3.曲线上离焦点越远的点，其到焦点的距离趋近于曲线的半径：即当P到焦点的距离无限增大时，这个距离与曲线的半径趋于相等。

二级结论二：卡西尼卵形线与力学在力学领域中，卡西尼卵形线也有一些相关的二级结论：1.卡西尼卵形线的轨迹：如果一个质点被两个力限制在卡西尼卵形线上，那么该质点的轨迹将是卡西尼卵形线。

2.卡西尼卵形线的稳定性：在某些力学系统中，卡西尼卵形线是一个稳定的平衡位置，当质点偏离卡西尼卵形线时，力将会将其拉回。

3.卡西尼卵形线与天体运动的关系：天体的运动轨迹中存在一类特殊情况，即当天体被两个引力中心所限制时，其运动轨迹将形成卡西尼卵形线。

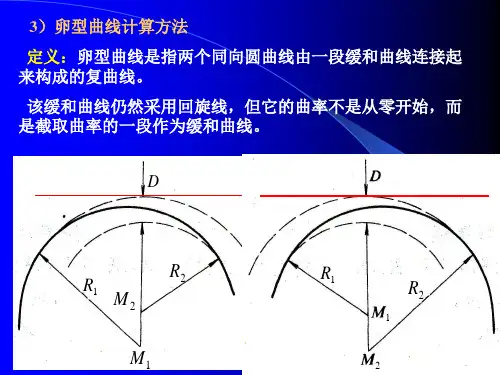
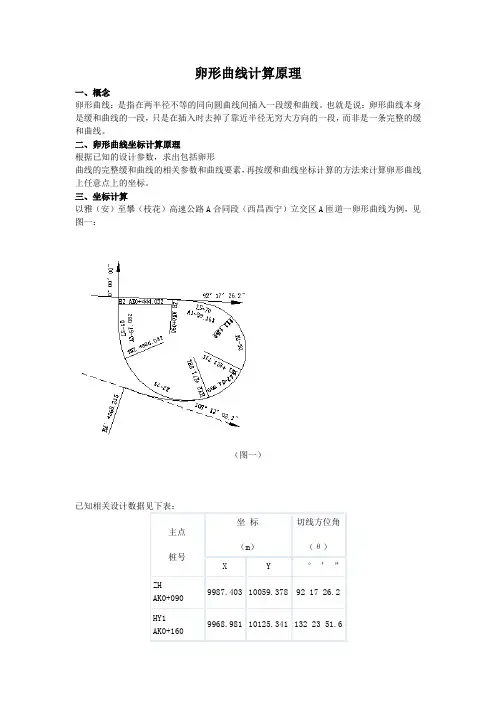
卵形曲线计算原理一、概念卵形曲线：是指在两半径不等的同向圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：1、缓和曲线（卵形曲线）参数计算A1==59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2==84.999A3==67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ'点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ'的弧长）=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ'-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ'点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH'或HZ'的弧长HZ'：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ'-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

高等级公路卵形曲线的计算方法周烨摘要在高等级公路施工过程中，常遇到卵形曲线，而设计单位的出发点不同，中线的解算方法也大相径庭。

本文着重从卵形中线几种计算方法入手，在此基础之上阐述了卵形曲线的测设。

关键词卵形曲线复曲线匝道桥高等级公路卵形曲线是高等级公路、立交桥匝道常见的曲线形式，它由基本的三部分构成：第一圆曲线段、缓和曲线段和第二圆曲线段。

中间段缓和曲线用来连接两个不同半径的圆曲线。

其中线坐标解算方法有如下几种：1 补全缓和曲线我国公路上采用的缓和曲线为辐射螺旋线，夹在两圆曲线中间的缓和曲线为整个缓和曲线的一部分，缓和曲线上任一点半径与该点至该缓和曲线起点的距离乘积为一定值：R×L＝A，假设R1＞R2，可由两圆半径及两圆间的缓和段长ls，求缓和曲线的总长L。

Δl＝L－ls(1)Δl就是夹在两圆曲线间缓和段省去的部分，由YH点补长Δl至o点，以o点为该缓和曲线起点，起点的切线方向为x轴，与之垂直的曲线内侧方向为y轴方向建立坐标系（图1）。

缓和曲线公式（推导过程略）如下：(2)(3)图 1利用x、y值可以求得o—YH弦与x轴的夹角：β＝3δ。

α1为YH点的切线方位角，则ox的方位：α＝α1±β。

o点的坐标可由几何关系求得为（x0，y）。

缓和段上任一点统一坐标可求得：(4)y=yo+xsinα±ycosα(5)2 曲率推算缓和曲线段曲率半径由第一段圆曲线半径R1变为第二段曲率半径R2（假设R1＞R2），则缓和曲线曲率半径变化为：(6)其中ls为中间段缓和曲线长，为求缓和曲线方程，现建立以缓和曲线起点为坐标原点，起点的切线方向为x轴，与之垂直的曲线内侧方向为y 轴的坐标系（图2），设P点为缓和曲线上任一点，距原点的曲线长为l，该点附近的微分弧长为dl，缓和曲线偏角为β，则有dx=dlcosβ(7)dy=dlsinβ(8)图 2由于将其代入上式并进行积分可得缓和曲线方程：(9)(10)中间缓和段统一坐标计算为：(11)xsinα±ycosα(12)Y＝yYHα为曲线YH点切线方位。

卵形曲线设计运用摘要：近年来，伴随我国城市化进程的快速发展，我国的城市基础设施建设工程的数量和规模也有了明显增加，其中，道路工程作为区域间经济文化交流的纽带，其建设质量更是得到了社会各界的广泛关注。

文章对卵形曲线设计运用进行了研究分析，以供参考。

关键词：卵形；曲线设计；运用1前言现如今，社会飞速发展，人们的出行需求也在不断增加。

大量车辆在道路上造成道路交通拥堵，造成一系列交通问题，影响道路交通安全。

此外，大型城镇不断扩张，中小城镇快速发展，城市的结构和规模发生了巨大的变化。

因此，研究城市道路交通分析和交通工程设计显得尤为重要。

2卵形曲线从结构上来看，卵形曲线是由一段回旋线将两段圆曲线组合在一起的一种曲线形式。

该曲线主要用于无法在相同方向的网曲线中插入直线的情况。

事实上，卵形曲线的设计原型是基本型单曲线，且基本型但曲线的应用范围要比卵形曲线更加广阔。

这主要是因为卵形曲线极易受到地形、路面设置和其他特殊条件的限制。

此外，C形曲线也是以单曲线为原型发展出来的一种曲线形式，其具体表现形式为由两段圆曲线在曲率为零处相连接。

由于C形曲线线路会给车辆的正常行驶造成影响，因此应用范围也较为狭窄，尽在部门特殊路段使用。

与C形曲线相比，卵形曲线的过渡方式更加优良，为汽车的行驶提供了更多的便利，因此在选择使用卵形曲线或者是C形曲线时，多以卵形曲线为主。

在设计卵形曲线时，为了发挥卵形曲线的优势应该将卵形曲线的回旋线参数设置在规定之上，连接两侧的圆曲线半径比例不应超过五倍，网曲线之间的距离应控制在极小的界限范围之内。

从卵形曲线的类型来看，通常将一道回旋线连接两道网曲线的组合形式规定为基本形式，在此基础上添加其他圆曲线，则依次被成为卵形曲线、四心卵形曲线等。

3卵形曲线采用的相关规定在公路勘测设计工作进行的过程中，之所以需要使用到卵形曲线，是为了可以让两个同向圆曲线直线插入长度不充足这个问题得到有效地解决，应用缓和曲线将两个同向圆曲线相互连接在一起，为了规避处于中间位置上的缓和曲线长度过大，或者曲率变化速度过快，一般情况下 R2/R1=0.2 ～ 0.8；缓和曲线各项参数的取值范围一般情况下是 0.5R2. 为宜，这是为了使连接两个同向圆曲线的回旋线曲率的变化不致过于急促；两圆曲线的间距 D 取值为 0.003 R2 ～ 0.03 R2 为宜。

5800卵形曲线坐标计算歪哥收集整理50卵形曲线辅助点计算（即完整缓和曲线起点的支距）解算步骤卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线，计算前只需要把不完整的缓和曲线（也就是卵型曲线）补充完整即可。

在计算小半径的缓和曲线或卵形曲线坐标时,由于切线支距公式取项少而造成计算精度低,现有书中一般介绍也就只有2~4项,为提高计算精度就需要将支距公式多展开几项。

以下计算卵型曲线的完整缓和曲线长支距模型：重在学习掌握解算流程，现在空间里有更好的计算程序。

曲线参数A2=LS×R1×R2÷(R2-R1)=卵形曲线长×小半径×大半径÷（大半径-小半径）在同一段回旋线内,它的参数永远是不变的。

LS=卵型曲线长. （已知）完整缓和曲线长L= A2÷R1=曲线参数÷小半径当L=LS时：代入完整缓和曲线切线支距公式：(式中R均为小半径R1)E=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10]F=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] 完整缓和曲线切线角（即两切线交角）L所对应玄长C=√（E2+F2）大半径处偏角P1=tan- 1(F2÷E2)小半径处偏角P3=180- P1-(180- p2)O=小半径处切线方位角（已知）小半径处至完整缓和曲线起点方位角Q=O±P3 (右向取+号；左向取-号)完整缓和曲线（起点）坐标：X=A+CcosQY=B=CsihQ完整缓和曲线（起点）处切线方位角：O=Q+180±p2 (右向取+号；左向取-号)以起点为基点用回旋线编程计算卵型曲线上任意桩号的中边桩点位坐标。

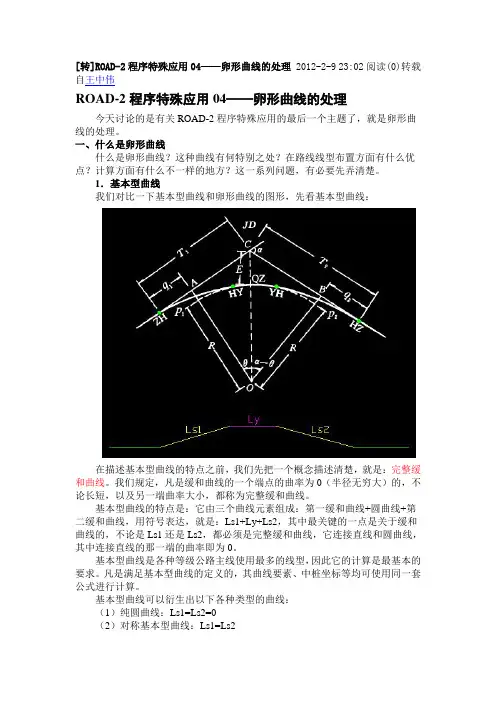
[转]ROAD-2程序特殊应用04——卵形曲线的处理2012-2-9 23:02阅读(0)转载自王中伟ROAD-2程序特殊应用04——卵形曲线的处理今天讨论的是有关ROAD-2程序特殊应用的最后一个主题了，就是卵形曲线的处理。

一、什么是卵形曲线什么是卵形曲线？这种曲线有何特别之处？在路线线型布置方面有什么优点？计算方面有什么不一样的地方？这一系列问题，有必要先弄清楚。

1．基本型曲线我们对比一下基本型曲线和卵形曲线的图形，先看基本型曲线：在描述基本型曲线的特点之前，我们先把一个概念描述清楚，就是：完整缓和曲线。

我们规定，凡是缓和曲线的一个端点的曲率为0（半径无穷大）的，不论长短，以及另一端曲率大小，都称为完整缓和曲线。

基本型曲线的特点是：它由三个曲线元素组成：第一缓和曲线+圆曲线+第二缓和曲线，用符号表达，就是：Ls1+Ly+Ls2，其中最关键的一点是关于缓和曲线的，不论是Ls1还是Ls2，都必须是完整缓和曲线，它连接直线和圆曲线，其中连接直线的那一端的曲率即为0。

基本型曲线是各种等级公路主线使用最多的线型，因此它的计算是最基本的要求。

凡是满足基本型曲线的定义的，其曲线要素、中桩坐标等均可使用同一套公式进行计算。

基本型曲线可以衍生出以下各种类型的曲线：（1）纯圆曲线：Ls1=Ls2=0（2）对称基本型曲线：Ls1=Ls2（3）凸形曲线：Ly=0（4）一侧带缓和曲线：Ls1=0，或者Ls2=0以上曲线的计算均可按基本型曲线公式计算。

也就是说，要使用基本型曲线公式计算，要么不带缓和曲线，如果要带，必须是完整缓和曲线。

两个基本型曲线直接相连的复曲线，均可按独立的两个基本型曲线进行计算，其中，两个同转向的基本型曲线直接连接的称为C型曲线，而两个相反转向的基本型曲线直接连接的称为S型曲线。

S型曲线在各种公路的平面线型中经常使用，而C型曲线则很少有使用的，究其原因，是因为其线型不好，仔细看一看吧，两曲率不相同的圆曲线之间缓和曲线的连接不合理。

公路路线设计中卵形曲线的运用张泽发布时间：2021-09-30T07:53:59.561Z 来源：《防护工程》2021年14期作者：张泽[导读] 卵形曲线是由一个回旋线连接两个同向圆曲线的组合形式。

其组成形式为直线—缓和曲线(A1)—圆曲线(R1)—缓和曲线—圆曲线(R2)—缓和曲线(A2)—直线的顺序组合构成的路线线形。

本文根据相关规范以及设计经验，经过计算论证对卵形曲线从设置条件、计算方法、交通安全性评价三方面对其运用探析，以期能在相关工作中提供参考。

张泽四川公路工程咨询监理有限公司四川成都 610000摘要：卵形曲线是由一个回旋线连接两个同向圆曲线的组合形式。

其组成形式为直线—缓和曲线(A1)—圆曲线(R1)—缓和曲线—圆曲线(R2)—缓和曲线(A2)—直线的顺序组合构成的路线线形。

本文根据相关规范以及设计经验，经过计算论证对卵形曲线从设置条件、计算方法、交通安全性评价三方面对其运用探析，以期能在相关工作中提供参考。

关键词：卵形曲线；回旋线；回旋线参数；卵形曲线计算；交通安全性评价0引言平面线形的三要素为直线、圆曲线和缓和曲线，在路线平面线形设计中通过灵活运用基本要素可组合成多种平面线形的组合形式。

主要有：基本型、S形、C形、卵形、凸形、回头曲线和复合型等。

设计中对于曲线的选择主要以基本型、S形为主，低等级道路设计中对于回头曲线的采用也较为常见，而C形、卵形、凸形、复合型曲线除了卵形在砸道设计中常见，一般仅在地形条件特殊困难，路线严格受限时采用。

对与各种曲线组合的使用在《公路路线设计规范》（JTG D20-2017）（以下称《规范》）中对其使用条件均作了相关规定。

卵形曲线的应用除匝道设计中使用外在低等级道路设计中因其较C形和凸形曲线安全性、驾驶体验较好。

通常在地形地貌、地质水文、建设规模受限时采用卵形曲线，因卵形曲线具有连续的曲率，能保持较好的线形协调性，受到了设计者的青睐，在道路设计中被越来越多的采用。

论文THESIS112 China Highway道路路线设计中，平面线形主要由直线、圆曲线和回旋线3种要素组成。

曲线形式的选用要根据曲线半径、地形及地物、技术规范要求等来选择。

一般曲线分为单曲线和复曲线两种。

单曲线是指设计一个半径的曲线。

根据技术规范要求及地形情况考虑是否设置回旋线。

复曲线为两个或两个以上圆曲线半径径相连接，包括同向复曲线和反向复曲线。

其中，同向复曲线分为卵形复曲线、凸形复曲线及C 形复曲线等几种形式。

路线设计中，卵形曲线在受地形、地物及其他条件限制时应用较为广泛。

卵形曲线卵形曲线是两同向圆曲线半径用回旋线径相衔接。

最基本的组合形式为回旋线—圆曲线—回旋线—圆曲线—回旋线。

常用的卵形曲线有双心和三心卵形曲线2种。

一个回旋线连接2个同向圆曲线的组合线形，叫双心卵形曲线。

在双心卵形曲线基础上，再用一个回旋线连接第三个同向圆曲线的组合线形，叫三心卵形曲线。

在实际应用当中要注意与C 形曲线的区别：与卵形曲线相比，C 形曲线也是2个同向不同半径的圆曲线相连接的一种形式，不同之处在于C 形曲线在两同向圆曲线回旋线曲率为零处径相衔接，等同于在两同向曲线之间设置的直线长度为零。

这种设置无论对线形还是行车舒适都有一定的影响，而卵形曲线是在不同半径的同向圆曲线之间，用1条回旋线A 相衔接，回旋线曲率半径是从半径R 1过渡到半径R 2。

卵形曲线两同向曲线间的衔接方式要比C 形曲线两同向曲线间的衔接方式要好，同时线形的整体性及行车舒适性都要比C 形曲线优，故C 形曲线仅限于地形条件特殊困难，路线严格受限时方可采用。

卵形曲线回旋线长度的计算《公路路线设计规范》（JTG D20—2006）9.2.4回旋线的运用第（4）条规定：①卵形曲线的回旋线参数宜选R 2/2≤A ≤R2 (R2为小圆曲线半径)。

②两曲线半径之比，以R 2/R 1=0.2～0.8卵形曲线规范条文适应性及应用分析文/中交第二航务工程勘察设计院有限公司 戴琪 曾庆桓为宜。

卵形线方程
摘要：
1.卵形线方程的定义
2.卵形线的性质
3.卵形线在数学和物理学中的应用
4.卵形线的发展历程
5.我国在卵形线研究方面的贡献
正文：
卵形线方程是描述一种特殊曲线的数学方程，该曲线形状类似于鸟卵，因此得名卵形线。

在数学和物理学中，卵形线具有很多独特的性质和应用，如在波动理论、统计物理和天体物理学等领域都有重要的应用。

卵形线是三阶代数曲线，其方程一般可以写成：x^3 + y^3 + 3axy = 0。

通过改变参数a、x 和y 的值，可以得到不同形状的卵形线。

卵形线具有如下一些性质：首先，卵形线具有三个分支，每个分支都呈卵形；其次，卵形线的分支在x 轴和y 轴上都有渐近线；最后，卵形线具有一个对称中心，即原点。

卵形线的研究历程可以追溯到19 世纪。

当时，德国数学家卡尔·魏尔斯特拉斯（Carl Weierstrass）首次提出了卵形线的概念，并研究了其一些基本性质。

自那时以来，许多数学家和物理学家都对卵形线进行了深入研究，发现了它在波动理论、统计物理和天体物理学等领域的重要应用。

我国在卵形线研究方面也取得了一定的成果。

近年来，我国数学家和物理
学家在卵形线的理论研究和应用方面做出了很多贡献。

例如，我国学者在卵形线的稳定性、振动特性和拓扑结构等方面取得了一系列重要成果，为卵形线的研究发展做出了贡献。

总之，卵形线是一种具有独特性质和应用的曲线，其研究在数学和物理学等领域具有重要意义。

从魏尔斯特拉斯提出卵形线的概念，到现代学者在卵形线研究方面取得的一系列成果，卵形线的研究历程充满了挑战和发现。

一．概述近年来随着我国公路建设的发展，全封闭、全立交的高等级公路已经成为我国公路网中的重要组成部分，组成立交的基本单元是匝道，匝道的平面线形组合相对比较复杂，计算烦琐，特别是卵形曲线的计算更加抽象难懂。

卵形曲线的计算方法主要有曲直法、解析法、拟合法、积木法、综合法、弦切法等。

由于其他方法理论抽象、计算烦琐。

因此一般工程放样中主要以弦切法为主。

本文重点介绍弦切法在立交匝道卵形曲线敷设计算中的应用。

二、弦切法的基本原理及计算思路对于路线平面线形而言，无论是绵延不断的公路，还是局部线形组合复杂的立交匝道，其基本构成单元不外是圆曲线、缓和曲线、直线。

一段圆曲线的终点，可以认为是其弦长（弧长所对应的）在相应方向上的延伸所构成的；一段缓和曲线的终点，也可以认为是由一方向和距离所构成的。

因此，在一段路线的起终点坐标和切线方位角固定的情况下，便能容易的求出坐标增量，方位增量的计算式，进而求得各曲线参数。

对于任何一种线形单元，只要知道起点坐标（X0，Y0）和切线方位角ɑ（可以假设为任意值），即可根据弦长S和相关参数确定其线形。

以下图2-1所示卵形曲线为例，若给定R1、R2和回旋曲线参数A，即、终可求得该缓和曲线长、交点坐标（XM，YM）、切线长T1、T2、偏角ɑJ点坐标（XZ，YZ）和终点切线方位角。

这样求得的终点坐标，曲率半径和切线方位角又可以作为下一线形单元起点的相应资料。

交点J的坐标：Xm=T1×COS（ɑ）+X0Ym=T1×SIN（ɑ）+Y0终点坐标：Xz=Xm+T2×COS（a+aj)Yz=Ym+T2×SIN(a+aj)根据卵形曲线的特点，可以计算出如下参数：L1=A2/R1，L2= A2/R2，L=L2-L1（R1>R2),或L=L1-L2 （R1<R2)根据回旋曲线上任意点的相对坐标计算公式：X=L S-L S5/40/A4+L S9/3456/A8，Y=L S3/6/A2-L S7/336/A6+L S11/42240/A10即可计算出卵形曲线起终点在相对坐标系中的坐标(X1,Y1) 和（X2，Y2）。

卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：主点桩号坐标（m）切线方位角（θ）XY°’‖ZHAK0+0909987.40310059.37892 17 26.2 HY1AK0+1609968.98110125.341132 23 51.6 YH1AK0+223.715 9910.60310136.791205 24 33.6HY2AK0+271.8819880.43810100.904251 24 18.5YH2AK0+384.0329922.31610007.909337 04 54.2HZAK0+444.0329981.36310000.0000 00 001、缓和曲线（卵形曲线）参数计算A1==59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2==84.999A3==67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ―点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ―的弧长）=A2÷R1=7224.900÷50=144.498∴HZ―桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ―的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ―-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ―点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8] - L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH―或HZ―的弧长HZ―：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ―-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2‖* 偏角计算用反正切公式，不要用其它公式。

笛卡儿卵形线推导
笛卡儿卵形线是由法国数学家笛卡儿在17世纪提出的一种特殊曲线，它的方程是(x^2/a^2) + (y^2/b^2) = 1。

它的名字来源于它的形状，它看起来像一枚椭圆形的蛋。

要推导笛卡儿卵形线的方程，我们可以从椭圆形的方程出发，椭圆形的方程是(x^2/a^2) + (y^2/b^2) = 1。

我们可以将椭圆形的方程转化为极坐标方程r^2 = a^2cos^2θ + b^2sin^2θ。

接着，我们可以将极坐标方程转化为笛卡儿坐标方程，即x = rcos θ，y = rsinθ。

将这两个方程代入极坐标方程中，我们可以得到(x^2/a^2) + (y^2/b^2) = cos^2θ/a^2 + sin^2θ/b^2。

化简后，我们可以得到(x^2/a^2) + (y^2/b^2) = 1。

这就是笛卡儿卵形线的方程。

因此，我们可以得出结论：笛卡儿卵形线是由椭圆形的方程转化而来的，它是一种特殊的椭圆形。

- 1 -。