卵形曲线计算方法

卵形曲线计算原理一、概念卵形曲线：是指在两半径不等的同向圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

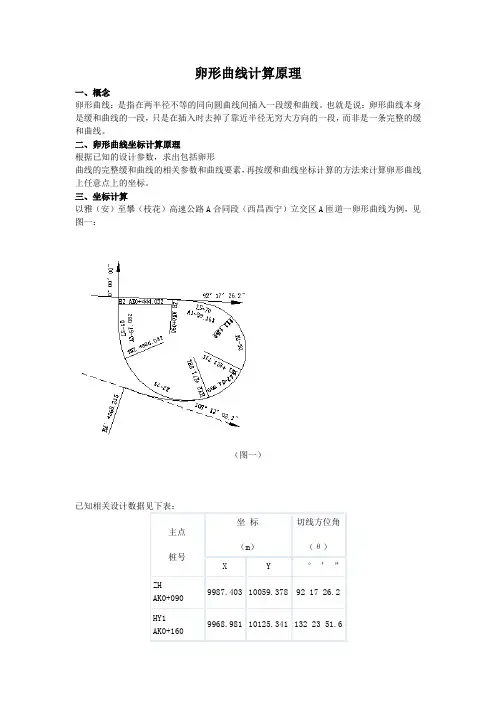
三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：1、缓和曲线（卵形曲线）参数计算A1==59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2==84.999A3==67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ'点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ'的弧长）=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ'-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ'点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH'或HZ'的弧长HZ'：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ'-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

卵形曲线坐标计算方法一、概念卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

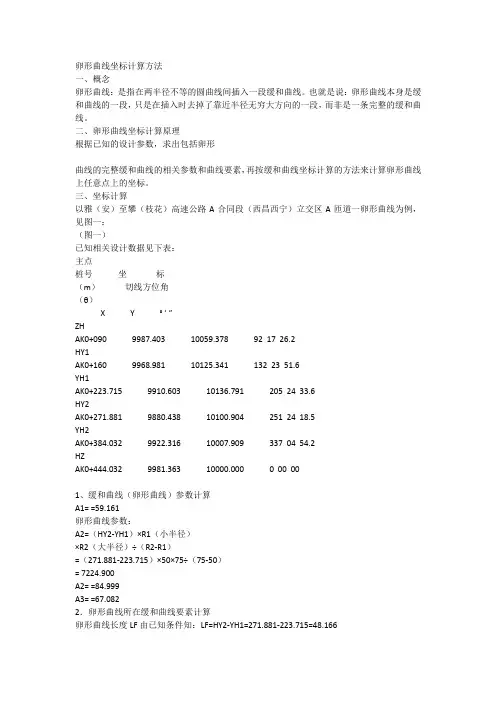
三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：主点桩号坐标（m）切线方位角（θ）X Y ° ’ ”ZHAK0+090 9987.403 10059.378 92 17 26.2HY1AK0+160 9968.981 10125.341 132 23 51.6YH1AK0+223.715 9910.603 10136.791 205 24 33.6HY2AK0+271.881 9880.438 10100.904 251 24 18.5YH2AK0+384.032 9922.316 10007.909 337 04 54.2HZAK0+444.032 9981.363 10000.000 0 00 001、缓和曲线（卵形曲线）参数计算A1= =59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2= =84.999A3= =67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ'点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ'的弧长）=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ'-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ'点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH'或HZ'的弧长HZ'：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ'-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

卡西尼卵形线二级结论卡西尼卵形线是一种在数学和物理领域中非常重要的曲线，它由法国天文学家吉安·达米安·德·卡西尼于1673年首次发现。

这条曲线是由两个焦点之间的点所绘制的曲线，其中两个焦点之间的距离等于该曲线的长轴长度。

卡西尼卵形线在天文学、物理学、工程学和计算机图形学中都有广泛应用。

一、卡西尼卵形线的定义和性质1. 定义：卡西尼卵形线是由两个焦点A和B之间距离为2a的所有点P构成的曲线，其中a是长轴长度。

2. 性质：（1）对于任意一条经过A、B两点的直线l，其与曲线交点P满足PA×PB=2a²。

（2）当l通过A、B两点时，交点P位于中垂线上；当l与长轴平行时，交点P位于短轴上。

（3）该曲线对称于长轴和短轴，并且具有四分之一旋转对称性。

（4）当a=b时，该曲线变成一个圆。

二、卡西尼卵形线的历史和应用1. 历史：卡西尼卵形线是由法国天文学家吉安·达米安·德·卡西尼于1673年首次发现的。

他使用望远镜观察土星的环，发现环上的某些部分呈现出奇特的形状，后来经过计算，他发现这些形状正是由卡西尼卵形线所描述的。

2. 应用：（1）天文学：在天文学中，卡西尼卵形线被用来描述行星和恒星之间的引力场。

（2）物理学：在物理学中，卡西尼卵形线被用来描述电子云和原子核之间的相互作用力。

（3）工程学：在工程学中，卡西尼卵形线被用来设计一些特殊的机械结构。

（4）计算机图形学：在计算机图形学中，卡西尼卵形线被用来绘制一些复杂的图案和曲线。

三、卡西尼卵形线与其他曲线的关系1. 椭圆和双曲线：当焦点A、B重合时，该曲线变成一个椭圆；当焦点A、B无限远时，该曲线变成一个双曲线。

2. 柯西曲线和阿斯滕曲线：柯西曲线是由两个复数之间距离为常数的所有点构成的曲线，与卡西尼卵形线密切相关；阿斯滕曲线则是由两个点P、Q之间距离差为常数的所有点构成的曲线，也与卡西尼卵形线密切相关。

50卵形曲线辅助点计算（即完整缓和曲线起点的支距）解算步骤卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线，计算前只需要把不完整的缓和曲线（也就是卵型曲线）补充完整即可。

在计算小半径的缓和曲线或卵形曲线坐标时,由于切线支距公式取项少而造成计算精度低,现有书中一般介绍也就只有2~4项,为提高计算精度就需要将支距公式多展开几项。

以下计算卵型曲线的完整缓和曲线长支距模型：重在学习掌握解算流程，现在空间里有更好的计算程序。

曲线参数A2=LS×R1×R2÷(R2-R1)=卵形曲线长×小半径×大半径÷（大半径-小半径）在同一段回旋线内,它的参数永远是不变的。

LS=卵型曲线长. （已知）完整缓和曲线长L= A2÷R1=曲线参数÷小半径当L=LS时：代入完整缓和曲线切线支距公式：(式中R均为小半径R1)E=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10]F=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] -L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] -L23÷[1.8802409472×1012（RLS）11]完整缓和曲线切线角（即两切线交角）p2=90L2÷(A2)L所对应玄长C=√（E2+F2）大半径处偏角P1=tan- 1(F2÷E2)小半径处偏角P3=180- P1-(180- p2)O=小半径处切线方位角（已知）小半径处至完整缓和曲线起点方位角Q=O±P3 (右向取+号；左向取-号)完整缓和曲线（起点）坐标：X=A+CcosQY=B=CsihQ完整缓和曲线（起点）处切线方位角：O=Q+180±p2 (右向取+号；左向取-号)以起点为基点用回旋线编程计算卵型曲线上任意桩号的中边桩点位坐标。

卵形线方程
摘要：
1.卵形线方程的定义
2.卵形线的性质
3.卵形线在数学和物理学中的应用
4.卵形线的发展历程
5.我国在卵形线研究方面的贡献
正文：
卵形线方程是描述一种特殊曲线的数学方程，该曲线形状类似于鸟卵，因此得名卵形线。

在数学和物理学中，卵形线具有很多独特的性质和应用，如在波动理论、统计物理和天体物理学等领域都有重要的应用。

卵形线是三阶代数曲线，其方程一般可以写成：x^3 + y^3 + 3axy = 0。

通过改变参数a、x 和y 的值，可以得到不同形状的卵形线。

卵形线具有如下一些性质：首先，卵形线具有三个分支，每个分支都呈卵形；其次，卵形线的分支在x 轴和y 轴上都有渐近线；最后，卵形线具有一个对称中心，即原点。

卵形线的研究历程可以追溯到19 世纪。

当时，德国数学家卡尔·魏尔斯特拉斯（Carl Weierstrass）首次提出了卵形线的概念，并研究了其一些基本性质。

自那时以来，许多数学家和物理学家都对卵形线进行了深入研究，发现了它在波动理论、统计物理和天体物理学等领域的重要应用。

我国在卵形线研究方面也取得了一定的成果。

近年来，我国数学家和物理
学家在卵形线的理论研究和应用方面做出了很多贡献。

例如，我国学者在卵形线的稳定性、振动特性和拓扑结构等方面取得了一系列重要成果，为卵形线的研究发展做出了贡献。

总之，卵形线是一种具有独特性质和应用的曲线，其研究在数学和物理学等领域具有重要意义。

从魏尔斯特拉斯提出卵形线的概念，到现代学者在卵形线研究方面取得的一系列成果，卵形线的研究历程充满了挑战和发现。

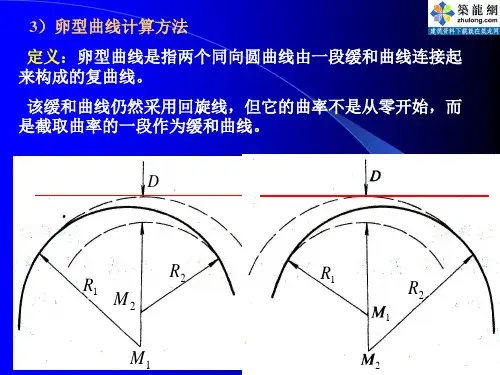
带卵形曲线的组合曲线的坐标计算作者：柴进全来源：《城市建设理论研究》2013年第34期摘要:以攀枝花至田房高速公路E8合同段线路组合曲线为例，介绍带卵形曲线的组合曲线坐标计算的公式和方法）关键词:卵形曲线;组合曲线;坐标计算中图分类号：U213.2+3文献标识码： A1、前言随着我国公路主骨架的初步形成，今后几年乃至十几年，我国公路建设的重点将转移到市县一级的交通网络上，地形复杂、展线较困难的山区将是公路建设的主战场，在线路的平面设计上，将越来越多的采用卵形曲线设计；同时高速公路的连接线和匝道的线路平面设计也经常采用卵形曲线过渡，而带卵形曲线的组合曲线的坐标计算是现阶段工程技术人员面临的一个难题。

2、工程概述攀枝花至田房高速公路是交通部规划建设的八条西部大通道之一—兰州～成都～昆明～磨憨公路四川境内的末端，在E8合同段与E9合同段的交接地段，由于地形限制和展线的需要，在K209+129.417～K210+875.768段为一两同向圆曲线以一回旋曲线相连的卵形曲线，曲线要素及主点里程坐标见图1：图1 组合曲线资料3、组合曲线结构分析卵形曲线是指在两半径不等的同向圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大或无穷小方向的一段，而非是一条完整的缓和曲线。

本例中的K209+800.477～K209+957.884段，就是经复原后的曲线组合图2中的缓和曲线ZH‘～HY中的一段。

图2 还原的曲线图所以该组合曲线的结构为：缓和曲线+圆曲线+卵形曲线+圆曲线+缓和曲线的组合。

4、缓和曲线及圆曲线任意点的坐标计算根据对组合曲线的结构分析可知，卵形曲线两端的圆曲线、缓和曲线，实际就是两个标准的缓和曲线+圆曲线的曲线组合一端去掉一个缓和曲线，所以计算这两个组合曲线上的任意点坐标的思路就是：将组合曲线拆分为两个已知圆曲线和缓和曲线长度的标准组合曲线，如图3、图4，分别计算其坐标。

一．概述近年来随着我国公路建设的发展，全封闭、全立交的高等级公路已经成为我国公路网中的重要组成部分，组成立交的基本单元是匝道，匝道的平面线形组合相对比较复杂，计算烦琐，特别是卵形曲线的计算更加抽象难懂。

卵形曲线的计算方法主要有曲直法、解析法、拟合法、积木法、综合法、弦切法等。

由于其他方法理论抽象、计算烦琐。

因此一般工程放样中主要以弦切法为主。

本文重点介绍弦切法在立交匝道卵形曲线敷设计算中的应用。

二、弦切法的基本原理及计算思路对于路线平面线形而言，无论是绵延不断的公路，还是局部线形组合复杂的立交匝道，其基本构成单元不外是圆曲线、缓和曲线、直线。

一段圆曲线的终点，可以认为是其弦长（弧长所对应的）在相应方向上的延伸所构成的；一段缓和曲线的终点，也可以认为是由一方向和距离所构成的。

因此，在一段路线的起终点坐标和切线方位角固定的情况下，便能容易的求出坐标增量，方位增量的计算式，进而求得各曲线参数。

对于任何一种线形单元，只要知道起点坐标（X0，Y0）和切线方位角ɑ（可以假设为任意值），即可根据弦长S和相关参数确定其线形。

以下图2-1所示卵形曲线为例，若给定R1、R2和回旋曲线参数A，即、终可求得该缓和曲线长、交点坐标（XM，YM）、切线长T1、T2、偏角ɑJ点坐标（XZ，YZ）和终点切线方位角。

这样求得的终点坐标，曲率半径和切线方位角又可以作为下一线形单元起点的相应资料。

交点J的坐标：Xm=T1×COS（ɑ）+X0Ym=T1×SIN（ɑ）+Y0终点坐标：Xz=Xm+T2×COS（a+aj)Yz=Ym+T2×SIN(a+aj)根据卵形曲线的特点，可以计算出如下参数：L1=A2/R1，L2= A2/R2，L=L2-L1（R1>R2),或L=L1-L2 （R1<R2)根据回旋曲线上任意点的相对坐标计算公式：X=L S-L S5/40/A4+L S9/3456/A8，Y=L S3/6/A2-L S7/336/A6+L S11/42240/A10即可计算出卵形曲线起终点在相对坐标系中的坐标(X1,Y1) 和（X2，Y2）。

一、概念卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：1、缓和曲线（卵形曲线）参数计算A1==59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2==84.999A3==67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度L F由已知条件知：L F=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度L S，由此找出HZ'点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）L M=L S（YH1至HZ'的弧长）=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+L M=223.715+144.498=368.213L E=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或L E= L M-L F=144.498-48.166=96.332卵形曲线长度L F=L M-L E=144.498-96.332=48.166（校核）HY2=HZ'-L E=368.213-96.332=271.881（校核）由上说明计算正确3．HZ'点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RL S）2]+L9÷[3456（RL S）4]–L13÷[599040（RL S）6]+L17÷[175472640（RL S）8]- L21÷[7.80337152×1010（RL S）10] （公式1）Y=L3÷[6（RL S）] - L7÷[336（RL S）3]+L11÷[42240（RL S）5] - L15÷[9676800（RL S）7]+L19÷[3530096640（RL S）9] - L23÷[1.8802409472×1012（RL S）11] （公式2）公式中L为计算点至ZH'或HZ'的弧长HZ'：AK0+368.213的坐标从YH1：AK0+223.715推算，L=L S=HZ'-YH1=368.213-223.715=144.498将L=L S代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

卡西尼卵形线的证明卡西尼卵形线，也称为卡西尼椭圆，是由法国天文学家吉安·多梅尼科·卡西尼在17世纪提出的一种椭圆曲线。

卡西尼卵形线的定义是一个动点沿着一对焦点之间距离之积保持不变的轨迹。

下面是对卡西尼卵形线的证明：假设卡西尼卵形线的焦点为F1和F2，距离为2a，点P为动点，距离F1和F2的距离分别为d1和d2，且d1 * d2 = a²。

我们可以使用坐标来证明卡西尼卵形线。

假设焦点为F1(-c, 0)和F2(c, 0)，其中c为焦距的一半。

点P的坐标为(x, y)。

首先，根据焦半径定义，我们可以得到：PF1² = (x + c)² + y² (1)PF2² = (x - c)² + y² (2)根据卡西尼椭圆的定义，有：PF1 * PF2 = a²将PF1和PF2的平方代入上式，我们得到：[(x + c)² + y²] * [(x - c)² + y²] = a²展开后化简，我们可以得到：(x² + y² + c²) * (x² + y² - c²) = a²再次进行展开化简，可以得到：x^4 + y^4 + (2c² - 2x² - 2y²)x² = 0这是一个四次方程，可以通过进一步的代数运算化简为标准的椭圆方程形式。

因此，我们证明了卡西尼卵形线满足上述方程，即为一椭圆曲线。

请注意，以上是一种简要的证明，可能并不涵盖所有细节。

在更详细的证明中，可能会见到更多的代数推导和几何推理。

高速公路及其匝道的特殊线形“卵型曲线”的中边桩坐标计算方法摘要：在高速公路工程施工测量过程中，会经常遇到复合型的回旋曲线，这些复合型的回旋曲线，有些是标准对称的平曲线，而有些是不标准不对称的平曲线（多出现在高速公路匝道线路中）。

对于不标准不对称的平曲线，线路中边桩坐标计算是测量工程师很头疼的问题。

本文将深入分析在高速公路匝道中经常出现的一种特殊复杂线形“卵形曲线”，并成功解决这种特殊线路的中、边桩坐标标准化计算问题。

关键词：高速公路及匝道；卵型曲线；中、边桩坐标；标准化计算程序改革开放三十多年以来，我国高速公路建设从无到有，从少到多，经过无数工程技术人员和工人的辛勤劳动和付出，现在，我国高速公路纵横交错，已遍布全国各大城市与乡村，目前高速公路总里程已突破13万公里。

高速公路的迅速发展，促进了中国经济的腾飞。

本人从1991年就参与到了高速公路建设大军中，直到现在，亲身见证了我国高速公路建设成果和经济发展成就。

高速公路建设从设计到施工均离不开测量工作，测量工作是公路工程建设的排头兵，先行者。

工程测量工作自始至终贯穿于公路工程施工的全过程，每一段路基的填筑、路面的铺设，每一座涵洞、桥梁、隧道的施工均需要测量工作者精确计算出中、边桩坐标，然后运用测量仪器进行施工放样。

所以线路的中、边桩坐标计算是测量工作的重中之重，只有准确计算出中桩坐标，才能进行准确的工程放样。

只有工程及构造物位置准确，才能确保工程的质量与进度。

下面就以本人在湖南省G5513长沙至益阳段高速公路扩容工程第一标段观音岩互通作为工程案例来解析平曲线，卵型曲线的组成及概念，以及特殊线路的中、边桩坐标计算方法。

1 平曲线的概念1.1 标准平曲线的组成平曲线一般由直线、缓和曲线和圆曲线三部分组成，现以长益高速复线观音岩互通C匝道为例，如下图一所示。

通过上图一可以分析得出：从CK0+856.4831至CK1+318.2096线路为标准的平曲线型，标准的平曲线型必须同时满足下列三个条件：第一：LS1段缓和曲线在ZH点必须与T1切线相切。

目录一、定义 (1)二、卵形曲线的应用 (1)三、计算卵形曲线上点坐标的方法 (1)1、一般坐标计算 (1)辛甫生公式 (2)四、案例计算 (3)1、使用一半坐标计算方法 (3)2、使用辛甫生公式计算 (4)卵形曲线一、定义卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线的应用西直门立交桥是北京市二环路西北的一座立交桥，位于北京市老城墙西北角，原北京内城西直门原址上。

从1994年开始，北京市政工程设计研究院用了整整4年的时间，做出了新立交桥的设计。

1999年，投资2个亿的崭新的西直门立交桥拔地而起……仅仅过了两年，这里成了北京最堵车的地方之一。

三、计算卵形曲线上点坐标的方法1、一般坐标计算首先补全缓和曲线。

在缓和曲线中R1L1= R2(L1+L2) ,使用此公式求的所补缓和曲线的长度。

利用缓和曲线的切线角公式求得YH点切线与x轴夹角β，而δ=1β/3。

α1为YH 点的切线方位角，则ox 的方位角α＝α1- β。

o-YH 的坐标方位角α =α+δ+180°。

使用缓和曲线的参数方程求得YH 点在自定义坐标系下的坐标，进一步求得o-YH 的距离，o 点的坐标可由几何关系求得为（ x 0 ，y 0 ）。

缓和段上任一点可利用缓和曲线参数方程计算出在自定义坐标系下的坐标，再利用坐标转换求得各点在施工坐标系下的坐标。

缓和曲线参数方程：坐标转换公式：辛甫生公式[]i A Ai A i n DK DK x x αααααcos cos cos 4cos 2cos 6434121+⎪⎪⎭⎫+ ⎝⎛++-+=[]i A Ai A i n DK DK y y αααααsin sin sin 4sin 2sin 6434121+⎪⎪⎭⎫+ ⎝⎛++-+=ZHZHy y x Y x y x X +∆+∆-=+∆+∆=ααααcos sin sin cos 旧旧新旧旧新四、案例计算1、使用一半坐标计算方法AB 段以A （ZH ）点为原点切线方向为X 轴，垂直于切线方向为Y 轴，使用缓和曲线参BC 段与AB 段在同一个自定义坐标系中，使用公式CD 段缓和曲线是不全的缓和曲线，需要将其补全后再使用缓和曲线参数方程计算。