卵形曲线参数计算

卵形曲线缓和曲线参数
卵形曲线的缓和曲线参数包括Ls1、Ly和Ls2。

其中，Ls1和Ls2是缓和曲线的长度，Ly是圆曲线的长度。

这些参数可以根据实际需求进行计算和调整，以适应不同的道路设计和行驶需求。

在计算这些参数时，需要考虑道路的曲线半径、设计速度、车辆的行驶特性等因素。

例如，根据缓和曲线的设置要求，Ls1和Ls2应满足一定的长度范围，以保证车辆在缓和曲线上的行驶平稳性和安全性。

同时，Ly的长度也需要根据圆曲线的半径和设计速度进行计算，以确保车辆在圆曲线上的行驶稳定性。

在实际应用中，可以使用专业的道路设计软件来计算这些参数，并根据计算结果进行道路设计和施工。

同时，还需要考虑道路的实际情况和交通流量等因素，对参数进行适当的调整和优化，以保证道路的安全、舒适和可靠性。

1。

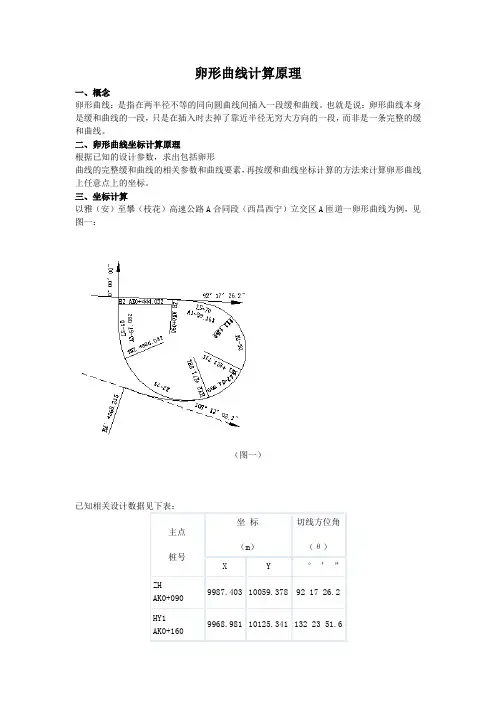
卵形曲线计算原理一、概念卵形曲线：是指在两半径不等的同向圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：1、缓和曲线（卵形曲线）参数计算A1==59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2==84.999A3==67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ'点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ'的弧长）=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ'-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ'点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH'或HZ'的弧长HZ'：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ'-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

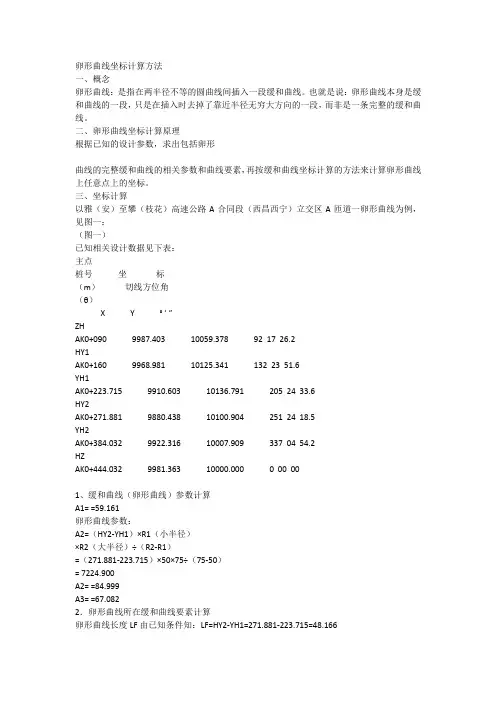
卵形曲线坐标计算方法一、概念卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：主点桩号坐标（m）切线方位角（θ）X Y ° ’ ”ZHAK0+090 9987.403 10059.378 92 17 26.2HY1AK0+160 9968.981 10125.341 132 23 51.6YH1AK0+223.715 9910.603 10136.791 205 24 33.6HY2AK0+271.881 9880.438 10100.904 251 24 18.5YH2AK0+384.032 9922.316 10007.909 337 04 54.2HZAK0+444.032 9981.363 10000.000 0 00 001、缓和曲线（卵形曲线）参数计算A1= =59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2= =84.999A3= =67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度LF由已知条件知：LF=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度LS，由此找出HZ'点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）LM=LS（YH1至HZ'的弧长）=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+LM=223.715+144.498=368.213LE=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或LE= LM-LF=144.498-48.166=96.332卵形曲线长度LF=LM-LE=144.498-96.332=48.166（校核）HY2=HZ'-LE=368.213-96.332=271.881（校核）由上说明计算正确3．HZ'点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10] （公式1）Y=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] - L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] - L23÷[1.8802409472×1012（RLS）11] （公式2）公式中L为计算点至ZH'或HZ'的弧长HZ'：AK0+368.213的坐标从YH1：AK0+223.715推算，L=LS=HZ'-YH1=368.213-223.715=144.498将L=LS 代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

浅谈道路线形设计中卵型平曲线的计算方法摘要:在当今社会发展中,人们对交通运输的要求越来越高,且道路建设水平在国民经济建设中占有重要地位,因此合理的线形设计至关重要。

卵型曲线作为道路线形设计中的一种,其设计复杂,计算繁琐,参数较多,在实际工作中对其进行研究。

关键词:公路工程线形设计卵型平曲线道路线形设计在道路整体设计中占有重要地位,设计合理的线形可以提高道路行车安全保障,同时对道路连续性和美观都起到重要作用。

道路线形设计中一般包括6种线形,即:基本型、S型、卵型、凸型、复合型和C型。

其中,基本型是现代道路线形设计中最基本、最常用、计算最简单的线形之一,但在设计中往往由于地形或其它因素的影响不能采用基本型设计,而采用其他5种线形中的一种,其中卵型是计算最为复杂的线形。

卵型平曲线是指用一个回旋线连接两个同向圆曲线的组合形式。

卵型组合的前提条件:(1)大圆必须把小圆完全包含在内,但不是同心圆。

(2)延长两相邻圆曲线的圆弧不能相互交叉。

(3)连接的回旋线不是由回旋线的原点开始,而是曲率为的部分。

下面我将结合自己的实践经验对道路线形设计中的卵型平曲线进行案例分析。

本案例中,和构成卵形平曲线,并且两交点的坐标分别为(76816.62,45314.107),(76615.557,45541.151),两交点的偏角分别为30°30’07″和23°21’06″,初拟的半径R1=400,缓和曲线。

本案例采用切线长度控制曲线半径法(直线型定线)进行计算,按两同向曲线(未设缓和曲线时)在公切点处直接相接在的思想进行设计(公切线即为两交点的连线)两曲线应满足:参考文献[1] 赵永平,唐勇.道路勘测设计[M].北京:高等教育出版社,2004(8).[2] 中华人民共和国行业标准.公路路线设计规范JTGD20-2006[S].北京:人民交通出版社,2006(10).[3] 许娅娅.测量学[M].北京:人民交通出版社,2004(5).。

50卵形曲线辅助点计算（即完整缓和曲线起点的支距）解算步骤卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线，计算前只需要把不完整的缓和曲线（也就是卵型曲线）补充完整即可。

在计算小半径的缓和曲线或卵形曲线坐标时,由于切线支距公式取项少而造成计算精度低,现有书中一般介绍也就只有2~4项,为提高计算精度就需要将支距公式多展开几项。

以下计算卵型曲线的完整缓和曲线长支距模型：重在学习掌握解算流程，现在空间里有更好的计算程序。

曲线参数A2=LS×R1×R2÷(R2-R1)=卵形曲线长×小半径×大半径÷（大半径-小半径）在同一段回旋线内,它的参数永远是不变的。

LS=卵型曲线长. （已知）完整缓和曲线长L= A2÷R1=曲线参数÷小半径当L=LS时：代入完整缓和曲线切线支距公式：(式中R均为小半径R1)E=L-L5÷[40（RLS）2]+L9÷[3456（RLS）4]–L13÷[599040（RLS）6]+L17÷[175472640（RLS）8]- L21÷[7.80337152×1010（RLS）10]F=L3÷[6（RLS）] - L7÷[336（RLS）3]+L11÷[42240（RLS）5] -L15÷[9676800（RLS）7]+L19÷[3530096640（RLS）9] -L23÷[1.8802409472×1012（RLS）11]完整缓和曲线切线角（即两切线交角）p2=90L2÷(A2)L所对应玄长C=√（E2+F2）大半径处偏角P1=tan- 1(F2÷E2)小半径处偏角P3=180- P1-(180- p2)O=小半径处切线方位角（已知）小半径处至完整缓和曲线起点方位角Q=O±P3 (右向取+号；左向取-号)完整缓和曲线（起点）坐标：X=A+CcosQY=B=CsihQ完整缓和曲线（起点）处切线方位角：O=Q+180±p2 (右向取+号；左向取-号)以起点为基点用回旋线编程计算卵型曲线上任意桩号的中边桩点位坐标。

标准卵圆方程
标准卵圆方程，又称轨道方程，是物理和数学领域中重要的问题。

标准卵圆方程用来描述一个物体在两个定点之间的轨迹以及由此产生
的几何形状。

根据参数，标准卵圆方程可以表示为:
x=acos θ
y=bsinθ
在标准卵圆方程中，θ 是一个变量，a 和 b 是卵圆的两个长轴。

如果 a=b，标准卵圆方程将描绘出一个完美的圆形。

如果a≠b，则会
描绘出一个椭圆形。

标准卵圆方程具有广泛的应用，从提供任意小臂间距弧线理解，
例如拱形桥梁，到附在圆机床上的铣削头，到在空气动力学，自动控
制和机器人动力学，以及航空运动等领域，它都扮演着重要的角色。

最为广泛的应用包括天文学和航空运动，特别是运载火箭和人造卫星，这些传感器影响着大气湍流，地球的引力场，太阳的磁场等等。

总之，标准卵圆方程是一个重要的数学模型，提供了许多其他应
用的理论基础，也提供了多种解决性能机构动力学问题的方法。

它对
科学非常重要，学习它也极其重要，因此，我们应当抓住机会，深入
研究，以便实现这些科学模型带来的收益。

带卵形曲线的组合曲线的坐标计算作者：柴进全来源：《城市建设理论研究》2013年第34期摘要:以攀枝花至田房高速公路E8合同段线路组合曲线为例，介绍带卵形曲线的组合曲线坐标计算的公式和方法）关键词:卵形曲线;组合曲线;坐标计算中图分类号：U213.2+3文献标识码： A1、前言随着我国公路主骨架的初步形成，今后几年乃至十几年，我国公路建设的重点将转移到市县一级的交通网络上，地形复杂、展线较困难的山区将是公路建设的主战场，在线路的平面设计上，将越来越多的采用卵形曲线设计；同时高速公路的连接线和匝道的线路平面设计也经常采用卵形曲线过渡，而带卵形曲线的组合曲线的坐标计算是现阶段工程技术人员面临的一个难题。

2、工程概述攀枝花至田房高速公路是交通部规划建设的八条西部大通道之一—兰州～成都～昆明～磨憨公路四川境内的末端，在E8合同段与E9合同段的交接地段，由于地形限制和展线的需要，在K209+129.417～K210+875.768段为一两同向圆曲线以一回旋曲线相连的卵形曲线，曲线要素及主点里程坐标见图1：图1 组合曲线资料3、组合曲线结构分析卵形曲线是指在两半径不等的同向圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大或无穷小方向的一段，而非是一条完整的缓和曲线。

本例中的K209+800.477～K209+957.884段，就是经复原后的曲线组合图2中的缓和曲线ZH‘～HY中的一段。

图2 还原的曲线图所以该组合曲线的结构为：缓和曲线+圆曲线+卵形曲线+圆曲线+缓和曲线的组合。

4、缓和曲线及圆曲线任意点的坐标计算根据对组合曲线的结构分析可知，卵形曲线两端的圆曲线、缓和曲线，实际就是两个标准的缓和曲线+圆曲线的曲线组合一端去掉一个缓和曲线，所以计算这两个组合曲线上的任意点坐标的思路就是：将组合曲线拆分为两个已知圆曲线和缓和曲线长度的标准组合曲线，如图3、图4，分别计算其坐标。

一．概述近年来随着我国公路建设的发展，全封闭、全立交的高等级公路已经成为我国公路网中的重要组成部分，组成立交的基本单元是匝道，匝道的平面线形组合相对比较复杂，计算烦琐，特别是卵形曲线的计算更加抽象难懂。

卵形曲线的计算方法主要有曲直法、解析法、拟合法、积木法、综合法、弦切法等。

由于其他方法理论抽象、计算烦琐。

因此一般工程放样中主要以弦切法为主。

本文重点介绍弦切法在立交匝道卵形曲线敷设计算中的应用。

二、弦切法的基本原理及计算思路对于路线平面线形而言，无论是绵延不断的公路，还是局部线形组合复杂的立交匝道，其基本构成单元不外是圆曲线、缓和曲线、直线。

一段圆曲线的终点，可以认为是其弦长（弧长所对应的）在相应方向上的延伸所构成的；一段缓和曲线的终点，也可以认为是由一方向和距离所构成的。

因此，在一段路线的起终点坐标和切线方位角固定的情况下，便能容易的求出坐标增量，方位增量的计算式，进而求得各曲线参数。

对于任何一种线形单元，只要知道起点坐标（X0，Y0）和切线方位角ɑ（可以假设为任意值），即可根据弦长S和相关参数确定其线形。

以下图2-1所示卵形曲线为例，若给定R1、R2和回旋曲线参数A，即、终可求得该缓和曲线长、交点坐标（XM，YM）、切线长T1、T2、偏角ɑJ点坐标（XZ，YZ）和终点切线方位角。

这样求得的终点坐标，曲率半径和切线方位角又可以作为下一线形单元起点的相应资料。

交点J的坐标：Xm=T1×COS（ɑ）+X0Ym=T1×SIN（ɑ）+Y0终点坐标：Xz=Xm+T2×COS（a+aj)Yz=Ym+T2×SIN(a+aj)根据卵形曲线的特点，可以计算出如下参数：L1=A2/R1，L2= A2/R2，L=L2-L1（R1>R2),或L=L1-L2 （R1<R2)根据回旋曲线上任意点的相对坐标计算公式：X=L S-L S5/40/A4+L S9/3456/A8，Y=L S3/6/A2-L S7/336/A6+L S11/42240/A10即可计算出卵形曲线起终点在相对坐标系中的坐标(X1,Y1) 和（X2，Y2）。

一、概念卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线坐标计算原理根据已知的设计参数，求出包括卵形曲线的完整缓和曲线的相关参数和曲线要素，再按缓和曲线坐标计算的方法来计算卵形曲线上任意点上的坐标。

三、坐标计算以雅（安）至攀（枝花）高速公路A合同段（西昌西宁）立交区A匝道一卵形曲线为例，见图一：（图一）已知相关设计数据见下表：1、缓和曲线（卵形曲线）参数计算A1==59.161卵形曲线参数：A2=（HY2-YH1）×R1（小半径）×R2（大半径）÷（R2-R1）=（271.881-223.715）×50×75÷（75-50）= 7224.900A2==84.999A3==67.0822．卵形曲线所在缓和曲线要素计算卵形曲线长度L F由已知条件知：L F=HY2-YH1=271.881-223.715=48.166卵形曲线作为缓和曲线的一段，因此先求出整条缓和曲线的长度L S，由此找出HZ'点的桩号及坐标（实际上不存在，只是作为卵形曲线辅助计算用）L M=L S（YH1至HZ'的弧长）=A2÷R1=7224.900÷50=144.498∴HZ'桩号=YH1+L M=223.715+144.498=368.213L E=HY2至HZ'的弧长=A2÷R2=7224.900÷75=96.332或L E= L M-L F=144.498-48.166=96.332卵形曲线长度L F=L M-L E=144.498-96.332=48.166（校核）HY2=HZ'-L E=368.213-96.332=271.881（校核）由上说明计算正确3．HZ'点坐标计算（见图二）（图二）①用缓和曲线切线支距公式计算，缓和曲线切线支距公式通式：Xn=[(-1)n+1×L4n–3]÷[(2n-2)!×22n–2×(4n-3)×(RLs)2n–2]Yn=[(-1)n+1×L4n–1]÷[(2n-1)!×22n–1×(4n-1)×(RLs)2n–1]公式中符号含义：n —项数序号(1、2、3、……n)！—阶乘R —圆曲线半径Ls —缓和曲线长②现取公式前6项计算（有关书籍中一般为2-3项，不能满足小半径的缓和曲线计算精度要求，如本例中AK0+090~AK0+160段缓和曲线，如AK0+160中桩坐标带2项算误差达8cm），公式如下：X=L-L5÷[40（RL S）2]+L9÷[3456（RL S）4]–L13÷[599040（RL S）6]+L17÷[175472640（RL S）8]- L21÷[7.80337152×1010（RL S）10] （公式1）Y=L3÷[6（RL S）] - L7÷[336（RL S）3]+L11÷[42240（RL S）5] - L15÷[9676800（RL S）7]+L19÷[3530096640（RL S）9] - L23÷[1.8802409472×1012（RL S）11] （公式2）公式中L为计算点至ZH'或HZ'的弧长HZ'：AK0+368.213的坐标从YH1：AK0+223.715推算，L=L S=HZ'-YH1=368.213-223.715=144.498将L=L S代入公式（1）、（2）得：X=117.1072 Y=59.8839L对应弦长C=√（X2+Y2）=131.5301偏角a1=arctg（Y÷X）=27°05’00.2”* 偏角计算用反正切公式，不要用其它公式。

卡西尼卵形线二级结论卡西尼卵形线二级结论，指的是卡西尼卵形线上每一点处的切线与该点到两个焦点的连线垂直。

这个结论的发现和证明，对于理解卡西尼卵形线的性质和应用具有重要的意义。

我们可以通过几何推导来理解卡西尼卵形线二级结论。

假设卡西尼卵形线的方程为(x^2 + y^2)^2 = a^2(x^2 - y^2)，其中a为常数。

我们可以求得卡西尼卵形线上任一点处的切线方程为yy' = (x^2 - a^2)y - ax^2。

根据二级结论，切线与该点到两个焦点的连线垂直，即切线的斜率与该点到两个焦点连线的斜率的乘积为-1。

通过求解切线方程的斜率，我们可以得到该结论的表达式。

卡西尼卵形线二级结论也可以通过微积分的方法进行证明。

我们可以利用曲线的参数方程来推导卡西尼卵形线上任一点处的切线和该点到两个焦点连线的斜率之间的关系。

通过对参数方程进行求导，并考虑到卡西尼卵形线的特殊性质，我们可以得到该结论的证明。

卡西尼卵形线二级结论的应用非常广泛。

在物理学中，卡西尼卵形线的形状与天体的运动轨迹有关，通过研究卡西尼卵形线的性质，我们可以推导出天体的运动规律。

在工程学中，卡西尼卵形线的形状可以用于设计曲线形道路，提高交通的安全性和流畅性。

在数学的研究领域，卡西尼卵形线是一种非常有趣的曲线，通过研究其性质，可以拓展数学的深度和广度。

总结起来，卡西尼卵形线二级结论是对卡西尼卵形线性质的一个重要结论。

通过几何推导和微积分的方法，我们可以理解和证明该结论。

卡西尼卵形线二级结论的应用非常广泛，涉及到物理学、工程学和数学等领域。

研究和应用卡西尼卵形线二级结论，对于推动科学的发展和应用的创新具有重要的意义。

卡西尼卵形线的证明卡西尼卵形线，也称为卡西尼椭圆，是由法国天文学家吉安·多梅尼科·卡西尼在17世纪提出的一种椭圆曲线。

卡西尼卵形线的定义是一个动点沿着一对焦点之间距离之积保持不变的轨迹。

下面是对卡西尼卵形线的证明：假设卡西尼卵形线的焦点为F1和F2，距离为2a，点P为动点，距离F1和F2的距离分别为d1和d2，且d1 * d2 = a²。

我们可以使用坐标来证明卡西尼卵形线。

假设焦点为F1(-c, 0)和F2(c, 0)，其中c为焦距的一半。

点P的坐标为(x, y)。

首先，根据焦半径定义，我们可以得到：PF1² = (x + c)² + y² (1)PF2² = (x - c)² + y² (2)根据卡西尼椭圆的定义，有：PF1 * PF2 = a²将PF1和PF2的平方代入上式，我们得到：[(x + c)² + y²] * [(x - c)² + y²] = a²展开后化简，我们可以得到：(x² + y² + c²) * (x² + y² - c²) = a²再次进行展开化简，可以得到：x^4 + y^4 + (2c² - 2x² - 2y²)x² = 0这是一个四次方程，可以通过进一步的代数运算化简为标准的椭圆方程形式。

因此，我们证明了卡西尼卵形线满足上述方程，即为一椭圆曲线。

请注意，以上是一种简要的证明，可能并不涵盖所有细节。

在更详细的证明中，可能会见到更多的代数推导和几何推理。