卵曲线计算

鸡蛋曲线方程数学中充满了许多神奇的函数，而鸡蛋曲线就是其中一种令人着迷的函数。

由于它得名自它和一个蛋形非常相似的外形，因而得名为鸡蛋曲线。

函数的形式为 y^2 = x(x-1)(x-\lambda)，其中 lambda 为系数。

这个方程曲线的逆向运动是经典的连锁垂降问题，也就是将一条长度不变的链子从杆子上滑下的运动。

更具体地说，如果一条链子放在两个支架之间，那么当链子的长度为L时，连锁坠落的时间为 \sqrt{2L/g} ,g 为重力加速度。

鸡蛋曲线最初是在18世纪由瑞士数学家雅各布·伯努利所发现的。

他是一个有才华的数学家，而鸡蛋曲线也是他最为有名的数学成就之一。

伯努利将这个函数引入微积分，为许多其他数学家和物理学家提供了宝贵的工具。

鸡蛋曲线并没有一个标准的系数，而是可以根据需求进行调整。

这使得它成为了一种十分灵活的工具，能够应用于各种不同的情形中。

在许多领域中，鸡蛋曲线可以被用来模拟各种物理现象。

其中最为著名的应用是在天文学中，鸡蛋曲线被用来对黑洞的重力场进行描述。

当物质进入一个黑洞时，它将受到强烈的引力，因此一般的牛顿定律不再适用。

这时候，鸡蛋曲线便成为了描述黑洞重力场的完美工具。

除此之外，鸡蛋曲线还可以用来描述流体运动。

刚开始时，人们并不相信鸡蛋曲线能够用来描述流体运动，因为其形状非常奇怪。

但是，随着时间的推移，越来越多的科学家开始使用这个函数，以描述各种不同的液体动力学现象。

尽管鸡蛋曲线看起来非常的奇怪，但是它却在许多领域中发挥了十分重要的作用。

从物理学到数学，再到天文学和液体动力学，这个函数都有着丰富的应用。

通过深入研究鸡蛋曲线，我们可以更好地理解自然界中的许多现象，并且能够为人类提供更好的解决方案。

卵型曲线测量坐标的计算方法
王晓光;赵凯红
【期刊名称】《吉林建筑工程学院学报》
【年(卷),期】2001(000)004
【摘要】在高速公路的互通立交中,卵型曲线被广泛采用.本文对两圆曲线之间缓和曲线的各种情况作了全面的分析,把计算各种情况下两圆曲线之间缓和曲线的问题,转化为同一圆曲线上两相邻缓和曲线的计算,并推导出了相应的计算公式.在此基础上,给出了解算卵型曲线的完整计算方法.最终解决了卵型曲线逐桩坐标计算的问题.【总页数】6页(P47-52)
【作者】王晓光;赵凯红
【作者单位】吉林建筑工程学院交通工程系,长春,130021;吉林建设银行,长
春,130021
【正文语种】中文
【中图分类】U412.2
【相关文献】
1.公路卵型曲线坐标计算 [J], 王寿武;李厚贤
2.复曲线及卵型曲线计算方法 [J], 孙斌
3.长输管道伴行公路测量中卵型曲线的坐标求解 [J], 焦全德
4.运用坐标变换求解卵型曲线的坐标 [J], 伊文天
5.还原方法计算卵型曲线中间缓和曲线点坐标 [J], 张福荣;焦广彦
因版权原因，仅展示原文概要，查看原文内容请购买。

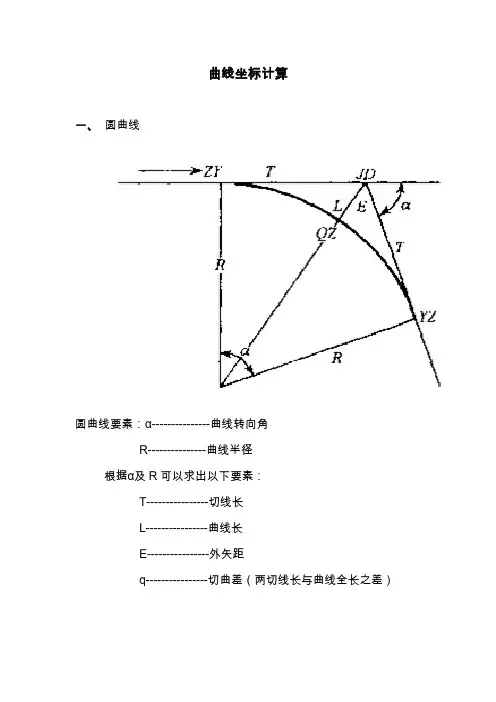
曲线坐标计算一、圆曲线圆曲线要素：α---------------曲线转向角R---------------曲线半径根据α及R可以求出以下要素：T----------------切线长L----------------曲线长E----------------外矢距q----------------切曲差（两切线长与曲线全长之差）各要素的计算公式为：2αtgR T ⋅=︒⋅=180παR L (弧长))12(sec -=αR E （sec α=cos α的倒数）圆曲线主点里程：ZY=JD －TQZ=ZY ＋L ／2 或 QZ=JD －q /2 YZ=QZ ＋L ／2 或 YZ=JD ＋T －qJD=QZ＋q／2（校核用）1、基本知识◆里程：由线路起点算起，沿线路中线到该中线桩的距离。

◆表示方法：DK26＋284.56。

“+”号前为公里数，即26km，“+”后为米数，即284.56m。

CK ——表示初测导线的里程。

DK ——表示定测中线的里程。

Ｋ——表示竣工后的连续里程。

铁路和公路计算方法略有不同。

2、曲线点坐标计算（偏角法或弦切角法）已知条件：起点、终点及各交点的坐标。

1）计算ZY、YZ点坐标通用公式：2）计算曲线点坐标①计算坐标方位角i 点为曲线上任意一点。

li 为i 点与ZY点里程之差。

弧长所对的圆心角弦切角弦的方位角当曲线左转时用“-”，右转时用“+”。

计算弦长②③计算曲线点坐标此时的已知数据为：ZY（x ZY，y ZY）、αZY- i、C。

根据坐标正算原理：切线支距法这种方法是以曲线起点ZY或终点YZ为坐标原点，以切线为X轴，以过原点的半径为Y轴，则圆曲线上任意一点的切线支距坐标可通过以下公式求得：πϕϕϕ︒⋅=-==180,)cos 1(sin R l R y R x 式中利用坐标平移和旋转，该点在大地平面直角坐标系中的坐标可由以下公式求得：式中：α为ZY(YZ)点沿线路前进方向的切线方位角。

高等级公路卵形曲线的计算方法周烨摘要在高等级公路施工过程中，常遇到卵形曲线，而设计单位的出发点不同，中线的解算方法也大相径庭。

本文着重从卵形中线几种计算方法入手，在此基础之上阐述了卵形曲线的测设。

关键词卵形曲线复曲线匝道桥高等级公路卵形曲线是高等级公路、立交桥匝道常见的曲线形式，它由基本的三部分构成：第一圆曲线段、缓和曲线段和第二圆曲线段。

中间段缓和曲线用来连接两个不同半径的圆曲线。

其中线坐标解算方法有如下几种：1 补全缓和曲线我国公路上采用的缓和曲线为辐射螺旋线，夹在两圆曲线中间的缓和曲线为整个缓和曲线的一部分，缓和曲线上任一点半径与该点至该缓和曲线起点的距离乘积为一定值：R×L＝A，假设R1＞R2，可由两圆半径及两圆间的缓和段长ls，求缓和曲线的总长L。

Δl＝L－ls(1)Δl就是夹在两圆曲线间缓和段省去的部分，由YH点补长Δl至o点，以o点为该缓和曲线起点，起点的切线方向为x轴，与之垂直的曲线内侧方向为y轴方向建立坐标系（图1）。

缓和曲线公式（推导过程略）如下：(2)(3)图 1利用x、y值可以求得o—YH弦与x轴的夹角：β＝3δ。

α1为YH点的切线方位角，则ox的方位：α＝α1±β。

o点的坐标可由几何关系求得为（x0，y）。

缓和段上任一点统一坐标可求得：(4)y=yo+xsinα±ycosα(5)2 曲率推算缓和曲线段曲率半径由第一段圆曲线半径R1变为第二段曲率半径R2（假设R1＞R2），则缓和曲线曲率半径变化为：(6)其中ls为中间段缓和曲线长，为求缓和曲线方程，现建立以缓和曲线起点为坐标原点，起点的切线方向为x轴，与之垂直的曲线内侧方向为y 轴的坐标系（图2），设P点为缓和曲线上任一点，距原点的曲线长为l，该点附近的微分弧长为dl，缓和曲线偏角为β，则有dx=dlcosβ(7)dy=dlsinβ(8)图 2由于将其代入上式并进行积分可得缓和曲线方程：(9)(10)中间缓和段统一坐标计算为：(11)xsinα±ycosα(12)Y＝yYHα为曲线YH点切线方位。

复曲线及卵型曲线计算方法
孙斌
【期刊名称】《山西建筑》
【年(卷),期】2007(033)032
【摘要】针对中线设计的重要性,介绍了中线设计的方法,详细讨论了复曲线和卵型曲线的几何要素和中桩坐标的计算方法,指出导线法适用于大比例地形图上定线、优化设计和立交线形设计中.
【总页数】2页(P279-280)
【作者】孙斌
【作者单位】北京交通大学土木建筑工程学院,北京,100044
【正文语种】中文
【中图分类】U412.3
【相关文献】
1.卵型曲线测量坐标的计算方法 [J], 王晓光;赵凯红
2.公路缓和复曲线(卵型曲线)特性的研究及其应用 [J], 卢印刚
3.浅谈道路线形设计中卵型平曲线的计算方法 [J], 张鹏
4.新型复曲线的曲线要素计算方法 [J], 赵平
5.用曲线测设广义公式进行卵型和凸型回旋曲线的计算 [J], 许勇;李世庭
因版权原因，仅展示原文概要，查看原文内容请购买。

浅谈道路线形设计中卵型平曲线的计算方法摘要:在当今社会发展中,人们对交通运输的要求越来越高,且道路建设水平在国民经济建设中占有重要地位,因此合理的线形设计至关重要。

卵型曲线作为道路线形设计中的一种,其设计复杂,计算繁琐,参数较多,在实际工作中对其进行研究。

关键词:公路工程线形设计卵型平曲线道路线形设计在道路整体设计中占有重要地位,设计合理的线形可以提高道路行车安全保障,同时对道路连续性和美观都起到重要作用。

道路线形设计中一般包括6种线形,即:基本型、S型、卵型、凸型、复合型和C型。

其中,基本型是现代道路线形设计中最基本、最常用、计算最简单的线形之一,但在设计中往往由于地形或其它因素的影响不能采用基本型设计,而采用其他5种线形中的一种,其中卵型是计算最为复杂的线形。

卵型平曲线是指用一个回旋线连接两个同向圆曲线的组合形式。

卵型组合的前提条件:(1)大圆必须把小圆完全包含在内,但不是同心圆。

(2)延长两相邻圆曲线的圆弧不能相互交叉。

(3)连接的回旋线不是由回旋线的原点开始,而是曲率为的部分。

下面我将结合自己的实践经验对道路线形设计中的卵型平曲线进行案例分析。

本案例中,和构成卵形平曲线,并且两交点的坐标分别为(76816.62,45314.107),(76615.557,45541.151),两交点的偏角分别为30°30’07″和23°21’06″,初拟的半径R1=400,缓和曲线。

本案例采用切线长度控制曲线半径法(直线型定线)进行计算,按两同向曲线(未设缓和曲线时)在公切点处直接相接在的思想进行设计(公切线即为两交点的连线)两曲线应满足:参考文献[1] 赵永平,唐勇.道路勘测设计[M].北京:高等教育出版社,2004(8).[2] 中华人民共和国行业标准.公路路线设计规范JTGD20-2006[S].北京:人民交通出版社,2006(10).[3] 许娅娅.测量学[M].北京:人民交通出版社,2004(5).。

道路卵型曲线中间缓和曲线段放样方法探讨卵型曲线是道路设计中经常采用的一种线型，是当不同半径的2圆曲线直接相连不被设计标准所允许，或受地形制约时，为使线形顺畅、美观而在2圆曲线之间加入一段缓和曲线的一种复曲线形式。

其组成为：（缓和曲线）+圆曲线+中间缓和曲线+圆曲线+（缓和曲线）。

卵型曲线的数学模型比较复杂，特别是中间缓和曲线段，在道路施工过程中不易现场测设操作。

本文将就卵型曲线中间缓和曲线段的测设总结一种简便的方法。

对于缓和曲线，通常把直线与半径R 2的圆曲线间的缓和曲线作为完整的缓和曲线形式，其曲率是从0（这时R =∞）渐变为ρ2（ρ2=1/R 2），而卵性曲线中间缓和曲线曲率则是从ρ1（第1圆曲线半径为R 1 ，ρ1=1/R 1），渐变为ρ2 （ρ2=1/R 2）。

两者属于同一数学模型的回旋曲线，可以看出，中间缓和曲线是完整缓和曲线的一部分。

1.卵型曲线中间缓和曲线段的还原要对中间缓和曲线进行解算，就先要对它进行还原。

中间缓和曲线的还原就是找出其完整形式（即曲率变化区间为[0，ρ2]的形式），确定出缓和曲线起点的位置A 假定ZH 及起点切线方位T 假定ZH （如图1所示）。

图中B HY 2为中间缓和曲线终点，C YH 1为中间缓和曲线起点，T 为C YH 1点的路线方向。

如果假定缓和曲线的曲率增大方向与线路前进方向一致，则缓和曲线起点就是A 假定ZH点。

缓和曲线起点应位于半径较大的圆曲线的方向。

A 假定ZH 点到C YH 1的距离为l 1=A 2/R 1，这里A 为缓和曲线常数，未给出时可按下式计算：A =s s R l =()2111/R R R R l s - ① 式中：l s 为中间缓和曲线的长度。

假定ZH 点的切线方位角T 假定ZH =T YH 1-α ② 式中：α=l 12/2R s (l 1+l s )×180/π 其中 R s = R 1R 2/(R 1+R 2)，T YH 1可以通过对第1圆曲线的解算求得, π为圆周率。

使用计算器计算卵型曲线
刘宝全
【期刊名称】《辽宁交通科技》
【年(卷),期】1995(018)003
【摘要】本文介绍了编制程序计算卵型线插入的回旋曲线“起点”桩号及卵型曲线标定要求和计算操作方法。

【总页数】7页(P4-10)
【作者】刘宝全
【作者单位】无
【正文语种】中文
【中图分类】U412.12
【相关文献】
1.复曲线及卵型曲线计算方法 [J], 孙斌
2.卵型曲线中间段缓和曲线段的补全计算实例 [J], 吴勋海
3.袖珍电子计算器的使用方法（六）：第三讲函数型计算器的使用方法（续三）[J], 王健南
4.袖珍电子计算器的使用方法（七）：第四讲函数型计算器实际应用举例 [J], 王健南
5.用曲线测设广义公式进行卵型和凸型回旋曲线的计算 [J], 许勇;李世庭
因版权原因，仅展示原文概要，查看原文内容请购买。

应用样条表达式计算卵型曲线和反曲线
李洁;郁舒兰
【期刊名称】《南京林业大学学报：自然科学版》
【年(卷),期】2001(25)4
【摘要】应用样条表达式进行卵型曲线和反曲线的设计和计算 ,不但统一了各线元的数学表达式 ,且由于在各表达式中引入了方位角 ,使计算方法简便 ;确定参数的同时进行参数合理性的检验 ,避免参数选择的错误 ,可大大提高程序运行的效率 ;利用积分计算缓和曲线 (螺旋线 )上各点的坐标 ,计算结果比近似计算精确。

此外 ,根据样条表达式衔接点处的位置关系 ,可核实同时位于不同线元上衔接点处参数计算的准确性。

【总页数】4页(P81-84)
【关键词】样条表达式;卵型曲线;反曲线;算法设计;公路;路线线形设计
【作者】李洁;郁舒兰
【作者单位】南京林业大学
【正文语种】中文
【中图分类】U412.34
【相关文献】
1.反算三次B样条曲线的等距曲线 [J], 杨红梅;张德强;关伟琪
2.公路缓和复曲线(卵型曲线)特性的研究及其应用 [J], 卢印刚
3.参数有理三次B样条曲线的一种反求顶点技术及在CAGD中的应用举例 [J], 王
相海;李会玲
4.用曲线测设广义公式进行卵型和凸型回旋曲线的计算 [J], 许勇;李世庭
5.电极挤压机型咀曲线初探——用三次样条数设计型咀曲线的设想 [J], 蒋文忠因版权原因，仅展示原文概要，查看原文内容请购买。

一、如何将外业期间已经通过老的定线方法确定的卵型等复杂曲线转换为纬地系统所采用的新的计算方法：1、此类问题出现的原因参见下图，图示为路线中出现的典型的卵型曲线，其中JD1 和JD2 为纬地系统中采用的新方法所对应的曲线交点（交点边和路线相切），而JD-1 和JD-2 为与之对应的老的定线方法所使用的交点（存在内移值的）。

另外，老的计算方法是一种近似的方法，其原理假设是将中间的缓和曲线一分为二，前后交点各含一半长度。

这种方法仅能适用于低等级公路且缓和曲线长度较小时的情况，根本不能满足高等级公路缓和曲线数百米长时的高精度要求。

2、转换方法a、参考外业采用老的方法所形成的直曲表，点击纬地系统菜单的“立交平面设计”命令，在确定起点位置和方向后，逐段输入卵型曲线范围的曲线单元，请注意输入时圆曲线、缓和曲线的长度应输为负值（代表弧长），注意曲线单元的转向和曲率半径；输入中可随时“计算显示”路线图形，以直观判断输入是否正确，桩号是否吻合。

b、在输入完成后，单击“存盘”按钮将数据存盘为*.pm文件；然后点击纬地系统菜单的“平面数据转换”→“曲线→交点（pm→jd）”命令，根据提示将*.pm文件转换为*.jd 文件，在此转换过程中系统已经自动反推得到新的交点坐标及曲线设置，保存在*jd 中。

c、打开“项目管理器”，在其中点击鼠标右键菜单的“添加文件”命令，选择将刚刚转换得到的*.jd 文件添加到项目中，保存项目后，点击纬地系统菜单的“路线平面设计”命令启动路线设计对话框，即可看到新的交点和曲线设置情况。

二、如何在纬地系统中设计卵型等复杂曲线a、先设定大圆曲线的半径、前或后缓和曲线长度；b、再设定小圆曲线的前后缓和曲线长度，注意卵型曲线时与大圆相接的缓和曲线的曲率半径变化应是从R1->R2；c、实时拖动小圆的半径变化，并监视两交点曲线间的直线段长度，使之趋近于零即可。

d、也可在小圆曲线的交点中选用“T1+Rc+S2”或“T1+S1+Rc”反算模式，直接完成曲线反算。

4800计算器（卵型曲线）程序一、文件名（LXQX）主程序Lb1 0:{DZG}:A“XA”:B“YA”:C“FW”:D“1/RA”:Z“1/RB”:F“DKA”:G“DKB”←Lb1 1:{H}:H“DKI”:H＞G⇒Goto 2△P=(Z-D)/Abs(G-F):K=Abs(H-F):S=P×K:Q=C+(S+2D)K×90/л:V=C+(S/4+2D)K×45/(2л):N=C+(3S/4+2D)K×135/(2л):J=C+(S/2+2D)K×45/л←X=A+K/12*(cosC+4(cosV+cosN)+2cosJ+cosQ)◣Y=B+K/12*(sinC+4(sinV+sinN)+2sinJ+sinQ)◣{T}:T“LR”:T=2⇒{LW}:L“LD=”:W“RA=”:X“XW”=X+Lcos(Q+W)◣Y“YW”=Y+Lsin(Q+W)◣△{P}:P“QH=”:P=3⇒{L}:L“LQ=”:X“XQ”=X+Lcos Q◣Y“YQ”=Y+LsinQ◣△M=X:U=Y:Prog“XY”:Goto 1←Lb1 2:H＞G+0.0001⇒Goto 1△A=X:B=Y:F=G:C=Q:Goto 0 二、坐标反算（XY）E“X0”:O“Y0”:M“XI”:U“YI”:po1(M-E,U-O):J<0⇒J=J+360△J◣I◣说明：1.该程序对任意曲线都实用。

2.对该程序要求输入数据的说明：输入： XA？YA？：要求输入曲线计算起点X，Y坐标；FW？：要求输入曲线计算起点的切线方位角（沿计算方向）；1/RA？：要求输入曲线起点半径的倒数(左偏为负，右偏为正)；1/RB？：要求输入曲线终点半径的倒数(左偏为负，右偏为正)；DKA？：要求输入曲线计算段起点里程（以米为单位，反算时为负值）；DKB？：要求输入曲线计算段终点里程（以米为单位，反算时为负值）；DKI？：要求输入曲线计算段内待求点里程（以米为单位，反算时为负值）；LR=？：是否测设左右点，输0为只计算线路中心，2为计算左右；LD？：左右距离（左为负，右为正）；RA? : 结构物与线路前进方向夹角（左为负，右为正）；QH=？：是否计算相对左右点的前后点坐标，输3时则计算；LQ？：相对左右点的前后距离（前为正，后为负。

高速公路及其匝道的特殊线形“卵型曲线”的中边桩坐标计算方法摘要：在高速公路工程施工测量过程中，会经常遇到复合型的回旋曲线，这些复合型的回旋曲线，有些是标准对称的平曲线，而有些是不标准不对称的平曲线（多出现在高速公路匝道线路中）。

对于不标准不对称的平曲线，线路中边桩坐标计算是测量工程师很头疼的问题。

本文将深入分析在高速公路匝道中经常出现的一种特殊复杂线形“卵形曲线”，并成功解决这种特殊线路的中、边桩坐标标准化计算问题。

关键词：高速公路及匝道；卵型曲线；中、边桩坐标；标准化计算程序改革开放三十多年以来，我国高速公路建设从无到有，从少到多，经过无数工程技术人员和工人的辛勤劳动和付出，现在，我国高速公路纵横交错，已遍布全国各大城市与乡村，目前高速公路总里程已突破13万公里。

高速公路的迅速发展，促进了中国经济的腾飞。

本人从1991年就参与到了高速公路建设大军中，直到现在，亲身见证了我国高速公路建设成果和经济发展成就。

高速公路建设从设计到施工均离不开测量工作，测量工作是公路工程建设的排头兵，先行者。

工程测量工作自始至终贯穿于公路工程施工的全过程，每一段路基的填筑、路面的铺设，每一座涵洞、桥梁、隧道的施工均需要测量工作者精确计算出中、边桩坐标，然后运用测量仪器进行施工放样。

所以线路的中、边桩坐标计算是测量工作的重中之重，只有准确计算出中桩坐标，才能进行准确的工程放样。

只有工程及构造物位置准确，才能确保工程的质量与进度。

下面就以本人在湖南省G5513长沙至益阳段高速公路扩容工程第一标段观音岩互通作为工程案例来解析平曲线，卵型曲线的组成及概念，以及特殊线路的中、边桩坐标计算方法。

1 平曲线的概念1.1 标准平曲线的组成平曲线一般由直线、缓和曲线和圆曲线三部分组成，现以长益高速复线观音岩互通C匝道为例，如下图一所示。

通过上图一可以分析得出：从CK0+856.4831至CK1+318.2096线路为标准的平曲线型，标准的平曲线型必须同时满足下列三个条件：第一：LS1段缓和曲线在ZH点必须与T1切线相切。

目录一、定义 (1)二、卵形曲线的应用 (1)三、计算卵形曲线上点坐标的方法 (1)1、一般坐标计算 (1)辛甫生公式 (2)四、案例计算 (3)1、使用一半坐标计算方法 (3)2、使用辛甫生公式计算 (4)卵形曲线一、定义卵形曲线：是指在两半径不等的圆曲线间插入一段缓和曲线。

也就是说：卵形曲线本身是缓和曲线的一段，只是在插入时去掉了靠近半径无穷大方向的一段，而非是一条完整的缓和曲线。

二、卵形曲线的应用西直门立交桥是北京市二环路西北的一座立交桥，位于北京市老城墙西北角，原北京内城西直门原址上。

从1994年开始，北京市政工程设计研究院用了整整4年的时间，做出了新立交桥的设计。

1999年，投资2个亿的崭新的西直门立交桥拔地而起……仅仅过了两年，这里成了北京最堵车的地方之一。

三、计算卵形曲线上点坐标的方法1、一般坐标计算首先补全缓和曲线。

在缓和曲线中R1L1= R2(L1+L2) ,使用此公式求的所补缓和曲线的长度。

利用缓和曲线的切线角公式求得YH点切线与x轴夹角β，而δ=1β/3。

α1为YH 点的切线方位角，则ox 的方位角α＝α1- β。

o-YH 的坐标方位角α =α+δ+180°。

使用缓和曲线的参数方程求得YH 点在自定义坐标系下的坐标，进一步求得o-YH 的距离，o 点的坐标可由几何关系求得为（ x 0 ，y 0 ）。

缓和段上任一点可利用缓和曲线参数方程计算出在自定义坐标系下的坐标，再利用坐标转换求得各点在施工坐标系下的坐标。

缓和曲线参数方程：坐标转换公式：辛甫生公式[]i A Ai A i n DK DK x x αααααcos cos cos 4cos 2cos 6434121+⎪⎪⎭⎫+ ⎝⎛++-+=[]i A Ai A i n DK DK y y αααααsin sin sin 4sin 2sin 6434121+⎪⎪⎭⎫+ ⎝⎛++-+=ZHZHy y x Y x y x X +∆+∆-=+∆+∆=ααααcos sin sin cos 旧旧新旧旧新四、案例计算1、使用一半坐标计算方法AB 段以A （ZH ）点为原点切线方向为X 轴，垂直于切线方向为Y 轴，使用缓和曲线参BC 段与AB 段在同一个自定义坐标系中，使用公式CD 段缓和曲线是不全的缓和曲线，需要将其补全后再使用缓和曲线参数方程计算。