当前位置：文档之家 › 快速傅里叶变换教程文件

快速傅里叶变换教程文件

  • 格式：ppt
  • 大小：984.00 KB
  • 文档页数：14

下载文档原格式

  / 14

合集下载

快速傅里叶变换

快速傅里叶变换

N X 2 ( k ) X 2 (k ) 2
第4章 快速傅里叶变换（FFT）
(N k ) 2 又由于WN
k WN WN
N 2

k WN
,所以
N N N k N 2 X (k ) X 1 (k ) WN X 2 (k ) 2 2 2
k X 1 (k ) WN X 2 (k ),
X 1 (k ) x1 (r )W x(2r )W
r 0 rk 4 r 0
3
3
rk 4
k 0,1,2,3
第4章 快速傅里叶变换（FFT）
(2) n为奇数时,分别记作:
x2 (0) x (1), x2 (1) x (3), x2 ( 2) x (5), x2 (3) x (7);
k N
1 1
k WN
-1
N X ( k ) X 1 (k ) WNk X 2 (k ) (后一半) 2
5.计算工作量分析
按奇、偶分组后的计算量：
第4章 快速傅里叶变换（FFT）
由上图可知，N点DFT的复乘为N2 ;复加N(N-1); 与分解后相比可知,计算工作点差不多减少 一半。
第4章 快速傅里叶变换（FFT）
一个X(k)的值的工作量,如X(1)
0 1 X (1) x(0)WN x(1)WN x(2)WN2 x( N 1)WNN 1
nk 通常x(n)和 W 都是复数,所以计算一个 N X(k)的值需要N次复数乘法运算,和N 1 次 复数加法运算.那么,所有的X(k)就要N2次复 数乘法运算,N(N-1)次复数加法运算.当N很 大时,运算量将是惊人的,如N=1024,则要完 成1048576 次(一百多万次)运算.这样,难 以做到实时处理.

《快速傅里叶变换》课件

《快速傅里叶变换》课件
FFT算法的出现极大地推动了数字信号 处理技术的发展和应用。
FFT的历史背景
01
1960年代，Cooley和Tukey提 出了基于“分治”思想的FFT 算法，为快速傅里叶变换的实 用化奠定了基础。
02
随后，出现了多种FFT算法的 变种和优化，如Radix-2、 Radix-4等。
03
随着计算机技术的发展，FFT 算法在硬件实现上也得到了广 泛应用，如FPGA、GPU等。
《快速傅里叶变换》ppt课件
contents
目录
• FFT简介 • FFT基本原理 • FFT实现 • FFT的应用 • FFT的优化与改进 • FFT的挑战与未来发展
01 FFT简介
FFT的定义
快速傅里叶变换（FFT）：一种高效计算离散傅里叶变换（DFT）及其逆变换的 算法。它将复杂度为$O(N^2)$的DFT计算降低到$O(Nlog N)$，大大提高了计 算效率。
详细描述
混合基数FFT算法结合了基数-2和基数-4算法的特点，利用两者在计算过程中的 互补性，减少了计算量，提高了计算效率。同时，该算法在处理大规模数据时 ，能够保持较高的精度。
分段FFT算法
总结词
分段FFT算法将输入数据分成若干段，对每一段进行快速傅里叶变换，以降低计算复杂度和提高计算效率。
详细描述
02 FFT基本原理
离散傅里叶变换（DFT）
定义
应用
DFT是时间域信号到频域的变换，通 过计算信号中各个频率成分的幅度和 相位，可以分析信号的频谱特性。
DFT在信号处理、图像处理、频谱分 析等领域有广泛应用。
计算量
DFT的计算量随着信号长度N的增加 而呈平方关系增长，因此对于长信号 ，计算量巨大。

《快速傅里叶变换》PPT课件

《快速傅里叶变换》PPT课件
然后计算圆周卷积
此时y(n)能代表线性卷积结果。
用FFT计算y(n)步骤如下： （1）求
，N点
（2）求
，N点
（3）计算
；
（4）求
，N点
工作量分析 FFT计算工作量
（4.105）
用线性相位滤波器来比较直接计算线性卷积和FFT法 计算线性卷积时比值
（4.106）
运算量分析：
（1）x(n)与h(n)点数差不多，设M＝L，
2
X1 k
x1
r
W rk N2
x
2r
W rk N2
r0
r0
（4.6）
N 1
N 1
2
2
X2 k
x2
r
W rk N2
x
2r
1
W rk N2
（4.7）
r 0
r0
应用系数的周期性
可得
N 1
X1
N 2
k
2 r 0
x1
r
W x r
N 2
k
N2
N 1 2
1
r0
比较可知，只要把DFT运算中的每一个系数
变成
，最后再乘常数1/N，则以上所有
按时间抽选或按频率抽选的FFT都可以拿来运算
IDFT。
不改FFT的程序计算IFFT方法： 对4.29式取共轭
因而
4.6 N为复合数的FFT算法 －－混合基算法
当N不满足
时，可有以下几种办法
（1）将x(n)补一些零值点的办法
y(n)也是有限长序列，其点数为L＋M－1。 2. 线性卷积运算量 乘法次数
线性相位滤波器满足条件
运算结构如图5.26,5.27所示 线性相位FIR滤波器的乘法运算量

快速傅里叶变换及其应用实验文档及程序

快速傅里叶变换及其应用实验文档及程序

试验二快速傅里叶变换及其应用一、试验目的（1）.在理论学习的基础上。

加深对FFT的理解，熟悉matlab中的有关函数。

（2）.应用FFT对典型信号进行频谱分析。

（3）.了解应用FFT进行信号频谱分析过程中可能出现的问题。

（4）.应用FFT实现序列的线性卷积和相关。

二、实验内容1．观察高斯序列的时域和幅频特性，固定信号xa(n)中参数p=8,改变q的值使q分别等于2、4、8，观察他们的时域和幅频特性，了解当q取不同值时，对信号序列的时域和幅频特性的影响；固定q=8，改变p,使p分别等于8、13、14，观察参数p变化对信号序列的时域和幅频特性的影响，注意p等于多少时会发生明显的泄漏现象，混叠是否也随之出现？记录实验中观察到的现象，绘出相应的时域序列和幅频特性曲线。

(1)固定p=8，使q=2和4的时域和频域图n=0:15x=exp((16*n-n.^2-64)./2)subplot(2,2,1);plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))subplot(2,2,2);stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');x=exp((16*n-n.^2-64)./4)subplot(2,2,3);plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))subplot(2,2,4);stem(n,y,'-o');xlabel('k');ylabel('y(k)')title('幅频特性');使q=8的时域和频域图n=0:15x=exp((16*n-n.^2-64)./8)plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');(2)固定q=8，使q=8和13的时域和频域图n=0:15x=exp((16*n-n.^2-64)./8)subplot(2,2,1);plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))subplot(2,2,2);stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');x=exp((26*n-n.^2-169)./8) subplot(2,2,3);plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))subplot(2,2,4);stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');使p=14的时域和频域图x=exp((28*n-n.^2-196)./8)plot(n,x,'-o')title('时域特性');xlabel('n');ylabel('y(n)')y=abs(fft(x))stem(n,y,'-o')xlabel('k');ylabel('y(k)')title('幅频特性');实验结果分析：由图形可知，当固定p,q取不同值时，随着q的增大，其相对应的时域幅值会增大，而且容易看出，它们的时域图关于n=8对称。

快速傅里叶变换PPT课件

快速傅里叶变换PPT课件

WNk
-
6
4.3 按时间抽取的基2-FFT算法
算法原理
DIT-FFT(Decimation-In-Time)
按时间抽取基-2FFT算法与直接计算 DFT运算量的比较
按时间抽取的FFT算法的特点
按时间抽取FFT算法的其它形式流程图
-
7
4.3.1 算法原理
设N＝2M，将x(n)按 n 的奇偶分为两组：
直接按DFT变换进行计算，当序列长度N很大时，计算
量非常大，所需时间会很长,实时处理难以实现。 1965年，图基和库利发表了《机器计算快速傅立叶级
数的一种算法》论文后，很快形成了快速计算DFT的计 算机算法FFT。（Fast Fourier Transform) FFT并不是一种与DFT不同的变换，而是DFT的一种快速 计算的算法。
2
28
观察原位运算规律
-
29
序列的逆序排列
序列的逆序排列
由于 x(n) 被反复地按奇、偶分组，所以流图输入端的 排列不再是顺序的，但仍有规律可循：
因为 N=2M ，对于任意 n（0≤n ≤N-1)，可以用M个 二进制码表示为：
n (D)E C (n M 1 n M 2 n 2 n 1 n 0)(B)IN 0
nM1,nM2,,n2,n1,n0 1
n 反复按奇、偶分解时，即按二进制码的“0” “1” 分解。
-
30
倒位序的树状图（N=8）
-
31
码位的倒位序(N=8)
自然顺序 n 二进制数 倒位序二进制数 倒位序顺序nˆ 数
0
000
000
0
1
001
100
4
2
010
010

FFT快速傅里叶变换word精品文档16页

FFT快速傅里叶变换word精品文档16页

快速傅里叶变换[编辑]维基百科，自由的百科全书跳转至：导航、搜索傅里叶变换Z变换傅里叶级数傅里叶变换离散傅里叶级数离散时间傅里叶变换离散傅里叶变换快速傅里叶变换分数傅里叶变换短时距傅立叶变换小波变换离散小波变换连续小波变换快速傅里叶变换（英语：Fast Fourier Transform, FFT），是离散傅里叶变换的快速算法，也可用于计算离散傅里叶变换的逆变换。

快速傅里叶变换有广泛的应用，如数字信号处理、计算大整数乘法、求解偏微分方程等等。

本条目只描述各种快速算法。

对于复数序列，离散傅里叶变换公式为：直接变换的计算复杂度是（参见大O符号）。

快速傅里叶变换可以计算出与直接计算相同的结果，但只需要的计算复杂度。

通常，快速算法要求n能被因数分解，但不是所有的快速傅里叶变换都要求n是合数，对于所有的整数n，都存在复杂度为的快速算法。

除了指数的符号相反、并多了一个1/n的因子，离散傅里叶变换的正变换与逆变换具有相同的形式。

因此所有的离散傅里叶变换的快速算法同时适用于正逆变换。

目录[隐藏]∙ 1 一般的简化理论∙ 2 快速傅里叶变换乘法量的计算∙ 3 Cooley-Tukey算法o 3.1 设计思想∙ 4 其他算法∙ 5 实数或对称资料专用的算法∙ 6 复杂度以及运算量的极限∙7 参考资料∙8 参阅一般的简化理论[编辑]假设一个M*N Sub-rectangular matrix S可分解成列向量以及行向量相乘：若有个相异的non-trivialvalues( where )有个相异的non-trivial values则S共需要个乘法。

Step 1：Step 2：简化理论的变型：也是一个M*N的矩阵。

若有个值不等于0，则的乘法量上限为。

快速傅里叶变换乘法量的计算[编辑]假设，其中彼此互质点DFT的乘法量为，则点DFT的乘法量为：假设，P是一个质数。

若点的DFT需要的乘法量为且当中 () 有个值不为及的倍数，有个值为及的倍数，但不为的倍数，则N点DFT的乘法量为：Cooley-Tukey算法[编辑]主条目：Cooley-Tukey快速傅里叶变换算法Cooley-Tukey算法是最常见的FFT算法。

04快速傅里叶变换


3 / 30
Beijing Institute of Technology
第四章 快速傅里叶变换
§4-2 直接计算DFT的问题和改善DFT运算效率的途径
一、直接计算DFT的问题
N 1
X (k) x(n)WNkn 0 k N 1 n0
x(n)
1 N
N 1
X (k )WNkn
0
0 n N 1
§4-3 按时间抽取(DIT)的FFT算法(Cooley-Tukey算法) 例：N=8 (P129)
26 / 30
6 / 30
？ 如何提高计算效率
Beijing Institute of Technology
第四章 快速傅里叶变换
§4-2 直接计算DFT的问题和改善DFT运算效率的途径
二、改善DFT运算效率的基本途径
1.利用WNkn的特性
①
W k(Nn) N
WNkn
(WNkn
)
（共轭）对称性
② WNkn WNk(nN) WNn(k N) 周期性
0 k N 1 2
归纳起来有
X (k) X1(k) WNk X 2 (k)
k 0,1,..., N 1 2
(4-13)
X
(N 2
k)
X1(k ) WNk
X 2 (k )
k 0,1,..., N 1 (4-14) 2
可见，
N DFT 2
N DFT
N DFT 2
N DFT19 / 30
18 / 30
代入(4-7)式，有:
Beijing Institute of Technology
§4-3 按时间抽取(DIT)的FFT算法(Cooley-Tukey算法)

快速傅里叶变换

n 0 N 1
r 0,1,
, N 2 1

N / 2 1

r 0
x(2r )WN
2 rk

N / 2 1

r 0
x(2r 1)WN
(2 r 1) k

N / 2 1

r 0
rk k x(2r )WN W /2 N
N / 2 1

r 0
rk x(2r 1)WN /2
N 2 N N ( N 1） N 2 所以8点FFT求X (k )共需 36次复数乘法, 2 2 2 2 N N2 N ( 1) N 32次复数加法, 共计为68次。看出仅做一次 2 2 分解就可以节省约一半计算量。
(2)N/2(4点)-->N/4(2点)FFT
N/2点 DFT
X1(1)
X1(2)
X1(3) X2(0)
WN
0
X(0) X(1) X(2) X(3)
1 2
x2(r) x2(0)=x(1)
奇 数 序 列
x2(1)=x(3) x2(2)=x(5) x2(3)=x(7)
N/2点 DFT
X2(1)
X2(2)
WN
WN
X2(3)
3 WN
X(4) -1 X(5) -1 X(6) -1 X(7)
-1 X(4)~X(7)
如：X（0） X 1 (0) X 2 (0)W80 X（2） X 1 (2) X 2 (2)W82
X（ 1） X 1 (1) X 2 (1)W81
X（3） X 1 (3) X 2 (3)W83
同学们自已写
比较直接计算N=8点DFT 与分解2个4点DFT的

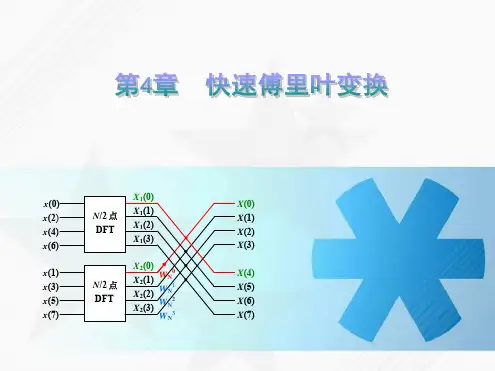
第4章快速傅里叶变换


例如： x(n)：
N=1024，N2=1048576
4
x(n)为N长，DFT变换对：
N 1
X (k ) x(n)WNkn n0
k 0,1, N 1
x(n)
1 N
N 1
X (k )WNnk
k 0
n 0,1, N 1
x(n)：时域信号，X(k)：频域频谱
物理意义不同，
但它们都是N长的序列，如果作为程序入口，没有什么
x1(r)= x(2r)
x2(r)= x(2r+1) r =0,1…N/2-1（长度为N/2）
N 1
则 X (k)
x(
n)W
nk N
x(n)WNnk
x(n)WNnk
n0
n为 偶 数
n为 奇 数
N / 21
N / 21
x(
2r
)W
2 rk N
x(2r 1)WN(2r1)k
r0
r0
N / 21
N2次
经过一次分解，运算量减少将近一半！
经过一次分解后，N→N/2； N/2仍为偶数，仍可进一步分解：
N/2 →N/4
l 0,1,
,
N 4
1
x(n)
x1(r) x(2r)
r 0,1,
,
N 2
1
x2(r) x(2r 1)
x3(l) x1(2l) (偶中偶) x4(l) x1(2l 1) (偶中奇)
问题是如何分最有效？
其中：基-2 FFT 是最基本的 FFT 算法，它要求 FFT 的 点数 N=2L（L为正整数）；
如果序列长度不满足这一条件，需要用后补零值点的 方法来补齐。
4.3 按时间抽取（DIT）的基-2FFT算法

FFT快速傅里叶变换23页word文档

快速傅里叶变换[编辑]维基百科，自由的百科全书跳转至：导航、搜索傅里叶变换Z变换傅里叶级数傅里叶变换离散傅里叶级数离散时间傅里叶变换离散傅里叶变换快速傅里叶变换分数傅里叶变换短时距傅立叶变换小波变换离散小波变换连续小波变换快速傅里叶变换（英语：Fast Fourier Transform, FFT），是离散傅里叶变换的快速算法，也可用于计算离散傅里叶变换的逆变换。

快速傅里叶变换有广泛的应用，如数字信号处理、计算大整数乘法、求解偏微分方程等等。

本条目只描述各种快速算法。

对于复数序列，离散傅里叶变换公式为：直接变换的计算复杂度是（参见大O符号）。

快速傅里叶变换可以计算出与直接计算相同的结果，但只需要的计算复杂度。

通常，快速算法要求n能被因数分解，但不是所有的快速傅里叶变换都要求n是合数，对于所有的整数n，都存在复杂度为的快速算法。

除了指数的符号相反、并多了一个1/n的因子，离散傅里叶变换的正变换与逆变换具有相同的形式。

因此所有的离散傅里叶变换的快速算法同时适用于正逆变换。

目录[隐藏]• 1 一般的简化理论• 2 快速傅里叶变换乘法量的计算• 3 Cooley-Tukey算法o 3.1 设计思想• 4 其他算法• 5 实数或对称资料专用的算法• 6 复杂度以及运算量的极限•7 参考资料•8 参阅一般的简化理论[编辑]假设一个M*N Sub-rectangular matrix S可分解成列向量以及行向量相乘：若有个相异的non-trivialvalues( where )有个相异的non-trivial values则S共需要个乘法。

Step 1：Step 2：简化理论的变型：也是一个M*N的矩阵。

若有个值不等于0，则的乘法量上限为。

快速傅里叶变换乘法量的计算[编辑]假设，其中彼此互质点DFT的乘法量为，则点DFT的乘法量为：假设，P是一个质数。

若点的DFT需要的乘法量为且当中 ()有个值不为及的倍数，有个值为及的倍数，但不为的倍数，则N点DFT的乘法量为：Cooley-Tukey算法[编辑]主条目：Cooley-Tukey快速傅里叶变换算法Cooley-Tukey算法是最常见的FFT算法。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。