C语言实现FFT(快速傅里叶变换)

傅里叶变换c程序傅里叶变换是一种用于分析和处理信号的重要数学工具，广泛应用于信号处理、图像处理、通信系统等领域。

在数学上，傅里叶变换可以将一个时域上的连续或离散信号转换为频域上的连续或离散信号，从而提供了一种将信号从时域转换为频域表示的方法。

在计算机科学中，傅里叶变换也有很大的应用。

通过使用傅里叶变换算法，可以对信号进行频谱分析，提取信号的频率成分，并在频域上进行滤波、去噪等处理。

傅里叶变换的计算可以使用多种方法，包括连续傅里叶变换（FFT）和离散傅里叶变换（DFT）。

为了实现傅里叶变换的计算，可以使用C语言编写相应的程序。

下面是一个简单的傅里叶变换C程序的示例：```c#include <stdio.h>#include <stdlib.h>#include <math.h>#define PI 3.14159265typedef struct {double real;double imag;} Complex;void fft(Complex* x, int N) {if (N <= 1) {}Complex* even = (Complex*) malloc(N/2 * sizeof(Complex)); Complex* odd = (Complex*) malloc(N/2 * sizeof(Complex)); for (int i = 0; i < N/2; i++) {even[i] = x[2*i];odd[i] = x[2*i + 1];}fft(even, N/2);fft(odd, N/2);for (int k = 0; k < N/2; k++) {Complex t;double angle = -2 * PI * k / N;t.real = cos(angle) * odd[k].real + sin(angle) * odd[k].imag; t.imag = cos(angle) * odd[k].imag - sin(angle) * odd[k].real; x[k].real = even[k].real + t.real;x[k].imag = even[k].imag + t.imag;x[k + N/2].real = even[k].real - t.real;x[k + N/2].imag = even[k].imag - t.imag;}free(even);}int main(void) {int N = 8;Complex* x = (Complex*) malloc(N * sizeof(Complex));// 初始化输入信号for (int i = 0; i < N; i++) {x[i].real = i;x[i].imag = 0;}fft(x, N);printf("傅里叶变换结果：\n");for (int i = 0; i < N; i++) {printf("X[%d] = %.2f + %.2fi\n", i, x[i].real, x[i].imag);}free(x);return 0;}```该程序演示了如何通过C代码实现傅里叶变换。

快速傅里叶变换fft的c程序代码实现标题：一种高效实现快速傅里叶变换(FFT)的C语言程序代码导言：快速傅里叶变换（Fast Fourier Transform，FFT）是一种在信号处理、图像处理、通信系统等领域广泛应用的重要算法。

它通过将输入信号从时域转换到频域，实现了对信号的频谱分析和频率成分提取。

在实际应用中，为了获得高效的FFT计算过程，我们需要使用合适的算法和优化技巧，并将其转化为高质量的C语言代码。

本文将介绍一种基于Cooley-Tukey算法的快速傅里叶变换的C语言程序代码实现。

我们将从原理开始详细讲解FFT算法，然后逐步引入代码实现的步骤，并进行相关优化。

我们将总结整个实现过程，并分享一些个人对FFT算法的理解和观点。

一、快速傅里叶变换（FFT）的原理（1）傅里叶级数与离散傅里叶变换傅里叶级数是将一个周期函数分解为一系列正弦和余弦函数的和的方法。

然而，实际数字信号往往是离散的。

我们需要离散傅里叶变换（Discrete Fourier Transform，DFT）来对离散信号进行频谱分析。

（2）DFT的定义及其计算复杂度离散傅里叶变换通过对离散信号的变换矩阵进行乘法运算，得到其频谱表示。

然而，直接使用定义式计算DFT的时间复杂度为O(N^2)，其中N为信号长度，这对于大规模信号计算是不可接受的。

（3）引入快速傅里叶变换 (FFT)Cooley-Tukey算法是一种最常用的FFT算法，通过将DFT分解为多个较小规模的DFT计算来降低计算复杂度。

FFT的时间复杂度为O(NlogN)，大大提高了计算效率。

二、快速傅里叶变换（FFT）的C语言实现（1）算法流程和数据结构设计以一维FFT为例，我们需要定义合适的数据结构来表示复数和存储输入输出信号，同时设计实现FFT的主要流程。

（2）递归实现方法递归实现是最直观的FFT实现方法，基于Cooley-Tukey算法的思想。

将输入信号分为偶数和奇数两部分，然后递归计算它们的FFT。

c语言傅里叶处理函数C语言傅里叶处理函数傅里叶变换是一种重要的信号处理方法，广泛应用于图像处理、音频处理、通信等领域。

在C语言中，我们可以使用傅里叶处理函数来实现对信号的频域分析和频谱变换。

本文将介绍C语言中常用的傅里叶处理函数及其使用方法。

一、傅里叶变换简介傅里叶变换是一种将时域信号转换为频域信号的数学方法，可以将信号分解为一组不同频率的正弦和余弦函数的叠加。

傅里叶变换的基本原理是利用正弦和余弦函数的周期性特点，将信号分解为不同频率的谐波分量，从而得到信号的频谱信息。

二、C语言中的傅里叶处理函数在C语言中，我们可以使用多种库函数或自定义函数来实现傅里叶变换。

以下是常用的傅里叶处理函数及其功能介绍。

1. FFT（快速傅里叶变换）FFT是一种高效的傅里叶变换算法，能够快速计算离散信号的频域分析。

在C语言中，我们可以使用FFTW库或自己实现FFT算法来进行快速傅里叶变换。

2. DFT（离散傅里叶变换）DFT是一种将离散信号转换为离散频谱的变换方法。

在C语言中，我们可以使用库函数如fftw_plan_dft_1d()来计算离散傅里叶变换。

3. IFFT（逆傅里叶变换）IFFT是傅里叶变换的逆运算，可以将频域信号恢复为时域信号。

在C语言中，我们可以使用库函数如fftw_plan_dft_1d()和fftw_execute()来计算逆傅里叶变换。

三、傅里叶处理函数的使用方法使用傅里叶处理函数进行信号处理的一般步骤如下：1. 导入相关库函数或自定义函数。

2. 定义输入信号和输出信号的数组。

3. 对输入信号进行傅里叶变换或逆傅里叶变换。

4. 分析或处理得到的频谱数据。

5. 可选地进行逆傅里叶变换，将频域信号恢复为时域信号。

以下是一个简单的示例，展示了如何使用FFTW库函数进行傅里叶变换和逆傅里叶变换：```c#include <stdio.h>#include <fftw3.h>#define N 16int main() {double in[N], out[N];fftw_complex *out_complex;fftw_plan plan;// 初始化输入信号for (int i = 0; i < N; i++) {in[i] = i;}// 创建傅里叶变换的输入输出数组out_complex = (fftw_complex*) fftw_malloc(sizeof(fftw_complex) * (N/2+1));// 创建傅里叶变换的计划plan = fftw_plan_dft_r2c_1d(N, in, out_complex, FFTW_ESTIMATE);// 执行傅里叶变换fftw_execute(plan);// 输出频谱数据for (int i = 0; i < N/2+1; i++) {printf("频率%d: 幅度%f 相位%f\n", i, cabs(out_complex[i]), carg(out_complex[i]));}// 销毁计划和临时数组fftw_destroy_plan(plan);fftw_free(out_complex);return 0;}```四、总结本文介绍了C语言中常用的傅里叶处理函数及其使用方法。

标题：C语言实现快速傅里叶变换输出频谱一、简介在信号处理和频域分析中，快速傅里叶变换（FFT）是一种常用的算法，用于将时域的信号转换为频域的频谱。

在C语言中实现快速傅里叶变换可以帮助我们对信号进行高效的频域分析。

本文将从基础开始，介绍C语言实现快速傅里叶变换并输出频谱的方法。

二、快速傅里叶变换概述快速傅里叶变换是一种将离散信号转换为频域表示的算法，它将N个离散时间域采样点转换成N个频域采样点。

快速傅里叶变换算法的核心是分治法，通过递归地将信号分解为奇偶部分，然后合并计算，从而实现高效的频谱分析。

三、C语言实现快速傅里叶变换1. 我们需要定义一个复数结构体，用于表示实部和虚部。

在C语言中，可以使用结构体来表示复数，例如：```ctypedef struct {double real; // 实部double imag; // 虚部} Complex;```2. 接下来，我们可以编写一个函数来实现快速傅里叶变换。

在函数中，我们可以按照快速傅里叶变换的递归算法，将信号分解为奇偶部分，并进行合并计算，最终得到频域表示的频谱。

```cvoid FFT(Complex* x, int N, int inv) {// 实现快速傅里叶变换的代码// ...}```3. 在实现快速傅里叶变换的过程中，我们还需要编写一些辅助函数，例如计算旋转因子和进行信号分解合并等操作。

四、输出频谱在C语言中实现快速傅里叶变换后，我们可以将得到的频域表示的频谱输出到文件或者直接在终端进行可视化。

通过频谱分析，我们可以了解信号的频域特性，包括频率成分、频谱密度等信息。

五、个人观点和理解C语言实现快速傅里叶变换需要深入理解算法的原理，同时对C语言的数据结构和递归算法有一定的掌握。

在实际应用中，我们可以将快速傅里叶变换应用于音频处理、图像处理、通信系统等领域，对信号的特性进行频域分析。

六、总结通过本文的介绍，我们了解了C语言实现快速傅里叶变换并输出频谱的方法。

c语言快速傅里叶变快速傅里叶变换的实现可以使用递归或迭代两种方式：1. 递归实现递归版本的快速傅里叶变换（FFT）是一种标准实现方法，它的时间复杂度为O(n * log2(n))。

快速傅里叶变换的代码实现如下：```void fft(double complex* x, int n){if(n == 1)return;double complex odd[n/2], even[n/2];for(int i=0, j=0; i<n; i+=2, j++){even[j] = x[i];odd[j] = x[i+1];}fft(even, n/2);fft(odd, n/2);for(int i=0; i<n/2; i++){double complex t = cexp(-I * 2 * M_PI * i / n) * odd[i];x[i] = even[i] + t;x[i+n/2] = even[i] - t;}}```2. 迭代实现迭代实现 FFT 的主要思路是根据蝴蝶定理将一次变换的复杂度降为 O(n)，多次迭代后复杂度为 O(n*logn)。

代码实现如下：```void fft(double complex* x, int n){int k = log2(n);double complex w[n/2];for (int i=0; i<n/2; i++)w[i] = cexp(-I * 2 * M_PI * i / n);for (int i=0; i<k; i++)for (int j=0; j<n; j++)if (!(j & (1<<i))){int x1 = j, x2 = j | (1<<i);double complex t = x[x2] * w[x2 & ((1<<i)-1)];x[x2] = x[x1] - t;x[x1] += t;}}```以上两种方式都是可行的，但是迭代实现方式更加快速。

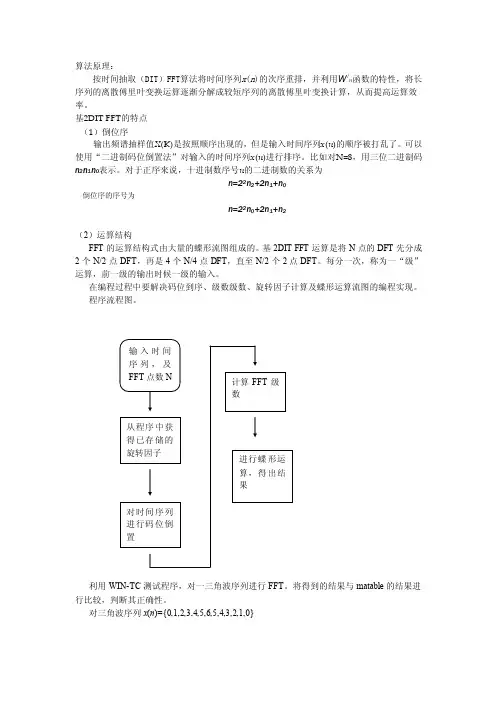
算法原理：按时间抽取（DIT）FFT算法将时间序列x(n)的次序重排，并利用W i n函数的特性，将长序列的离散傅里叶变换运算逐渐分解成较短序列的离散傅里叶变换计算，从而提高运算效率。

基2DIT FFT的特点（1）倒位序输出频谱抽样值X(K)是按照顺序出现的，但是输入时间序列x(n)的顺序被打乱了。

可以使用“二进制码位倒置法”对输入的时间序列x(n)进行排序。

比如对N=8，用三位二进制码n2n1n0表示。

对于正序来说，十进制数序号n的二进制数的关系为n=22n2+2n1+n0倒位序的序号为n=22n0+2n1+n2（2）运算结构FFT的运算结构式由大量的蝶形流图组成的。

基2DIT FFT运算是将N点的DFT先分成2个N/2点DFT，再是4个N/4点DFT，直至N/2个2点DFT。

每分一次，称为一“级”运算，前一级的输出时候一级的输入。

在编程过程中要解决码位到序、级数级数、旋转因子计算及蝶形运算流图的编程实现。

程序流程图。

利用WIN-TC测试程序，对一三角波序列进行FFT。

将得到的结果与matable的结果进行比较，判断其正确性。

对三角波序列x(n)={0,1,2,3,4,5,6,5,4,3,2,1,0}在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是XKN2 =Columns 1 through 636.0000 34.2084 -10.3770i 29.1007 -19.4445i 21.4292 -26.1115i 12.2946 -29.6817i 2.9501 -29.9525i前半段波形对比显示WIN-TC结果能保证小数点后2位的精度。

对方波序列x(n),长度为64，前32为1，幅值为1的序列在WIN-TC进行128点FFT，得到前6个结果Matable仿真的前6个结果是Columns 1 through 632.0000 20.8677 -19.8677i 1.0000 -20.3555i -6.2783 - 7.2783i 04.5539 - 3.5539i仿真波形对比显示WIN-TC结果能保证小数点后2位的精度。

[C++]频谱图中FFT快速傅⾥叶变换C++实现在项⽬中，需要画波形频谱图，因此进⾏查找，不是很懂相关知识，下列代码主要是针对这篇⽂章。

//快速傅⾥叶变换/*⼊⼝参数：inv： =1,傅⾥叶变换; =-1,逆傅⾥叶变换N：输⼊的点数，为偶数，⼀般为2的幂次级，2,4,8,16...k: 满⾜N=2^k（k>0）,实质上k是N个采样数据可以分解为偶次幂和奇次幂的次数real[]: inv=1时，存放N个采样数据的实部，inv=-1时，存放傅⾥叶变换的N个实部imag[]: inv=1时，存放N个采样数据的虚部，inv=-1时，存放傅⾥叶变换的N个虚部出⼝参数：real[]: inv=1时，返回傅⾥叶变换的实部，inv=-1时，返回逆傅⾥叶变换的实部imag[]: inv=1时，返回傅⾥叶变换的虚部，inv=-1时，返回逆傅⾥叶变换的虚部*/void FFT::dealFFT(double real[], double imag[], double dSp[], int N, int k, int inv){int i, j, k1, k2, m, step, factor_step;double temp_real, temp_imag, factor_real, factor_imag;if (inv != 1 && inv != -1)return;//double *real = new double[N];//double *imag = new double[N];//倒序j = 0;for (i = 0; i < N; i++){if (j>i){temp_real = real[j];real[j] = real[i];real[i] = temp_real;temp_imag = imag[j];imag[j] = imag[i];imag[i] = temp_imag;}m = N / 2;while (j >= m&&m != 0){j -= m;m >>= 1;}j += m;}//蝶形运算for (i = 0; i < k; i++){step = 1 << (i + 1);factor_step = N >> (i + 1); //旋转因数变化速度//初始化旋转因⼦factor_real = 1.0;factor_imag = 0.0;for (j = 0; j < step / 2; j++){for (k1 = j; k1 < N; k1 += step){k2 = k1 + step / 2; //蝶形运算的两个输⼊/* temp_real = real[k1] + real[k2] * factor_real - imag[k2] * factor_imag;temp_imag = imag[k1] + real[k2] * factor_imag + imag[k2] * factor_real;real[k2] = real[k1] - (real[k2] * factor_real - imag[k2] * factor_imag);imag[k2] = imag[k1] - (real[k2] * factor_imag + imag[k2] * factor_real);real[k1] = temp_real;imag[k1] = temp_imag;*///上⾯⽅法虽然直⽩，但效率太低，稍微改变结构如下：temp_real = real[k2] * factor_real - imag[k2] * factor_imag;temp_imag = real[k2] * factor_imag + imag[k2] * factor_real;real[k2] = real[k1] - temp_real;imag[k2] = imag[k1] - temp_imag;real[k1] = real[k1] + temp_real;imag[k1] = imag[k1] + temp_imag;}factor_real = inv*cos(-2 * PI*(j + 1)*factor_step / N);factor_imag = inv*sin(-2 * PI*(j + 1)*factor_step / N);}}if (inv == -1){for (i = 0; i <= N - 1; i++){real[i] = real[i] / N;imag[i] = imag[i] / N;}}for (i = 0; i<N;i++){dSp[i] = sqrt(real[i] * real[i] + imag[i] * imag[i]);}}⼀般好像需要进⾏下转换，即后半部分和前半部分置换，即1234变成3412.void FFT::FFTShift(double dp[], int len){for (int i = 0; i < len / 2; i++){double tmp = dp[i];dp[i] = dp[i + len / 2];dp[i + len / 2] = tmp;}}此时得到的应该是实部和虚部解出来的频谱图的Y轴电压值，⼀般频谱图Y轴为dB，因此需要进⾏转换void FFT::getFFT(double dRe[], double dIm[], double dSp[], int len, int nBits, double dWorkingImpedance){dealFFT(dRe, dIm, dSp, len, nBits, 1);FFTShift(dSp,len); //此时得到的应该是实部和虚部解出来的频谱图的Y轴电压值，还需要转换////dBW = 10lg(电压^2/阻抗);dBm =dBW+30，注意电压单位是Vfor (int i = 0; i<len; i++){dSp[i] = 10 * log10(dSp[i] * dSp[i] / dWorkingImpedance)+30;}}getFFT()输出之后的dp才是要的频谱图Y轴值，频谱图X轴的坐标得到通过以下⽅式：//X轴精确度，采样频率/数据个数 = 步长m_DeltaX_S = m_dataPara.nSampleFrequency / nDataNumOfPage_S;data_SX[i / 2] = m_dataPara.nCenterFrequency + count*m_DeltaX_S - m_dataPara.nWorkingBandWidth/2;//中⼼频率+当前点*步长-带宽/2在项⽬中，实际代码如下：int count = 0;for (int i = 0; i < nDataNumOfPage_S * 2; i++){if (i % 2 == 0)data_SQ[i / 2] = data_S[i] * m_DeltaY_S;elsedata_SI[i / 2] = data_S[i] * m_DeltaY_S;if (i % 2 == 0){count++;data_SX[i / 2] = m_dataPara.nCenterFrequency + count*m_DeltaX_S - m_dataPara.nWorkingBandWidth/2;}}m_dataPara.nWorkingImpedance = 50;FFT fft;int nBits = log10(nDataNumOfPage_S) / log10(2);//因为参数需要是2的N次⽅fft.getFFT(data_SQ, data_SI, data_SS, nDataNumOfPage_S, nBits, m_dataPara.nWorkingImpedance); LoadData_S(data_SX, data_SS, nDataNumOfPage_S);。

fft算法c语言实现快速傅里叶变换（FFT）是一种高效的离散傅里叶变换算法，用于计算信号在频域的表示。

下面是一个简单的使用 C 语言实现的 FFT 算法示例，它可以用于对输入的时域信号进行离散傅里叶变换。

```c#include <stdio.h>#include <stdlib.h>#include <math.h>#define N 16// 复数结构体typedef struct {double real;double imag;} Complex;// 初始化复数void initComplex(Complex *c, double real, double imag) {c->real = real;c->imag = imag;}// FFT 算法void fft(Complex *c, int n) {int i, j, k;Complex w, u, v;// 层次遍历for (i = 1; i < n; i <<= 1) {// 旋转因子w.real = cos(2 * M_PI * i / n);w.imag = -sin(2 * M_PI * i / n);for (j = 0; j < n; j += i) {for (k = 0; k < i / 2; k++) {u.real = c[j + k].real;u.imag = c[j + k].imag;v.real = c[j + i / 2 + k].real;v.imag = c[j + i / 2 + k].imag;c[j + k].real = u.real + w.real * v.real - w.imag * v.imag; c[j + k].imag = u.imag + w.real * v.imag + w.imag * v.real; c[j + i / 2 + k].real = u.real - w.real * v.real + w.imag * v.imag; c[j + i / 2 + k].imag = u.imag - w.real * v.imag - w.imag * v.real; }}}}// 打印复数void printComplex(Complex c) {printf("%f + %fi\n", c.real, c.imag);}int main() {Complex c[N];// 输入的时域信号for (int i = 0; i < N; i++) {c[i].real = rand() / RAND_MAX;c[i].imag = rand() / RAND_MAX;}printf("输入的时域信号：\n");// 打印输入的时域信号for (int i = 0; i < N; i++) {printComplex(c[i]);}fft(c, N);printf("经过 FFT 变换后的频域信号：\n");// 打印经过 FFT 变换后的频域信号for (int i = 0; i < N; i++) {printComplex(c[i]);}return 0;}```上述代码是一个简单的 C 语言实现的 FFT 算法示例。

C语言实现FFT快速傅里叶变换（Fast Fourier Transform, FFT）是一种高效进行离散傅里叶变换（Discrete Fourier Transform, DFT）计算的算法。

它通过利用对称性和递归的方法，将O(n^2)的计算复杂度优化为O(nlogn)。

本文将介绍C语言实现FFT的基本步骤和代码。

首先，需要定义一个复数结构体来表示复数，包含实部和虚部两个成员变量：```ctypedef structdouble real; // 实部double imag; // 虚部```接着，需要实现FFT的关键函数，包括以下几个步骤：1. 进行位逆序排列（bit-reversal permutation）：FFT中的输入数据需要按照位逆序排列，这里使用蝶形算法来实现位逆序排列。

先将输入序列按照索引位逆序排列，再将复数序列按照实部和虚部进行重新排列。

```cint i, j, k;for (i = 1, j = size / 2; i < size - 1; i++)if (i < j)temp = data[j];data[j] = data[i];data[i] = temp;}k = size / 2;while (j >= k)j=j-k;k=k/2;}j=j+k;}```2. 计算旋转因子（twiddle factor）：FFT中的旋转因子用于对复数进行旋转变换，这里采用的旋转因子为e^( -2*pi*i/N )，其中N为DFT点数。

```cint i;double angle;for (i = 0; i < size; i++)angle = -2 * M_PI * i / size;twiddleFactors[i].real = cos(angle);twiddleFactors[i].imag = sin(angle);}```3.执行蝶形算法计算DFT：蝶形算法是FFT算法的核心部分，通过递归地将DFT问题一分为二，并将计算结果根据旋转因子进行两两合并，最终得到FFT结果。

#include <iom128、h>#include <intrinsics、h>/*********************************************************************快速傅立叶变换C函数函数简介:此函数就是通用的快速傅里叶变换C语言函数,移植性强,以下部分不依赖硬件。

此函数采用联合体的形式表示一个复数,输入为自然顺序的复数(输入实数就是可令复数虚部为0),输出为经过FFT变换的自然顺序的复数使用说明:使用此函数只需更改宏定义FFT_N的值即可实现点数的改变,FFT_N应该为2的N次方,不满足此条件时应在后面补0函数调用:FFT(s);时间:2010-2-20版本:Ver1、0参考文献:**********************************************************************/#include<math、h>#define PI 3、14932384626433832795028841971 //定义圆周率值#define FFT_N 128 //定义傅立叶变换的点数struct compx {float real,imag;}; //定义一个复数结构struct compx s[FFT_N]; //FFT输入与输出:从S[1]开始存放,根据大小自己定义/*******************************************************************函数原型:struct compx EE(struct compx b1,struct compx b2)函数功能:对两个复数进行乘法运算输入参数:两个以联合体定义的复数a,b输出参数:a与b的乘积,以联合体的形式输出*******************************************************************/struct compx EE(struct compx a,struct compx b){struct compx c;c、real=a、real*b、real-a、imag*b、imag;c、imag=a、real*b、imag+a、imag*b、real;return(c);}/*****************************************************************函数原型:void FFT(struct compx *xin,int N)函数功能:对输入的复数组进行快速傅里叶变换(FFT)输入参数:*xin复数结构体组的首地址指针,struct型*****************************************************************/void FFT(struct compx *xin){int f,m,nv2,nm1,i,k,l,j=0;struct compx u,w,t;nv2=FFT_N/2; //变址运算,即把自然顺序变成倒位序,采用雷德算法nm1=FFT_N-1;for(i=0;i<nm1;i++){if(i<j) //如果i<j,即进行变址{t=xin[j];xin[j]=xin[i];xin[i]=t;}k=nv2; //求j的下一个倒位序while(k<=j) //如果k<=j,表示j的最高位为1{j=j-k; //把最高位变成0k=k/2; //k/2,比较次高位,依次类推,逐个比较,直到某个位为0}j=j+k; //把0改为1}{int le,lei,ip; //FFT运算核,使用蝶形运算完成FFT运算f=FFT_N;for(l=1;(f=f/2)!=1;l++) ; //计算l的值,即计算蝶形级数for(m=1;m<=l;m++) // 控制蝶形结级数{ //m表示第m级蝶形,l为蝶形级总数l=log(2)Nle=2<<(m-1); //le蝶形结距离,即第m级蝶形的蝶形结相距le点lei=le/2; //同一蝶形结中参加运算的两点的距离u、real=1、0; //u为蝶形结运算系数,初始值为1u、imag=0、0;w、real=cos(PI/lei); //w为系数商,即当前系数与前一个系数的商w、imag=-sin(PI/lei);for(j=0;j<=lei-1;j++) //控制计算不同种蝶形结,即计算系数不同的蝶形结{for(i=j;i<=FFT_N-1;i=i+le) //控制同一蝶形结运算,即计算系数相同蝶形结{ip=i+lei; //i,ip分别表示参加蝶形运算的两个节点t=EE(xin[ip],u); //蝶形运算,详见公式xin[ip]、real=xin[i]、real-t、real;xin[ip]、imag=xin[i]、imag-t、imag;xin[i]、real=xin[i]、real+t、real;xin[i]、imag=xin[i]、imag+t、imag;}u=EE(u,w); //改变系数,进行下一个蝶形运算}}}}/************************************************************函数原型:void main()函数功能:测试FFT变换,演示函数使用方法输入参数:无输出参数:无************************************************************/void main(){int i;for(i=0;i<FFT_N;i++) //给结构体赋值{s[i]、real=sin(2*3、1493*i/FFT_N); //实部为正弦波FFT_N点采样,赋值为1s[i]、imag=0; //虚部为0}FFT(s); //进行快速傅立叶变换for(i=0;i<FFT_N;i++) //求变换后结果的模值,存入复数的实部部分s[i]、real=sqrt(s[i]、real*s[i]、real+s[i]、imag*s[i]、imag);while(1);}#include <iom128、h>#include <intrinsics、h>/*********************************************************************快速傅立叶变换C程序包函数简介:此程序包就是通用的快速傅里叶变换C语言函数,移植性强,以下部分不依赖硬件。

§2.4 快速傅里叶变换 (FFT) 实现一、实验目的 1. 掌握FFT 算法的基本原理；2. 掌握用C 语言编写DSP 程序的方法。

二、实验设备 1. 一台装有CCS3.3软件的计算机； 2. DSP 实验箱的TMS320F2812主控板；3. DSP 硬件仿真器。

三、实验原理傅里叶变换是一种将信号从时域变换到频域的变换形式，是信号处理的重要分析工具。

离散傅里叶变换（DFT ）是傅里叶变换在离散系统中的表示形式。

但是DFT 的计算量非常大， FFT 就是DFT 的一种快速算法, FFT 将DFT 的N 2 步运算减少至 ( N/2 )log 2N 步。

离散信号x(n)的傅里叶变换可以表示为∑=-=10][)(N N nk N W n x k X ， Nj N e W /2π-=式中的W N 称为蝶形因子，利用它的对称性和周期性可以减少运算量。

一般而言，FFT 算法分为时间抽取（DIT ）和频率抽取（DIF ）两大类。

两者的区别是蝶形因子出现的位置不同，前者中蝶形因子出现在输入端，后者中出现在输出端。

本实验以时间抽取方法为例。

时间抽取FFT 是将N 点输入序列x(n) 按照偶数项和奇数项分解为偶序列和奇序列。

偶序列为：x(0), x(2), x(4),…, x(N-2)；奇序列为：x(1), x(3), x(5),…, x(N-1)。

这样x(n) 的N 点DFT 可写成：()()∑++∑=-=+-=12/0)12(12/02122)(N n kn NN n nkNW n x Wn x k X考虑到W N 的性质，即2/)2//(22/)2(2][N N j N j N W e e W ===--ππ因此有：()()∑++∑=-=-=12/02/12/02/122)(N n nkN kNN n nkN W n x W Wn x k X或者写成：()()k Z W k Y k X kN +=)(由于Y(k) 与Z(k) 的周期为N/2，并且利用W N 的对称性和周期性，即：k NN k N W W -=+2/可得：()()k Z W k Y N k X kN -=+)2/(对Y(k) 与Z(k) 继续以同样的方式分解下去，就可以使一个N 点的DFT 最终用一组2点的DFT 来计算。

快速傅里叶变换(FFT)算法C++实现代码#include <math.h>#define DOUBLE_PI 6.283185307179586476925286766559// 快速傅里叶变换// data 长度为 (2 * 2^n), data 的偶位为实数部分, data 的奇位为虚数部分// isInverse表示是否为逆变换void FFT(double * data, int n, bool isInverse = false){int mmax, m, j, step, i;double temp;double theta, sin_htheta, sin_theta, pwr, wr, wi, tempr, tempi;n = 2 * (1 << n);int nn = n >> 1;// 长度为1的傅里叶变换, 位置交换过程j = 1;for(i = 1; i < n; i += 2){if(j > i){temp = data[j - 1];data[j - 1] = data[i - 1];data[i - 1] = temp;data[j] = temp;data[j] = data[i];data[i] = temp;}// 相反的二进制加法m = nn;while(m >= 2 && j > m){j -= m;m >>= 1;}j += m;}// Danielson - Lanczos 引理应用mmax = 2;while(n > mmax){step = mmax << 1;theta = DOUBLE_PI / mmax;if(isInverse){theta = -theta;}sin_htheta = sin(0.5 * theta);sin_theta = sin(theta);pwr = -2.0 * sin_htheta * sin_htheta;wr = 1.0;wi = 0.0;for(m = 1; m < mmax; m += 2){for(i = m; i <= n; i += step){j = i + mmax;tempr = wr * data[j - 1] - wi * data[j];tempi = wr * data[j] + wi * data[j - 1];data[j - 1] = data[i - 1] - tempr;data[j] = data[i] - tempi;data[i - 1] += tempr;data[i] += tempi;}sin_htheta = wr;wr = sin_htheta * pwr - wi * sin_theta + wr;wi = wi * pwr + sin_htheta * sin_theta + wi;}mmax = step;}}输入数据为data，data是一组复数，偶数位存储的是复数的实数部分，奇数位存储的是复数的虚数部分。

快速傅⾥叶变换（fft）及其逆变换（iff）的c代码实现#define float sample_t// data的长度为n,必须是2的指数倍，result的长度为2n，其中奇数项保存虚数，偶数项保存的是实数int fft(sample_t *data, int sample_number, sample_t *result){// 需要给奇数部分填充虚数0for(int i = 0; i < sample_number; ++i){result[2*i] = data[i];result[2*i+1] = 0;}int flag = 1;flag = fft_ifft_implement(result, sample_number, flag);return flag;}// data的长度是2n，result的长度为n,n必须是2的指数倍int ifft(sample_t *data, int sample_number, sample_t *result){int flag = -1;flag = fft_ifft_implement(data, sample_number, flag);// 奇数部分是虚数，需要舍弃for (int i = 0; i < sample_number; i++){result[i] = data[2*i] / sample_number;}return flag;}static int fft_ifft_implement(sample_t *data, int sample_number, int flag){// 判断样本个数是不是2的指数倍，如果不是能否补零成指数倍？sample_t number_log = log(sample_number) / log(2);int mmax = 2, j=0;int n = sample_number<<1;int istep, m;sample_t theta, wtemp, wpr, wpi, wr, wi, tempr, tempi;if (((int)number_log - number_log) != 0){return 0;}for(int i = 0; i < n-1; i=i+2){if(j > i){swap(data, j ,i);swap(data, j + 1 ,i + 1);}m = n / 2;while(m >= 2 && j >= m){j = j - m;m = m / 2;}j = j + m;}while(n > mmax){istep = mmax<<1;theta = -2 * PI / (flag * mmax);wtemp = sin(0.5 * theta);wpr = -2.0 * wtemp * wtemp;wpi = sin(theta);wr = 1.0;wi = 0.0;for(int m = 1; m < mmax; m = m + 2){for(int i = m; i < n + 1; i = i + istep){int j = i + mmax;tempr = wr * data[j-1] - wi * data[j];tempi = wr * data[j] + wi * data[j-1];data[j-1] = data[i-1] - tempr;data[j] = data[i] - tempi;data[i-1] += tempr;data[i] += tempi;}wtemp = wr;wr += wr * wpr - wi * wpi;wi += wi * wpr + wtemp * wpi;}mmax = istep;}return 1;}static void swap(sample_t *data ,int m, int n) {sample_t temp = data[m];data[m] = data[n];data[n] = temp;}。

C语言实现FFT变换FFT（快速傅里叶变换）是一种高效的算法，用于将时域信号转换为频域信号。

在C语言中，可以使用以下步骤实现FFT变换。

1.首先，需要定义复数结构体，用于表示实部和虚部。

```ctypedef structdouble real;double imag;```2.实现一个函数来进行复数的乘法操作。

```cresult.real = a.real * b.real - a.imag * b.imag;result.imag = a.real * b.imag + a.imag * b.real;return result;```3.编写一个函数来执行FFT变换。

```c//基线条件if (n == 1)return;}//分解信号for (int i = 0; i < n / 2; i++) even[i] = x[2 * i];odd[i] = x[2 * i + 1];}//递归计算FFTfft(even, n / 2, is_inverse);fft(odd, n / 2, is_inverse);//合并结果double angle = 2 * PI / n;if (is_inverse)angle = -angle;}for (int k = 0; k < n / 2; k++)x[k] = add(even[k], t);x[k + n / 2] = subtract(even[k], t); w = multiply(w, wn);}//释放内存free(even);free(odd);```4.编写一个函数来计算FFT结果的模值。

```cdouble* magnitude = (double*)malloc(n * sizeof(double));for (int i = 0; i < n; i++)magnitude[i] = sqrt(x[i].real * x[i].real + x[i].imag * x[i].imag);}return magnitude;```5.在主函数中使用上述函数进行FFT变换。

数字信号处理_快速傅里叶变换FFT实验报告快速傅里叶变换(FFT)实验报告1. 引言数字信号处理是一门研究如何对数字信号进行处理、分析和提取信息的学科。

傅里叶变换是数字信号处理中常用的一种方法，可以将信号从时域转换到频域。

而快速傅里叶变换(FFT)是一种高效的计算傅里叶变换的算法，广泛应用于信号处理、图象处理、通信等领域。

2. 实验目的本实验旨在通过编写程序实现快速傅里叶变换算法，并对不同信号进行频谱分析。

3. 实验原理快速傅里叶变换是一种基于分治策略的算法，通过将一个N点离散傅里叶变换(DFT)分解为多个较小规模的DFT，从而实现高效的计算。

具体步骤如下： - 如果N=1，直接计算DFT；- 如果N>1，将输入序列分为偶数和奇数两部份，分别计算两部份的DFT；- 将两部份的DFT合并为整体的DFT。

4. 实验步骤此处以C语言为例，给出实验的具体步骤：(1) 定义输入信号数组和输出频谱数组；(2) 实现快速傅里叶变换算法的函数，输入参数为输入信号数组和输出频谱数组；(3) 在主函数中调用快速傅里叶变换函数，得到输出频谱数组；(4) 对输出频谱数组进行可视化处理，如绘制频谱图。

5. 实验结果与分析为了验证快速傅里叶变换算法的正确性和有效性，我们设计了以下实验：(1) 生成一个正弦信号，频率为100Hz，采样频率为1000Hz，时长为1秒；(2) 对生成的正弦信号进行快速傅里叶变换，并绘制频谱图；(3) 生成一个方波信号，频率为200Hz，采样频率为1000Hz，时长为1秒；(4) 对生成的方波信号进行快速傅里叶变换，并绘制频谱图。

实验结果显示，对于正弦信号，频谱图中存在一个峰值，位于100Hz处，且幅度较大；对于方波信号，频谱图中存在多个峰值，分别位于200Hz的奇数倍处，且幅度较小。

这与我们的预期相符，说明快速傅里叶变换算法能够正确地提取信号的频谱信息。

6. 实验总结通过本次实验，我们成功实现了快速傅里叶变换算法，并对不同信号进行了频谱分析。

一、对FFT的介绍1。

FFT（Fast Fourier Transformation）,即为快速傅里叶变换，是离散傅里叶变换的快速算法，它是根据离散傅里叶变换的奇、偶、虚、实等特性,对离散傅里叶变换的算法进行改进获得的。

2.FFT算法的基本原理FFT算法是把长序列的DFT逐次分解为较短序列的DFT。

按照抽取方式的不同可分为DIT-FFT(按时间抽取)和DIF—FFT(按频率抽取)算法。

按蝶形运算的构成不同可分为基2，基4，基8,以及任意因子的类型。

3。

迭代关系4、本次程序的基本过程我们这次所研究的是数字信号处理中的FFT算法，我们这次所用的数字信号是复数类型的.(1）所以首先，我们先定义了一个复数结构体，因为是进行复数的运算，我们又相继定义复数的加减乘运算的函数.（2）紧接着,我们定义了进行FFT计算的fft（)快速傅里叶变换函数initW（) 初始化变换核函数即旋转因子的计算，change（) 变址函数,output()输出傅里叶变换的结果的函数.（3）定义主函数，并调用定义好的相关子函数，利用fft（)中的蝶形运算以及change(）函数来完成从时间域上选取的DIT-FFT。

二、FFT中码位倒置排序1、码位倒置的实现方法：(1)简单的利用按位与、或循环实现(2）利用公式推导的迭代方法2、为什么要进行码位倒置因为由于FFT的计算特性,如果按照正常顺序输入，而没有进行码位倒置的话,就会以乱序输出，就不便于我们后续对信号的相关性质进行研究了，所以DIT—FFT算法就是在进行FFT计算之前，进行分奇偶后的码位倒置运算，即二进制数的倒位。

3、倒位序由奇偶分组造成，以N=8为例，说明如下：三、蝶形运算由按照上述公式的规律进行逐级分解,直到2点DFT，如下是N=8时的蝶形算法分析图：四、FFT算法中蝶形算法的基本思想分析（1）我们知道N点FFT运算可以分成log2(N)级，每一级都有N/2个碟形，FFT的基本思想是用3层循环完成全部运算（N点FFT）。

C语言、MATLAB实现FFT几种方法总结前人经验，仅供参考///一、///////////////////////////////////////////////////////////////////// ////////////////////////////////////////////////////////////////////////////////////////////////////////c语言程序/////////////////////////////////////////////////////////////////////////////////////////////////////////////////// //////////////////////////////////////////////////#include <iom128.h>#include <intrinsics.h>#include<math.h>#define PI 3.1415926535897932384626433832795028841971 //定义圆周率值#define FFT_N 128 //定义福利叶变换的点数struct compx {float real,imag;}; //定义一个复数结构struct compx s[FFT_N]; //FFT输入和输出：从S[1]开始存放，根据大小自己定义/******************************************************************* 函数原型：struct compx EE(struct compx b1,struct compx b2)函数功能：对两个复数进行乘法运算输入参数：两个以联合体定义的复数a,b输出参数：a和b的乘积，以联合体的形式输出*******************************************************************/ struct compx EE(struct compx a,struct compx b){struct compx c;c.real=a.real*b.real-a.imag*b.imag;c.imag=a.real*b.imag+a.imag*b.real;return(c);}/*****************************************************************函数原型：void FFT(struct compx *xin,int N)函数功能：对输入的复数组进行快速傅里叶变换（FFT）输入参数：*xin复数结构体组的首地址指针，struct型*****************************************************************/ void FFT(struct compx *xin){int f,m,nv2,nm1,i,k,l,j=0;struct compx u,w,t;nv2=FFT_N/2; //变址运算，即把自然顺序变成倒位序，采用雷德算法 nm1=FFT_N-1;for(i=0;i<nm1;i++){if(i<j) //如果i<j,即进行变址{t=xin[j];xin[j]=xin[i];xin[i]=t;}k=nv2; //求j的下一个倒位序while(k<=j) //如果k<=j,表示j的最高位为1{j=j-k; //把最高位变成0k=k/2; //k/2，比较次高位，依次类推，逐个比较，直到某个位为0}j=j+k; //把0改为1}{int le,lei,ip; //FFT运算核，使用蝶形运算完成FFT 运算f=FFT_N;for(l=1;(f=f/2)!=1;l++) //计算l的值，即计算蝶形级数;for(m=1;m<=l;m++) // 控制蝶形结级数{ //m表示第m级蝶形，l为蝶形级总数l=log（2）Nle=2<<(m-1); //le蝶形结距离，即第m级蝶形的蝶形结相距le 点lei=le/2; //同一蝶形结中参加运算的两点的距离u.real=1.0; //u为蝶形结运算系数，初始值为1u.imag=0.0;w.real=cos(PI/lei); //w为系数商，即当前系数与前一个系数的商w.imag=-sin(PI/lei);for(j=0;j<=lei-1;j++) //控制计算不同种蝶形结，即计算系数不同的蝶形结{for(i=j;i<=FFT_N-1;i=i+le) //控制同一蝶形结运算，即计算系数相同蝶形结{ip=i+lei; //i，ip分别表示参加蝶形运算的两个节点 t=EE(xin[ip],u); //蝶形运算，详见公式xin[ip].real=xin[i].real-t.real;xin[ip].imag=xin[i].imag-t.imag;xin[i].real=xin[i].real+t.real;xin[i].imag=xin[i].imag+t.imag;}u=EE(u,w); //改变系数，进行下一个蝶形运算 }}}}/************************************************************函数原型：void main()函数功能：测试FFT变换，演示函数使用方法输入参数：无输出参数：无************************************************************/void main(){int i;for(i=0;i<FFT_N;i++) //给结构体赋值{s[i].real=sin(2*3.141592653589793*i/FFT_N); //实部为正弦波FFT_N 点采样，赋值为1s[i].imag=0; //虚部为0}FFT(s); //进行快速福利叶变换for(i=0;i<FFT_N;i++) //求变换后结果的模值，存入复数的实部部分s[i].real=sqrt(s[i].real*s[i].real+s[i].imag*s[i].imag);while(1);}%////二、%//////////////////////////////////////////////////////////////////// /////////////////////////////////////////%//////////////////////////////////////////////////////////////////// ///////////////////////////////////////%////////////////////////////////MATLAB仿真信号源的源程序:: Clear;Clc;t=O:O.01:3;yl=100*sin(pi/3*t);for t=-O:O.01:10;y2(1,n)=-61.1614*exp(-0.9*t);n=n+;endmin(y2)y=[yl，y2];figure(1);plot(y); %funboxing(O.001+1/3)%////////////////////////%/////////快速傅里叶变换matlab程序:%////////////////////////clc;clear;clf;N=input('Node number')T=input('cai yang jian ge')f=input('frenquency')choise=input('add zero or not? 1/0 ')n=0:T:(N-1)*T; %采样点k=0:N-1;x=sin(2*pi*f*n);if choise==1e=input('Input the number of zeros!')x=[x zeros(1,e)]N=N+e;elseend %加零k=0:N-1; %给k重新赋值，因为有可能出现加零状况bianzhi=bi2de(fliplr(de2bi(k,length(de2bi(N-1)))))+1;%利用库函数进行变址运算for l=1:NX(l)=x(bianzhi(l));%将采样后的值按照变址运算后的顺序放入X矩阵中endfor m=1:log2(N)d2=d1; %做蝶形运算的两个数之间的距离d1=d1*2; %同一级之下蝶形结之间的距离W=1; %蝶形运算系数的初始值dw=exp(-j*pi/d2); %蝶形运算系数的增加量for t=1:d2 %for i=t:d1:Ni1=i+d2;if(i1>N)break; %判断是否超出范围elsep=X(i1)*W;X(i1)=X(i)-p;X(i)=X(i)+p; %蝶形运算endendW=W*dw; %蝶形运算系数的变化endendsubplot(2,2,1);t=0:0.0000001:N*T;plot(t,sin(2*pi*f*t)); %画原曲线subplot(2,2,2);stem(k,x); %画采样后的离散信号subplot(2,2,3);stem(k,abs(X)/max(abs(X))); %画自己的fft的运算结果subplot(2,2,4);stem(k,abs(fft(x))/max(abs(fft(x)))); %调用系统的函数绘制结果，与自己的结果进行比较//////三、///////////////////////////////////////////////////////////////////// ////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////FFT的C语言算法实现////////////程序如下：/************FFT***********/#include <stdio.h>#include <math.h>#include <stdlib.h>#define N 1000typedef struct{double real;double img;}complex;void fft(); /*快速傅里叶变换*/void ifft(); /*快速傅里叶逆变换*/void initW();void change();void add(complex ,complex ,complex *); /*复数加法*/ void mul(complex ,complex ,complex *); /*复数乘法*/ void sub(complex ,complex ,complex *); /*复数减法*/ void divi(complex ,complex ,complex *);/*复数除法*/ void output(); /*输出结果*/complex x[N], *W;/*输出序列的值*/int size_x=0;/*输入序列的长度，只限2的N次方*/double PI;int main(){int i,method;system("cls");PI=atan(1)*4;printf("Please input the size of x:\n");/*输入序列的长度*/scanf("%d",&size_x);printf("Please input the data in x[N]:(such as:5 6)\n"); /*输入序列对应的值*/for(i=0;i<size_x;i++)scanf("%lf %lf",&x[i].real,&x[i].img);initW();/*选择FFT或逆FFT运算*/printf("Use FFT(0) or IFFT(1)?\n");scanf("%d",&method);if(method==0)fft();elseifft();output();return 0;}/*进行基-2 FFT运算*/void fft(){int i=0,j=0,k=0,l=0;complex up,down,product;change();for(i=0;i< log(size_x)/log(2) ;i++){l=1<<i;for(j=0;j<size_x;j+= 2*l ){for(k=0;k<l;k++){mul(x[j+k+l],W[size_x*k/2/l],&product);add(x[j+k],product,&up);sub(x[j+k],product,&down);x[j+k]=up;x[j+k+l]=down;}}}void ifft(){int i=0,j=0,k=0,l=size_x;complex up,down;for(i=0;i< (int)( log(size_x)/log(2) );i++) /*蝶形运算*/ {l/=2;for(j=0;j<size_x;j+= 2*l ){for(k=0;k<l;k++){add(x[j+k],x[j+k+l],&up);up.real/=2;up.img/=2;sub(x[j+k],x[j+k+l],&down);down.real/=2;down.img/=2;divi(down,W[size_x*k/2/l],&down);x[j+k]=up;x[j+k+l]=down;}}}change();}void initW(){int i;W=(complex *)malloc(sizeof(complex) * size_x);for(i=0;i<size_x;i++){W[i].real=cos(2*PI/size_x*i);W[i].img=-1*sin(2*PI/size_x*i);}void change(){complex temp;unsigned short i=0,j=0,k=0;double t;for(i=0;i<size_x;i++){k=i;j=0;t=(log(size_x)/log(2));while( (t--)>0 ){j=j<<1;j|=(k & 1);k=k>>1;}if(j>i){temp=x[i];x[i]=x[j];x[j]=temp;}}}void output() /*输出结果*/{int i;printf("The result are as follows\n"); for(i=0;i<size_x;i++){printf("%.4f",x[i].real);if(x[i].img>=0.0001)printf("+%.4fj\n",x[i].img);else if(fabs(x[i].img)<0.0001)printf("\n");elseprintf("%.4fj\n",x[i].img);}}void add(complex a,complex b,complex *c){c->real=a.real+b.real;c->img=a.img+b.img;}void mul(complex a,complex b,complex *c){c->real=a.real*b.real - a.img*b.img;c->img=a.real*b.img + a.img*b.real;}void sub(complex a,complex b,complex *c){c->real=a.real-b.real;c->img=a.img-b.img;}void divi(complex a,complex b,complex *c){c->real=( a.real*b.real+a.img*b.img )/(b.real*b.real+b.img*b.img);c->img=( a.img*b.real-a.real*b.img)/(b.real*b.real+b.img*b.img); }/////四、///////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////////%//////选带傅里叶变换(zoom-fft) MATLAB%移频（将选带的中心频率移动到零频）%数字低通滤波器（防止频率混叠）%重新采样（将采样的数据再次间隔采样，间隔的数据取决于分析的带宽，就是放大倍数）%复FFT （由于经过了移频，所以数据不是实数了）%频率调整（将负半轴的频率成分移到正半轴）function [f, y] = zfft(x, fi, fa, fs)% x为采集的数据% fi为分析的起始频率% fa为分析的截止频率% fs为采集数据的采样频率% f为输出的频率序列% y为输出的幅值序列(实数）f0 = (fi + fa) / 2; %中心频率N = length(x); %数据长度r = 0:N-1;b = 2*pi*f0.*r ./ fs;x1 = x .* exp(-1j .* b); %移频bw = fa - fi;B = fir1(32, bw / fs); %滤波截止频率为0.5bwx2 = filter(B, 1, x1);c = x2(1:floor(fs/bw):N); %重新采样N1 = length(c);f = linspace(fi, fa, N1);y = abs(fft(c)) ./ N1 * 2;y = circshift(y, [0, floor(N1/2)]); %将负半轴的幅值移过来end///////////////////////////////////////////////////////////////////// ////////////////////////////////////////////////////////////////////////////////////////////////////////////////////// /////////////////////////////////////%上边四程序测试应用实例：fs = 2048;T = 100;t = 0:1/fs:T;x = 30 * cos(2*pi*110.*t) + 30 * cos(2*pi*111.45.*t) + 25*c os(2*pi*112.3*t) + 48*cos(2*pi*113.8.*t)+50*cos(2*pi*114.5.*t); [f, y] = zfft(x, 109, 115, fs);plot(f, y);///////////////////////////////////////////////////////////////////// ////////////////////////////////////////////////图片效果：。