当前位置：文档之家 › 结构图及其等效变换

结构图及其等效变换

  • 格式：ppt
  • 大小：1.61 MB
  • 文档页数：15

下载文档原格式

  / 15

合集下载

控制系统的结构图及其等效变换

控制系统的结构图及其等效变换

2.
通路
沿支路箭头方向穿过各相 连支路的路径。
前向通路
从源节点到阱节点的通路上通过任何节点
不多于一次的通路。前向通路上各支路增益之 乘积，称前向通路总增益，一般用pk表示。
回路
起点与终点重合且通过任何节点不多于一次的
闭合通路。回路中所有支路增益之乘积称为回 路增益，用Lk表示。
不接触回路
相互间没有任何公共节点的回路
反馈通路断开。 系统开环传递函数：前向通道传递函数与反馈通道传 递函数的乘积。
B( s ) Gk ( s) G1 ( s)G2 ( s) H ( s) E (s)
(反馈信号B(s)和偏差信号E (s)之间的传递函数)
系统的开环传递函数
GK (s) G1 (s)G2 (s) H (s)
注：开环传递函数并非指开环控制系统的传递函数， 而是指闭环系统断开反馈点后整个环路的传递函数。
例2.9 简化下图，求出系统的传递函数。
解： 上图是具有交叉连接的结构图。为消除交叉，可采 用比较点、引出点互换的方法处理。 （1）将相加点a移至G2之后
（2）再与b点交换
（3）因 G4与G1G2并联， G3与G2H是负反馈环节
（4）上图两环节串联，函数相乘后得系统的传递函数为
注： ①以上为原系统的闭环传递函数，不是开环系统的传递函数， 而是闭环系统简化的结果； ②分母中不能看成原闭环系统的开环传递函数，闭环系统开 环传递函数应根据定义和具体框图定。
闭环系统的传递函数
反馈控制系统的典型结构 ：
R( s) E (s) G1(s) B(s)
N (s)
G2(s)
C (s)
H(s)
输入量R(s)、干扰量N(s)同时作用于系统

系统结构图及等效变换、梅森公式

系统结构图及等效变换、梅森公式
统结构图基础上应用等效变换和梅森 公式进行系统设计和实现，确保系统稳定性和可靠性。
05
结论与展望
BIG DATA EMPOWERS TO CREATE A NEW
ERA
研究结论
• 通过分析和比较不同系统结构图的特点和性能，本文得出了一些重要的结论。首先，等效变换在系统分析和设 计中具有重要的作用，它可以帮助我们简化复杂的系统结构，降低分析和设计的难度。其次，梅森公式是一种 有效的系统性能评估方法，它可以用于计算系统的传递函数和频率响应等关键性能指标。最后，通过实例分析 和仿真验证，本文证明了等效变换和梅森公式在系统分析和设计中的有效性和实用性。
案例一
分析一个简单的RC电路，利用梅 森公式计算其传递函数，并与实 验结果进行对比分析。
案例二
针对一个控制系统，利用梅森公 式分析其稳定性，并给出相应的 控制器设计建议。
案例三
考虑一个复杂的信号流图，利用 梅森公式进行化简，得到简化的 数学模型，便于后续分析和设计。
BIG DATA EMPOWERS TO CREATE A NEW ERA
案例分析
案例一
串联等效变换的应用。在某控制系统中，存在两个串联的控制器，通过串联等效变换，可以将这两个控制器 合并为一个等效控制器，从而简化系统分析。
案例二
并联等效变换的应用。在某电力系统中，存在两个并联的电源，通过并联等效变换，可以将这两个电源合并 为一个等效电源，方便进行系统性能评估。
案例三
反馈等效变换的应用。在某通信系统中，存在一个反馈环节，通过反馈等效变换，可以将该反馈环节进行简 化，使得简化后的系统与原系统在性能上保持一致。
系统结构图及等效变换、
BIG DATA EMPOWERS TO CREATE A NEW

动态结构图及其等效变换

动态结构图及其等效变换
再进行内回路反馈和并联变换，得下图。
22
N1 +
解：
（2）求C/N1,设R=0,N2=0, 得右图。
C(s) G3(1 G2 ) N1(s) 1 G2 G1G2G3
23
解（3）求C(s)/N2(s)，设R=0,N1=0，得下图。
则：
0 N2(s) C(s)
C(s) 1 N2 (s)
24
X(s)
X(s)
R(s)
C(s)
R(s)
C(s)
Y(s)
C(s) R(s) X (s) Y (s)
Y(s)
C(s) R(s) Y (s) X (s)
7. 相邻的比较点和引出点之间可以调换位置，如下图 所示。
17
相邻引出点之间的移动
R(s)
R(s)
R(s)
R(s) C(s)
R(s)
R(s) R(s)
动态结构图及其等效变换
1
§ 2.3 动态结构图及其等效变换
一、动态结构图(方块图) 1.定义
动态结构图是图形化的数学模型，它是一种系 统输入和输出之间因果关系的简略图示方法，表示 了系统输出、输入信号之间的动态传递关系。
2
2. 组成要素 传递方块: 表示输入、输出信号之间的传递关系 C(s)=G(s)E(s)，B(s)=H(s)C(s)
(s) )
RI CsU
(s) I(s) c (s) Uc (
s)
1 R
U r
1 Cs
( I
s) (s)
U
c
(
s)
绘制上式各子方程的方框图：
r ( s ) r ( s ) - c ( s ) r ( s ) - c ( s ) I ( s ) I ( s ) c ( s )

动态结构图.

动态结构图.
U1 ( s )
I1 ( s )

1 U1 ( s ) C1 s
I 2 ( s)

1 I 2 ( s) R2
UC ( s)
I 2 ( s)
1 UC ( s) sC 2
动态结构图的建立
按图中关系联接各个方框
U r ( s)
1 I1 ( s ) R


I 2 ( s)
1 U1 ( s ) C1 s
U1 ( s )
( m)
∆k ——第k条前向通路特征式的余因子，即对于结构图的特征式∆，将与第k
条前向通路相接触的回路传递函数代以零值，余下的∆即为∆k。

1 I 2 ( s) R2
UC ( s)
1 UC ( s) sC 2
传递函数可由方程组消去中间变量得到
UC ( s) 1 2 U r ( s ) R1C1 R2C 2 s ( R1C1 R2C 2 R1C 2 ) s 1
动态结构图的建立
注意:双T网络不可看成两个RC网络的串联，即：
1 R 1 sC
I ( s)
UC ( s)
动态结构图的建立
连接各方框,得到动态结构图
U r ( s)
U ( s)
C
U R ( s) U R ( s)
1 R
I ( s)
I ( s)
1 sC
UC ( s)
R I(s) Ur(s)
1 sC
U r ( s)
UC(s)
U ( s)
C
U R ( s)
1 接的传递函数
X1(s) G1(s) G2(s) X3(s) X2(s) ±
X 2 (s) G ( s) X 1 (s) X 3 (s) X 4 (s) X 1 ( s)

2.3 等效变换

2.3 等效变换
G ( s ) Gi ( s ) (n为相串联 接传递函数的乘积。 的环节数) i 1
2
(b)
n
(2) 并联连接
特点：各环节的输入信号是相同的，均为R(s)， 输出C(s)为各环节的输出之和。
Ｒ(s)
G1 ( s) G2 ( s)
C1(s)
C2(s)
C(s)
±
Ｒ(s)

G1 (s) G2 (s)
± R (s) ± R (s) 2 3

± R (s) ± R (s) 3 2

± R (s) 3
(a)
(b) C(s)＝R1(s)±R2(s)±R3(s)
(c)
(6) 相邻引出点位置的交换
R(s) R(s) R(s) R(s) R(s)

R(s)
R(s) R(s)
(a)
(b)
8
二、结构图等效变换举例
1
一、结构图的等效变换法则
１、环节的合并 (1) 串联连接 特点：前一环节的输出量就是后一环节的输入量。
Ｒ(s)
G1 ( s)
D(s)
G2 ( s)
C(s)

Ｒ(s)
G1 ( s)G2 ( s)
C(s)
(a)
图2-35 串联连接的等效变换 D(s)＝G1(s)R(s) C(s)＝G2(s) G1(s)R(s) C(s)＝G2(s)D(s) C ( s) 结论：环节串联的等效 G ( s) G1 ( s)G2 ( s ) R( s) 传递函数等于各串联连
例 试化简如图所示系统结构图，求出传递函数 Φ(s)=C(s)/R(s)。
R(s)
－
G1 G2
＋
G3

研讨题5方框图的等效变换的原则和简化方法总结

研讨题5方框图的等效变换的原则和简化方法总结

研讨题5 方框图的等效变换的原则和简化方法总结
结构图的基本组成形式可分为三种：
（1）串联连接方框与方框首尾相连。

前一个方框的输出，作为后一个方框的输入。

（2）并联连接两个或多个方框，具有同一个输入，而以各方框输出的代数和作为总输出。

（3）反馈连接一个方框的输出，输入到另一个方框，得到的输出再返回作用于前一个方框的输入端。

方框图的等效变换的原则
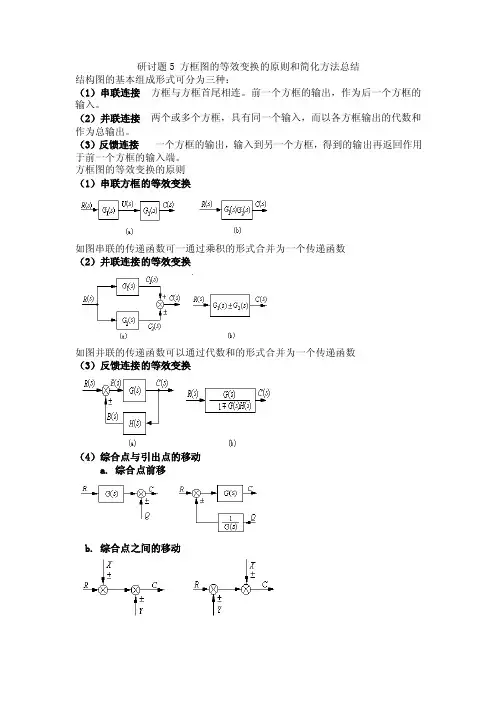
（1）串联方框的等效变换
如图串联的传递函数可一通过乘积的形式合并为一个传递函数
（2）并联连接的等效变换
如图并联的传递函数可以通过代数和的形式合并为一个传递函数
（3）反馈连接的等效变换
（4）综合点与引出点的移动
a. 综合点前移
b. 综合点之间的移动
c. 引出点后移
d. 相邻引出点之间的移动
简化结构图求总传递函数的一般步骤：
1. 确定输入量与输出量，如果作用在系统上的输入量有多个（分别作用在系统的不同部位），则必须分别对每个输入量逐个进行结构变换，求得各自的传递函数。

对于有多个输出量的情况，也应分别变换。

2. 若结构图中有交叉关系，应运用等效变换法则，首先将交叉消除，化为无交叉的多回路结构。

3. 对多回路结构，可由里向外进行变换，直至变换为一个等效的方框，即得到所求的传递函数。

自动控制原理02结构图及其等效变换

自动控制原理02结构图及其等效变换
e)
R( s )
G 1 G 2 G3G 4 C (s) 1 G 1 G 2 G3G 4 G 2 G3 H 1 G3G 4 H 2
f)
2.3 控制系统的结构图及等效变换
2.3.4 系统传递函数
典型闭环控制系统
N (s)
R( s )
E ( s)
G1 (s)
结构图。
2.3.2 结构图的建立
例2-7 RLC电路网络的结构图
解： U (s) U (s) U (s) U (s) i R L 0
U R ( s) RI ( s)
U L ( s) LsI ( s)
{
I ( s)
U i ( s) U 0 ( s ) U R ( s ) U L ( s )
C 传输到 ( s)
单位反馈： H ( s) 1 开环传递函数：
G( s) H ( s)
2.3.3 结构图的等效变换和简化
（4）比较点的移动
R1 (s)
G(s)
R2 ( s )
a)
C (s)
R2 ( s )
R1 (s)
G(s)
C (s)
1/ G(s)
b)
R1 (s)
R2 ( s )
a)
G(s)
C (s) G(s) ( s) R( s) 1 G ( s) H ( s )
2.3.3 结构图的等效变换和简化
反馈连接中的术语：
R( s)
E (s)

G (s)
H (s)
C (s)
B( s)
前向通道：信号从 R( 传输到 s) 反馈通道：信号从
的通道 C ( s) 的通道 R( s )
R(s)

# 23传递函数方块图(系统动态结构图)及其等效变换

# 23传递函数方块图(系统动态结构图)及其等效变换

r (s)
–
e
e ( s)
c ( s)
US(s)
U S (s) KSe (s)
Ua(s) –
(s)
KS
U a (s) Ra I a (s) La SIa (s) Eb (s)
Eb(s)
1 Ra La S
Ia(s)
M m (s) Cm I a (s)
2
Ia(s)
Cm
根据传递函数的定义，每一个方块单元，一 般有以下的运算关系： X0(s) = W(s) Xi(s)
# 2—3 传递函数方块图（系统动态结构图） 及其等效变换 图中：指向方块单元的箭头表示输入量 的象函数Xi(s),离开方块单元的箭头表示 输出量的象函数X0(s),写在方块单元中的 是传递函数G(s)。
Mm(s)
JS m (s) fSm (s) M m (s) M L (s)
Mm(s)
–
1 JS 2 fS
m ( s)
Eb(s)
Eb (s) Kb Sm (s) m ( s)
ML(s)
K bS
1 c ( s ) m ( s ) i
e (s)
m ( s) 1 c ( s)
# 2—5 传递函数方块图（系统动态结构图） 及其等效变换 作业：系统结构方图的绘制 R1 L Xi Uc R2 Ur C
L Ur C R2 Uc
X0
2、系统结构方块图的绘制步骤 （1）列写系统中各元件的运动方程 （2）在零初始条件下，对微分方程进行拉氏变 换 （3）用元件方块图等表示出信号间的关系 （4）根据系统中各信号的传递方向和顺序将各 方块图连接起来，就得到系统的动态结构 图
–
U1(s)

第2章第4节控制系统的结构图

第2章第4节控制系统的结构图
R（s） G1(s) U（s） G2(s) C（s） R（s） G1(s) G2(s) C（s）
C ( s ) = G 2 ( s )U ( s ) = G 2 ( s )G1 ( s ) R ( s ) = G ( s ) R ( s ) G( s) = G1 ( s)G2 ( s)
推广到n个方框串联连接
+ ψ 电位器1 up 放大器 电动机 If 励磁绕组 电位器2 Ia 发电机原动机 发电机 齿轮传 动机构 φ 负载
J.Z. Xiao, CEIE, HBU
随动系统原理结构图
6
（1）电位器组：
u p = k p (ψ − ϕ)
ψ(s) -
U p ( s ) = k pψ ( s ) − k p ϕ ( s )
ψ(s) kp
UP(s) ka -
I f (s) 1 R f (Tf s + 1)
kg
1 kd (TaTm s 2 + Tm s + 1)
kp
ω(s)
kt s
φ(s)
J.Z. Xiao, CEIE, HBU
随动系统结构框图
9
三、结构图的等效变换
等效变换原则： 变换前后各变量之间的传递关系保持不变。 三种基本连接形式： 串联、并联和反馈 1、串联连接的等效传递函数
§2.4 控制系统的结构图(方框图)
结构图的组成 结构图的绘制 结构图的等效变换
由代数关系，是否可将复杂系统视为其 各子系统间的输入输出连接形式呢？
R1
L
C1
R2
ui (t )
′ uo (t )
ui′(t )
C2
uo (t )
组合后的 系统模型 是什么？

系统的结构图及其等效变换

系统的结构图及其等效变换

控制系统的结构图及其等效变换项目内容学习目的掌握结构图的化简方法。

重点熟练掌握结构图化简求取传递函数的方法。

难点典型结构变换、结构图化简方法的灵活应用。

结构图的组成和绘制结构图的等效变换→求系统传递函数一结构图的组成和绘制系统的结构图是表示系统各元件特性、系统结构和信号流向的图示方法。

定义：将方块图中各时间域中的变量用其拉氏变换代替，各方框中元件的名称换成各元件的传递函数,这时方框图就变成了动态结构图，简称结构图，即传递函数的几何表达形式。

组成(1)信号线：带有箭头的直线，箭头表示信号的流向，在直线旁边标有信号的时间函数或象函数。

一条信号线上的信号处处相同。

X(s)(2)引出点:表示信号引出或测量的位置，同一位置引出的信号大小和性质完全相同。

(3)比较点(综合点、相加点)：表示对两个以上的信号进行加减运算，加号常省略,减号必须标出。

G(s)X(s)Y(s)(4)方框：表示对信号进行的数学变换，方框内的函数为元件或系统的传递函数。

结构图的绘制R C i （a ）i u ou 一阶RC 网络例1画出RC 电路的结构图。

解：利用复阻抗的概念及元件特性可得每一元件的输入量和输出量之间的关系如下：()()()(1)i o U s U s I s R -=()()(2)o I s U s sC =R ：C ：绘制每一元件的结构图，并把相同变量连接起来，得到系统的结构图。

1/sC U i (s)U o (s)-U o (s)I (s)1/R RC i （a ）i u ou 1/sc例2：绘制两级RC 网络的结构图。

r U cU 11sC 21sC 1R 2R 1I 2I 1U111112112222()()()1()[()()]()()()1()()r C C U s U s I s R U s I s I s sC U s U s I s R U s I s sC -⎧=⎪⎪⎪=-⋅⎪⎪⎨-⎪=⎪⎪⎪=⋅⎪⎩r U cU 11sC 21sC 1R 2R 1I 2I 1U 解：利用复阻抗的概念及元件特性可得每一元件的输入量和输出量之间的关系如下：111112112222()()()1()[()()]()()()1()()r C C U s U s I s R U s I s I s sC U s U s I s R U s I s sC -⎧=⎪⎪⎪=-⋅⎪⎪⎨-⎪=⎪⎪⎪=⋅⎪⎩1/R 11/sC 11/R 21/sC 2U C (s)U r (s)U 1(s)I 1(s)I 2(s)--U 1(s)-U C (s)绘制每一元件的结构图，并把相同变量连接起来，得到系统的结构图。

2.3动态结构图

2.3动态结构图

X1(s) C(s)
R(s) B(s)
E(s)
G1(s)
C(s)
G2 ( s )
±
X2(s)
H(s)
并联连接
反馈连接
《自动控制技术及应用》电子课件
西安航空职业技术学院 自动化工程学院
2.3.2 动态结构图的等效变换
一、等效变换
（三）反馈连接框图的等效变化
R(s) B(s) H(s) E(s) G1(s) C(s)
《自动控制技术及应用》电子课件
2.3.1 动态结构图的建立
【例2-16】 对RC串联电路建立动态结构图.
（3）依据信号的流向，将图中相同的信号连 起来，就组成了RC串联电路的动态结构图
U R ( s) U r ( s) U C ( s)
Ur(s) UC(s) UR(s)
1 I (s) U R (s) R
R(s) C(s)
G(s)
R(s)
G(s) 1 G(s)
C(s)
西安航空职业技术学院 自动化工程学院
《自动控制技术及应用》电子课件
2.3.2 动态结构图的等效变换
练一练1:对下图中的各结构图进行等效化简.
（1）
R(s)
R1
R2
C(s)
R(s)
（2）
R(s)
R1 R2
C(s)
-
（ 3）
R(s)
-
一、动态结构图的组成
4 分支点
X(s)
X(s) X(s)
分支点又称引出点，表示在此位置处将 该信号分成多路输出.由于信号线上只传送 信号，不传送能量，因此分出的每路信号大 小均与原信号相等.
西安航空职业技术学院 自动化工程学院

自动控制原理 动态结构图及变换

自动控制原理 动态结构图及变换

U s (s)
Ka Ua (s)
系统各元部件的动态结构图(4)
e (s) r (s) c (s)
M m (s) CmIa (s)
U s (s) Kse (s)
U a (s) KaU s (s) Ua (s) Ra Ia (s) LasIa (s)
Eb (s)
Eb (s) Kbsm (s)
二、动态结构图的基本连接形式
1. 串联连接
X(s) G1(s)
Y(s) G2(s)
方框与方框通过信号线相连，前一个方框的输 出作为后一个方框的输入，这种形式的连接称 为串联连接。
2. 并联连接
G1(s)
X(s)
－ Y(s)
＋
G2(s)
两个或两个以上的方框，具有同一个输入信号，并 以各方框输出信号的代数和作为输出信号，这种形
式的连接称为并联连接。
3. 反馈连接
R(s)
－
C(s) G(s)
H(s)
一个方框的输出信号输入到另一个方框后，得 到的输出再返回到这个方框的输入端，构成输 入信号的一部分。这种连接形式称为反馈连接。
三、系统动态结构图的构成
• 构成原则：
按照动态结构图的基本连接形式，构 成系统的各个环节，连接成系统的动 态结构图。
Ua (s) Ra Ia (s) LasIa (s) Eb (s)
Js2 m (s) M m fsm (s)
c
(s)
1
i
m
(s)
r (s)
e (s)
c (s)
系统各元部件的动态结构图(2)
e (s) r (s) c (s) Us (s) Kse (s)
Ua (s) KaU s (s) Ua (s) Ra Ia (s) LasIa (s)

自动控制原理2.4 结构图的等效变换及简化计算

自动控制原理2.4 结构图的等效变换及简化计算
Pk—从R(s)到C(s)的第k条前向通道增益 △k —第k条前向通道的余子式
在△中，去掉与第k条前向通 道相接触的回路对应的项后
剩余的部分。
求法: 去掉第k条前向通路后所求的△ 用梅森公式求上例信号流图对应的传函。
南京工业职业技术学院机械工程学院——自动控制原理
梅森公式例1
GG44((ss))
R(s)
注：比较点和引出点之间不能换位。 3. 通过在被变换的支路上乘或除某个传函来保持等效。 4. 根据环节方框的连接方式（串联、并联和反馈）进行简化
计算。
南京工业职业技术学院机械工程学院——自动控制原理
结构图三种连接形式及其计算
串联
G1
G2
G1 G2
n
G(s) Gi (s) i 1
并联 G1 G2
反馈 G1
G5
R –
X1 G1
– G2 X2 –
G3 X3
G4
C
X3
G6
G7
南京工业职业技术学院机械工程学院——自动控制原理
G8 G5
R – G1 X1
X2 – G2
–
X3
G3
G4
C
X3 G6
G7
（2）求传函。用梅逊公式：
1 G1G2G3G4G7 G1G2G3G4G8 G2G3G6 G3G4G5
R(s)
-
G4
A
G1
-
B
G2
H1
G3 H2
C C(s)
P1 G1G2G3 1 1
P2 G1G4 2 1
C(S) P(S) P11 P22
P11 P22
R(S)
1 (L1 L2 L3 L4 L5 )

控制系统的结构图及其等效变换

控制系统的结构图及其等效变换

Y (s)
前移 R1(s) G(s) Y (s)
注：
R2 (s)
R1 ( s )
Y (s)
G(s)
1/G(s) R2 (s)
相加点进入和出去的信号量纲必须相同，否则不能加减。
b引出点（信号由某一点分开）
分支点分出信号，数值相同
R(s) 后移
G(s)
Y (s)
R(s)
R(s) G(s)
Y (s) R(s)
4.比较点（求和点、综合点） 1.用符号“ ”及相应的信号箭头表示 2.箭头前方的“+”或“-”表示加上此信号 或减去此信号
! 注意量纲：相同量纲的物理量
例：二阶RC电气网络
结构图的等效变换和简化
➢系统的结构图通过等效变换和简化后可以方便、快速 地求取闭环系统的传递函数或系统输出量的响应。
➢等效变换和简化的过程对应于消去中间变量求系统传
信号流图的绘制 1. 根据微分方程绘制信号流图 2. 根据方框图绘制信号流图
1. 根据微分方程绘制信号流图
i
A
取Ui(s)、I1(s)、UA(s)、I2(s)、 Uo (s)作为信号流图的节点 Ui(s)、Uo(s)分别为输入及输出节点
2. 根据方框图绘制信号流图
方块图转换为信号流 图
信号流图的等效变换法则
•支路增益——支路传输定量地表明变量从支路一端沿箭头方 向传送到另一端的函数关系。用标在支路旁边的传递函数 “G”表示支路传输。
2.
通路
沿支路箭头方向穿过各相 连支路的路径。
前向通路 从源节点到阱节点的通路上通过任何节点 不多于一次的通路。前向通路上各支路增益之 乘积，称前向通路总增益，一般用pk表示。
信号流图梅森公式

梅逊公式

梅逊公式

2-7 结构图等效变换及梅逊公式求传递函数时，需要对微分方程组（或变换方程组）进行消元，最后仅剩下输入、输出两个变量，因此中间变量的传递过程得不到反映。

若采用结构图，它就能形象地表明输入信号在系统或元件中的传递过程。

另外，下面将会看到，利用结构图，也便于求取传递函数。

所以，结构图在控制理论中应用十分广泛。

一、结构图在第2-6节中，我们曾采用消元法求得图2-24所示RC 网络的传递函数。

这里，我们采用结构图的方法求其传递函数。

RC 网络的微分方程组如下：⎪⎩⎪⎨⎧=+=⎰idt C u u Ri u c cr 1对上两式进行拉氏变换，得)()()(s U s RI s U c r +=或[])()()(1s I s U s U Rc r =- （2-54） )(1)(s I Css U r =（2-55）方程（2-54）可用图2-29)(a 表示，方程（2-55）可用图2-29)(b 表示。

将图2-29)(a )(b 按信号传递方向结合起来，网络的输入量置于图示的左端，输出量置于最右端，并将同一变量的信号连在一起，如图2-30)(a 所示，即得RC 网络结构图。

对图2-30)(a 进行所谓“等效变换”就可得出网络传递函数，因此网络结构就更为简单,如图2-30)(b 所示。

关于结构图等效变换的方法将另作介绍。

（1）建立控制系统各元、部件的微分方程。

（2）对各元、部件的微分方程进行拉氏变换，并做出各元、部件的结构图。

（3）按系统中各信号的传递顺序，依次将各元件结构图连接起来，便得到系统的结构图。

下面以图1-7所示随动系统为例。

把组成该系统各元部件的微分方程（2-18）进行拉氏变换，可得方程组（2-56e a ~），其中比较元件 )()()(s s s c r θθθε-=（2-56a ） 电位器 )()(1s K s U εεθ= （2-56b ） 放大器 )()(2s U k s U ε=（2-56c ） 电动机 )()()1(s U K s s T s m m =+εθ（2-56d ） 减速器)(1)(s is c θθ=（2-56e ）各元、部件的结构图如图2-31所示。

  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
G(s)
信号分支点的移动和互换
G(s) N(s)
Tuesday, June 30, 2020
9
分支点从环节的输出端移到输入端：
G(s)
信号相加点和分支点的移动和互换
G(s) N(s)
[注意]： 相临的信号相加点位置可以互换而不改变其等效性；见下例
Tuesday, June 30, 2020
10
信号相加点和分支点的移动和互换
比较环节：
运放Ⅰ：
运放Ⅱ：
K1
功放环节：
K2 (s 1)
Tuesday, June 30, 2020
K3
2
反馈环节：
电动机环节：
K3
M c (s) Km (Tas 1)
TaTms2 Tms 1
Ua (s)
Ku
TaTms2 Tms 1
-
(s)
将上面几部分按照信号传递方向连接起来，形成下页所示的完整结构图。 通常将输入信号画在最左边,输出信号画在最右边.
-1
1
-
R1
C1s
1 R2C2s 1
1 R2C2s 1
R1C2 s
-
1
1
-
R1
C1s
1 R2C2s 1
Tuesday, June 30, 2020
16
R1C2 s
-
1
R1C1s 1
1 R2C2s 1
Tuesday, June 30, 2020
17
解法二：
-
1
1
1
1
-
R1
C1s
-
R2
C2s
-
1
1
4
二、结构图的等效变换： [定义]：在结构图上进行数学方程的运算。 [类型]：①环节的合并；
--串联 --并联 --反馈连接 ②信号分支点或相加点的移动。 [原则]：变换前后环节的数学关系保持不变。
Tuesday, June 30, 2020
结构图的等效变换
5
（一）环节的合并：有串联、并联和反馈三种形式。
1 R2C2s 1
Tuesday, June 30, 2020
22
结构图等效变换例子||例2-12
[例2-12]系统结构图如下，求传递函数
1
-
R2
1 C2s
14
为了求出总的传递函数，需要进行适当的等效变换。一个可能的变换过程如下：
-
1
1
1
1
-
R1
C1s
-
R2
C2s
C2s
-
1
1
1
1
-
R1
C1s
-
R2
C2s
1
-
R1
C2s
-
1 C1s
1 R2C2s 1
Tuesday, June 30, 2020
15
1
-
R1
C2s
-
1 C1s
R1C2 s
X(t) 电结位构器图：Y(t)
微分方程：y(t)=kx(t)
X(s)
Y(s)
G(s)=K
若已知系统的组成和各部分的传递函数，则可以画出各个部分的结构图并连成整个 系统的结构图。
Tuesday, June 30, 2020
1
结构图的基本概念
[例2-10].求例2-6所示的速度控制系统的结构图。各部分传递函数见例2-8，罗列如 下：
结构图的基本概念
一、结构图的基本概念：
我们可以用结构图表示系统的组成和信号流向。在引入传递函数后，可以把环 节的传递函数标在结构图的方块里，并把输入量和输出量用拉氏变换表示。这时 Y(s)=G(s)X(s)的关系可以在结构图中体现出来。
[定义]表示变量之间数学关系的方块图称为函数结构图或方块图。
[例]：结构：
1
1
R1
-
C1s
-
R2
C2s
1
1
R1
C2s
-
1
1
1
1
R1
-
C1s
-
R2
C2s
Tuesday, June 30, 2020
1
1
R1
C2s
18
1
-
R1
C2s
1
R1
R1C1s 1 R2C2s 1
C2s
1
R1C2 s
1
R1 (R1C1s 1)( R2C2s 1) R1C2s
C2s
Tuesday, June 30, 2020
支点。
①信号相加点的移动： 把相加点从环节的输入端移到输出端
G(s)G(s)N( Nhomakorabea)Tuesday, June 30, 2020
7
信号相加点的移动和互换
把相加点从环节的输出端移到输入端：
G(s)
N(s)
G(s)
Tuesday, June 30, 2020
8
②信号分支点的移动： 分支点从环节的输入端移到输出端
19
解法三：
1
-
R1
1
-
R1
1
C1s
1 R2 1 C1s
1
-
R1
Tuesday, June 30, 2020
1
R2
+-
1
C1s
1
1
-
R2
C2s
1
1
-
R2
C2s
1 R2
1
-
R2
1 C2s
20
1
R2
1
+-
1
-
R1
C1s
1 R2
1
1
-
R2
C2s
+
1
-
R1
R2 R2C1s 1
1 R2
1 R2C2s 1
[解]：不能把左图简单地看成两个RC电路的串
联,因有负载效应。根据电路定理，有以下等式
i2
和结构图：
Tuesday, June 30, 2020
-
1 C1s
-
1
13
C2s
结构图等效变换例子||例2-11
-
1
C1s
-
总的结构图如下：
1
-
R1
-
1 C1s
Tuesday, June 30, 2020
1 C2s
同一信号的分支点位置可以互换而不改变其等效性；见下例
G(s)
相加点和分支点在一般情况下，不能互换。
G(s)
G(s)
G(s)
✓在一般情况下，相加点向相加点移动，分支点向分支点移动。
常用的结构图等效变换见表2-1
Tuesday, June 30, 2020
11
结构图等效变换例子||例2-11
[例2-11]利用结构图等效变换讨论两级RC串联电路的传递函数。
Tuesday, June 30, 2020
3
结构图的基本概念
K1
K2 (s 1)
K3
Kf
Km (Tas 1) TaTms Tms 1
Ku
-
TaTms Tms 1
在结构图中，不仅能反映系统的组成和信号流向，还能表示信号传递过程中的数 学关系。系统结构图也是系统的数学模型，是复域的数学模型。
Tuesday, June 30, 2020
环节的串联：
X (s) G1(s) …
环节的并联：
Y (s) Gn (s)
反馈联接：
G1 ( s )
G(s)
Gn (s)
H (s)
环节的合并
Tuesday, June 30, 2020
6
信号相加点的移动
（二）信号相加点和分支点的移动和互换： 如果上述三种连接交叉在一起而无法化简，则要考虑移动某些信号的相加点和分
1
R2 (R2C2s 1)
+
1
R2
1
-
R1
Tuesday, June 30, 2020
R2C1s 1
R2C2s 1
21
+
1
-
R1
1 R2 (R2C2s 1)
R2 R2C1s 1
1 R2C2s 1
1
R2C2s 1
-
R1
R2C1C2s2 (C1 C2 )s
1 R2C2s 1
R2C2s 1 R1R2C1C2s2 (R1C1 R1C2 )s R2C2s 1