当前位置：文档之家 › 10山东建筑大学结构力学动力学1解析

10山东建筑大学结构力学动力学1解析

  • 格式：ppt
  • 大小：895.00 KB
  • 文档页数：21

下载文档原格式

  / 21

合集下载

结构力学课后答案第10章结构动力学

结构力学课后答案第10章结构动力学
\
解：
若 为静力荷载，弹簧中反力为 。
已知图示体系为静定结构，具有一个自由度。设为B点处顺时针方向转角 为坐标。建立动力方程：
则弹簧支座的最大动反力为 。
10-21设图a所示排架在横梁处受图b所示水平脉冲荷载作用，试求各柱所受的最大动剪力。已知EI=6×106Nm2，t1＝，FP0＝8×104N。
(a)
则同样有： 。
10-9图示结构AD和DF杆具有无限刚性和均布质量 ，A处转动弹簧铰的刚度系数为kθ，C、E处弹簧的刚度系数为k，B处阻尼器的阻尼系数为c，试建立体系自由振动时的运动方程。
*
解：
取DF隔离体， ：
取AE隔离体：
将R代入，整理得：
/
10-10试建立图示各体系的运动方程。
(a)
解：（1）以支座B处转角作为坐标，绘出梁的位移和受力图如下所示。图中惯性力为三角形分布，方向与运动方向相反。
图 图
（1）求结构运动方程
如所示弯矩图，图乘后，
其中 ，稳态解：
所示结构的运动方程为 ，C点最大动位移幅值为
（2）求B点的动位移反应
，
！
B点的动位移幅值为
（3）绘制最大动力弯矩图
图 图
最大动力弯矩图
10-20试求图示集中质量体系在均布简谐荷载作用下弹簧支座的最大动反力。设杆件为无限刚性，弹簧的刚度系数为k。
（2）画出 和 图（在B点处作用一附加约束）
…
（3）列出刚度法方程
， ，
代入 、 的值，整理得：
(b)
解：
图 图
】
试用柔度法解题
此体系自由度为1 。设质量集中处的竖向位移y为坐标。
y是由动力荷载 和惯性力矩 共同引起的。

结构力学的动力特性分析

结构力学的动力特性分析

结构力学的动力特性分析结构力学是工程学中重要的学科，它研究物体在外界作用力的作用下产生的力学行为及其相互关系。

动力特性分析是结构力学中的一个重要方向，它研究结构在外部激励下的振动特性以及对结构的影响。

本文将探讨结构力学的动力特性分析方法及其在实际工程中的应用。

一、动力特性分析的基本方法动力特性分析是研究结构振动行为的一种方法，它主要通过求解结构的固有频率、模态形态和频率响应等来描述结构对外界激励的响应情况。

以下是动力特性分析的基本方法：1. 固有频率分析：通过求解结构的本征值和本征向量，得到结构的固有频率和模态形态。

固有频率是结构在自由振动状态下的频率，也是结构振动的基本特性之一。

2. 频率响应分析：通过对结构施加外部激励，计算结构在不同频率下的响应特性。

频率响应分析可以帮助工程师了解结构对不同频率激励的响应情况，从而做出相应的优化设计。

3. 模态超几何分析：对于非线性结构或者多自由度结构，可以采用模态超几何分析方法来描述结构的动力特性。

该方法主要是在模态基础上引入非线性效应，研究结构在不同模态下的非线性行为。

二、动力特性分析的应用动力特性分析在工程实践中具有广泛的应用，以下是动力特性分析在各个领域的具体应用案例：1. 建筑工程：在建筑工程中，动力特性分析可以用于研究大楼、桥梁等结构的抗震性能。

通过分析结构的固有频率和模态形态，可以对结构进行合理的抗震设计，提高结构的地震安全性能。

2. 车辆工程：在汽车、火车等交通工具的设计中，动力特性分析可以用于优化车辆的悬挂系统、减震器等部件。

通过分析车辆在不同频率下的响应特性，可以改善车辆的行驶平稳性和乘坐舒适度。

3. 航空航天工程：在航空航天领域，动力特性分析可以用于研究飞机、火箭等载具的结构振动特性。

通过对结构的固有频率和模态形态的研究，可以对飞行器的结构强度和稳定性进行评估和设计。

4. 机械工程：在机械设计中，动力特性分析可以用于优化机械系统的结构和参数。

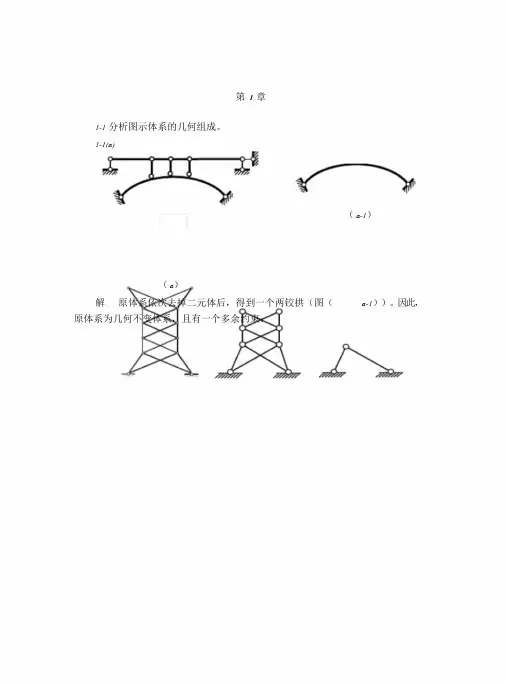
最新结构力学第1章习题及参考答案文件.doc

最新结构力学第1章习题及参考答案文件.doc

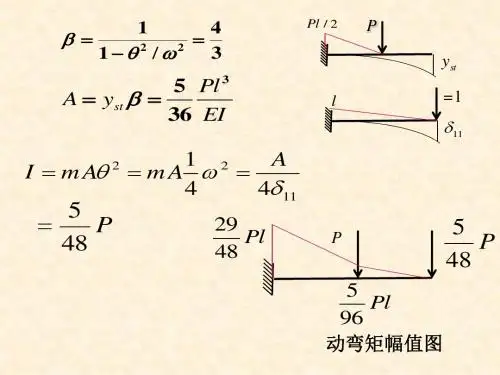
第1章1-1 分析图示体系的几何组成。

1-1(a)（a-1）（a）解原体系依次去掉二元体后，得到一个两铰拱（图（a-1））。

因此，原体系为几何不变体系，且有一个多余约束。

1-1 (b)（b）（b-1）（b-2）解原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (c)（c）（c-1）（c-2）（c-3）解原体系依次去掉二元体后，得到一个三角形。

因此，原体系为几何不变体系，且无多余约束。

1-1 (d)（d）（d-1）（d-2）（d-3）解原体系依次去掉二元体后，得到一个悬臂杆，如图（d-1）-（d-3）所示。

因此，原体系为几何不变体系，且无多余约束。

注意：这个题的二元体中有的是变了形的，分析要注意确认。

1-1 (e)AABB C（e）（e-1）（e-2）解原体系去掉最右边一个二元体后，得到（e-1）所示体系。

在该体系中，阴影所示的刚片与支链杆 C 组成了一个以 C 为顶点的二元体，也可以去掉，得到（e-2）所示体系。

在图（e-2）中阴影所示的刚片与地基只用两个链杆连接，很明显，这是一个几何可变体系，缺少一个必要约束。

因此，原体系为几何可变体系，缺少一个必要约束。

1-1 (f)（f-1）（f ）解原体系中阴影所示的刚片与体系的其它部分用一个链杆和一个定向支座相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉只分析其余部分。

很明显，余下的部分（图（f-1））是一个几何不变体系，且无多余约束。

因此，原体系为几何不变体系，且无多余约束。

1-1 (g)（g）（g-1）（g-2）解原体系中阴影所示的刚片与体系的其它部分用三个链杆相连，符合几何不变体系的组成规律。

因此，可以将该刚片和相应的约束去掉，只分析其余部分。

余下的部分（图（g-1））在去掉一个二元体后，只剩下一个悬臂杆（图（g-2））。

因此，原体系为几何不变体系，且无多余约束。

1-1 (h)（h）（h-1）解原体系与基础用一个铰和一个支链杆相连，符合几何不变体系的组成规律。

10山东建筑大学结构力学动力学4解析

10山东建筑大学结构力学动力学4解析

Pl ( P
P ( P m )l P(1 2 )l k
2 2
两个自由度体系的自由振动
一、刚度法
D
(k11 2m1 ) k21
k12 (k22 m2 )
2
0
特征方程
频率方程
(k11 2m1 )(k22 2m2 ) k12k21 0




荷载幅值产生的静位移和静内力 yst1= yst2=P/k 层间剪力: Qst1= P P
yst2=P/k
θ2mY2 k θ2mY1 k
动荷载产生的位移幅值和内力幅值
yst1
Y1 1 2 2 P (1 2 )(1 2 ) k 1 2 Y2 1 2 2 2 P (1 2 )(1 2 ) k 1 2
Y2
3.0 2.0
P k
3.0 2.0
k
0.618
1.618
0.618
k
1.618
1.0 0 -1.0 -2.0 -3.0

m
1.0 0 -1.0 -2.0 -3.0

k m
3.0
3.0
两个质点的 位移动力系 数不同。
当 0.618 k m 1 和 1.618 k m 2时,Y1和Y2 趋于无穷大。 可见在两个自由度体系中，在两种情况下可能出现共振。 但也有特例
Psinθt k2 m2
2n 2 300 31.4 1 s 60 60
频率比在共振区之内应设置吸振器。
P 2）由 k2 弹簧刚度系数为： Y2 1000 k2 110 5 N/m 0.01 k 2 1105 =102 kg m2 2 2 31.4

山东建筑大学理论力复习要点

山东建筑大学理论力复习要点
分别为R和r,且R = 2r,物体
A
C重P,作用于A轮的转矩M
为一常量.求物体 C上升的 加速度.
B
C
25
解:取系统为研究对象进 行运动分析.
A作定轴转动,B作平面运动,C作直线平动. R A = 2r B A = B =
M

A
A = B =
vC = vB = r
aC = aB = r
A M
B
C
20
YA
解:取系统为研究对象进行运动分析. A作定轴转动,B作平面运动I为 瞬心,C作直线平动. R A = 2r B A = B = vC = vB = r αA = αB = α a C = a B = rα
I
A M W1 XA
B W2 C
取系统为研究对象进行受力分析. 内力和约束力均不作功.
P 解除B点约束代之RB
Q1 rC
1
Q2
2
M
rC ( AC)1 (CD)2
1 2
A
B
C
D
RB
1 1 1 1
W ( P) 1 4900 1 4900
1
1
2
W (Q1 ) 3 4900 1 14700 W (Q2 ) 3 4900 2 14700
1 l 2 J O 0 W sin 2 2
x y
O A
C
acn ac
3g sin l
3g cos 2l
ac
l 3g cos 2 4
acn
l 2 3g sin 2 2
30
x
取杆为研究对象画受力图. y

第10章 结构动力学

第10章 结构动力学

TMD又称为固体阻尼器，液体阻尼器TLD（ Tuned Liquid Damper ）工程中也有应用。
调质阻尼器按启动机制可分为被动式调质阻尼器（Passive Tuned Mass Damper）和主动式调质阻尼器（Active Tuned Mass Damper）。台北101所采用的是被动式调质阻尼器。 世界上采用被动式TMD的其它代表性建筑有：加拿大多伦多 的CN Tower、日本大阪的Crystal Tower、澳洲悉尼的 Centerpoint Tower、美国纽约的Citicorp Center、日本的明石 海峡大桥 Akashi Kaikyo Bridge ，等等。
4 ( x) sin
2014-1-10
…
广义坐标法是一种数学简化方法
第10章
10.2体系的动力自由度
有限单元法：
可以看作是分区的广义坐标法，其要点与静力问题一样，是先把结构划分 成适当数量的区域（称为单元），然后对每一单元施行广义坐标法。详见 有限单元法参考资料，这里不再赘述。 一般地说，有限元法是最灵活有效的离散化方法，它提供了既方便又可靠 的理想化模型，并特别适合于用电子计算机进行分析，是目前最为流行的 方法，已有不少专用的或通用的程序可供结构动力学分析之用。 有限单元法也是一种数学简化方法
m ml 4 m l 4
EI l 4
m3 m2 m1
l 4
l 4
假定刚梁 质量向楼面集中 动力自由度＝3
3层框架 楼面刚度和质量比柱子大
2014-1-10
集中质量法是一种物理简化方法
第10章
10.2体系的动力自由度
广义坐标法：以图示简支梁无限自由度体系为例说明。
例：
m EI l

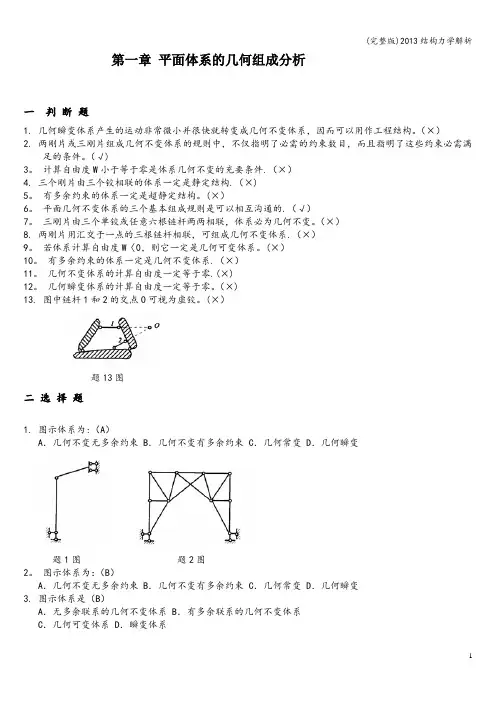
(完整版)结构力学解析

(完整版)结构力学解析

第一章平面体系的几何组成分析一判断题1. 几何瞬变体系产生的运动非常微小并很快就转变成几何不变体系，因而可以用作工程结构。

（×）2. 两刚片或三刚片组成几何不变体系的规则中，不仅指明了必需的约束数目，而且指明了这些约束必需满足的条件。

（√)3。

计算自由度W小于等于零是体系几何不变的充要条件.（×）4. 三个刚片由三个铰相联的体系一定是静定结构.（×)5。

有多余约束的体系一定是超静定结构。

(×）6。

平面几何不变体系的三个基本组成规则是可以相互沟通的.（√）7。

三刚片由三个单铰或任意六根链杆两两相联，体系必为几何不变。

（×）8. 两刚片用汇交于一点的三根链杆相联，可组成几何不变体系.（×）9。

若体系计算自由度W〈0，则它一定是几何可变体系。

(×）10。

有多余约束的体系一定是几何不变体系.（×）11。

几何不变体系的计算自由度一定等于零.(×)12。

几何瞬变体系的计算自由度一定等于零。

（×)13. 图中链杆1和2的交点O可视为虚铰。

(×）题13图二选择题1. 图示体系为:（A）A．几何不变无多余约束 B．几何不变有多余约束 C．几何常变 D．几何瞬变题1图题2图2。

图示体系为：（B）A．几何不变无多余约束 B．几何不变有多余约束 C．几何常变 D．几何瞬变3. 图示体系是（B）A．无多余联系的几何不变体系 B．有多余联系的几何不变体系C．几何可变体系 D．瞬变体系题3图4。

图示体系的几何组成为（B）A．几何不变无多余约束 B．几何不变有多余约束 C．瞬变体系 D．可变体系题4图5. 图示平面体系的几何组成为（C)A。

几何不变无多余约束 B。

几何不变有多余约束 C.瞬变体系 D.几何可变体系题5图6. 图示体系为（A）A。

几何不变,无多余约束 B.几何不变,有多余约束 C。

几何常变 D。

几何瞬变题6图题7图7. 图示体系为（D）A。

山东建筑大学《结构力学》——1

山东建筑大学《结构力学》——1

桁架特点：理想铰、平直杆、力结点 ⑸组合结构： 这是由桁架和
梁或桁架和刚架等组合在一起的 结构。在这种结构中，有些杆件 只承受轴力，而另一些杆件则同 时承受弯矩、剪力和轴力。
§1—4 荷载的分类
1.荷载：指作用在结构上的主动力。 如：自重、荷重、风载、雪载……等。 2.荷载的分类
按作用时间久暂 恒载(长期且不变), 如自重、土压力等。

§1—2 杆件结构的计算简图
计算简图: 能表现结构的主要特点,略去次要因素 的原结构的简化图形。 1.杆件的简化; 简化的内容 2.荷载的简化； 3.支座和结点的简化。
例如: q
P
一、杆件的简化 根据杆件受力后的变形特点，由材料力学可知， 各种杆件在计算简图中均用其轴线来代替。等截 面直杆的轴线是一直线，曲杆是一曲线。一根变 截面杆件也都近似地以一条直线或曲线来代替。
工业厂房 高层建筑
薄壳屋面
圆形水池
矩形水池
挡土墙
塔式起重机结构
展车台结构
立体车库结构
3. 结构力学的具体任务：
(1) 研究荷载等因素在结构中所产生的内力（强度计算）； (2)计算荷载等因素所产生的变形（刚度计算）； (3)分析结构的稳定性（稳定性计算）； (4)探讨结构的组成规律及合理形式。 进行强度、稳定性计算的目的，在于保证结构满足安全和 经济的要求。 计算刚度的目的，在于保证结构不至于发生过大的变形， 以至于影响正常使用。 研究组成规律目的，在于保证结构各部分，不至于发生相 对的刚体运动，而能承受荷载维持平衡。 探讨结构合理的形式，是为了有效地利用材料，使其性能 得到充分发挥。
X Y
M
Y
X Y
（4）定向支座
M Y
三.结点的简化

在线网课《结构力学A1(山东联盟-山东建筑大学)》课后章节测试答案

在线网课《结构力学A1(山东联盟-山东建筑大学)》课后章节测试答案

第一章测试1【多选题】(100分)结构力学的主要内容是（）A.讨论结构的稳定性，以及在动力荷载作用下的反应B.结构的组成规律与合理形式计算简图的合理选择C.在外力或其他因素影响下，结构的内力和变形计算第二章测试1【单选题】(20分)作为结构的体系应是：A.几何不变体系或瞬变体系B.几何不变体系C.几何可变体系D.瞬变体系2【单选题】(20分)图示体系虽有3个多余约束，但为保证其几何不变，哪两根链杆是不能同时去掉的。

A.a和eB.a和cC.a和bD.c和e3【单选题】(20分)图示体系为：A.几何不变无多余约束B.几何不变有多余约束C.几何可变D.几何瞬变4【单选题】(20分)图示体系为：A.几何不变有多余约束B.几何可变C.几何不变无多余约束D.几何瞬变5【判断题】(20分)有多余约束的体系一定是几何不变体系。

A.错B.对第三章测试1【判断题】(15分)几何不变体系一定是静定结构。

A.错B.对2【单选题】(15分)静定结构在荷载作用下，其全部反力和内力：A.都可由静力平衡条件求得，而且数值是确定的B.特殊情况下，才可由静力平衡条件唯一地确定C.可由静力平衡条件求得，但数值有时是不确定的D.不能只由平衡条件来确定，还必须考虑变形条件3【判断题】(15分)静定结构在支座移动、变温及荷载分别作用下，均产生位移和内力。

A.错B.对4【判断题】(15分)多跨静定梁仅当基本部分承受荷载时，其它部分的内力和反力均为零。

A.对B.错5【单选题】(15分)A.B.-0.5pC.0.5pD.p6【判断题】(15分)图示为一杆段的M、Q图，若Q图是正确的，则M图一定是的。

A.错B.对7【判断题】(15分)图示梁上的荷载P将使CD杆产生内力。

A.错B.对8【单选题】(15分)图示桁架内力为零的杆有（）A.6根B.7根C.8根D.9根9【单选题】(10分)A.B.C.D.10【判断题】(10分)图示三铰拱左支座的竖向反力为零。

《结构力学》习题解答(内含解答图)

《结构力学》习题解答(内含解答图)
习题2-12图习题2-12解答图
习题2-13试对图示体系进行几何组成分析。
习题2-13图习题2-13解答图
解：将原图结点进行编号，并将支座6换为单铰，如图（b）。取基础为刚片Ⅰ，△134为刚片Ⅱ，△235为刚片Ⅲ，由规则一知，三刚片用三个不共线的铰联结组成几何不变体。在此基础上增加二元体674、785，而杆38看作多余约束。杆910由铰联结着链杆10，可看作二元体，则整个体系为有一个多余约束的几何不变体系。
习题2-7试对图示体系进行几何组成分析。
习题2-7图习题2-7解答图
解：将题中的折杆用直杆代替，如图（b）所示。杆CD和链杆1由铰D联结构成二元体可以去掉；同理，去掉二元体杆CE和链杆2，去掉二元体ACB,则只剩下基础，故整个体系为几何不变体系，且无多余约束。
另外也可用基础与杆AC、杆BC是由不共线的三个铰联结，组成几何不变体，在此几何不变体上增加二元体杆CD和链杆1、杆CE和链杆2的方法分析。，
习题2-8试对图示体系进行几何组成分析。
习题2-8图习题2-8解答图
解：为了便于分析，对图中的链杆和刚片进行编号，分析过程见图2-21(b)。首先去掉二元体NMI、JNI，然后分析剩余部分。杆AD由固定支撑与基础联结形成一体，构成几何不变体，在此基础上增加二元体DEB、EFC、EHF形成刚片Ⅰ（注意固定铰支座与铰相同）；铰结△GIJ为刚片Ⅱ；刚片I与刚片Ⅱ之间用不交于一点的杆DI、杆GI、杆HJ相连，组成几何不变体。
习题2-18试对图示体系进行几何组成分析。
解：将原图结点进行编号，并将固定铰支座换为单铰，如图（b）。折杆AD上联结杆EF，从几何组成来说是多余约束；同理，折杆CD上联结杆EF也是多余约束。取基础为刚片Ⅰ，折杆AD为刚片Ⅱ，折杆CD为刚片Ⅲ。刚片Ⅰ与刚片Ⅱ是由链杆A和杆BD相连，刚片Ⅰ与刚片Ⅲ是由链杆C相连，注意，杆BD只能使用一次。由规则二知，体系为几何可变体系。

结构力学1习题答案

结构力学1习题答案

结构力学1习题答案结构力学1习题答案结构力学是土木工程中非常重要的一门学科，它研究物体在外力作用下的变形和破坏规律。

在学习过程中，习题是帮助我们巩固知识和提高解题能力的重要途径。

下面将为大家提供一些结构力学1习题的答案，希望能对大家的学习有所帮助。

1. 一根长为L的悬臂梁，在其自重和集中力F的作用下，左端A有一个水平位移δ，求右端B的水平位移。

解答：由于是悬臂梁，右端B受到的力只有集中力F。

根据结构力学的基本原理，我们可以得到以下方程：F * L = k * δ其中，k是悬臂梁的刚度。

根据悬臂梁的刚度公式 k = 3EI / L^3，我们可以将上述方程改写为：F * L = 3EI * δ / L^3整理得到：δ = F * L^3 / 3EI所以，右端B的水平位移为δ = F * L^3 / 3EI。

2. 一根长度为L、截面积为A的均匀梁，在其自重和均匀分布载荷q的作用下，求梁的最大弯矩和最大挠度。

解答：首先求解最大弯矩。

根据梁的平衡条件，我们可以得到以下方程：M_max = q * L^2 / 8其中，M_max为最大弯矩。

根据梁的挠度公式δ = q * L^4 / (8EI)，我们可以将上述方程改写为：M_max = δ * EI / L^2所以，梁的最大弯矩为 M_max = q * L^2 / 8，最大挠度为δ = q * L^4 / (8EI)。

3. 一根长度为L、截面积为A的均匀梁，在其自重和均匀分布载荷q的作用下，求梁的中点处的弯矩和挠度。

解答：由于是均匀分布载荷，梁在中点处的受力为 qL/2。

根据梁的平衡条件和挠度公式，我们可以得到以下方程：M_mid = q * L^2 / 8δ_mid = q * L^4 / (192EI)所以，梁在中点处的弯矩为 M_mid = q * L^2 / 8，挠度为δ_mid = q * L^4 / (192EI)。

4. 一根长度为L、截面积为A的均匀梁，在其自重和均匀分布载荷q的作用下，求梁的最大应力和最大挠度。

山东建筑大学结构力学

山东建筑大学结构力学

1. 一个点与一个刚片之间的组成方式 一个点与一个刚片之间用两根链杆相连,且三铰不 在一直线上,则组成无多余约束的几何不变体系。
2. 两个刚片之间的组成方式 两个刚片之间用一个铰和一根链杆相连, 且 三铰不在一直线上,则组成无多余约束的几何 不变体系. 或两个刚片之间用三根链杆相连, 且三根链杆不交于一点,则组成无多余约束的 几何不变体系。
第二章 结构的几何构造分析
1
概述
本章内容：研究平面杆件体系的组成规律。
研究体系几何组成的任务和目的： １、研究体系的基本组成规则，用以判定体系是否 可作为结构。 ２、根据体系的几何组成，选择相应的计算方法和 计算途径。
2
§2-1 基本概念
1 几何不变体系、几何可变体系
体系受到某种荷载作用，在不考虑材料应变的 前提下，体系若不能保证几何形状、位置不变，称 为几何可变体系。
组成几何不变体系的条件：
• 具有必要的约束数；
• 约束布置方式合理
14
瞬变体系 体系在特定位置时是几何可变，
离开此位置，是几何不变。
FP
FP
15
有限交点
无限交点
常变体系 瞬变体系
16
瞬变体系受力不合理，不可作为结构
FP
FP
FN
FN
FN

FP
2 sin

17
利用组成规律可以两种方式构造一般的结构： （1）从基础出发构造
6
4、约束
约束：能减少体系自由度数的装置。
7
结论: 一个链杆相当一个约束 一个单铰相当两个约束 一个固定支座相当三个约束 一个刚结点相当三个约束
8
5、多余约束
在体系上加上或撤除某一约束并不改变原体系的 自由度数，则该约束就是多余约束。

山东建筑大学结构力试卷 答案与评分标准

山东建筑大学结构力试卷 答案与评分标准

山东建筑大学试卷 答案与评分标准 共 2页第1页2012 2013 学年第 1 学期 考试时间： 120 分钟课程名称： 结构力学A2 （A √、B ）卷 考试形式：（√闭卷、开卷） 年级：辅修2011级 专业： 土木工程 ；层次：（√本、专科） 题号 一 二 三 四 五 总分 分数一、用力矩分配法计算图示结构，作出弯矩图。

EI = 常 数 。

（20分）- /8/8- /32-5 /32=1- /16/16=4/32分 ()2分 ()2分 ()5 /32/16图M 6分 ()i i Pl Pl Pl Pl Pl Pl Pl Pl Pl 1/21/29/64计算分配系数 6分 固端弯矩 2分 分配传递 6分 弯矩图 6分二、用矩阵位移法，求图示连续梁的总刚度矩阵和节点荷载列矩阵。

（20分）EI 20kNm20kNm80kN4m4m3m3m2EI EI编号、坐标系 2分 定位向量 2分等效荷载 4分 最后荷载矩阵 4分1233020226033402033EI EI EIEI EI EI EI θθθ⎡⎤⎢⎥-⎛⎫⎛⎫⎢⎥ ⎪ ⎪⎢⎥= ⎪ ⎪⎢⎥ ⎪ ⎪-⎢⎥⎝⎭⎝⎭⎢⎥⎢⎥⎣⎦三、图 示 梁 自 重 不 计 ，W EI ==⨯⋅2002104kN kN m 2,，求自振圆频率。

（20分）EI WABC2m2m由 于 对 称 ，跨 中 无 转 角 ，求 刚 度 k k EI k k ,/,114322610===⨯kN /m(15分 )ω=-542.s 1 (5分 )∆2m=1k 1考场 班级 姓名 学号 线 装订线 装订线山东建筑大学试卷 答案与评分标准 共2页第2页四、求 图 示 刚 架 的 临 界 荷 载 。

（20分）PlllEIEI O OEI简 化 为 轴 压 杆 ， 下 端 转 动 刚 度 r k =6EIl。

（ 10 分 ） P crABδk r θθ小 挠 度 ， 中 性 平 衡 ，A M =∑0 ，P δθ-⋅=r k 0 ，θδδ=-⋅=lP k lr,()0 ，cr δ≠==062,P kl EI lr（ 10 分 ）五、图示梁的截面极限弯矩为M u 。

山东建筑大学《结构力学》——互等定理

山东建筑大学《结构力学》——互等定理

2
FN 2 EA
2
M2 EI
F N1 N2 M 1 M 2 kF Q1 Q2 F F + + ds W12 P1 2 EI GA EA
F Ｎ２N1 M 2 M 1 kF Q2 Q1 F F + + W21 F2 1 ds EI GA EA
（4-11） 位移互等定理：（P74） 在任一线性变形体系中，由荷载P1所引起的与荷载P2相应 的位移影响系数δ21 等于由荷载P2所引起的与荷载P1相应的位移影 响系数δ12 。或者说,由单位荷载P1=1所引起的与荷载P2相应的位移 δ21等于由单位荷载P2=1所引起的与荷载P1相应的位移δ12 。
4、图示结构桁架中，腹杆 截面的大小对C点的竖向位 14 移有影响。（ ） 题 5、虚位移原理等价于变形 图 协调条件，可用于求体系 的位移。（ ） 6、在荷载作用下，刚架和梁的位移主要由于各个杆的弯曲 变形引起。（ ）
7、图示桁架C点的水平位移不等于零。 7 （ ） 题 8、应用虚力原理求体系的位移时，虚 图 设力状态可在需求位移处添加相应的非 单位力，亦可求的该位移。（ ） 9、图示结构L>a>0 B点的水平位移是 （ ） A、向右 B、向左 C、等于零 D、不一定
四、互等定理 •适用条件 •内容 W12= W21
ql2/8
↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓↓
MP
d12d 21
r12=r21 l
ql
B
EI
l
求B点竖向位移
M
1
BV
1 1 3 ql 2 l 2 l ql l 11 ql l EI 2 2 3 3 8 2 24 EI

10结构动力学概论

10结构动力学概论

当 FP (t)为简谐荷载时，其解的形式为
第十章 结构动力学简介
y(t)
y0
cos ωt
ν0 ω
sin ωt
F
θ sin ωt
F
sin θt
m(ω2 θ 2 ) ω
m(ω2 θ 2 )
前两项为初始条件引起的自由振动;第三项为荷载（干扰力）引起的自由振 动，称为伴生自由振动。实际上，由于阻尼的存在，自由振动部分都很快 衰减掉。自由振动消失前的振动阶段称为过渡阶段。第四项为按荷载频率 进行的振动，此阶段为振动的平稳阶段，称为纯受迫振动或稳态振动。
2、平衡方程的建立
平衡方程的建立有两种方法：一是刚度法；一是柔度法。
my
y k
k
m
刚度法：根据达兰贝尔原理，沿位移正向，在质点上加上惯性力，列动态平 衡方程
ky my
k y ——总是与位移方向相反，指向平衡位置
平m衡y 方—程—与加速m度y方向相k反y 0
第十章 结构动力学简介
柔度法：在惯性力作用下，质点的位移等于实际位移
结构力学
STRUCTURAL MECHANICS
第十章 结构动力学简介
§10-1 概述
一、动力计算的内容
动力计算的内容：研究结构在动荷载作用下的动力反应的计算原理和方法。 涉及到内外两方面的因素： 1）确定动力荷载（外部因素，即干扰力）； 2）确定结构的动力特性（内部因素，如结构的自振频率、周期、振型和 阻尼等等），类似静力学中的I、S等； 计算动位移及其幅值；计算动内力及其幅值。
纯受迫振动解的讨论请同学们课下自学完成！
第十章 结构动力学简介
三、阻尼对振动的影响
§10-3 单自由度体系的振动分析

山东建筑大学结构力学静定结构的内力分析

山东建筑大学结构力学静定结构的内力分析
返回
1、单元的形式及未知力 结点：桁架的结点法、刚架计算中已知FQ求FN时取结点为单元。 杆件：多跨静定梁的计算、刚架计算中已知M求FQ时取杆件为单元。 杆件体系：桁架的截面法取杆件体系为单元。
未知力的数目是由所截断的约束的性质决定的。 截断链杆只有未知轴力；在平面结构中，截断梁式杆，未知 力有轴力、剪力和弯矩；在铰处截断，有水平和竖向未知力。
作用，为了画弯矩图，可将该梁 分为b示两段，分别绘弯矩图然 后相连。（ ）
7 题 图
8、图示结构 的支反力是 正确的。 （）
8题图
10、图示梁的弯矩图 是正确的。（ ）
9、两杆相交的刚结点， 其杆端弯矩一定等值同侧 （即两杆端弯矩代数和为 零）。（ ）
10题图
返回
11、图示刚架，AD中截面C的 弯矩等于： （A） (左拉) （B） (右拉) （C） (左拉) （D） (右拉)
15题图
返回
作业
第50页 3-18（a）、3-20（a）
返回
休息一下
返回
2PΒιβλιοθήκη 变荷部载当分分上静布的定不荷结同载构，作的但等一合效个力变几相换何同时不，
A
B
其余部分的内力不变。
＝
结论：桁架在非结点荷载 作用除下A的B杆内内力力，不等同于，桁其架在等效 荷载余作部用分下的的内内力力相，同再。叠加上在 局部平衡荷载作用下所产生的局 部内力。
P
P
A
B
仅AB杆受力，其余杆内力为零
12、图示多跨 梁截面B左的 弯矩等于（ ）， （ ）侧受拉。
12题图
13、图示刚架中，无论跨 度L和高度h如何变化， 永远等于 的（ ）倍， BC杆（ ）侧受拉。
7题图
13题图

【结构力学】第十三章 结构动力计算(1)汇总

【结构力学】第十三章 结构动力计算(1)汇总

11
1 EI
lh 2
2h 3
lh 2 3EI
w 1 3EI m11 mlh2
15
例6
k11
k11
解：求 k
3EI
3EI
m
k l3
1
k
EI
k11 k l 3
l
w k11 3EI l3 k
m
m
•对于静定结构一般计算柔度系数方便。
•如果让振动体系沿振动方向发生单位位移时，所有刚节点
都不能发生转动（如横梁刚度为无穷大的刚架)计算刚度系数方
2
1
m
l/2
11
1 EI
(
1 2
l 2
l 2
2 3
l 2
1 2
l 2
l
l 2
2 3
)
l3 8EI
w
1
m11
8EI ml3
14
例5 1
k Am
h
I=∞ EI
B
θ
1
1
h
解法1：求 k θ=1/h
MBA=kh
=
MBC
3
EI l
3EI lh
C
k 3EI lh2
w
k11 m
3EI mh2l
解法2：求 δ
2n
6023.14500
6052.3
1 S
52.3/57.4=0.91
2）求动力系数β
1
1
5.88
1 2 w 2 152.32 5379.742 1.35
max
Ql 4W
Pl 4W
(Q P)l
4W
175.6MPa
149.2
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

度与加速度的关系，及结构在动内力与静内力共同作用下力学状态。
动力计算的内容：研究结构在动荷载作用下的动力反应的计算原理和方法。 涉及到内外两方面的因素： 1）确定动力荷载（外部因素，即干扰力）； 2）确定结构的动力特性（内部因素，如结构的质量分布、自振频率、周 期、振型和阻尼等等），类似静力学中的I、S等； 计算动位移及其幅值；计算动内力及其幅值。
由平衡位置计量。以质点受力平衡建立方程，引用了刚度系数，称刚度法。
2、 柔度法：研究结构上(质点位置)的位移，建立位移协调方程。
静平衡位置
m
. y(t) I (t) m (t ) y .
(t ) y 0 m y
设已知结构的柔度系数δ
.......... .(c)
1 可得与 (b) 相同的方程 k 刚度法常用于刚架类结构，柔度法常用于梁式结构。
m m>>m梁 m +αm梁 I
厂房排架水平振 时的计算简图
m+αm柱
I 2I
单自由度体系
y2 y1
2个自由度 2个自由度
自由度与质量数不一定相等
m1
m2
2个自由度
m3
4个自由度
v( t ) θ( t )
u(t)
水平振动时的计算体系
构架式基础顶板简化成刚性块
多自由度体系
m ( x)
无限自由度体系
二、自由振动微分方程的解
I(t)
改写为
ky 0 m y k y 0 y m
.......... .......... .......... ......(b)
k y 0 其中 y m
2
2
它是二阶线性齐次微分方程，其一般解为：
y(t ) C1 sin t C2 cost
恒与位移反向
(t ) m( j d ) y y y 惯性力 I (t ) m
其中 或
j d ) k ( y j yd ) W ……………(a) m( y y j 0 上式可以简化为 y kyj=W 及 d kyd 0 m y ky 0 m y .......... .......... .......... ......(b)
.......... .....(d )
积分常数C1，C2由初始条件确定
a1， a2，…….. an
y ( x, t ) ak k ( x )
k 1
的函数，称为形状函数。
ak(t) ——称广义座标，为一组待定
参数，其个数即为自由度数，用此法可将
无限自由度体系简化为有限自由度体系。
x
n
y
3、有限单元法
四、动力计算的方法
动力平衡法（达朗伯尔原理）
m
(t ) P(t ) m y
荷载对结构产生的惯性力不能忽略，因动力荷载将使结构产生相当大的加速度，
由它所引起的内力和变形都是时间的函数。 与静力计算的对比：两者都是建立平衡方程，但动力计算，利用动静法，
建立的是形式上的平衡方程。力系中包含了惯性力，考虑的是瞬间平衡，荷 载、内力都是时间的函数。建立的平衡方程是微分方程。 2、目的和内容 计算结构的动力反应：结构的刚度、质量等性能与振动中内力、位移、速
P(t)
(t ) ＝I(t) m y
m
(t ) P(t ) m y
改写成 设其中
…………..运动方程
…………..平衡方程
(t ) 0 P(t ) m y
(t ) I (t ) m y
I(t)－惯性力，与加速度成正比，方向相反
虚功原理（拉格朗日方程） 哈米顿原理（变分方程）
x
y(x,t)
2、广义座标法： 如简支梁的变形曲线可用三角级数来表示
y ( x, t ) ak (t ) sin
k 1
n
kx l
x y(x,t)
用几条函数曲线来描述体系的振动曲 线就称它是几个自由度体系，其中
kx sin —— 是根据边界约束条件选取 l
1( x),2 ( x),........ .n ( x)
都要用到抽象的虚位移概念
§10-2 单自由度体系的自由振动 自由振动：体系在振动过程中没有动荷载的作用。 自由振动产生原因：体系在初始时刻（t=0）受到外界的干扰。
静平衡位置
m获得初位移y
m获得初速度 y
研究单自由度体系的自由振动重要性在于： 1、它代表了许多实际工程问题，如水塔、单层厂房等。 2、它是分析多自由度体系的基础，包含了许多基本概念。 自由振动反映了体系的固有动力特性。 要解决的问题包括： 建立运动方程、计算自振频率、周期，阻尼的影响……….
一、运动微分方程的建立
方法：达朗伯尔原理 应用条件：微幅振动（线性微分方程） 力学模型 1、 刚度法：研究作用于被隔离的质量上的
力，建立平衡方程。
静平衡位置
重力
W
m 质量m在任一时刻的位移 y(t)=yj+yd
. y . .y
k
S(t)
m m
j d
.y
d
W
I(t)
+
弹性力 S (t ) ky(t ) k ( y j yd )
二、动力荷载分类
P(t )按其变化规律及源自作用特点可分为：1）周期荷载：随时间作周期性变化。（转动电机的偏心力） P
t 简谐荷载（按正、余弦规律变化） 一般周期荷载
t
2）冲击荷载：短时内剧增或剧减。（如爆炸荷载）
P P tr t P(t )
P
tr t
3）随机荷载：(非确定性荷载) 荷载在将来任一时刻的数值无法事先确定。 （如地震荷载、风荷载）
§10-1
动力计算概述
一、动力计算的特点、目的和内容
1、特点：静力荷载与动力荷载的特点及其效应。 “静力荷载”是指其大小、方向和作用位置不随时间而变化的荷载。这 类荷载对结构产生的惯性力可以忽略不计，由它所引起的内力和变形都是确定 的。(绝大部分的恒载、活载） “动力荷载”是指其大小、方向和作用位置随时间而变化的荷载。这类
塔克马海峡大桥在大风中垮塌
三、动力计算中体系的自由度
确定体系上全部质量位置所需独立参数的个数称为体系的振动自由度。 实际结构的质量都是连续分布的，严格地说来都是无限自由度体系。计算 困难，常取如下简化方法： 1、集中质量法 把连续分布的质量集中为几个质点，将一个无限自由度的问题简化成有限
自由度问题。