结构线性静力分析

结构的稳定性分析结构的稳定性是指在外力作用下，结构是否能保持其原有的形状和稳定性能。

在工程领域中，结构的稳定性分析是非常重要的一项内容，它关系到工程结构的性能和安全性。

本文将从理论基础、分析方法和实际案例三个方面，对结构的稳定性分析进行探讨。

一、理论基础结构的稳定性分析依托于力学和结构力学的基本理论。

结构的稳定性问题可以归结为结构的等效刚度和等效长度的问题。

等效刚度是指结构在外力作用下的变形程度，而等效长度则是指结构的几何形状与尺寸。

通过对结构的等效刚度和等效长度进行计算和分析，可以判断结构的稳定性。

二、分析方法1. 静力分析法静力分析法是最常用的结构稳定性分析方法之一。

它基于结构在平衡状态下的力学平衡方程，通过计算结构内力和外力的平衡关系，确定结构是否能保持稳定。

静力分析法主要适用于简单的结构体系，如悬臂梁、简支梁等。

2. 动力分析法动力分析法是一种基于结构的振动特性进行稳定性判断的方法。

通过分析结构的自然频率、振型和阻尼比等参数，可以确定结构的稳定性。

动力分析法适用于复杂的结构体系，如桥梁、高层建筑等。

3. 线性稳定性分析法线性稳定性分析法是一种通过求解结构的特征方程，得到结构的临界荷载（临界力）的方法。

线性稳定性分析法适用于线弹性结构，在分析过程中通常假设结构材料的性质符合线弹性假设，结构的变形量较小，且作用于结构的荷载为线性荷载。

三、实际案例以钢柱稳定性为例，介绍结构的稳定性分析在实际工程中的应用。

钢柱是承受垂直荷载的重要组成部分，其稳定性直接关系到整个结构的安全性。

通过使用静力分析法和线性稳定性分析法，可以确定钢柱的临界荷载并判断其稳定性。

在静力分析中，需要计算钢柱受力状态下的内力和外力之间的平衡关系。

通过引入等效长度和等效刚度的概念，可以将实际的钢柱简化为等效的杆件模型，从而进行稳定性计算。

在线性稳定性分析中，通过建立钢柱的特征方程，并求解其特征值和特征向量，可以得到钢柱的临界荷载。

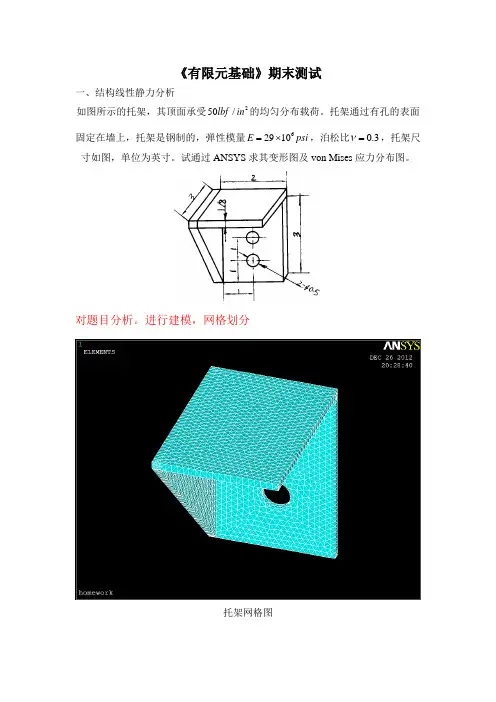
《有限元基础》期末测试一、结构线性静力分析如图所示的托架，其顶面承受2lbf in的均匀分布载荷。

托架通过有孔的表面50/ν=，托架尺固定在墙上，托架是钢制的，弹性模量6=⨯，泊松比0.3E psi2910寸如图，单位为英寸。

试通过ANSYS求其变形图及von Mises应力分布图。

对题目分析。

进行建模，网格划分托架网格图施加约束后，就可以对实体进行加载求解，托架变形图托架变形图输出的是原型托架和施加载荷后托架变形图的对比，虚线部分即为托架的原型，托架变形图可看出，由于载荷的作用，托架上面板明显变形了，变形最严重的就是红色部分，这是因为其离托板就远，没有任何物体与其分担载荷，故其较容易变形甚至折断。

这是我们在应用托架的时候应当注意的。

节点位移图托架von Mises 应力分布图上面两个图为托架的应力分布图，由图可看出主要在两孔处出现应力集中，也就是说这些地方所受的应力的最大的，比较容易出现裂痕。

我们在应用托架的时候，应当注意采取一些设施，以便减缓其应力集中。

特别是在施加载荷时，绝对不能够超过托架所能承受的极限，否则必将导致事故的发生。

二、动力分析如图1有一梁板结构，板的四角由四根梁固定支撑，板质量集中于中央。

梁板材料相关参数为弹性模量112210/E Nm =⨯，泊松比0.3ν=，密度337.810/kg m ρ=⨯。

板的厚度0.02t =，板长2000L mm =，宽1000B mm =，板的质量100M kg =。

梁长1000h mm =，截面面积为42210A m -=⨯，惯性矩为84210J m -=⨯，现在板的表面施加均匀压力载荷如图2。

试研究该梁板结构的瞬态动力响应。

图1图2建立有限元分析模型并附加动力节点146的位移时间历程结果三、非线性屈曲分析如图，一根长200L in =，截面高度0.5h in =，截面面积20.25A in =，惯性矩24/120.0052083J Ah in ==的细长杆受轴向载荷的作用，若沿X 方向取10个主自由度，求其屈曲模态。

一、结构线性静力分析结构静力分析是ANSYS产品家族中7种结构分析之一，主要用来分析由于稳态外载荷所引起的系统或零部件的位移、应力、应变和作用力，很适合求解惯性及阻尼的时间相关作用对结构响应的影响并不显著地问题，其中稳态载荷主要包括外部施加的力和压力、稳态的惯性力，如重力和旋转速度、施加位移、温度和热量等。

ANSYS的静力分析过程一般包括建立模型、施加载荷并求解和检查结果3个步骤。

连杆受力分析实例（a）问题描述如图所示为汽车连杆的几何模型，连杆的厚度为0.5m，在小头孔的内侧90度范围内承受P=1000N的面载荷作用，利用有限元分析该杆的受力状态。

连杆的材料属性为弹性模量E=30e6 Pa，泊松比为0.3。

(由于连杆的结构和载荷均对称，因此在分析时只采用了一般进行分析）（b）分析步骤[步骤1]设置系统环境（1）设置界面选择菜单Utility Menu：MenuCtrls,选择相应菜单，即可将其现实或隐藏。

（2）显示工作平面选择菜单Utility Menu：WorkPlane→Display Working Plane.（3）设置工作平面选择菜单Utility Menu：WorkPlane→WP Settings，在工作平面设置对话框中选Grid Only单选钮，设置Snap Incr为0.5，Minimum为0，Maximum为10，Spacing为1。

（4）显示网格选择菜单Utility Menu：PlotCtrls→Pan，Zoom, Rotate,单击控制按钮，使网格满窗口。

（5）设置分析类型选择菜单Main Menu：Preferences，选择分析类型对话框中的Structural复选框。

[步骤2]定义单元属性（1）定义单元类型选择菜单Main Menu：Preprocessor→Add/Edit/Delete 命令，在单元库列表中选择Solid和Brick 8node 45。

（2）定义材料属性选择菜单Main Menu：Preprocessor→Material Props →Materia Model，在材料属性窗口中依次点击Structure，Linear，Elastic和Isotropic，在弹出的对话框里设置EX=30e6，PRXY=0.3。

静力计算手册一、引言静力计算是结构工程中的一项基本技术，主要用于分析结构在恒定载荷作用下的响应。

本手册将详细介绍静力计算的相关理论、方法和应用，旨在为工程师和研究者提供实用的参考。

二、静力学基础1.静力学的概念：静力学主要研究物体在恒定外力作用下，如何维持平衡状态。

2.力的合成与分解：介绍了力的矢量表示方法，以及力的合成与分解的基本原理。

3.力的矩：介绍了力矩的概念，以及如何计算力对点之矩。

4.平衡条件：阐述了静力学中的平衡条件，包括力的平衡和力矩平衡。

三、结构分析方法1.结构分析概述：介绍了结构分析的基本概念、目的和方法。

2.线性静力分析：阐述了线性静力分析的基本原理和步骤，包括建立模型、施加载荷和求解等。

3.非线性静力分析：介绍了非线性静力分析的特点、常见问题和解决方法。

4.有限元法：详细介绍了有限元法的基本原理、实施步骤和应用。

四、杆件内力计算1.杆件内力的计算：介绍了如何通过平衡条件计算杆件的内力。

2.弯矩和剪力：阐述了弯矩和剪力的概念，以及如何计算它们。

3.轴力和扭矩：介绍了轴力和扭矩的概念，以及如何计算它们。

五、截面承载能力计算1.截面几何特性：介绍了截面的面积、惯性矩等基本几何特性。

2.截面承载能力分析：分析了各种形式截面的承载能力，如抗弯、抗剪、抗扭等。

3.材料的强度指标：介绍了常用材料的抗拉、抗压、抗剪强度等指标。

六、结构位移计算1.结构位移的计算方法：介绍了结构位移的几种主要计算方法，如虚功原理、单位载荷法等。

2.常见结构的位移特性：分析了常见结构的位移特性，如梁、柱、拱等。

3.位移与内力的关系：阐述了位移与内力之间的关系，以及如何通过位移计算内力。

七、结构优化设计1.结构优化设计概述：介绍了结构优化设计的基本概念、方法和应用领域。

2.结构优化设计的数学模型：阐述了结构优化设计的数学模型，包括设计变量、约束条件和目标函数等。

3.结构优化算法：介绍了常见的结构优化算法，如梯度法、遗传算法等。

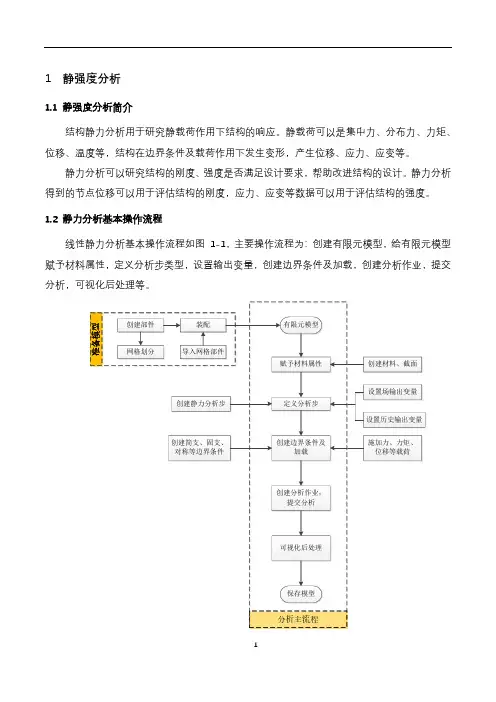
1静强度分析1.1静强度分析简介结构静力分析用于研究静载荷作用下结构的响应。

静载荷可以是集中力、分布力、力矩、位移、温度等，结构在边界条件及载荷作用下发生变形，产生位移、应力、应变等。

静力分析可以研究结构的刚度、强度是否满足设计要求，帮助改进结构的设计。

静力分析得到的节点位移可以用于评估结构的刚度，应力、应变等数据可以用于评估结构的强度。

1.2静力分析基本操作流程线性静力分析基本操作流程如图1-1，主要操作流程为：创建有限元模型，给有限元模型赋予材料属性，定义分析步类型，设置输出变量，创建边界条件及加载，创建分析作业，提交分析，可视化后处理等。

图1-1 静力分析流程图1.3边界条件的确定边界条件的包括载荷和约束的施加。

1.3.1载荷条件施加注意事项集中载荷和弯矩•实体单元只有旋转平动自由度，不能将弯矩直接施加在实体单元节点上，如果要在实体单元上施加弯矩，可以通过定义Coupling约束的方法来实现；•定义集中载荷或弯矩时，可以在Edit Load对话框中选中”Follow nodal rotation”实现；图1-2 载荷方向分析过程中随节点转动而变化定义方法 线载荷•线载荷只适用于梁单元；•在三维实体模型的边上施加分布载荷，可通过将需要施加载荷的边和一个参考点耦合在一起，然后再参考点上施加集中载荷。

面载荷与压力载荷•面载荷和压力载荷都是单位面积上的载荷，二者的区别是：压力载荷是一个标量，力的方向总是与面垂直；面载荷是一个矢量，其方向可以是任意的，定义面载荷时必须指定其方向矢量（direction vector）。

重力载荷与体载荷•重力载荷中给出的是各个方向上的重力加速度，受力区域上所受的合力等于受力区域的体积X密度X重力载荷•体载荷中给出的是单位体积上的力，与密度无关，受力区域上所受合力等于受力区域的体积X体载荷1.3.2约束条件初学者在施加边界约束条件时时常遇到以下两个问题：1）约束条件的施加是只需要施加在单独的零部件上还是将部件周围的零部件都建立出来，然后将约束条件施加在周边的零部件上；2）在部件什么位置施加约束，该约束几个自由度。

常用的有限元分析方法1、结构静力分析结构静力分析用来分析由于稳态外部载荷引起的系统或部件的位移、应力、应变和力。

静力分析很适合于求解惯性及阻力的时间相关作用对结构响应的影响并不显著的问题。

这种分析类型有很广泛的应用，如确定结构的应力集中程度，或预测结构中由温度引起的应力等。

静力分析包括线性静力分析和非线性静力分析。

如图1、图2所示。

非线性静力分析允许有大变形、蠕变、应力刚化、接触单元、超弹性单元等。

结构非线性可以分为：几何非线性，材料非线性和状态非线性三种类型。

几何非线性指物体在外部载荷作用下所产生的变形与其本身的几何尺寸相比不能忽略时，由物体的变形引起的非线性响应。

材料非线性指物体材料变形时，材料所表现的非线性应力应变关系。

常见的材料非线性有弹塑性、超弹性、粘弹塑性等。

许多因素可以影响材料的非线性应力-应变关系，如加载历史、环境温度、加载的时间总量等。

状态非线性是指结构表现出来的一种与状态相关的非线性行为，如二个变形体之间的接触。

随着接触状态的变化，其刚度矩阵发生显著的变化。

图1 图2汽车车架的线性结构静力分析应用云图发动机连杆小头连接部分的结构静力分析云图2、结构动力分析结构动力分析一般包括结构模态分析、谐响应分析和瞬态动力学分析。

结构模态分析用于确定结构或部件的振动特性（固有频率和振型）。

它也是其它瞬态动力学分析的起点，如谐响应分析、谱分析等。

结构模态分析中常用的模态提取方法有：子空间(Subspace)法、分块的兰索斯(BlockLanczos)法、PowerDynamics法、豪斯霍尔德(ReducedHouseholder)法、Damped法以及Unsysmmetric法等。

谐响应分析用于分析持速的周期载荷在结构系统中产生的持速的周期响应（谐响应），以及确定线性结构承受随时间按正弦（简谐）规律变化的载荷时稳态响应的一种分析方法，这种分析只计算结构的稳态受迫振动，不考虑发生在激励开始时的瞬态振动，谐响应分析是一种线性分析，但也可以分析有预应力的结构。

工程结构分析的方法工程结构分析是研究和评估工程结构在负载作用下的力学特性和稳定性的过程。

它涉及工程结构的设计、建造和维护，并对结构的安全性和可靠性提出要求。

在工程实践中，有许多不同的方法可以用于进行结构分析。

下面将介绍常用的几种工程结构分析方法。

一、静力分析静力分析是最基本的结构分析方法之一。

它基于牛顿第二定律和力平衡原理，假设结构在负载作用下保持静止。

通过计算结构中各个部位的受力情况，可以评估结构的强度、刚度和稳定性。

静力分析方法可以使用解析方法或数值方法进行计算，常见的解析方法有力法、位移法和弹性法，数值方法有有限元法和有限差分法。

静力分析的主要优点是计算简单、直观，并且可以在设计和施工过程中提供快速的结果。

然而，它的缺点是忽略了结构的动态效应和材料的非线性行为。

二、动力分析动力分析是一种考虑结构在振动或冲击负载作用下的分析方法。

它适用于对结构的动态响应进行评估，从而确定结构是否具有足够的刚度和稳定性来抵抗动力负载。

动力分析方法可以分为自由振动分析和强迫振动分析。

在自由振动分析中，结构受到一个初始扰动后开始自由振动，通过求解结构的振动模态和固有频率，可以得到结构的固有振动特性。

在强迫振动分析中，结构受到外部激励力的作用，通过求解结构的强迫响应和频率响应函数，可以评估结构在动力负载下的振动状况。

动力分析的优点是能够考虑结构的动态特性，对于受到动力负载的结构具有更准确的评估。

然而，动力分析的计算复杂度较高，通常需要使用数值方法进行求解。

三、塑性分析塑性分析是一种考虑结构的塑性变形和屈服破坏的分析方法。

它适用于对材料塑性变形和结构破坏的问题进行评估。

塑性分析方法可以分为弹塑性分析和完全塑性分析。

在弹塑性分析中，结构中的材料被假定为在一定范围内具有线性弹性行为，超过该范围时为塑性行为。

通过计算结构在负载作用下的延性变形和塑性区域的分布，可以评估结构在塑性变形作用下的安全性和可靠性。

在完全塑性分析中，结构中的材料被假定为完全塑性，在达到材料的屈服强度后，将继续产生塑性变形。

第二章结构线性静力分析2.1静力分析的定义静力分析计算在固定不变载荷作用下结构的响应，它不考虑惯性和阻尼影响，如结构受随时间变化载荷作用的情况。

可是静力分析可以计算那些固定不变的惯性载荷对结构的影响(如重力和离心力)，以及那些可以近似为等价静力作用的随时间变化载荷(如通常在许多建筑规范中所定义的等价静力风载和地震载荷)的作用。

静力分析用于计算由那些不包括惯性和阻尼效应的载荷作用于结构或部件上引起的位移、应力、应变和力。

固定不变的载荷和响应是一种假定，即假定载荷和结构响应随时间的变化非常缓慢。

静力分析所施加的载荷包括：外部施加的作用力和压力稳态的惯性力(如重力和离心力)强迫位移温度载荷(对于温度应变)能流(对于核能膨胀)关于载荷，还可参见§2.3.4。

2.2线性静力分析与非线性静力分析静力分析既可以是线性的也可以是非线性的。

非线性静力分析包括所有类型的非线性：大变形、塑性、蠕变、应力刚化、接触(间隙)单元、超弹性单元等。

本章主要讨论线性静力分析。

对非线性静力分析只作简单介绍。

2.3静力分析的求解步骤2.3.1建模首先用户应指定作业名和分析标题，然后通过PREP7前处理程序定义单元类型、实常数、材料特性、模型的几何元素。

这些步骤是大多数分析类型共同的，并已在《ANSYS Basic Analysis Guide》§1.2论述。

有关建模的进一步论述，见《ANSYS Modeling and Meshing Guide》。

2.3.1.1注意事项在进行静力分析时，要注意如下内容：1、可以采用线性或非线性结构单元。

2、材料特性可以是线性或非线性，各向同性或正交各向异性，常数或与温度相关的：必须按某种形式定义刚度(如弹性模量EX，超弹性系数等)。

对于惯性载荷(如重力等)，必须定义质量计算所需的数据，如密度DENS。

对于温度载荷，必须定义热膨胀系数ALPX。

3、对于网格密度，要注意：应力或应变急剧变化的区域(通常是用户感兴趣的区域)，需要比应力或应变近乎常数的区域较密的网格：在考虑非线性的影响时，要用足够的网格来得到非线性效应。

建筑结构设计中的力学分析方法建筑结构设计是一门综合性学科，旨在确保建筑物能够在不同的力学荷载下保持结构稳定和安全。

力学分析是建筑结构设计中的关键环节之一，它通过深入研究和分析不同荷载对建筑结构产生的影响，以确定和优化结构的设计。

1. 引言在建筑结构设计中，力学分析是一项至关重要的技术。

通过运用力学原理和方法，可以预测建筑结构在外界荷载作用下的响应，为设计提供可靠的基础和指导。

本文将介绍建筑结构设计中常用的力学分析方法。

2. 静力分析静力分析是建筑结构设计中最基本的分析方法之一。

它基于力和力的平衡原理，通过计算建筑结构受力情况来确定结构的承载能力和稳定性。

静力分析常用的方法包括受力图法、弯矩计算、剪力计算等。

这些方法能够准确地描述结构在静力荷载下的受力状态。

3. 动力分析动力分析是一种更为复杂的分析方法，适用于考虑到地震、风载等动力荷载的建筑结构。

动力分析主要包括静力等效法、模态超静力法和时程分析等。

其中，静力等效法和模态超静力法都是基于模态分析的思想，并在考虑动力荷载的情况下简化了计算过程。

时程分析是一种更为精确的方法，通过模拟荷载和结构之间的相互作用来评估结构的响应。

4. 有限元分析有限元分析是一种广泛应用于建筑结构设计领域的数值分析方法。

它将结构划分为有限个单元，利用数学模型和计算机技术模拟结构的受力行为。

有限元分析可以综合考虑结构的几何形状、材料性质和边界条件等因素，对结构的受力性能进行精确分析。

由于有限元分析具有较高的计算精度和灵活性，因此在复杂建筑结构的设计和优化中得到广泛应用。

5. 非线性分析非线性分析是一种针对具有非线性特征的结构进行分析的方法。

在许多情况下，建筑结构在受到极限荷载或变形限制时会发生非线性响应。

非线性分析通过考虑结构材料的非线性特性、几何非线性和接触非线性等因素，准确地描述结构的受力性能，并提供合理的设计参考。

6. 结构优化方法结构优化方法在建筑结构设计中发挥着重要的作用。

如何使用CAD进行线性静力分析CAD软件是一种广泛应用于机械设计领域的工具，它允许工程师们创建、编辑和分析各种类型的图纸和模型。

在设计中，静力学分析是一个重要的环节，它用于评估设计的结构的静态行为和强度。

本教程将介绍如何使用CAD软件进行线性静力学分析。

首先，打开CAD软件并创建一个新的工程文件。

接下来，在绘图界面上选择合适的测量单位，这将决定我们在后续制图和分析过程中所用的单位。

然后，开始绘制模型。

根据设计需求，使用CAD软件的绘图工具创建所需的几何形状。

确保使用准确的尺寸和比例来绘制模型，这将对后续的分析结果产生重要影响。

完成绘图后，我们需要给模型添加约束和加载条件以进行分析。

约束是指限制模型自由度的条件，例如固定支座或约束运动。

加载条件是指施加在模型上的力或压力，例如重力、外部力或约束。

在CAD软件中，我们可以使用不同工具来添加约束和加载条件。

通常情况下，约束可以通过设置特定点的绝对坐标或定义点之间的相对移动来实现。

加载条件可以通过施加所需力或压力的数值来实现。

一旦添加了约束和加载条件，我们就可以开始进行线性静力学分析。

在CAD软件中，这通常通过选择相应的分析功能来实现。

根据不同的软件，操作步骤可能会有所不同，但基本原理是相似的。

在进行分析之前，我们需要选择适当的材料属性和截面特性。

这些属性将在分析过程中用于计算应力和变形。

确保选择准确的材料属性和截面特性对于得到准确的分析结果至关重要。

开始分析后，CAD软件将根据我们提供的约束、加载条件和模型几何来计算模型的应力和变形。

计算过程可能需要花费一些时间，具体取决于模型的复杂性和计算机性能。

完成分析后，我们可以查看模型的结果。

CAD软件通常会提供各种分析结果，包括应力分布、变形图和因子安全系数。

这些结果可以帮助我们评估设计的结构的强度和稳定性。

根据分析结果，我们可以进行必要的修改和优化，以满足设计要求和规范要求。

这可以包括改变材料选择、增加结构支撑或调整模型几何。

常用CAE分析类型作者：冒小萍审校：顾伯达适用版本：所有CAE软件CAE分析时根据结构实际工况准确判断分析类型至关重要，根据分析类型我们决定采用何种分析软件进行分析求解更合理。

如果分析类型判断不准确，或者由于软件功能限制不能完成某种分析类型而做过多的简化，分析的结果是不可靠的，对实际工程项目没有多少参考价值。

目前我们常用的结构分析类型主要有以下几种：1．线性结构静力分析结构线性静力分析是结构设计与强度校核的基础，主要是计算在固定不变的载荷作用下（包含由定常加速度引起的平衡惯性载荷）结构的响应（位移、应力、应变和力），不考虑惯性和阻尼的影响；固定不变的载荷和响应是一种假定，即假定载荷和结构的响应随时间的变化非常缓慢。

结构线性静力分析中，假定结构中的工作应力小于结构材料的屈服应力，因此应力应变关系服从虎克定理，具有线性关系．同时结构的变形（位移）相对结构的总体尺寸来说，又是很小的，所以问题可以用线性方程计算．从应用的角度看，多数情况下，结构的线性分析是评估很多结构设计问题的最有效的方法．2．模态分析结构的模态分析是结构动力分析的基础。

模态也就是结构产生自由振动时的振动形态，也称为振型．每一个自由振动的固有频率都对应一个振型，一般说系统有多少自由度就有多少个固有频率。

实际的分析对象是连续体，具有无限多的自由度，所以其模态具有无穷阶，要求用弹性动力学的偏微分方程解决，因为实际结构的复杂性，一般无法得到封闭解，通常都是用近似的方法来求解．有限单元法就是一种常用的近似方法，可以比较正确的计算出足够多的结构振动模态．有限元中模态分析的本质是求方程的特征值问题，所分析的结构振动模态的“阶数” 就是指要求的对应数学方程的特征值的个数。

将特征值从小到大排列就是阶次。

模态分析的目标是确定系统的模态参数，即系统的各阶固有频率和振型，为结构系统的动力特性分析和优化设计提供依据。

屈曲分析在通常的结构分析中，结构处于一个稳定平衡的状态。