当前位置：文档之家 › 【最新】一章系统的状态变量分析

【最新】一章系统的状态变量分析

  • 格式：ppt
  • 大小：506.50 KB
  • 文档页数：87

下载文档原格式

  / 87

合集下载

系统的状态变量分析

系统的状态变量分析

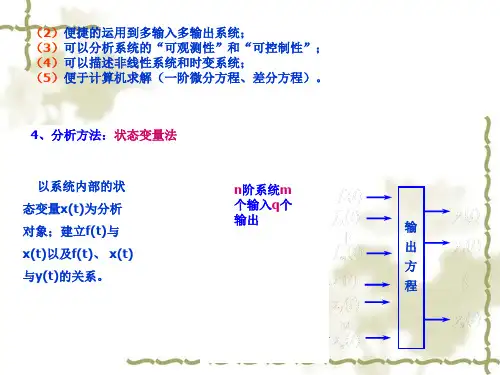
Chap.9 系统的状态变量分析1.系统状态及状态方程的基本概念2. 信号流图signal flow graph信号流图的代数运算1. 只有一个输入支路的结点值等于输入信号乘以支路增益。

3. 并联支路的合并：并联支路的总增益等于所有各支路增益之和（并联相加）。

2. 串联支路的合并：串联支路的总增益等于所有各支路增益的乘积（串联相乘）。

x 3信号流图的代数运算（续）4.结点的吸收和变换：输出结点可以消掉，混合结点也可以通过增加一个具有单位传输的支路变为输出结点。

5. 环路吸收：带有环路系统的总增益等于断开环路后所有输入输出支路增益乘积除以因式（1-环路增益）。

信号流图简化步骤环路吸收，去掉结点1X 例2结点吸收环路吸收信号流图简化步骤（续）环路吸收，去掉结点闭环4X 结点吸收，去掉结点4X信号流图简化步骤（续）442233221432443322432133222244444321332243211)1)(1(1)1)(1(G H G H G H G H G H H H G H G H G H H H H H H G H G G H H G H G H H H G H G H G H H H H H ++++++=++−−−−++=得到系统函数并联相加环路吸收)()(14422332214324433224321G H G H G H G H G H H H G H G H G H H H H H H ++++++=对于例2, 用梅森公式求系统的转移函数。

求信号流图的特征行列式△△=1+(H 2G 2+ H 3G 3+ H 4G 4+H 2H 3H 4G 1)+(H 2G 2H 3G 3+ H 2G 2H 4G 4)系统具有4个环路，分别为：L1=（X 1→X 2→X 1）=-H 2G 2L2= （X 3→X 4→X 3）=-H 3G 3L3= （X 4→Y →X 4）=-H 4G 4L4= （X 1→X 2→X 3→X 4→Y →X 1）=-H 2H 3H 4G 1互不接触环路为：L1和L2, L1和L3前向通路只有一条：g1=H 1H 2H 3H 4，其特征行列式的余子式△1为△1=1 –0 + 0 -……22)()0t e b)(t e i βp 1i α−1)(t r i p α+321===λλλ&&&321⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡λλλ&&&。

系统的状态变量分析法

系统的状态变量分析法

出
状
方
态
程
方
程
9-1 连续系统状态空间方程建立
一、引例 t<0，K在2；t=0，K从2打到1。求t>0时，电压uR和uL。
（
状
态
方
程
）
（ 输 出
uR t Ri(t)
方 程
uL t Ri(t) uc (t) us (t)
）
状态方程和输出方程通称为
状态空间方程
uc(t)和i(t)称为状态变量
说明：同一系统函数或微分方程，可以有不同的模拟图或信号流图，所以 可以得到不同的状态方程和输出方程，但特征根相同，同一系统，它的系 统矩阵A相似。
练习1：列写状态方程和输出方程，已知系统函数为
状态变量：选积分器输出。
练习2：已知系统函数，用级联型信号流图列写状态方程和 输出方程
状态变量：选积分器输出。来自3、系统函数矩阵与单位冲激响应矩阵 1）系统函数矩阵
2）单位冲激响应矩阵： 3）系统自然频率：
意义：第j个激励单独作用时 与所产生的第i个响应之间的 关系。
3、状态方程：描述系统状态变量和激励与状态变量一阶导数关系 的微分方程组。
4、输出方程：描述系统状态变量和激励与输出响应关系的代数方程组。 5、状态向量：由状态变量做分量所构成的向量。（n维） 6、状态空间：状态变量所有取值的集合。即状态向量所在的空间。 7、状态轨迹：在状态空间中状态向量端点随时间变化所形成的轨迹。
（2）便捷的运用到多输入多输出系统； （3）可以分析系统的“可观测性”和“可控制性”； （4）可以描述非线性系统和时变系统； （5）便于计算机求解（一阶微分方程、差分方程）。
4、分析方法：状态变量法
以系统内部的状

系统的状态变量分析

系统的状态变量分析

则状态方程和输出方程分别为：
12((tt))
a111(t) a211(t)
a1nn (t) b11x1(t) b1m xm (t) a2nn (t) b21x1(t) b2m xm (t)
n (t) an11(t) annn (t) bn1x1(t) bnm xm (t)
X (s)
Y (s)
H(s)
X (s) H(s) Y (s)
Y(s) H(s)X (s)
例：将下图所示系统的方框图转化成信号流图。
X (s)
解：
s1 • s1 • s1
b1
b2
•
Y (s)
a1 a2 a3
由两个及两个以上的 箭头指向的节点可兼 做加法器。
b1
X (s)
1
s 1
a1
s 1
2 1 La 1 G2H 2
a
1 (G1H1 G2H 2G3H3 G1G2G3H4 ) G1G3H1H3
G1 H1H2H3H5, 1 1
G2 H4H5, 2 1 La 1 G2 H 2
a
H
1
K
GK K
1
(G11
G22 )
H1H2 H3H5 H4 H5 (1 G2 H2 )
上述状态方程和输出方程可以写成矩阵形式：
状态方程： 输出方程：
[n
1] k 1
[ A]kk
[n]k1
[B]km
x[n] m1
y[n] r1 [C]rk
[n] k1 [D]rm
x[n] m1
其中：
1[n 1]
[n
1]
2 [n
L
1]
k
[n
1]

状态变量分析

状态变量分析

RiL (t)
vs
（3）消除中间变量 vC2，将 vC2 vS vC1 代入，得
C1
d vC1 dt
iL
C2
d(vS vC1 ) dt
0
（4）整理，得
diL dt
R L iL
1 L vC1
1 L vS
d
vC1
dt
1 C1 C2
iL
C2 C1 C2
dvS dt
写成矩阵形式，为
diL
x2
dx1 dt
(b1 a1b2 ) f
dy dt
b2
df dt
(b1 a1b2 ) f
正如前面所述，状态变量的选取可以是多种形式的。
输出方程为 y x1 b2 f
写成矩阵形式，为
y 1
0
x1 x2
b2
f
7.2.4 从模拟图建立状态方程
根据系统的输入－输出方程或系统函数可以作出系 统的时域或复频域模拟图，然后选择每一个积分器的输 出端信号作为状态变量，最后得到系统的状态方程和输 出方程。
信号与系统
第七章 状态变量分析
第七章 状态变量分析
状态变量分析概述 7.1 状态与状态空间 7.2 连续系统状态方程的建立 7.3 系连续系统状态方程的 本章要点
状态变量分析概述
系统的描述方法 – 输入－输出描述法、状态变量描述法
输入－输出描述法（端口分析法、外部法） – 用系统的输入－输出变量之间的关系来描述系统的 特性； – 数学模型是 n 阶微分（或差分）方程。
方程。
iS (t)
解 选取 vC (t) 和 iL (t) 为状态变量， 它们都是独立的状态变量。
vC
(t)

[工学]系统的状态变量分析法

[工学]系统的状态变量分析法

前向通路的增益 : g1 H1H2H3
由于所有环路都与该条 前向通路接触
H1(s) g111
H1H2H3
1[H1H2G1 H2H3G3 H3G2 H1H2H3G1G2]
§9.4连续时间系统状态方程的建立
状态方程的建立方法
直接编写法
直观编写 网络拓扑分析编写 系统编写（借助计算机自动编写）
+


e(t-)
I1 L
uL I2
UR
ห้องสมุดไป่ตู้
I 2 (s) [uL (s) uR (s)]c2 s
uR (s) RI2 (s)
E(s)
I1(s)
uL (s)
I2 (s)
uR (s)
R(s)
c1s
Ls
c2s
R
1
c1s ls c2s
H (s) 1

k
Tk k
1 (Lc1s 2 Lc2 s 2 Rc2 s) Lc1c2 Rs 3
a
nn

x
n

b n1
b12 . b1n f1
b 22
.
b
2p

f
2

. . . .
bn2
.
b
2p

f
p

n p
y1 c11 c12 .
y .
2


c 21 .
c 22 .
. .
yq
cq1

1RL
C
1 L 0

iL (t) vC (t)

连续和离散系统的状态变量分析

连续和离散系统的状态变量分析
开始 上一页 下一页 结束
已知系统的输入输出方程或模拟图建立状态方程和输出方程 到目前为止，我们对系统已经有两种描述方法了 输入输出描述（激励响应的微分方程）；状态变量描述 对同一系统只是描述方式不同，两种描述方式之间一定有一定的关系，就象输入输 出描述中的输入输出方程，模拟图，系统函数等可以表述同一系统一样。输入输出 方程，模拟图，系统函数之间可以相互转换，两种描述方式之间也可以 【1】由输入输出描述的系统直接模拟图或系统函数、微分方程求状态方程和输出方程 4s 10 实例2：系统函数为 H ( s) 3 s 8s 2 19 s 12 系统方程为：
x1 0 e(t ) y 1 2 3 x 2 x3
规律：1.A阵为对角线阵，其对角线上的元素是H(S)的极点值。 其它元素全为零 2.B阵为1列阵 3.C阵是行阵，依次为H (s)部分分式的系数 4.D阵为零 这种状态变量～对角线变量，它是真实存在的。 还可以有其它方法建立状态方程和输出方程，但以上两种较为常用。但是这样一些状态变量 一般是无法测量或观察的。 注意 1.是以上的类型的模拟图可以用以上方法直接写状态方程及输出方程 2.不是以上的类型的模拟图不可以用以上方法直接写状态方程及输出方程 3.其它类型的模拟图都可以选积分号后面的变量作状态变量 离散系统的状态方程和输出方程形式与连续系统的相似，只不过将t变成k一阶导数变成增序1 （将一阶微分方程组变成一阶差分方程组）。

系统模拟图为：
y 8 y 19y 12 4 x 10x
开始 上一页
下一页 结束
选每个积分号后的变量为状态变量
x2 x1 x3 x2 12x1 19x2 8 x3 x x3
状态方程标准矩阵形式

状态变量分析法

状态变量分析法

B b1 b2 D d
式(5.5.8)和式(5.5.9)分别称为图5.5.2二阶网络的状
态方程和输出方程。 如果系统中有N个单位延时支路，M个输入信号： x1(n),x2(n),…,xM(n) ， L 个输出信号 y1(n),y2(n),… ， yL(n) ， 则状态方程和输出方程分别为
y(n) [c1c2 ][1(n)2 (n)]T dx(n)
再用矩阵符号表示：
(5.5.6)
(5.5.7)
W (n 1) AW (n ) Bx(n) Y (n) CW (n ) Dx(n)
(5.5.8) (5.5.9)
T
a11 a12 A , a21 a22 C c1 c2 ,
状态变量分析法
1. 状态方程和输出方程 状态变量分析法有两个基本方程，即状态方程和 输出方程。状态方程把系统内部一些称为状态变量的 节点变量和输入联系起来；而输出方程则把输出信号 和那些状态变量联系起来。 一般状态变量选在基本信
号流图中单位延时支路输出节点处。
图5.5.1是二阶网络基本信号流图，有两个延时支路， 因此建立两个状态变量w1(n)和w2(n)。下面建立流图中其 它节点w′2和输出y(n)与状态变量之间的关系。
将以上w1(n+1)、w2(n+1)和y(n)写成矩阵形式：
(5.5.1) (5.5.2)
(5.5.3)
1 (n 1) 0 (n 1) 2 a2
1
1 (n) 0 x(n) a1 2 (n) 1
2 (n 1) 2 2 (n 1) a21 (n ) a1 2 (n ) x(n ) 1 (n 1) 2 (n ) y (n ) b21 (n ) b1 2 (n ) b0 2 (b2 a2b0 )1 (n ) (b1 a1b0 ) 2 ( n ) b0 x( n )

MATLAB系统的状态变量分析

MATLAB系统的状态变量分析

MATLAB系统的状态变量分析MATLAB是一种强大的数值计算和数据分析软件，具有广泛的应用领域。

在MATLAB中，状态变量分析是一种用于研究和描述系统动态特性的方法。

状态变量分析通常涉及到线性系统和微分方程的求解。

在本文中，我们将探讨MATLAB系统的状态变量分析。

在MATLAB中，使用状态空间模型表示系统。

状态空间模型是一种数学模型，通过描述系统的状态变量和输入之间的关系来表示系统的动态行为。

状态变量是系统的内部变量，可以描述系统的状态。

输入是系统的控制变量，用于影响系统的行为。

首先，我们需要在MATLAB中创建系统的状态空间模型。

可以使用"ss"命令创建一个简单的状态空间模型。

例如，以下代码创建一个一阶系统的状态空间模型：A=[0-2;1-1];B=[1;1];C=[10];D=0;sys = ss(A, B, C, D);在这个例子中，A矩阵表示状态变量的演化方程，B矩阵表示输入对系统状态的影响，C矩阵是用于输出状态变量的观测方程，D矩阵是直接影响输出的输入。

接下来，我们可以使用MATLAB的函数来分析系统的状态变量。

以下是一些常用的状态变量分析函数：1. "step"函数：用于计算系统的阶跃响应。

可以使用以下命令计算系统对阶跃信号的响应：[y, t] = step(sys);plot(t, y);2. "impulse"函数：用于计算系统的脉冲响应。

可以使用以下命令计算系统对脉冲信号的响应：[y, t] = impulse(sys);plot(t, y);3. "initial"函数：用于计算系统的初值响应。

可以使用以下命令计算系统对给定初始条件的响应：[y, t] = initial(sys, x0);plot(t, y);其中，x0是系统的初始状态变量值。

4. "lsim"函数：用于计算系统对任意输入信号的响应。

系统的状态变量分析

系统的状态变量分析

形式与连续时间系统的形式相同。
用状态变量分析法研究系统具有如下优点。
(1) 便于研究系统内部的一些物理量在信号转换过程中的变化。这些物理量可以用状态矢
量的一个分量表现出来，从而便于研究其变化规律。
361
(2) 系统的状态变量分析法与系统的复杂程度无关，它和简单系统的数学模型相似，都表 现为一些状态变量的线性组合，因而这种分析法更适用于多输入多输出系统。
(3) 状态变量分析法还适用于非线性和时变系统，因为一阶微分方程或差分方程是研究非 线性和时变系统的有效方法。
(4) 状态变量分析法可以用来定性地研究系统的稳定性及如何控制各个参数使系统的性能 达到最佳等。
(5) 由于状态方程都是一阶联立微分方程组或一阶联立差分方程组，因而便于采用数值解 法，从而为使用计算机进行分析系统提供有效的途径。
时间信号。
上述关于状态变量和状态方程的基本概念，可用于讨论系统状态方程和输出方程的一般形
式。
1. 连续时间系统状态方程和输出方程的一般形式
一个动态连续时间系统的时域数学模型都是用输入、输出信号的各阶导数来描述的。作为
连续时间系统的状态方程表现为状态变量的一阶联立微分方程组，对于线性时不变系统，状态
方程和输出方程简化为状态变量和输入信号的线性组合，即线性时不变系统的状态方程和输出
的一阶导数与状态变量和激励的关系。式(8-3)形式的代数方程称为输出方程(output equation)，
它描述了系统输出与状态变量和激励之间的关系。
状态变量分析法对于离散时间系统也是同样适用的，即上面给出的概念对离散时间系统同
样有效。只不过对于离散时间系统，其状态方程是一阶联立差分方程组，状态变量λ[n]是离散
（8-8）

系统的状态变量分析共37页

系统的状态变量分析共37页
14
例1 写出图示电路的状态方程和输出方程。
R1
x2(t) L
+
+ f (t)

i1(t)
+
x1(t)
C

i2(t)
R2 y(t)

解： 选择电容的电压x1(t)和电感的电流x2(t)作为系 统的状态变量。
回路电流和状态变量的关系为
x2(t)i2(t)
C x 1(t)i1(t)i2(t)
15


y

x
2

x 3


0
0
3
0


x
2



1

f
0 4 x 3 1
x1
y0.511.5
x
2

x 3
28
离散时间系统状态方程的建立
由模拟框图建立状态方程 由差分方程或系统函数建立状态方程
s1 2
x2 s1 2.5


的矩阵表示式为
2
3
s1 x3 y

4
x 1 2

x
2



2
x 3 2
0 0 x1
3
0


x
2

0.5 4 x 3
0


0

f
1
x1
x[k1]A[xk]B[fk] y[k]C[xk]D[fk]
9
二、离散时间系统状态方程的一般形式
x[k1]A[xk]B[fk] y[k]C[xk]D[fk]

信号与系统课件：系统的状态变量分析

信号与系统课件：系统的状态变量分析
状态变量，得到状态方程为
输出方程为
系统的状态变量分析 写成矩阵形式，状态方程和输出方程分别为
系统的状态变量分析
2. 并联模拟 由式(7. 2－15b )，系统函数可写为
系统的状态变量分析 即可用 3 个简单的子系统的并联来表示。其中每个简 单子系统的系统函数为
其模拟框图如图 7.2－4 所示。
系统的状态变量分析
(1)可以有效地提供系统内部的信息，使人们能够较为 容易地解决那些与系统内部情况有关的分析设计问题。
(2)状态变量描述法不仅适用于线性非时变的单输入单 输出系统特性的描述，也适用于非线性时变多输入多输出系 统特性的描述。
(3)描述方法规律性强，便于应用计算机技术解决复杂 系统的分析设计问题。
系统的状态变量分析 【例 7.2－1 】 电路如图 7. 2 1 所示，激励为 u s ( t )，
响应为 i (t )，试写出其状态方程和输出方程。
图 7.2－1 例 7. 2－1 用图
系统的状态变量分析
系统的状态变量分析
将式(7. 2－2 )中状态变量的一阶导数放在等式左端，把状态 变量和激励放在等式右端，则可写成
前面几章讨论的分析方法属于输入 输出描述法( Input-OutputDescription )，又称端口分析法，也称外部法。 它主要关心的是系统的激励与响应之间的关系，而不直接涉 及系统的内部情况。这种分析法对于较为简单系统的分析是 合适的。其相应的数学模型是 n 阶微分(或差分)方程。
系统的状态变量分析
系统的状态变量分析 将式(7. 2－12 )最高阶导数项留在等式左边，其余各项移到 等式右边，代入状态变量符号，得
于是，写出其状态方程和输出方程为
系统的状态变量分析 写成矩阵形式，状态方程为

系统的状态变量分析

系统的状态变量分析

第7-9页
H 1
k
gk k
1
H1H
2
H
3
H
4
9
桂林电子科技大学信息工程教研室
信号与系统分析
7.1 系统的信号流图
三、系统的信号流图模拟
1.直接型（正则型）
以连续系统为例，设
H
s
bmsm bm1sm1 ... b0 sn an1sn1 ... a0
（m≤n）
将之变为： H s bmsnm bm1snm1 ... b0sn
（2）节点：表示信号或变量的圆点，具有加法器的功能
共有三类节点：
源点：只有输出支路的节点，通常对应系统的
输入信号；
阱点：只有输入支路的节点，通常对应系统的
输出信号；
混合节点：既有输入支路又有输出支路的节点。
4
第7-4页
桂林电子科技大学信息工程教研室
信号与系统分析
7.1 系统的信号流图
（3）通路与开通路：沿箭头方向所经过的支路组成的路 径称为通路；与通路上任意节点相交不多于一次的通路 称为开通路；
信号与系统分析
第七章
7.1 系统的信号流图
一、信号流图 二、梅森公式 三、系统信号流图模拟
7.2 系统的状态方程和输出方程
一、状态和状态变量 二、连续系统的状态方程和输出方程 三、离散系统的状态方程和输出方程
点击目录 ，进入相关章节
1
第7-1页
桂林电子科技大学信息工程教研室
信号与系统分析
7.1 系统的信号流图
7.1 系统的信号流图
一、信号流图---模拟框图的简化表示
1、信号流图：对系统s域或z域模拟框图的简化，具体 说来，就是用有向线段表示信号的传输路径，有向线段 起点和终点表示信号，起点信号与终点信号之间的转移 关系（传输函数）标于线段的上方，加法器用节点表示。 比如，下图（a）所示的模拟框图经简化后得到的流图 如图（b）所示。

信号与系统9-1系统的状态变量分析课件

信号与系统9-1系统的状态变量分析课件

s 1
x1
b0
y(t)
x1 x2
x2 x3
x1
y(t)
y(t)
x3
(b0a2ax03b3) b0 x1 b1x2
a1bx(b221x3 aa01bbx313x)3
f(b(t2)
a2b3
)
x2
b3
x3
f
(t)
b0 x1 b1x2 b2 x3 b3[ f (t) a2 x3 a1x2 a0 x1]
状态变量描述法：是以系统内部某些变量作为状态变量，
这种描述法表达出系统的全部状态和性能，构成了对系统的 内部描述，称为内部表达法。
状态和状态变量：
对于一个动态系统，状态是表示系统的一组最少变量（被称为 状态变量），它满足两条：
只要知道t=t0时这组变量和tt0的输入函数； 决定tt0的系统的全部的其它变量。
4
系统的状态变量表达式
系统动态方程由两部分组成：
状态方程：一阶微分方程组或一阶差分方程组。
输出方程：由状态变量和激励表示的输出响应。
一般形式为：
连续系统
x(t) Ax(t) Bf(t) 状态方程 y(t) C x(t) Df (t) 输出方程
其中 x (t)为状态变量的一阶导数
离散系统 x(k 1) Ax(k) Bf (k) 状态方程
11
由H(s)求状态方程
H(s) 信号流图 状态方程
并联模拟
数的节点电流方程。 消去非状态变量。 写成标准形式。
6
例 9.2
列写电路的状态方程和输出方程。
解 列写连接电容支路的A节点电流方程 和含有电感的回路电压方程。
C
x1 (t)
x2 (t)

§6.01 系统的状态变量分析-全章

§6.01 系统的状态变量分析-全章
i1 (t ) iS (t ) i2 (t ) iS (t ) 2 (t )
根据电容回路的KVL有，
根据电感节点的KCL有，
电容C1所在的节点 a 的 KCL
d d 1 C1 1 (t ) C2 v2 (t ) v2 (t ) 2 (t ) dt dt R2
根据C1 L2 L1 R1 组成的回路KVL有
d L1 1 (t ) R11 (t ) 3 (t ) x1 (t ) dt d L2 2 (t ) R22 (t ) x2 (t ) 3 (t ) dt
上述三个方程代入具体参数得
1 (t ) 2 0 1 1 (t ) 1 0 (t ) 0 3 x1 (t ) 2 (t ) 0 3 3 2 x (t ) 2 2 0 (t ) 0 0 2 3 3 (t )
信号与系统
三、由电路图建立状态方程
R1
L1
a
例：列写如图所示电路的状态方程
1 t v1 t


i1 t
L2
v S t


பைடு நூலகம்
C1 C2


v 2 t
2 t i2 t iS t
R2
解：电源 Vs(t) 与电容 C1、C2 组成一个回路，所以只能选一个电容电压作 为状态变量，同样，电源 is(t) 与电感 L1、L2 组成一个节点，所以也只能选

设系统有 p 个激励 x1 (t ), x2 (t ),, x p (t )
系统有 q 个响应
y1 (t ), y2 (t ),, yq (t )

信号与线性系统分析 第20讲 系统的状态变量分析(二)

信号与线性系统分析 第20讲 系统的状态变量分析(二)

移项，两边同乘 eAt ，得
xt e At x0 t e At Bf d e At x0 e At Bf t 0 e At x0 e At B f t
可见它就是式 xt Axt Bf t 的解。式中第一项与输入无 关，只取决于初始条件（零输入分量）；第二项与初始条件 无关，只取决于输入（零状态分量）。
仿照单位矩阵的概念，定义一个单位冲激函数矩阵为一个为：
t 0 0
t
t
0
t
0
（任意阶次的方阵）
0
0 t
上一页
2021/4/26
信号与线性系统分析——系统的状态变量分析
12
∴ f t t f t
yt Ce At x0 Ce At Bf t D t f t
Ce At x0 Ce AtB D t f t yzi t yzs t
f 3 2
f11 g11 f12 g21 g12
f21 g11 f22 g21 g22
f31 g11 f32 g21
f11 g12 f12 g22
f21 g12 f22 g22
f31 g12 f32 g22
与乘积相比，把乘积运算换成卷积运算，应注意前面的积 分限是 0 t，因而严格地说 eAt 的所有分量，其含义应该乘以 一个单位阶跃 t 。
dt
dt
③ e At eAt ， e At eAt eAAt e0t
④ eAt 的逆阵为 e-At ， ∵ A A1 , ∴ ③ 由 知： e At 1 eAt
上一页 返 回
2021/4/26
信号与线性系统分析——系统的状态变量分析
7
状态方程组
xt Axt Bf t 是一个一阶微分方程。如果它是一个标 量方程式，就可以写成：xt axt bf t
  1. 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
  2. 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
  3. 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

1(t) 0 1 0 1(t) 0
2(t) 0
3(t)
a0
0 a1
1a232((tt))10[f(t)]
(7―16)
《信号与线性系统》
第7章 系统的状态变量分析
输出方程为
1(t)
[y(t)][b 0b 3a0 b 1b 3a1 b2b3a2] 2(t) [b3][f(t)]
当m＜n时，例如，
3(t)
λ(k+1)=Aλ(k)+Bf(k)
(7―7)
y(k)=Cλ(k)+Df(k)
(7―8)
其中
λ(k)=［λ1(k)，λ2(k)，…，λn(k)］T f(k)=［f1(k)，f2(k)，…，fm(k)］T y(k)=［y1(k)，y2(k)，…，yL(k)］T
《信号与线性系统》
第7章 系统的状态变量分析
7.2 连续时间系统状态方程的建立
7.2.1 根据电路图列写状态方程 对于纯正电路，其状态方程直观列写的一般步骤是： （1）选所有独立电容电压和独立电感电流作为状态
变量； （2）为保证所列出的状态方程等号左端只为一个状
态变量的一阶导数，必须对每一个独立电容写出只含此 独立电容电压一阶导数在内的节点（割集）KCL方程， 对每一个独立电感写出只含此电感电流一阶导数在内的 回路KVL方程；
yL(k)
图7.2 多输入―输出离散时间系统 《信号与线性系统》
第7章 系统的状态变量分析
设有n阶多输入―输出离散系统如图7.2所示。它
的m个输入为f1(k)，f2(k)，…，fm(k) ，其L个输出为 y1(k) ， y2(k) ， … ， yL(k) ， 系 统 的 状 态 变 量 为 λ1(k) ， λ2(k)，…，λn(k)。则其状态方程和输出方程可写为
7.1 状态变量与状态方程
7.1.1 系统用状态变量描述的基本术语 1．状态 状态可理解为事物的某种特征。状态发生了变化就
意味着事物有了发展和变化，所以状态是划分阶段的依 据。系统的状态就是指系统的过去、现在和将来的状况。 当系统的所有外部输入已知时，为确定系统未来运动， 必要与充分的信息的集合叫做系统的状态。状态通常可 以用一个数（变量）或一组数来描述。
3．状态变量分析法 以状态变量为独立完备变量，以状态方程和输出方程 为研究对象，对多输入多输出系统进行分析的方法，称为 状态变量分析法，也称状态空间法。该方法的基本步骤是： (1)选取一组独立的、完备的状态变量； (2)列写系统的状态方程，并将其写成标准的矩阵形式； (3)求解该状态方程，得到状态向量λ(t)或λ(k)； (4)列写标准形式的输出方程，并将所求得的状态向量 λ(t)或λ (k)代入其中，即得到输出向量y(t)或y(k)。
λ(t)=［λ1(t0)λ2(t0)…λn(t0)］T
《信号与线性系统》
第7章 系统的状态变量分析
状态变量在t0=0－时刻的值称为系统的初始状态 或起始状态 。即
λ(0-)=［λ1(0-)λ2(0-)…λn(0-)］T 5．状态空间 以n个状态变量为坐标轴而构成的n维空间称为状 态空间，或者说安放状态向量的空间即称为状态空间。 状态向量在状态空间n个坐标轴上的投影即相应为n个 状态变量。
yL(t)
图7.1 多输入―输出连续时间系统 《信号与线性系统》
第7章 系统的状态变量分析
系统的状态方程也可以用矢量矩阵的形式来表示，即
12aa1211
n
a31
a12 a22 a32
aa123312bb1211 a33n b31
b12 b22 b32
b13f1 bb3233ff23
(7―3)
上式可简记为
① ＋ uC － ②
＋
iCቤተ መጻሕፍቲ ባይዱＣ iL2
iL3
uS －
L2
④
L3 ③ ＋
(iS＋iL3) iS
R
－
《信号与线性系统》
图7.3 例7―1图
第7章 系统的状态变量分析
解该系统中有三个独立动态元件，故需三个状
态变量。选取电容电压uC和电感电流iL2、iL3为状态变 量。
对接有电容C的节点②运用KCL可得
iCCuCiL2iL3
H(s)bs33s3ab2s2s22ab1s1sab00
(7―15)
《信号与线性系统》
第7章 系统的状态变量分析
设H(s)的分子与分母无公因子相消，则可根据系统 的微分方程或H(s)，画出直接形式、并联形式、级联 形式的模拟框图或信号流图，然后再从模拟框图或信 号流图建立系统的状态方程。
1. 直接模拟法——相变量 取积分器的输出信号为状态变量，则状态方程为
(7―9)
选包含L2的回路L2－uS－C以及包含L3的回路L3
－R－uS－C，运用KVL可得两个独立电压方程
uS uC L2iL2 uS uC L3iL3R(iS iL3)
(7―10)
《信号与线性系统》
第7章 系统的状态变量分析
将式（7―9）和式（7―10）稍加整理，即可得到 状态方程
uC
1 C
《信号与线性系统》
第7章 系统的状态变量分析
1(t)
(t)
2(t)
[1(t)
2(t)n(t)]T
n(t)
(7―1)
此列矩阵λ(t)即称为n维状态向量，简称状态向量 。 由状态变量的定义可知，当λ(t0)及系统的输入给定时， λ(t)便可唯一的被确定。
4．初始状态 状态变量在某一时刻t0的值称为系统在t0时刻的状 态 。即
0
R L3
i
L3
1
L3
输出方程为
iC iL2 iL3 u RiS RiL3
《信号与线性系统》
0
0
uS
iS
(7―12)
R L3
(7―13)
第7章 系统的状态变量分析
写成标准矩阵形式为
iuC00
1 0
1RiiuL LC3200
0uS
RiS
(7―14)
《信号与线性系统》
第7章 系统的状态变量分析
7.1.2 系统的状态变量描述 1．状态方程 对于一个有m个输入f1(t)，f2(t)，…，fm(t)，L个输出
y1(t)，y2(t)，…，yL(t)的连续时间系统(如图7.1所示),假 设能充分描述该系统的n个状态变量为λ1(t)λ2(t)，…， λn(t)，则每个状态变量在任何时刻t的一阶导数可表示 为该时刻的n个状态变量和m个输入的一个函数，即
《信号与线性系统》
第7章 系统的状态变量分析
b2
f
1
3 s－1
2 s－1
1 s－1
b1
b0
－a2 3
2
1
y
－a1
－a0
图7.6 例7―2对应的信号流图 《信号与线性系统》
第7章 系统的状态变量分析
7.2.3 由微分方程或系统函数建立状态方程 若已知系统的微分方程，为了更具一般性，设其
分子、分母多项式中s的最高幂次相同（即取m=n的一 般情况），为 （p3+a2p2+a1p+a0）y(t)=（b3p3+b2p2+b1p+b0）f(t) 则进而可写出系统函数为
《信号与线性系统》
第7章 系统的状态变量分析
4．状态变量的选取 用状态变量描述系统的关键是选择状态变量。一 般来说，能充分描述因果动态系统的一组状态变量的 选择并不是唯一的。但只要状态变量的个数是充分的， 选择不同的状态变量来描述系统都是充分的。因此， 如何选择合适的状态变量，主要是看其是否方便于状 态方程和输出方程的编写，以及初始状态向量是否容 易确定。
第7章 系统的状态变量分析
7.2.2 由系统的模拟框图或信号流图建立状态方程 由系统的模拟框图或信号流图建立状态方程是一
种比较直观和简单的方法，其一般规则是： (1）选积分器的输出（或微分器的输入）作为状态
变量。 （2）围绕加法器列写状态方程或输出方程。
《信号与线性系统》
第7章 系统的状态变量分析
《信号与线性系统》
第7章 系统的状态变量分析
6．状态轨迹 在描述一个动态系统的状态空间中，状态向量的 端点随时间变化所经历的路径称为系统的状态轨迹。 一个动态系统的状态轨迹不仅取决于系统的内部结构， 还与系统的输入有关，因此，系统的状态轨迹可以形 象地描绘出在确定的输入作用下系统内部的动态过程。
《信号与线性系统》
第7章 系统的状态变量分析
解 选择各积分器的输出为状态变量，从右边到 左边依次取为λ1(t)、λ2(t)和λ3(t)，如图所示。根据各 积分器输入―输出和加法器的关系，可写出状态方程 为
1(t) 2(t) 2(t) 3(t) 3(t) a01(t) a12(t) a23(t) f (t) y(t) b01(t) b12(t) b23(t)
《信号与线性系统》
第7章 系统的状态变量分析
1a111a122a1nnb11f1b12f2b1mfm 2a211a222a2nnb21f1b22f2b2mfm nan11an22annnbn1f1bn2f2bnmfm
(7―2)
f1(t) f2(t)
fm(t)
…
{i(t0)}
…
y1(t) y2(t)
《信号与线性系统》
第7章 系统的状态变量分析
（3）若第（2）步所列出KCL、KVL方程中含有非 状态变量，则利用适当的节点KCL方程和回路KVL方 程，将非状态变量消去；
（4）将列出的状态方程整理成式（7―3）的矩阵 标准形式。
《信号与线性系统》
第7章 系统的状态变量分析
例7―1 写出图7.3所示电路的状态方程，若以电流 iC和电压u为输出，列出输出方程。