2021高考数学二轮复习专题练大题每日一题规范练第二周含解析

创新设计（全国通用）2017届高考数学二轮复习大题规范天天练第二周星期六综合限时练文编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（创新设计（全国通用）2017届高考数学二轮复习大题规范天天练第二周星期六综合限时练文）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为创新设计（全国通用）2017届高考数学二轮复习大题规范天天练第二周星期六综合限时练文的全部内容。

星期六(综合限时练)2017年____月____日解答题综合练(设计意图：训练考生在规定时间内得高分，限时:80分钟）1.（本小题满分12分）某个团购网站为了更好地满足消费者,对在其网站发布的团购产品展开了用户调查，每个用户在使用了团购产品后可以对该产品进行打分，最高分是10分.上个月该网站共卖出了100份团购产品，所有用户打分的平均分作为该产品的参考分值，将这些产品按照得分分成以下几组:第一组[0，2),第二组［2，4),第三组［4，6)，第四组[6，8），第五组[8,10］，得到的频率分布直方图如图所示。

(1)分别求第三,四，五组的频率；（2）该网站在得分较高的第三、四，五组中用分层抽样的方法抽取了6个产品作为下个月团购的特惠产品，某人决定在这6个产品中随机抽取2个购买，求他抽到的两个产品均来自第三组的概率.解(1）第三组的频率是0.150×2＝0.3；第四组的频率是0。

100×2＝0.2;第五组的频率是0.050×2＝0。

1。

(2）设“抽到的两个产品均来自第三组”为事件A，由题意可知，分别抽取3个，2个，1个。

不妨设第三组抽到的是A1，A2，A3；第四组抽到的是B1，B2；第五组抽到的是C1，所含基本事件总数为：{A1，A2｝，｛A1，A3},{A2，A3}，｛A1,B1｝,｛A1，B2}，{A1，C1},{A2，B1}，｛A2，B2},｛A2，C1｝，｛A3,B1｝，｛A3，B2},｛A3,C1｝，{B1，B2},{B1，C1},{B2，C1}共15种。

20212021湖南高考数学第二轮备考专题练习及参考答案2021年高考复习做题是不可或缺的方法，下面是查字典数学网整理的湖南高考数学第二轮备考专题练习，请大家及时练习。

1.双曲线的方程为=1(a0，b0)，焦距为4，一个顶点是抛物线y2=4x的焦点，则双曲线的离心率e=()A.2B. 1C.3D.52.已知F1，F2是椭圆的两个焦点，满足=0的点M总在椭圆内部，则椭圆离心率的取值范围是()A. (0，1)B.(1，5)C. (1，3)D.(0，2)3.设F为抛物线y2=4x的焦点，A，B，C为该抛物线上三点。

若=0，则||+||+||=()A.9B.6C.4D.34.已知抛物线y2=2px(p0)，过其焦点且斜率为1的直线交抛物线于A，B两点，若线段AB的中点的纵坐标为2，则该抛物线的准线方程为()A.x=1B.x=1C.x=2D.x=25.已知A，B，P是双曲线=1上不同的三点，且A，B连线经过坐标原点，若直线PA，PB的斜率乘积kPAkPB=，则该双曲线的离心率为()A.1B.2C. 1D.26.已知抛物线y2=4x的焦点为F，准线为l，经过F且斜率为的直线与抛物线在x轴上方的部分相交于点A，AKl，垂足为K，则AKF的面积是()A.4B.3C.4D.87.过抛物线y2=2px(p0)的焦点F作倾斜角为45的直线交抛物线于A，B两点，若线段AB的长为8，则p=( )。

8.(2021湖南，文14)平面上一机器人在行进中始终保持与点F(1，0)的距离和到直线x=1的距离相等。

若机器人接触不到过点P(1，0)且斜率为k的直线，则k的取值范围是( )。

9.已知双曲线的中心在原点，且一个焦点为F(，0)，直线y=x1与其相交于M， N两点，线段MN中点的横坐标为，求此双曲线的方程。

10.(2021安徽，文21)设F1，F2分别是椭圆E:=1(a0)的左、右焦点，过点F1的直线交椭圆E于A，B两点，|AF1|=3|F1B|。

2021年安徽高考数学理二轮模拟试题及答案1．复数为虚数单位，那么复数的共轭复数为( )ABCD分值: 5分查看题目解析 >22．“〞是“直线与互相平行〞的( )A充分不必要条件B必要不充分条件C充要条件D既不充分也不必要条件分值: 5分查看题目解析 >33．如右程序框图的算法思路源于数学名著<几何原本>中的“辗转相除法〞，执行该程序框图〔图中“〞表示除以的余数〕，假设输入的分别为，那么输出的A0B5C45D90分值: 5分查看题目解析 >44．将三颗骰子各掷一次，记事件“三个点数都不同〞，“至少出现一个６点〞，那么条件概率，分别是A，B，C，D，分值: 5分查看题目解析 >55．某几何体的三视图如下图，那么该几何体的体积为A12B18C24D30分值: 5分查看题目解析 >66．点在双曲线上，直线过坐标原点，且直线、的斜率之积为，那么双曲线的离心率为ABCD分值: 5分查看题目解析 >77．在边长为的正中，是边的两个三等分点〔靠近于点〕，那么等于A1/6B2/9C13/18D1/3分值: 5分查看题目解析 >88．函数的局部图象如下图，假设将图像上的所有点向右平移个单位得到函数的图像，那么函数的单调递增区间为ABCD分值: 5分查看题目解析 >99．数列是首项为，公差为的等差数列，数列满足．假设对任意的, 都有成立, 那么实数的取值范围是ABCD分值: 5分查看题目解析 >1010．函数为自然对数的底数的图象可能是ABCD分值: 5分查看题目解析 >1111．当，满足不等式组时，恒成立，那么实数的取值范围是ABCD分值: 5分查看题目解析 >1212．底面为边长为的正方形，侧棱长为的直四棱柱中，是面上的动点．给出以下四个结论中，那么正确的个数是与点距离为的点形成一条曲线，且该曲线的长度是；假设平面，那么与平面所成角的正切值取值范围是；假设，那么在该四棱柱六个面上的正投影长度之和的值为．A0B1C2D3分值: 5分查看题目解析 >填空题本大题共4小题，每题5分，共20分。

限时练二2021年高考数学二轮复习 专题训练 限时练2 理一、选择题1．设U ＝{1,2,3,4,5}，A ＝{1,5}，B ＝{2,4}，则B ∩(∁U A )＝ ( )．A ．{2,3,4}B ．{2}C ．{2,4}D ．{1,3,4,5}解析 ∁U A ＝{2,3,4}，所以B ∩(∁U A )＝{2,4}．答案 C2．已知复数z 1＝3－b i ，z 2＝1－2i ，若z 1z 2是实数，则实数b 的值为( )．A ．0B ．－32C ．6D ．－6解析z 1z 2＝3－b i 1－2i ＝3－b i 1＋2i1－2i 1＋2i＝3＋2b ＋6－b i5，因为z 1z 2是实数，所以6－b ＝0，所以实数b 的值为6.答案 C3．已知{a n }是由正数组成的等比数列，S n 表示{a n }的前n 项的和，若a 1＝3，a 2a 4＝144，则S 5的值是( )．A.692B ．69C ．93D ．189解析 因为{a n }是由正数组成的等比数列，所以a 23＝a 2a 4＝144，即a 3＝12，又因为a 1＝3，所以q ＝2，所以S 5＝31－251－2＝93.答案 C4．在△ABC 中，A ＝60°，b ＝1，△ABC 的面积为3，则边a 的值为( )．A ．27B ．21 C.13D ．3解析 因为△ABC 的面积为3，所以12bc sin A ＝3，所以c ＝4，由余弦定理得：a2＝b2＋c2－2bc cos A＝13，所以a＝13.答案 C5．如果log a8＞log b8＞0，那么a，b间的关系是( )．A．0＜a＜b＜1 B．1＜a＜bC．0＜b＜a＜1 D．1＜b＜a解析因为log a8＞log b8＞0，所以log8b＞log8a＞0＝log81，所以1＜a＜b.答案 B6．若(x－2x)n的二项展开式中的第5项是常数，则自然数n的值为( )．A．6 B．10 C．12 D．15解析∵T r＋1＝C r n(x)n－r(－2x)r＝C r n(－1)r2r x，∴T5＝C4n·24·x.令n－12＝0，∴n＝12.答案 C7.某学生一个学期的数学测试成绩一共记录了6个数据：x1＝52，x2＝70，x3＝68，x4＝55，x5＝85，x6＝90，执行如图所示的程序框图，那么输出的s是( )．A．1 B．2C．3 D．4解析初始值i＝1，s＝0，输入x 1＝52，此时不满足大于60，i ＝i ＋1＝2；输入x 2＝70，此时满足大于60，s ＝s ＋1＝1；i ＝i ＋1＝3； 输入x 3＝68，此时满足大于60，s ＝s ＋1＝2；i ＝i ＋1＝4； 输入x 4＝55，此时不满足大于60，i ＝i ＋1＝5；输入x 5＝85，此时满足大于60，s ＝s ＋1＝3；i ＝i ＋1＝6；输入x 6＝90，此时满足大于60，s ＝s ＋1＝4；i ＝i ＋1＝7，满足i ＞6，结束循环，所以输出的s 是4. 答案 D8．已知某几何体的三视图如图所示，其中俯视图是圆，且该几何体的体积为V 1；直径为2的球的体积为V 2.则V 1∶V 2＝( )．A ．1∶4B ．1∶2C ．1∶1D ．2∶1解析 易知：该几何体为一个圆柱内挖去一个圆锥，其中圆柱的底面半径为1，高为1，所以该几何体的体积V 1＝π×12×1－13π×12×1＝23π，直径为2的球的体积为V 2＝43πr 3＝43π，所以V 1∶V 2＝1∶2.答案 B9．已知实数x ，y 满足不等式组⎩⎪⎨⎪⎧0≤x ≤2，x ＋y －2≥0，x －y ＋2≥0，则目标函数z ＝3x －4y 的最小值m 与最大值M 的积为( )．A ．－60B ．－48C ．－80D ．36解析 画出约束条件⎩⎪⎨⎪⎧0≤x ≤2，x ＋y －2≥0，x －y ＋2≥0的可行域，由可行域知：目标函数z ＝3x －4y过点(2,0)时，取最大值6，所以M ＝6；过点(2,4)时，取最小值－10，所以m ＝－10.所以目标函数z ＝3x －4y 的最小值m 与最大值M 的积为－60. 答案 A10．双曲线x 2a 2－y 2b2＝1(a ＞0，b ＞0)的左、右焦点分别是F 1，F 2，过F 1作倾斜角为30°的直线交双曲线右支于M 点，若MF 2⊥x 轴，则双曲线的离心率为( )．A. 6 B ． 3 C. 4D ．33解析 ∵MF 2⊥x 轴，∴M (c ，b 2a )，∴tan 30°＝b 2a 2c ＝b 22ac ＝33，即3c 2－23ac －3a 2＝0，e ＝ 3.答案 B11．已知函数f (x )＝e x－mx ＋1的图象为曲线C ，若曲线C 存在与直线y ＝12x 垂直的切线，则实数m 的取值范围是( )．A ．m ≤2B ．m ＞2C ．m ≤－12D ．m ＞－12解析 由题意可知f ′(x )＝e x－m ，存在x 使得e x－m ＝－2有解，则m ＝e x＋2有解，e x＋2＞2，知m ＞2成立． 答案 B12．f (x )是定义在[－c ，c ]上的奇函数，其图象如图所示，令g (x )＝af (x )＋b ，则下列关于函数g (x )的叙述正确的是( )．A．若a＜0，则函数g(x)的图象关于原点对称B．若a＝－1，－2＜b＜0，则方程g(x)＝0有大于2的实根C．若a≠0，b＝2，则方程g(x)＝0有两个实根D．若a≥1，b＜2，则方程g(x)＝0有两个实根解析A中，若a＝－1，b＝1，则函数g(x)不是奇函数，其图象不可能关于原点对称，所以选项A错误；B中，当a＝－1时，－f(x)仍是奇函数，2仍是它的一个零点，但单调性与f(x)相反，若再加b，－2＜b＜0，则图象又向下平移－b个单位长度，所以g(x)＝－f(x)＋b＝0有大于2的实根，所以选项B正确；C中，若a＝12，b＝2，则g(x)＝12f(x)＋2，其图象由f(x)的图象向上平移2个单位长度，那么g(x)只有1个零点，所以g(x)＝0只有1个实根，所以选项C错误；D中，若a＝1，b＝－3，则g(x)的图象由f(x)的图象向下平移3个单位长度，它只有1个零点，即g(x)＝0只有一个实根，所以选项D错误．答案 B二、填空题13．某公司300名员工xx年年薪情况的频率分布直方图如图所示，由图可知，员工中年薪在1.4～1.6万元的共有________人．解析由频率分布直方图知年薪低于1.4万元或者高于1.6万元的频率为(0.2＋0.8＋0.8＋1.0＋1.0)×0.2＝0.76，因此，年薪在1.4到1.6万元间的频率为1－0.76＝0.24，所以300名员工中年薪在1.4到1.6万元间的员工人数为300×0.24＝72. 答案 7214．已知e 1，e 2是两个单位向量，若向量a ＝e 1－2e 2，b ＝3e 1＋4e 2，且a ·b ＝－6，则向量e 1与e 2的夹角是______．解析 ∵a ·b ＝(e 1－2e 2)·(3e 1＋4e 2)＝3e 21－8e 21－2e 1·e 2＝－6，即e 1·e 2＝12，设向量e 1与e 2的夹角为θ，则cos θ ＝12，又θ∈[0，π]，∴θ＝π3.答案π315．某铁路货运站对6列货运列车进行编组调度，决定将这6列列车编成两组，每组3列，且甲与乙两列列车不在同一小组，如果甲所在小组3列列车先开出，那么这6列列车先后不同的发车顺序共有种数为______．解析 除甲乙外的四辆车现分为两组，共有C 242种分组，再将甲乙分别放入两组，有A 22种，甲所在小组列车开出顺序有A 33种，乙所在小组列车开出顺序同样有A 33种，所以这六列列车开出顺序共有C 242A 22A 33A 33＝216种．答案 21616．将正奇数按下表的规律填在5列的数表中，则第20行第3列的数字与第20行第2列数字的和为________.解析 易知前194列的奇数为2×77－1＝153，所以第20行第3列的数字与第20行第2列数字分别为155,157，所以它们的和为312.答案 312d28403 6EF3 滳25447 6367 捧pd27148 6A0C 樌30805 7855 硕&M25893 6525 攥J 30635 77AB 瞫*26170 663A 昺。

2021年高三下学期第二次双周考试数学（理）试题 含答案一.选择题（本大题共12小题，每小题5分，共60分.在小题给出的四个选项中，只有一项是符合题目要求的.）1.已知集合，则=（ ） A ． B ． C ． D ． 2、复数z ＝1－3i1＋2i，则（ ）A 、 |z |＝2B 、z 的实部为1C 、 z 的虚部为－iD 、z 的共轭复数为－1＋i 3、下列判断错误的是（ ） A ．“”是“a < b ”的充分不必要条件 B ．命题“”的否定是“”C ．“若a =1，则直线和直线互相垂直”的逆否命题为真命题D ．若为假命题，则p ，q 均为假命题4、已知f (x )＝2sin(ωx ＋)的部分图像如图所示，则f (x )的表达式为( ) A ．f (x )＝2sin(32x ＋) B ．f (x )＝2sin(32x ＋)C ．f (x )＝2sin(43x ＋)D ．f (x )＝2sin(43x ＋2518)5、若x 、y 满足不等式，则z =3x +y 的最大值为（ ） A 、11B 、C 、13D 、6、若函数与函数在上的单调性相同，则的一个值为( ) A ．B ．C ．D ．7、过点可作圆的两条切线，则实数的取值范围为（ ） A ．或 B ．C ． 或D ．或8、在△ABC 中，若AB →2＝AB →·AC →＋BA →·BC →＋CA →·CB →，则△ABC 是( )A ．等边三角形B ．锐角三角形C ．钝角三角形D ．直角三角形 9.已知函数是定义在上的奇函数，且满足，当时，，则函数的零点是（ ） A ． B ． C ．D ．10、一个三棱的三视图是三个直角三角形，如图所示，则该三棱锥外接球表面积为（ ）A 、29B 、30C 、D 、21611、已知抛物线C ：y 2=8x 的焦点为F ，准线为l ，P 为l 上一点，Q 是直线PF 与C 的一个交点，若，则｜｜=（ ）A 、B 、C 、3D 、612、设定义域为R 的函数f （x ）=⎪⎪⎩⎪⎪⎨⎧<-=>-1 111 11 11x x x x x 若关于x 的方程f 2（x ）+bf （x ）+c =0有三个不同的解x 1，x 2，x 3，则x 12+x 22+x 32的值为（ ）A 、1B 、3C 、5D 、10二. 填空题（本大题共4小题，每小题5分，共20分.请把正确答案填写在横线上） 13.执行如图所示的程序框图，输出的T= ．14.若log a (a 2＋1)<log a 2a <0，则实数a 的取值范围是 ．15.已知函数，若数列满足（），且是递增数列，则实数的取值范围是 ___________． 16、设k 是一个正整数，（1+）k 的展开式中第三项的系数为，任取x ∈[0，4]，y ∈[0，16]，则点（x ，y ）满足条件y ≤kx 的概率是__________。

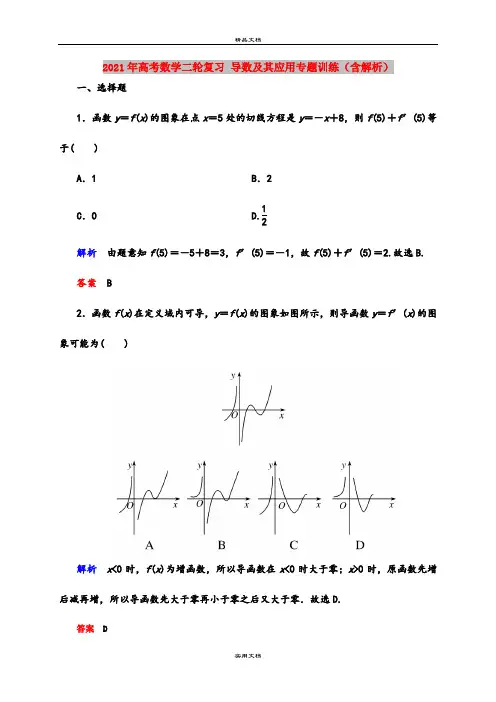
2021年高考数学二轮复习导数及其应用专题训练（含解析）一、选择题1．函数y＝f(x)的图象在点x＝5处的切线方程是y＝－x＋8，则f(5)＋f′(5)等于( )A．1 B．2C．0 D.1 2解析由题意知f(5)＝－5＋8＝3，f′(5)＝－1，故f(5)＋f′(5)＝2.故选B.答案B2．函数f(x)在定义域内可导，y＝f(x)的图象如图所示，则导函数y＝f′(x)的图象可能为( )解析x<0时，f(x)为增函数，所以导函数在x<0时大于零；x>0时，原函数先增后减再增，所以导函数先大于零再小于零之后又大于零．故选D.答案 D3．(理)(xx·山东淄博一模)若函数f (x )的导函数在区间(a ，b )上的图象关于直线x ＝a ＋b2对称，则函数y ＝f (x )在区间[a ，b ]上的图象可能是( )A ．①④B ．②④C ．②③D ．③④解析 因为函数y ＝f (x )的导函数在区间(a ，b )上的图象关于直线x ＝a ＋b2对称，即导函数要么图象无增减性，要么在直线x ＝a ＋b2两侧单调性相反．由图①得，在a 处切线斜率最小，在b 处切线斜率最大，故导函数图象不关于直线x ＝a ＋b2对称，故①不成立；由图②得，在a 处切线斜率最大，在b 处切线斜率最小，故导函数图象不关于直线x ＝a ＋b2对称，故②不成立；由图③得，原函数为一次函数，其导函数为常数函数，故导函数图象关于直线x ＝a ＋b2对称，③成立；由图④得，原函数有一对称中心，在直线x ＝a ＋b2与原函数图象的交点处，故导函数图象关于直线x ＝a ＋b2对称，④成立；所以满足要求的有③④，故选D.答案 D3．(文)函数f (x )＝3x 2＋ln x －2x 的极值点的个数是( ) A ．0 B ．1 C ．2D ．无数个解析 函数定义域为(0，＋∞)， 且f ′(x )＝6x ＋1x －2＝6x 2－2x ＋1x，由于x >0，g (x )＝6x 2－2x ＋1中Δ＝－20<0， ∴g (x )>0恒成立， 故f ′(x )>0恒成立，即f (x )在定义域上单调递增，无极值点． 答案 A4．(xx·重庆七校联盟联考)已知函数f (x )在R 上满足f (x )＝2f (2－x )－x 2＋8x －8，则曲线y ＝f (x )在点(1，f (1))处切线的斜率是( )A ．2B ．1C ．3D ．－2解析 由f (x )＝2f (2－x )－x 2＋8x －8两边求导得，f ′(x )＝2f ′(2－x )×(－1)－2x ＋8.令x ＝1得f ′(1)＝2f ′(1)×(－1)－2＋8⇒f ′(1)＝2，∴k ＝2.答案 A5．(xx·云南昆明一模)已知函数f (x )＝ln x ＋1ln x，则下列结论中正确的是( ) A ．若x 1，x 2(x 1<x 2)是f (x )的极值点，则f (x )在区间(x 1，x 2)内是增函数 B ．若x 1，x 2(x 1<x 2)是f (x )的极值点，则f (x )在区间(x 1，x 2)内是减函数 C ．∀x >0，且x ≠1，f (x )≥2D ．∃x 0>0，f (x )在(x 0，＋∞)上是增函数解析 由已知f ′(x )＝1x －1x ln 2x ＝ln 2x －1x ln 2x (x >0，且x ≠1)，令f ′(x )＝0，得x ＝e 或x ＝1e.当x ∈⎝⎛⎭⎪⎫0，1e 时，f ′(x )>0；当x ∈⎝⎛⎭⎪⎫1e，1∪(1，e)时，f ′(x )<0；当x ∈(e ，＋∞)时，f ′(x )>0.故x ＝1e和x ＝e 分别是函数f (x )的极大值点和极小值点，故函数f (x )在⎝ ⎛⎭⎪⎫1e，1和(1，e)内单调递减，所以A 、B 错；当0<x <1时，ln x <0，f (x )<0，故C 错；若x 0≥e，f (x )在(x 0，＋∞)上是增函数，D 正确．答案 D6．f (x )是定义在(0，＋∞)上的非负可导函数，且满足xf ′(x )－f (x )≤0，对任意正数a ，b ，若a <b ，则必有( )A ．af (b )≤bf (a )B ．bf (a )≤af (b )C ．af (a )≤f (b )D ．bf (b )≤f (a )解析 设F (x )＝f x x ，则F ′(x )＝xf ′x －f xx 2≤0， 故F (x )＝f xx为减函数． 由0<a <b ，有f a a ≥f bb⇒af (b )≤bf (a )，故选A. 答案 A 二、填空题7．(理)(xx·广东卷)曲线y ＝e －5x＋2在点(0,3)处的切线方程为________．解析 y ′＝－5e－5x，∴y ′|x ＝0＝－5，∴所求切线方程为y －3＝－5x ，即5x ＋y －3＝0.答案 5x ＋y －3＝07．(文)已知函数f (x )＝x e x，则f ′(x )＝________；函数f (x )的图象在点(0，f (0))处的切线方程为________．解析 ∵f ′(x )＝1·e x ＋x ·e x ＝(1＋x )e x；f ′(0)＝1，f (0)＝0，因此f (x )在点(0，f (0))处的切线方程为y －0＝x －0，即y ＝x .答案 (1＋x )e xy ＝x8．若点P 是曲线y ＝x 2－ln x 上任意一点，则点P 到直线y ＝x －2的最小距离为________． 解析 过点P 作y ＝x －2的平行直线，且与曲线y ＝x 2－ln x 相切． 设P (x 0，x 20－ln x 0)，则有k ＝y ′|x ＝x 0＝2x 0－1x 0.∴2x 0－1x 0＝1.∴x 0＝1或x 0＝－12(舍去)．∴P (1,1)，∴d ＝|1－1－2|1＋1＝ 2. 答案29．已知函数f (x )＝x 3＋2bx 2＋cx ＋1有两个极值点x 1，x 2，且x 1∈[－2，－1]，x 2∈[1,2]，则f (－1)的取值范围是________．解析 由于f ′(x )＝3x 2＋4bx ＋c ，据题意方程3x 2＋4bx ＋c ＝0有两个根x 1，x 2，且x 1∈[－2，－1]，x 2∈[1,2]，令g (x )＝3x 2＋4bx ＋c ，结合二次函数图象可得⎩⎪⎨⎪⎧g －2＝12－8b ＋c ≥0，g －1＝3－4b ＋c ≤0，g 1＝3＋4b ＋c ≤0，g2＝12＋8b ＋c ≥0，此即为关于点(b ，c )的线性约束条件，作出其对应的平面区域，f (－1)＝2b －c ，问题转化为在上述线性约束条件下确定目标函数f (－1)＝2b －c 的最值问题，由线性规划易知3≤f (－1)≤12.答案 [3,12] 三、解答题10．已知函数f (x )＝4x 3＋3tx 2－6t 2x ＋t －1，x ∈R ，其中t ∈R . (1)当t ＝1时，求曲线y ＝f (x )在点(0，f (0))处的切线方程； (2)t ≠0时，求f (x )的单调区间．解 (1)当t ＝1时，f (x )＝4x 3＋3x 2－6x ，f (0)＝0，f ′(x )＝12x 2＋6x －6，f ′(0)＝－6， 所以曲线y ＝f (x )在点(0，f (0))处的切线方程为y ＝－6x . (2)f ′(x )＝12x 2＋6tx －6t 2.令f ′(x )＝0，解得x ＝－t 或x ＝t2.因为t ≠0，以下分两种情况讨论：①若t <0，则t2<－t .当x 变化时，f ′(x )，f (x )的变化情况如下表：所以，f (x )的单调递增区间是⎝ ⎛⎭⎪⎫－∞，2，(－t ，＋∞)；f (x )的单调递减区间是⎝ ⎛⎭⎪⎫2，－t .②若t >0，则－t <t2.当x 变化时，f ′(x )，f (x )的变化情况如下表：所以，f (x )的单调递增区间是(－∞，－t )，⎝ ⎛⎭⎪⎫2，＋∞；f (x )的单调递减区间是⎝ ⎛⎭⎪⎫－t ，t 2.11．(理)(xx·福建卷)已知函数f (x )＝e x－ax (a 为常数)的图象与y 轴交于点A ，曲线y ＝f (x )在点A 处的切线斜率为－1.(1)求a 的值及函数f (x )的极值； (2)证明：当x >0时，x 2<e x；(3)证明：对任意给定的正数c ，总存在x 0，使得当x ∈(x 0，＋∞)时，恒有x 2<c e x. 解 (1)由f (x )＝e x －ax ，得f ′(x )＝e x－a . 又f ′(0)＝1－a ＝－1，得a ＝2. 所以f (x )＝e x －2x ，f ′(x )＝e x－2. 令f ′(x )＝0，得x ＝ln2.当x <ln2时，f ′(x )<0，f (x )单调递减； 当x >ln2时，f ′(x )>0，f (x )单调递增．所以当x ＝ln2时，f (x )取得极小值，且极小值为f (ln2)＝e ln2－2ln2＝2－ln4，f (x )无极大值． (2)令g (x )＝e x －x 2，则g ′(x )＝e x－2x . 由(1)得g ′(x )＝f (x )≥f (ln2)>0， 故g (x )在R 上单调递增，又g (0)＝1>0， 因此，当x >0时，g (x )>g (0)>0，即x 2<e x.(3)①若c≥1，则e x≤c e x.又由(2)知，当x>0时，x2<e x.所以当x>0时，x2<c e x.取x0＝0，当x∈(x0，＋∞)时，恒有x2<c e x.②若0<c<1，令k＝1c>1，要使不等式x2<c e x成立，只要e x>kx2成立．而要使e x>kx2成立，则只要x>ln(kx2)，只要x>2ln x＋ln k成立．令h(x)＝x－2ln x－ln k，则h′(x)＝1－2x＝x－2x，所以当x>2时，h′(x)>0，h(x)在(2，＋∞)内单调递增．取x0＝16k>16，所以h(x)在(x0，＋∞)内单调递增，又h(x0)＝16k－2ln(16k)－ln k＝8(k－ln2)＋3(k－ln k)＋5k，易知k>ln k，k>ln2,5k>0，所以h(x0)>0.即存在x0＝16c，当x∈(x0，＋∞)时，恒有x2<c e x.综上，对任意给定的正数c，总存在x0，当x∈(x0，＋∞)时，恒有x2<c e x.11．(文)已知函数f(x)＝－x3＋ax2＋bx＋c在(－∞，0)上是减函数，在(0,1)上是增函数，函数f(x)在R上有三个零点，且1是其中一个零点．(1)求b的值；(2)求f(2)的取值范围．解(1)∵f(x)＝－x3＋ax2＋bx＋c，∴f′(x)＝－3x2＋2ax＋b.∵f(x)在(－∞，0)上是减函数，在(0,1)上是增函数，∴当x＝0时，f(x)取得极小值，即f′(0)＝0.∴b＝0.(2)由(1)知，f(x)＝－x3＋ax2＋c，∵1是函数f(x)的一个零点，即f(1)＝0，∴c＝1－a.∵f′(x)＝－3x2＋2ax＝0的两个根分别为x1＝0，x2＝2a 3.∵f(x)在(0,1)上是增函数，且函数f(x)在R上有三个零点，∴x 2＝2a3>1，即a >32.∴f (2)＝－8＋4a ＋(1－a )＝3a －7>－52.故f (2)的取值范围为⎝ ⎛⎭⎪⎫－52，＋∞. B 级——能力提高组1．(理)(xx·江西卷)若f (x )＝x 2＋2⎠⎛01f(x)d x ，则⎠⎛01f(x)d x ＝( )A ．－1B ．－13C .13D ．1解析 直接求解定积分，再利用方程思想求解． ∵f(x)＝x 2＋2⎠⎛01f(x)d x ，∴⎠⎛01f(x)d x ＝⎝ ⎛⎭⎪⎫13x 3＋2x ⎠⎛01f x d x ⎪⎪ 1＝13＋2⎠⎛01f(x)d x ， ∴⎠⎛01f(x)d x ＝－13.答案 B 1．(文)(理)2.(xx·中原名校二模)已知函数g(x)＝ax 3＋bx 2＋cx ＋d(a≠0)的导函数为f(x)，且a ＋2b ＋3c ＝0，f(0)·f(1)>0，设x 1，x 2是方程f(x)＝0的两根，则|x 1－x 2|的取值范围是( )A .⎣⎢⎡⎭⎪⎫0，23B .⎣⎢⎡⎭⎪⎫0，49C .⎝ ⎛⎭⎪⎫13，23 D .⎝ ⎛⎭⎪⎫19，49 解析 因为f(x)＝3ax 2＋2bx ＋c ，所以f(0)f(1)＝c(3a ＋2b ＋c)＝c(2a －2c)>0,0<c a<1，又|x 1－x 2|＝Δ|3a|＝2b 2－3ac |3a|＝|a －3c||3a|＝⎪⎪⎪⎪⎪⎪13－c a ∈⎣⎢⎡⎭⎪⎫0，23.答案 A2．(理)(xx·中原名校二模)已知函数g(x)＝ax 3＋bx 2＋cx ＋d(a≠0)的导函数为f(x)，且a ＋2b ＋3c ＝0，f(0)·f(1)>0，设x 1，x 2是方程f(x)＝0的两根，则|x 1－x 2|的取值范围是( )A .⎣⎢⎡⎭⎪⎫0，23B .⎣⎢⎡⎭⎪⎫0，49C .⎝⎛⎭⎪⎫13，23D .⎝⎛⎭⎪⎫19，49解析 因为f(x)＝3ax 2＋2bx ＋c ，所以f(0)f(1)＝c(3a ＋2b ＋c)＝c(2a －2c)>0,0<c a<1，又|x 1－x 2|＝Δ|3a|＝2b 2－3ac |3a|＝|a －3c||3a|＝⎪⎪⎪⎪⎪⎪13－c a ∈⎣⎢⎡⎭⎪⎫0，23.答案 A2．(文)已知函数f(x)＝ax 3＋bx 2＋cx ，其导函数y ＝f′(x)的图象经过点(1,0)，(2,0)，如图所示，则下列说法中不正确的是________． ①当x ＝32时函数取得极小值；②f(x )有两个极值点； ③当x ＝2时函数取得极小值； ④当x ＝1时函数取得极大值．解析 从图象上可以看到：当x∈(0,1)时，f′(x)>0；当x∈(1,2)时，f′(x)<0；当x∈(2，＋∞)时，f′(x)>0，所以f(x)有两个极值点1和2，且当x ＝2时函数取得极小值，当x ＝1时函数取得极大值．只有①不正确．答案 ①3．(理)(xx·课标全国卷Ⅱ)已知函数f(x)＝e x－e －x－2x. (1)讨论f(x)的单调性；(2)设g(x)＝f(2x)－4bf(x)，当x>0时，g(x)>0，求b 的最大值； (3)已知1.414 2<2<1.414 3，估计ln 2的近似值(精确到0.001)． 解 (1)f′(x)＝e x＋e －x－2≥0，等号仅当x ＝0时成立．所以f(x)在(－∞，＋∞)上单调递增． (2)g(x)＝f(2x)－4bf(x)＝e 2x－e －2x－4b(e x －e －x)＋(8b －4)x ，g′(x)＝2[e 2x＋e－2x－2b(e x＋e －x )＋(4b －2)]＝2(e x＋e －x－2)(e x＋e －x－2b ＋2)．①当b≤2时，g′(x)≥0，等号仅当x ＝0时成立，所以g(x)在(－∞，＋∞)上单调递增．而g(0)＝0，所以对任意x>0，g(x)>0；②当b>2时，若x 满足2<e x＋e －x<2b －2，即0<x<ln (b －1＋b 2－2b)时g′(x)<0.而g(0)＝0，因此当0<x≤ln (b －1＋b 2－2b)时，g(x)<0.综上，b 的最大值为2.(3)由(2)知，g(ln 2)＝32－22b ＋2(2b －1)ln 2.当b ＝2时，g(ln 2)＝32－42＋6ln 2>0，ln 2>82－312>0.692 8；当b ＝324＋1时，ln (b －1＋b 2－2b)＝ln 2， g(ln 2)＝－32－22＋(32＋2)ln 2<0，ln 2<18＋228<0.693 4. 所以ln 2的近似值为0.693.3．(文)(xx·课标全国卷Ⅱ)已知函数f(x)＝x 3－3x 2＋ax ＋2，曲线y ＝f(x)在点(0,2)处的切线与x 轴交点的横坐标为－2.(1)求a ；(2)证明：当k<1时，曲线y ＝f(x)与直线y ＝kx －2只有一个交点． 解 (1)f′(x)＝3x 2－6x ＋a ，f′(0)＝a. 曲线y ＝f(x)在点(0,2)处的切线方程为y ＝ax ＋2. 由题设得－2a ＝－2，所以a ＝1.(2)证明：由(1)知，f(x)＝x 3－3x 2＋x ＋2. 设g(x)＝f(x)－kx ＋2＝x 3－3x 2＋(1－k)x ＋4. 由题设知1－k>0.当x≤0时，g′(x)＝3x 2－6x ＋1－k>0，g(x)单调递增，g(－1)＝k －1<0，g(0)＝4， 所以g(x)＝0在(－∞，0]有唯一实根． 当x>0时，令h(x)＝x 3－3x 2＋4， 则g(x)＝h(x)＋(1－k)x>h(x)．h′(x)＝3x2－6x＝3x(x－2)，h(x)在(0,2)单调递减，在(2，＋∞)单调递增，所以g(x)>h(x)≥h(2)＝0.所以g(x)＝0在(0，＋∞)没有实根．综上，g(x)＝0在R有唯一实根，即曲线y＝f(x)与直线y＝kx－2只有一个交点．20226 4F02 伂31220 79F4 秴]38002 9472 鑲39341 99AD 馭30496 7720 眠24691 6073 恳 "35323 89FB 觻 26755 6883 梃35769 8BB9 讹]7。

2021年高考数学二轮复习规范滚动训练(I)解答题(解答应写出文字说明，证明过程或演算步骤)1．设函数f (x )＝x2＋sin x 的所有正的极小值点从小到大排成的数列为{x n }．(1)求数列{x n }的通项公式；(2)设{x n }的前n 项和为S n ，求sin S n .解：(1)令f ′(x )＝12＋cos x ＝0，即cos x ＝－12，解得x ＝2k π±23π(k ∈Z )．由x n 是f (x )的第n 个正极小值点知x n ＝2n π－23π(n ∈N *)．(2)由(1)可知S n ＝2π(1＋2＋…＋n )－23n π＝n (n ＋1)π－2n π3，所以sin S n ＝sin ⎣⎢⎡⎦⎥⎤nn ＋1π－2n π3. 因为n (n ＋1)表示两个连续正整数的乘积， 所以n (n ＋1)一定为偶数，所以sin S n ＝－sin 2n π3.当n ＝3m －2(m ∈N *)时，sin S n ＝－sin ⎝ ⎛⎭⎪⎫2m π－4π3＝－32； 当n ＝3m －1(m ∈N *)时，sin S n ＝－sin ⎝ ⎛⎭⎪⎫2m π－2π3＝32； 当n ＝3m (m ∈N *)时，sin S n ＝－sin2m π＝0. 综上，当n ＝3m －2(m ∈N *)sin S n ＝－32当n ＝3m －1，(m ∈N *)sin S n ＝32当n ＝3m ，(m ∈N *)sin S n ＝0.2．为了迎接国家卫生城市复审，创设干净整洁的城市环境，某高中要从高一、高二、高三三个年级推出的班级中分别选1个，组成“巩卫”小组，利用周末进行义务创城活动．其中高一推出3个班且标号分别为A 1，A 2，A 3，高二推出2个班且标号分别为B 1，B 2，高三推出2个班且标号分别为C 1，C 2. (1)求A 1被选中的概率；(2)求A 1和C 2不全被选中的概率．解：通解：组成“巩卫”小组的所有结果如下：(A 1，B 1，C 1)，(A 1，B 1，C 2)，(A 1，B 2，C 1)，(A 1，B 2，C 2)，(A 2，B 1，C 1)，(A 2，B 1，C 2)，(A 2，B 2，C 1)，(A 2，B 2，C 2)，(A 3，B 1，C 1)，(A 3，B 1，C 2)，(A 3，B 2，C 1)，(A 3，B 2，C 2)，共12种．(1)记“A 1被选中”为事件E ，则E 包含的结果有：(A 1，B 1，C 1)，(A 1，B 1，C 2)，(A 1，B 2，C 1)，(A 1，B 2，C 2)，共4种，所以P (E )＝412＝13.(2)记事件M 表示“A 1和C 2不全被选中”，则其对立事件M 表示“A 1和C 2全被选中”． 由于事件M 包含(A 1，B 1，C 2)，(A 1，B 2，C 2)，共2种结果，所以P (M )＝212＝16. 由对立事件的概率计算公式得P (M )＝1－P (M )＝1－16＝56.故A 1和C 2不全被选中的概率为56.3．如图，在平行四边形ABCD 中，BC ＝2AB ，∠ABC ＝60°，四边形BEFD 是矩形，且BE ＝BA ，平面BEFD ⊥平面ABCD .(1)求证：AE ⊥CF ；(2)若AB ＝1，求该几何体的表面积．解：(1)法一：连接AC ，记EC ，EF ，BD 的中点分别为G ，M ，N ，连接GM ，GN ，MN ，则GM ∥FC ，GN ∥AE ，如图1.由题意，易证BE ⊥AB ， 不妨设AB ＝1，则GM ＝GN ＝22，MN ＝BE ＝1， 由勾股定理的逆定理知GM ⊥GN . 故AE ⊥CF .法二：如图2，将原几何体补成直四棱柱，则依题意，其侧面ABEG 为正方形，对角线AE ，BG 显然垂直，故AE ⊥CF .(2)连接AC ，根据题意易证AB ⊥AC ，BE ⊥平面ABCD ，易知BE ＝AB ＝CD ＝DF ＝1，BC ＝AD ＝2，AE ＝CF ＝2，CE ＝AF ＝5，EF ＝BD ＝7， 从而CE ⊥CF ，AE ⊥AF . 所以所求几何体的表面积S ＝2×⎝ ⎛⎭⎪⎫12×1×1＋12×1×2＋12×2×5＋2×1×32＝3＋10＋ 3. 4．已知椭圆C ：x 2a 2＋y 2b 2＝1(a ＞b ＞0)的左、右焦点分别为F 1，F 2，离心率e 为12，过F 1的直线l 1与椭圆C 交于M ，N 两点，且△MNF 2的周长为8. (1)求椭圆C 的方程；(2)设直线l 2与椭圆C 交于A ，B 两点，O 为坐标原点，且OA →·OB →＝0.过点O 作直线l 2的垂线，垂足为Q ，求点Q 的轨迹方程． 解：(1)由题意知4a ＝8，∴a ＝2. ∵e ＝12，∴c ＝1，b 2＝3.∴椭圆C 的方程为x 24＋y 23＝1.(2)∵OA →·OB →＝0，∴OA ⊥OB .①若直线l 2的斜率不存在，则点Q 在x 轴上． 设点Q 的坐标为(x 0,0)，则A (x 0，x 0)，B (x 0，－x 0)． 又∵A ，B 两点在椭圆C 上，∴x 204＋x 203＝1，x 20＝127.∴点Q 的坐标为⎝ ⎛⎭⎪⎫±127，0，即|OQ |＝127. ②若直线l 2的斜率存在，设直线l 2的方程为y ＝kx ＋m .由⎩⎪⎨⎪⎧y ＝kx ＋m ，x 24＋y23＝1消去y 得(3＋4k 2)x 2＋8kmx ＋4m 2－12＝0. 由Δ＞0得，m 2＜3＋4k 2. 设A (x 1，y 1)，B (x 2，y 2)，则x 1＋x 2＝－8km 3＋4k 2，x 1x 2＝4m 2－123＋4k 2.∵OA ⊥OB ，∴x 1x 2＋y 1y 2＝0. ∴x 1x 2＋(kx 1＋m )(kx 2＋m )＝0， 即(k 2＋1)x 1x 2＋km (x 1＋x 2)＋m 2＝0. ∴(k 2＋1)4m 2－123＋4k 2－8k 2m 23＋4k2＋m 2＝0.整理得7m 2＝12(k 2＋1)，满足m 2＜3＋4k 2.又由已知可得过原点O 与直线l 2垂直的直线方程为y ＝－1kx ，解方程组⎩⎪⎨⎪⎧y ＝－1k x ，y ＝kx ＋m ，得点Q 的横坐标与纵坐标分别为x ＝－kk 2＋1m ，y ＝1k 2＋1m ， ∴x 2＋y 2＝k 2k 2＋12m 2＋1k 2＋12m 2＝m 2k 2＋1＝127，即|OQ |＝127. 综合(1)(2)可知，点Q 的轨迹是以坐标原点为圆心，半径为127的一个圆，且该圆的方程为x 2＋y 2＝127.23707 5C9B 岛537633 9301 錁 21921 55A1 喡M28172 6E0C 渌33084 813C 脼20135 4EA7 产f-24685 606D 恭f38080 94C0 铀m。

2021年高三上学期第二次周练数学（理）试题 含答案一、选择题：（本题包括6小题，共60分，每小题只有一个选项符合题意）1.设函数，则是( )A 、奇函数，且在（0,1）上是增函数B 、奇函数，且在（0,1）上是减函数C 、偶函数，且在（0,1）上是增函数D 、偶函数，且在（0,1）上是减函数2.设，若，，，则下列关系式中正确的是（ ）A ．B ．C ．D ．3.函数f (x )＝|log 3x |在区间[a ，b ]上的值域为[0,1]，则b －a 的最小值为( )A.13B.23C ．1D ．2 4.已知f (x )＝3x －b (2≤x ≤4，b 为常数)的图像经过点(2,1)，则f (x )的值域( )A ．[9,81]B ．[3,9] C. [1,9] D ．[1，＋∞)5.f (x )的定义域为R ，且f (x )＝⎩⎪⎨⎪⎧2－x －1(x ≤0)，f (x －1)(x ＞0)， 若方程f (x )＝x ＋a 有两个不同实根，则a 的取值范围为( )A ．(－∞，1)B ．(－∞，1]C ．(0,1)D ．(－∞，＋∞)6.设函数的图像与的图像关于直线对称，且，则( )（A ） （B ） （C ） （D ）7.设a >0且a ≠1，函数f (x )＝a lg(x 2－2x ＋3)有最大值，则不等式log a (x 2－5x ＋7)>0的解集为__________．8.已知函数，（其中）.对于不相等的实数，设，.现有如下命题：（1）对于任意不相等的实数，都有；（2）对于任意的a 及任意不相等的实数，都有；（3）对于任意的a ，存在不相等的实数，使得；（4）对于任意的a ，存在不相等的实数，使得.其中的真命题有 （写出所有真命题的序号）.})(|{)3(.1)()2(.)(,)1(.|34|)(.92有四个不相等的实根使方程求集合解不等式增减性的单调区间，并指出其并求函数画出函数的图像已知函数m x f m M x f x f x x x f ==≥+-=10附加题（零班） 图像对称中心函数利用题设中的真命题求对应的函数解析式，并个单位，求此时图像个单位，再向上平移的图像向左平移将函数是奇函数函数的充要条件为成中心对称图形的图像关于点函数已知真命题：)(213)()1(".)(""),()("23x g x x x g b a x f y b a P x f y -=-+==的坐标..42log )(22图像对称中心的坐标）求函数（xx x h -= （2）证明）使之成为真命题（不必的真命题对它进行修改说明理由，并类比题设如果是假命题，果是真命题，请证明，判断该命题的真假，如是偶函数函数使得和存在实数的充要条件为对称图像的图像关于某直线成轴函数已知命题：,,")(,"")(")3(b a x f y b a x f y -+==1.A 【解析】函数，函数的定义域为（-1，1），函数所以函数是奇函数． ，在（0,1）上 ，所以在(0,1)上单调递增，故选A.2.C【解析】；；因为，由是个递增函数，所以，故答案选3.B解析：令f (x )＝0，得x ＝1；令f (x )＝1，得x ＝13或3.因为函数f (x )在(0,1]上为减函数，在[1，＋∞)上为增函数，故b －a 的最小值为1－13＝23. 4.C5.A 解析：x ≤0时，f (x )＝2－x －1,0＜x ≤1时，－1＜x －1≤0，f (x )＝f (x －1)＝2－(x －1)－1，故x ＞0时，f (x )是周期函数．如图：欲使方程f (x )＝x ＋a 有两个不同的实数解，即函数f (x )的图像与直线y ＝x ＋a 有两个不同的交点，故a ＜1.6.C 【解析】选C 设是函数的图像上任意一点，它关于直线对称为（），由已知知（）在函数的图像上，∴，解得，即，∴22(2)(4)log 2log 41f f a a -+-=-+-+=，解得，故选C.7.答案：(2,3)解析：∵函数y ＝lg(x 2－2x ＋3)有最小值，f (x )＝a lg(x 2－2x ＋3)有最大值，∴0<a <1.∴由log a (x 2－5x ＋7)>0，得0<x 2－5x ＋7<1，解得2<x <3.∴不等式log a (x 2－5x ＋7)>0的解集为(2,3)．8.【答案】①④【解析】设11221122(,()),(,()),(,()),(,())A x f x B x f x C x g x D x g x .对（1），从的图象可看出，恒成立，故正确.对（2），直线CD 的斜率可为负，即，故不正确.对（3），由m =n 得，即.令，则.由得：，作出的图象知，方程不一定有解，所以不一定有极值点，即对于任意的a ，不一定存在不相等的实数，使得，即不一定存在不相等的实数，使得.故不正确.对（4），由m =－n 得，即.令，则.由得：，作出的图象知，方程必一定有解，所以一定有极值点，即对于任意的a，一定存在不相等的实数，使得，即一定存在不相等的实数，使得.故正确.所以（1）（4）9.略10附加题（1）（2,1）（3）假命题xxay==f=y+f的充要条件为"(),")(是偶函数函数a的图像关于直线成轴对称图像x34264 85D8 藘K36412 8E3C 踼39622 9AC6 髆38645 96F5 雵28544 6F80 澀9 24164 5E64 幤4pq36135 8D27 货39260 995C 饜。

大题每日一题规范练星期一(三角) 2021年____月____日【题目1】 已知△ABC 的内角A ，B ，C 的对边分别为a ，b ，c ，在①(a ＋b )(sin A －sin B )＝(c －b )sin C ， ②b sinB ＋C2＝a sin B ，③cos 2A －3cos(B ＋C )＝1这三个条件中任选一个解答下列问题： (1)求A 的大小； (2)若△ABC 的面积S ＝53，b ＝5，求sin B sin C 值.(注：如果选择多个条件分别解答，按第一个解答计分) 解 选择①.(1)由正弦定理，得(a ＋b )(a －b )＝(c －b )c ， 即a 2－b 2＝c 2－bc . 由余弦定理，得cos A ＝b 2＋c 2－a 22bc＝12. ∵0<A <π，∴A ＝π3.(2)由S ＝12bc sin A ＝53，b ＝5，A ＝π3，得c ＝4.由余弦定理，得a 2＝b 2＋c 2－2bc cos A ＝21.由正弦定理，得asin A ＝2R (R 为△ABC 的外接圆的半径)，∴(2R )2＝⎝ ⎛⎭⎪⎫a sin A 2＝28， ∴sin B sin C ＝bc（2R ）2＝57.选择②.(1)由正弦定理，得sin B sin B ＋C2＝sin A sin B .∵sin B ≠0，A ＋B ＋C ＝π，∴sin ⎝ ⎛⎭⎪⎫π2－A 2＝sin A ，即cos A 2＝2sin A 2cos A 2.又cos A 2≠0，∴sin A 2＝12.∵0<A <π，∴A 2＝π6，即A ＝π3.(2)由S ＝12bc sin A ＝53，b ＝5，A ＝π3，得c ＝4.由余弦定理，得a 2＝b 2＋c 2－2bc cos A ＝21.由正弦定理，得asin A＝2R (R 为△ABC 的外接圆的半径)，∴(2R )2＝⎝ ⎛⎭⎪⎫a sin A 2＝28， ∴sin B sin C ＝bc（2R ）2＝57.选择③.(1)由cos 2A －3cos(B ＋C )＝1，A ＋B ＋C ＝π， 得2cos 2A ＋3cos A －2＝0.解得cos A ＝12或cos A ＝－2(舍去).∵0<A <π，∴A ＝π3.(2)由S ＝12bc sin A ＝53，b ＝5，A ＝π3，得c ＝4.由余弦定理，得a 2＝b 2＋c 2－2bc cos A ＝21.由正弦定理，得asin A ＝2R (R 为△ABC 的外接圆的半径)，∴(2R )2＝⎝ ⎛⎭⎪⎫a sin A 2＝28， ∴sin B sin C ＝bc（2R ）2＝57.星期二(数列) 2021年____月____日【题目2】 已知数列{a n }的前n 项和S n ＝2n ＋1－2，记b n ＝a n S n (n ∈N *). (1)求数列{a n }的通项公式； (2)求数列{b n }的前n 项和T n . 解 (1)∵S n ＝2n ＋1－2.∴当n ＝1时，a 1＝S 1＝21＋1－2＝2. 当n ≥2时，a n ＝S n －S n －1＝2n ＋1－2n ＝2n ， 又a 1＝2＝21适合上式， 故a n ＝2n (n ∈N *).(2)由(1)知b n ＝a n S n ＝2n (2n ＋1－2)＝2·4n －2n ＋1. ∴T n ＝b 1＋b 2＋b 3＋…＋b n＝2(4＋42＋…＋4n )－(22＋23＋…＋2n ＋1)＝2×4（1－4n ）1－4－4（1－2n ）1－2＝23·4n ＋1－2n ＋2＋43.星期三(概率与统计) 2021年____月____日【题目3】 第24届冬奥会将于2022年在中国北京和张家口举行.为宣传冬奥会，让更多的人了解、喜爱冰雪项目，某大学举办了冬奥会知识竞赛，并从中随机抽取了100名学生的成绩，绘制成如图所示的频率分布直方图：(1)试根据频率分布直方图估计这100人的平均成绩(同一组数据用该组区间的中点值代替)； (2)若采用分层抽样的方法从成绩在[70，80)，[80，90)，[90，100]的学生中共抽取6人，再将其随机地分配到3个社区开展冬奥会宣传活动(每个社区2人)，求“成绩在同一区间的学生分配到不同社区”的概率.解 (1)平均成绩x －＝0.02×45＋0.16×55＋0.22×65＋0.30×75＋0.20×85＋0.10×95＝73.00.(2)由题意知，从成绩在[70，80)，[80，90)，[90，100]的学生中分别选取了3人，2人，1人.6人平均分成3组分配到3个社区，共有C 26C 24＝90(种)方法. 成绩在同一区间的学生分配到不同社区的方法有A 33A 23＝36(种)，所以“成绩在同一区间的学生分配到不同社区”的概率p ＝3690＝25.星期四(立体几何) 2021年____月____日【题目4】 如图，在四棱锥P －ABCD 中，底面ABCD 是菱形，PA ＝PD ，∠DAB ＝60°.(1)证明：AD⊥PB；(2)若PB＝6，AB＝PA＝2，求直线PB与平面PDC所成角的正弦值.(1)证明取AD的中点为O，连接PO，BO，BD，如图1，图1∵底面ABCD是菱形，且∠DAB＝60°，∴△ABD是等边三角形，∴BO⊥AD.又PA＝PD，即△PAD是等腰三角形，∴PO⊥AD.又PO∩BO＝O，PO，BO⊂平面PBO，∴AD⊥平面PBO，又PB⊂平面PBO，∴AD⊥PB.(2)解∵AB＝PA＝2，∴由(1)知△PAD，△ABD均是边长为2的正三角形，则PO＝3，BO＝3，又PB＝6，∴PO2＋BO2＝PB2，即PO⊥BO，又由(1)知，BO⊥AD，PO⊥AD，∴以O为坐标原点，OA，OB，OP所在直线分别为x，y，z轴建立如图2所示的空间直角坐标系.图2则D (－1，0，0)，P (0，0，3)，C (－2，3，0)，B (0，3，0)，PB →＝(0，3，－3)，DP →＝(1，0，3)，CD →＝(1，－3，0).设n ＝(x ，y ，z )是平面PCD 的法向量，则⎩⎨⎧n ·DP→＝0，n ·CD →＝0，∴⎩⎪⎨⎪⎧x ＋3z ＝0，x －3y ＝0，取y ＝1，解得⎩⎪⎨⎪⎧x ＝3，z ＝－1，即n ＝(3，1，－1)为平面PCD 的一个法向量.设直线PB 与平面PDC 所成的角为θ， 则sin θ＝|cos 〈PB →，n 〉|＝|0×3＋3×1＋（－3）×（－1）|6×5＝105，∴直线PB 与平面PDC 所成角的正弦值为105.星期五(解析几何) 2021年____月____日【题目5】 已知定点A (－3，0)，B (3，0)，直线AM ，BM 相交于点M ，且它们的斜率之积为－19，记动点M 的轨迹为曲线C .(1)求曲线C 的方程；(2)过点T (1，0)的直线l 与曲线C 交于P ，Q 两点，是否存在定点S (x 0，0)，使得直线SP 与SQ 斜率之积为定值？若存在，求出S 的坐标；若不存在，请说明理由.解 (1)设动点M (x ，y )，则直线MA 的斜率k MA ＝yx ＋3(x ≠－3)，直线MB 的斜率k MB ＝yx －3(x ≠3).因为k MA ·k MB ＝－19，所以y x ＋3·y x －3＝－19，化简得x 29＋y 2＝1.又x ≠±3，所以曲线C 的方程为x 29＋y 2＝1(x ≠±3).(2)由题意得直线l 的斜率不为0，根据直线l 过点T (1，0)，可设直线l 的方程为x ＝my ＋1，P (x 1，y 1)，Q (x 2，y 2)，联立⎩⎪⎨⎪⎧x ＝my ＋1，x 2＋9y 2＝9，消去x 得(m 2＋9)y 2＋2my －8＝0.则⎩⎪⎨⎪⎧y 1＋y 2＝－2mm 2＋9，y 1y 2＝－8m 2＋9.又k SP ＝y 1x 1－x 0＝y 1my 1＋1－x 0，k SQ ＝y 2x 2－x 0＝y 2my 2＋1－x 0，k SP ·k SQ ＝y 1y 2（my 1＋1－x 0）（my 2＋1－x 0）＝y 1y 2m 2y 1y 2＋m （1－x 0）（y 1＋y 2）＋（1－x 0）2＝－8（x 20－9）m 2＋9（1－x 0）2， 当x 0＝3时，∀m ∈R ，k SP ·k SQ ＝－89（1－x 0）2＝－29；当x 0＝－3时，∀m ∈R ，k SP ·k SQ ＝－89（1－x 0）2＝－118. 所以存在定点S ，其坐标为(3，0)或(－3，0)使得直线SP 与SQ 斜率之积为定值.星期六(函数与导数) 2021年____月____日【题目6】 已知f (x )＝e x ，g (x )＝x ＋1(e 为自然对数的底数). (1)求证：f (x )≥g (x )恒成立；(2)设m 是正整数，对任意正整数n ，⎝ ⎛⎭⎪⎫1＋13⎝ ⎛⎭⎪⎫1＋132·…·⎝ ⎛⎭⎪⎫1＋13n ＜m ，求m 的最小值.(1)证明 令h (x )＝f (x )－g (x )＝e x －x －1， 则h ′(x )＝e x －1，当x ∈(－∞，0)时，h ′(x )＜0，当x ∈(0，＋∞)时，h ′(x )＞0， 故h (x )在(－∞，0)上单调递减，在(0，＋∞)上单调递增， 所以h (x )min ＝h (0)＝0，即h (x )≥0恒成立， 所以f (x )≥g (x )恒成立.(2)解 由(1)可知1＜1＋13n ≤e 13n ，由不等式的性质得⎝ ⎛⎭⎪⎫1＋13⎝ ⎛⎭⎪⎫1＋132⎝ ⎛⎭⎪⎫1＋133·…·⎝ ⎛⎭⎪⎫1＋13n ≤e 13·e 132·e 133·…·e 13n ＝e13＋132＋133＋…＋13n＝e13[1－⎝ ⎛⎭⎪⎫13n ]1－13＝e 12⎣⎢⎡⎦⎥⎤1－⎝ ⎛⎭⎪⎫13n ＜e 12＝e ＜2.所以m 的最小值为2(m ∈N *).。

2021年高三数学第二次周练含解析考试时间：100分钟 班级 姓名 一、填空题：本大题共14小题，每小题5分，共70分. 请注意答题的准确度.1．若a ＋i 1－i (i 是虚数单位)是实数，则实数a 的值是 ．【解析】因为是实数，所以a ＋1＝0，所以a ＝－1．2．已知集合A ＝{x ∣y ＝lg(x ＋1)}，B ＝{x ∣x ≥2}，则A ∪B ＝ ． 【解析】因为A ＝{x ∣x ＞－1}，B ＝{x ∣x ≥2}，则A ∪B ＝{x ∣x ＞－1}． 3．现有4名学生A ，B ，C ，D 平均分乘两辆车，则“A ，B 两人 恰好乘坐在同一辆车”的概率为 ．【解析】因为4名学生平均分配共有(AB ，CD )，(AC ，BD )，(AD ，BC ) 共三种情况，“A ，B 两人恰好乘坐在同一辆车”只有(AB ，CD )故其概率为．4．已知一组数据：9.7，9.9，x ，10.2，10.1，若这组数据的均值为10 则这组数据的方差为 ．【解析】由这组数据的均值为10，可得x ＝10.1，所以方差为：032.0)1.02.01.01.03.0(5122222=++++． 5．右图是一个算法的流程图，最后输出的k ＝ ．【解析】6．在△ABC 中，已知A ＝45º，C ＝105º，BC ＝，则AC ＝ . 【解析】因为A ＝45º，C ＝105º，所以B ＝30º，由，解得AC ＝1．7．若S n 为等差数列{a n }的前n 项和，S 9＝－36，S 13＝－104，则a 5与a 7的等比中项为 ．【解析】由S 9＝－36，S 13＝－104，可解得a 1＝4，d ＝－2，所以a 5＝－4，a 7＝－8. 设a 5与a 7的等比中项为x ，则x 2＝a 5a 7＝32，所以x ＝±4. 8．若正四棱锥的底面边长为，体积为8，则其侧面积为 . 【解析】因为V ＝＝8，所以h ＝3，所以斜高.(第5题图)所以其侧面积为.9．已知f (x )是定义在R 上的奇函数，当x ∈(0，＋∞)时，f (x )＝log 2x ，则不等式f (x )＜－1 的解集是 ．【解析】因为当x ∈(0，＋∞)时，f (x )＝log 2x ，且f (x )是定义在R 上的奇函数， 所以当x ∈(－∞，0)时，－x ∈(0，＋∞)，则f (x )＝－f (－x )＝－log 2(－x )． 又因为f (x )＜－1，显然f (0)＝0不成立，故 22101)log(01log 02-<<<⇒⎩⎨⎧-<--<⎩⎨⎧-<>x x x x x x 或或，所以解集为．10. 设P 是函数图象上异于原点的动点，且该图象在点P 处的切线的倾斜角 为θ，则θ的取值范围是 ． 【解析】因为321232)0(2123213)1(21=⋅≥>+=+=++='x xx x x x x xy ．所以，又θ∈[0，π)，所以θ∈． 11．设为锐角，若，则的值为 ． 【解析】因为为锐角，所以，所以． 所以10222532254]4)6sin[()12sin(=⨯-⨯=-+=-ππαπα． 12．已知椭圆E ：x 2a 2＋y 2b 2＝1(a >b >0)的左、右焦点分别为F 1，F 2，焦距为2c ，若椭圆E 与直线y ＝3(x ＋c )的一个交点M 满足∠MF 1F 2＝2∠MF 2F 1，则椭圆的离心率为 ． 【解析】因为直线y ＝3(x ＋c )的斜率为3，所以倾斜角∠MF 1F 2＝60º， 又∠MF 1F 2＝2∠MF 2F 1，所以∠MF 2F 1＝30º，所以∠F 1MF 2＝90º． 因为F 1F 2＝2c ，所以MF 1＝c ，MF 2＝3c ，又MF 1＋MF 2＝2a ，备课人：雷蕾所以c ＋3c ＝2a ，即，所以离心率．13．在边长为1的正△ABC 中，已知，，x ＞0，y ＞0，且x ＋y ＝1， 则的最大值为 ． 【解析】如图建系，则)23,21(),0,21(),23,21(),0,21(y y E B x x D C ----， 因为x ＋y ＝1，所以y ＝1－x ，则，0＜x ＜1． 所以)2)1(3,21(),23,22(x x x x -+=-=， xy O AB C DE所以]43)21[(21)1(214)1(34)1)(2(22+--=+--=-++-=⋅x x x x x x x ．所以当时，的最大值为．14. 已知f (x )＝x 3－2x 2＋x ＋a ，g (x )＝－2x ＋.若对任意的x 1∈[－1，2]，存在x 2∈[2，4]，使得f (x 1)＝g (x 2)，则实数a 的取值范围是 ．【解析】先求得f (x )＝x 3－2x 2＋x ＋a 在x ∈[－1，2]上的值域为[a －4，a ＋2]， 再求得g (x )＝－2x ＋在x ∈[2，4]上的值域为． 由已知，可得[a －4，a ＋2]， 所以．二、解答题：本大题共4小题，共计58分. 请注意：答题要规范，步骤要完整.15. (本小题满分14分)在△ABC 中，角A ，B ，C 的对边分别为a ，b ，c ．已知 ．(1) 求A 的大小；(2) 若，求△ABC 的面积． 【解析】（1）法一：在△ABC 中，由正弦定理，及， 得，………………………………… 3分 即，因为A ∈(0，π)，所以，所以，…………………………6分所以. ……………………………………………………………………8分 法二：在△ABC 中，由余弦定理，及，得2222222222222a b c a c b b c a b c a ab ac bc+-+-+-+=，…………………………3分所以，所以， ………………………………………………6分因为A ∈(0，π)，所以.…………………………………………………8分 （2）由，得，………………………………11分 所以△ABC 的面积为. ……………… 14分16. (本小题满分14分)如图，四棱锥P ABCD 中，为菱形ABCD 对角线的交点，M 为棱PD 的中点，MA ＝MC . (1) 求证：PB 平面AMC ；(2) 求证：平面PBD 平面AMC ．【解析】（1）连结，因为为菱形ABCD 对角线的交点， 所以为BD 的中点，又M 为棱PD 的中点， 所以，…… 4分又平面AMC ，平面AMC ， 所以PB 平面AMC ； …… 6分 （2）在菱形ABCD 中，ACBD ，且为AC 的中点，又MAMC ，故A ， …… 8分 而OMBD ，OM ，BD 平面PBD ，所以AC 平面PBD ， …… 11分AP DCOM （第16题）备课人：雷蕾 备课人：雷蕾又AC 平面AMC ，所以平面PBD 平面AMC . …… 14分17. (本小题满分14分)烟囱向其周围地区散落烟尘而污染环境．已知落在地面某处的烟尘浓度与该处到烟囱的距离成反比．．，现有两座烟囱相距10km ，其中甲烟囱喷出的烟尘浓 度是乙烟囱的2倍，在距甲烟囱1km 处的烟尘浓度为2个单位/m 3，现要在甲、乙两 烟囱之间建立一所学校. 问学校建在何处，烟尘对学校的影响最小？【解析】设学校建立在距离甲烟囱x km 处，则该处甲、乙两烟囱的烟尘浓度分别为： ，，…………………3分由已知，可得：当x=1时，. …………………5分所以在学校的烟尘浓度为. ……………7分 所以2002301]20200)20[(301200)20(30)20(20)10(20)(2-≥-+--=--+---=--=xx x x x x x x x f 当且仅当，即时，取=. ……………13分故学校应建在距离甲烟囱()处，烟尘对学校的影响最小. ………14分18. (本小题满分16分)已知函数． (1) 求函数的最小值；(2) 若，使得成立，求实数的最大值；(3) 令1122()()(),(,()),(,())h x g x f x A x h x B x h x =-是函数图象上任意两点，且满足求实数的取值范围． 【解析】（1）因为，所以，令，得． ………………………1分因为当时，；当时，，所以在(0，1)上单调递减，在(1，+∞) 上单调递增． …………………2分 所以当x ﹦1时，的最小值为1． …………………3分 （2）， . ，，使得成立．令，则， ………………………6分 令，则由 可得或（舍） 当时，则在上单调递减； 当时，则在上单调递增.，在上恒成立. 在上单调递增.，即. ………………………9分实数的最大值为. ………………………10分 （3）,对于任意的，不妨取，则， 则由可得，变形得恒成立， ………………………12分 令，则在上单调递增，故在恒成立， ………………………14分 在恒成立.，当且仅当时取，. ………………………16分21177 52B9 効35743 8B9F 讟401239CBB 鲻21093 5265 剥V33957 84A5 蒥39399 99E7 駧930831 786F 硯32171 7DAB 綫-38422 9616 阖 30385 76B1 皱7备课人：雷蕾。

湖南高考数学二轮备考专项练习（含答案）数学的温习离不开多做题，下面是2021年湖南高考数学二轮备考专项练习，希望对考生有所协助。

题型一、频率散布直方图的运用例1：某校100名先生期中考试语文效果的频率散布直方图如下图，其中效果分组区间是[50,60)，[60,70)，[70,80)，[80,90)，[90,100]。

(1)求图中a的值;(2)依据频率散布直方图，估量这100名先生语文效果的平均分;(3)假定这100名先生语文效果某些分数段的人数(x)与数学效果相应分数段的人数(y)之比如下表所示，求数学效果在[50,90)之外的人数。

分数段[50,60)[60,70)[70,80)[80,90) x∶y 1∶1 2∶1 3∶4 4∶5破题切入点：(1)依据样本频率之和为1，求出参数a的值。

(2)依据频率散布直方图战争均值的计算公式，求出样本平均值。

(3)由直方图可计算语文效果在每分段上的频数，再依据语文和数学效果在同一段上的人数比，便可计算数学效果在[50,90)之间的人数，进而求解。

解：(1)由频率散布直方图知(2a+0.02+0.03+0.04)10=1，解得a=0.005。

(2)由频率散布直方图知这100名先生语文效果的平均分为550.00510+650.0410+750.0310+850.0210+950.00510=73(分)。

(3)由频率散布直方图知语文效果在[50,60)，[60,70)，[70,80)，[80,90)各分数段的人数依次为0.00510100=5,0.0410100=40,0.0310100=30,0.0210100=20。

由题中给出的比例关系知数学效果在上述各分数段的人数依次为5,40=20,30=40,20=25。

故数学效果在[50,90)之外的人数为100-(5+20+40+25)=10。

题型二茎叶图的运用例2：从甲、乙两个城市区分随机抽取16台自动售货机，对其销售额停止统计，统计数据用茎叶图表示(如下图)。

2021年高考数学二轮复习 专题大模拟（二）一、选择题(本大题共12个小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项符合题目要求．)1．(xx·全国新课标Ⅰ高考)设z ＝11＋i＋i ，则|z |＝( )A.12B.22C.32 D ．2 【解析】 ∵z ＝11＋i ＋i ＝1－i 1＋i 1－i＋i ＝1－i 2＋i ＝12＋12i ， ∴|z |＝122＋122＝22， 故选B.【答案】 B2．(xx·湖北高考)命题“∀x ∈R ，x 2≠x ”的否定是( )A ．∀x ∉R ，x 2≠xB ．∀x ∈R ，x 2＝xC ．∃x ∉R ，x 2≠xD ．∃x ∈R ，x 2＝x 【解析】 将∀改写成∃，否定结论，故选D. 【答案】 D3．(xx·全国大纲高考)设集合M ＝{x |x 2－3x －4<0}，N ＝{x |0≤x ≤5}，则M ∩N ＝( ) A ．(0,4] B ．[0,4) C ．[－1,0) D ．(－1,0]【解析】 M ＝{x |x 2－3x －4<0}＝{x |－1<x <4}， N ＝{x |0≤x ≤5}∴M ∩N ＝{x |0≤x ＜4}，故选B. 【答案】 B4．已知函数f (x )＝⎩⎪⎨⎪⎧log 21－x ，x ≤0fx －1＋1，x ＞0，则f (2 015)＝( )A ．2 015B ．2 014C ．2 013D ．2 012【解析】 f (2 015)＝f (2 014)＋1＝f (2 013)＋2 ＝…＝f (0)＋2 015＝log 21＋2 015 ＝2 015.故选A. 【答案】 A5．(xx·全国新课标Ⅰ高考)若tan α＞0，则( )A ．sin α＞0B ．cos α＞0C ．sin 2α＞0D ．cos 2α＞0【解析】 ∵tan α＝sin αcos α＞0，∴sin α·cos α＞0，∴sin 2α＝2sin α·cos α＞0， 故选C.【答案】 C6．(xx·广东广州综合测试)若函数f (x )＝x 2＋ax ＋1的定义域为实数集R ，则实数a 的取值范围为( )A ．(－2,2)B ．(－∞，－2)∪(2，＋∞)C ．(－∞，－2)∪[2，＋∞)D ．[－2,2]【解析】 依题意x 2＋ax ＋1≥0对x ∈R 恒成立，∴Δ＝a 2－4≤0，∴－2≤a ≤2.故选D. 【答案】 D7．(xx·山东济南一模)函数y ＝ln x －sin xx ＋sin x的图象大致是( )【解析】 因为f (－x )＝ln(－x －sin －x －x ＋sin －x )＝ln x －sin xx ＋sin x )＝f (x )，所以f (x )为偶函数，排除B 、D ，又因为当0<x <π2时，0<sin x <x ，所以0<x －sin x <x ＋sin x,0<x －sin xx ＋sin x<1，f (x )<0，排除C.故选A.【答案】 A8．若a ＞0，b ＞0，且函数f (x )＝4x 3－ax 2－2bx ＋2在x ＝1处有极值，则ab 的最大值等于( )A ．2B ．3C ．6D ．9【解析】 函数的导数为f ′(x )＝12x 2－2ax －2b ，由函数f (x )在x ＝1处有极值，可知函数f (x )在x ＝1处的导数值为零，12－2a －2b ＝0，所以a ＋b ＝6，由题意知a ，b 都是正实数，所以ab ≤(a ＋b 2)2＝(62)2＝9，当且仅当a ＝b ＝3时取到等号，故选D.【答案】 D9．(文)(xx·福建高考)将函数y ＝sin x 的图象向左平移π2个单位，得到函数y ＝f (x )的图象，则下列说法正确的是( )A ．y ＝f (x )是奇函数B ．y ＝f (x )的周期为πC ．y ＝f (x )的图象关于直线x ＝π2对称D ．y ＝f (x )的图象关于点(－π2，0)对称【解析】 函数y ＝sin x 图象向左平移π2得f (x )＝sin(x ＋π2)，∴f (x )＝cos x ，故选D.【答案】 D(理)(xx·湖南高考)已知函数f(x)＝sin(x－φ)，且∫2π30f(x)d x＝0，则函数f(x)的图象的一条对称轴是( )A．x＝5π6B．x＝7π12C．x＝π3D．x＝π6【解析】由∫2π30f(x)d x＝0，得∫2π30sin(x－φ)d x＝0，即－cos (x－φ)|2π30＝0，解得φ＝kπ＋π3，∴f(x)＝sin ⎣⎢⎡⎦⎥⎤x－⎝⎛⎭⎪⎫kπ＋π3，由x－kπ－π3＝k′π＋π2得x＝(k＋k′)π＋56π(k，k′∈Z)，故选A.【答案】 A10．(xx·陕西高考)如图，修建一条公路需要一段环湖弯曲路段与两条直道平滑连接(相切)．已知环湖弯曲路段为某三次函数图象的一部分，则该函数的解析式为( )A．y＝12x3－12x2－x B．y＝12x3＋12x2－3xC．y＝14x3－x D．y＝14x3＋12x2－2x【解析】由题图知函数过(0,0)，可设三次函数为f(x)＝ax3＋bx2＋cx，f′(x)＝3ax2＋2bx＋c，函数f(x)过点(2,0)且f′(0)＝－1，f′(2)＝3，由⎩⎪⎨⎪⎧f2＝0，f′0＝－1，f′2＝3，∴⎩⎪⎨⎪⎧4a＋2b＋c＝0，c＝－1，12a＋4b＋c＝3⇒⎩⎪⎨⎪⎧a＝12，b＝－12，c＝－1，∴f(x)＝12x3－12x2－x，故选A.【答案】 A11．(xx·江西高考)在△ABC中，内角A，B，C所对的边分别是a，b，c.若c2＝(a－b)2＋6，C ＝π3，则△ABC 的面积是( )A ．3 B.932 C.332 D ．3 3【解析】 由c 2＝(a －b )2＋6得c 2＝a 2＋b 2－2ab ＋6.由余弦定理得c 2＝a 2＋b 2－ab ，∴ab ＝6，∴S ＝12ab sin C ＝12×6×32＝332，故选C.【答案】 C12．(xx·江西南昌模拟)若数列{a n }，{b n }的通项公式分别是a n ＝(－1)n ＋2 013·a ，b n ＝2＋－1n ＋2 014n，且a n <b n 对任意n ∈N *恒成立，则常数a 的取值范围是( )A ．(－2,1)B ．[－2,1)C ．(－2,1]D ．[－2,1] 【解析】 由a n <b n ，得－(－1)n·a <2＋－1nn，要使其对任意n ∈N *恒成立，则当n ＝2k －1(k ∈N *)时，a <2－12k －1恒成立，又(12k －1)max ＝1，所以a <2－1＝1；当n ＝2k (k ∈N *)时，－a <2＋12k 恒成立，又12k ∈(0，12]，所以－a ≤2，得a ≥－2.综上所述，－2≤a <1.故选B.【答案】 B第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题，每小题5分，共20分．把答案填在题中横线上．)13．已知等比数列{a n }为递增数列，且a 25＝a 10,2(a n ＋a n ＋2)＝5a n ＋1，则数列{a n }的通项公式a n ＝________.【解析】 先判断数列的项是正数，再求出公比和首项．a 25＝a 10＞0，根据已知条件得2(1q＋q )＝5，解得q ＝2.所以a 21q 8＝a 1q 9，所以a 1＝2，所以a n ＝2n.【答案】 2n14．(xx·山东高考)执行如图所示的程序框图，若输入的x 的值为1，则输出的n 的值为________．【解析】 x ＝1 n ＝0 12－4×1＋3＝0 x ＝1＋1＝2； n ＝1 22－4×2＋3＝－1<0 x ＝2＋1＝3； n ＝2 32－4×3＋3＝0 x ＝3＋1＝4； n ＝3 42－4×4＋3＝3>0 输出3. 【答案】 315．(预测题)已知某生产厂家的年利润y (单位：万元)与年产量x (单位：万件)的函数关系式为y ＝－13x 3＋81x －234，则使该生产厂家获取最大年利润的年产量为________万件．【解析】 因为y ′＝－x 2＋81，所以当x ＞9时，y ′＜0；当x ∈(0,9)时，y ′＞0，所以函数y ＝－13x 3＋81x －234在(9，＋∞)上单调递减，在(0,9)上单调递增，所以x ＝9是函数的极大值点，又因为函数在(0，＋∞) 上只有一个极大值点，所以函数在x ＝9处取得最大值．【答案】 9 16.如图，在平面直角坐标系xOy 中，一单位圆的圆心的初始位置在(0,1)，此时圆上一点P的位置在(0,0)，圆在x 轴上沿正向滚动．当圆滚动到圆心位于(2,1)时，OP →的坐标为________．【解析】利用平面向量的坐标定义、解三角形知识以及数形结合思想求解．设A (2,0)，B (2,1)，由题意知劣弧PA 长为2，∠ABP ＝21＝2.设P (x ，y )，则x ＝2－1×cos(2－π2) ＝2－sin 2，y ＝1＋1×sin(2－π2)＝1－cos 2，∴OP →的坐标为(2－sin 2,1－cos 2)． 【答案】 (2－sin 2,1－cos 2)三、解答题(本大题共6小题，共70分．解答应写出文字说明、证明过程或演算步骤．)17．(10分)(xx·陕西高考)已知向量a ＝(cos x ，－12)，b ＝(3sin x ，cos 2x )，x ∈R ，设函数f (x )＝a ·b .(1)求f (x )的最小正周期；(2)求f (x )在[0，π2]上的最大值和最小值．【解】 f (x )＝(cos x ，－12)·(3sin x ，cos 2x )＝3cos x sin x －12cos 2x ＝32sin 2x －12cos 2x＝cos π6sin 2x －sin π6cos 2x ＝sin(2x －π6)．(1)f (x )的最小正周期为T ＝2πω＝2π2＝π，即函数f (x )的最小正周期为π.(2)∵0≤x ≤π2，∴－π6≤2x －π6≤5π6.由正弦函数的性质，得当2x －π6＝π2，即x ＝π3时，f (x )取得最大值1；当2x －π6＝－π6，即x ＝0时，f (0)＝－12；当2x －π6＝56π，即x ＝π2时，f (π2)＝12，∴f (x )的最小值为－12.因此，f (x )在[0，π2]上的最大值是1，最小值是－12. 18．(12分)(文)(xx·山东高考)已知{a n }是等差数列，满足a 1＝3，a 4＝12，数列{b n }满足b 1＝4，b 4＝20，且{b n －a n }为等比数列．(1)求数列{a n }和{b n }的通项公式； (2)求数列{b n }的前n 项和．【解】 (1)设等差数列{a n }的公差为d ，由题意得d ＝a 4－a 13＝12－33＝3.所以a n ＝a 1＋(n －1)d ＝3n (n ＝1,2，…)． 设等比数列{b n －a n }的公比为q ，由题意得q 3＝b 4－a 4b 1－a 1＝20－124－3＝8，解得q ＝2.所以b n －a n ＝(b 1－a 1)q n －1＝2n －1.从而b n ＝3n ＋2n －1(n ＝1,2，…)．(2)由(1)知b n ＝3n ＋2n －1(n ＝1,2，…)．数列{3n }的前n 项和为32n (n ＋1)，数列{2n －1}的前n 项和为1×1－2n1－2＝2n－1.所以，数列{b n }的前n 项和为32n (n ＋1)＋2n－1.(理)设各项均为正数的数列{a n }的前n 项和为S n ，且S n 满足S 2n －(n 2＋n －3)S n －3(n 2＋n )＝0，n ∈N *.(1)求a 1的值；(2)求数列{a n }的通项公式；(3)证明：对一切正整数n ，有1a 1a 1＋1＋1a 2a 2＋1＋…＋1a n a n ＋1＜13.(1)【解】 由题意知，S 2n －(n 2＋n －3)S n －3(n 2＋n )＝0，n ∈N *.令n ＝1，有S 21－(12＋1－3)S 1－3×(12＋1)＝0，可得有S 21＋S 1－6＝0，解得S 1＝－3或2，即a 1＝－3或2，又a n 为正数，所以a 1＝2.(2)【解】 由S 2n －(n 2＋n －3)S n －3(n 2＋n )＝0，n ∈N *可得，(S n ＋3)(S n －n 2－n )＝0，则S n ＝n 2＋n 或S n ＝－3，又数列{a n }的各项均为正数，所以S n ＝n 2＋n ，S n －1＝(n －1)2＋(n －1)，所以当n ≥2时，a n ＝S n －S n －1＝n 2＋n －[(n －1)2＋(n －1)]＝2n . 又a 1＝2＝2×1，所以a n ＝2n .(3)【证明】 当n ＝1时，1a 1a 1＋1＝12×3＝16＜13成立；当n ≥ 2时，1a n a n ＋1＝12n 2n ＋1＜12n －12n ＋1＝12(12n －1－12n ＋1)，所以1a 1a 1＋1＋1a 2a 2＋1＋…＋1a n a n ＋1＜16＋12[(13－15)＋…＋(12n －1－12n ＋1)]＝16＋12(13－12n ＋1)＜16＋16＝13. 所以对一切正整数n ，有1a 1a 1＋1＋1a 2a 2＋1＋…＋1a n a n ＋1＜13.19．(12分)(xx·陕西高考)△ABC 的内角A ，B ，C 所对的边分别为a ，b ，c . (1)若a ，b ，c 成等差数列，证明：sin A ＋sin C ＝2sin(A ＋C )； (2)若a ，b ，c 成等比数列，求cos B 的最小值． (1)【证明】 ∵a ，b ，c 成等差数列，∴a ＋c ＝2b . 由正弦定理得sin A ＋sin C ＝2sin B .∵sin B ＝sin [π－(A ＋C )]＝sin(A ＋C )， ∴sin A ＋sin C ＝2sin(A ＋C )．(2)【解】 ∵a ，b ，c 成等比数列，∴b 2＝ac . 由余弦定理得cos B ＝a 2＋c 2－b 22ac ＝a 2＋c 2－ac 2ac ≥2ac －ac 2ac ＝12，当且仅当a ＝c 时等号成立．∴cos B 的最小值为12.20．(12分)(xx·江西高考)已知函数f (x )＝(4x 2＋4ax ＋a 2)x ，其中a ＜0. (1)当a ＝－4时，求f (x )的单调递增区间；(2)若f (x )在区间[1,4]上的最小值为8，求a 的值．【解】 (1)当a ＝－4时，由f ′(x )＝25x －2x －2x ＝0得x ＝25或x ＝2，由f ′(x )＞0得x ∈(0，25)或x ∈(2，＋∞)，故函数f (x )的单调递增区间为(0，25)和(2，＋∞)．(2)f ′(x )＝10x ＋a 2x ＋a 2x ，a ＜0，由f ′(x )＝0得x ＝－a 10或x ＝－a2.当x ∈(0，－a 10)时，f (x )单调递增；当x ∈(－a 10，－a 2)时，f (x )单调递减；当x ∈(－a2，＋∞)时，f (x )单调递增．易知f (x )＝(2x ＋a )2x ≥0，且f (－a 2)＝0.①当－a2≤1时，即－2≤a ＜0时，f (x )在[1,4]上的最小值为f (1)，由f (1)＝4＋4a ＋a2＝8，得a ＝±22－2，均不符合题意．②当1＜－a 2≤4时，即－8≤a ＜－2时，f (x )在[1,4]上的最小值为f (－a2)＝0，不符合题意．③当－a2＞4时，即a ＜－8时，f (x )在[1,4]上的最小值可能在x ＝1或x ＝4处取得，而f (1)≠8，由f (4)＝2(64＋16a ＋a 2)＝8得a ＝－10或a ＝－6(舍去)，当a ＝－10时，f (x )在(1,4)单调递减，f (x )在[1,4]上的最小值为f (4)＝8，符合题意．综上有，a ＝－10.21．(12分)(xx·山东济宁模拟)已知函数f (x )＝a x＋ln x (a ∈R )． (1)当a ＝－1时，求f (x )在(1，f (1))处的切线方程； (2)求f (x )的最小值；(3)当a ＝2时，求证：ln(n ＋1)＋2ni ＝1ii ＋1>n ln(2e)(n ∈N *)．【解】 (1)当a ＝－1时，f (x )＝－1x ＋ln x ，∴f ′(x )＝1x 2＋1x ，∴k ＝f ′(1)＝12.又f (1)＝－1，∴切点为(1，－1)，所以切线方程为y －(－1)＝12(x －1)，即x －2y －3＝0.(2)因为f (x )＝a x＋ln x (x >0)所以f ′(x )＝－a x2＋1x＝x －ax2，①当a ≤0时， f ′(x )≥0，f (x )在(0，＋∞)上单调递增，所以f (x )无最值；②当a >0时，的变化情况如下：由表可知，当所以f (x )min ＝f (a )＝ln a ＋1；综上所述：当a ≤0时，f (x )无最值； 当a >0时，f (x )最小值为f (a )＝ln a ＋1.(3)当a ＝2时，由(1)知：f (x )≥ln 2＋1，(当且仅当x ＝2时，等号成立) 即2x ＋ln x ≥ln 2＋1，从而ln x ≥ln 2＋1－2x ＝ln(2e)－2x，(*)所以分别令x ＝21，32，43，…，n ＋1n代入(*)式得下列n 个不等式：ln 21>ln(2e)－221＝ln(2e)－2×12，ln 32>ln(2e)－232ln(2e)－2×23，ln 43>ln(2e)－243ln(2e)－2×34，……ln n ＋1n >ln(2e)－2n ＋1n＝ln(2e)－2×n n ＋1，将上述n 个不等式相加得： ln 21＋ln 32＋ln 43＋…＋ln n ＋1n >n ln(2e)－(2×12＋2×23＋2×34＋…＋2×n n ＋1)，即ln(21×32×43×…×n ＋1n )>n ln(2e)－2(12＋23＋34＋…＋n n ＋1)，所以ln(n ＋1)>n ln(2e)－2(12＋23＋34＋…＋nn ＋1)，即ln(n ＋1)＋2 i ＝1nii ＋1>n ln(2e)．22．(12分)(预测题)已知点(1，13)是函数f (x )＝a x(a ＞0且a ≠1)图象上的一点，等比数列{a n }的前n 项和为f (n )－c ，数列{b n }(b n ＞0)的首项为c ，且前n 项和S n 满足S n －S n －1＝S n ＋S n －1(n ≥2)．(1)求数列{a n }和{b n }的通项公式；(2)若数列{1b n b n ＋1}的前n 项和为T n ，问使T n ≥1 0012 015的最小正整数n 是多少？(3)若c n ＝－12a n ·b n ，求数列{c n }的前n 项和．【解】 (1)∵f (1)＝a ＝13，∴f (x )＝(13)x.∴a 1＝f (1)－c ＝13－c ，a 2＝[f (2)－c ]－[f (1)－c ]＝－29，a 3＝[f (3)－c ]－[f (2)－c ]＝－227.又数列{a n }成等比数列，a 1＝a 22a 3＝481－227＝－23＝13－c ，∴c ＝1.又公比q ＝a 2a 1＝13，∴a n ＝－23(13)n －1＝－23n ，(n ∈N *)．S n －S n －1＝(S n －S n －1)(S n ＋S n －1)＝S n ＋S n －1(n ≥2)．又∵b n ＞0，S n ＞0，∴S n －S n －1＝1.∴数列{S n }构成一个首项为1，公差为1的等差数列，S n ＝1＋(n －1)×1＝n ，S n ＝n 2.当n ≥2时，b n ＝S n －S n －1＝n 2－(n －1)2＝2n －1，当n ＝1时，b 1＝1也适合该通项公式，∴b n ＝2n －1(n ∈N *)．(2)T n ＝1b 1b 2＋1b 2b 3＋1b 3b 4＋…＋1b n b n ＋1＝11×3＋13×5＋15×7＋…＋12n －1×2n ＋1 ＝12(1－13)＋12(13－15)＋12(15－17)＋…＋12(12n －1－12n ＋1)＝12(1－12n ＋1)＝n 2n ＋1. 由T n ＝n 2n ＋1≥1 0012 015，得n ≥1 00113≈77，满足T n ≥1 0012 014的最小正整数为77.(3)c n ＝－12a n ·b n ＝－12·－23n ·(2n －1)＝13n ·(2n －1)设数列{c n }的前n 项和为P n ，则P n ＝c 1＋c 2＋…＋c n＝1·13＋3·132＋5·133＋…＋(2n －3)·13n －1＋(2n －1)·13n ①则3P n ＝1＋3·13＋5·132＋…＋(2n －1)·13n －1②②－①得：2P n ＝1＋2·13＋2·132＋…＋2·13n －1－(2n －1)·13n＝1＋2(13＋132＋…＋13n －1)－(2n －1)·13n＝1＋2·131－13n －11－13－(2n －1)·13n ＝2－2n ＋13n∴P n ＝1－n ＋13n即{c n }的前n 项和为1－n ＋13n .L27335 6AC7 櫇+=28843 70AB 炫26611 67F3 柳s38944 9820 頠27057 69B1 榱31438 7ACE 竎33308 821C 舜625271 62B7抷36265 8DA9 趩/。